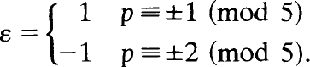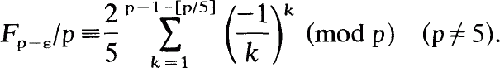Skip to main content Accessibility help
×
  1. Home
  2. Search

Refine search

Refine search

Access:
Content type:
Publication date:
Apply   From and To filters
Subject: Show more
Journals Show more
Publishers: Show more
Societies Show more
Series: Show more
Collections: Show more

Actions for selected content:

Select all | Deselect all
  • View selected items
  • Export citations
  • Download PDF (zip)
  • Save to Kindle
  • Save to Dropbox
  • Save to Google Drive

Save Search

You can save your searches here and later view and run them again in "My saved searches".

Please provide a title, maximum of 40 characters.
Cancel
×

3 results

  • Half-Silvered Mirrors and Wythoff's Game

  • Horacio Porta, Kenneth B. Stolarsky
  • Journal:
    Canadian Mathematical Bulletin / Volume 33 / Issue 1 / 01 March 1990
    Published online by Cambridge University Press:
    20 November 2018, pp. 119-125
    Print publication:
    01 March 1990
    • Article
      • You have access
    • PDF
    • Export citation

  • We propose the following problem. Given an array of vertical mirrors that simultaneously transmit and reflect, and a single incoming ray of light, describe the configuration of all light rays that are generated. We solve the problem here for a certain infinite configuration of mirrors; the solution involves the winning positions (a(n), b(n)) of Wythoff's game.

  • A Note on the Fibonacci Quotient F p-ε/p

  • H. C. Williams
  • Journal:
    Canadian Mathematical Bulletin / Volume 25 / Issue 3 / 01 September 1982
    Published online by Cambridge University Press:
    20 November 2018, pp. 366-370
    Print publication:
    01 September 1982
    • Article
      • You have access
    • PDF
    • Export citation

  • In this note a formula analogous to Eisenstein's well known formula is presented for F p-ε/p, where F n is the nth Fibonacci number (F 0 = 0, F 1 = 1), p an odd prime, and

    This formula is:

  • Beatty Sequences, Continued Fractions, and Certain Shift Operators

  • Kenneth B. Stolarsky
  • Journal:
    Canadian Mathematical Bulletin / Volume 19 / Issue 4 / 01 December 1976
    Published online by Cambridge University Press:
    20 November 2018, pp. 473-482
    Print publication:
    01 December 1976
    • Article
      • You have access
    • PDF
    • Export citation

  • Let θ = θ(k) be the positive root of θ 2 + (k-2)θ-k = 0. Let f(n) = [(n + l)θ]-[nθ] for positive integers n, where [x] denotes the greatest integer in x. Then the elements of the infinite sequence (f(l), f(2), f(3),…) can be rapidly generated from the finite sequence (f(l), f(2),…,f(k)) by means of certain shift operators. For k = 1 we can generate (the characteristic function of) the sequence [n θ] itself in this manner.