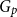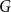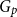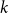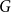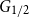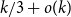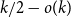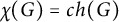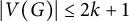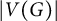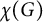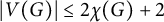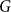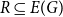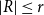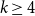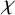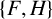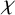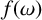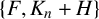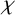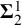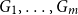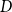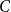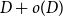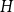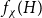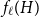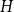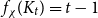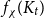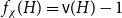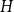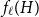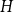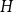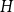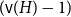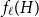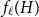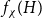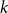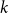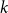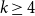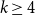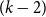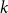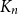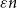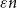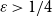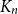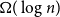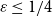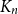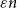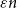Refine search
Actions for selected content:
93 results
Chi-Boundedness of graphs containing no cycles with k chords
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 November 2025, e189
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the existence of reflecting n-queens configurations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 October 2025, e169
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTEREXAMPLE TO CONJECTURES ON COMPLEMENTED ZERO-DIVISOR GRAPHS OF SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 26 September 2025, pp. 1-5
-
- Article
- Export citation
Random independent sets in triangle-free graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 25 September 2025, e156
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the multicolor Turán conjecture for color-critical graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 10 September 2025, pp. 1-31
-
- Article
- Export citation
Colouring random subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 28 April 2025, pp. 585-595
-
- Article
- Export citation
COLORING EQUILATERAL TRIANGLES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-14
-
- Article
- Export citation
Common graphs with arbitrary chromatic number
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 03 July 2025, pp. 594-634
- Print publication:
- March 2025
-
- Article
- Export citation
Measurable Vizing’s theorem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 February 2025, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimum non-chromatic-choosable graphs with given chromatic number
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 27 December 2024, pp. 1-32
-
- Article
- Export citation
Vertex-critical graphs far from edge-criticality
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 151-157
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON
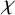 $\chi $-BINDING FUNCTIONS AND LINEAR FORESTS
$\chi $-BINDING FUNCTIONS AND LINEAR FORESTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 27 September 2024, pp. 23-29
- Print publication:
- August 2025
-
- Article
- Export citation
List packing number of bounded degree graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 18 September 2024, pp. 807-828
-
- Article
- Export citation
ON HOMOMORPHISM GRAPHS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 May 2024, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A special case of Vu’s conjecture: colouring nearly disjoint graphs of bounded maximum degree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 10 November 2023, pp. 179-195
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the choosability of
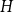 $H$-minor-free graphs
$H$-minor-free graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 03 November 2023, pp. 129-142
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COLORING ISOSCELES TRIANGLES IN CHOICELESS SET THEORY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 11 September 2023, pp. 105-134
- Print publication:
- March 2025
-
- Article
- Export citation
On the maximum number of edges in
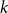 $k$-critical graphs
$k$-critical graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 24 July 2023, pp. 900-911
-
- Article
- Export citation
COMPUTABLE VS DESCRIPTIVE COMBINATORICS OF LOCAL PROBLEMS ON TREES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 04 July 2023, pp. 1835-1849
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unavoidable patterns in locally balanced colourings
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 01 June 2023, pp. 796-808
-
- Article
- Export citation