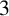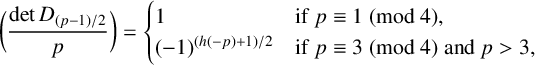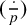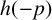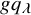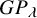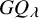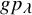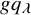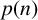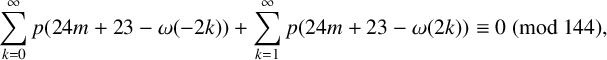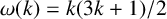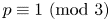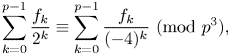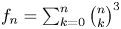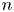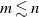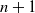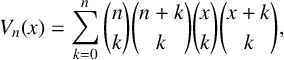Refine search
Actions for selected content:
40 results
Alternating sign matrices with reflective symmetry and plane partitions:
 $n+3$ pairs of equivalent statistics and a Cauchy-type identity
$n+3$ pairs of equivalent statistics and a Cauchy-type identity
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 October 2025, e168
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hook length inequalities for t-regular partitions in the t-aspect
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 24 July 2025, pp. 1-12
-
- Article
- Export citation
Zero-one dual characters of flagged Weyl modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 08 July 2025, pp. 1-23
-
- Article
- Export citation
Exact solution to the Chow–Robbins game for almost all n, by using a catalan triangle
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 16 May 2025, pp. 1-36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWO NEW TRUNCATED IDENTITIES AND PARTITION THEOREMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 21 March 2025, pp. 1-8
-
- Article
- Export citation
ON NEW MINIMAL EXCLUDANTS OF OVERPARTITIONS RELATED TO SOME q-SERIES OF RAMANUJAN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 11 February 2025, pp. 1-13
- Print publication:
- August 2025
-
- Article
- Export citation
Bounded Littlewood identity related to alternating sign matrices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 December 2024, e124
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONGRUENCES FOR SUMS OF MACMAHON’S q-CATALAN POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 08 October 2024, pp. 416-427
- Print publication:
- June 2025
-
- Article
- Export citation
Supercongruences involving Motzkin numbers and central trinomial coefficients
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 03 October 2024, pp. 1060-1084
-
- Article
- Export citation
ON GENERALISED LEGENDRE MATRICES INVOLVING ROOTS OF UNITY OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 22 April 2024, pp. 199-210
- Print publication:
- October 2024
-
- Article
- Export citation
Combinatorial formulas for shifted dual stable Grothendieck polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 February 2024, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Pipe Dream Perspective on Totally Symmetric Self-Complementary Plane Partitions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 29 January 2024, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DIVISIBILITY OF SUMS OF PARTITION NUMBERS BY MULTIPLES OF 2 AND 3
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 22 December 2023, pp. 271-279
- Print publication:
- October 2024
-
- Article
- Export citation
Skew RSK dynamics: Greene invariants, affine crystals and applications to q-Whittaker polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 18 October 2023, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MacMahon’s statistics on higher-dimensional partitions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 July 2023, e63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On two congruence conjectures of Z.-W. Sun involving Franel numbers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 16 May 2023, pp. 887-905
- Print publication:
- June 2024
-
- Article
- Export citation
Negative moments of orthogonal polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 29 March 2023, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The moduli space of polynomial maps and their fixed-point multipliers: II. Improvement to the algorithm and monic centered polynomials
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 03 February 2023, pp. 3777-3795
- Print publication:
- November 2023
-
- Article
- Export citation
Parking functions: interdisciplinary connections
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 17 January 2023, pp. 768-792
- Print publication:
- September 2023
-
- Article
- Export citation
ON THE DIVISIBILITY OF SUMS INVOLVING APÉRY-LIKE POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 14 March 2022, pp. 203-208
- Print publication:
- October 2022
-
- Article
- Export citation