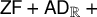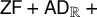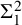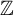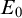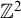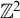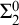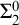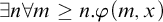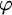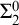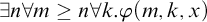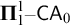Refine search
Actions for selected content:
156 results
SIZE OF PIECES IN DECOMPOSITIONS INTO THE FIRST UNCOUNTABLE CARDINAL MANY PIECES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 09 October 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ZOO OF IDEAL SCHAUDER BASES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 05 September 2025, pp. 1-31
-
- Article
- Export citation
ON WINNING STRATEGIES FOR
 $F_\sigma $ GAMES
$F_\sigma $ GAMES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-15
-
- Article
- Export citation
MEASURABLE DOMATIC PARTITIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-25
-
- Article
- Export citation
A model of the Axiom of Determinacy in which every set of reals is universally Baire
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 11 June 2025, e94
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A counterexample regarding an equivalence relation on a product space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 16 April 2025, pp. 1-5
-
- Article
- Export citation
Borel complexity of sets of points with prescribed Birkhoff averages in Polish dynamical systems with a specification property
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 02 April 2025, pp. 2695-2723
- Print publication:
- September 2025
-
- Article
- Export citation
Tree-like graphings, wallings, and median graphings of equivalence relations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 March 2025, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN ORDER ANALYSIS OF HYPERFINITE BOREL EQUIVALENCE RELATIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 21 March 2025, pp. 1-23
-
- Article
- Export citation
ON SOME OF BROUWER’S AXIOMS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 16 April 2025, pp. 1-52
- Print publication:
- March 2025
-
- Article
- Export citation
INFINITE GAMES AND RAMSEY PROPERTIES OF
 $F_\sigma $ IDEALS
$F_\sigma $ IDEALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 17 February 2025, pp. 1-25
-
- Article
- Export citation
Measurable Vizing’s theorem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 February 2025, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LEARNING EQUIVALENCE RELATIONS ON POLISH SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 February 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON EQUIVALENCE RELATIONS INDUCED BY POLISH GROUPS ADMITTING COMPATIBLE TWO-SIDED INVARIANT METRICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 February 2025, pp. 1-38
-
- Article
- Export citation
MORE ON YET ANOTHER IDEAL VERSION OF THE BOUNDING NUMBER
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-16
-
- Article
- Export citation
MANY-ONE REDUCIBILITY WITH REALIZABILITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-39
-
- Article
- Export citation
THE WEIHRAUCH LATTICE AT THE LEVEL OF
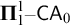 $\boldsymbol {\Pi }^1_1{-}\mathsf{CA}_0$: THE CANTOR–BENDIXSON THEOREM
$\boldsymbol {\Pi }^1_1{-}\mathsf{CA}_0$: THE CANTOR–BENDIXSON THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 27 January 2025, pp. 752-790
- Print publication:
- June 2025
-
- Article
- Export citation
THE GENERIC MULTIVERSE IS NOT GOING AWAY
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 27 December 2024, pp. 671-703
- Print publication:
- September 2025
-
- Article
- Export citation
SCOTT SENTENCE COMPLEXITIES OF LINEAR ORDERINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 13 December 2024, pp. 1-30
-
- Article
- Export citation
Generic properties of topological groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation