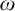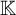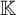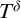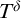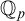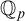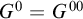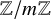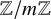Refine search
Actions for selected content:
80 results
THE CLASS OF KRASNER HYPERFIELDS IS NOT ELEMENTARY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Universal-existential theories of fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 03 September 2025, pp. 1-30
-
- Article
- Export citation
Semisimple groups interpretable in various valued fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 01 August 2025, e127
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A TWO-SORTED THEORY OF NILPOTENT LIE ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 22 July 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONTRACTING ENDOMORPHISMS OF VALUED FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 08 May 2025, pp. 2047-2106
- Print publication:
- September 2025
-
- Article
- Export citation
Motivic Vitushkin invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 20 August 2025, pp. 959-992
- Print publication:
- May 2025
-
- Article
- Export citation
DP AND OTHER MINIMALITIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-30
-
- Article
- Export citation
MODEL THEORY OF DIFFERENTIAL-HENSELIAN PRE-H-FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 08 April 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON THE NON-EXISTENCE OF PRIME MODELS OF THEORIES OF PSEUDO-FINITE FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 52-67
- Print publication:
- March 2025
-
- Article
- Export citation
OMEGA-CATEGORICAL PSEUDOFINITE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 15 January 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On ordinary differentially large fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DEFINABLE HENSELIAN VALUATIONS IN POSITIVE RESIDUE CHARACTERISTIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERIC DERIVATIONS ON ALGEBRAICALLY BOUNDED STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 13 November 2024, pp. 1-27
-
- Article
- Export citation
ARTIN–SCHREIER EXTENSIONS AND COMBINATORIAL COMPLEXITY IN HENSELIAN VALUED FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 03 September 2024, pp. 1747-1767
- Print publication:
- December 2024
-
- Article
- Export citation
ONE-DIMENSIONAL SUBGROUPS AND CONNECTED COMPONENTS IN NON-ABELIAN p-ADIC DEFINABLE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 April 2024, pp. 1-19
-
- Article
- Export citation
MORE ON GALOIS COHOMOLOGY, DEFINABILITY, AND DIFFERENTIAL ALGEBRAIC GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 496-515
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWO EXAMPLES CONCERNING EXISTENTIAL UNDECIDABILITY IN FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 23 November 2023, pp. 552-563
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON MODEL-THEORETIC CONNECTED GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 14 November 2023, pp. 50-79
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PAC STRUCTURES AS INVARIANTS OF FINITE GROUP ACTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 20 October 2023, pp. 1340-1375
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Decidability of the class of all the rings
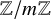 $\mathbb {Z}/m\mathbb {Z}$: A problem of Ax
$\mathbb {Z}/m\mathbb {Z}$: A problem of Ax
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 July 2023, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation