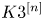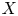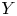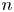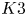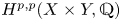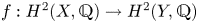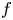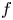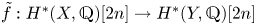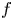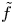1. Introduction
1.1 Algebraicity of rational Hodge isometries
An irreducible holomorphic symplectic manifold (IHSM) is a simply connected compact Kähler manifold ![]() $X$ such that
$X$ such that ![]() $H^0(X,\Omega ^2_X)$ is spanned by a nowhere degenerate holomorphic
$H^0(X,\Omega ^2_X)$ is spanned by a nowhere degenerate holomorphic ![]() $2$-form. Such manifolds admit hyper-Kähler structures and are examples of compact hyper-Kähler manifolds. When two-dimensional, such a manifold is a
$2$-form. Such manifolds admit hyper-Kähler structures and are examples of compact hyper-Kähler manifolds. When two-dimensional, such a manifold is a ![]() $K3$ surface. If
$K3$ surface. If ![]() $X$ is a Kähler manifold which is deformation equivalent to the Hilbert scheme
$X$ is a Kähler manifold which is deformation equivalent to the Hilbert scheme ![]() $S^{[n]}$ of length
$S^{[n]}$ of length ![]() $n$ subschemes of a
$n$ subschemes of a ![]() $K3$ surface
$K3$ surface ![]() $S$, then
$S$, then ![]() $X$ is an IHSM [Reference BeauvilleBea83]. The latter are said to be of
$X$ is an IHSM [Reference BeauvilleBea83]. The latter are said to be of ![]() $K3^{[n]}$ type. The second integral cohomology
$K3^{[n]}$ type. The second integral cohomology ![]() $H^2(X,{\mathbb {Z}})$ of an IHSM
$H^2(X,{\mathbb {Z}})$ of an IHSM ![]() $X$ is endowed with a symmetric integral primitive non-degenerate bilinear pairing of signature
$X$ is endowed with a symmetric integral primitive non-degenerate bilinear pairing of signature ![]() $(3,b_2(X)-3)$ known as the Beauville–Bogomolov–Fujiky (BBF) pairing, where
$(3,b_2(X)-3)$ known as the Beauville–Bogomolov–Fujiky (BBF) pairing, where ![]() $b_2(X)$ is the second Betti number [Reference BeauvilleBea83]. A homomorphism
$b_2(X)$ is the second Betti number [Reference BeauvilleBea83]. A homomorphism ![]() $f:H^2(X,{\mathbb {Z}})\rightarrow H^2(Y,{\mathbb {Z}})$ between the second cohomologies of two IHSMs is said to be an integral Hodge isometry, if it is an isometry with respect to the BBF pairings as well as an isomorphism of Hodge structures. If
$f:H^2(X,{\mathbb {Z}})\rightarrow H^2(Y,{\mathbb {Z}})$ between the second cohomologies of two IHSMs is said to be an integral Hodge isometry, if it is an isometry with respect to the BBF pairings as well as an isomorphism of Hodge structures. If ![]() $f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ has these properties it is said to be a rational Hodge isometry.
$f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ has these properties it is said to be a rational Hodge isometry.
Let ![]() $X$ be an IHSM. Given a class
$X$ be an IHSM. Given a class ![]() $\alpha$ in the even cohomology
$\alpha$ in the even cohomology ![]() $H^{ev}(X,{\mathbb {Q}})$ of
$H^{ev}(X,{\mathbb {Q}})$ of ![]() $X$, denote by
$X$, denote by ![]() $\alpha _i$ its graded summand in
$\alpha _i$ its graded summand in ![]() $H^{2i}(X,{\mathbb {Q}})$. Let
$H^{2i}(X,{\mathbb {Q}})$. Let ![]() $\alpha ^\vee \in H^{ev}(X,{\mathbb {Q}})$ be the class satisfying
$\alpha ^\vee \in H^{ev}(X,{\mathbb {Q}})$ be the class satisfying ![]() $(\alpha ^\vee )_i=(-1)^i\alpha _i$. The Mukai pairing on the even cohomology
$(\alpha ^\vee )_i=(-1)^i\alpha _i$. The Mukai pairing on the even cohomology ![]() $H^{ev}(X,{\mathbb {Q}})$ is defined by
$H^{ev}(X,{\mathbb {Q}})$ is defined by
The Mukai vector of an object ![]() $F$ in the bounded derived category
$F$ in the bounded derived category ![]() $D^b(X)$ of coherent sheaves on
$D^b(X)$ of coherent sheaves on ![]() $X$ is
$X$ is ![]() $v(F):=ch(F)\sqrt {td_X}\in H^{ev}(X,{\mathbb {Q}})$. Grothendieck–Riemann–Roch yields
$v(F):=ch(F)\sqrt {td_X}\in H^{ev}(X,{\mathbb {Q}})$. Grothendieck–Riemann–Roch yields
for objects ![]() $E$ and
$E$ and ![]() $F$ in
$F$ in ![]() $D^b(X)$, where
$D^b(X)$, where ![]() $E^\vee :=R{\mathcal {H}}om(E,{\mathcal {O}}_{X})$ is the derived dual object. When
$E^\vee :=R{\mathcal {H}}om(E,{\mathcal {O}}_{X})$ is the derived dual object. When ![]() $X$ is of
$X$ is of ![]() $K3^{[n]}$ type the odd cohomology vanishes and
$K3^{[n]}$ type the odd cohomology vanishes and ![]() $H^{ev}(X,{\mathbb {Z}})=H^*(X,{\mathbb {Z}})$ (see [Reference MarkmanMar07]).
$H^{ev}(X,{\mathbb {Z}})=H^*(X,{\mathbb {Z}})$ (see [Reference MarkmanMar07]).
Let ![]() $X$ be a
$X$ be a ![]() $2n$-dimensional IHSM. Denote by
$2n$-dimensional IHSM. Denote by ![]() $H^*(X,{\mathbb {Q}})[2n]$ the shifted cohomology of
$H^*(X,{\mathbb {Q}})[2n]$ the shifted cohomology of ![]() $X$, where
$X$, where ![]() $H^k(X,{\mathbb {Q}})[2n]=H^{k+2n}(X,{\mathbb {Q}})$. We say that a homomorphism
$H^k(X,{\mathbb {Q}})[2n]=H^{k+2n}(X,{\mathbb {Q}})$. We say that a homomorphism ![]() $f:H^*(X,{\mathbb {Q}})[2n]\rightarrow H^*(Y,{\mathbb {Q}})[2n]$ is degree reversing, if it maps
$f:H^*(X,{\mathbb {Q}})[2n]\rightarrow H^*(Y,{\mathbb {Q}})[2n]$ is degree reversing, if it maps ![]() $H^k(X,{\mathbb {Q}})[2n]$ to
$H^k(X,{\mathbb {Q}})[2n]$ to ![]() $H^{-k}(Y,{\mathbb {Q}})[2n]$, for all
$H^{-k}(Y,{\mathbb {Q}})[2n]$, for all ![]() $k$. The homomorphism is degree preserving up to sign, if it is either degree preserving or degree reversing.
$k$. The homomorphism is degree preserving up to sign, if it is either degree preserving or degree reversing.
Let ![]() $X$ and
$X$ and ![]() $Y$ be IHSMs of
$Y$ be IHSMs of ![]() $K3^{[n]}$ type and
$K3^{[n]}$ type and ![]() $f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ a Hodge isometry.
$f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ a Hodge isometry.
Theorem 1.1 There exists an analytic correspondence ![]() $\tilde {f}:H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$, which is an isometry with respect to the Mukai pairings and satisfies one of the following:
$\tilde {f}:H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$, which is an isometry with respect to the Mukai pairings and satisfies one of the following:
(1)
 $\tilde {f}$ is degree preserving and it restricts to
$\tilde {f}$ is degree preserving and it restricts to  $H^2(X,{\mathbb {Q}})$ as
$H^2(X,{\mathbb {Q}})$ as  $f$;
$f$;(2)
 $\tilde {f}$ is degree reversing and the composition
of
$\tilde {f}$ is degree reversing and the composition
of \[ H^*(X,{\mathbb{Q}})\stackrel{c_2(X)^{n-1} \cup}{\longrightarrow} H^*(X,{\mathbb{Q}})\stackrel{\tilde{f}}{\longrightarrow} H^*(X,{\mathbb{Q}}) \]
\[ H^*(X,{\mathbb{Q}})\stackrel{c_2(X)^{n-1} \cup}{\longrightarrow} H^*(X,{\mathbb{Q}})\stackrel{\tilde{f}}{\longrightarrow} H^*(X,{\mathbb{Q}}) \]
 $\tilde {f}$ with cup product with
$\tilde {f}$ with cup product with  $c_2(X)^{n-1}$ restricts to
$c_2(X)^{n-1}$ restricts to  $H^2(X,{\mathbb {Q}})$ as a non-zero rational multiple of
$H^2(X,{\mathbb {Q}})$ as a non-zero rational multiple of  $f$.
$f$.
In particular, ![]() $f$ is algebraic whenever
$f$ is algebraic whenever ![]() $X$ and
$X$ and ![]() $Y$ are projective.
$Y$ are projective.
The theorem is proved in § 9. When ![]() $n=1$ and
$n=1$ and ![]() $X$ and
$X$ and ![]() $Y$ are
$Y$ are ![]() $K3$ surfaces Theorem 1.1 was proved by Mukai for projective surfaces with Picard number
$K3$ surfaces Theorem 1.1 was proved by Mukai for projective surfaces with Picard number ![]() $\geq 11$ (see [Reference MukaiMuk87]), by Nikulin for projective surfaces with Picard number
$\geq 11$ (see [Reference MukaiMuk87]), by Nikulin for projective surfaces with Picard number ![]() $\geq 5$ (see [Reference NikulinNik87]), announced by Mukai in [Reference MukaiMuk02], and proved by Buskin in complete generality [Reference BuskinBus19]. Another proof for projective
$\geq 5$ (see [Reference NikulinNik87]), announced by Mukai in [Reference MukaiMuk02], and proved by Buskin in complete generality [Reference BuskinBus19]. Another proof for projective ![]() $K3$ surfaces
$K3$ surfaces ![]() $X$ and
$X$ and ![]() $Y$, without further restrictions on their Picard numbers, is due to Huybrechts [Reference HuybrechtsHuy19].
$Y$, without further restrictions on their Picard numbers, is due to Huybrechts [Reference HuybrechtsHuy19].
A more direct relationship between the Hodge isometries ![]() $f$ and
$f$ and ![]() $\tilde {f}$ in Theorem 1.1 is described in terms of Taelman's Looijenga–Lunts–Verbitsky (LLV) lattice in Theorem 1.4 below.
$\tilde {f}$ in Theorem 1.1 is described in terms of Taelman's Looijenga–Lunts–Verbitsky (LLV) lattice in Theorem 1.4 below.
Definition 1.2 Let ![]() $X_1$ and
$X_1$ and ![]() $X_2$ be deformation equivalent compact Kähler manifolds. An isomorphism
$X_2$ be deformation equivalent compact Kähler manifolds. An isomorphism ![]() $f:H^*(X_1,{\mathbb {Z}})\rightarrow H^*(X_2,{\mathbb {Z}})$ is said to be a parallel-transport operator, if it arises as follows. There exist a smooth and proper family of compact Kähler manifolds
$f:H^*(X_1,{\mathbb {Z}})\rightarrow H^*(X_2,{\mathbb {Z}})$ is said to be a parallel-transport operator, if it arises as follows. There exist a smooth and proper family of compact Kähler manifolds ![]() $\pi :{\mathcal {X}}\rightarrow B$ over an analytic space
$\pi :{\mathcal {X}}\rightarrow B$ over an analytic space ![]() $B$, points
$B$, points ![]() $b_1$,
$b_1$, ![]() $b_2$ in
$b_2$ in ![]() $B$, isomorphisms
$B$, isomorphisms ![]() $g_i:X_i\rightarrow {\mathcal {X}}_{b_i}$ with the fibers
$g_i:X_i\rightarrow {\mathcal {X}}_{b_i}$ with the fibers ![]() ${\mathcal {X}}_{b_i}$ of
${\mathcal {X}}_{b_i}$ of ![]() $\pi$ over
$\pi$ over ![]() $b_i$,
$b_i$, ![]() $i=1,2$, and a continuous path
$i=1,2$, and a continuous path ![]() $\gamma$ from
$\gamma$ from ![]() $b_1$ to
$b_1$ to ![]() $b_2$, such that parallel transport along the path
$b_2$, such that parallel transport along the path ![]() $\gamma$ in the local system
$\gamma$ in the local system ![]() $R\pi _*{\mathbb {Z}}$ induces
$R\pi _*{\mathbb {Z}}$ induces ![]() $g_{2,*}\circ f\circ g_1^*:H^*({\mathcal {X}}_{b_1},{\mathbb {Z}})\rightarrow H^*({\mathcal {X}}_{b_2},{\mathbb {Z}})$. When
$g_{2,*}\circ f\circ g_1^*:H^*({\mathcal {X}}_{b_1},{\mathbb {Z}})\rightarrow H^*({\mathcal {X}}_{b_2},{\mathbb {Z}})$. When ![]() $X_1=X_2$ the parallel-transport operator
$X_1=X_2$ the parallel-transport operator ![]() $f$ is also called a monodromy operator. The monodromy group
$f$ is also called a monodromy operator. The monodromy group ![]() ${\rm Mon}(X)$ of a compact Kähler manifold
${\rm Mon}(X)$ of a compact Kähler manifold ![]() $X$ is the subgroup of
$X$ is the subgroup of ![]() $GL(H^*(X,{\mathbb {Z}}))$ consisting of all monodromy operators.
$GL(H^*(X,{\mathbb {Z}}))$ consisting of all monodromy operators.
Recall that a groupoid is a category all of whose morphisms are isomorphisms. Let
be the groupoid, whose objects are pairs ![]() $(X,\epsilon )$ consisting of an IHSM
$(X,\epsilon )$ consisting of an IHSM ![]() $X$ and an orientationFootnote 1
$X$ and an orientationFootnote 1 ![]() $\epsilon$ of
$\epsilon$ of ![]() $H^2(X,{\mathbb {Q}})$. If
$H^2(X,{\mathbb {Q}})$. If ![]() $\dim (X)$ is divisible by
$\dim (X)$ is divisible by ![]() $4$, assumeFootnote 2 that
$4$, assumeFootnote 2 that ![]() $b_2(X)$ is odd. Morphisms in
$b_2(X)$ is odd. Morphisms in ![]() ${\rm Hom}_{\mathcal {G}}((X,\epsilon ),(Y,\epsilon '))$ are compositions of three types of rational isometries from
${\rm Hom}_{\mathcal {G}}((X,\epsilon ),(Y,\epsilon '))$ are compositions of three types of rational isometries from ![]() $H^*(X,{\mathbb {Q}})$ to
$H^*(X,{\mathbb {Q}})$ to ![]() $H^*(Y,{\mathbb {Q}})$ with respect to the Mukai pairing.
$H^*(Y,{\mathbb {Q}})$ with respect to the Mukai pairing.
(1) A parallel-transport operator
 $f:H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$.
$f:H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$.(2) The isometry
 $H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ induced by the correspondence
$H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ induced by the correspondence  $ch({\mathcal {P}})\sqrt {td_{X\times Y}}$, where
$ch({\mathcal {P}})\sqrt {td_{X\times Y}}$, where  ${\mathcal {P}}\in D^b(X\times Y)$ is the Fourier–Mukai kernel of an equivalence
${\mathcal {P}}\in D^b(X\times Y)$ is the Fourier–Mukai kernel of an equivalence  $D^b(X)\rightarrow D^b(Y)$ of derived categories between two deformation equivalent IHSMs
$D^b(X)\rightarrow D^b(Y)$ of derived categories between two deformation equivalent IHSMs  $X$ and
$X$ and  $Y$.
$Y$.(3) An isometry of
 $H^*(X,{\mathbb {Q}})$ induced by cup product with
$H^*(X,{\mathbb {Q}})$ induced by cup product with  $\exp (\lambda ):=\sum _{k=0}^{\dim (X)}\lambda ^k/k!$ for some
$\exp (\lambda ):=\sum _{k=0}^{\dim (X)}\lambda ^k/k!$ for some  $\lambda \in H^2(X,{\mathbb {Q}})$.
$\lambda \in H^2(X,{\mathbb {Q}})$.
The set of morphisms ![]() ${\rm Hom}_{\mathcal {G}}((X,\epsilon ),(Y,\epsilon '))$ is independent of the orientations and is also denoted by
${\rm Hom}_{\mathcal {G}}((X,\epsilon ),(Y,\epsilon '))$ is independent of the orientations and is also denoted by ![]() ${\rm Hom}_{\mathcal {G}}(X,Y)$. Note that the latter is empty, by definition, if
${\rm Hom}_{\mathcal {G}}(X,Y)$. Note that the latter is empty, by definition, if ![]() $X$ and
$X$ and ![]() $Y$ are not deformation equivalent.
$Y$ are not deformation equivalent.
Definition 1.3 Given an object ![]() $F$ of positive rank
$F$ of positive rank ![]() $r$ in the derived category of coherent sheaves, set
$r$ in the derived category of coherent sheaves, set ![]() $\kappa (F):=ch(F)\exp \big ({-}c_1(F)/r\big )$, where
$\kappa (F):=ch(F)\exp \big ({-}c_1(F)/r\big )$, where ![]() $\exp (x)=\sum _{j=0}^\infty x^j/j!$. Then
$\exp (x)=\sum _{j=0}^\infty x^j/j!$. Then ![]() $\kappa (F)^r=ch(F^{\otimes r}\otimes \det (F)^{-1})$, where the tensor power is taken in the derived category. If
$\kappa (F)^r=ch(F^{\otimes r}\otimes \det (F)^{-1})$, where the tensor power is taken in the derived category. If ![]() $F$ is an object of positive rank
$F$ is an object of positive rank ![]() $r$ in the derived category of twisted coherent sheaves with respect to some Brauer class, then
$r$ in the derived category of twisted coherent sheaves with respect to some Brauer class, then ![]() $F^{\otimes r}\otimes \det (F)^{-1}$ is an untwisted object and we define
$F^{\otimes r}\otimes \det (F)^{-1}$ is an untwisted object and we define ![]() $\kappa (F)$ as the
$\kappa (F)$ as the ![]() $r$th root of the Chern character of the latter with degree-
$r$th root of the Chern character of the latter with degree-![]() $0$ summand equal to
$0$ summand equal to ![]() $r$. If
$r$. If ![]() $F$ has negative rank, set
$F$ has negative rank, set ![]() $\kappa (F):=-\kappa (F[1])$.
$\kappa (F):=-\kappa (F[1])$.
Let
be the subgroupoid of ![]() ${\mathcal {G}}$ with the same objects. Morphisms of
${\mathcal {G}}$ with the same objects. Morphisms of ![]() ${\mathcal {G}}_{an}$ are compositions of two types of rational isometries: (1) parallel-transport operators
${\mathcal {G}}_{an}$ are compositions of two types of rational isometries: (1) parallel-transport operators ![]() $f:H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$, which are Hodge isometries; (2) Hodge isometries
$f:H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$, which are Hodge isometries; (2) Hodge isometries
induced by classes ![]() $\kappa ({\mathcal {P}})\sqrt {td_{X\times Y}}$, where
$\kappa ({\mathcal {P}})\sqrt {td_{X\times Y}}$, where ![]() ${\mathcal {P}}$ is a locally free twisted sheaf over
${\mathcal {P}}$ is a locally free twisted sheaf over ![]() $X\times Y$, such that the Azumaya
$X\times Y$, such that the Azumaya ![]() ${\mathcal {O}}_{X\times Y}$-algebra
${\mathcal {O}}_{X\times Y}$-algebra ![]() ${\mathcal {E}}nd({\mathcal {P}})$ is a deformation (in the sense of Definition 5.13) of the endomorphism algebra of a locally free Fourier–Mukai kernel of an equivalence of derived categories.Footnote 3 Morphisms in
${\mathcal {E}}nd({\mathcal {P}})$ is a deformation (in the sense of Definition 5.13) of the endomorphism algebra of a locally free Fourier–Mukai kernel of an equivalence of derived categories.Footnote 3 Morphisms in ![]() ${\mathcal {G}}_{an}$ are induced by analytic correspondences. Indeed, this follows from the Torelli theorem for parallel-transport Hodge isometries (Theorem 5.2 and Lemma 5.3) and by definition for morphisms of type (2) above.
${\mathcal {G}}_{an}$ are induced by analytic correspondences. Indeed, this follows from the Torelli theorem for parallel-transport Hodge isometries (Theorem 5.2 and Lemma 5.3) and by definition for morphisms of type (2) above.
The rational LLV lattice of an IHSM ![]() $X$ is the vector space
$X$ is the vector space
endowed with the non-degenerate symmetric bilinear pairing, which restricts to ![]() $H^2(X,{\mathbb {Q}})$ as the BBF pairing, such that
$H^2(X,{\mathbb {Q}})$ as the BBF pairing, such that ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ are isotropic and orthogonal to
$\beta$ are isotropic and orthogonal to ![]() $H^2(X,{\mathbb {Q}})$ and satisfy
$H^2(X,{\mathbb {Q}})$ and satisfy ![]() $(\alpha,\beta )=-1$. An orientation for
$(\alpha,\beta )=-1$. An orientation for ![]() $H^2(X,{\mathbb {Q}})$ determines an orientation of
$H^2(X,{\mathbb {Q}})$ determines an orientation of ![]() $\widetilde {H}(X,{\mathbb {Q}})$, and so the LLV lattice of objects of
$\widetilde {H}(X,{\mathbb {Q}})$, and so the LLV lattice of objects of ![]() ${\mathcal {G}}$ has a chosen orientation. We assign
${\mathcal {G}}$ has a chosen orientation. We assign ![]() $\widetilde {H}(X,{\mathbb {Q}})$ the grading where
$\widetilde {H}(X,{\mathbb {Q}})$ the grading where ![]() $\alpha$ has degree
$\alpha$ has degree ![]() $-2$,
$-2$, ![]() $\beta$ has degree
$\beta$ has degree ![]() $2$, and
$2$, and ![]() $H^2(X,{\mathbb {Q}})$ has degree
$H^2(X,{\mathbb {Q}})$ has degree ![]() $0$.
$0$.
Let ![]() $\widetilde {{\mathcal {G}}}$ be the groupoid, whose objects are IHSMs and such that morphisms are isometries of their rational LLV lattices. Results of Taelman's yield a functor
$\widetilde {{\mathcal {G}}}$ be the groupoid, whose objects are IHSMs and such that morphisms are isometries of their rational LLV lattices. Results of Taelman's yield a functor
(see Definition 3.3).
We show that the morphism (1.3) is degree reversing (Lemma 4.1). It follows that every morphism ![]() $\phi$ in
$\phi$ in ![]() ${\rm Hom}_{{\mathcal {G}}_{an}}((X,\epsilon ),(Y,\epsilon '))$ preserves the grading up to sign. Consequently,
${\rm Hom}_{{\mathcal {G}}_{an}}((X,\epsilon ),(Y,\epsilon '))$ preserves the grading up to sign. Consequently, ![]() $\widetilde {H}(\phi )$ preserves the grading of
$\widetilde {H}(\phi )$ preserves the grading of ![]() $\widetilde {H}(X,{\mathbb {Q}})$ up to sign and maps
$\widetilde {H}(X,{\mathbb {Q}})$ up to sign and maps ![]() $H^2(X,{\mathbb {Q}})$ to
$H^2(X,{\mathbb {Q}})$ to ![]() $H^2(Y,{\mathbb {Q}})$ and restricts to
$H^2(Y,{\mathbb {Q}})$ and restricts to ![]() $H^2(X,{\mathbb {Q}})$ as a Hodge isometry
$H^2(X,{\mathbb {Q}})$ as a Hodge isometry ![]() $\widetilde {H}(\phi )_0$ (Lemma 3.4).
$\widetilde {H}(\phi )_0$ (Lemma 3.4).
Let ![]() ${\mathcal {H}dg}$ be the groupoid, whose objects are IHSMs, and whose morphisms in
${\mathcal {H}dg}$ be the groupoid, whose objects are IHSMs, and whose morphisms in ![]() ${\rm Hom}_{{\mathcal {H}dg}}(X,Y)$ are rational Hodge isometries
${\rm Hom}_{{\mathcal {H}dg}}(X,Y)$ are rational Hodge isometries ![]() $f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ preserving the orientations of the positive cones (Definition 5.17). We get the functor
$f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ preserving the orientations of the positive cones (Definition 5.17). We get the functor
forgetting the orientation of objects and mapping a morphism ![]() $\phi$ to
$\phi$ to ![]() $\widetilde {H}(\phi )_0$ or
$\widetilde {H}(\phi )_0$ or ![]() $-\widetilde {H}(\phi )_0$ (whichever preserves the orientations of the positive cones). Let
$-\widetilde {H}(\phi )_0$ (whichever preserves the orientations of the positive cones). Let ![]() ${\mathcal {G}}_{an}^{[n]}$ be the full subgroupoid of
${\mathcal {G}}_{an}^{[n]}$ be the full subgroupoid of ![]() ${\mathcal {G}}_{an}$, whose objects are of
${\mathcal {G}}_{an}$, whose objects are of ![]() $K3^{[n]}$ type. Define the subgroupoid
$K3^{[n]}$ type. Define the subgroupoid ![]() ${\mathcal {H}dg}^{[n]}$ of
${\mathcal {H}dg}^{[n]}$ of ![]() ${\mathcal {H}dg}$ analogously. The following theorem is proved in § 9.
${\mathcal {H}dg}$ analogously. The following theorem is proved in § 9.
Theorem 1.4 The functor ![]() $\widetilde {H}_0:{\mathcal {G}}_{an}^{[n]}\rightarrow {\mathcal {H}dg}^{[n]}$ is full.Footnote 4 In particular, the analytic correspondence
$\widetilde {H}_0:{\mathcal {G}}_{an}^{[n]}\rightarrow {\mathcal {H}dg}^{[n]}$ is full.Footnote 4 In particular, the analytic correspondence ![]() $\tilde {f}$ of Theorem 1.1 can be chosen to be a morphism in
$\tilde {f}$ of Theorem 1.1 can be chosen to be a morphism in ![]() ${\rm Hom}_{{\mathcal {G}}^{[n]}_{an}}((X,\epsilon ),(Y,\epsilon '))$ satisfying
${\rm Hom}_{{\mathcal {G}}^{[n]}_{an}}((X,\epsilon ),(Y,\epsilon '))$ satisfying ![]() $\widetilde {H}_0(\tilde {f})=f$, possibly after replacing
$\widetilde {H}_0(\tilde {f})=f$, possibly after replacing ![]() $f$ by
$f$ by ![]() $-f$, so that it would preserve the orientations of the positive cones.
$-f$, so that it would preserve the orientations of the positive cones.
Let ![]() $f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ be a rational isometry between two IHSMs of
$f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ be a rational isometry between two IHSMs of ![]() $K3^{[n]}$ type
$K3^{[n]}$ type ![]() $X$ and
$X$ and ![]() $Y$. We say that
$Y$. We say that ![]() $f$ is of
$f$ is of ![]() $r$-cyclic type, for some positive integer
$r$-cyclic type, for some positive integer ![]() $r$, if there exists a primitive class
$r$, if there exists a primitive class ![]() $u\in H^2(X,{\mathbb {Z}})$, satisfying
$u\in H^2(X,{\mathbb {Z}})$, satisfying ![]() $(u,u)=2r$ and
$(u,u)=2r$ and ![]() $(u,\bullet )\in H^2(X,{\mathbb {Z}})^*$ is primitive as well, and there exists a parallel-transport operator
$(u,\bullet )\in H^2(X,{\mathbb {Z}})^*$ is primitive as well, and there exists a parallel-transport operator ![]() $g:H^2(X,{\mathbb {Z}})\rightarrow H^2(Y,{\mathbb {Z}})$, such that
$g:H^2(X,{\mathbb {Z}})\rightarrow H^2(Y,{\mathbb {Z}})$, such that ![]() $f=-g\rho _u$, where
$f=-g\rho _u$, where ![]() $\rho _u\in O(H^2(X,{\mathbb {Q}}))$ is the reflection in
$\rho _u\in O(H^2(X,{\mathbb {Q}}))$ is the reflection in ![]() $u$ given by
$u$ given by ![]() $\rho _u(x)=x-({2(u,x)}/{(u,u)})u$. Such
$\rho _u(x)=x-({2(u,x)}/{(u,u)})u$. Such ![]() $f$ is necessarily compatible with the orientations of the positive cones. The proof of Theorem 1.4 relies on the following.
$f$ is necessarily compatible with the orientations of the positive cones. The proof of Theorem 1.4 relies on the following.
Theorem 1.5 (Corollary 8.5)
Let ![]() $f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ be a rational Hodge isometry of
$f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ be a rational Hodge isometry of ![]() $r$-cyclic type between two IHSMs
$r$-cyclic type between two IHSMs ![]() $X$ and
$X$ and ![]() $Y$ of
$Y$ of ![]() $K3^{[n]}$ type. There exists over
$K3^{[n]}$ type. There exists over ![]() $X\times Y$ a (possibly twisted) locally free coherent sheaf
$X\times Y$ a (possibly twisted) locally free coherent sheaf ![]() $E$ of rank
$E$ of rank ![]() $n!r^n$, such that
$n!r^n$, such that ![]() $\phi :=[\kappa (E)\sqrt {td_{X\times Y}}]_*$ is a degree-reversing morphism in
$\phi :=[\kappa (E)\sqrt {td_{X\times Y}}]_*$ is a degree-reversing morphism in ![]() ${\rm Hom}_{{\mathcal {G}}^{[n]}_{an}}(X,Y)$ and
${\rm Hom}_{{\mathcal {G}}^{[n]}_{an}}(X,Y)$ and ![]() $\widetilde {H}_0(\phi )=f$.
$\widetilde {H}_0(\phi )=f$.
1.2 Fourier–Mukai kernels of positive rank and the Lefschetz standard conjecture
Theorem 1.5 leads to an alternative short proof of the Lefschetz standard conjecture for projective IHSMs of ![]() $K3^{[n]}$ type, originally proved in [Reference Charles and MarkmanCM13]. Let
$K3^{[n]}$ type, originally proved in [Reference Charles and MarkmanCM13]. Let ![]() $X$ be a projective IHSM of
$X$ be a projective IHSM of ![]() $K3^{[n]}$ type. Let
$K3^{[n]}$ type. Let ![]() $\lambda \in H^{1,1}(X,{\mathbb {Q}})$ be an ample class. Let
$\lambda \in H^{1,1}(X,{\mathbb {Q}})$ be an ample class. Let ![]() $h\in {\rm End}(H^*(X,{\mathbb {Q}}))$ multiply
$h\in {\rm End}(H^*(X,{\mathbb {Q}}))$ multiply ![]() $H^{k}(X,{\mathbb {Q}})[2n]$ by
$H^{k}(X,{\mathbb {Q}})[2n]$ by ![]() $k$. Denote by
$k$. Denote by ![]() $e_\lambda \in {\rm End}(H^*(X,{\mathbb {Q}}))$ the Lefschetz operator of cup product with
$e_\lambda \in {\rm End}(H^*(X,{\mathbb {Q}}))$ the Lefschetz operator of cup product with ![]() $\lambda$ and let
$\lambda$ and let ![]() $e^\vee _\lambda \in {\rm End}(H^*(X,{\mathbb {Q}}))$ be dual Lefschetz operator, i.e. the unique element satisfying
$e^\vee _\lambda \in {\rm End}(H^*(X,{\mathbb {Q}}))$ be dual Lefschetz operator, i.e. the unique element satisfying
Choose an IHSM ![]() $Y$, such that there exists a rational Hodge isometry
$Y$, such that there exists a rational Hodge isometry ![]() $f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ of
$f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ of ![]() $r$-cyclic type, for some integer
$r$-cyclic type, for some integer ![]() $r>0$. The existence of such
$r>0$. The existence of such ![]() $Y$ follows, for every
$Y$ follows, for every ![]() $r>0$, by Theorem 1.5 and the surjectivity of the period map [Reference HuybrechtsHuy99].Footnote 5 The morphism
$r>0$, by Theorem 1.5 and the surjectivity of the period map [Reference HuybrechtsHuy99].Footnote 5 The morphism ![]() $\phi \in {\rm Hom}_{{\mathcal {G}}^{[n]}_{an}}(X,Y)$ in Theorem 1.5 is degree reversing. We get that
$\phi \in {\rm Hom}_{{\mathcal {G}}^{[n]}_{an}}(X,Y)$ in Theorem 1.5 is degree reversing. We get that ![]() $e_\lambda ^\vee$ is algebraic, by the following elementary lemma.
$e_\lambda ^\vee$ is algebraic, by the following elementary lemma.
Let ![]() $X$ and
$X$ and ![]() $Y$ be IHSMs and let
$Y$ be IHSMs and let ![]() $\phi \in {\rm Hom}_{{\mathcal {G}}_{an}}((X,\epsilon ),(Y,\epsilon '))$ be a degree-reversing morphism. Then
$\phi \in {\rm Hom}_{{\mathcal {G}}_{an}}((X,\epsilon ),(Y,\epsilon '))$ be a degree-reversing morphism. Then ![]() $\tilde {\phi }:=\widetilde {H}(\phi )$ is degree reversing as well (Lemma 3.4). Let
$\tilde {\phi }:=\widetilde {H}(\phi )$ is degree reversing as well (Lemma 3.4). Let ![]() $t\in {\mathbb {Q}}$ be such that
$t\in {\mathbb {Q}}$ be such that ![]() $\tilde {\phi }(\beta )=t\alpha$. Let
$\tilde {\phi }(\beta )=t\alpha$. Let ![]() $\lambda \in H^2(X,{\mathbb {Q}})$ be such that
$\lambda \in H^2(X,{\mathbb {Q}})$ be such that ![]() $(\lambda,\lambda )\neq 0$.
$(\lambda,\lambda )\neq 0$.
Lemma 1.6 The dual Lefschetz operator is given by ![]() $e_\lambda ^\vee = ({2}/{t(\lambda,\lambda )})\phi ^{-1}e_{\tilde {\phi }(\lambda )}\phi$ and is algebraic if
$e_\lambda ^\vee = ({2}/{t(\lambda,\lambda )})\phi ^{-1}e_{\tilde {\phi }(\lambda )}\phi$ and is algebraic if ![]() $\lambda$ is, as
$\lambda$ is, as ![]() $e_{\tilde {\phi }(\lambda )}$ and the morphisms
$e_{\tilde {\phi }(\lambda )}$ and the morphisms ![]() $\phi$ and
$\phi$ and ![]() $\phi ^{-1}$ are.
$\phi ^{-1}$ are.
The short proof of the lemma is given at the end of § 4.
Example 1.7 If ![]() $X$ is an IHSM of
$X$ is an IHSM of ![]() $K3^{[n]}$ type,
$K3^{[n]}$ type, ![]() $n=1,2$, then
$n=1,2$, then ![]() ${\rm Aut}_{{\mathcal {G}}^{[n]}_{an}}(X)$ contains a degree-reversing involution. When
${\rm Aut}_{{\mathcal {G}}^{[n]}_{an}}(X)$ contains a degree-reversing involution. When ![]() $X$ is a
$X$ is a ![]() $K3$ surface such an involution is induced by the ideal sheaf of the diagonal in
$K3$ surface such an involution is induced by the ideal sheaf of the diagonal in ![]() $X\times X$, as the ideal sheaf is the kernel of a derived auto-equivalence. When
$X\times X$, as the ideal sheaf is the kernel of a derived auto-equivalence. When ![]() $X$ is of
$X$ is of ![]() $K3^{[2]}$ type, a rank-
$K3^{[2]}$ type, a rank-![]() $2$ twisted reflexive sheaf
$2$ twisted reflexive sheaf ![]() $E$ was constructed on
$E$ was constructed on ![]() $X\times X$ in [Reference MarkmanMar20]. When
$X\times X$ in [Reference MarkmanMar20]. When ![]() $X=S^{[2]}$, for a
$X=S^{[2]}$, for a ![]() $K3$ surface
$K3$ surface ![]() $S$, Addington showed that
$S$, Addington showed that ![]() $E$ is the Fourier–Mukai kernel of an auto-equivalence of
$E$ is the Fourier–Mukai kernel of an auto-equivalence of ![]() $D^b(S^{[2]})$ acting on cohomology as an involution [Reference AddingtonAdd16]. It follows that
$D^b(S^{[2]})$ acting on cohomology as an involution [Reference AddingtonAdd16]. It follows that ![]() $[\kappa (E)\sqrt {td_{X\times X}}]_*$ is a degree-reversing involution in
$[\kappa (E)\sqrt {td_{X\times X}}]_*$ is a degree-reversing involution in ![]() ${\rm Aut}_{{\mathcal {G}}^{[2]}_{an}}(X)$, for every
${\rm Aut}_{{\mathcal {G}}^{[2]}_{an}}(X)$, for every ![]() $X$ of
$X$ of ![]() $K3^{[2]}$ type. Does a degree-reversing automorphism exist in
$K3^{[2]}$ type. Does a degree-reversing automorphism exist in ![]() ${\rm Aut}_{{\mathcal {G}}^{[n]}_{an}}(X)$ for every
${\rm Aut}_{{\mathcal {G}}^{[n]}_{an}}(X)$ for every ![]() $X$ of
$X$ of ![]() $K3^{[n]}$ type for
$K3^{[n]}$ type for ![]() $n\geq 3$? What about other deformation types?
$n\geq 3$? What about other deformation types?
1.3 The Pontryagin product
In § 10 we define a Pontryagin product ![]() $\star$ on the cohomology
$\star$ on the cohomology ![]() $H^*(X,{\mathbb {Q}})$ of every IHSM
$H^*(X,{\mathbb {Q}})$ of every IHSM ![]() $X$ with vanishing odd cohomology. The unit with respect to
$X$ with vanishing odd cohomology. The unit with respect to ![]() $\star$ is
$\star$ is ![]() $c_X[pt]/n!$, where
$c_X[pt]/n!$, where ![]() $\dim (X)=2n$,
$\dim (X)=2n$, ![]() $[pt]\in H^{\textrm{top}}(X,{\mathbb {Q}})$ is the class Poincaré dual to the class of a point, and
$[pt]\in H^{\textrm{top}}(X,{\mathbb {Q}})$ is the class Poincaré dual to the class of a point, and ![]() $c_X$ is the Fujiki constant.Footnote 6 The product
$c_X$ is the Fujiki constant.Footnote 6 The product ![]() $\star$ maps
$\star$ maps ![]() $H^k(X,{\mathbb {Q}})\otimes H^l(X,{\mathbb {Q}})$ to
$H^k(X,{\mathbb {Q}})\otimes H^l(X,{\mathbb {Q}})$ to ![]() $H^{k+l-4n}(X,{\mathbb {Q}})$, so that
$H^{k+l-4n}(X,{\mathbb {Q}})$, so that ![]() $\star$ is compatible with the grading for which
$\star$ is compatible with the grading for which ![]() $H^k(X,{\mathbb {Q}})$ has degree
$H^k(X,{\mathbb {Q}})$ has degree ![]() $4n-k$. Parallel-transport operators induce isomorphisms of the Pontryagin rings (Lemma 10.2).
$4n-k$. Parallel-transport operators induce isomorphisms of the Pontryagin rings (Lemma 10.2).
The Pontryagin product ![]() $\star$ on the cohomology
$\star$ on the cohomology ![]() $H^*(S,{\mathbb {Z}})$ of a
$H^*(S,{\mathbb {Z}})$ of a ![]() $K3$ surface
$K3$ surface ![]() $S$ is simple to describe. The unit with respect to
$S$ is simple to describe. The unit with respect to ![]() $\star$ is the class
$\star$ is the class ![]() $[pt]\in H^4(X,{\mathbb {Z}})$ Poincaré dual to a point. The product
$[pt]\in H^4(X,{\mathbb {Z}})$ Poincaré dual to a point. The product ![]() $\star$ maps
$\star$ maps ![]() $H^k(S,{\mathbb {Z}})\otimes H^l(S,{\mathbb {Z}})$ to
$H^k(S,{\mathbb {Z}})\otimes H^l(S,{\mathbb {Z}})$ to ![]() $H^{k+l-4}(S,{\mathbb {Z}})$ and satisfies
$H^{k+l-4}(S,{\mathbb {Z}})$ and satisfies ![]() $\lambda _1\star \lambda _2=(\lambda _1,\lambda _2)\in H^0(S,{\mathbb {Z}})$, for classes
$\lambda _1\star \lambda _2=(\lambda _1,\lambda _2)\in H^0(S,{\mathbb {Z}})$, for classes ![]() $\lambda _1,\lambda _2\in H^2(S,{\mathbb {Z}})$. Let
$\lambda _1,\lambda _2\in H^2(S,{\mathbb {Z}})$. Let ![]() $\rho _u:\widetilde {H}(S,{\mathbb {Z}})\rightarrow \widetilde {H}(S,{\mathbb {Z}}),$ be the reflection
$\rho _u:\widetilde {H}(S,{\mathbb {Z}})\rightarrow \widetilde {H}(S,{\mathbb {Z}}),$ be the reflection ![]() $\rho _u(r,c,s)=(-s,c,-r)$ in the Mukai vector
$\rho _u(r,c,s)=(-s,c,-r)$ in the Mukai vector ![]() $u:=(1,0,1)$ of the structure sheaf
$u:=(1,0,1)$ of the structure sheaf ![]() ${\mathcal {O}}_{S}$. Then
${\mathcal {O}}_{S}$. Then ![]() $-\rho _u$ conjugates the usual product on
$-\rho _u$ conjugates the usual product on ![]() $H^*(S,{\mathbb {Z}})$ to the Pontryagin product. Note that
$H^*(S,{\mathbb {Z}})$ to the Pontryagin product. Note that ![]() $-\rho _u$ corresponds to the action on cohomology of the autoequivalence
$-\rho _u$ corresponds to the action on cohomology of the autoequivalence ![]() $\Phi _{{\mathcal {I}}_{\Delta }}$ of
$\Phi _{{\mathcal {I}}_{\Delta }}$ of ![]() $D^b(S)$, whose Fourier–Mukai kernel is the ideal sheaf
$D^b(S)$, whose Fourier–Mukai kernel is the ideal sheaf ![]() ${\mathcal {I}}_{\Delta }$ of the diagonal
${\mathcal {I}}_{\Delta }$ of the diagonal ![]() $\Delta$ in
$\Delta$ in ![]() $S\times S$.
$S\times S$.
Morphisms in ![]() ${\mathcal {G}}_{[an]}$, which are associated to equivalences of derived categories with a Fourier–Mukai kernel of positive rank, are degree reversing. This corresponds to a normalization which annihilates the first Chern class of the Fourier–Mukai kernel. We introduce a further normalization, which assures that the compositions of any two such degree-reversing morphisms would map the usual identity
${\mathcal {G}}_{[an]}$, which are associated to equivalences of derived categories with a Fourier–Mukai kernel of positive rank, are degree reversing. This corresponds to a normalization which annihilates the first Chern class of the Fourier–Mukai kernel. We introduce a further normalization, which assures that the compositions of any two such degree-reversing morphisms would map the usual identity ![]() $1\in H^0(X,{\mathbb {Q}})$ to itself. We speculate in the following that thus normalized, the degree-reversing morphisms conjugate the cup product to the Pontryagin product. We introduce this further normalization in the next paragraph.
$1\in H^0(X,{\mathbb {Q}})$ to itself. We speculate in the following that thus normalized, the degree-reversing morphisms conjugate the cup product to the Pontryagin product. We introduce this further normalization in the next paragraph.
Let ![]() ${\mathbb {Q}}^\times$ be the multiplicative group of rational numbers. Let
${\mathbb {Q}}^\times$ be the multiplicative group of rational numbers. Let
be the groupoid homomorphism sending every object to ![]() ${\mathbb {Q}}^\times$ and sending a morphism
${\mathbb {Q}}^\times$ and sending a morphism ![]() $\phi$ to
$\phi$ to ![]() $t$, if
$t$, if ![]() $\phi$ is degree preserving and
$\phi$ is degree preserving and ![]() $\widetilde {H}(\phi )(\alpha )=t\alpha$, or if
$\widetilde {H}(\phi )(\alpha )=t\alpha$, or if ![]() $\phi$ is degree reversing and
$\phi$ is degree reversing and ![]() $\widetilde {H}(\phi )(\alpha )= ({1}/{t})\beta$. Given a non-zero rational number
$\widetilde {H}(\phi )(\alpha )= ({1}/{t})\beta$. Given a non-zero rational number ![]() $t$, denote by
$t$, denote by ![]() $\mu _t:H^*(X,{\mathbb {Q}})[2n]\rightarrow H^*(X,{\mathbb {Q}})[2n]$ the graded linear transformation multiplying
$\mu _t:H^*(X,{\mathbb {Q}})[2n]\rightarrow H^*(X,{\mathbb {Q}})[2n]$ the graded linear transformation multiplying ![]() $H^{2k}(X,{\mathbb {Q}})[\dim (X)]$ by
$H^{2k}(X,{\mathbb {Q}})[\dim (X)]$ by ![]() $t^k$. Let
$t^k$. Let
be the subgroupoid of ![]() ${\mathcal {G}}^{[n]}_{an}$ with the same objects, but whose morphisms
${\mathcal {G}}^{[n]}_{an}$ with the same objects, but whose morphisms ![]() $\phi$ have the property that
$\phi$ have the property that ![]() $\mu _{\chi (\phi )}\circ \phi$ conjugates the usual product on
$\mu _{\chi (\phi )}\circ \phi$ conjugates the usual product on ![]() $H^*(X,{\mathbb {Q}})$ to itself, if
$H^*(X,{\mathbb {Q}})$ to itself, if ![]() $\phi$ is degree preserving and to
$\phi$ is degree preserving and to ![]() $\star$ if
$\star$ if ![]() $\phi$ is degree reversing.
$\phi$ is degree reversing.
Conjecture 1.8 The subgroupoid ![]() ${\mathcal {R}}^{[n]}_{an}$ is, in fact, the whole of
${\mathcal {R}}^{[n]}_{an}$ is, in fact, the whole of ![]() ${\mathcal {G}}^{[n]}_{an}$. Furthermore, if an object of positive rank
${\mathcal {G}}^{[n]}_{an}$. Furthermore, if an object of positive rank ![]() $F$ in
$F$ in ![]() $D^b(X\times Y)$ is the Fourier–Mukai kernel of an equivalence
$D^b(X\times Y)$ is the Fourier–Mukai kernel of an equivalence ![]() $\Phi _F:D^b(X)\rightarrow D^b(Y)$ of derived categories of projective IHSMs
$\Phi _F:D^b(X)\rightarrow D^b(Y)$ of derived categories of projective IHSMs ![]() $X$ and
$X$ and ![]() $Y$ of
$Y$ of ![]() $K3^{[n]}$ type, then the rank of
$K3^{[n]}$ type, then the rank of ![]() $F$ is
$F$ is ![]() $n!t^n$, for some rational number
$n!t^n$, for some rational number ![]() $t$, and setting
$t$, and setting ![]() $\phi :=\mu _t\circ [\kappa (F)\sqrt {td_{X\times Y}}]_*:H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ we have
$\phi :=\mu _t\circ [\kappa (F)\sqrt {td_{X\times Y}}]_*:H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ we have
for all ![]() $\gamma _1,\gamma _2\in H^*(X,{\mathbb {Q}})$.
$\gamma _1,\gamma _2\in H^*(X,{\mathbb {Q}})$.
The stated equality ![]() ${\rm rank}(F)=n!t^n$, for some rational number
${\rm rank}(F)=n!t^n$, for some rational number ![]() $t$, is known [Reference BeckmannBec23, Theorem 4.14]. As evidence for the conjecture, we show that the examples of morphisms of
$t$, is known [Reference BeckmannBec23, Theorem 4.14]. As evidence for the conjecture, we show that the examples of morphisms of ![]() ${\mathcal {G}}^{[n]}_{an}$ used in the proof of Theorem 1.4 all satisfy Conjecture 1.8. Consequently, Theorem 1.4 holds even after replacing
${\mathcal {G}}^{[n]}_{an}$ used in the proof of Theorem 1.4 all satisfy Conjecture 1.8. Consequently, Theorem 1.4 holds even after replacing ![]() ${\mathcal {G}}^{[n]}_{an}$ by
${\mathcal {G}}^{[n]}_{an}$ by ![]() ${\mathcal {R}}^{[n]}_{an}$ and we get the following result proven in § 10.
${\mathcal {R}}^{[n]}_{an}$ and we get the following result proven in § 10.
Proposition 1.9 (Proposition 10.7)
The restriction of the functor ![]() $\widetilde {H}_0:{\mathcal {G}}^{[n]}_{an}\rightarrow {\mathcal {H}dg}^{[n]}$ to the subgroupoid
$\widetilde {H}_0:{\mathcal {G}}^{[n]}_{an}\rightarrow {\mathcal {H}dg}^{[n]}$ to the subgroupoid ![]() ${\mathcal {R}}^{[n]}_{an}$ remains full.
${\mathcal {R}}^{[n]}_{an}$ remains full.
Let ![]() $X$ and
$X$ and ![]() $Y$ be projective IHSMs of
$Y$ be projective IHSMs of ![]() $K3^{[n]}$ type. The proof of Proposition 10.7 implies that the degree-reversing correspondence
$K3^{[n]}$ type. The proof of Proposition 10.7 implies that the degree-reversing correspondence ![]() $\kappa (E)\sqrt {td_{X\times Y}}$ in Theorem 1.5 satisfies Conjecture 1.8. Set
$\kappa (E)\sqrt {td_{X\times Y}}$ in Theorem 1.5 satisfies Conjecture 1.8. Set ![]() $\phi :=\mu _t\circ [\kappa (E)\sqrt {td_{X\times Y}}]_*$, as in the conjecture. Let
$\phi :=\mu _t\circ [\kappa (E)\sqrt {td_{X\times Y}}]_*$, as in the conjecture. Let ![]() $[\Delta ]\in H^*(X^3,{\mathbb {Q}})$ the class of the small diagonal
$[\Delta ]\in H^*(X^3,{\mathbb {Q}})$ the class of the small diagonal ![]() $\Delta$ in
$\Delta$ in ![]() $X^3$. The following corollary is proved in § 10.2.
$X^3$. The following corollary is proved in § 10.2.
Corollary 1.10 The Pontryagin product ![]() $\star : H^*(Y\times Y,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ is induced by the algebraic class
$\star : H^*(Y\times Y,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ is induced by the algebraic class ![]() $\phi ^3([\Delta ])$ in
$\phi ^3([\Delta ])$ in ![]() $H^*(Y^3,{\mathbb {Q}})$. In particular, Pontryagin product
$H^*(Y^3,{\mathbb {Q}})$. In particular, Pontryagin product ![]() $\gamma \star :H^*(Y,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ by an algebraic class
$\gamma \star :H^*(Y,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ by an algebraic class ![]() $\gamma$ is induced by an algebraic correspondence.
$\gamma$ is induced by an algebraic correspondence.
The algebraicity of the dual Lefschetz operator ![]() $e_\lambda ^\vee$ in Lemma 1.6 is a special case of the above corollary, since
$e_\lambda ^\vee$ in Lemma 1.6 is a special case of the above corollary, since ![]() $e_\lambda ^\vee$ is a scalar multiple of the operator of Pontryagin product with the algebraic class
$e_\lambda ^\vee$ is a scalar multiple of the operator of Pontryagin product with the algebraic class ![]() $\phi ^{-1}(\tilde {\phi }(\lambda ))$.
$\phi ^{-1}(\tilde {\phi }(\lambda ))$.
1.4 Outline of the proof of Theorem 1.4
The reader familiar with Buskin's proof of the case ![]() $n=1$ of the theorem will note the similarity of our strategy to his. Buskin considers examples of two-dimensional moduli spaces
$n=1$ of the theorem will note the similarity of our strategy to his. Buskin considers examples of two-dimensional moduli spaces ![]() $M$ of vector bundles over a
$M$ of vector bundles over a ![]() $K3$ surface
$K3$ surface ![]() $S$ and the universal bundle
$S$ and the universal bundle ![]() ${\mathcal {U}}$ over
${\mathcal {U}}$ over ![]() $M\times S$. Here
$M\times S$. Here ![]() $M$ is a
$M$ is a ![]() $K3$ surface and so the product
$K3$ surface and so the product ![]() $M\times S$ is a hyper-Kähler manifold. Buskin uses Verbitsky's results on hyperholomorphic vector bundles over hyper-Kähler manifolds to deform the pair
$M\times S$ is a hyper-Kähler manifold. Buskin uses Verbitsky's results on hyperholomorphic vector bundles over hyper-Kähler manifolds to deform the pair ![]() $(M\times S,{\mathcal {U}})$ to twisted vector bundles
$(M\times S,{\mathcal {U}})$ to twisted vector bundles ![]() $(X_1\times X_2,{\mathcal {U}}')$ over products of not necessarily projective
$(X_1\times X_2,{\mathcal {U}}')$ over products of not necessarily projective ![]() $K3$ surfaces
$K3$ surfaces ![]() $X_1$ and
$X_1$ and ![]() $X_2$. Buskin proves that the groupoid
$X_2$. Buskin proves that the groupoid ![]() ${\mathcal {H}dg}^{[1]}$ is generated by parallel-transport operators, which are isomorphisms of Hodge structures, and by the restrictions to
${\mathcal {H}dg}^{[1]}$ is generated by parallel-transport operators, which are isomorphisms of Hodge structures, and by the restrictions to ![]() $H^2(X_1,{\mathbb {Q}})$ of the degree-reversing isometries
$H^2(X_1,{\mathbb {Q}})$ of the degree-reversing isometries ![]() $[\kappa ({\mathcal {U}}')\sqrt {td_{X_1\times X_2}}]_*:\widetilde {H}(X_1,{\mathbb {Q}})\rightarrow \widetilde {H}(X_2,{\mathbb {Q}})$.
$[\kappa ({\mathcal {U}}')\sqrt {td_{X_1\times X_2}}]_*:\widetilde {H}(X_1,{\mathbb {Q}})\rightarrow \widetilde {H}(X_2,{\mathbb {Q}})$.
We first construct the functor ![]() $\widetilde {H}_0:{\mathcal {G}}_{an}\rightarrow {\mathcal {H}dg}$ and establish its properties in §§ 3 and 4. The construction depends heavily on the recent work of Taelman [Reference TaelmanTae23], as well as on the work of the author and independently of Beckmann describing the action of equivalences of derived categories on the LLV lattice [Reference BeckmannBec23, Reference MarkmanMar21a]. In § 7 we lift the equivalence of derived categories
$\widetilde {H}_0:{\mathcal {G}}_{an}\rightarrow {\mathcal {H}dg}$ and establish its properties in §§ 3 and 4. The construction depends heavily on the recent work of Taelman [Reference TaelmanTae23], as well as on the work of the author and independently of Beckmann describing the action of equivalences of derived categories on the LLV lattice [Reference BeckmannBec23, Reference MarkmanMar21a]. In § 7 we lift the equivalence of derived categories ![]() $\Phi _{\mathcal {U}}:D^b(M)\rightarrow D^b(S)$, with the universal bundle
$\Phi _{\mathcal {U}}:D^b(M)\rightarrow D^b(S)$, with the universal bundle ![]() ${\mathcal {U}}$ as a kernel, to an equivalence
${\mathcal {U}}$ as a kernel, to an equivalence ![]() $\Phi _{{\mathcal {U}}^{[n]}}:D^b(M^{[n]})\rightarrow D^b(S^{[n]})$ of derived categories of Hilbert schemes. This is done by conjugating the equivalence of equivariant derived categories on the cartesian products
$\Phi _{{\mathcal {U}}^{[n]}}:D^b(M^{[n]})\rightarrow D^b(S^{[n]})$ of derived categories of Hilbert schemes. This is done by conjugating the equivalence of equivariant derived categories on the cartesian products ![]() $\Phi _{{\mathcal {U}}^{\boxtimes n}}:D^b_{{\mathfrak {S}}_n}(M^n)\rightarrow D^b_{{\mathfrak {S}}_n}(S^n)$, obtained from the cartesian power of
$\Phi _{{\mathcal {U}}^{\boxtimes n}}:D^b_{{\mathfrak {S}}_n}(M^n)\rightarrow D^b_{{\mathfrak {S}}_n}(S^n)$, obtained from the cartesian power of ![]() $\Phi _{\mathcal {U}}$, with the Bridgeland–King–Reid equivalence
$\Phi _{\mathcal {U}}$, with the Bridgeland–King–Reid equivalence ![]() $\textit{BKR}:D^b_{{\mathfrak {S}}_n}(S^n)\rightarrow D^b(S^{[n]})$ and its analogue for
$\textit{BKR}:D^b_{{\mathfrak {S}}_n}(S^n)\rightarrow D^b(S^{[n]})$ and its analogue for ![]() $M$. The Bridgeland–King–Reid equivalence is reviewed in § 6. The assignment
$M$. The Bridgeland–King–Reid equivalence is reviewed in § 6. The assignment ![]() $S\mapsto S^{[n]}$ and
$S\mapsto S^{[n]}$ and ![]() $\Phi _{\mathcal {U}}\mapsto \Phi _{{\mathcal {U}}^{[n]}}$ extends to define a functor
$\Phi _{\mathcal {U}}\mapsto \Phi _{{\mathcal {U}}^{[n]}}$ extends to define a functor
constructed in (7.12). The Fourier–Mukai kernel ![]() ${\mathcal {U}}^{[n]}$ is again a locally free sheaf over
${\mathcal {U}}^{[n]}$ is again a locally free sheaf over ![]() $M^{[n]}\times S^{[n]}$. Again we use Verbitsky's results on hyperholomorphic vector bundles on hyper-Kähler manifolds to deform the pair
$M^{[n]}\times S^{[n]}$. Again we use Verbitsky's results on hyperholomorphic vector bundles on hyper-Kähler manifolds to deform the pair ![]() $(M^{[n]}\times S^{[n]},{\mathcal {U}}^{[n]})$ to pairs
$(M^{[n]}\times S^{[n]},{\mathcal {U}}^{[n]})$ to pairs ![]() $(X_1\times X_2,E)$ consisting of a twisted vector bundle
$(X_1\times X_2,E)$ consisting of a twisted vector bundle ![]() $E$ over the product
$E$ over the product ![]() $X_1\times X_2$ of not necessarily projective IHSMs of
$X_1\times X_2$ of not necessarily projective IHSMs of ![]() $K3^{[n]}$ type. The general techniques are developed in § 5 and applied to
$K3^{[n]}$ type. The general techniques are developed in § 5 and applied to ![]() ${\mathcal {U}}^{[n]}$ in § 8.
${\mathcal {U}}^{[n]}$ in § 8.
It remains to prove that we get a full functor already when we restrict the functor ![]() $\widetilde {H}_0:{\mathcal {G}}^{[n]}_{an}\rightarrow {\mathcal {H}dg}^{[n]}$ to the subgroupoid of
$\widetilde {H}_0:{\mathcal {G}}^{[n]}_{an}\rightarrow {\mathcal {H}dg}^{[n]}$ to the subgroupoid of ![]() ${\mathcal {G}}_{an}^{[n]}$ generated by parallel-transport operators, which are Hodge isometries, and morphisms in the image of
${\mathcal {G}}_{an}^{[n]}$ generated by parallel-transport operators, which are Hodge isometries, and morphisms in the image of ![]() $\Theta _n$. This is done as follows.
$\Theta _n$. This is done as follows.
Step 1 (generators for the group of rational isometries). Let ![]() $L$ be a lattice isometric to the second cohomology of a
$L$ be a lattice isometric to the second cohomology of a ![]() $K3$ surface. Let
$K3$ surface. Let ![]() $\Lambda$ be the orthogonal direct sum
$\Lambda$ be the orthogonal direct sum ![]() $L\oplus {\mathbb {Z}}\delta$, where
$L\oplus {\mathbb {Z}}\delta$, where ![]() $(\delta,\delta )=2-2n$. Then
$(\delta,\delta )=2-2n$. Then ![]() $\Lambda$ is isometric to the second cohomology of an IHSM
$\Lambda$ is isometric to the second cohomology of an IHSM ![]() $X$ of
$X$ of ![]() $K3^{[n]}$ type endowed with the BBF pairing [Reference BeauvilleBea83]. The monodromy group of
$K3^{[n]}$ type endowed with the BBF pairing [Reference BeauvilleBea83]. The monodromy group of ![]() $X$ acts on
$X$ acts on ![]() $H^2(X,{\mathbb {Z}})$ via a normal subgroup of
$H^2(X,{\mathbb {Z}})$ via a normal subgroup of ![]() $O(H^2(X,{\mathbb {Z}}))$ and so corresponds to a well-defined subgroup
$O(H^2(X,{\mathbb {Z}}))$ and so corresponds to a well-defined subgroup ![]() ${\rm Mon}(\Lambda )$ of
${\rm Mon}(\Lambda )$ of ![]() $O(\Lambda )$, by [Reference MarkmanMar08, Theorem 1.6 and Lemma 4.10]. We first prove that the group
$O(\Lambda )$, by [Reference MarkmanMar08, Theorem 1.6 and Lemma 4.10]. We first prove that the group ![]() $O(\Lambda _{\mathbb {Q}})$ of rational isometries is generated by
$O(\Lambda _{\mathbb {Q}})$ of rational isometries is generated by ![]() ${\rm Mon}(\Lambda )$ and
${\rm Mon}(\Lambda )$ and ![]() $O(L_{\mathbb {Q}})$ (Proposition 2.1). It follows from the Cartan–Dieudonné theorem that every rational isometry
$O(L_{\mathbb {Q}})$ (Proposition 2.1). It follows from the Cartan–Dieudonné theorem that every rational isometry ![]() $\psi :\Lambda _{\mathbb {Q}}\rightarrow \Lambda _{\mathbb {Q}}$, which preserves the orientation of the positive cone, decomposes as the composition
$\psi :\Lambda _{\mathbb {Q}}\rightarrow \Lambda _{\mathbb {Q}}$, which preserves the orientation of the positive cone, decomposes as the composition ![]() $\psi =\psi _k\circ \cdots \circ \psi _1$, where
$\psi =\psi _k\circ \cdots \circ \psi _1$, where ![]() $\psi _i$ belongs to the double orbit
$\psi _i$ belongs to the double orbit ![]() ${\rm Mon}(\Lambda )(-\rho _{u}){\rm Mon}(\Lambda )$, where
${\rm Mon}(\Lambda )(-\rho _{u}){\rm Mon}(\Lambda )$, where ![]() $\rho _u$ is the reflection in a primitive integral class
$\rho _u$ is the reflection in a primitive integral class ![]() $u\in L$ with
$u\in L$ with ![]() $(u,u)>0$ (Corollary 2.5). The double orbit
$(u,u)>0$ (Corollary 2.5). The double orbit ![]() ${\rm Mon}(\Lambda )(-\rho _{u}){\rm Mon}(\Lambda )$ depends only on
${\rm Mon}(\Lambda )(-\rho _{u}){\rm Mon}(\Lambda )$ depends only on ![]() $(u,u)$ and is otherwise independent of the class
$(u,u)$ and is otherwise independent of the class ![]() $u$, since so does the double orbit
$u$, since so does the double orbit ![]() $O^+(L)(-\rho _{u})O^+(L),$ by [Reference BuskinBus19, Proposition 3.3], and
$O^+(L)(-\rho _{u})O^+(L),$ by [Reference BuskinBus19, Proposition 3.3], and ![]() ${\rm Mon}(\Lambda )$ contains
${\rm Mon}(\Lambda )$ contains ![]() $O^+(L)$.
$O^+(L)$.
Step 2 (reduction to the double orbit of a reflection). Let ![]() $f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ be a rational Hodge isometry preserving the orientations of the positive cones, where
$f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ be a rational Hodge isometry preserving the orientations of the positive cones, where ![]() $X$ and
$X$ and ![]() $Y$ are of
$Y$ are of ![]() $K3^{[n]}$ type. Choose isometries
$K3^{[n]}$ type. Choose isometries ![]() $\eta _X:H^2(X,{\mathbb {Z}})\rightarrow \Lambda$ and
$\eta _X:H^2(X,{\mathbb {Z}})\rightarrow \Lambda$ and ![]() $\eta _Y:H^2(Y,{\mathbb {Z}})\rightarrow \Lambda$, so that the marked pairs
$\eta _Y:H^2(Y,{\mathbb {Z}})\rightarrow \Lambda$, so that the marked pairs ![]() $(X,\eta _X)$ and
$(X,\eta _X)$ and ![]() $(Y,\eta _Y)$ belong to the same connected component
$(Y,\eta _Y)$ belong to the same connected component ![]() ${\mathfrak {M}}_\Lambda ^0$ of the moduli space of marked IHSMs of
${\mathfrak {M}}_\Lambda ^0$ of the moduli space of marked IHSMs of ![]() $K3^{[n]}$ type. Let
$K3^{[n]}$ type. Let ![]() $\Omega _\Lambda$ be the period domain of marked IHSMs of
$\Omega _\Lambda$ be the period domain of marked IHSMs of ![]() $K3^{[n]}$ type and let
$K3^{[n]}$ type and let ![]() $P:{\mathfrak {M}}_\Lambda ^0\rightarrow \Omega _\Lambda$ be the period map (see (5.1) for the definitions of
$P:{\mathfrak {M}}_\Lambda ^0\rightarrow \Omega _\Lambda$ be the period map (see (5.1) for the definitions of ![]() $\Omega _\Lambda$ and
$\Omega _\Lambda$ and ![]() $P$). Set
$P$). Set ![]() $\psi :=\eta _Y\circ f\circ \eta _X^{-1}\in O(\Lambda _{\mathbb {Q}})$ and choose a decomposition
$\psi :=\eta _Y\circ f\circ \eta _X^{-1}\in O(\Lambda _{\mathbb {Q}})$ and choose a decomposition ![]() $\psi =\psi _k\circ \cdots \circ \psi _1$ as in Step 1. The group
$\psi =\psi _k\circ \cdots \circ \psi _1$ as in Step 1. The group ![]() $O^+(\Lambda _{\mathbb {Q}})$ acts on
$O^+(\Lambda _{\mathbb {Q}})$ acts on ![]() $\Omega _\Lambda$ and
$\Omega _\Lambda$ and ![]() $\psi (P(X,\eta _X))=P(Y,\eta _Y)$. Set
$\psi (P(X,\eta _X))=P(Y,\eta _Y)$. Set ![]() $\ell _i:=(\psi _i\circ \cdots \circ \psi _1)(P(X,\eta _X))$,
$\ell _i:=(\psi _i\circ \cdots \circ \psi _1)(P(X,\eta _X))$, ![]() $0\leq i \leq k$. The surjectivity of the period map implies the existence of marked pairs
$0\leq i \leq k$. The surjectivity of the period map implies the existence of marked pairs ![]() $(X_i,\eta _i)\in {\mathfrak {M}}_\Lambda ^0$, such that
$(X_i,\eta _i)\in {\mathfrak {M}}_\Lambda ^0$, such that ![]() $P(X_i,\eta _i)=\ell _i$, where we choose
$P(X_i,\eta _i)=\ell _i$, where we choose ![]() $(X_0,\eta _0):=(X,\eta _X)$ and
$(X_0,\eta _0):=(X,\eta _X)$ and ![]() $(X_k,\eta _k):=(Y,\eta _Y)$. Set
$(X_k,\eta _k):=(Y,\eta _Y)$. Set ![]() $f_i:=\eta _i^{-1}\psi _i\circ \eta _{i-1}:H^2(X_{i-1},{\mathbb {Q}})\rightarrow H^2(X_i,{\mathbb {Q}})$. Then
$f_i:=\eta _i^{-1}\psi _i\circ \eta _{i-1}:H^2(X_{i-1},{\mathbb {Q}})\rightarrow H^2(X_i,{\mathbb {Q}})$. Then ![]() $f=f_k\circ \cdots \circ f_1$. If
$f=f_k\circ \cdots \circ f_1$. If ![]() $k=0$, so that
$k=0$, so that ![]() $\psi =\eta _Y\circ f\circ \eta _X^{-1}$ is the identity, then
$\psi =\eta _Y\circ f\circ \eta _X^{-1}$ is the identity, then ![]() $f=\eta _Y^{-1}\eta _X$ is a parallel-transport operator and a Hodge isometry, and so
$f=\eta _Y^{-1}\eta _X$ is a parallel-transport operator and a Hodge isometry, and so ![]() $f$ lifts to a morphism
$f$ lifts to a morphism ![]() $\phi \in {\rm Hom}_{{\mathcal {G}}_{an}}(X,Y)$ with
$\phi \in {\rm Hom}_{{\mathcal {G}}_{an}}(X,Y)$ with ![]() $\widetilde {H}_0(\phi )=f$, by Verbitsky's Torelli theorem (Theorem 5.2). It remains to prove that each
$\widetilde {H}_0(\phi )=f$, by Verbitsky's Torelli theorem (Theorem 5.2). It remains to prove that each ![]() $f_i$ belongs to the image of
$f_i$ belongs to the image of ![]() $\widetilde {H}_0$.
$\widetilde {H}_0$.
Step 3. The equivalence of derived categories ![]() $\Phi _{{\mathcal {U}}^{[n]}}:D^b(M^{[n]})\rightarrow D^b(S^{[n]})$ described previously yields a morphism in
$\Phi _{{\mathcal {U}}^{[n]}}:D^b(M^{[n]})\rightarrow D^b(S^{[n]})$ described previously yields a morphism in ![]() ${\mathcal {G}}^{[n]}_{an}$ which is mapped via
${\mathcal {G}}^{[n]}_{an}$ which is mapped via ![]() $\widetilde {H}_0$ to a Hodge isometry
$\widetilde {H}_0$ to a Hodge isometry ![]() $H^2(M^{[n]},{\mathbb {Q}})\rightarrow H^2(S^{[n]},{\mathbb {Q}})$ which, in turn, is simply the extensionFootnote 7 of the isometry
$H^2(M^{[n]},{\mathbb {Q}})\rightarrow H^2(S^{[n]},{\mathbb {Q}})$ which, in turn, is simply the extensionFootnote 7 of the isometry ![]() $H^2(M,{\mathbb {Q}})\rightarrow H^2(S,{\mathbb {Q}})$ associated to
$H^2(M,{\mathbb {Q}})\rightarrow H^2(S,{\mathbb {Q}})$ associated to ![]() $\Phi _{\mathcal {U}}$ (Corollary 7.3). The resulting Hodge isometry
$\Phi _{\mathcal {U}}$ (Corollary 7.3). The resulting Hodge isometry ![]() $H^2(M^{[n]},{\mathbb {Q}})\rightarrow H^2(S^{[n]},{\mathbb {Q}})$ is thus in the double orbit
$H^2(M^{[n]},{\mathbb {Q}})\rightarrow H^2(S^{[n]},{\mathbb {Q}})$ is thus in the double orbit ![]() ${\rm Mon}(\Lambda )(-\rho _{u}){\rm Mon}(\Lambda )$, where
${\rm Mon}(\Lambda )(-\rho _{u}){\rm Mon}(\Lambda )$, where ![]() $\rho _u$ is the reflection in a primitive integral class
$\rho _u$ is the reflection in a primitive integral class ![]() $u\in L$ with
$u\in L$ with ![]() $(u,u)>0$. The proof of Corollary 7.3 relies on [Reference MarkmanMar21a, Theorem 12.2] obtained independently by Beckman [Reference BeckmannBec23, Theorem 7.4]. All such double orbits are obtained that way by varying the Mukai vector of the two-dimensional moduli space
$(u,u)>0$. The proof of Corollary 7.3 relies on [Reference MarkmanMar21a, Theorem 12.2] obtained independently by Beckman [Reference BeckmannBec23, Theorem 7.4]. All such double orbits are obtained that way by varying the Mukai vector of the two-dimensional moduli space ![]() $M$, by [Reference BuskinBus19, Proposition 3.3]. We prove that every rational Hodge isometry
$M$, by [Reference BuskinBus19, Proposition 3.3]. We prove that every rational Hodge isometry ![]() $f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$, with
$f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$, with ![]() $f$ in a fixed double orbit of a reflection in
$f$ in a fixed double orbit of a reflection in ![]() $u\in L$ and preserving the orientation of the positive cones, is of the form
$u\in L$ and preserving the orientation of the positive cones, is of the form ![]() $\widetilde {H}_0([\kappa (E)\sqrt {td_{X\times Y}}]_*)$, for a pair
$\widetilde {H}_0([\kappa (E)\sqrt {td_{X\times Y}}]_*)$, for a pair ![]() $(X\times Y,E)$, which is a deformation of
$(X\times Y,E)$, which is a deformation of ![]() $(M^{[n]}\times S^{[n]},{\mathcal {U}}^{[n]})$ for a suitable choice of
$(M^{[n]}\times S^{[n]},{\mathcal {U}}^{[n]})$ for a suitable choice of ![]() $M$ (Corollary 8.5).
$M$ (Corollary 8.5).
2. Generators for the rational isometry group
Let ![]() $U$ be the rank-
$U$ be the rank-![]() $2$ lattice with basis
$2$ lattice with basis ![]() $\{e_1,e_2\}$ satisfying
$\{e_1,e_2\}$ satisfying ![]() $(e_i,e_i)=0$,
$(e_i,e_i)=0$, ![]() $i=1,2$, and
$i=1,2$, and ![]() $(e_1,e_2)=-1$. Let
$(e_1,e_2)=-1$. Let ![]() $L$ be an even unimodular lattice of signature
$L$ be an even unimodular lattice of signature ![]() $(3,s_-)$,
$(3,s_-)$, ![]() $s_-\geq 3$, which contains a sublattice isometric to the orthogonal direct sum of three copies of
$s_-\geq 3$, which contains a sublattice isometric to the orthogonal direct sum of three copies of ![]() $U$. Let the lattice
$U$. Let the lattice ![]() $\Lambda$ be the orthogonal direct sum
$\Lambda$ be the orthogonal direct sum ![]() $L\oplus {\mathbb {Z}}\delta$, where
$L\oplus {\mathbb {Z}}\delta$, where ![]() $(\delta,\delta )=-2d$ for some positive integer
$(\delta,\delta )=-2d$ for some positive integer ![]() $d$. Given a non-degenerate lattice
$d$. Given a non-degenerate lattice ![]() $M$, denote by
$M$, denote by ![]() $O^+(M)$ the subgroup of isometries of
$O^+(M)$ the subgroup of isometries of ![]() $M$ which preserve the orientation of the positive cone of
$M$ which preserve the orientation of the positive cone of ![]() $M\otimes _{\mathbb {Z}}{\mathbb {R}}$ (see [Reference MarkmanMar11, § 4]). Let
$M\otimes _{\mathbb {Z}}{\mathbb {R}}$ (see [Reference MarkmanMar11, § 4]). Let ![]() $\Gamma \subset O^+(\Lambda )$ be the subgroup which acts on the discriminant group
$\Gamma \subset O^+(\Lambda )$ be the subgroup which acts on the discriminant group ![]() $\Lambda ^*/\Lambda$ by multiplication by
$\Lambda ^*/\Lambda$ by multiplication by ![]() $\pm 1$. Set
$\pm 1$. Set ![]() $\Lambda _{\mathbb {Q}}:=\Lambda \otimes _{\mathbb {Z}}{\mathbb {Q}}$ and
$\Lambda _{\mathbb {Q}}:=\Lambda \otimes _{\mathbb {Z}}{\mathbb {Q}}$ and ![]() $L_{\mathbb {Q}}:=L\otimes _{\mathbb {Z}}{\mathbb {Q}}$. We regard
$L_{\mathbb {Q}}:=L\otimes _{\mathbb {Z}}{\mathbb {Q}}$. We regard ![]() $O(L_{\mathbb {Q}})$ as a subgroup of
$O(L_{\mathbb {Q}})$ as a subgroup of ![]() $O(\Lambda _{\mathbb {Q}})$ by extending each isometry so that it leaves
$O(\Lambda _{\mathbb {Q}})$ by extending each isometry so that it leaves ![]() $\delta$ invariant.
$\delta$ invariant.
Proposition 2.1 The group ![]() $O(\Lambda _{\mathbb {Q}})$ is generated by
$O(\Lambda _{\mathbb {Q}})$ is generated by ![]() $\Gamma$ and
$\Gamma$ and ![]() $O(L_{\mathbb {Q}})$.
$O(L_{\mathbb {Q}})$.
The following lemmas are needed for the proof of the above proposition.
Lemma 2.2 Let ![]() $\alpha =\lambda +k\delta$, where
$\alpha =\lambda +k\delta$, where ![]() $\lambda$ is a primitive class in
$\lambda$ is a primitive class in ![]() $L$ and
$L$ and ![]() $k\in {\mathbb {Z}}$. There exists an isometry
$k\in {\mathbb {Z}}$. There exists an isometry ![]() $\gamma \in \Gamma$, such that
$\gamma \in \Gamma$, such that ![]() $\gamma (\alpha )$ belongs to
$\gamma (\alpha )$ belongs to ![]() $L$.
$L$.
Proof. Let ![]() $\widetilde {\Lambda }$ be the orthogonal direct sum of
$\widetilde {\Lambda }$ be the orthogonal direct sum of ![]() $L$ and
$L$ and ![]() $U$ and let
$U$ and let ![]() $\iota :\Lambda \rightarrow \widetilde {\Lambda }$ be the isometric embedding restricting to the identity on
$\iota :\Lambda \rightarrow \widetilde {\Lambda }$ be the isometric embedding restricting to the identity on ![]() $L$ and sending
$L$ and sending ![]() $\delta$ to the element of the second direct summand
$\delta$ to the element of the second direct summand ![]() $U$ with coordinate
$U$ with coordinate ![]() $(1,d)$ in the basis
$(1,d)$ in the basis ![]() $\{e_1,e_2\}$. Let
$\{e_1,e_2\}$. Let ![]() $v\in \widetilde {\Lambda }$ be the element with coordinates
$v\in \widetilde {\Lambda }$ be the element with coordinates ![]() $(1,-d)$ of the second direct summand
$(1,-d)$ of the second direct summand ![]() $U$, so that
$U$, so that ![]() $(v,v)=2d$ and
$(v,v)=2d$ and ![]() $v^\perp =\iota (\Lambda )$, where
$v^\perp =\iota (\Lambda )$, where ![]() $v^\perp$ is the co-rank-
$v^\perp$ is the co-rank-![]() $1$ sublattice of
$1$ sublattice of ![]() $\widetilde {\Lambda }$ orthogonal to
$\widetilde {\Lambda }$ orthogonal to ![]() $v$. The sublattice
$v$. The sublattice ![]() $\Sigma _1:={\rm span}_{\mathbb {Z}}\{\iota (\alpha ),v\}$ of
$\Sigma _1:={\rm span}_{\mathbb {Z}}\{\iota (\alpha ),v\}$ of ![]() $\widetilde {\Lambda }$ is saturated. Indeed, if
$\widetilde {\Lambda }$ is saturated. Indeed, if ![]() $a,b\in {\mathbb {Q}}$ and
$a,b\in {\mathbb {Q}}$ and ![]() $a\iota (\alpha )+bv=a\lambda +(ak+b)e_1+(adk-bd)e_2$ is an integral class of
$a\iota (\alpha )+bv=a\lambda +(ak+b)e_1+(adk-bd)e_2$ is an integral class of ![]() $\widetilde {\Lambda }$, then
$\widetilde {\Lambda }$, then ![]() $a$ must be an integer, since
$a$ must be an integer, since ![]() $\lambda$ is primitive, hence
$\lambda$ is primitive, hence ![]() $b$ must be an integer as well. Let
$b$ must be an integer as well. Let ![]() $\beta \in L$ be a primitive class satisfying
$\beta \in L$ be a primitive class satisfying ![]() $(\beta,\beta )=(\alpha,\alpha )$. The sublattice
$(\beta,\beta )=(\alpha,\alpha )$. The sublattice ![]() $\Sigma _2:={\rm span}_{\mathbb {Z}}\{\beta,v\}$ is saturated in
$\Sigma _2:={\rm span}_{\mathbb {Z}}\{\beta,v\}$ is saturated in ![]() $\widetilde {\Lambda }$ and is isometric to
$\widetilde {\Lambda }$ and is isometric to ![]() $\Sigma _1$. There exists an isometry
$\Sigma _1$. There exists an isometry ![]() $g\in O(\widetilde {\Lambda })$ satisfying
$g\in O(\widetilde {\Lambda })$ satisfying ![]() $g(v)=v$ and
$g(v)=v$ and ![]() $g(\iota (\alpha ))=\beta$, by results of Nikulin [Reference NikulinNik87, Reference MarkmanMar08, Lemma 8.1]. Set
$g(\iota (\alpha ))=\beta$, by results of Nikulin [Reference NikulinNik87, Reference MarkmanMar08, Lemma 8.1]. Set ![]() $\tilde {\gamma }:=g$, if
$\tilde {\gamma }:=g$, if ![]() $g$ belongs to
$g$ belongs to ![]() $O^+(\widetilde {\Lambda }),$ and
$O^+(\widetilde {\Lambda }),$ and ![]() $\tilde {\gamma }:=-g$ otherwise. Then
$\tilde {\gamma }:=-g$ otherwise. Then ![]() $\tilde {\gamma }\circ \iota =\iota \circ \gamma$, for a unique element
$\tilde {\gamma }\circ \iota =\iota \circ \gamma$, for a unique element ![]() $\gamma \in \Gamma$, by [Reference MarkmanMar08, Theorem 1.6 and Lemma 4.2], and
$\gamma \in \Gamma$, by [Reference MarkmanMar08, Theorem 1.6 and Lemma 4.2], and ![]() $\gamma (\alpha )$ belongs to
$\gamma (\alpha )$ belongs to ![]() $L$.
$L$.
Let ![]() $G$ be the subgroup of
$G$ be the subgroup of ![]() $O(\Lambda _{\mathbb {Q}})$ generated by
$O(\Lambda _{\mathbb {Q}})$ generated by ![]() $\Gamma$ and
$\Gamma$ and ![]() $O(L_{\mathbb {Q}})$.
$O(L_{\mathbb {Q}})$.
Lemma 2.3 Let ![]() $\lambda \in L_{\mathbb {Q}}$ and
$\lambda \in L_{\mathbb {Q}}$ and ![]() $t\in {\mathbb {Q}}$ and assume that
$t\in {\mathbb {Q}}$ and assume that ![]() $(\lambda,\lambda )\neq 0$. There exists an isometry
$(\lambda,\lambda )\neq 0$. There exists an isometry ![]() $g\in G$, such that
$g\in G$, such that ![]() $g(\lambda +t\delta )$ belongs to
$g(\lambda +t\delta )$ belongs to ![]() $L_{\mathbb {Q}}$.
$L_{\mathbb {Q}}$.
Proof. Let ![]() $q\in {\mathbb {Q}}^\times$ be such that
$q\in {\mathbb {Q}}^\times$ be such that ![]() $q(\lambda +t\delta )$ is integral. Choose an integral and primitive class
$q(\lambda +t\delta )$ is integral. Choose an integral and primitive class ![]() $\lambda '\in L$ satisfying
$\lambda '\in L$ satisfying ![]() $(\lambda ',\lambda ')=q^2(\lambda,\lambda )$. There exists an isometry
$(\lambda ',\lambda ')=q^2(\lambda,\lambda )$. There exists an isometry ![]() $f\in O(L_{\mathbb {Q}})$, such that
$f\in O(L_{\mathbb {Q}})$, such that ![]() $\lambda '=f(q\lambda )$, by [Reference GersteinGer08, Proposition 2.35]. Then
$\lambda '=f(q\lambda )$, by [Reference GersteinGer08, Proposition 2.35]. Then ![]() $f(q(\lambda +t\delta ))=\lambda '+qt\delta$ is integral and there exists
$f(q(\lambda +t\delta ))=\lambda '+qt\delta$ is integral and there exists ![]() $h\in \Gamma$, such that
$h\in \Gamma$, such that ![]() $h(f(q(\lambda +t\delta )))$ is a primitive class in
$h(f(q(\lambda +t\delta )))$ is a primitive class in ![]() $L$, by Lemma 2.2. The statement follows, since
$L$, by Lemma 2.2. The statement follows, since ![]() $h\circ f$ belongs to
$h\circ f$ belongs to ![]() $G$.
$G$.
Proof Proof of Proposition 2.1
Choose ![]() $u\in L$ satisfying
$u\in L$ satisfying ![]() $(u,u)=2d+2$. Then
$(u,u)=2d+2$. Then ![]() $(u+\delta,u+\delta )=2$. Let
$(u+\delta,u+\delta )=2$. Let ![]() $\rho _{u+\delta }$ be the reflection of
$\rho _{u+\delta }$ be the reflection of ![]() $\Lambda$ in
$\Lambda$ in ![]() $(u+\delta )^\perp$
$(u+\delta )^\perp$
Then ![]() $\rho _{u+\delta }(\delta )=(2d)u+(1+2d)\delta$. Furthermore,
$\rho _{u+\delta }(\delta )=(2d)u+(1+2d)\delta$. Furthermore, ![]() $-\rho _{u+\delta }$ belongs to
$-\rho _{u+\delta }$ belongs to ![]() $\Gamma$. There exists
$\Gamma$. There exists ![]() $g_1\in G$, such that
$g_1\in G$, such that ![]() $g_1(-\rho _{u+\delta }(\delta ))$ belongs to
$g_1(-\rho _{u+\delta }(\delta ))$ belongs to ![]() $L_{\mathbb {Q}}$, by Lemma 2.3.
$L_{\mathbb {Q}}$, by Lemma 2.3.
Let ![]() $\phi$ be an isometry in
$\phi$ be an isometry in ![]() $O(\Lambda _{\mathbb {Q}})$. Write
$O(\Lambda _{\mathbb {Q}})$. Write ![]() $\phi (\delta )=\lambda +t\delta$. If
$\phi (\delta )=\lambda +t\delta$. If ![]() $(\lambda,\lambda )=0$ choose
$(\lambda,\lambda )=0$ choose ![]() $u\in L$, such that
$u\in L$, such that ![]() $(u,\lambda )=0$ and
$(u,\lambda )=0$ and ![]() $(u,u)=2d+2$. Then
$(u,u)=2d+2$. Then ![]() $\rho _{u+\delta }(\phi (\delta ))=\lambda +(2d)u+(1+2d)\delta$ and the self-intersection
$\rho _{u+\delta }(\phi (\delta ))=\lambda +(2d)u+(1+2d)\delta$ and the self-intersection ![]() $(\lambda +(2d)u,\lambda +(2d)u)=4d^2(2d+2)$ is non-zero. Now,
$(\lambda +(2d)u,\lambda +(2d)u)=4d^2(2d+2)$ is non-zero. Now, ![]() $\phi$ belongs to
$\phi$ belongs to ![]() $G$, if and only if
$G$, if and only if ![]() $-\rho _{u+\delta }\phi$ belongs to
$-\rho _{u+\delta }\phi$ belongs to ![]() $G$. Hence, we may assume that
$G$. Hence, we may assume that ![]() $(\lambda,\lambda )\neq 0$. Then there exists
$(\lambda,\lambda )\neq 0$. Then there exists ![]() $g_2\in G$ such that
$g_2\in G$ such that ![]() $(g_2\circ \phi )(\delta )$ belongs to
$(g_2\circ \phi )(\delta )$ belongs to ![]() $L_{\mathbb {Q}}$, by Lemma 2.3. There exists
$L_{\mathbb {Q}}$, by Lemma 2.3. There exists ![]() $h\in O(L_{\mathbb {Q}})$, such that
$h\in O(L_{\mathbb {Q}})$, such that ![]() $h(g_2(\phi (\delta )))=g_1(-\rho _{u+\delta }(\delta ))$, by [Reference GersteinGer08, Proposition 2.35]. Hence,
$h(g_2(\phi (\delta )))=g_1(-\rho _{u+\delta }(\delta ))$, by [Reference GersteinGer08, Proposition 2.35]. Hence, ![]() $(-\rho _{u+\delta }g_1^{-1}hg_2\phi )(\delta )=\delta$, and so
$(-\rho _{u+\delta }g_1^{-1}hg_2\phi )(\delta )=\delta$, and so ![]() $-\rho _{u+\delta }g_1^{-1}hg_2\phi$ belongs to
$-\rho _{u+\delta }g_1^{-1}hg_2\phi$ belongs to ![]() $O(L_{\mathbb {Q}})$. Hence,
$O(L_{\mathbb {Q}})$. Hence, ![]() $\phi$ belongs to
$\phi$ belongs to ![]() $G$.
$G$.
Lemma 2.4 The group ![]() $O(L_{\mathbb {Q}})$ is generated by
$O(L_{\mathbb {Q}})$ is generated by ![]() $O(L)$ and reflections
$O(L)$ and reflections ![]() $\rho _u$ in
$\rho _u$ in ![]() $u^\perp$, for
$u^\perp$, for ![]() $u\in L$ satisfying
$u\in L$ satisfying ![]() $(u,u)>0$.
$(u,u)>0$.
Proof. The group ![]() $O(L_{\mathbb {Q}})$ is generated by reflections
$O(L_{\mathbb {Q}})$ is generated by reflections ![]() $\rho _u$, with
$\rho _u$, with ![]() $(u,u)\neq 0$, by [Reference GersteinGer08, Proposition 2.36]. The isometry group
$(u,u)\neq 0$, by [Reference GersteinGer08, Proposition 2.36]. The isometry group ![]() $O(L)$ acts transitively on the set
$O(L)$ acts transitively on the set ![]() $\{u \ : \ u \ \mbox {is} \mbox {primitive and} \ (u,u)=2d\}$,
$\{u \ : \ u \ \mbox {is} \mbox {primitive and} \ (u,u)=2d\}$, ![]() $d\in {\mathbb {Z}}$, by [Reference NikulinNik87, Theorem 1.14.4]. Consider the above basis
$d\in {\mathbb {Z}}$, by [Reference NikulinNik87, Theorem 1.14.4]. Consider the above basis ![]() $\{e_1,e_2\}$ of
$\{e_1,e_2\}$ of ![]() $U$ and observe that
$U$ and observe that ![]() $\rho _{e_1-de_2}\rho _{e_1+de_2}$ is minus the identity of
$\rho _{e_1-de_2}\rho _{e_1+de_2}$ is minus the identity of ![]() $U$. Hence, for every element
$U$. Hence, for every element ![]() $u\in L$ with
$u\in L$ with ![]() $(u,u)<0$, there exists an element
$(u,u)<0$, there exists an element ![]() $w\in L$ with
$w\in L$ with ![]() $(w,w)=-(u,u)$, such that
$(w,w)=-(u,u)$, such that ![]() $\rho _u\rho _w$ belongs to
$\rho _u\rho _w$ belongs to ![]() $O(L)$. Thus, it sufficed to consider reflections
$O(L)$. Thus, it sufficed to consider reflections ![]() $\rho _u$ with
$\rho _u$ with ![]() $(u,u)>0$.
$(u,u)>0$.
Corollary 2.5 Let ![]() $\phi$ be an isometry in
$\phi$ be an isometry in ![]() $O^+(\Lambda _{\mathbb {Q}})$. There exist a positive integer
$O^+(\Lambda _{\mathbb {Q}})$. There exist a positive integer ![]() $k$, integral elements
$k$, integral elements ![]() $u_i\in L$ satisfying
$u_i\in L$ satisfying ![]() $(u_i,u_i)\geq 2$,
$(u_i,u_i)\geq 2$, ![]() $1\leq i \leq k$, and elements
$1\leq i \leq k$, and elements ![]() $\gamma _i\in \Gamma$,
$\gamma _i\in \Gamma$, ![]() $0\leq i \leq k$, such that
$0\leq i \leq k$, such that
where ![]() $\rho _{u_i}(x)=x- ({2(u_i,x)}/{(u_i,u_i)})u_i$ is the reflection of
$\rho _{u_i}(x)=x- ({2(u_i,x)}/{(u_i,u_i)})u_i$ is the reflection of ![]() $\Lambda _{\mathbb {Q}}$ in
$\Lambda _{\mathbb {Q}}$ in ![]() $u_i^\perp$.
$u_i^\perp$.
Proof. This follows immediately from Proposition 2.1, Lemma 2.4, the fact that ![]() $O^+(L)$ is contained in
$O^+(L)$ is contained in ![]() $\Gamma$, and the fact that
$\Gamma$, and the fact that ![]() $-\rho _{u_i}$ belongs to
$-\rho _{u_i}$ belongs to ![]() $O^+(\Lambda _{\mathbb {Q}})$ if
$O^+(\Lambda _{\mathbb {Q}})$ if ![]() $(u_i,u_i)>0$, since the signature of
$(u_i,u_i)>0$, since the signature of ![]() $\Lambda$ is
$\Lambda$ is ![]() $(3,1+s_-)$ and
$(3,1+s_-)$ and ![]() $3$ is odd.
$3$ is odd.
Remark 2.6 Note that in Corollary 2.5 we can require ![]() $\gamma _i$ to belong to any subgroup
$\gamma _i$ to belong to any subgroup ![]() $\Gamma _0$ of
$\Gamma _0$ of ![]() $\Gamma$, such that
$\Gamma$, such that ![]() $\Gamma _0$ and
$\Gamma _0$ and ![]() $O^+(L)$ generate
$O^+(L)$ generate ![]() $\Gamma$. When
$\Gamma$. When ![]() $L$ is the
$L$ is the ![]() $K3$ lattice, the group
$K3$ lattice, the group ![]() $\Gamma$ is the monodromy group of IHSMs of
$\Gamma$ is the monodromy group of IHSMs of ![]() $K3^{[d+1]}$ deformation type [Reference MarkmanMar08, Theorem 1.6]. If
$K3^{[d+1]}$ deformation type [Reference MarkmanMar08, Theorem 1.6]. If ![]() $L=U^{\oplus 3}$, the monodromy of generalized Kummer varieties of dimension
$L=U^{\oplus 3}$, the monodromy of generalized Kummer varieties of dimension ![]() $2d-2$, for
$2d-2$, for ![]() $d\geq 3$, is the following index
$d\geq 3$, is the following index ![]() $2$ subgroup
$2$ subgroup ![]() $\Gamma _0$ of
$\Gamma _0$ of ![]() $\Gamma$. Here
$\Gamma$. Here ![]() $\Gamma$ acts on the discriminant group
$\Gamma$ acts on the discriminant group ![]() $\Lambda ^*/\Lambda$ by a character
$\Lambda ^*/\Lambda$ by a character ![]() $\xi :\Gamma \rightarrow \{\pm 1\}$, by the definition of
$\xi :\Gamma \rightarrow \{\pm 1\}$, by the definition of ![]() $\Gamma$. Let
$\Gamma$. Let ![]() $\det :\Gamma \rightarrow \{\pm 1\}$ be the determinant character. Then
$\det :\Gamma \rightarrow \{\pm 1\}$ be the determinant character. Then ![]() $\Gamma _0$ is the kernel of the product character
$\Gamma _0$ is the kernel of the product character ![]() $\det \cdot \xi :\Gamma \rightarrow \{\pm 1\}$, by [Reference MarkmanMar23, Theorem 1.4]. The character
$\det \cdot \xi :\Gamma \rightarrow \{\pm 1\}$, by [Reference MarkmanMar23, Theorem 1.4]. The character ![]() $\det \cdot \xi$ has value
$\det \cdot \xi$ has value ![]() $-1$ on a reflection
$-1$ on a reflection ![]() $\rho _\omega \in O^+(L)$ in a class
$\rho _\omega \in O^+(L)$ in a class ![]() $w \in L$ with
$w \in L$ with ![]() $(w,w)=-2$, and so
$(w,w)=-2$, and so ![]() $\Gamma _0$ and
$\Gamma _0$ and ![]() $O^+(L)$ generate
$O^+(L)$ generate ![]() $\Gamma$.
$\Gamma$.
3. The LLV Lie algebra
In § 3.1 we recall the LLV Lie algebra ![]() ${\mathfrak g}_X$ and its action on the cohomology of a
${\mathfrak g}_X$ and its action on the cohomology of a ![]() $2n$-dimensional IHSM
$2n$-dimensional IHSM ![]() $X$. We review the
$X$. We review the ![]() ${\mathfrak g}_X$-equivariant isomorphism between the subring
${\mathfrak g}_X$-equivariant isomorphism between the subring ![]() $SH^*(X,{\mathbb {Q}})$ of
$SH^*(X,{\mathbb {Q}})$ of ![]() $H^*(X,{\mathbb {Q}})$ generated by
$H^*(X,{\mathbb {Q}})$ generated by ![]() $H^2(X,{\mathbb {Q}})$ and the
$H^2(X,{\mathbb {Q}})$ and the ![]() $n$th symmetric power of the LLV lattice
$n$th symmetric power of the LLV lattice ![]() $\widetilde {H}(X,{\mathbb {Q}})$. In § 3.2 we recall Taelman's definition of the functor
$\widetilde {H}(X,{\mathbb {Q}})$. In § 3.2 we recall Taelman's definition of the functor ![]() $\widetilde {H}:{\mathcal {G}}\rightarrow \widetilde {{\mathcal {G}}}$, mentioned in (1.4), sending equivalences of derived categories to isometries of LLV lattices. Given a morphism
$\widetilde {H}:{\mathcal {G}}\rightarrow \widetilde {{\mathcal {G}}}$, mentioned in (1.4), sending equivalences of derived categories to isometries of LLV lattices. Given a morphism ![]() $\phi \in {\rm Hom}_{\mathcal {G}}((X,\epsilon _X),(Y,\epsilon _Y))$, which is degree preserving up to sign, we relate in Lemmas 3.6 and 3.7 the restrictions of
$\phi \in {\rm Hom}_{\mathcal {G}}((X,\epsilon _X),(Y,\epsilon _Y))$, which is degree preserving up to sign, we relate in Lemmas 3.6 and 3.7 the restrictions of ![]() $\phi$ and of
$\phi$ and of ![]() $\widetilde {H}(\phi )$ to
$\widetilde {H}(\phi )$ to ![]() $H^2(X,{\mathbb {Q}})$.
$H^2(X,{\mathbb {Q}})$.
A note about orientations: we take pains to carefully keep track of the sign of ![]() $\widetilde {H}(\phi )$, for a morphism
$\widetilde {H}(\phi )$, for a morphism ![]() $\phi \in {\rm Hom}_{\mathcal {G}}((X,\epsilon _X),(Y,\epsilon _Y))$. The sign depends in a subtle way on the orientations
$\phi \in {\rm Hom}_{\mathcal {G}}((X,\epsilon _X),(Y,\epsilon _Y))$. The sign depends in a subtle way on the orientations ![]() $\epsilon _X,\epsilon _Y$. We use the functor
$\epsilon _X,\epsilon _Y$. We use the functor ![]() $\widetilde {H}:{\mathcal {G}}\rightarrow \widetilde {{\mathcal {G}}}$ in order to define the functor
$\widetilde {H}:{\mathcal {G}}\rightarrow \widetilde {{\mathcal {G}}}$ in order to define the functor ![]() $\widetilde {H}_0:{\mathcal {G}}_{an}\rightarrow {\mathcal {H}dg}$ in (1.5) (see also (5.8)). The sign of
$\widetilde {H}_0:{\mathcal {G}}_{an}\rightarrow {\mathcal {H}dg}$ in (1.5) (see also (5.8)). The sign of ![]() $\widetilde {H}_0(\phi )$ is independent of the sign of
$\widetilde {H}_0(\phi )$ is independent of the sign of ![]() $\widetilde {H}(\phi )$, so the functor
$\widetilde {H}(\phi )$, so the functor ![]() $\widetilde {H}_0$ is independent of the orientations. The proof of Theorems 1.1 and 1.4 depends only on
$\widetilde {H}_0$ is independent of the orientations. The proof of Theorems 1.1 and 1.4 depends only on ![]() $\widetilde {H}_0$. The reader who is only interested in that proof may ignore the orientations of objects in
$\widetilde {H}_0$. The reader who is only interested in that proof may ignore the orientations of objects in ![]() ${\mathcal {G}}$ and redefine morphisms in
${\mathcal {G}}$ and redefine morphisms in ![]() $\widetilde {{\mathcal {G}}}$ as pairs
$\widetilde {{\mathcal {G}}}$ as pairs ![]() $\{\pm g\}$ of an isometry
$\{\pm g\}$ of an isometry ![]() $g:\widetilde {H}(X,{\mathbb {Q}})\rightarrow \widetilde {H}(Y,{\mathbb {Q}})$ and its negative. The resulting coarser version of the functor
$g:\widetilde {H}(X,{\mathbb {Q}})\rightarrow \widetilde {H}(Y,{\mathbb {Q}})$ and its negative. The resulting coarser version of the functor ![]() $\widetilde {H}$ is sufficient to define
$\widetilde {H}$ is sufficient to define ![]() $\widetilde {H}_0$.
$\widetilde {H}_0$.
3.1 The subring generated by  $H^2(X,{\mathbb {Q}})$
$H^2(X,{\mathbb {Q}})$
Let ![]() $X$ be a
$X$ be a ![]() $2n$-dimensional IHSM. Given a class
$2n$-dimensional IHSM. Given a class ![]() $\lambda \in H^2(X,{\mathbb {Q}})$ denote by
$\lambda \in H^2(X,{\mathbb {Q}})$ denote by ![]() $e_\lambda :H^*(X,{\mathbb {Q}})\rightarrow H^*(X,{\mathbb {Q}})$ the endomorphism given by the cup product with
$e_\lambda :H^*(X,{\mathbb {Q}})\rightarrow H^*(X,{\mathbb {Q}})$ the endomorphism given by the cup product with ![]() $\lambda$. The grading operator
$\lambda$. The grading operator
acts on ![]() $H^k(X,{\mathbb {Q}})[2n]=H^{2n+k}(X,{\mathbb {Q}})$,
$H^k(X,{\mathbb {Q}})[2n]=H^{2n+k}(X,{\mathbb {Q}})$, ![]() $-2n\leq k\leq 2n$, via multiplication by
$-2n\leq k\leq 2n$, via multiplication by ![]() $k$. A triple
$k$. A triple ![]() $(e,h,f)$ of endomorphisms of
$(e,h,f)$ of endomorphisms of ![]() $H^*(X,{\mathbb {Q}})$ is called an
$H^*(X,{\mathbb {Q}})$ is called an ![]() ${\mathfrak sl}_2$-triple, if
${\mathfrak sl}_2$-triple, if
Given ![]() $e$, if
$e$, if ![]() $f$ exists, then it is the unique endomorphism completing the pair
$f$ exists, then it is the unique endomorphism completing the pair ![]() $(e,h)$ to an
$(e,h)$ to an ![]() ${\mathfrak sl}_2$-triple. The LLV Lie algebra
${\mathfrak sl}_2$-triple. The LLV Lie algebra ![]() ${\mathfrak g}_X\subset {\rm End}(H^*(X,{\mathbb {Q}}))$ is the Lie algebra generated by all
${\mathfrak g}_X\subset {\rm End}(H^*(X,{\mathbb {Q}}))$ is the Lie algebra generated by all ![]() ${\mathfrak sl}_2$-triples
${\mathfrak sl}_2$-triples ![]() $(e_\lambda,h,f_\lambda )$,
$(e_\lambda,h,f_\lambda )$, ![]() $\lambda \in H^2(X,{\mathbb {Q}})$.
$\lambda \in H^2(X,{\mathbb {Q}})$.
Denote by ![]() $S_{[n]}\widetilde {H}(X,{\mathbb {Q}})$ the subspace of
$S_{[n]}\widetilde {H}(X,{\mathbb {Q}})$ the subspace of ![]() ${\rm Sym}^n(\widetilde {H}(X,{\mathbb {Q}}))$ generated by
${\rm Sym}^n(\widetilde {H}(X,{\mathbb {Q}}))$ generated by ![]() $n$th powers of isotropic elements of
$n$th powers of isotropic elements of ![]() $\widetilde {H}(X,{\mathbb {Q}})$. Verbitsky proved that the subring
$\widetilde {H}(X,{\mathbb {Q}})$. Verbitsky proved that the subring ![]() $SH^*(X,{\mathbb {Q}})$ is an irreducible
$SH^*(X,{\mathbb {Q}})$ is an irreducible ![]() ${\mathfrak g}_X$-submodule of
${\mathfrak g}_X$-submodule of ![]() $H^*(X,{\mathbb {Q}})$, appearing with multiplicity one, there exists a Lie algebra isomorphism
$H^*(X,{\mathbb {Q}})$, appearing with multiplicity one, there exists a Lie algebra isomorphism
and there exists a unique graded isomorphism of ![]() ${\mathfrak so}(\widetilde {H}(X,{\mathbb {Q}}))$-modules
${\mathfrak so}(\widetilde {H}(X,{\mathbb {Q}}))$-modules
satisfying ![]() $\Psi (1)= {\alpha ^n}/{n!}$, where the
$\Psi (1)= {\alpha ^n}/{n!}$, where the ![]() ${\mathfrak so}(\widetilde {H}(X,{\mathbb {Q}}))$-module structure of
${\mathfrak so}(\widetilde {H}(X,{\mathbb {Q}}))$-module structure of ![]() $SH^*(X,{\mathbb {Q}})[2n]$ is via
$SH^*(X,{\mathbb {Q}})[2n]$ is via ![]() $\dot {\rho }$ (see [Reference TaelmanTae23, Proposition 3.5]). The pairing on
$\dot {\rho }$ (see [Reference TaelmanTae23, Proposition 3.5]). The pairing on ![]() $\widetilde {H}(X,{\mathbb {Q}})$ induces a pairing
$\widetilde {H}(X,{\mathbb {Q}})$ induces a pairing ![]() $b_{[n]}$ on
$b_{[n]}$ on ![]() $S_{[n]}\widetilde {H}(X,{\mathbb {Q}})$, the Mukai pairing on
$S_{[n]}\widetilde {H}(X,{\mathbb {Q}})$, the Mukai pairing on ![]() $H^*(X,{\mathbb {Q}})$ restricts to a pairing
$H^*(X,{\mathbb {Q}})$ restricts to a pairing ![]() $b_{SH}$ on
$b_{SH}$ on ![]() $SH^*(X,{\mathbb {Q}})$, and
$SH^*(X,{\mathbb {Q}})$, and ![]() $c_X b_{[n]}(\Psi (x),\Psi (y))=b_{SH}(x,y),$ where
$c_X b_{[n]}(\Psi (x),\Psi (y))=b_{SH}(x,y),$ where ![]() $c_X$ is the Fujiki constant [Reference TaelmanTae23, Proposition 3.8].
$c_X$ is the Fujiki constant [Reference TaelmanTae23, Proposition 3.8].
The following is the explicit description of the isomorphism ![]() $\Psi$ (see [Reference TaelmanTae23, Proposition 3.5]). Given
$\Psi$ (see [Reference TaelmanTae23, Proposition 3.5]). Given ![]() $\lambda \in H^2(X,{\mathbb {Q}})$, denote by
$\lambda \in H^2(X,{\mathbb {Q}})$, denote by
also the endomorphism of ![]() $\widetilde {H}(X,{\mathbb {Q}})$ sending
$\widetilde {H}(X,{\mathbb {Q}})$ sending ![]() $\alpha$ to
$\alpha$ to ![]() $\lambda$, annihilating
$\lambda$, annihilating ![]() $\beta$, and sending
$\beta$, and sending ![]() $\lambda '\in H^2(X,{\mathbb {Q}})$ to
$\lambda '\in H^2(X,{\mathbb {Q}})$ to ![]() $(\lambda,\lambda ')\beta$. Extend
$(\lambda,\lambda ')\beta$. Extend ![]() $e_\lambda$ as an endomorphism of
$e_\lambda$ as an endomorphism of ![]() ${\rm Sym}^n\widetilde {H}(X,{\mathbb {Q}})$ via the product rule, so that
${\rm Sym}^n\widetilde {H}(X,{\mathbb {Q}})$ via the product rule, so that ![]() $e_\lambda (x_1\cdots x_n)=\sum _{i=1}^n x_1\cdots e_\lambda (x_i) \cdots x_n.$ Then
$e_\lambda (x_1\cdots x_n)=\sum _{i=1}^n x_1\cdots e_\lambda (x_i) \cdots x_n.$ Then
Let
be the grading operator multiplying ![]() $\alpha$ by
$\alpha$ by ![]() $-2$,
$-2$, ![]() $\beta$ by
$\beta$ by ![]() $2$, and
$2$, and ![]() $H^2(X,{\mathbb {Q}})$ by
$H^2(X,{\mathbb {Q}})$ by ![]() $0$.
$0$.
3.2 The functor  $\widetilde {H}$
$\widetilde {H}$
Let ![]() $\phi$ be a morphism in
$\phi$ be a morphism in ![]() ${\rm Hom}_{\mathcal {G}}((X,\epsilon ),(Y,\epsilon '))$, where
${\rm Hom}_{\mathcal {G}}((X,\epsilon ),(Y,\epsilon '))$, where ![]() ${\mathcal {G}}$ is the groupoid (1.1). Then
${\mathcal {G}}$ is the groupoid (1.1). Then ![]() $\phi$ is in particular an isometry
$\phi$ is in particular an isometry ![]() $\phi :H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ with respect to the Mukai pairing and we denote by
$\phi :H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ with respect to the Mukai pairing and we denote by
the Lie algebra isomorphism given by ![]() $Ad_\phi (\xi )=\phi \xi \phi ^{-1}$. Then
$Ad_\phi (\xi )=\phi \xi \phi ^{-1}$. Then ![]() $Ad_\phi$ restricts to a Lie algebra isomorphism from
$Ad_\phi$ restricts to a Lie algebra isomorphism from ![]() ${\mathfrak g}_X$ onto
${\mathfrak g}_X$ onto ![]() ${\mathfrak g}_Y$, by [Reference TaelmanTae23, Theorem A]. Hence,
${\mathfrak g}_Y$, by [Reference TaelmanTae23, Theorem A]. Hence, ![]() $\phi$ restricts to an isometry
$\phi$ restricts to an isometry ![]() $\phi _{\mid _{}}:SH^*(X,{\mathbb {Q}})\rightarrow SH^*(Y,{\mathbb {Q}})$. Consequently, when
$\phi _{\mid _{}}:SH^*(X,{\mathbb {Q}})\rightarrow SH^*(Y,{\mathbb {Q}})$. Consequently, when ![]() $X$ and
$X$ and ![]() $Y$ are deformation equivalent, so that
$Y$ are deformation equivalent, so that ![]() $c_X=c_Y$, then
$c_X=c_Y$, then ![]() $\Psi _Y\circ \phi _{\mid _{}}\circ \Psi _X^{-1}:S_{[n]}\widetilde {H}(X,{\mathbb {Q}})\rightarrow S_{[n]}\widetilde {H}(Y,{\mathbb {Q}})$ is an isometry, which conjugates
$\Psi _Y\circ \phi _{\mid _{}}\circ \Psi _X^{-1}:S_{[n]}\widetilde {H}(X,{\mathbb {Q}})\rightarrow S_{[n]}\widetilde {H}(Y,{\mathbb {Q}})$ is an isometry, which conjugates ![]() $S_{[n]}{\mathfrak so}(\widetilde {H}(X,{\mathbb {Q}}))$ to
$S_{[n]}{\mathfrak so}(\widetilde {H}(X,{\mathbb {Q}}))$ to ![]() $S_{[n]}{\mathfrak so}(\widetilde {H}(Y,{\mathbb {Q}}))$, where
$S_{[n]}{\mathfrak so}(\widetilde {H}(Y,{\mathbb {Q}}))$, where ![]() $S_{[n]}{\mathfrak so}(\widetilde {H}(X,{\mathbb {Q}}))$ is the image of
$S_{[n]}{\mathfrak so}(\widetilde {H}(X,{\mathbb {Q}}))$ is the image of ![]() ${\mathfrak so}(\widetilde {H}(X,{\mathbb {Q}}))$ in
${\mathfrak so}(\widetilde {H}(X,{\mathbb {Q}}))$ in ![]() ${\rm End}(S_{[n]}\widetilde {H}(X,{\mathbb {Q}}))$.
${\rm End}(S_{[n]}\widetilde {H}(X,{\mathbb {Q}}))$.
Given an isomorphism ![]() $f:V_1\rightarrow V_2$ of oriented vector spaces, we set
$f:V_1\rightarrow V_2$ of oriented vector spaces, we set ![]() $\det (f)=1$, if
$\det (f)=1$, if ![]() $f$ is orientation preserving and
$f$ is orientation preserving and ![]() $\det (f)=-1$ otherwise.
$\det (f)=-1$ otherwise.
Proposition 3.1 [Reference TaelmanTae23, Proposition 4.4, Theorem 4.10, and Theorem 4.11]
Let ![]() $V_1$ and
$V_1$ and ![]() $V_2$ be
$V_2$ be ![]() $d$-dimensional vector spaces over
$d$-dimensional vector spaces over ![]() ${\mathbb {Q}}$ with non-degenerate bilinear parings and
${\mathbb {Q}}$ with non-degenerate bilinear parings and ![]() $\phi :S_{[n]}V_1\rightarrow S_{[n]}V_2$ an isometry, such that
$\phi :S_{[n]}V_1\rightarrow S_{[n]}V_2$ an isometry, such that ![]() $\phi (S_{[n]}{\mathfrak so}(V_1))\phi ^{-1}=S_{[n]}{\mathfrak so}(V_2)$. If
$\phi (S_{[n]}{\mathfrak so}(V_1))\phi ^{-1}=S_{[n]}{\mathfrak so}(V_2)$. If ![]() $n$ is even assume that
$n$ is even assume that ![]() $d$ is odd and choose an orientation for each of
$d$ is odd and choose an orientation for each of ![]() $V_1$ and
$V_1$ and ![]() $V_2$. Then there exists a unique isometry
$V_2$. Then there exists a unique isometry ![]() $\widetilde {H}(\phi ):V_1\rightarrow V_2$, such that the restriction
$\widetilde {H}(\phi ):V_1\rightarrow V_2$, such that the restriction ![]() $S_{[n]}(\widetilde {H}(\phi ))$ of its
$S_{[n]}(\widetilde {H}(\phi ))$ of its ![]() $n$-symmetric power to
$n$-symmetric power to ![]() $S_{[n]}V_1$ satisfies
$S_{[n]}V_1$ satisfies ![]() $S_{[n]}(\widetilde {H}(\phi ))=\phi$, if
$S_{[n]}(\widetilde {H}(\phi ))=\phi$, if ![]() $n$ is odd, and
$n$ is odd, and ![]() $\det (\widetilde {H}(\phi ))S_{[n]}(\widetilde {H}(\phi ))=\phi$, if
$\det (\widetilde {H}(\phi ))S_{[n]}(\widetilde {H}(\phi ))=\phi$, if ![]() $n$ is even.
$n$ is even.
Remark 3.2 Fix a positive integer ![]() $n$. Consider the two groupoids
$n$. Consider the two groupoids ![]() ${\mathcal {V}}$ and
${\mathcal {V}}$ and ![]() $S_{[n]}{\mathcal {V}}$, whose objects are vector spaces over
$S_{[n]}{\mathcal {V}}$, whose objects are vector spaces over ![]() ${\mathbb {Q}}$, which are odd dimensional if
${\mathbb {Q}}$, which are odd dimensional if ![]() $n$ is even, with non-degenerate symmetric quadratic forms and with the additional choice of orientations, if
$n$ is even, with non-degenerate symmetric quadratic forms and with the additional choice of orientations, if ![]() $n$ is even. The morphisms of
$n$ is even. The morphisms of ![]() ${\mathcal {V}}$ are isometries. The morphisms in
${\mathcal {V}}$ are isometries. The morphisms in ![]() ${\rm Hom}_{S_{[n]}{\mathcal {V}}}(V_1,V_2)$ are isometries
${\rm Hom}_{S_{[n]}{\mathcal {V}}}(V_1,V_2)$ are isometries ![]() $\phi :S_{[n]}V_1\rightarrow S_{[n]}V_2$ satisfying
$\phi :S_{[n]}V_1\rightarrow S_{[n]}V_2$ satisfying ![]() $\phi (S_{[n]}{\mathfrak so}(V_1))\phi ^{-1}=S_{[n]}{\mathfrak so}(V_2)$. We have the obvious functor
$\phi (S_{[n]}{\mathfrak so}(V_1))\phi ^{-1}=S_{[n]}{\mathfrak so}(V_2)$. We have the obvious functor ![]() $S_{[n]} : {\mathcal {V}} \rightarrow S_{[n]}{\mathcal {V}}$, which is the identity on objects, and which sends an isometry from
$S_{[n]} : {\mathcal {V}} \rightarrow S_{[n]}{\mathcal {V}}$, which is the identity on objects, and which sends an isometry from ![]() $V_1$ to
$V_1$ to ![]() $V_2$ to the restriction of its
$V_2$ to the restriction of its ![]() $n$th symmetric power to the subrepresentation
$n$th symmetric power to the subrepresentation ![]() $S_{[n]}V_1$. Proposition 3.1 gives rise to a functor
$S_{[n]}V_1$. Proposition 3.1 gives rise to a functor ![]() $\widetilde {H}:S_{[n]}{\mathcal {V}}\rightarrow {\mathcal {V}}$. If
$\widetilde {H}:S_{[n]}{\mathcal {V}}\rightarrow {\mathcal {V}}$. If ![]() $n$ is odd, the functors
$n$ is odd, the functors ![]() $S_{[n]}$ and
$S_{[n]}$ and ![]() $\widetilde {H}$ are inverses of each other. If
$\widetilde {H}$ are inverses of each other. If ![]() $n$ is even, then
$n$ is even, then ![]() $S_{[n]}$ is not faithful, since
$S_{[n]}$ is not faithful, since ![]() $S_{[n]}(\phi )=S_{[n]}(-\phi )$. Proposition 3.1 asserts that if
$S_{[n]}(\phi )=S_{[n]}(-\phi )$. Proposition 3.1 asserts that if ![]() $n$ is even, then the functor
$n$ is even, then the functor ![]() $F:{\mathcal {V}}\rightarrow S_{[n]}{\mathcal {V}}$, which is the identity on objects, and which sends
$F:{\mathcal {V}}\rightarrow S_{[n]}{\mathcal {V}}$, which is the identity on objects, and which sends ![]() $f\in {\rm Hom}_{\mathcal {V}}((V_1,\epsilon _1),(V_2,\epsilon _2))$ to
$f\in {\rm Hom}_{\mathcal {V}}((V_1,\epsilon _1),(V_2,\epsilon _2))$ to ![]() $\det (f)S_{[n]}(f)$, is an equivalence and defines
$\det (f)S_{[n]}(f)$, is an equivalence and defines ![]() $\widetilde {H}$ as its inverse. We have
$\widetilde {H}$ as its inverse. We have ![]() $S_{[n]}(-f)=-S_{[n]}(f)$, if
$S_{[n]}(-f)=-S_{[n]}(f)$, if ![]() $n$ is odd, and
$n$ is odd, and ![]() $F(-f)=-F(f)$, if
$F(-f)=-F(f)$, if ![]() $n$ is even, and so
$n$ is even, and so ![]() $\widetilde {H}(-\phi )=-\widetilde {H}(\phi )$. Let
$\widetilde {H}(-\phi )=-\widetilde {H}(\phi )$. Let ![]() $f_i\in O(V_i)$,
$f_i\in O(V_i)$, ![]() $i=1,2$. We have
$i=1,2$. We have
 \begin{equation} \widetilde{H}(S_{[n]}(f_2)\circ \phi\circ S_{[n]}(f_1))= \begin{cases} f_2\circ \widetilde{H}(\phi)\circ f_1 & \mbox{if}\ n \ \mbox{is odd},\\ \det(f_1)\det(f_2)f_2\circ \widetilde{H}(\phi)\circ f_1 & \mbox{if}\ n \ \mbox{is even}. \end{cases} \end{equation}
\begin{equation} \widetilde{H}(S_{[n]}(f_2)\circ \phi\circ S_{[n]}(f_1))= \begin{cases} f_2\circ \widetilde{H}(\phi)\circ f_1 & \mbox{if}\ n \ \mbox{is odd},\\ \det(f_1)\det(f_2)f_2\circ \widetilde{H}(\phi)\circ f_1 & \mbox{if}\ n \ \mbox{is even}. \end{cases} \end{equation}Definition 3.3 The functor ![]() $\widetilde {H}:{\mathcal {G}}\rightarrow \widetilde {{\mathcal {G}}}$, given in (1.4), sends a morphism
$\widetilde {H}:{\mathcal {G}}\rightarrow \widetilde {{\mathcal {G}}}$, given in (1.4), sends a morphism ![]() $\phi$ in
$\phi$ in ![]() ${\rm Hom}_{\mathcal {G}}((X,\epsilon _X),(Y,\epsilon _Y))$ to
${\rm Hom}_{\mathcal {G}}((X,\epsilon _X),(Y,\epsilon _Y))$ to ![]() $\widetilde {H}(\Psi _Y\circ \phi _{\mid _{}}\circ \Psi _X^{-1}):\widetilde {H}(X,{\mathbb {Q}})\rightarrow \widetilde {H}(Y,{\mathbb {Q}})$, where the latter functor
$\widetilde {H}(\Psi _Y\circ \phi _{\mid _{}}\circ \Psi _X^{-1}):\widetilde {H}(X,{\mathbb {Q}})\rightarrow \widetilde {H}(Y,{\mathbb {Q}})$, where the latter functor ![]() $\widetilde {H}$ is from Remark 3.2 (with
$\widetilde {H}$ is from Remark 3.2 (with ![]() $V_1=\widetilde {H}(X,{\mathbb {Q}})$ with orientation
$V_1=\widetilde {H}(X,{\mathbb {Q}})$ with orientation ![]() $\epsilon _X$ and
$\epsilon _X$ and ![]() $V_2=\widetilde {H}(Y,{\mathbb {Q}})$ with orientation
$V_2=\widetilde {H}(Y,{\mathbb {Q}})$ with orientation ![]() $\epsilon _Y$) and
$\epsilon _Y$) and ![]() $\phi _{\mid _{}}$ is the restriction of
$\phi _{\mid _{}}$ is the restriction of ![]() $\phi$ to
$\phi$ to ![]() $SH^*(X,{\mathbb {Q}})$.
$SH^*(X,{\mathbb {Q}})$.
Lemma 3.4 Let ![]() $X$ and
$X$ and ![]() $Y$ be
$Y$ be ![]() $2n$-dimensional IHSMs. Let
$2n$-dimensional IHSMs. Let ![]() $\phi$ be a morphism in
$\phi$ be a morphism in ![]() ${\rm Hom}_{{\mathcal {G}}}((X,\epsilon _X),(Y,\epsilon _Y))$. Set
${\rm Hom}_{{\mathcal {G}}}((X,\epsilon _X),(Y,\epsilon _Y))$. Set ![]() $\tilde {\phi }:=\widetilde {H}(\phi ):\widetilde {H}(X,{\mathbb {Q}})\rightarrow \widetilde {H}(Y,{\mathbb {Q}})$. The equality
$\tilde {\phi }:=\widetilde {H}(\phi ):\widetilde {H}(X,{\mathbb {Q}})\rightarrow \widetilde {H}(Y,{\mathbb {Q}})$. The equality ![]() $\tilde {\phi }\tilde {h}_X=(-1)^k\tilde {h}_Y\tilde {\phi }$, for some
$\tilde {\phi }\tilde {h}_X=(-1)^k\tilde {h}_Y\tilde {\phi }$, for some ![]() $k\in \{0,1\}$, is equivalent to
$k\in \{0,1\}$, is equivalent to ![]() $\phi h_X=(-1)^kh_Y\phi$ for the same
$\phi h_X=(-1)^kh_Y\phi$ for the same ![]() $k$.
$k$.
Proof. The proof is modeled after that of [Reference TaelmanTae23, Theorem 5.3]. The isomorphism ![]() $\phi :H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ conjugates the LLV Lie algebra
$\phi :H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ conjugates the LLV Lie algebra ![]() ${\mathfrak g}_X$ to
${\mathfrak g}_X$ to ![]() ${\mathfrak g}_Y$, by [Reference TaelmanTae23, Theorem A], and it conjugates
${\mathfrak g}_Y$, by [Reference TaelmanTae23, Theorem A], and it conjugates ![]() $SH^*(X,{\mathbb {Q}})$ to
$SH^*(X,{\mathbb {Q}})$ to ![]() $SH^*(Y,{\mathbb {Q}})$, by [Reference TaelmanTae23, Theorem B]. Hence,
$SH^*(Y,{\mathbb {Q}})$, by [Reference TaelmanTae23, Theorem B]. Hence, ![]() $\phi h_X\phi ^{-1}$ belongs to
$\phi h_X\phi ^{-1}$ belongs to ![]() ${\mathfrak g}_Y$. Theorems 4.10 and 4.11 in [Reference TaelmanTae23] yield the commutative diagram
${\mathfrak g}_Y$. Theorems 4.10 and 4.11 in [Reference TaelmanTae23] yield the commutative diagram

where the left bottom vertical arrow is the restriction to the subrepresentation ![]() $SH^*(X,{\mathbb {Q}})$ of
$SH^*(X,{\mathbb {Q}})$ of ![]() $H^*(X,{\mathbb {Q}})$ and the right bottom vertical arrow is the analogue. The top left vertical arrow corresponds to
$H^*(X,{\mathbb {Q}})$ and the right bottom vertical arrow is the analogue. The top left vertical arrow corresponds to ![]() $f\mapsto \Psi _X^{-1}\circ (S_{[n]}f) \circ \Psi _X$ and the right is the analogue. All four vertical arrows are injective and each pair in the same column have the same image yielding the curved arrows which are isomorphisms (inverses of
$f\mapsto \Psi _X^{-1}\circ (S_{[n]}f) \circ \Psi _X$ and the right is the analogue. All four vertical arrows are injective and each pair in the same column have the same image yielding the curved arrows which are isomorphisms (inverses of ![]() $\dot {\rho }$ in (3.2)). The grading operator
$\dot {\rho }$ in (3.2)). The grading operator ![]() $h_X\in {\mathfrak g}_X$ restricts to the same element of
$h_X\in {\mathfrak g}_X$ restricts to the same element of ![]() ${\mathfrak sl}(SH^*(X,{\mathbb {Q}}))$ as the image of the grading operator
${\mathfrak sl}(SH^*(X,{\mathbb {Q}}))$ as the image of the grading operator ![]() $\tilde {h}_X\in {\mathfrak so}(\widetilde {H}(X,{\mathbb {Q}}))$, since
$\tilde {h}_X\in {\mathfrak so}(\widetilde {H}(X,{\mathbb {Q}}))$, since ![]() $\Psi _X$ is a graded isomorphism. The same holds for
$\Psi _X$ is a graded isomorphism. The same holds for ![]() $h_Y$ and
$h_Y$ and ![]() $\tilde {h}_Y$. Hence, the equality
$\tilde {h}_Y$. Hence, the equality ![]() $\tilde {\phi }\tilde {h}_X\tilde {\phi }^{-1}=(-1)^k\tilde {h}_Y$ is equivalent to the equality of the restrictions of
$\tilde {\phi }\tilde {h}_X\tilde {\phi }^{-1}=(-1)^k\tilde {h}_Y$ is equivalent to the equality of the restrictions of ![]() $\phi h_X\phi ^{-1}$ and
$\phi h_X\phi ^{-1}$ and ![]() $(-1)^k h_Y$ to elements of
$(-1)^k h_Y$ to elements of ![]() ${\mathfrak sl}(SH^*(Y,{\mathbb {Q}}))$, by the commutativity of the diagram and the injectivity of the top right vertical arrow. The latter is equivalent to the equality
${\mathfrak sl}(SH^*(Y,{\mathbb {Q}}))$, by the commutativity of the diagram and the injectivity of the top right vertical arrow. The latter is equivalent to the equality ![]() $\phi h_X\phi ^{-1}=(-1)^kh_Y$, since the restriction homomorphism
$\phi h_X\phi ^{-1}=(-1)^kh_Y$, since the restriction homomorphism ![]() ${\mathfrak g}_Y\rightarrow {\mathfrak sl}(SH^*(Y,{\mathbb {Q}}))$ is injective.
${\mathfrak g}_Y\rightarrow {\mathfrak sl}(SH^*(Y,{\mathbb {Q}}))$ is injective.
The relation between ![]() $h_X$ and
$h_X$ and ![]() $\tilde {h}_X$ explains the following result of Verbitsky, Looijenga, and Lunts.
$\tilde {h}_X$ explains the following result of Verbitsky, Looijenga, and Lunts.
Lemma 3.5 [Reference Looijenga and LuntsLL97, Proposition 4.5(ii)]
The commutator of ![]() $h$ in
$h$ in ![]() ${\mathfrak g}_X$ decomposes as a direct sum
${\mathfrak g}_X$ decomposes as a direct sum ![]() $\bar {{\mathfrak g}}_X\oplus {\mathbb {Q}} h_X$, where
$\bar {{\mathfrak g}}_X\oplus {\mathbb {Q}} h_X$, where ![]() $\bar {{\mathfrak g}}_X$ is the derived Lie subalgebra of the commutator, and
$\bar {{\mathfrak g}}_X$ is the derived Lie subalgebra of the commutator, and ![]() $\bar {{\mathfrak g}}_X$ is isomorphic to
$\bar {{\mathfrak g}}_X$ is isomorphic to ![]() ${\mathfrak so}(H^2(X,{\mathbb {Q}}))$.
${\mathfrak so}(H^2(X,{\mathbb {Q}}))$.
The Hodge operator
acts on ![]() $H^{p,q}(X)$ by multiplication by
$H^{p,q}(X)$ by multiplication by ![]() $q-p$. Verbitsky proved that it is an element of the subalgebra
$q-p$. Verbitsky proved that it is an element of the subalgebra ![]() $\bar {{\mathfrak g}}_{X,{\mathbb {C}}}$ of
$\bar {{\mathfrak g}}_{X,{\mathbb {C}}}$ of ![]() ${\mathfrak g}_{X,{\mathbb {C}}}$ (see [Reference VerbitskyVer99a, Theorem 8.1]; see also [Reference TaelmanTae23, Corollary 2.12]).
${\mathfrak g}_{X,{\mathbb {C}}}$ (see [Reference VerbitskyVer99a, Theorem 8.1]; see also [Reference TaelmanTae23, Corollary 2.12]).
Lemma 3.6 Assume that ![]() $\phi \in {\rm Hom}_{\mathcal {G}}((X,\epsilon _X),(Y,\epsilon _Y))$ is degree preserving and let
$\phi \in {\rm Hom}_{\mathcal {G}}((X,\epsilon _X),(Y,\epsilon _Y))$ is degree preserving and let ![]() $\phi _2$ be the restriction of
$\phi _2$ be the restriction of ![]() $\phi$ to
$\phi$ to ![]() $H^2(X,{\mathbb {Q}})$. Let
$H^2(X,{\mathbb {Q}})$. Let ![]() $t\in {\mathbb {Q}}^\times$ be such that
$t\in {\mathbb {Q}}^\times$ be such that ![]() $\widetilde {H}(\phi )(\alpha )=t^{-1}\alpha$. Then the restriction
$\widetilde {H}(\phi )(\alpha )=t^{-1}\alpha$. Then the restriction ![]() $\widetilde {H}(\phi )_0$ of
$\widetilde {H}(\phi )_0$ of ![]() $\widetilde {H}(\phi )$ to
$\widetilde {H}(\phi )$ to ![]() $H^2(X,{\mathbb {Q}})$ satisfies
$H^2(X,{\mathbb {Q}})$ satisfies
 \[ \widetilde{H}(\phi)_0=\begin{cases}
t^{n-1}\phi_2 & \mbox{if} \ n \ \mbox{is odd},\\
\det(\widetilde{H}(\phi))t^{n-1}\phi_2 & \mbox{if} \ n \
\mbox{is even}. \end{cases} \]
\[ \widetilde{H}(\phi)_0=\begin{cases}
t^{n-1}\phi_2 & \mbox{if} \ n \ \mbox{is odd},\\
\det(\widetilde{H}(\phi))t^{n-1}\phi_2 & \mbox{if} \ n \
\mbox{is even}. \end{cases} \]
Proof. Assume that ![]() $\phi \in {\rm Hom}_{\mathcal {G}}((X,\epsilon _X),(Y,\epsilon _Y))$ is degree preserving. Then so is
$\phi \in {\rm Hom}_{\mathcal {G}}((X,\epsilon _X),(Y,\epsilon _Y))$ is degree preserving. Then so is ![]() $\widetilde {H}(\phi )$, by Lemma 3.4. Let
$\widetilde {H}(\phi )$, by Lemma 3.4. Let ![]() $\lambda$ be a class in
$\lambda$ be a class in ![]() $H^2(X,{\mathbb {Q}})$. We have
$H^2(X,{\mathbb {Q}})$. We have
 \begin{align*} (S_{[n]}\widetilde{H}(\phi))(\Psi(\lambda)) &= (S_{[n]}\widetilde{H}(\phi))(e_\lambda(\alpha^n/n!))=(S_{[n]}\widetilde{H}(\phi))(\alpha^{n-1}\lambda/(n-1)!)\\ &=\frac{t^{1-n}}{(n-1)!}\alpha^{n-1}\widetilde{H}(\phi)(\lambda),\\ {}(S_{[n]}\widetilde{H}(\phi))(\Psi(\lambda)) &= a \Psi(\phi(\lambda))= a e_{\phi(\lambda)}(\alpha^n/n!)=a \alpha^{n-1}\phi(\lambda)/(n-1)!, \end{align*}
\begin{align*} (S_{[n]}\widetilde{H}(\phi))(\Psi(\lambda)) &= (S_{[n]}\widetilde{H}(\phi))(e_\lambda(\alpha^n/n!))=(S_{[n]}\widetilde{H}(\phi))(\alpha^{n-1}\lambda/(n-1)!)\\ &=\frac{t^{1-n}}{(n-1)!}\alpha^{n-1}\widetilde{H}(\phi)(\lambda),\\ {}(S_{[n]}\widetilde{H}(\phi))(\Psi(\lambda)) &= a \Psi(\phi(\lambda))= a e_{\phi(\lambda)}(\alpha^n/n!)=a \alpha^{n-1}\phi(\lambda)/(n-1)!, \end{align*}
where ![]() $a=1$, if
$a=1$, if ![]() $n$ is odd, and
$n$ is odd, and ![]() $a=\det (\widetilde {H}(\phi ))$, if
$a=\det (\widetilde {H}(\phi ))$, if ![]() $n$ is even (Proposition 3.1). The statement follows from the equality of the right-hand sides in the two equations above.
$n$ is even (Proposition 3.1). The statement follows from the equality of the right-hand sides in the two equations above.
Lemma 3.7 Let ![]() $\phi \in {\rm Hom}_{\mathcal {G}}((X,\epsilon _X),(Y,\epsilon _Y))$ be a degree-reversing morphism, where
$\phi \in {\rm Hom}_{\mathcal {G}}((X,\epsilon _X),(Y,\epsilon _Y))$ be a degree-reversing morphism, where ![]() $X$ and
$X$ and ![]() $Y$ are
$Y$ are ![]() $2n$-dimensional. Then the value
$2n$-dimensional. Then the value ![]() $\widetilde {H}_0(\phi ):H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ at
$\widetilde {H}_0(\phi ):H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ at ![]() $\phi$ of the functor
$\phi$ of the functor ![]() $\widetilde {H}_0$ given in (1.5) is a scalar multiple of the composition
$\widetilde {H}_0$ given in (1.5) is a scalar multiple of the composition
Proof. Note first that ![]() $H^2(X,{\mathbb {Q}})$ and
$H^2(X,{\mathbb {Q}})$ and ![]() $H^{4n-2}(X,{\mathbb {Q}})$ are subspaces of
$H^{4n-2}(X,{\mathbb {Q}})$ are subspaces of ![]() $SH^*(X,{\mathbb {Q}})$. Let
$SH^*(X,{\mathbb {Q}})$. Let ![]() $\phi _{\mid _{}}$ be the restriction of
$\phi _{\mid _{}}$ be the restriction of ![]() $\phi$ to
$\phi$ to ![]() $SH^*(X,{\mathbb {Q}})$. Given an isometry
$SH^*(X,{\mathbb {Q}})$. Given an isometry ![]() $f\in O(\widetilde {H}(X,{\mathbb {Q}}))$, let
$f\in O(\widetilde {H}(X,{\mathbb {Q}}))$, let
be given by ![]() $\eta _f:=\Psi _X^{-1}\circ S_{[n]}(f)\circ \Psi _X$. Then
$\eta _f:=\Psi _X^{-1}\circ S_{[n]}(f)\circ \Psi _X$. Then
 \[ \widetilde{H}(\phi_{\mid_{}}\circ
\eta_f)= \begin{cases} \widetilde{H}(\phi)\circ f &
\mbox{if} \ n \ \mbox{is odd},\\
\det(f)\widetilde{H}(\phi)\circ f & \mbox{if}\ n \
\mbox{is even}, \end{cases} \]
\[ \widetilde{H}(\phi_{\mid_{}}\circ
\eta_f)= \begin{cases} \widetilde{H}(\phi)\circ f &
\mbox{if} \ n \ \mbox{is odd},\\
\det(f)\widetilde{H}(\phi)\circ f & \mbox{if}\ n \
\mbox{is even}, \end{cases} \]
by (3.6). The left-hand side is defined to be ![]() $\widetilde {H}(\Psi _X\circ (\phi _{\mid _{}}\circ \eta _f)\circ \Psi _X^{-1})$ where
$\widetilde {H}(\Psi _X\circ (\phi _{\mid _{}}\circ \eta _f)\circ \Psi _X^{-1})$ where ![]() $\widetilde {H}$ is the functor in Proposition 3.1.
$\widetilde {H}$ is the functor in Proposition 3.1.
Let ![]() $\tau \in O(\widetilde {H}(X,{\mathbb {Q}}))$ be the element which interchanges
$\tau \in O(\widetilde {H}(X,{\mathbb {Q}}))$ be the element which interchanges ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ and multiplies
$\beta$ and multiplies ![]() $H^2(X,{\mathbb {Q}})$ by
$H^2(X,{\mathbb {Q}})$ by ![]() $-1$. Then
$-1$. Then ![]() $\tau \tilde {h}_X=-\tilde {h}_X\tau$ and so
$\tau \tilde {h}_X=-\tilde {h}_X\tau$ and so ![]() $\eta _\tau$ is degree reversing. Hence,
$\eta _\tau$ is degree reversing. Hence, ![]() $\phi _{\mid _{}}\circ \eta _\tau$ is degree preserving and so the restriction
$\phi _{\mid _{}}\circ \eta _\tau$ is degree preserving and so the restriction ![]() $\widetilde {H}(\phi _{\mid _{}}\circ \eta _\tau )_0$ of
$\widetilde {H}(\phi _{\mid _{}}\circ \eta _\tau )_0$ of ![]() $\widetilde {H}(\phi _{\mid _{}}\circ \eta _\tau )$ to
$\widetilde {H}(\phi _{\mid _{}}\circ \eta _\tau )$ to ![]() $H^2(X,{\mathbb {Q}})$ is a scalar multiple of
$H^2(X,{\mathbb {Q}})$ is a scalar multiple of ![]() $(\phi _{\mid _{}}\circ \eta _\tau )_2$, by Lemma 3.6. Furthermore,
$(\phi _{\mid _{}}\circ \eta _\tau )_2$, by Lemma 3.6. Furthermore, ![]() $\widetilde {H}(\phi _{\mid _{}}\circ \eta _\tau )_0=\widetilde {H}(\phi )_0\circ \widetilde {H}(\eta _\tau )_0$ and
$\widetilde {H}(\phi _{\mid _{}}\circ \eta _\tau )_0=\widetilde {H}(\phi )_0\circ \widetilde {H}(\eta _\tau )_0$ and ![]() $\widetilde {H}(\eta _\tau )_0=-id,$ so
$\widetilde {H}(\eta _\tau )_0=-id,$ so ![]() $\widetilde {H}(\phi _{\mid _{}}\circ \eta _\tau )_0=- \widetilde {H}(\phi )_0=\pm \widetilde {H}_0(\phi )$. We conclude that
$\widetilde {H}(\phi _{\mid _{}}\circ \eta _\tau )_0=- \widetilde {H}(\phi )_0=\pm \widetilde {H}_0(\phi )$. We conclude that ![]() $\widetilde {H}_0(\phi )$ is a scalar multiple of
$\widetilde {H}_0(\phi )$ is a scalar multiple of ![]() $(\phi _{\mid _{}}\circ \eta _\tau )_2$.
$(\phi _{\mid _{}}\circ \eta _\tau )_2$.
It remains to prove that ![]() $\eta _\tau :H^2(X,{\mathbb {Q}})\rightarrow H^{4n-2}(X,{\mathbb {Q}})$ is a scalar multiple of cup product with
$\eta _\tau :H^2(X,{\mathbb {Q}})\rightarrow H^{4n-2}(X,{\mathbb {Q}})$ is a scalar multiple of cup product with ![]() $c_2(X)^{n-1}$. Let
$c_2(X)^{n-1}$. Let ![]() $G$ be the subgroup of
$G$ be the subgroup of ![]() $SO(\widetilde {H}(X,{\mathbb {Q}}))$ leaving each of
$SO(\widetilde {H}(X,{\mathbb {Q}}))$ leaving each of ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ invariant. Then
$\beta$ invariant. Then ![]() $G$ commutes with
$G$ commutes with ![]() $\tau$ and its
$\tau$ and its ![]() $\eta$-action on
$\eta$-action on ![]() $SH^*(X,{\mathbb {Q}})$ is via degree-preserving isometries with respect to which
$SH^*(X,{\mathbb {Q}})$ is via degree-preserving isometries with respect to which ![]() $\eta _\tau$ is
$\eta _\tau$ is ![]() $G$-equivariant. Now,
$G$-equivariant. Now, ![]() $H^2(X,{\mathbb {Q}})$ and
$H^2(X,{\mathbb {Q}})$ and ![]() $H^{4n-2}(X,{\mathbb {Q}})$ are dual irreducible
$H^{4n-2}(X,{\mathbb {Q}})$ are dual irreducible ![]() $G$-representations and
$G$-representations and ![]() $\cup c_2(X)^{n-1}:H^2(X,{\mathbb {Q}})\rightarrow H^{4n-2}(X,{\mathbb {Q}})$ is
$\cup c_2(X)^{n-1}:H^2(X,{\mathbb {Q}})\rightarrow H^{4n-2}(X,{\mathbb {Q}})$ is ![]() $G$-equivariant as well and non-vanishing, by [Reference Looijenga and LuntsLL97, Theorem 4.7]. Hence, a scalar multiple of the latter is equal to the restriction of
$G$-equivariant as well and non-vanishing, by [Reference Looijenga and LuntsLL97, Theorem 4.7]. Hence, a scalar multiple of the latter is equal to the restriction of ![]() $\eta _\tau$ to
$\eta _\tau$ to ![]() $H^2(X,{\mathbb {Q}})$.
$H^2(X,{\mathbb {Q}})$.
Let ![]() $X$ and
$X$ and ![]() $Y$ be projective IHSMs and
$Y$ be projective IHSMs and ![]() ${\mathcal {P}}\in D^b(X\times Y)$ the Fourier–Mukai kernel of an equivalence
${\mathcal {P}}\in D^b(X\times Y)$ the Fourier–Mukai kernel of an equivalence ![]() $\Phi _{\mathcal {P}}:D^b(X)\rightarrow D^b(Y)$. Assume that the rank
$\Phi _{\mathcal {P}}:D^b(X)\rightarrow D^b(Y)$. Assume that the rank ![]() $r$ of
$r$ of ![]() ${\mathcal {P}}$ does not vanish. Let
${\mathcal {P}}$ does not vanish. Let ![]() $x$ be a point of
$x$ be a point of ![]() $X$, denote by
$X$, denote by ![]() ${\mathcal {P}}_x\in D^b(Y)$ the restriction of
${\mathcal {P}}_x\in D^b(Y)$ the restriction of ![]() ${\mathcal {P}}$ to
${\mathcal {P}}$ to ![]() $\{x\}\times Y$, and set
$\{x\}\times Y$, and set ![]() $\lambda :=c_1({\mathcal {P}}_x)\in H^2(Y,{\mathbb {Z}})$. Note that the object
$\lambda :=c_1({\mathcal {P}}_x)\in H^2(Y,{\mathbb {Z}})$. Note that the object ![]() ${\mathcal {P}}_x$ of
${\mathcal {P}}_x$ of ![]() $D^b(Y)$ is the image of the skyscraper sheaf at
$D^b(Y)$ is the image of the skyscraper sheaf at ![]() $x$ via
$x$ via ![]() $\Phi _{\mathcal {P}}$. Set
$\Phi _{\mathcal {P}}$. Set ![]() $\widetilde {H}(\Phi _{\mathcal {P}}):=\widetilde {H}([ch({\mathcal {P}})\sqrt {td_{X\times Y}}]_*)$. The following was proved independently by Beckmann [Reference BeckmannBec23, Lemma 4.13(iv)] and the author [Reference MarkmanMar21a, Theorem 6.13(3)].
$\widetilde {H}(\Phi _{\mathcal {P}}):=\widetilde {H}([ch({\mathcal {P}})\sqrt {td_{X\times Y}}]_*)$. The following was proved independently by Beckmann [Reference BeckmannBec23, Lemma 4.13(iv)] and the author [Reference MarkmanMar21a, Theorem 6.13(3)].
Proposition 3.8 The isometry ![]() $\widetilde {H}(\Phi _{\mathcal {P}}):\widetilde {H}(X,{\mathbb {Q}})\rightarrow \widetilde {H}(Y,{\mathbb {Q}})$ maps
$\widetilde {H}(\Phi _{\mathcal {P}}):\widetilde {H}(X,{\mathbb {Q}})\rightarrow \widetilde {H}(Y,{\mathbb {Q}})$ maps ![]() $\beta$ to the isotropic line spanned by
$\beta$ to the isotropic line spanned by ![]() $r\alpha +\lambda +s\beta$, where
$r\alpha +\lambda +s\beta$, where ![]() $s=(\lambda,\lambda )/2r$ so that the line is isotropic.
$s=(\lambda,\lambda )/2r$ so that the line is isotropic.
4. The degree-reversing Hodge isometry of a Fourier–Mukai kernel of non-zero rank
Consider an object ![]() $E$ of non-zero rank in the derived category of a product
$E$ of non-zero rank in the derived category of a product ![]() $X\times Y$ of
$X\times Y$ of ![]() $2n$-dimensional deformation equivalent IHSMs
$2n$-dimensional deformation equivalent IHSMs ![]() $X$ and
$X$ and ![]() $Y$. Assume that
$Y$. Assume that ![]() $E$ is the Fourier–Mukai kernel of an equivalence of derived categories. This means that the functor
$E$ is the Fourier–Mukai kernel of an equivalence of derived categories. This means that the functor ![]() $\Phi _E:D^b(X)\rightarrow D^b(Y)$, given by
$\Phi _E:D^b(X)\rightarrow D^b(Y)$, given by ![]() $\Phi _E(\bullet )=R\pi _{Y,*}(L\pi _X^*(\bullet )\otimes E)$, is an equivalence of triangulated categories.
$\Phi _E(\bullet )=R\pi _{Y,*}(L\pi _X^*(\bullet )\otimes E)$, is an equivalence of triangulated categories.
Lemma 4.1
(1) The class
 $\kappa (E)\sqrt {td_{X\times Y}}$, with
$\kappa (E)\sqrt {td_{X\times Y}}$, with  $\kappa (E)$ as in Definition 1.3, induces a degree-reversing Hodge isometry
$\kappa (E)$ as in Definition 1.3, induces a degree-reversing Hodge isometry
 \[ \phi:H^*(X,{\mathbb{Q}})\rightarrow H^*(Y,{\mathbb{Q}}). \]
\[ \phi:H^*(X,{\mathbb{Q}})\rightarrow H^*(Y,{\mathbb{Q}}). \]
(2) The Hodge isometry
 $\widetilde {H}(\phi ):\widetilde {H}(X,{\mathbb {Q}})\rightarrow \widetilde {H}(Y,{\mathbb {Q}})$, associated to
$\widetilde {H}(\phi ):\widetilde {H}(X,{\mathbb {Q}})\rightarrow \widetilde {H}(Y,{\mathbb {Q}})$, associated to  $\phi$ and any choice of orientations of
$\phi$ and any choice of orientations of  $H^2(X,{\mathbb {Q}})$ and
$H^2(X,{\mathbb {Q}})$ and  $H^2(Y,{\mathbb {Q}})$, restricts to a Hodge isometry
(4.1)
$H^2(Y,{\mathbb {Q}})$, restricts to a Hodge isometry
(4.1) \begin{equation} \widetilde{H}(\phi)_0:H^2(X,{\mathbb{Q}})\rightarrow H^2(Y,{\mathbb{Q}}). \end{equation}
\begin{equation} \widetilde{H}(\phi)_0:H^2(X,{\mathbb{Q}})\rightarrow H^2(Y,{\mathbb{Q}}). \end{equation}(3) The Lie algebras isomorphism
 $Ad_\phi :{\mathfrak g}_X\rightarrow {\mathfrak g}_Y$ is graded and restricts to
$Ad_\phi :{\mathfrak g}_X\rightarrow {\mathfrak g}_Y$ is graded and restricts to
 \[ Ad_{\widetilde{H}_0(\phi)}:\bar{{\mathfrak g}}_X\rightarrow \bar{{\mathfrak g}}_Y. \]
\[ Ad_{\widetilde{H}_0(\phi)}:\bar{{\mathfrak g}}_X\rightarrow \bar{{\mathfrak g}}_Y. \]
Proof. Let ![]() $r$ be the rank of
$r$ be the rank of ![]() $E$ and let
$E$ and let ![]() $\lambda _X\in H^2(X,{\mathbb {Z}})$ and
$\lambda _X\in H^2(X,{\mathbb {Z}})$ and ![]() $\lambda _Y\in H^2(Y,{\mathbb {Z}})$ satisfy
$\lambda _Y\in H^2(Y,{\mathbb {Z}})$ satisfy ![]() $c_1(E)=\pi _X^*(\lambda _X)+\pi _Y^*(\lambda _Y)$. Given
$c_1(E)=\pi _X^*(\lambda _X)+\pi _Y^*(\lambda _Y)$. Given ![]() $\lambda \in H^2(X,{\mathbb {Q}})$, let
$\lambda \in H^2(X,{\mathbb {Q}})$, let ![]() $e_\lambda$ be the endomorphism of
$e_\lambda$ be the endomorphism of ![]() $\widetilde {H}(X,{\mathbb {Q}})$ given in (3.4). Set
$\widetilde {H}(X,{\mathbb {Q}})$ given in (3.4). Set ![]() $B_\lambda :=\exp (e_\lambda )$.
$B_\lambda :=\exp (e_\lambda )$.
The isometry ![]() $\widetilde {H}(\Phi _E)$ maps
$\widetilde {H}(\Phi _E)$ maps ![]() ${\rm span}\{\beta _X\}$ to
${\rm span}\{\beta _X\}$ to ![]() ${\rm span}\{r\alpha _Y+\lambda _Y+ ({(\lambda _Y,\lambda _Y)}/{2r})\beta _Y\}$, by Proposition 3.8. We have
${\rm span}\{r\alpha _Y+\lambda _Y+ ({(\lambda _Y,\lambda _Y)}/{2r})\beta _Y\}$, by Proposition 3.8. We have ![]() $B_{-\lambda _X/r}(\beta _X)=\beta _X$ and
$B_{-\lambda _X/r}(\beta _X)=\beta _X$ and
The equality ![]() $\widetilde {H}(\phi )=B_{-\lambda _Y/r}\widetilde {H}(\Phi _E)B_{-\lambda _X/r}$ implies that
$\widetilde {H}(\phi )=B_{-\lambda _Y/r}\widetilde {H}(\Phi _E)B_{-\lambda _X/r}$ implies that ![]() $\widetilde {H}(\phi )$ maps
$\widetilde {H}(\phi )$ maps ![]() ${\rm span}\{\beta _X\!\}$ to
${\rm span}\{\beta _X\!\}$ to ![]() ${\rm span}\{\alpha _Y\!\}$. The adjoint
${\rm span}\{\alpha _Y\!\}$. The adjoint ![]() $\Phi _E^{\dagger}$ has Fourier–Mukai kernel
$\Phi _E^{\dagger}$ has Fourier–Mukai kernel ![]() $E^*[2n]$. The argument above applied to the adjoint shows that
$E^*[2n]$. The argument above applied to the adjoint shows that ![]() $\widetilde {H}(\phi )^{-1}$ maps
$\widetilde {H}(\phi )^{-1}$ maps ![]() ${\rm span}\{\beta _Y\!\}$ to
${\rm span}\{\beta _Y\!\}$ to ![]() ${\rm span}\{\alpha _X\!\}$. Hence,
${\rm span}\{\alpha _X\!\}$. Hence, ![]() $\widetilde {H}(\phi )$ maps
$\widetilde {H}(\phi )$ maps ![]() ${\rm span}\{\alpha _X\!\}$ to
${\rm span}\{\alpha _X\!\}$ to ![]() ${\rm span}\{\beta _Y\!\}$. It follows that
${\rm span}\{\beta _Y\!\}$. It follows that ![]() $\widetilde {H}(\phi )$ maps the subspace
$\widetilde {H}(\phi )$ maps the subspace ![]() $H^2(X,{\mathbb {Q}})$ orthogonal to
$H^2(X,{\mathbb {Q}})$ orthogonal to ![]() ${\rm span}\{\alpha _X,\beta _X\!\}$ to the subspace
${\rm span}\{\alpha _X,\beta _X\!\}$ to the subspace ![]() $H^2(Y,{\mathbb {Q}})$ orthogonal to
$H^2(Y,{\mathbb {Q}})$ orthogonal to ![]() ${\rm span}\{\alpha _Y,\beta _Y\!\}$. This proves part (2) of the Lemma. We denote by
${\rm span}\{\alpha _Y,\beta _Y\!\}$. This proves part (2) of the Lemma. We denote by ![]() $\widetilde {H}(\phi )_0$ the restriction of
$\widetilde {H}(\phi )_0$ the restriction of ![]() $\widetilde {H}(\phi )$ to
$\widetilde {H}(\phi )$ to ![]() $H^2(X,{\mathbb {Q}})$.
$H^2(X,{\mathbb {Q}})$.
The isometry ![]() $\widetilde {H}(\phi )$ conjugates the grading operator
$\widetilde {H}(\phi )$ conjugates the grading operator ![]() $\tilde {h}_X$ of
$\tilde {h}_X$ of ![]() $\widetilde {H}(X,{\mathbb {Q}})$, given in (3.5), to
$\widetilde {H}(X,{\mathbb {Q}})$, given in (3.5), to ![]() $-\tilde {h}_Y$, where
$-\tilde {h}_Y$, where ![]() $\tilde {h}_Y$ is the grading operator of
$\tilde {h}_Y$ is the grading operator of ![]() $\widetilde {H}(Y,{\mathbb {Q}})$. Lemma 3.4 implies that
$\widetilde {H}(Y,{\mathbb {Q}})$. Lemma 3.4 implies that ![]() $\phi$ is degree reversing and part (1) is proven.
$\phi$ is degree reversing and part (1) is proven.
(3) The subalgebra ![]() $\bar {{\mathfrak g}}_X$ is the semi-simple part of the degree-
$\bar {{\mathfrak g}}_X$ is the semi-simple part of the degree-![]() $0$ subalgebra of the LLV algebra
$0$ subalgebra of the LLV algebra ![]() ${\mathfrak g}_X$, by [Reference Looijenga and LuntsLL97, Proposition 4.5(ii)], and
${\mathfrak g}_X$, by [Reference Looijenga and LuntsLL97, Proposition 4.5(ii)], and ![]() $Ad_\phi :{\mathfrak g}_X\rightarrow {\mathfrak g}_Y$ is a graded Lie algebra isomorphism, by part (1), and so
$Ad_\phi :{\mathfrak g}_X\rightarrow {\mathfrak g}_Y$ is a graded Lie algebra isomorphism, by part (1), and so ![]() $Ad_\phi$ maps
$Ad_\phi$ maps ![]() $\bar {{\mathfrak g}}_X$ to the semi-simple part
$\bar {{\mathfrak g}}_X$ to the semi-simple part ![]() $\bar {{\mathfrak g}}_Y$ of the degree-
$\bar {{\mathfrak g}}_Y$ of the degree-![]() $0$ subalgebra of
$0$ subalgebra of ![]() ${\mathfrak g}_Y$. Furthermore, the restriction of
${\mathfrak g}_Y$. Furthermore, the restriction of ![]() $Ad_\phi$ to
$Ad_\phi$ to ![]() $\bar {{\mathfrak g}}_Y$ is equal to
$\bar {{\mathfrak g}}_Y$ is equal to ![]() $Ad_{\widetilde {H}(\phi )_0}$, by part (2) and the commutativity of the outer square in diagram (3.7). Finally,
$Ad_{\widetilde {H}(\phi )_0}$, by part (2) and the commutativity of the outer square in diagram (3.7). Finally, ![]() $Ad_{\widetilde {H}(\phi )_0}=Ad_{\widetilde {H}_0(\phi )}$, as
$Ad_{\widetilde {H}(\phi )_0}=Ad_{\widetilde {H}_0(\phi )}$, as ![]() $\widetilde {H}_0(\phi )=\pm \widetilde {H}(\phi )_0$, by definition (1.5).
$\widetilde {H}_0(\phi )=\pm \widetilde {H}(\phi )_0$, by definition (1.5).
Set ![]() $\gamma :=\kappa (E)\sqrt {td_{X\times Y}}$ and let
$\gamma :=\kappa (E)\sqrt {td_{X\times Y}}$ and let ![]() $\gamma _i$ be the graded summand in
$\gamma _i$ be the graded summand in ![]() $H^{2i}(X\times Y,{\mathbb {Q}})$.
$H^{2i}(X\times Y,{\mathbb {Q}})$.
Corollary 4.2 If the odd cohomology of ![]() $X$ vanishes, then
$X$ vanishes, then ![]() $\gamma _i=0$, for odd
$\gamma _i=0$, for odd ![]() $i$. In that case
$i$. In that case ![]() $\kappa (E)=\kappa (E^\vee )$.
$\kappa (E)=\kappa (E^\vee )$.
Proof. The class ![]() $\gamma _i$ induces the homomorphism
$\gamma _i$ induces the homomorphism ![]() $H^{k-2n}(X,{\mathbb {Q}})[2n]\rightarrow H^{k+2i-6n}(Y,{\mathbb {Q}})[2n]$. As
$H^{k-2n}(X,{\mathbb {Q}})[2n]\rightarrow H^{k+2i-6n}(Y,{\mathbb {Q}})[2n]$. As ![]() $\phi$ is degree reversing, this homomorphism vanishes unless
$\phi$ is degree reversing, this homomorphism vanishes unless ![]() $k+i-4n=0$. Hence, it vanishes unless the parities of
$k+i-4n=0$. Hence, it vanishes unless the parities of ![]() $i$ and
$i$ and ![]() $k$ are the same, and it vanishes if
$k$ are the same, and it vanishes if ![]() $k$ is odd, by assumption.
$k$ is odd, by assumption.
Proof Proof of Lemma 1.6
Set ![]() $\tilde {\phi }:=\widetilde {H}(\phi )$. The morphism
$\tilde {\phi }:=\widetilde {H}(\phi )$. The morphism ![]() $\phi$ conjugates the LLV Lie algebra of
$\phi$ conjugates the LLV Lie algebra of ![]() $X$ to that of
$X$ to that of ![]() $Y$, by [Reference TaelmanTae23, Theorem A]. The LLV Lie algebras act faithfully on the rational LLV lattices. Hence, it suffices to verify the equality
$Y$, by [Reference TaelmanTae23, Theorem A]. The LLV Lie algebras act faithfully on the rational LLV lattices. Hence, it suffices to verify the equality ![]() $e_\lambda ^\vee = ({2}/{t(\lambda,\lambda )})\tilde {\phi }^{-1}e_{\tilde {\phi }(\lambda )}\tilde {\phi }$ for the endomorphisms of
$e_\lambda ^\vee = ({2}/{t(\lambda,\lambda )})\tilde {\phi }^{-1}e_{\tilde {\phi }(\lambda )}\tilde {\phi }$ for the endomorphisms of ![]() $\widetilde {H}(X,{\mathbb {Q}})$. We have
$\widetilde {H}(X,{\mathbb {Q}})$. We have
 \begin{align*} (\tilde{\phi}^{-1}e_{\tilde{\phi}(\lambda)}\tilde{\phi})(\alpha) &= \tilde{\phi}^{-1}(e_{\tilde{\phi}(\lambda)}(t^{-1}\beta))=0,\\ (\tilde{\phi}^{-1}e_{\tilde{\phi}(\lambda)}\tilde{\phi})(\beta) &= \tilde{\phi}^{-1}(e_{\tilde{\phi}(\lambda)}(t\alpha))= t\tilde{\phi}^{-1}(\tilde{\phi}(\lambda))=t\lambda,\\ (\tilde{\phi}^{-1}e_{\tilde{\phi}(\lambda)}\tilde{\phi})(\lambda') &=\tilde{\phi}^{-1}((\tilde{\phi}(\lambda),\tilde{\phi}(\lambda'))\beta)=t(\lambda,\lambda')\alpha. \end{align*}
\begin{align*} (\tilde{\phi}^{-1}e_{\tilde{\phi}(\lambda)}\tilde{\phi})(\alpha) &= \tilde{\phi}^{-1}(e_{\tilde{\phi}(\lambda)}(t^{-1}\beta))=0,\\ (\tilde{\phi}^{-1}e_{\tilde{\phi}(\lambda)}\tilde{\phi})(\beta) &= \tilde{\phi}^{-1}(e_{\tilde{\phi}(\lambda)}(t\alpha))= t\tilde{\phi}^{-1}(\tilde{\phi}(\lambda))=t\lambda,\\ (\tilde{\phi}^{-1}e_{\tilde{\phi}(\lambda)}\tilde{\phi})(\lambda') &=\tilde{\phi}^{-1}((\tilde{\phi}(\lambda),\tilde{\phi}(\lambda'))\beta)=t(\lambda,\lambda')\alpha. \end{align*}
Set ![]() $\psi :=\tilde {\phi }^{-1}e_{\tilde {\phi }(\lambda )}\tilde {\phi }$. We get
$\psi :=\tilde {\phi }^{-1}e_{\tilde {\phi }(\lambda )}\tilde {\phi }$. We get
 \begin{align*} [e_\lambda,\psi](\alpha)&=-\psi(e_\lambda(\alpha))=-t(\lambda,\lambda)\alpha,\\ [e_\lambda,\psi](\beta)&=e_\lambda(t\lambda)=t(\lambda,\lambda)\beta,\\ [e_\lambda,\psi](\lambda')&=t(\lambda,\lambda')\lambda-t(\lambda,\lambda')\lambda=0. \end{align*}
\begin{align*} [e_\lambda,\psi](\alpha)&=-\psi(e_\lambda(\alpha))=-t(\lambda,\lambda)\alpha,\\ [e_\lambda,\psi](\beta)&=e_\lambda(t\lambda)=t(\lambda,\lambda)\beta,\\ [e_\lambda,\psi](\lambda')&=t(\lambda,\lambda')\lambda-t(\lambda,\lambda')\lambda=0. \end{align*}
Hence, ![]() $[e_\lambda,\psi ]= ({t(\lambda,\lambda )}/{2})h$. Clearly,
$[e_\lambda,\psi ]= ({t(\lambda,\lambda )}/{2})h$. Clearly, ![]() $[h,\psi ]=-2\psi$, since
$[h,\psi ]=-2\psi$, since ![]() $\psi$ has degree
$\psi$ has degree ![]() $-2$. Thus,
$-2$. Thus, ![]() $e_\lambda ^\vee = ({2}/{t(\lambda,\lambda )})\psi$.
$e_\lambda ^\vee = ({2}/{t(\lambda,\lambda )})\psi$.
5. Hyperholomorphic vector bundles deforming a Fourier–Mukai kernel
Let ![]() $X$ and
$X$ and ![]() $Y$ be deformation equivalent IHSMs and
$Y$ be deformation equivalent IHSMs and ![]() $E$ a locally free sheaf over
$E$ a locally free sheaf over ![]() $X\times Y$ which is the Fourier–Mukai kernel of an equivalence
$X\times Y$ which is the Fourier–Mukai kernel of an equivalence ![]() $\Phi _E:D^b(X)\rightarrow D^b(Y)$ of derived categories. Let
$\Phi _E:D^b(X)\rightarrow D^b(Y)$ of derived categories. Let ![]() $\phi :H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ be the morphism in
$\phi :H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ be the morphism in ![]() ${\rm Hom}_{{\mathcal {G}}_{an}}(X,Y)$ induced by
${\rm Hom}_{{\mathcal {G}}_{an}}(X,Y)$ induced by ![]() $\kappa (E)\sqrt {td_{X\times Y}}$. Let
$\kappa (E)\sqrt {td_{X\times Y}}$. Let ![]() $\widetilde {H}_0(\phi ):H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ be the value on
$\widetilde {H}_0(\phi ):H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ be the value on ![]() $\phi$ of the functor
$\phi$ of the functor ![]() $\widetilde {H}_0$, given in (1.5). Let
$\widetilde {H}_0$, given in (1.5). Let ![]() $\pi _X$ and
$\pi _X$ and ![]() $\pi _Y$ be the projections from
$\pi _Y$ be the projections from ![]() $X\times Y$. We prove in this section the following theorem.
$X\times Y$. We prove in this section the following theorem.
Theorem 5.1 (Proposition 5.22 and Lemma 5.7)
Assume that there exists an open subcone of the Kähler cone of ![]() $X$, such that
$X$, such that ![]() $\widetilde {H}_0(\phi )$ maps each Kähler class
$\widetilde {H}_0(\phi )$ maps each Kähler class ![]() $\omega _1$ in this subcone to a Kähler class
$\omega _1$ in this subcone to a Kähler class ![]() $\omega _2:=\widetilde {H}_0(\phi )(\omega _1)$ on
$\omega _2:=\widetilde {H}_0(\phi )(\omega _1)$ on ![]() $Y$ with respect to which
$Y$ with respect to which ![]() $E$ is
$E$ is ![]() $[\pi _X^*(\omega _1)+\pi _Y^*(\omega _2)]$-slope stable. Then for every IHSM
$[\pi _X^*(\omega _1)+\pi _Y^*(\omega _2)]$-slope stable. Then for every IHSM ![]() $X'$ deformation equivalent to
$X'$ deformation equivalent to ![]() $X$ there exists an IHSM
$X$ there exists an IHSM ![]() $Y'$ and a locally free (possibly twisted) coherent sheaf
$Y'$ and a locally free (possibly twisted) coherent sheaf ![]() $E'$ over
$E'$ over ![]() $X'\times Y'$, such that the pair
$X'\times Y'$, such that the pair ![]() $(X'\times Y',E')$ is deformation equivalent to
$(X'\times Y',E')$ is deformation equivalent to ![]() $(X\times Y,E)$.
$(X\times Y,E)$.
Note that the assumptions of the theorem are symmetric with respect to ![]() $X$ and
$X$ and ![]() $Y$, upon replacing
$Y$, upon replacing ![]() $E$ by
$E$ by ![]() $E^*$ and
$E^*$ and ![]() $\phi$ by
$\phi$ by ![]() $\phi ^{-1}$, and so the conclusions are symmetric as well. Proposition 5.22 is a slightly stronger version of the theorem, allowing the assumptions in the statement of the theorem to hold instead for a deformation
$\phi ^{-1}$, and so the conclusions are symmetric as well. Proposition 5.22 is a slightly stronger version of the theorem, allowing the assumptions in the statement of the theorem to hold instead for a deformation ![]() $(X_0\times Y_0,E_0)$ of the Fourier–Mukai kernel
$(X_0\times Y_0,E_0)$ of the Fourier–Mukai kernel ![]() $(X\times Y,E)$. Theorem 5.1 may be viewed as a global analogue, in the special case of classical and gerby deformations of locally free Fourier–Mukai kernels between IHSMs, of the infinitesimal deformability result of Toda for generalized deformations of Fourier–Mukai kernels [Reference TodaTod09, Theorem 1.1].
$(X\times Y,E)$. Theorem 5.1 may be viewed as a global analogue, in the special case of classical and gerby deformations of locally free Fourier–Mukai kernels between IHSMs, of the infinitesimal deformability result of Toda for generalized deformations of Fourier–Mukai kernels [Reference TodaTod09, Theorem 1.1].
The proof of Theorem 5.1 uses Verbitsky's results on hyperholomorphic vector bundles over hyper-Kähler manifolds and their deformability along twistor paths in moduli [Reference VerbitskyVer99b]. In § 5.1 we recall the notion of a twistor line in the moduli space of marked IHSMs. In § 5.2 we define the moduli space ![]() ${\mathfrak {M}}_\psi$ of rational Hodge isometries. Given a lattice
${\mathfrak {M}}_\psi$ of rational Hodge isometries. Given a lattice ![]() $\Lambda$ and a rational isometry
$\Lambda$ and a rational isometry ![]() $\psi \in O(\Lambda _{\mathbb {Q}})$, the moduli space
$\psi \in O(\Lambda _{\mathbb {Q}})$, the moduli space ![]() ${\mathfrak {M}}_\psi$ parametrizes isomorphism classes of quadruples
${\mathfrak {M}}_\psi$ parametrizes isomorphism classes of quadruples ![]() $(X_1,\eta _1,X_2,\eta _2)$ of deformation equivalent marked pairs
$(X_1,\eta _1,X_2,\eta _2)$ of deformation equivalent marked pairs ![]() $(X_i,\eta _i)$, where
$(X_i,\eta _i)$, where ![]() $\eta _i:H^2(X_i,{\mathbb {Z}})\rightarrow \Lambda$ is an isometry,
$\eta _i:H^2(X_i,{\mathbb {Z}})\rightarrow \Lambda$ is an isometry, ![]() $i=1,2$, such that
$i=1,2$, such that ![]() $\eta _2^{-1}\psi \eta _1:H^2(X_1,{\mathbb {Q}})\rightarrow H^2(X_2,{\mathbb {Q}})$ is a Hodge isometry which maps some Kähler class to a Kähler class. In § 5.3 we define diagonal twistor lines in
$\eta _2^{-1}\psi \eta _1:H^2(X_1,{\mathbb {Q}})\rightarrow H^2(X_2,{\mathbb {Q}})$ is a Hodge isometry which maps some Kähler class to a Kähler class. In § 5.3 we define diagonal twistor lines in ![]() ${\mathfrak {M}}_\psi$. In § 5.4 we define the notion of generic twistor paths and prove that every two points in the same connected component of
${\mathfrak {M}}_\psi$. In § 5.4 we define the notion of generic twistor paths and prove that every two points in the same connected component of ![]() ${\mathfrak {M}}_\psi$ are connected by such a path. In § 5.5 we review Verbitsky's result about hyperholomorphic vector bundles and their deformability along twistor paths in
${\mathfrak {M}}_\psi$ are connected by such a path. In § 5.5 we review Verbitsky's result about hyperholomorphic vector bundles and their deformability along twistor paths in ![]() ${\mathfrak {M}}_\psi$. In § 5.6 we associate to an equivalence
${\mathfrak {M}}_\psi$. In § 5.6 we associate to an equivalence ![]() $\Phi _E$ as in Theorem 5.1 a connected component
$\Phi _E$ as in Theorem 5.1 a connected component ![]() ${\mathfrak {M}}_\psi ^0$ of the moduli space of rational Hodge isometries. In § 5.7 we prove Theorem 5.1.
${\mathfrak {M}}_\psi ^0$ of the moduli space of rational Hodge isometries. In § 5.7 we prove Theorem 5.1.
5.1 Twistor lines
A marking of an IHSM ![]() $X$ is an isometry
$X$ is an isometry ![]() $\eta :H^2(X,{\mathbb {Z}})\rightarrow \Lambda$ with a fixed lattice
$\eta :H^2(X,{\mathbb {Z}})\rightarrow \Lambda$ with a fixed lattice ![]() $\Lambda$. Two marked pairs
$\Lambda$. Two marked pairs ![]() $(X_1,\eta _1)$ and
$(X_1,\eta _1)$ and ![]() $(X_2,\eta _2)$ are isomorphic, if there exists an isomorphism
$(X_2,\eta _2)$ are isomorphic, if there exists an isomorphism ![]() $f:X_1\rightarrow X_2$, such that
$f:X_1\rightarrow X_2$, such that ![]() $\eta _2=\eta _1\circ f^*$. The moduli space
$\eta _2=\eta _1\circ f^*$. The moduli space ![]() ${\mathfrak {M}}_\Lambda$ of isomorphism classes of marked IHSMs is a non-Hausdorff complex manifold of dimension
${\mathfrak {M}}_\Lambda$ of isomorphism classes of marked IHSMs is a non-Hausdorff complex manifold of dimension ![]() ${\rm rank}(\Lambda )-2$ (see [Reference HuybrechtsHuy99]).
${\rm rank}(\Lambda )-2$ (see [Reference HuybrechtsHuy99]).
Set ![]() $\Omega _\Lambda :=\{\ell \in {\mathbb {P}}(\Lambda _{\mathbb {C}}) \ : \ (\ell,\ell )=0 \ \mbox {and}\ (\lambda,\bar {\lambda })>0 \ \mbox {for all non-zero} \ \lambda \in \ell \}$. The period map
$\Omega _\Lambda :=\{\ell \in {\mathbb {P}}(\Lambda _{\mathbb {C}}) \ : \ (\ell,\ell )=0 \ \mbox {and}\ (\lambda,\bar {\lambda })>0 \ \mbox {for all non-zero} \ \lambda \in \ell \}$. The period map
is given by ![]() $P(X,\eta )=\eta (H^{2,0}(X))$. The restriction of the period map to every connected component of
$P(X,\eta )=\eta (H^{2,0}(X))$. The restriction of the period map to every connected component of ![]() ${\mathfrak {M}}_\Lambda$ is known to be surjective and generically injective, by Verbitsky's Torelli theorem [Reference HuybrechtsHuy12, Reference VerbitskyVer13]. Furthermore, if
${\mathfrak {M}}_\Lambda$ is known to be surjective and generically injective, by Verbitsky's Torelli theorem [Reference HuybrechtsHuy12, Reference VerbitskyVer13]. Furthermore, if ![]() ${\rm Pic}(X)$ is trivial, or cyclic generated by a class of non-negative BBF degree, then
${\rm Pic}(X)$ is trivial, or cyclic generated by a class of non-negative BBF degree, then ![]() $(X,\eta )$ is the unique point in the fiber of
$(X,\eta )$ is the unique point in the fiber of ![]() $P$ through the connected component of
$P$ through the connected component of ![]() ${\mathfrak {M}}_\Lambda$ containing
${\mathfrak {M}}_\Lambda$ containing ![]() $(X,\eta )$.
$(X,\eta )$.
The Torelli theorem solves the case of Theorem 1.1 in which the Hodge isometry ![]() $f$ is a parallel-transport operator.
$f$ is a parallel-transport operator.
Theorem 5.2 Let ![]() $(X,\eta )$ and
$(X,\eta )$ and ![]() $(X',\eta ')$ be two marked pairs in the same connected component of
$(X',\eta ')$ be two marked pairs in the same connected component of ![]() ${\mathfrak {M}}_\Lambda$ satisfying
${\mathfrak {M}}_\Lambda$ satisfying ![]() $P(X,\eta )=P(X',\eta ')$. There exist an analytic cycle
$P(X,\eta )=P(X',\eta ')$. There exist an analytic cycle ![]() $Z$ in
$Z$ in ![]() $X\times X'$, such that
$X\times X'$, such that ![]() $[Z]_*:H^*(X',{\mathbb {Z}})\rightarrow H^*(X,{\mathbb {Z}})$ is a parallel-transport operator, which restricts to
$[Z]_*:H^*(X',{\mathbb {Z}})\rightarrow H^*(X,{\mathbb {Z}})$ is a parallel-transport operator, which restricts to ![]() $H^2(X'_i,{\mathbb {Z}})$ as
$H^2(X'_i,{\mathbb {Z}})$ as ![]() $\eta ^{-1}\circ \eta '$.
$\eta ^{-1}\circ \eta '$.
Proof. The assumption that ![]() $(X,\eta )$ and
$(X,\eta )$ and ![]() $(X',\eta ')$ belong to the same connected component of
$(X',\eta ')$ belong to the same connected component of ![]() ${\mathfrak {M}}_\Lambda$ and have the same period implies that
${\mathfrak {M}}_\Lambda$ and have the same period implies that ![]() $(X,\eta )$ and
$(X,\eta )$ and ![]() $(X',\eta ')$ are inseparable points of
$(X',\eta ')$ are inseparable points of ![]() ${\mathfrak {M}}_\Lambda$, by Verbitsky's Torelli theorem [Reference HuybrechtsHuy12, Reference VerbitskyVer13]. Note also that
${\mathfrak {M}}_\Lambda$, by Verbitsky's Torelli theorem [Reference HuybrechtsHuy12, Reference VerbitskyVer13]. Note also that ![]() $\eta '\circ \eta ^{-1}$ is a parallel-transport operator, which is a Hodge isometry. The existence of the analytic cycle
$\eta '\circ \eta ^{-1}$ is a parallel-transport operator, which is a Hodge isometry. The existence of the analytic cycle ![]() $Z$ with the claimed properties thus follows from results of Huybrechts in [Reference HuybrechtsHuy03b] (see [Reference MarkmanMar11, Theorem 3.2]).
$Z$ with the claimed properties thus follows from results of Huybrechts in [Reference HuybrechtsHuy03b] (see [Reference MarkmanMar11, Theorem 3.2]).
Lemma 5.3 Let ![]() $X$ and
$X$ and ![]() $X'$ be IHSMs and let
$X'$ be IHSMs and let ![]() $f_i:H^*(X,{\mathbb {Z}})\rightarrow H^*(X',{\mathbb {Z}})$ be a parallel-transport operator,
$f_i:H^*(X,{\mathbb {Z}})\rightarrow H^*(X',{\mathbb {Z}})$ be a parallel-transport operator, ![]() $i=1,2$. Assume that
$i=1,2$. Assume that ![]() $f_1$ and
$f_1$ and ![]() $f_2$ restrict to the same parallel-transport operator
$f_2$ restrict to the same parallel-transport operator ![]() $f:H^2(X,{\mathbb {Z}})\rightarrow H^2(X',{\mathbb {Z}})$. Then there exist automorphisms
$f:H^2(X,{\mathbb {Z}})\rightarrow H^2(X',{\mathbb {Z}})$. Then there exist automorphisms ![]() $g\in {\rm Aut}(X)$ and
$g\in {\rm Aut}(X)$ and ![]() $g'\in {\rm Aut}(X')$, acting trivially on the second cohomologies, such that
$g'\in {\rm Aut}(X')$, acting trivially on the second cohomologies, such that ![]() $f_2=g'_*\circ f_1\circ g_*$.
$f_2=g'_*\circ f_1\circ g_*$.
Proof. There exist families ![]() $\pi _i:{\mathcal {X}}_i\rightarrow B_i$ over connected analytic spaces
$\pi _i:{\mathcal {X}}_i\rightarrow B_i$ over connected analytic spaces ![]() $B_i$, points
$B_i$, points ![]() $b_i$,
$b_i$, ![]() $b_i'\in B_i$, and continuous paths
$b_i'\in B_i$, and continuous paths ![]() $\gamma _i$ from
$\gamma _i$ from ![]() $b_i$ to
$b_i$ to ![]() $b_i'$ in
$b_i'$ in ![]() $B_i$, such that
$B_i$, such that ![]() $f_i$ is the parallel-transport operator along
$f_i$ is the parallel-transport operator along ![]() $\gamma _i$ in the local system
$\gamma _i$ in the local system ![]() $R\pi _{i,*}{\mathbb {Z}}$,
$R\pi _{i,*}{\mathbb {Z}}$, ![]() $i=1,2$. We may and do assume that
$i=1,2$. We may and do assume that ![]() $B_i$ is simply connected, possibly after passing to the universal cover and lifting the path
$B_i$ is simply connected, possibly after passing to the universal cover and lifting the path ![]() $\gamma _i$. Choose an isometric trivialization
$\gamma _i$. Choose an isometric trivialization ![]() $\eta _i:R^2\pi _{i,*}{\mathbb {Z}}\rightarrow \underline {\Lambda }$, where
$\eta _i:R^2\pi _{i,*}{\mathbb {Z}}\rightarrow \underline {\Lambda }$, where ![]() $\underline {\Lambda }$ is the trivial local system over
$\underline {\Lambda }$ is the trivial local system over ![]() $B_i$ with a fixed lattice
$B_i$ with a fixed lattice ![]() $\Lambda$, with
$\Lambda$, with ![]() $\eta _{1,b_1}=\eta _{2,b_2}:H^2(X,{\mathbb {Z}})\rightarrow \Lambda$. Set
$\eta _{1,b_1}=\eta _{2,b_2}:H^2(X,{\mathbb {Z}})\rightarrow \Lambda$. Set ![]() $\eta :=\eta _{1,b_1}$. Set
$\eta :=\eta _{1,b_1}$. Set ![]() $\eta ':=\eta \circ f^{-1}$. We get that
$\eta ':=\eta \circ f^{-1}$. We get that ![]() $\eta _{i,b_i'}=\eta '$, for
$\eta _{i,b_i'}=\eta '$, for ![]() $i=1,2$.
$i=1,2$.
Let ![]() ${\mathfrak {M}}_\Lambda ^0$ be the connected component of the moduli space of isomorphism classes of marked IHSMs containing the isomorphism class
${\mathfrak {M}}_\Lambda ^0$ be the connected component of the moduli space of isomorphism classes of marked IHSMs containing the isomorphism class ![]() $[(X,\eta )]$ of
$[(X,\eta )]$ of ![]() $(X,\eta )$. Let
$(X,\eta )$. Let ![]() $s_i:B_i\rightarrow {\mathfrak {M}}_\Lambda ^0$ be the classifying morphism associated to
$s_i:B_i\rightarrow {\mathfrak {M}}_\Lambda ^0$ be the classifying morphism associated to ![]() $\eta _i$. Set
$\eta _i$. Set ![]() $q:=[(X,\eta )]=s_1(X,\eta _{1,b_1})=s_2(X,\eta _{2,b_2})$ and
$q:=[(X,\eta )]=s_1(X,\eta _{1,b_1})=s_2(X,\eta _{2,b_2})$ and ![]() $q':=[(X,\eta ')]=s_1(X',\eta _{1,b_1'})=s_2(X',\eta _{2,b_2'})$.
$q':=[(X,\eta ')]=s_1(X',\eta _{1,b_1'})=s_2(X',\eta _{2,b_2'})$.
There exists over ![]() ${\mathfrak {M}}_\Lambda ^0$ a universal family
${\mathfrak {M}}_\Lambda ^0$ a universal family ![]() $\Pi :{\mathcal {Y}}\rightarrow {\mathfrak {M}}_\Lambda ^0$ and isomorphisms
$\Pi :{\mathcal {Y}}\rightarrow {\mathfrak {M}}_\Lambda ^0$ and isomorphisms ![]() $h_i:{\mathcal {X}}_i\rightarrow s_i^{-1}({\mathcal {Y}})$ of the two families
$h_i:{\mathcal {X}}_i\rightarrow s_i^{-1}({\mathcal {Y}})$ of the two families ![]() $\pi _i$ and
$\pi _i$ and ![]() $s_i^{-1}(\Pi )$ over
$s_i^{-1}(\Pi )$ over ![]() $B_i$, by [Reference MarkmanMar21b, Theorem 1.1] and our assumption that
$B_i$, by [Reference MarkmanMar21b, Theorem 1.1] and our assumption that ![]() $B_i$ is simply connected, for
$B_i$ is simply connected, for ![]() $i=1,2$. Furthermore, the local system
$i=1,2$. Furthermore, the local system ![]() $R\Pi _*{\mathbb {Z}}$ over
$R\Pi _*{\mathbb {Z}}$ over ![]() ${\mathfrak {M}}_\Lambda ^0$ is trivial, by [Reference MarkmanMar21b, Lemma 2.1]. Hence, the paths
${\mathfrak {M}}_\Lambda ^0$ is trivial, by [Reference MarkmanMar21b, Lemma 2.1]. Hence, the paths ![]() $s_i\circ \gamma _i$,
$s_i\circ \gamma _i$, ![]() $i=1,2$, from
$i=1,2$, from ![]() $q$ to
$q$ to ![]() $q'$ in
$q'$ in ![]() ${\mathfrak {M}}_\Lambda ^0$ induce the same parallel-transport operator from the fiber
${\mathfrak {M}}_\Lambda ^0$ induce the same parallel-transport operator from the fiber ![]() $Y_q$ of
$Y_q$ of ![]() ${\mathcal {Y}}$ over
${\mathcal {Y}}$ over ![]() $q$ to the fiber
$q$ to the fiber ![]() $Y_{q'}$ of
$Y_{q'}$ of ![]() ${\mathcal {Y}}$ over
${\mathcal {Y}}$ over ![]() $q'$. Let
$q'$. Let ![]() $h_{i,b_i}:X\rightarrow Y_q$ and
$h_{i,b_i}:X\rightarrow Y_q$ and ![]() $h_{i,b_i'}:X'\rightarrow Y_{q'}$ be the isomorphism associated to
$h_{i,b_i'}:X'\rightarrow Y_{q'}$ be the isomorphism associated to ![]() $h_i$,
$h_i$, ![]() $i=1,2$. We conclude that
$i=1,2$. We conclude that ![]() $h_{i,b_i'}\circ f_i\circ h^{-1}_{i,b_i}$ is the parallel-transport along
$h_{i,b_i'}\circ f_i\circ h^{-1}_{i,b_i}$ is the parallel-transport along ![]() $s_i\circ \gamma _i$,
$s_i\circ \gamma _i$, ![]() $i=1,2$, and so
$i=1,2$, and so
Then ![]() $g:=h_{1,b_1}^{-1}\circ h_{2,b_2}\in {\rm Aut}(X)$ and
$g:=h_{1,b_1}^{-1}\circ h_{2,b_2}\in {\rm Aut}(X)$ and ![]() $g':=h_{2,b_2'}^{-1}\circ h_{1,b_1'}\in {\rm Aut}(X')$ are automorphisms satisfying
$g':=h_{2,b_2'}^{-1}\circ h_{1,b_1'}\in {\rm Aut}(X')$ are automorphisms satisfying ![]() $f_2=g'_*\circ f_1\circ g_*$.
$f_2=g'_*\circ f_1\circ g_*$.
Given a positive-definite three-dimensional subspace ![]() $W$ of
$W$ of ![]() $\Lambda _{\mathbb {R}}$, set
$\Lambda _{\mathbb {R}}$, set ![]() $W_{\mathbb {C}}:=W\otimes _{\mathbb {R}}{\mathbb {C}}$. We get the projective conic curve
$W_{\mathbb {C}}:=W\otimes _{\mathbb {R}}{\mathbb {C}}$. We get the projective conic curve ![]() ${\mathbb {P}}(W_{\mathbb {C}})\cap \Omega _\Lambda$, which is called a twistor line. Let
${\mathbb {P}}(W_{\mathbb {C}})\cap \Omega _\Lambda$, which is called a twistor line. Let ![]() $(X,\eta )$ be a marked pair in
$(X,\eta )$ be a marked pair in ![]() ${\mathfrak {M}}_\Lambda$ and
${\mathfrak {M}}_\Lambda$ and ![]() $\omega \in H^{1,1}(X,{\mathbb {R}})$ a Kähler class. The intersection of
$\omega \in H^{1,1}(X,{\mathbb {R}})$ a Kähler class. The intersection of ![]() $W_{\mathbb {C}}:=H^{2,0}(X)\oplus H^{0,2}(X)\oplus {\mathbb {C}}\omega$ with
$W_{\mathbb {C}}:=H^{2,0}(X)\oplus H^{0,2}(X)\oplus {\mathbb {C}}\omega$ with ![]() $H^2(X,{\mathbb {R}})$ is a positive-definite three-dimensional subspace
$H^2(X,{\mathbb {R}})$ is a positive-definite three-dimensional subspace ![]() $W$ and the twistor line
$W$ and the twistor line ![]() $Q_{(X,\eta,\omega )}:={\mathbb {P}}(\eta (W_{\mathbb {C}}))\cap \Omega _\Lambda$ passes through
$Q_{(X,\eta,\omega )}:={\mathbb {P}}(\eta (W_{\mathbb {C}}))\cap \Omega _\Lambda$ passes through ![]() $P(X,\eta )$. We endow
$P(X,\eta )$. We endow ![]() $W$ with the orientation associated to the basis
$W$ with the orientation associated to the basis
for a non-zero class ![]() $\sigma \in H^{2,0}(X)$. There exists a family
$\sigma \in H^{2,0}(X)$. There exists a family
of IHSMs with fiber ![]() $X$ over the point
$X$ over the point ![]() $P(X,\eta )$, known as the twistor family associated to
$P(X,\eta )$, known as the twistor family associated to ![]() $\omega$, with the following properties [Reference HuybrechtsHuy99, paragraph 1.17, p. 76]. The marking
$\omega$, with the following properties [Reference HuybrechtsHuy99, paragraph 1.17, p. 76]. The marking ![]() $\eta$ extends to a trivialization of the local system
$\eta$ extends to a trivialization of the local system ![]() $R^2\pi _*{\mathbb {Z}}$, as
$R^2\pi _*{\mathbb {Z}}$, as ![]() $Q_{(X,\eta,\omega )}$ is simply connected. Denote by
$Q_{(X,\eta,\omega )}$ is simply connected. Denote by ![]() $\eta _t$ the resulting marking of the fiber
$\eta _t$ the resulting marking of the fiber ![]() $X_t$ of
$X_t$ of ![]() $\pi$ over
$\pi$ over ![]() $t\in Q_{(X,\eta,\omega )}$. Then
$t\in Q_{(X,\eta,\omega )}$. Then
for each ![]() $t\in Q_{(X,\eta,\omega )}$ and the line in
$t\in Q_{(X,\eta,\omega )}$ and the line in ![]() $H^2(X_t,{\mathbb {R}})$, which is contained in
$H^2(X_t,{\mathbb {R}})$, which is contained in ![]() $\eta _t^{-1}(\eta (W))$ and orthogonal to
$\eta _t^{-1}(\eta (W))$ and orthogonal to ![]() $H^{2,0}(X_t)$, is spanned by a Kähler class
$H^{2,0}(X_t)$, is spanned by a Kähler class ![]() $\omega _t$. The twistor family depends only on the ray in the Kähler cone of
$\omega _t$. The twistor family depends only on the ray in the Kähler cone of ![]() $X$ through
$X$ through ![]() $\omega$. Denote by
$\omega$. Denote by
the ray through ![]() $\omega _t$ in the Kähler cone
$\omega _t$ in the Kähler cone ![]() ${\mathcal {K}}_{X_t}$ of
${\mathcal {K}}_{X_t}$ of ![]() $X_t$. The curve
$X_t$. The curve
in ![]() ${\mathfrak {M}}^0_\Lambda$ is mapped isomorphically onto
${\mathfrak {M}}^0_\Lambda$ is mapped isomorphically onto ![]() $Q_{(X,\eta,\omega )}$ via the period map. The curve
$Q_{(X,\eta,\omega )}$ via the period map. The curve ![]() $\widetilde {Q}_{(X,\eta,\omega )}$ is called the twistor line through
$\widetilde {Q}_{(X,\eta,\omega )}$ is called the twistor line through ![]() $(X,\eta )$ associated to
$(X,\eta )$ associated to ![]() $\omega$. The twistor line
$\omega$. The twistor line ![]() $\widetilde {Q}_{(X,\eta,\omega )}$ is said to be generic, if
$\widetilde {Q}_{(X,\eta,\omega )}$ is said to be generic, if ![]() ${\rm Pic}(X_t)$ is trivial, for some
${\rm Pic}(X_t)$ is trivial, for some ![]() $t\in Q_{(X,\eta,\omega )}$. This is the case for
$t\in Q_{(X,\eta,\omega )}$. This is the case for ![]() $\omega$ in the complement of a countable union of hyperplanes in the Kähler cone.
$\omega$ in the complement of a countable union of hyperplanes in the Kähler cone.
5.2 Moduli spaces of rational Hodge isometries
Fix a deformation class of IHSMs with a second integral cohomology lattice isometric to a lattice ![]() $\Lambda$. Let
$\Lambda$. Let ![]() $\psi \in O(\Lambda _{\mathbb {Q}})$ be a rational isometry. Let
$\psi \in O(\Lambda _{\mathbb {Q}})$ be a rational isometry. Let ![]() ${\mathfrak {M}}_\psi$ be the moduli space of isomorphism classes of quadruples
${\mathfrak {M}}_\psi$ be the moduli space of isomorphism classes of quadruples ![]() $(X_1,\eta _1,X_2,\eta _2)$, where
$(X_1,\eta _1,X_2,\eta _2)$, where ![]() $\eta _i:H^2(X_i,{\mathbb {Z}})\rightarrow \Lambda$ is a marking, such that
$\eta _i:H^2(X_i,{\mathbb {Z}})\rightarrow \Lambda$ is a marking, such that ![]() $\eta _2^{-1}\psi \eta _1:H^2(X_1,{\mathbb {Q}})\rightarrow H^2(X_2,{\mathbb {Q}})$ is a Hodge isometry which maps some Kähler class to a Kähler class. Two quadruples
$\eta _2^{-1}\psi \eta _1:H^2(X_1,{\mathbb {Q}})\rightarrow H^2(X_2,{\mathbb {Q}})$ is a Hodge isometry which maps some Kähler class to a Kähler class. Two quadruples ![]() $(X_1,\eta _1,X_2,\eta _2)$ and
$(X_1,\eta _1,X_2,\eta _2)$ and ![]() $(X'_1,\eta '_1,X'_2,\eta '_2)$ are isomorphic, if the marked pair
$(X'_1,\eta '_1,X'_2,\eta '_2)$ are isomorphic, if the marked pair ![]() $(X_i,\eta _i)$ is isomorphic to
$(X_i,\eta _i)$ is isomorphic to ![]() $(X'_i,\eta '_i)$, for
$(X'_i,\eta '_i)$, for ![]() $i=1,2$. The moduli space
$i=1,2$. The moduli space ![]() ${\mathfrak {M}}_\psi$ has a natural structure of a non-Hausdorff complex manifold. The proof of the latter statement is identical to that of [Reference BuskinBus19, Proposition 4.9]. The isometry
${\mathfrak {M}}_\psi$ has a natural structure of a non-Hausdorff complex manifold. The proof of the latter statement is identical to that of [Reference BuskinBus19, Proposition 4.9]. The isometry ![]() $\psi$ induces an automorphism of
$\psi$ induces an automorphism of ![]() $\Omega _\Lambda$ which we denote by
$\Omega _\Lambda$ which we denote by ![]() $\psi$ as well.
$\psi$ as well.
Lemma 5.4 If ![]() $(X_1,\eta _1,X_2,\eta _2)$ belongs to
$(X_1,\eta _1,X_2,\eta _2)$ belongs to ![]() ${\mathfrak {M}}_\psi$, then
${\mathfrak {M}}_\psi$, then ![]() $P(X_2,\eta _2)=\psi (P(X_1,\eta _1))$.
$P(X_2,\eta _2)=\psi (P(X_1,\eta _1))$.
Proof. The composition ![]() $\eta _2^{-1}\psi \eta _1:H^2(X_1,{\mathbb {Q}})\rightarrow H^2(X_2,{\mathbb {Q}})$ is a Hodge isometry. Hence,
$\eta _2^{-1}\psi \eta _1:H^2(X_1,{\mathbb {Q}})\rightarrow H^2(X_2,{\mathbb {Q}})$ is a Hodge isometry. Hence, ![]() $P(X_2,\eta _2):=\eta _2(H^{2,0}(X_2))=[\eta _2\circ (\eta _2^{-1}\psi \eta _1)](H^{2,0}(X_1))=\psi (P(X_1,\eta _1)).$
$P(X_2,\eta _2):=\eta _2(H^{2,0}(X_2))=[\eta _2\circ (\eta _2^{-1}\psi \eta _1)](H^{2,0}(X_1))=\psi (P(X_1,\eta _1)).$
Given a quadruple ![]() $q:=(X_1,\eta _1,X_2,\eta _2)$ in
$q:=(X_1,\eta _1,X_2,\eta _2)$ in ![]() ${\mathfrak {M}}_\psi$ set
${\mathfrak {M}}_\psi$ set
Let ![]() $\omega _1$ be a Kähler class on
$\omega _1$ be a Kähler class on ![]() $X_1$, such that
$X_1$, such that ![]() $\omega _2:=\psi _q(\omega _1)$ is a Kähler class on
$\omega _2:=\psi _q(\omega _1)$ is a Kähler class on ![]() $X_2$. Note that
$X_2$. Note that ![]() $\psi :\Omega _\Lambda \rightarrow \Omega _\Lambda$ maps the twistor line
$\psi :\Omega _\Lambda \rightarrow \Omega _\Lambda$ maps the twistor line ![]() $Q_{(X_1,\eta _1,\omega _1)}$ to the twistor line
$Q_{(X_1,\eta _1,\omega _1)}$ to the twistor line ![]() $Q_{(X_2,\eta _2,\omega _2)}$. Let
$Q_{(X_2,\eta _2,\omega _2)}$. Let ![]() $(X_{i,t},\eta _{i,t})$,
$(X_{i,t},\eta _{i,t})$, ![]() $t\in Q_{(X_i,\eta _i,\omega _i)}$, be the point of
$t\in Q_{(X_i,\eta _i,\omega _i)}$, be the point of ![]() $\widetilde {Q}_{(X_i,\eta _i,\omega _i)}$ over
$\widetilde {Q}_{(X_i,\eta _i,\omega _i)}$ over ![]() $t$, for
$t$, for ![]() $i=1,2$.
$i=1,2$.
Lemma 5.5 The rays ![]() $R_t$ and
$R_t$ and ![]() $R_{\psi (t)}$ in the Kähler cones of
$R_{\psi (t)}$ in the Kähler cones of ![]() $X_{1,t}$ and
$X_{1,t}$ and ![]() $X_{2,\psi (t)}$, given in (5.4), satisfy the equality
$X_{2,\psi (t)}$, given in (5.4), satisfy the equality ![]() $\psi (\eta _{1,t}(R_t))=\eta _{2,\psi (t)}(R_{\psi (t)})$, for each
$\psi (\eta _{1,t}(R_t))=\eta _{2,\psi (t)}(R_{\psi (t)})$, for each ![]() $t\in Q_{(X_1,\eta _1,\omega _1)}$. Consequently, the quadruple
$t\in Q_{(X_1,\eta _1,\omega _1)}$. Consequently, the quadruple ![]() $(X_{1,t},\eta _{1,t},X_{2,\psi (t)},\eta _{2,\psi (t)})$ belongs to
$(X_{1,t},\eta _{1,t},X_{2,\psi (t)},\eta _{2,\psi (t)})$ belongs to ![]() ${\mathfrak {M}}_\psi$, for all
${\mathfrak {M}}_\psi$, for all ![]() $t\in Q_{(X_1,\eta _1,\omega _1)}$.
$t\in Q_{(X_1,\eta _1,\omega _1)}$.
Proof. Let ![]() ${\mathcal {C}}_{X_i}:=\{\lambda \in H^{1,1}(X_i,{\mathbb {R}}) \ : \ (\lambda,\lambda )>0\}$ be the positive cone,
${\mathcal {C}}_{X_i}:=\{\lambda \in H^{1,1}(X_i,{\mathbb {R}}) \ : \ (\lambda,\lambda )>0\}$ be the positive cone, ![]() $i=1,2$. Each
$i=1,2$. Each ![]() ${\mathcal {C}}_{X_i}$ has two connected components and we denote by
${\mathcal {C}}_{X_i}$ has two connected components and we denote by ![]() ${\mathcal {C}}_{X_i}^+$ the one which contains the Kähler cone. The isometry
${\mathcal {C}}_{X_i}^+$ the one which contains the Kähler cone. The isometry ![]() $\psi _q$ maps
$\psi _q$ maps ![]() ${\mathcal {C}}_{X_1}$ isomorphically onto
${\mathcal {C}}_{X_1}$ isomorphically onto ![]() ${\mathcal {C}}_{X_2}$ and
${\mathcal {C}}_{X_2}$ and ![]() $\psi _q({\mathcal {K}}_{X_1})\cap K_{X_2}$ is non-empty, hence
$\psi _q({\mathcal {K}}_{X_1})\cap K_{X_2}$ is non-empty, hence ![]() $\psi _q({\mathcal {C}}_{X_1}^+)={\mathcal {C}}_{X_2}^+$. Equivalently,
$\psi _q({\mathcal {C}}_{X_1}^+)={\mathcal {C}}_{X_2}^+$. Equivalently, ![]() $\psi (\eta _{1,t_0}({\mathcal {C}}^+_{X_{t_0}}))=\eta _{2,\psi (t_0)}({\mathcal {C}}^+_{X_{\psi (t_0)}})$, where
$\psi (\eta _{1,t_0}({\mathcal {C}}^+_{X_{t_0}}))=\eta _{2,\psi (t_0)}({\mathcal {C}}^+_{X_{\psi (t_0)}})$, where ![]() $t_0=P(X_1,\eta _1)$. Hence,
$t_0=P(X_1,\eta _1)$. Hence, ![]() $\psi (\eta _{1,t}({\mathcal {C}}^+_{X_{t}}))=\eta _{2,\psi (t)}({\mathcal {C}}^+_{X_{\psi (t)}})$, for all
$\psi (\eta _{1,t}({\mathcal {C}}^+_{X_{t}}))=\eta _{2,\psi (t)}({\mathcal {C}}^+_{X_{\psi (t)}})$, for all ![]() $t\in Q_{(X_1,\eta _1,\omega _1)}$, by continuity and connectedness of
$t\in Q_{(X_1,\eta _1,\omega _1)}$, by continuity and connectedness of ![]() $Q_{(X_1,\eta _1,\omega _1)}$. We know that
$Q_{(X_1,\eta _1,\omega _1)}$. We know that ![]() $\psi$ maps the line spanned by
$\psi$ maps the line spanned by ![]() $\eta _{1,t}(R_t)$ to the line spanned by
$\eta _{1,t}(R_t)$ to the line spanned by ![]() $\eta _{2,\psi (t)}(R_{\psi (t)})$, since
$\eta _{2,\psi (t)}(R_{\psi (t)})$, since ![]() $\eta _{2,t}^{-1}\psi \eta _{1,t}$ is a Hodge isometry which maps the positive-definite three-dimensional subspace
$\eta _{2,t}^{-1}\psi \eta _{1,t}$ is a Hodge isometry which maps the positive-definite three-dimensional subspace ![]() $W_1$ associated to
$W_1$ associated to ![]() $(X_1,\eta _1,\omega _1)$ to the positive-definite three-dimensional subspace
$(X_1,\eta _1,\omega _1)$ to the positive-definite three-dimensional subspace ![]() $W_2$ associated to
$W_2$ associated to ![]() $(X_2,\eta _2,\omega _2)$ and
$(X_2,\eta _2,\omega _2)$ and ![]() $\eta _{1,t}(R_t)$ spans the line in
$\eta _{1,t}(R_t)$ spans the line in ![]() $W_1$ orthogonal to
$W_1$ orthogonal to ![]() $\eta _{1,t}(H^{2,0}(X_t))$ and
$\eta _{1,t}(H^{2,0}(X_t))$ and ![]() $\eta _{2,t}(R_{\psi (t)})$ spans the line in
$\eta _{2,t}(R_{\psi (t)})$ spans the line in ![]() $W_2$ orthogonal to
$W_2$ orthogonal to ![]() $\eta _{2,t}(H^{2,0}(X_{\psi (t)}))$. Now,
$\eta _{2,t}(H^{2,0}(X_{\psi (t)}))$. Now, ![]() $R_t$ is the intersection of the line spanned by it with
$R_t$ is the intersection of the line spanned by it with ![]() ${\mathcal {C}}^+_{X_{t}}$ and the similar statement holds for
${\mathcal {C}}^+_{X_{t}}$ and the similar statement holds for ![]() $R_{\psi (t)}$. Hence,
$R_{\psi (t)}$. Hence, ![]() $\psi (\eta _{1,t}(R_{t}))=\eta _{2,\psi (t)}(R_{\psi (t)})$.
$\psi (\eta _{1,t}(R_{t}))=\eta _{2,\psi (t)}(R_{\psi (t)})$.
Lemma 5.5 enables us to define the twistor line in ![]() ${\mathfrak {M}}_\psi ^0$ through
${\mathfrak {M}}_\psi ^0$ through ![]() $(X_1,\eta _1,X_2,\eta _2)$ determined by
$(X_1,\eta _1,X_2,\eta _2)$ determined by ![]() $\omega _1\in {\mathcal {K}}_{X_1}\cap \psi _q^{-1}({\mathcal {K}}_{X_2})$ to be the curve
$\omega _1\in {\mathcal {K}}_{X_1}\cap \psi _q^{-1}({\mathcal {K}}_{X_2})$ to be the curve
5.3 Diagonal twistor lines
We explain next that the twistor line (5.6) in the above definition is associated to a hyper-Kähler structure on the differential manifold underlying the product ![]() $X_1\times X_2$. This fact is used in the proof of Proposition 5.15. A Kähler class on an IHSM
$X_1\times X_2$. This fact is used in the proof of Proposition 5.15. A Kähler class on an IHSM ![]() $X$ determines a Ricci-flat hermitian metric
$X$ determines a Ricci-flat hermitian metric ![]() $g$ on the manifold
$g$ on the manifold ![]() $M$ underlying
$M$ underlying ![]() $X$, by the Calabi–Yau theorem [Reference BeauvilleBea83]. The metric
$X$, by the Calabi–Yau theorem [Reference BeauvilleBea83]. The metric ![]() $g$ admits three complex structures
$g$ admits three complex structures ![]() $I$,
$I$, ![]() $J$, and
$J$, and ![]() $K$, satisfying the quaternionic relation
$K$, satisfying the quaternionic relation ![]() $IJ=K$, such that
$IJ=K$, such that ![]() $X$ is the complex manifold
$X$ is the complex manifold ![]() $(M,I)$. For each point
$(M,I)$. For each point ![]() $t$ in the unit sphere
$t$ in the unit sphere ![]() $S^2:=\{(a,b,c) \ : \ a^2+b^2+c^2=1\!\}$, we get the unit purely imaginary quaternion
$S^2:=\{(a,b,c) \ : \ a^2+b^2+c^2=1\!\}$, we get the unit purely imaginary quaternion ![]() $I_t:=aI+bJ+cK$, which is a complex structure on
$I_t:=aI+bJ+cK$, which is a complex structure on ![]() $M$. The
$M$. The ![]() $2$-form
$2$-form ![]() $\omega _{I_t}:=g(I_t(\bullet ),(\bullet ))$ is a Kähler form. The original class
$\omega _{I_t}:=g(I_t(\bullet ),(\bullet ))$ is a Kähler form. The original class ![]() $\omega$ is the cohomology class of the
$\omega$ is the cohomology class of the ![]() $2$-form
$2$-form ![]() $\omega _I:=g(I(\bullet ),(\bullet ))$. The classes of
$\omega _I:=g(I(\bullet ),(\bullet ))$. The classes of ![]() $\{\omega _I,\omega _J,\omega _K\!\}$ form a basis for the positive-definite three-dimensional subspace
$\{\omega _I,\omega _J,\omega _K\!\}$ form a basis for the positive-definite three-dimensional subspace ![]() $W\subset H^2(X,{\mathbb {R}})$ whose complexification is
$W\subset H^2(X,{\mathbb {R}})$ whose complexification is ![]() $H^{2,0}(X)\oplus H^{0,2}(X)\oplus {\mathbb {C}}\omega$. The latter basis is orthogonal with respect to the BBF pairing, and the BBF degrees of the three classes are the same. Conversely, a choice of an orthogonal basis of
$H^{2,0}(X)\oplus H^{0,2}(X)\oplus {\mathbb {C}}\omega$. The latter basis is orthogonal with respect to the BBF pairing, and the BBF degrees of the three classes are the same. Conversely, a choice of an orthogonal basis of ![]() $W$ with the same orientation consisting of
$W$ with the same orientation consisting of ![]() $\omega$ and two classes of the same BBF degree as
$\omega$ and two classes of the same BBF degree as ![]() $\omega$ determines complex structures
$\omega$ determines complex structures ![]() $J$ and
$J$ and ![]() $K$ and an action of the unit purely imaginary quaternions on the tangent bundle of
$K$ and an action of the unit purely imaginary quaternions on the tangent bundle of ![]() $M$ via parallel complex structures. The above
$M$ via parallel complex structures. The above ![]() $2$-sphere of complex structures is thus naturally identified with the unit sphere in
$2$-sphere of complex structures is thus naturally identified with the unit sphere in ![]() $W$.
$W$.
The standard complex structure on the unit sphere combines with the above construction to define a complex structure on ![]() $S^2\times M$, such that the first projection
$S^2\times M$, such that the first projection ![]() $\pi :S^2\times M\rightarrow S^2$ is holomorphic and the fiber over
$\pi :S^2\times M\rightarrow S^2$ is holomorphic and the fiber over ![]() $t$ is
$t$ is ![]() $(M,I_t)$, giving rise to the twistor family (5.3) (see [Reference Hitchin, Karlhede, Lindström and RočekHKLR87]). The base of the twistor family is thus naturally identified with the unit sphere in the positive-definite three-dimensional subspace
$(M,I_t)$, giving rise to the twistor family (5.3) (see [Reference Hitchin, Karlhede, Lindström and RočekHKLR87]). The base of the twistor family is thus naturally identified with the unit sphere in the positive-definite three-dimensional subspace ![]() $W$ of
$W$ of ![]() $H^2(X,{\mathbb {R}})$ via the isomorphism sending a class
$H^2(X,{\mathbb {R}})$ via the isomorphism sending a class ![]() $\omega '$ in the unit sphere in
$\omega '$ in the unit sphere in ![]() $W$ to the uniqueFootnote 8 isotropic line in
$W$ to the uniqueFootnote 8 isotropic line in ![]() ${\mathbb {P}}(W_{\mathbb {C}})$, which is orthogonal to
${\mathbb {P}}(W_{\mathbb {C}})$, which is orthogonal to ![]() $\omega '$ and induces on
$\omega '$ and induces on ![]() $W$ the same orientation induced by
$W$ the same orientation induced by ![]() $H^{2,0}(X)$ in (5.2).
$H^{2,0}(X)$ in (5.2).
Let ![]() $M_i$ be the differential manifold underlying
$M_i$ be the differential manifold underlying ![]() $X_i$,
$X_i$, ![]() $i=1,2$. Let
$i=1,2$. Let ![]() $g_1$ be the Ricci-flat hermitian metric on
$g_1$ be the Ricci-flat hermitian metric on ![]() $M_1$ associated with the Kähler class
$M_1$ associated with the Kähler class ![]() $\omega _1$ in (5.6) and let
$\omega _1$ in (5.6) and let ![]() $g_2$ be the metric on
$g_2$ be the metric on ![]() $M_2$ associated with the Kähler class
$M_2$ associated with the Kähler class ![]() $\omega _2:=\psi _q(\omega _1)$. Let
$\omega _2:=\psi _q(\omega _1)$. Let ![]() $W_i$ be the positive-definite three-dimensional subspace of
$W_i$ be the positive-definite three-dimensional subspace of ![]() $H^2(X_i,{\mathbb {R}})$, whose complexification is
$H^2(X_i,{\mathbb {R}})$, whose complexification is ![]() $H^{2,0}(X_i)\oplus H^{0,2}(X_i)\oplus {\mathbb {C}} w_i$. We have the equality
$H^{2,0}(X_i)\oplus H^{0,2}(X_i)\oplus {\mathbb {C}} w_i$. We have the equality ![]() $W_2=\psi _q(W_1)$, and
$W_2=\psi _q(W_1)$, and ![]() $\psi _q$ maps the unit sphere in
$\psi _q$ maps the unit sphere in ![]() $W_1$ to that in
$W_1$ to that in ![]() $W_2$, as
$W_2$, as ![]() $\psi _q$ is a Hodge isometry. Hence,
$\psi _q$ is a Hodge isometry. Hence, ![]() $\psi$ restricts to an isometry from
$\psi$ restricts to an isometry from ![]() $\eta _1(W_1)$ onto
$\eta _1(W_1)$ onto ![]() $\eta _2(W_2)$, which maps the twistor line
$\eta _2(W_2)$, which maps the twistor line ![]() $Q_{(X_1,\eta _1,\omega _1)}$ isomorphically onto
$Q_{(X_1,\eta _1,\omega _1)}$ isomorphically onto ![]() $Q_{(X_2,\eta _2,\omega _2)}$. Denote by
$Q_{(X_2,\eta _2,\omega _2)}$. Denote by
the graph of the restriction of ![]() $\psi$. Let
$\psi$. Let ![]() $\pi _i:{\mathcal {X}}_i\rightarrow Q_{(X_i,\eta _i,\omega _i)}$ be the twistor family through
$\pi _i:{\mathcal {X}}_i\rightarrow Q_{(X_i,\eta _i,\omega _i)}$ be the twistor family through ![]() $(X_i,\eta _i)$ associated to
$(X_i,\eta _i)$ associated to ![]() $\omega _i$,
$\omega _i$, ![]() $i=1,2$. The twistor line (5.6) is the lift of
$i=1,2$. The twistor line (5.6) is the lift of ![]() $Q_{(X_1,\eta _1,X_2,\eta _2),\omega _1}$ to a curve in
$Q_{(X_1,\eta _1,X_2,\eta _2),\omega _1}$ to a curve in ![]() ${\mathfrak {M}}^0_\psi$ obtained via the extensions of
${\mathfrak {M}}^0_\psi$ obtained via the extensions of ![]() $\eta _i$ to a trivialization of
$\eta _i$ to a trivialization of ![]() $R\pi _{i,*}^2{\mathbb {Z}}$,
$R\pi _{i,*}^2{\mathbb {Z}}$, ![]() $i=1,2$. Choose an orthogonal basis of
$i=1,2$. Choose an orthogonal basis of ![]() $W_1$, extending
$W_1$, extending ![]() $\omega _1$ and consisting of classes of the same BBF degree, and let
$\omega _1$ and consisting of classes of the same BBF degree, and let ![]() $I_1$,
$I_1$, ![]() $J_1$, and
$J_1$, and ![]() $K_1$ be the resulting basis of the purely imaginary quaternions acting via complex structures on the tangent bundle of
$K_1$ be the resulting basis of the purely imaginary quaternions acting via complex structures on the tangent bundle of ![]() $M_1$. Define the complex structures
$M_1$. Define the complex structures ![]() $I_2$,
$I_2$, ![]() $J_2$,
$J_2$, ![]() $K_2$ on
$K_2$ on ![]() $M_2$ associated to the orthogonal basis of
$M_2$ associated to the orthogonal basis of ![]() $W_2$, which is the image via
$W_2$, which is the image via ![]() $\psi _q$ of the chosen basis of
$\psi _q$ of the chosen basis of ![]() $W_1$. Given a point
$W_1$. Given a point ![]() $t$ in the unit sphere in
$t$ in the unit sphere in ![]() $W_i$ denote by
$W_i$ denote by ![]() $I_{i,t}$ the corresponding complex structure on
$I_{i,t}$ the corresponding complex structure on ![]() $M_i$ such that
$M_i$ such that ![]() $g_i(I_{i,t}(\bullet ),\bullet )$ is the Kähler form with class
$g_i(I_{i,t}(\bullet ),\bullet )$ is the Kähler form with class ![]() $t$,
$t$, ![]() $i=1,2$. We get the
$i=1,2$. We get the ![]() $2$-sphere of complex structures
$2$-sphere of complex structures ![]() $I_t:=(I_{1,t},I_{2,\psi (t)})$ on
$I_t:=(I_{1,t},I_{2,\psi (t)})$ on ![]() $M_1\times M_2$ compatible with the Ricci-flat hermitian metric
$M_1\times M_2$ compatible with the Ricci-flat hermitian metric ![]() $(g_1,g_2)$ on
$(g_1,g_2)$ on ![]() $M_1\times M_2$. Then the fiber product
$M_1\times M_2$. Then the fiber product
of the two twistor families is the twistor family associated to the above sphere of complex structures on ![]() $M_1\times M_2$.
$M_1\times M_2$.
5.4 Diagonal twistor paths
Let
be the morphism sending the isomorphism class of ![]() $(X_1,\eta _1,X_2,\eta _2)$ to that of
$(X_1,\eta _1,X_2,\eta _2)$ to that of ![]() $(X_i,\eta _i)$. Note that
$(X_i,\eta _i)$. Note that ![]() $\Pi _i$ maps
$\Pi _i$ maps ![]() $\widetilde {Q}_{(X_1,\eta _1,X_2,\eta _2),\omega _1}$ isomorphically onto
$\widetilde {Q}_{(X_1,\eta _1,X_2,\eta _2),\omega _1}$ isomorphically onto ![]() $\widetilde {Q}_{(X_i,\eta _i,\omega _i)}$,
$\widetilde {Q}_{(X_i,\eta _i,\omega _i)}$, ![]() $i=1,2$. Fix a connected component
$i=1,2$. Fix a connected component ![]() ${\mathfrak {M}}_\Lambda ^0$ of
${\mathfrak {M}}_\Lambda ^0$ of ![]() ${\mathfrak {M}}_\Lambda$.
${\mathfrak {M}}_\Lambda$.
Definition 5.6 (1) A twistor path in ![]() ${\mathfrak {M}}_\Lambda ^0$ from a marked pair
${\mathfrak {M}}_\Lambda ^0$ from a marked pair ![]() $(X,\eta )$ to a marked pair
$(X,\eta )$ to a marked pair ![]() $(X',\eta ')$ consists of the data of a sequence of marked pairs
$(X',\eta ')$ consists of the data of a sequence of marked pairs ![]() $(X_i,\eta _i)$,
$(X_i,\eta _i)$, ![]() $0\leq i\leq k+1$, with
$0\leq i\leq k+1$, with ![]() $(X_0,\eta _0)=(X,\eta )$ and
$(X_0,\eta _0)=(X,\eta )$ and ![]() $(X_{k+1},\eta _{k+1})=(X',\eta ')$, together with a twistor line
$(X_{k+1},\eta _{k+1})=(X',\eta ')$, together with a twistor line ![]() $\widetilde {Q}_{(X_i,\eta _i,\omega _i)}$ through
$\widetilde {Q}_{(X_i,\eta _i,\omega _i)}$ through ![]() $(X_i,\eta _i)$ passing through
$(X_i,\eta _i)$ passing through ![]() $(X_{i+1},\eta _{i+1})$ as well, for
$(X_{i+1},\eta _{i+1})$ as well, for ![]() $0\leq i \leq k$. The twistor path is said to be generic if
$0\leq i \leq k$. The twistor path is said to be generic if ![]() ${\rm Pic}(X_i)$ is trivial, for
${\rm Pic}(X_i)$ is trivial, for ![]() $1\leq i\leq k$.
$1\leq i\leq k$.
(2) A twistor path in ![]() ${\mathfrak {M}}_\psi ^0$ from a quadruple
${\mathfrak {M}}_\psi ^0$ from a quadruple ![]() $(X_1,\eta _1,X_2,\eta _2)$ to a quadruple
$(X_1,\eta _1,X_2,\eta _2)$ to a quadruple ![]() $(Y_1,e_1,Y_2,e_2)$ consists of the data of a sequence
$(Y_1,e_1,Y_2,e_2)$ consists of the data of a sequence ![]() $(X_{1,i},\eta _{1,i},X_{2,i},\eta _{2,i})$,
$(X_{1,i},\eta _{1,i},X_{2,i},\eta _{2,i})$, ![]() $0\leq i\leq k+1$, with
$0\leq i\leq k+1$, with ![]() $(X_{1,0},\eta _{1,0},X_{2,0},\eta _{2,0})=(X_1,\eta _1,X_2,\eta _2)$ and
$(X_{1,0},\eta _{1,0},X_{2,0},\eta _{2,0})=(X_1,\eta _1,X_2,\eta _2)$ and ![]() $(X_{1,k+1},\eta _{1,k+1},X_{2,k+1},\eta _{2,k+1})=(Y_1,e_1,Y_2,e_2)$, together with a twistor line
$(X_{1,k+1},\eta _{1,k+1},X_{2,k+1},\eta _{2,k+1})=(Y_1,e_1,Y_2,e_2)$, together with a twistor line ![]() $\widetilde {Q}_{(X_{1,i},\eta _{1,i},X_{2,i},\eta _{2,i}),\omega _i}$ through
$\widetilde {Q}_{(X_{1,i},\eta _{1,i},X_{2,i},\eta _{2,i}),\omega _i}$ through ![]() $(X_{1,i},\eta _{1,i},X_{2,i},\eta _{2,i})$ passing through
$(X_{1,i},\eta _{1,i},X_{2,i},\eta _{2,i})$ passing through ![]() $(X_{1,i+1},\eta _{1,i+1},X_{2,i+1},\eta _{2,i+1})$ as well, for
$(X_{1,i+1},\eta _{1,i+1},X_{2,i+1},\eta _{2,i+1})$ as well, for ![]() $0\leq i \leq k$. The twistor path is said to be generic if
$0\leq i \leq k$. The twistor path is said to be generic if ![]() ${\rm Pic}(X_{1,i})$ is trivial, for
${\rm Pic}(X_{1,i})$ is trivial, for ![]() $1\leq i\leq k$.
$1\leq i\leq k$.
Lemma 5.7 The morphism ![]() $\Pi _i:{\mathfrak {M}}_\psi ^0\rightarrow {\mathfrak {M}}_\Lambda ^0$ is surjective, for
$\Pi _i:{\mathfrak {M}}_\psi ^0\rightarrow {\mathfrak {M}}_\Lambda ^0$ is surjective, for ![]() $i=1,2$.
$i=1,2$.
Proof. Let ![]() $q:=(X_1,\eta _1,X_2,\eta _2)$ be a quadruple in
$q:=(X_1,\eta _1,X_2,\eta _2)$ be a quadruple in ![]() ${\mathfrak {M}}_\psi ^0$ and let
${\mathfrak {M}}_\psi ^0$ and let ![]() $(Y'_1,\eta '_1)$ be a marked pair in
$(Y'_1,\eta '_1)$ be a marked pair in ![]() ${\mathfrak {M}}_\Lambda ^0$. Choose a generic Kähler class
${\mathfrak {M}}_\Lambda ^0$. Choose a generic Kähler class ![]() $\omega _1$ in
$\omega _1$ in ![]() ${\mathcal {K}}_{X_1}\cap \psi _q^{-1}({\mathcal {K}}_{X_2})$ so that the twistor line
${\mathcal {K}}_{X_1}\cap \psi _q^{-1}({\mathcal {K}}_{X_2})$ so that the twistor line ![]() $\widetilde {Q}_{(X_1,\eta _1,\omega _1)}$ is generic and let
$\widetilde {Q}_{(X_1,\eta _1,\omega _1)}$ is generic and let ![]() $(Y_1,e_1)$ be a marked pair in
$(Y_1,e_1)$ be a marked pair in ![]() $\widetilde {Q}_{(X_1,\eta _1,\omega _1)}$ with a trivial
$\widetilde {Q}_{(X_1,\eta _1,\omega _1)}$ with a trivial ![]() ${\rm Pic}(Y_1)$. A pair
${\rm Pic}(Y_1)$. A pair ![]() $(Y_2,e_2)$ in the fiber of the period map through
$(Y_2,e_2)$ in the fiber of the period map through ![]() ${\mathfrak {M}}_\Lambda ^0$ over
${\mathfrak {M}}_\Lambda ^0$ over ![]() $\psi (P(Y_1,e_1))$ must be the unique marked pair in this fiber, since
$\psi (P(Y_1,e_1))$ must be the unique marked pair in this fiber, since ![]() ${\rm Pic}(Y_2)$ is trivial as well. The equalities
${\rm Pic}(Y_2)$ is trivial as well. The equalities ![]() ${\mathcal {K}}_{Y_i}={\mathcal {C}}_{Y_i}^+$,
${\mathcal {K}}_{Y_i}={\mathcal {C}}_{Y_i}^+$, ![]() $i=1,2$, imply that
$i=1,2$, imply that ![]() ${\mathcal {K}}_{Y_1}= (e_1^{-1}\psi e_2)({\mathcal {K}}_{Y_2})$ and so the quadruple
${\mathcal {K}}_{Y_1}= (e_1^{-1}\psi e_2)({\mathcal {K}}_{Y_2})$ and so the quadruple ![]() $(Y_1,e_1,Y_2,e_2)$ belongs to the diagonal twistor line
$(Y_1,e_1,Y_2,e_2)$ belongs to the diagonal twistor line ![]() $Q_{(X_1,\eta _1,X_2,\eta _2),\omega _1}$ and, hence, to the connected component
$Q_{(X_1,\eta _1,X_2,\eta _2),\omega _1}$ and, hence, to the connected component ![]() ${\mathfrak {M}}_\psi ^0$ of
${\mathfrak {M}}_\psi ^0$ of ![]() ${\mathfrak {M}}_\psi$. Furthermore, every twistor path
${\mathfrak {M}}_\psi$. Furthermore, every twistor path ![]() $Q_{(Y_1,e_1,\omega '_1)}$ through
$Q_{(Y_1,e_1,\omega '_1)}$ through ![]() $(Y_1,e_1)$ lifts to a twistor path
$(Y_1,e_1)$ lifts to a twistor path ![]() $Q_{(Y_1,e_1,Y_2,e_2),\omega '_1}$ through
$Q_{(Y_1,e_1,Y_2,e_2),\omega '_1}$ through ![]() $(Y_1,e_1,Y_2,e_2)$, by Lemma 5.5. There exists a generic twistor path from
$(Y_1,e_1,Y_2,e_2)$, by Lemma 5.5. There exists a generic twistor path from ![]() $(Y_1,e_1)$ to
$(Y_1,e_1)$ to ![]() $(Y'_1,\eta '_1)$, by [Reference VerbitskyVer96, Theorems 3.2 and 5.2.e]. Repeating the above argument we get that this twistor path lifts to a twistor path from
$(Y'_1,\eta '_1)$, by [Reference VerbitskyVer96, Theorems 3.2 and 5.2.e]. Repeating the above argument we get that this twistor path lifts to a twistor path from ![]() $(Y_1,e_1,Y_2,e_2)$ to
$(Y_1,e_1,Y_2,e_2)$ to ![]() $(Y'_1,\eta '_1,Y'_2,\eta '_2)$, for some
$(Y'_1,\eta '_1,Y'_2,\eta '_2)$, for some ![]() $(Y'_2,\eta '_2)$ in
$(Y'_2,\eta '_2)$ in ![]() ${\mathfrak {M}}^0_\Lambda$, by the genericity assumption. Hence,
${\mathfrak {M}}^0_\Lambda$, by the genericity assumption. Hence, ![]() $(Y'_1,\eta '_1)$ belongs to the image of
$(Y'_1,\eta '_1)$ belongs to the image of ![]() $\Pi _1$ and
$\Pi _1$ and ![]() $\Pi _1$ is surjective. The isomorphism
$\Pi _1$ is surjective. The isomorphism ![]() ${\mathfrak {M}}_\psi \rightarrow {\mathfrak {M}}_{\psi ^{-1}}$ sending
${\mathfrak {M}}_\psi \rightarrow {\mathfrak {M}}_{\psi ^{-1}}$ sending ![]() $(X_1,\eta _1,X_2,\eta _2)$ to
$(X_1,\eta _1,X_2,\eta _2)$ to ![]() $(X_2,\eta _2,X_1,\eta _1)$ interchanges the roles of
$(X_2,\eta _2,X_1,\eta _1)$ interchanges the roles of ![]() $\Pi _1$ and
$\Pi _1$ and ![]() $\Pi _2$. It follows that
$\Pi _2$. It follows that ![]() $\Pi _2$ is surjective as well.
$\Pi _2$ is surjective as well.
Lemma 5.8 Every two points in ![]() ${\mathfrak {M}}^0_\psi$ are connected by a generic twistor path in
${\mathfrak {M}}^0_\psi$ are connected by a generic twistor path in ![]() ${\mathfrak {M}}^0_\psi$.
${\mathfrak {M}}^0_\psi$.
Proof. Let ![]() $q:=(X_1,\eta _1,X_2,\eta _2)$ be a quadruple in
$q:=(X_1,\eta _1,X_2,\eta _2)$ be a quadruple in ![]() ${\mathfrak {M}}^0_\psi$, such that
${\mathfrak {M}}^0_\psi$, such that ![]() ${\rm Pic}(X_1)$ is trivial. Then
${\rm Pic}(X_1)$ is trivial. Then ![]() ${\rm Pic}(X_2)$ is trivial as well, since
${\rm Pic}(X_2)$ is trivial as well, since ![]() $\psi _q:H^2(X_1,{\mathbb {Q}})\rightarrow H^2(X_2,{\mathbb {Q}})$ is a Hodge isometry. Hence,
$\psi _q:H^2(X_1,{\mathbb {Q}})\rightarrow H^2(X_2,{\mathbb {Q}})$ is a Hodge isometry. Hence, ![]() $(X_i,\eta _i)$ is the unique pair in its connected component in
$(X_i,\eta _i)$ is the unique pair in its connected component in ![]() ${\mathfrak {M}}_\Lambda$ over its period
${\mathfrak {M}}_\Lambda$ over its period ![]() $P(X_i,\eta _i)$, by Verbitsky's Torelli theorem [Reference HuybrechtsHuy12, Reference VerbitskyVer13]. Consequently,
$P(X_i,\eta _i)$, by Verbitsky's Torelli theorem [Reference HuybrechtsHuy12, Reference VerbitskyVer13]. Consequently, ![]() $q$ is the unique point in
$q$ is the unique point in ![]() ${\mathfrak {M}}^0_\psi$ mapping via
${\mathfrak {M}}^0_\psi$ mapping via ![]() $P\circ \Pi _i$ to
$P\circ \Pi _i$ to ![]() $P(X_i,\eta _i)$, for each of
$P(X_i,\eta _i)$, for each of ![]() $i=1,2$. It follows that every two such quadruples are connected by a generic twistor path in
$i=1,2$. It follows that every two such quadruples are connected by a generic twistor path in ![]() ${\mathfrak {M}}^0_\psi$, by the analogous theorem for marked pairs and the liftability of such paths to
${\mathfrak {M}}^0_\psi$, by the analogous theorem for marked pairs and the liftability of such paths to ![]() ${\mathfrak {M}}^0_\psi$ demonstrated in the proof of Lemma 5.7. Now, through each point in
${\mathfrak {M}}^0_\psi$ demonstrated in the proof of Lemma 5.7. Now, through each point in ![]() ${\mathfrak {M}}^0_\psi$ passes a generic twistor line. Hence, every two points in
${\mathfrak {M}}^0_\psi$ passes a generic twistor line. Hence, every two points in ![]() ${\mathfrak {M}}^0_\psi$ are connected by a generic twistor path.
${\mathfrak {M}}^0_\psi$ are connected by a generic twistor path.
5.5 Deforming vector bundles along diagonal twistor paths
A universal family ![]() $f:{\mathcal {X}}\rightarrow {\mathfrak {M}}_\Lambda ^0$ exists, by [Reference MarkmanMar21b]. We get the universal families
$f:{\mathcal {X}}\rightarrow {\mathfrak {M}}_\Lambda ^0$ exists, by [Reference MarkmanMar21b]. We get the universal families ![]() $\Pi _i^*(f):\Pi _i^*{\mathcal {X}}\rightarrow {\mathfrak {M}}_\psi ^0$,
$\Pi _i^*(f):\Pi _i^*{\mathcal {X}}\rightarrow {\mathfrak {M}}_\psi ^0$, ![]() $i=1,2$, as well as the universal fiber product
$i=1,2$, as well as the universal fiber product
The local system ![]() $Rf_*{\mathbb {Z}}$ over
$Rf_*{\mathbb {Z}}$ over ![]() ${\mathfrak {M}}_\Lambda ^0$ is trivial, by [Reference MarkmanMar21b, Lemma 2.1]. Hence, so are the local system
${\mathfrak {M}}_\Lambda ^0$ is trivial, by [Reference MarkmanMar21b, Lemma 2.1]. Hence, so are the local system ![]() $R\tilde {f}_*{\mathbb {Z}}$ and
$R\tilde {f}_*{\mathbb {Z}}$ and ![]() $R\tilde {f}_*{\mathbb {Q}}$.
$R\tilde {f}_*{\mathbb {Q}}$.
Definition 5.9 Let ![]() $M$ be a
$M$ be a ![]() $d$-dimensional compact Kähler manifold. Set
$d$-dimensional compact Kähler manifold. Set ![]() $H^{ev}(M,{\mathbb {Q}}):=\oplus _{i=0}^{2d} H^{2i}(M,{\mathbb {Q}})$. Given a class
$H^{ev}(M,{\mathbb {Q}}):=\oplus _{i=0}^{2d} H^{2i}(M,{\mathbb {Q}})$. Given a class ![]() $\gamma \in H^{ev}(M,{\mathbb {Q}})$ denote by
$\gamma \in H^{ev}(M,{\mathbb {Q}})$ denote by ![]() $\gamma _i$ the graded summand in
$\gamma _i$ the graded summand in ![]() $H^{2i}(M,{\mathbb {Q}})$. We say that
$H^{2i}(M,{\mathbb {Q}})$. We say that ![]() $\gamma$ is a Hodge class, if
$\gamma$ is a Hodge class, if ![]() $\gamma _i$ belongs to
$\gamma _i$ belongs to ![]() $H^{i,i}(M)$, for all
$H^{i,i}(M)$, for all ![]() $0\leq i\leq 2d$.
$0\leq i\leq 2d$.
Definition 5.10 Let ![]() $q:=(X_1,\eta _1,X_2,\eta _2)$ be a quadruple in
$q:=(X_1,\eta _1,X_2,\eta _2)$ be a quadruple in ![]() ${\mathfrak {M}}^0_\psi$ and let
${\mathfrak {M}}^0_\psi$ and let ![]() $\gamma$ be a Hodge class in
$\gamma$ be a Hodge class in ![]() $H^{ev}(X_1\times X_2,{\mathbb {Q}})$. We say that
$H^{ev}(X_1\times X_2,{\mathbb {Q}})$. We say that ![]() $\gamma$ remains a Hodge class under every deformation in
$\gamma$ remains a Hodge class under every deformation in ![]() ${\mathfrak {M}}^0_\psi$, if for every quadruple
${\mathfrak {M}}^0_\psi$, if for every quadruple ![]() $q':=(X'_1,\eta '_1,X'_2,\eta '_2)$ in
$q':=(X'_1,\eta '_1,X'_2,\eta '_2)$ in ![]() ${\mathfrak {M}}^0_\psi$ the parallel transport
${\mathfrak {M}}^0_\psi$ the parallel transport ![]() $\gamma '\in H^{ev}(X'_1\times X'_2,{\mathbb {Q}})$ of
$\gamma '\in H^{ev}(X'_1\times X'_2,{\mathbb {Q}})$ of ![]() $\gamma$ in the local system
$\gamma$ in the local system ![]() $R\tilde {f}_*{\mathbb {Q}}$ along some, hence any, continuous path from
$R\tilde {f}_*{\mathbb {Q}}$ along some, hence any, continuous path from ![]() $q$ to
$q$ to ![]() $q'$ in
$q'$ in ![]() ${\mathfrak {M}}^0_\psi$ is a Hodge class.
${\mathfrak {M}}^0_\psi$ is a Hodge class.
Definition 5.11 An Azumaya ![]() ${\mathcal {O}}_{X}$-algebra of rank
${\mathcal {O}}_{X}$-algebra of rank ![]() $r$ over a complex manifold
$r$ over a complex manifold ![]() $X$ is a sheaf
$X$ is a sheaf ![]() ${\mathcal {A}}$ of locally free coherent
${\mathcal {A}}$ of locally free coherent ![]() ${\mathcal {O}}_{X}$-modules, with a global section
${\mathcal {O}}_{X}$-modules, with a global section ![]() $1_{\mathcal {A}}$, and an
$1_{\mathcal {A}}$, and an ![]() ${\mathcal {O}}_{X}$-linear associative multiplication
${\mathcal {O}}_{X}$-linear associative multiplication ![]() $m:{\mathcal {A}}\otimes _{{\mathcal {O}}_{X}}{\mathcal {A}}\rightarrow {\mathcal {A}}$ with identity
$m:{\mathcal {A}}\otimes _{{\mathcal {O}}_{X}}{\mathcal {A}}\rightarrow {\mathcal {A}}$ with identity ![]() $1_{\mathcal {A}}$, admitting an open covering
$1_{\mathcal {A}}$, admitting an open covering ![]() $\{U_\alpha \}$ of
$\{U_\alpha \}$ of ![]() $X$ and an isomorphism
$X$ and an isomorphism ![]() $\eta _\alpha :{\mathcal {A}}_{\mid _{U_\alpha }}\rightarrow {\mathcal {E}}nd(F_\alpha )$ of unital associative algebras for some locally free
$\eta _\alpha :{\mathcal {A}}_{\mid _{U_\alpha }}\rightarrow {\mathcal {E}}nd(F_\alpha )$ of unital associative algebras for some locally free ![]() ${\mathcal {O}}_{U_\alpha }$-module
${\mathcal {O}}_{U_\alpha }$-module ![]() $F_\alpha$ of rank
$F_\alpha$ of rank ![]() $r$ over each
$r$ over each ![]() $U_\alpha$. We will also refer to such
$U_\alpha$. We will also refer to such ![]() ${\mathcal {A}}$ as an Azumaya algebra over
${\mathcal {A}}$ as an Azumaya algebra over ![]() $X$.
$X$.
Remark 5.12 The endomorphism sheaf ![]() ${\mathcal {E}}nd(F)$ of a locally free twisted sheaf
${\mathcal {E}}nd(F)$ of a locally free twisted sheaf ![]() $F$ over
$F$ over ![]() $X$ is an Azumaya algebra over
$X$ is an Azumaya algebra over ![]() $X$. Conversely, an Azumaya algebra corresponds to a natural equivalence class of locally free twisted sheaves over
$X$. Conversely, an Azumaya algebra corresponds to a natural equivalence class of locally free twisted sheaves over ![]() $X$, modulo tensorization by line bundles [Reference CăldăraruCăl00]. The class
$X$, modulo tensorization by line bundles [Reference CăldăraruCăl00]. The class ![]() $\kappa (F)$ depends only on this equivalence class and so may be regarded as a characteristic class of the pair
$\kappa (F)$ depends only on this equivalence class and so may be regarded as a characteristic class of the pair ![]() $({\mathcal {A}},m)$ of the locally free sheaf
$({\mathcal {A}},m)$ of the locally free sheaf ![]() ${\mathcal {A}}$ underlying the Azumaya algebra over
${\mathcal {A}}$ underlying the Azumaya algebra over ![]() $X$ and its multiplication
$X$ and its multiplication ![]() $m$ (see [Reference MarkmanMar20, § 2.3]).
$m$ (see [Reference MarkmanMar20, § 2.3]).
Definition 5.13 Let ![]() $M_1$ and
$M_1$ and ![]() $M_2$ be compact Kähler manifolds. Let
$M_2$ be compact Kähler manifolds. Let ![]() ${\mathcal {A}}_i$ be an Azumaya algebra over
${\mathcal {A}}_i$ be an Azumaya algebra over ![]() $M_i$. We say that
$M_i$. We say that ![]() ${\mathcal {A}}_2$ is deformation equivalent to
${\mathcal {A}}_2$ is deformation equivalent to ![]() ${\mathcal {A}}_1$, if there exists a proper family
${\mathcal {A}}_1$, if there exists a proper family ![]() $\pi :{\mathcal {M}}\rightarrow B$ of compact Kähler manifolds over a connected analytic base
$\pi :{\mathcal {M}}\rightarrow B$ of compact Kähler manifolds over a connected analytic base ![]() $B$, points
$B$, points ![]() $b_i\in B$, isomorphisms
$b_i\in B$, isomorphisms ![]() $f_i:M_i\rightarrow {\mathcal {M}}_{b_i}$ with the fiber of
$f_i:M_i\rightarrow {\mathcal {M}}_{b_i}$ with the fiber of ![]() $\pi$ over
$\pi$ over ![]() $b_i$, and an Azumaya algebra
$b_i$, and an Azumaya algebra ![]() ${\mathcal {A}}$ over
${\mathcal {A}}$ over ![]() ${\mathcal {M}}$, such that
${\mathcal {M}}$, such that ![]() $f_i^*{\mathcal {A}}$ is isomorphic to
$f_i^*{\mathcal {A}}$ is isomorphic to ![]() ${\mathcal {A}}_i$, for
${\mathcal {A}}_i$, for ![]() $i=1,2$.
$i=1,2$.
Let ![]() $X$ be a
$X$ be a ![]() $d$-dimensional compact Kähler manifold and let
$d$-dimensional compact Kähler manifold and let ![]() $\omega$ be a Kähler class on
$\omega$ be a Kähler class on ![]() $X$. The
$X$. The ![]() $\omega$-slope of a torsion-free coherent sheaf
$\omega$-slope of a torsion-free coherent sheaf ![]() $F$ on
$F$ on ![]() $X$ is
$X$ is ![]() $\mbox {slope}_\omega (F):=\int _Xc_1(F)\omega ^{d-1}/{\rm rank}(F)$.
$\mbox {slope}_\omega (F):=\int _Xc_1(F)\omega ^{d-1}/{\rm rank}(F)$.
Definition 5.14 [Reference MarkmanMar20, Definition 6.5]
Let ![]() $E$ be a torsion free coherent sheaf on
$E$ be a torsion free coherent sheaf on ![]() $X$, which is
$X$, which is ![]() $\theta$-twisted with respect to a class
$\theta$-twisted with respect to a class ![]() $\theta$ in
$\theta$ in ![]() $H^2(X,{\mathcal {O}}_{X}^*)$. We say that
$H^2(X,{\mathcal {O}}_{X}^*)$. We say that ![]() $E$ is
$E$ is ![]() $\omega$-slope-stable, if for every non-zero
$\omega$-slope-stable, if for every non-zero ![]() $\theta$-twisted subsheaf
$\theta$-twisted subsheaf ![]() $F$ of
$F$ of ![]() $E$ of lower rank we have
$E$ of lower rank we have ![]() $\mbox {slope}_\omega ({\mathcal {H}}om(E,F))<0$.
$\mbox {slope}_\omega ({\mathcal {H}}om(E,F))<0$.
Proposition 5.15 Let ![]() $q:=(X_1,\eta _1,X_2,\eta _2)$ be a quadruple in
$q:=(X_1,\eta _1,X_2,\eta _2)$ be a quadruple in ![]() ${\mathfrak {M}}^0_\psi$ and let
${\mathfrak {M}}^0_\psi$ and let ![]() $F$ be a locally free sheaf over
$F$ be a locally free sheaf over ![]() $X_1\times X_2$ with the following properties.
$X_1\times X_2$ with the following properties.
(1) The locally free sheaf
 $F$ is
$F$ is  $\big (\pi _{X_1}^*(\omega )+\pi _{X_2}^*(\psi _q(\omega ))\big )$-slope-stable, for every Kähler class
$\big (\pi _{X_1}^*(\omega )+\pi _{X_2}^*(\psi _q(\omega ))\big )$-slope-stable, for every Kähler class  $\omega$ in some non-empty open subcone
$\omega$ in some non-empty open subcone  ${\mathcal {C}}_F$ of
${\mathcal {C}}_F$ of  ${\mathcal {K}}_{X_1}\cap \psi _q^{-1}({\mathcal {K}}_{X_2})$.
${\mathcal {K}}_{X_1}\cap \psi _q^{-1}({\mathcal {K}}_{X_2})$.(2) The class
 $c_2({\mathcal {E}}nd(F))$ remains of Hodge type
$c_2({\mathcal {E}}nd(F))$ remains of Hodge type  $(2,2)$ along every deformation in
$(2,2)$ along every deformation in  ${\mathfrak {M}}^0_\psi$.
${\mathfrak {M}}^0_\psi$.
For every point ![]() $q':=(X'_1,\eta '_1,X'_2,\eta '_2)$ in
$q':=(X'_1,\eta '_1,X'_2,\eta '_2)$ in ![]() ${\mathfrak {M}}^0_\psi$ there exists a possibly twisted locally free sheaf
${\mathfrak {M}}^0_\psi$ there exists a possibly twisted locally free sheaf ![]() $F'$ over
$F'$ over ![]() $X'_1\times X'_2$, such that the Azumaya algebra
$X'_1\times X'_2$, such that the Azumaya algebra ![]() ${\mathcal {E}}nd(F')$ is deformation equivalent to
${\mathcal {E}}nd(F')$ is deformation equivalent to ![]() ${\mathcal {E}}nd(F)$. Furthermore,
${\mathcal {E}}nd(F)$. Furthermore, ![]() $F'$ is
$F'$ is ![]() $\big (\pi _{X'_1}^*(\omega )+\pi _{X'_2}^*(\psi _{q'}(\omega ))\big )$-slope-stable with respect to some Kähler class
$\big (\pi _{X'_1}^*(\omega )+\pi _{X'_2}^*(\psi _{q'}(\omega ))\big )$-slope-stable with respect to some Kähler class ![]() $\omega$ in
$\omega$ in ![]() ${\mathcal {K}}_{X'_1}\cap \psi _{q'}^{-1}({\mathcal {K}}_{X'_2})$.
${\mathcal {K}}_{X'_1}\cap \psi _{q'}^{-1}({\mathcal {K}}_{X'_2})$.
Proof. The slope stability property (1) of ![]() $F$ implies that the first Chern class of every direct summand of
$F$ implies that the first Chern class of every direct summand of ![]() ${\mathcal {E}}nd(F)$ vanishes, by [Reference MarkmanMar20, Lemma 7.2]. Property (2), that
${\mathcal {E}}nd(F)$ vanishes, by [Reference MarkmanMar20, Lemma 7.2]. Property (2), that ![]() $c_2({\mathcal {E}}nd(F))$ remains of Hodge type, implies that the Azumaya algebra
$c_2({\mathcal {E}}nd(F))$ remains of Hodge type, implies that the Azumaya algebra ![]() ${\mathcal {E}}nd(F)$ deforms along the twistor family over a generic twistor line
${\mathcal {E}}nd(F)$ deforms along the twistor family over a generic twistor line ![]() $\widetilde {Q}_{(X_1,\eta _1,X_2,\eta _2),\omega _1}$ in
$\widetilde {Q}_{(X_1,\eta _1,X_2,\eta _2),\omega _1}$ in ![]() ${\mathfrak {M}}^0_\psi$ associated to a Kähler class
${\mathfrak {M}}^0_\psi$ associated to a Kähler class ![]() $\omega _1$ in
$\omega _1$ in ![]() ${\mathcal {C}}_F$, by [Reference VerbitskyVer99b, Theorem 3.19], which is generalized to Azumaya algebras in [Reference MarkmanMar20, Corollary 6.12]. Here we use the fact that the twistor line in
${\mathcal {C}}_F$, by [Reference VerbitskyVer99b, Theorem 3.19], which is generalized to Azumaya algebras in [Reference MarkmanMar20, Corollary 6.12]. Here we use the fact that the twistor line in ![]() ${\mathfrak {M}}^0_\psi$ is associated to a hyper-Kähler structure, as explained in § 5.3, as well as the fact that the first Chern class of every direct summand of
${\mathfrak {M}}^0_\psi$ is associated to a hyper-Kähler structure, as explained in § 5.3, as well as the fact that the first Chern class of every direct summand of ![]() ${\mathcal {E}}nd(F)$ vanishes. Choose a quadruple
${\mathcal {E}}nd(F)$ vanishes. Choose a quadruple ![]() $q_0:=(Y_1,e_1,Y_2,e_2)$ in
$q_0:=(Y_1,e_1,Y_2,e_2)$ in ![]() $\widetilde {Q}_{(X_1,\eta _1,X_2,\eta _2),\omega _1}$ with a trivial Picard group
$\widetilde {Q}_{(X_1,\eta _1,X_2,\eta _2),\omega _1}$ with a trivial Picard group ![]() ${\rm Pic}(Y_1)$ and let
${\rm Pic}(Y_1)$ and let ![]() ${\mathcal {A}}$ be the Azumaya algebra over
${\mathcal {A}}$ be the Azumaya algebra over ![]() $Y_1\times Y_2$ resulting by deforming
$Y_1\times Y_2$ resulting by deforming ![]() ${\mathcal {E}}nd(F)$ along
${\mathcal {E}}nd(F)$ along ![]() $\widetilde {Q}_{(X_1,\eta _1,X_2,\eta _2),\omega _1}$. The Azumaya algebra
$\widetilde {Q}_{(X_1,\eta _1,X_2,\eta _2),\omega _1}$. The Azumaya algebra ![]() ${\mathcal {A}}$ further deforms along every generic twistor path in
${\mathcal {A}}$ further deforms along every generic twistor path in ![]() ${\mathfrak {M}}^0_\psi$ from
${\mathfrak {M}}^0_\psi$ from ![]() $q_0$ to any point in
$q_0$ to any point in ![]() ${\mathfrak {M}}^0_\psi$, by [Reference MarkmanMar20, Proposition 6.17]. The existence of an Azumaya algebra
${\mathfrak {M}}^0_\psi$, by [Reference MarkmanMar20, Proposition 6.17]. The existence of an Azumaya algebra ![]() ${\mathcal {A}}'$ over
${\mathcal {A}}'$ over ![]() $X'_1\times X'_2$ deformation equivalent to
$X'_1\times X'_2$ deformation equivalent to ![]() ${\mathcal {E}}nd(F)$ follows from that fact that every point
${\mathcal {E}}nd(F)$ follows from that fact that every point ![]() $q'$ in
$q'$ in ![]() ${\mathfrak {M}}_\psi ^0$ is connected to the point
${\mathfrak {M}}_\psi ^0$ is connected to the point ![]() $q_0$ via a generic twistor path, by Lemma 5.8. The existence of a locally free sheaf
$q_0$ via a generic twistor path, by Lemma 5.8. The existence of a locally free sheaf ![]() $F'$, such that the Azumaya algebras
$F'$, such that the Azumaya algebras ![]() ${\mathcal {E}}nd(F')$ and
${\mathcal {E}}nd(F')$ and ![]() ${\mathcal {A}}'$ are isomorphic, follows from the well-known correspondence between Azumaya algebras and equivalence classes of locally free twisted sheaves modulo tensorization by line bundles [Reference CăldăraruCăl00]. The existence of the Kähler class
${\mathcal {A}}'$ are isomorphic, follows from the well-known correspondence between Azumaya algebras and equivalence classes of locally free twisted sheaves modulo tensorization by line bundles [Reference CăldăraruCăl00]. The existence of the Kähler class ![]() $\omega$ in
$\omega$ in ![]() ${\mathcal {K}}_{X'_1}\cap \psi _{q'}^{-1}({\mathcal {K}}_{X'_2})$ for which
${\mathcal {K}}_{X'_1}\cap \psi _{q'}^{-1}({\mathcal {K}}_{X'_2})$ for which ![]() $F'$ is
$F'$ is ![]() $\big (\pi _{X_1}^*(\omega )+\pi _{X_2}^*(\psi _q(\omega ))\big )$-slope-stable is automatic, since the twistor deformation
$\big (\pi _{X_1}^*(\omega )+\pi _{X_2}^*(\psi _q(\omega ))\big )$-slope-stable is automatic, since the twistor deformation ![]() $F'$ of the hyperholomorphic sheaf
$F'$ of the hyperholomorphic sheaf ![]() $F$ is slope-stable with respect to any such Kähler class for
$F$ is slope-stable with respect to any such Kähler class for ![]() $\omega$ in the ray given in (5.4) parametrized by the point
$\omega$ in the ray given in (5.4) parametrized by the point ![]() $q'$ of the twistor path, by Verbitsky's theorem (see [Reference MarkmanMar20, Corollary 6.12] for this statement in the case of twisted sheaves).
$q'$ of the twistor path, by Verbitsky's theorem (see [Reference MarkmanMar20, Corollary 6.12] for this statement in the case of twisted sheaves).
5.6 The rational Hodge isometry of a Fourier–Mukai kernel of non-zero rank
Let ![]() $X$ and
$X$ and ![]() $Y$ be the IHSMs in Lemma 4.1. Choose markings
$Y$ be the IHSMs in Lemma 4.1. Choose markings ![]() $\eta _X:H^2(X,{\mathbb {Z}})\rightarrow \Lambda$ and
$\eta _X:H^2(X,{\mathbb {Z}})\rightarrow \Lambda$ and ![]() $\eta _Y:H^2(Y,{\mathbb {Z}})\rightarrow \Lambda$ such that
$\eta _Y:H^2(Y,{\mathbb {Z}})\rightarrow \Lambda$ such that ![]() $(X,\eta _X)$ and
$(X,\eta _X)$ and ![]() $(Y,\eta _Y)$ belong to the same connected component
$(Y,\eta _Y)$ belong to the same connected component ![]() ${\mathfrak {M}}_\Lambda ^0$ of
${\mathfrak {M}}_\Lambda ^0$ of ![]() ${\mathfrak {M}}_\Lambda$.
${\mathfrak {M}}_\Lambda$.
Convention 5.16 Choose an orientation ![]() $\epsilon _\Lambda$ of
$\epsilon _\Lambda$ of ![]() $\Lambda \otimes _{\mathbb {Z}}{\mathbb {Q}}$. Given two pairs
$\Lambda \otimes _{\mathbb {Z}}{\mathbb {Q}}$. Given two pairs ![]() $(X_1,\eta _1)$ and
$(X_1,\eta _1)$ and ![]() $(X_2,\eta _2)$ in
$(X_2,\eta _2)$ in ![]() ${\mathfrak {M}}_\Lambda$, we endow
${\mathfrak {M}}_\Lambda$, we endow ![]() $H^2(X_i,{\mathbb {Q}})$ with the orientation
$H^2(X_i,{\mathbb {Q}})$ with the orientation ![]() $\epsilon _i$, such that
$\epsilon _i$, such that ![]() $\eta _i$ is orientation preserving. The homomorphism
$\eta _i$ is orientation preserving. The homomorphism
induced by the functor (1.4), is then always evaluated in terms of the orientations ![]() $\epsilon _1$ and
$\epsilon _1$ and ![]() $\epsilon _2$. The resulting homomorphism depends on the markings
$\epsilon _2$. The resulting homomorphism depends on the markings ![]() $\eta _1$ and
$\eta _1$ and ![]() $\eta _2$, but is independent of the choice of
$\eta _2$, but is independent of the choice of ![]() $\epsilon _\Lambda$.
$\epsilon _\Lambda$.
The unit sphere in any positive-definite three-dimensional subspace of ![]() $H^2(X,{\mathbb {R}})$ is a deformation retract of the positive cone
$H^2(X,{\mathbb {R}})$ is a deformation retract of the positive cone ![]() ${\mathcal {C}}'_X:=\{x\in H^2(X,{\mathbb {R}}) \ ; \ (x,x)>0\}$ (see [Reference MarkmanMar11, § 4]). Hence, the second cohomology of the positive cone is a one-dimensional representation of
${\mathcal {C}}'_X:=\{x\in H^2(X,{\mathbb {R}}) \ ; \ (x,x)>0\}$ (see [Reference MarkmanMar11, § 4]). Hence, the second cohomology of the positive cone is a one-dimensional representation of ![]() $O(H^2(X,{\mathbb {Q}}))$ corresponding to a character
$O(H^2(X,{\mathbb {Q}}))$ corresponding to a character ![]() $\nu :O(H^2(X,{\mathbb {Q}}))\rightarrow \mu _2:=\{\pm 1\}$. Set
$\nu :O(H^2(X,{\mathbb {Q}}))\rightarrow \mu _2:=\{\pm 1\}$. Set
The orientation given by the basis (5.2) is independent of the choices of a holomorphic ![]() $2$-form and of a Kähler class and determines a positive generator of the cyclic group
$2$-form and of a Kähler class and determines a positive generator of the cyclic group ![]() $H^2({\mathcal {C}}'_X,{\mathbb {Z}})$.
$H^2({\mathcal {C}}'_X,{\mathbb {Z}})$.
Definition 5.17 The orientation of the positive cone is the positive generator of ![]() $H^2({\mathcal {C}}'_X,{\mathbb {Z}})$. An isometry
$H^2({\mathcal {C}}'_X,{\mathbb {Z}})$. An isometry ![]() $g:H^2(X_1,{\mathbb {Q}})\rightarrow H^2(X_2,{\mathbb {Q}})$ is orientation preserving, if
$g:H^2(X_1,{\mathbb {Q}})\rightarrow H^2(X_2,{\mathbb {Q}})$ is orientation preserving, if ![]() $g_*:H^2({\mathcal {C}}'_{X_1},{\mathbb {Z}})\rightarrow H^2({\mathcal {C}}'_{X_2},{\mathbb {Z}})$ maps the positive generator to the positive generator.
$g_*:H^2({\mathcal {C}}'_{X_1},{\mathbb {Z}})\rightarrow H^2({\mathcal {C}}'_{X_2},{\mathbb {Z}})$ maps the positive generator to the positive generator.
Set
 \[ \nu(g) = \begin{cases} 1 & \mbox{if}\
g \ \mbox{is orientation preserving},\\ -1 & \mbox{if}\ g \
\mbox{is orientation reveresing}. \end{cases}
\]
\[ \nu(g) = \begin{cases} 1 & \mbox{if}\
g \ \mbox{is orientation preserving},\\ -1 & \mbox{if}\ g \
\mbox{is orientation reveresing}. \end{cases}
\]
Note that if ![]() $g$ is a Hodge isometry, which maps some Kähler class to a Kähler class, then
$g$ is a Hodge isometry, which maps some Kähler class to a Kähler class, then ![]() $\nu (g)=1$, as it maps a basis of the form (5.2) to such a basis. In particular, the isometry
$\nu (g)=1$, as it maps a basis of the form (5.2) to such a basis. In particular, the isometry ![]() $\eta _2^{-1}\psi \eta _1:H^2(X_1,{\mathbb {Q}})\rightarrow H^2(X_2,{\mathbb {Q}})$ associated to a quadruple
$\eta _2^{-1}\psi \eta _1:H^2(X_1,{\mathbb {Q}})\rightarrow H^2(X_2,{\mathbb {Q}})$ associated to a quadruple ![]() $(X_1,\eta _1,X_2,\eta _2)$ in
$(X_1,\eta _1,X_2,\eta _2)$ in ![]() ${\mathfrak {M}}_\psi$ is orientation preserving.
${\mathfrak {M}}_\psi$ is orientation preserving.
Remark 5.18 Keep the notation of Convention 5.16. Let ![]() $g:H^*(X_1,{\mathbb {Z}})\rightarrow H^*(X_2,{\mathbb {Z}})$ be a parallel-transport operator and denote by
$g:H^*(X_1,{\mathbb {Z}})\rightarrow H^*(X_2,{\mathbb {Z}})$ be a parallel-transport operator and denote by ![]() $\bar {g}$ its restriction to
$\bar {g}$ its restriction to ![]() $H^2(X_1,{\mathbb {Z}})$. One checks that if
$H^2(X_1,{\mathbb {Z}})$. One checks that if ![]() $\bar {g}$ is orientation preserving in the sense of Convention 5.16, so that
$\bar {g}$ is orientation preserving in the sense of Convention 5.16, so that ![]() $\det (\eta _2 \bar {g}\eta _1^{-1})=1$, then
$\det (\eta _2 \bar {g}\eta _1^{-1})=1$, then ![]() $\widetilde {H}(g)$ maps
$\widetilde {H}(g)$ maps ![]() $\alpha$ to
$\alpha$ to ![]() $\alpha$,
$\alpha$, ![]() $\beta$ to
$\beta$ to ![]() $\beta$, and restricts to
$\beta$, and restricts to ![]() $H^2(X_1,{\mathbb {Q}})$ as
$H^2(X_1,{\mathbb {Q}})$ as ![]() $\bar {g}$, so that
$\bar {g}$, so that ![]() $\widetilde {H}_0(g)=\bar {g}$ (seeFootnote 9 [Reference MarkmanMar21a, Remark 5.4]). In particular, this is the case when
$\widetilde {H}_0(g)=\bar {g}$ (seeFootnote 9 [Reference MarkmanMar21a, Remark 5.4]). In particular, this is the case when ![]() $(X_1,\eta _1)$ and
$(X_1,\eta _1)$ and ![]() $(X_2,\eta _2)$ belong to the same connected component of
$(X_2,\eta _2)$ belong to the same connected component of ![]() ${\mathfrak {M}}_\Lambda$ and
${\mathfrak {M}}_\Lambda$ and ![]() $\bar {g}=\eta _2^{-1}\eta _1$.
$\bar {g}=\eta _2^{-1}\eta _1$.
Let ![]() $E$ be the Fourier–Mukai kernel of non-zero rank of an equivalence
$E$ be the Fourier–Mukai kernel of non-zero rank of an equivalence ![]() $\Phi _E:D^b(X)\rightarrow D^b(Y)$ of derived categories of two deformation equivalent IHSMs
$\Phi _E:D^b(X)\rightarrow D^b(Y)$ of derived categories of two deformation equivalent IHSMs ![]() $X$ and
$X$ and ![]() $Y$. Set
$Y$. Set ![]() $\phi :=[\kappa (E)\sqrt {td_{X\times Y}}]_*:H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ and let
$\phi :=[\kappa (E)\sqrt {td_{X\times Y}}]_*:H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ and let ![]() $\widetilde {H}(\phi )_0$ be the restriction of
$\widetilde {H}(\phi )_0$ be the restriction of ![]() $\widetilde {H}(\phi )$ to
$\widetilde {H}(\phi )$ to ![]() $H^2(X,{\mathbb {Q}})$. Set
$H^2(X,{\mathbb {Q}})$. Set
We denote ![]() $\widetilde {H}_0(\phi )$ also by
$\widetilde {H}_0(\phi )$ also by ![]() $\psi _E$ to emphasize its dependence on
$\psi _E$ to emphasize its dependence on ![]() $E$:
$E$:
Let ![]() $\psi :\Lambda _{\mathbb {Q}}\rightarrow \Lambda _{\mathbb {Q}}$, be the isometry given by
$\psi :\Lambda _{\mathbb {Q}}\rightarrow \Lambda _{\mathbb {Q}}$, be the isometry given by
Then ![]() $\psi$ belongs to
$\psi$ belongs to ![]() $O^+(\Lambda _{\mathbb {Q}})$, since
$O^+(\Lambda _{\mathbb {Q}})$, since ![]() $(X,\eta _X)$ and
$(X,\eta _X)$ and ![]() $(Y,\eta _Y)$ belong to the same connected component of
$(Y,\eta _Y)$ belong to the same connected component of ![]() ${\mathfrak {M}}_\Lambda$ and
${\mathfrak {M}}_\Lambda$ and ![]() $\widetilde {H}_0(\phi )$ is orientation preserving (see [Reference MarkmanMar11, § 4]).
$\widetilde {H}_0(\phi )$ is orientation preserving (see [Reference MarkmanMar11, § 4]).
Assumption 5.19
(1) Assume that the Fourier–Mukai kernel
 $E$ in Lemma 4.1 is represented by a locally free sheaf, which we also denote by
$E$ in Lemma 4.1 is represented by a locally free sheaf, which we also denote by  $E$.
$E$.(2) Assume that there existFootnote 10 proper and smooth families of Kähler manifolds
 $p:{\mathcal {X}}\rightarrow B$ and
$p:{\mathcal {X}}\rightarrow B$ and  $q:{\mathcal {Y}}\rightarrow B$, over the same simply connected analytic base
$q:{\mathcal {Y}}\rightarrow B$, over the same simply connected analytic base  $B$, a possibly twisted vector bundle
$B$, a possibly twisted vector bundle  ${\mathcal {E}}$ over
${\mathcal {E}}$ over  ${\mathcal {X}}\times _B {\mathcal {Y}}$, a point
${\mathcal {X}}\times _B {\mathcal {Y}}$, a point  $b\in B$, isomorphisms
$b\in B$, isomorphisms  $f:X\rightarrow X_b$ and
$f:X\rightarrow X_b$ and  $g:Y\rightarrow Y_b$, and an isomorphism of Azumaya algebras
$g:Y\rightarrow Y_b$, and an isomorphism of Azumaya algebras  ${\mathcal {E}}nd(E)\cong (f\times g)^*{\mathcal {E}}nd({\mathcal {E}})$, where
${\mathcal {E}}nd(E)\cong (f\times g)^*{\mathcal {E}}nd({\mathcal {E}})$, where  $X_b$ and
$X_b$ and  $Y_b$ are the fibers of
$Y_b$ are the fibers of  ${\mathcal {X}}$ and
${\mathcal {X}}$ and  ${\mathcal {Y}}$ over
${\mathcal {Y}}$ over  $b$, such that the value of the parallel transport
$b$, such that the value of the parallel transport  $\psi _{E_0}$ of
$\psi _{E_0}$ of  $\psi _E$ in the local system
$\psi _E$ in the local system  $(R^2p_*{\mathbb {Q}})^*\otimes R^2q_*{\mathbb {Q}}$ at some point
$(R^2p_*{\mathbb {Q}})^*\otimes R^2q_*{\mathbb {Q}}$ at some point  $0\in B$ maps some Kähler class
$0\in B$ maps some Kähler class  $\omega _1$ on the fiber
$\omega _1$ on the fiber  $X_0$ of
$X_0$ of  $p$ to a Kähler class
$p$ to a Kähler class  $\omega _2$ over the fiber
$\omega _2$ over the fiber  $Y_0$ of
$Y_0$ of  $q$.
$q$.(3) We assume that
 $E_0$ is
$E_0$ is  $[\pi _{X_0}^*(\omega )+\pi _{Y_0}^*(\psi _{E_0}(\omega ))]$-slope-stable, for classes
$[\pi _{X_0}^*(\omega )+\pi _{Y_0}^*(\psi _{E_0}(\omega ))]$-slope-stable, for classes  $\omega$ in a non-empty subcone of the intersection
$\omega$ in a non-empty subcone of the intersection  ${\mathcal {K}}_{X_0}\cap \psi _{E_0}^{-1}({\mathcal {K}}_{Y_0})$.
${\mathcal {K}}_{X_0}\cap \psi _{E_0}^{-1}({\mathcal {K}}_{Y_0})$.
Remark 5.20 Note that the class ![]() $\kappa (E_0)\sqrt {td_{X_0\times Y_0}}$ induces the degree-reversing Hodge isometry (with respect to the Mukai pairings)
$\kappa (E_0)\sqrt {td_{X_0\times Y_0}}$ induces the degree-reversing Hodge isometry (with respect to the Mukai pairings)
which is the parallel transport of ![]() $\phi$ in Lemma 4.1, hence a morphism in
$\phi$ in Lemma 4.1, hence a morphism in ![]() ${\rm Hom}_{\mathcal {G}}(X_0,Y_0)$. Its image
${\rm Hom}_{\mathcal {G}}(X_0,Y_0)$. Its image ![]() $\widetilde {H}(\phi _0)$ restricts to a Hodge isometry
$\widetilde {H}(\phi _0)$ restricts to a Hodge isometry ![]() $\widetilde {H}(\phi _0)_0:H^2(X_0,{\mathbb {Q}})\rightarrow H^2(Y_0,{\mathbb {Q}})$, which is the parallel transport of
$\widetilde {H}(\phi _0)_0:H^2(X_0,{\mathbb {Q}})\rightarrow H^2(Y_0,{\mathbb {Q}})$, which is the parallel transport of ![]() $\widetilde {H}(\phi )_0$ in Lemma 4.1. The parallel transport
$\widetilde {H}(\phi )_0$ in Lemma 4.1. The parallel transport ![]() $\psi _{E_0}:H^2(X_0,{\mathbb {Q}})\rightarrow H^2(Y_0,{\mathbb {Q}})$ of
$\psi _{E_0}:H^2(X_0,{\mathbb {Q}})\rightarrow H^2(Y_0,{\mathbb {Q}})$ of ![]() $\psi _E$ in Assumption 5.19(2) is equal to
$\psi _E$ in Assumption 5.19(2) is equal to ![]() $\widetilde {H}_0(\phi _0)$.
$\widetilde {H}_0(\phi _0)$.
Let ![]() $\eta _{X_0}$ be the marking of
$\eta _{X_0}$ be the marking of ![]() $X_0$ resulting in the extension of
$X_0$ resulting in the extension of ![]() $\eta _X$ to a trivialization of
$\eta _X$ to a trivialization of ![]() $R^2p_*{\mathbb {Z}}$ for the family
$R^2p_*{\mathbb {Z}}$ for the family ![]() $p:{\mathcal {X}}\rightarrow B$ in Assumption 5.19. Define
$p:{\mathcal {X}}\rightarrow B$ in Assumption 5.19. Define ![]() $\eta _{Y_0}$ similarly. Note that
$\eta _{Y_0}$ similarly. Note that ![]() $\psi (\eta _{X_0}(\omega _1))=\eta _{Y_0}(\omega _2)$ for some Kähler classes
$\psi (\eta _{X_0}(\omega _1))=\eta _{Y_0}(\omega _2)$ for some Kähler classes ![]() $\omega _1$ and
$\omega _1$ and ![]() $\omega _2$, by Assumption 5.19, and so
$\omega _2$, by Assumption 5.19, and so ![]() $(X_0,\eta _{X_0},Y_0,\eta _{Y_0})$ belongs to
$(X_0,\eta _{X_0},Y_0,\eta _{Y_0})$ belongs to ![]() ${\mathfrak {M}}_\psi$. Denote by
${\mathfrak {M}}_\psi$. Denote by
the connected component of ![]() ${\mathfrak {M}}_\psi$ containing
${\mathfrak {M}}_\psi$ containing ![]() $(X_0,\eta _{X_0},Y_0,\eta _{Y_0})$.
$(X_0,\eta _{X_0},Y_0,\eta _{Y_0})$.
5.7 Deforming the Fourier–Mukai kernel
Definition 5.21 A quadruple ![]() $(X_1,\eta _1,X_2,\eta _2)$ in
$(X_1,\eta _1,X_2,\eta _2)$ in ![]() ${\mathfrak {M}}_\psi$ is said to support a compatible vector bundle if there exists a (possibly twisted) locally free coherent sheaf
${\mathfrak {M}}_\psi$ is said to support a compatible vector bundle if there exists a (possibly twisted) locally free coherent sheaf ![]() $F$ over
$F$ over ![]() $X_1\times X_2$ with the following properties.
$X_1\times X_2$ with the following properties.
(1) The class
 $\kappa (F)\sqrt {td_{X_1\times X_2}}$ induces a morphism
in
$\kappa (F)\sqrt {td_{X_1\times X_2}}$ induces a morphism
in \[ \phi_F:H^*(X_1,{\mathbb{Q}})\rightarrow H^*(X_2,{\mathbb{Q}}) \]
\[ \phi_F:H^*(X_1,{\mathbb{Q}})\rightarrow H^*(X_2,{\mathbb{Q}}) \]
 ${\rm Hom}_{{\mathcal {G}}_{an}}(X_1,X_2)$, where
${\rm Hom}_{{\mathcal {G}}_{an}}(X_1,X_2)$, where  ${\mathcal {G}}_{an}$ is the groupoid given in (1.2).
${\mathcal {G}}_{an}$ is the groupoid given in (1.2).(2) The equality
 $\psi =\eta _2\widetilde {H}_0(\phi _F)\eta _1^{-1}$ holds, where
$\psi =\eta _2\widetilde {H}_0(\phi _F)\eta _1^{-1}$ holds, where  $\widetilde {H}_0$ is given in (5.8).
$\widetilde {H}_0$ is given in (5.8).
Proposition 5.22 Every quadruple ![]() $(X_1,\eta _1,X_2,\eta _2)$ in the connected component
$(X_1,\eta _1,X_2,\eta _2)$ in the connected component ![]() ${\mathfrak {M}}_\psi ^0$ given in (5.11) supports a compatible vector bundle.
${\mathfrak {M}}_\psi ^0$ given in (5.11) supports a compatible vector bundle.
Proof. Step 1. Let ![]() $q\in {\mathfrak {M}}_\psi ^0$ be the isomorphism class of
$q\in {\mathfrak {M}}_\psi ^0$ be the isomorphism class of ![]() $(X_1,\eta _1,X_2,\eta _2)$. Consider the local system
$(X_1,\eta _1,X_2,\eta _2)$. Consider the local system ![]() $R\tilde {f}_*{\mathbb {Q}}$ over
$R\tilde {f}_*{\mathbb {Q}}$ over ![]() ${\mathfrak {M}}^0_\psi$ associated to the universal fiber product (5.7). Let
${\mathfrak {M}}^0_\psi$ associated to the universal fiber product (5.7). Let ![]() $\gamma _q\in H^*(X_1\times X_2,{\mathbb {Q}})$ be a flat deformation of the class
$\gamma _q\in H^*(X_1\times X_2,{\mathbb {Q}})$ be a flat deformation of the class
via a path in ![]() ${\mathfrak {M}}_\psi ^0$ from
${\mathfrak {M}}_\psi ^0$ from ![]() $(X_0,\eta _{X_0},Y_0,\eta _{Y_0})$ to
$(X_0,\eta _{X_0},Y_0,\eta _{Y_0})$ to ![]() $q$. If
$q$. If ![]() $\tilde {\eta }_1:H^*(X_1,{\mathbb {Q}})\rightarrow H^*(X_0,{\mathbb {Q}})$ denotes the parallel-transport operator in the local system
$\tilde {\eta }_1:H^*(X_1,{\mathbb {Q}})\rightarrow H^*(X_0,{\mathbb {Q}})$ denotes the parallel-transport operator in the local system ![]() $\Pi _1^*Rf_*{\mathbb {Q}}$ and
$\Pi _1^*Rf_*{\mathbb {Q}}$ and ![]() $\tilde {\eta }_2:H^*(X_2,{\mathbb {Q}})\rightarrow H^*(Y_0,{\mathbb {Q}})$ denotes the parallel-transport operator in the local system
$\tilde {\eta }_2:H^*(X_2,{\mathbb {Q}})\rightarrow H^*(Y_0,{\mathbb {Q}})$ denotes the parallel-transport operator in the local system ![]() $\Pi _2^*Rf_*{\mathbb {Q}}$, both with respect to the chosen path (backward), then
$\Pi _2^*Rf_*{\mathbb {Q}}$, both with respect to the chosen path (backward), then ![]() $\gamma =(\tilde {\eta }_1\otimes \tilde {\eta }_2)(\gamma _q)$. The class
$\gamma =(\tilde {\eta }_1\otimes \tilde {\eta }_2)(\gamma _q)$. The class ![]() $\gamma _q$ is independent of the path chosen, since the local system
$\gamma _q$ is independent of the path chosen, since the local system ![]() $R\tilde {f}_*{\mathbb {Q}}$ over
$R\tilde {f}_*{\mathbb {Q}}$ over ![]() ${\mathfrak {M}}_\Lambda ^0$ is trivial, by [Reference MarkmanMar21b, Lemma 2.1]. We prove in this step that
${\mathfrak {M}}_\Lambda ^0$ is trivial, by [Reference MarkmanMar21b, Lemma 2.1]. We prove in this step that ![]() $\gamma _q$ is a Hodge class. In particular,
$\gamma _q$ is a Hodge class. In particular, ![]() $c_2({\mathcal {E}}nd(E_0))$ remains of Hodge type over
$c_2({\mathcal {E}}nd(E_0))$ remains of Hodge type over ![]() $X_1\times X_2$, by the equality
$X_1\times X_2$, by the equality ![]() $c_2({\mathcal {E}}nd(E_0))=-2\,{\rm rank}(E_0)\kappa _2(E_0)$. Once it is proven that
$c_2({\mathcal {E}}nd(E_0))=-2\,{\rm rank}(E_0)\kappa _2(E_0)$. Once it is proven that ![]() $\gamma _q$ is a Hodge class, for all
$\gamma _q$ is a Hodge class, for all ![]() $q\in {\mathfrak {M}}^0_\psi$, Proposition 5.15 implies the existence of a locally free sheaf
$q\in {\mathfrak {M}}^0_\psi$, Proposition 5.15 implies the existence of a locally free sheaf ![]() $F$ over
$F$ over ![]() $X_1\times X_2$ such that
$X_1\times X_2$ such that ![]() ${\mathcal {E}}nd(F)$ is deformation equivalent to
${\mathcal {E}}nd(F)$ is deformation equivalent to ![]() ${\mathcal {E}}nd(E_0)$.
${\mathcal {E}}nd(E_0)$.
The isometryFootnote 11 ![]() $\phi _0:H^*(X_0,{\mathbb {Q}})\rightarrow H^*(Y_0,{\mathbb {Q}})$, induced by
$\phi _0:H^*(X_0,{\mathbb {Q}})\rightarrow H^*(Y_0,{\mathbb {Q}})$, induced by ![]() $\gamma$, is invariant under the action of
$\gamma$, is invariant under the action of ![]() $GL(H^*(X_0,{\mathbb {Q}}))$ on
$GL(H^*(X_0,{\mathbb {Q}}))$ on ![]() ${\rm Hom}(H^*(X_0,{\mathbb {Q}}),H^*(Y_0,{\mathbb {Q}}))$, where an element
${\rm Hom}(H^*(X_0,{\mathbb {Q}}),H^*(Y_0,{\mathbb {Q}}))$, where an element ![]() $g\in GL(H^*(X_0,{\mathbb {Q}}))$ acts by
$g\in GL(H^*(X_0,{\mathbb {Q}}))$ acts by ![]() $h\mapsto (\phi _0 g\phi _0^{-1})h g^{-1}$. The isometry
$h\mapsto (\phi _0 g\phi _0^{-1})h g^{-1}$. The isometry ![]() $\phi _0$ is related to the class
$\phi _0$ is related to the class ![]() $\gamma :=\kappa (E_0)\sqrt {td_{X_0\times Y_0}}$ via
$\gamma :=\kappa (E_0)\sqrt {td_{X_0\times Y_0}}$ via
where the middle isomorphism is induced by the Poincaré duality isomorphism ![]() $PD:H^*(X_0,{\mathbb {Q}})\rightarrow H^*(X_0,{\mathbb {Q}})^*$. Assume that
$PD:H^*(X_0,{\mathbb {Q}})\rightarrow H^*(X_0,{\mathbb {Q}})^*$. Assume that ![]() $g$ is an isometry with respect to the Poincaré pairing and so
$g$ is an isometry with respect to the Poincaré pairing and so ![]() $(g^{-1})^*= PD\circ g \circ PD^{-1}$. In this case
$(g^{-1})^*= PD\circ g \circ PD^{-1}$. In this case ![]() $\gamma$ is invariant with respect to the action by
$\gamma$ is invariant with respect to the action by ![]() $g\otimes (\phi _0 g\phi _0^{-1})$. The Lie algebra
$g\otimes (\phi _0 g\phi _0^{-1})$. The Lie algebra ![]() $\bar {{\mathfrak g}}_{X_0,{\mathbb {R}}}$ acts on
$\bar {{\mathfrak g}}_{X_0,{\mathbb {R}}}$ acts on ![]() $H^*(X_0,{\mathbb {R}})$ by derivations [Reference Looijenga and LuntsLL97, Proposition 4.5(ii)], and so it annihilates the cup product and is thus contained in the Lie algebra of the isometry group with respect to the Poincaré pairing. We get that the class
$H^*(X_0,{\mathbb {R}})$ by derivations [Reference Looijenga and LuntsLL97, Proposition 4.5(ii)], and so it annihilates the cup product and is thus contained in the Lie algebra of the isometry group with respect to the Poincaré pairing. We get that the class ![]() $\gamma$ is annihilated by
$\gamma$ is annihilated by ![]() $(\xi \otimes 1)+(1\otimes Ad_{\phi _0}(\xi ))$, for every element
$(\xi \otimes 1)+(1\otimes Ad_{\phi _0}(\xi ))$, for every element ![]() $\xi \in \bar {{\mathfrak g}}_{X_0}$. We conclude that
$\xi \in \bar {{\mathfrak g}}_{X_0}$. We conclude that ![]() $\gamma$ is annihilated by the Lie subalgebra
$\gamma$ is annihilated by the Lie subalgebra
where the inclusion follows from the equality ![]() $Ad_{\phi _0}({\mathfrak g}_{X_0})={\mathfrak g}_{Y_0}$ established in [Reference TaelmanTae23, Theorem A]. Note that
$Ad_{\phi _0}({\mathfrak g}_{X_0})={\mathfrak g}_{Y_0}$ established in [Reference TaelmanTae23, Theorem A]. Note that ![]() $\bar {{\mathfrak g}}_{\phi _0}$ is, in fact, the subalgebra
$\bar {{\mathfrak g}}_{\phi _0}$ is, in fact, the subalgebra
by Lemma 4.1(3) and Remark 5.20.
We have the commutative diagram

whose horizontal arrows are parallel-transport operators. The Lie algebra ![]() ${\mathfrak g}_{X_0}$ deforms flatly to
${\mathfrak g}_{X_0}$ deforms flatly to ![]() ${\mathfrak g}_{X_1}$, by the topological nature of both, and so the semi-simple part of its degree-
${\mathfrak g}_{X_1}$, by the topological nature of both, and so the semi-simple part of its degree-![]() $0$ summand
$0$ summand ![]() $\bar {{\mathfrak g}}_{X_0}$ deforms flatly to
$\bar {{\mathfrak g}}_{X_0}$ deforms flatly to ![]() $\bar {{\mathfrak g}}_{X_1}$. The Lie subalgebra
$\bar {{\mathfrak g}}_{X_1}$. The Lie subalgebra ![]() ${\mathfrak g}_{\psi _{E_0}}$ deforms flatly to
${\mathfrak g}_{\psi _{E_0}}$ deforms flatly to
by the commutativity of the above diagram. Indeed,
 \begin{align*} (Ad_{\eta_1^{-1}\eta_{X_0}}\otimes Ad_{\eta_2^{-1}\eta_{Y_0}}) \Big((\xi\otimes 1)+(1\otimes Ad_{\psi_{E_0}}(\xi))\Big) &= (Ad_{\eta_1^{-1}\eta_{X_0}}(\xi)\otimes 1)+(1\otimes Ad_{\eta_2^{-1}\eta_{Y_0}\psi_{E_0}}(\xi))\\ &= (\xi'\otimes 1)+(1\otimes Ad_{\psi_q}(\xi')), \end{align*}
\begin{align*} (Ad_{\eta_1^{-1}\eta_{X_0}}\otimes Ad_{\eta_2^{-1}\eta_{Y_0}}) \Big((\xi\otimes 1)+(1\otimes Ad_{\psi_{E_0}}(\xi))\Big) &= (Ad_{\eta_1^{-1}\eta_{X_0}}(\xi)\otimes 1)+(1\otimes Ad_{\eta_2^{-1}\eta_{Y_0}\psi_{E_0}}(\xi))\\ &= (\xi'\otimes 1)+(1\otimes Ad_{\psi_q}(\xi')), \end{align*}
where ![]() $\xi ':=Ad_{\eta _1^{-1}\eta _{X_0}}(\xi )\in \bar {{\mathfrak g}}_{X_1}$. It follows that
$\xi ':=Ad_{\eta _1^{-1}\eta _{X_0}}(\xi )\in \bar {{\mathfrak g}}_{X_1}$. It follows that ![]() $\gamma _q$ is annihilated by
$\gamma _q$ is annihilated by ![]() $\bar {{\mathfrak g}}_{\psi _q}$, as we have seen that
$\bar {{\mathfrak g}}_{\psi _q}$, as we have seen that ![]() $\gamma$ is annihilated by
$\gamma$ is annihilated by ![]() $\bar {{\mathfrak g}}_{\psi _{E_0}}$.
$\bar {{\mathfrak g}}_{\psi _{E_0}}$.
Let ![]() $h'_{X_i}$ be the Hodge operator of
$h'_{X_i}$ be the Hodge operator of ![]() $X_i$,
$X_i$, ![]() $i=1,2$, given in (3.8). Then
$i=1,2$, given in (3.8). Then ![]() $h'_{X_2}=Ad_{\psi _q}(h'_{X_1})$, since
$h'_{X_2}=Ad_{\psi _q}(h'_{X_1})$, since ![]() $\psi _q$ is an isomorphism of Hodge structures. Hence, the Hodge operator of
$\psi _q$ is an isomorphism of Hodge structures. Hence, the Hodge operator of ![]() $X_1\times X_2$
$X_1\times X_2$
belongs to ![]() $\bar {{\mathfrak g}}_{\psi _q}$ and, thus, annihilates
$\bar {{\mathfrak g}}_{\psi _q}$ and, thus, annihilates ![]() $\gamma _q$. We conclude that
$\gamma _q$. We conclude that ![]() $\gamma _q$ is a Hodge class.
$\gamma _q$ is a Hodge class.
Step 2. Consider first the quadruple ![]() $q_0:=(X_0,\eta _{X_0},Y_0,\eta _{Y_0})$, used in the definition of the connected component
$q_0:=(X_0,\eta _{X_0},Y_0,\eta _{Y_0})$, used in the definition of the connected component ![]() ${\mathfrak {M}}_\psi ^0$ in (5.11), and set
${\mathfrak {M}}_\psi ^0$ in (5.11), and set ![]() $F:=E_0$. Property (1) in Definition 5.21 follows in this case from Assumption 5.19 and property (2) follows from the definition of
$F:=E_0$. Property (1) in Definition 5.21 follows in this case from Assumption 5.19 and property (2) follows from the definition of ![]() $\psi$ in (5.9).
$\psi$ in (5.9).
Let ![]() $\phi _{\gamma _q}:H^*(X_1,{\mathbb {Q}})\rightarrow H^*(X_2,{\mathbb {Q}})$ be the homomorphism induced by
$\phi _{\gamma _q}:H^*(X_1,{\mathbb {Q}})\rightarrow H^*(X_2,{\mathbb {Q}})$ be the homomorphism induced by ![]() $\gamma _q$. The equality
$\gamma _q$. The equality ![]() $\phi _{\gamma _q}=\tilde {\eta }_2^{-1}\phi _0\tilde {\eta }_1$ exhibits
$\phi _{\gamma _q}=\tilde {\eta }_2^{-1}\phi _0\tilde {\eta }_1$ exhibits ![]() $\phi _{\gamma _q}$ as a composition of morphisms in the groupoid
$\phi _{\gamma _q}$ as a composition of morphisms in the groupoid ![]() ${\mathcal {G}}$, hence in
${\mathcal {G}}$, hence in ![]() ${\rm Hom}_{\mathcal {G}}(X_1,X_2)$. Choose a twistor path
${\rm Hom}_{\mathcal {G}}(X_1,X_2)$. Choose a twistor path ![]() $C$ in
$C$ in ![]() ${\mathfrak {M}}^0_\psi$ from
${\mathfrak {M}}^0_\psi$ from ![]() $q_0$ to
$q_0$ to ![]() $q$ along which the Azumaya algebra
$q$ along which the Azumaya algebra ![]() ${\mathcal {E}}nd(E_0)$ deforms via an Azumaya algebra
${\mathcal {E}}nd(E_0)$ deforms via an Azumaya algebra ![]() ${\mathcal {A}}$ over the twistor family
${\mathcal {A}}$ over the twistor family ![]() $\Pi _1^*{\mathcal {X}}\times _C\Pi _2^*{\mathcal {X}}\rightarrow C$. Such a path
$\Pi _1^*{\mathcal {X}}\times _C\Pi _2^*{\mathcal {X}}\rightarrow C$. Such a path ![]() $C$ exists, by Assumption 5.19 and Proposition 5.15. There exists a locally free twisted sheaf
$C$ exists, by Assumption 5.19 and Proposition 5.15. There exists a locally free twisted sheaf ![]() ${\mathcal {F}}$ over
${\mathcal {F}}$ over ![]() $\Pi _1^*{\mathcal {X}}\times _C\Pi _2^*{\mathcal {X}}$, such that
$\Pi _1^*{\mathcal {X}}\times _C\Pi _2^*{\mathcal {X}}$, such that ![]() ${\mathcal {E}}nd({\mathcal {F}})$ is isomorphic to
${\mathcal {E}}nd({\mathcal {F}})$ is isomorphic to ![]() ${\mathcal {A}}$.
${\mathcal {A}}$. ![]() ${\mathcal {F}}$ restricts to a locally free twisted sheaf
${\mathcal {F}}$ restricts to a locally free twisted sheaf ![]() $F_0$ over
$F_0$ over ![]() $X_0\times Y_0$ and a locally free sheaf
$X_0\times Y_0$ and a locally free sheaf ![]() $F$ over
$F$ over ![]() $X_1\times X_2$, such that the Azumaya algebras
$X_1\times X_2$, such that the Azumaya algebras ![]() ${\mathcal {E}}nd(F_0)$ is isomorphic to
${\mathcal {E}}nd(F_0)$ is isomorphic to ![]() ${\mathcal {E}}nd(E_0)$ and
${\mathcal {E}}nd(E_0)$ and ![]() $\kappa (F)$ is a parallel transport of
$\kappa (F)$ is a parallel transport of ![]() $\kappa (F_0)$ along a (real) path in
$\kappa (F_0)$ along a (real) path in ![]() $C$. Hence,
$C$. Hence, ![]() $\gamma _q$ is equal to
$\gamma _q$ is equal to ![]() $\kappa (F)\sqrt {td_{X_1\times X_2}}$ and property (1) in Definition 5.21 follows. Property (2) in Definition 5.21 is equivalent to the equality
$\kappa (F)\sqrt {td_{X_1\times X_2}}$ and property (1) in Definition 5.21 follows. Property (2) in Definition 5.21 is equivalent to the equality ![]() $\psi _q=\widetilde {H}_0([\kappa (F)\sqrt {td_{X_1\times X_2}}]_*)$. The latter equality follows at
$\psi _q=\widetilde {H}_0([\kappa (F)\sqrt {td_{X_1\times X_2}}]_*)$. The latter equality follows at ![]() $q$ via Remark 5.18 from the fact that it holds for
$q$ via Remark 5.18 from the fact that it holds for ![]() $q_0$. Explicitly,
$q_0$. Explicitly,
 \begin{align*} \psi_q&\qquad\! =\qquad (\eta_2^{-1}\eta_{Y_0})\psi_{E_0}(\eta_{X_0}^{-1}\eta_1)= (\eta_2^{-1}\eta_{Y_0})\widetilde{H}_0([\kappa(E_0)\sqrt{td_{X_0\times Y_0}}]_*)(\eta_{X_0}^{-1}\eta_1)\\ &\stackrel{{\rm Remark}\ \text{5.18}}= \widetilde{H}_0\big((\tilde{\eta}_2^{-1})\circ [\kappa(E_0)\sqrt{td_{X_0\times Y_0}}]_*\circ \tilde{\eta}_1\big)= \widetilde{H}_0([\kappa(F)\sqrt{td_{X_1\times X_2}}]_*). \end{align*}
\begin{align*} \psi_q&\qquad\! =\qquad (\eta_2^{-1}\eta_{Y_0})\psi_{E_0}(\eta_{X_0}^{-1}\eta_1)= (\eta_2^{-1}\eta_{Y_0})\widetilde{H}_0([\kappa(E_0)\sqrt{td_{X_0\times Y_0}}]_*)(\eta_{X_0}^{-1}\eta_1)\\ &\stackrel{{\rm Remark}\ \text{5.18}}= \widetilde{H}_0\big((\tilde{\eta}_2^{-1})\circ [\kappa(E_0)\sqrt{td_{X_0\times Y_0}}]_*\circ \tilde{\eta}_1\big)= \widetilde{H}_0([\kappa(F)\sqrt{td_{X_1\times X_2}}]_*). \end{align*}
6. The BKR equivalence
Let ![]() $S$ be a projective surface and denote by
$S$ be a projective surface and denote by ![]() $S^{[n]}$ the Hilbert scheme of length
$S^{[n]}$ the Hilbert scheme of length ![]() $n$ subscheme of
$n$ subscheme of ![]() $S$. The symmetric group
$S$. The symmetric group ![]() ${\mathfrak {S}}_n$ on
${\mathfrak {S}}_n$ on ![]() $n$ letters acts on the cartesian product
$n$ letters acts on the cartesian product ![]() $S^n$ permuting the factors. Let
$S^n$ permuting the factors. Let ![]() $\textit{Hilb}_{{\mathfrak {S}}_n}(S^n)$ be the Hilbert scheme of length
$\textit{Hilb}_{{\mathfrak {S}}_n}(S^n)$ be the Hilbert scheme of length ![]() $n!$ subschemes
$n!$ subschemes ![]() $Z$ of
$Z$ of ![]() $S^n$, which are
$S^n$, which are ![]() ${\mathfrak {S}}_n$-invariant, and such that
${\mathfrak {S}}_n$-invariant, and such that ![]() $H^0(Z,{\mathcal {O}}_{Z})$ is the regular representation of
$H^0(Z,{\mathcal {O}}_{Z})$ is the regular representation of ![]() ${\mathfrak {S}}_n$. Then
${\mathfrak {S}}_n$. Then ![]() $S^{[n]}$ is isomorphic to the closure in
$S^{[n]}$ is isomorphic to the closure in ![]() $\textit{Hilb}_{{\mathfrak {S}}_n}(S^n)$ of the locus of reduced subschemes which are
$\textit{Hilb}_{{\mathfrak {S}}_n}(S^n)$ of the locus of reduced subschemes which are ![]() ${\mathfrak {S}}_n$-orbits of
${\mathfrak {S}}_n$-orbits of ![]() $n$-tuples consisting of
$n$-tuples consisting of ![]() $n$ distinct points of
$n$ distinct points of ![]() $S$, by [Reference HaimanHai01]. The restriction
$S$, by [Reference HaimanHai01]. The restriction
to ![]() $S^{[n]}$ of the universal subscheme of
$S^{[n]}$ of the universal subscheme of ![]() $\textit{Hilb}_{{\mathfrak {S}}_n}(S^n)\times S^n$ is calledFootnote 12 the isospectral Hilbert scheme. The projections
$\textit{Hilb}_{{\mathfrak {S}}_n}(S^n)\times S^n$ is calledFootnote 12 the isospectral Hilbert scheme. The projections ![]() $S^{[n]}\stackrel {q}{\leftarrow } \Gamma _S\stackrel {b}{\rightarrow } S^n$ have the following properties. The morphism
$S^{[n]}\stackrel {q}{\leftarrow } \Gamma _S\stackrel {b}{\rightarrow } S^n$ have the following properties. The morphism ![]() $q$ is flat and
$q$ is flat and ![]() ${\mathfrak {S}}_n$-invariant of degree
${\mathfrak {S}}_n$-invariant of degree ![]() $n!$, by the proof of [Reference HaimanHai01, Proposition 3.7.4]. The morphism
$n!$, by the proof of [Reference HaimanHai01, Proposition 3.7.4]. The morphism ![]() $b$ restricts to an isomorphism over the complement of the union of the diagonals in
$b$ restricts to an isomorphism over the complement of the union of the diagonals in ![]() $S^n$. The isospectral Hilbert scheme
$S^n$. The isospectral Hilbert scheme ![]() $\Gamma _S$ is Gorenstein, by [Reference HaimanHai01, Theorem 3.1], and its dualizing sheaf
$\Gamma _S$ is Gorenstein, by [Reference HaimanHai01, Theorem 3.1], and its dualizing sheaf ![]() $\omega _{\Gamma _S}$ is isomorphic to the line bundle
$\omega _{\Gamma _S}$ is isomorphic to the line bundle ![]() $q^*(\omega _{S^{[n]}}(\delta ))$, by [Reference HaimanHai01, Theorem 3.1, Proposition 3.4.3, comment after Lemma 3.4.2]. Above
$q^*(\omega _{S^{[n]}}(\delta ))$, by [Reference HaimanHai01, Theorem 3.1, Proposition 3.4.3, comment after Lemma 3.4.2]. Above ![]() $\delta$ is the divisor class, such that
$\delta$ is the divisor class, such that ![]() ${\mathcal {O}}_{S^{[n]}}(-\delta )\cong \big (q_*({\mathcal {O}}_{\Gamma _S})\big )^\chi$, where
${\mathcal {O}}_{S^{[n]}}(-\delta )\cong \big (q_*({\mathcal {O}}_{\Gamma _S})\big )^\chi$, where ![]() $\chi$ is the sign character of
$\chi$ is the sign character of ![]() ${\mathfrak {S}}_n$. Note that
${\mathfrak {S}}_n$. Note that ![]() $2\delta$ is the class of the effective divisor in
$2\delta$ is the class of the effective divisor in ![]() $S^{[n]}$ of non-reduced subschemes.
$S^{[n]}$ of non-reduced subschemes.
Let ![]() $D^b_{{\mathfrak {S}}_n}(S^n)$ be the bounded derived category of
$D^b_{{\mathfrak {S}}_n}(S^n)$ be the bounded derived category of ![]() ${\mathfrak {S}}_n$-equivariant coherent sheaves on
${\mathfrak {S}}_n$-equivariant coherent sheaves on ![]() $S^n$ and
$S^n$ and ![]() $D^b_{{\mathfrak {S}}_n}(S^{[n]}\times S^n)$ its analogue with respect to the permutation action of
$D^b_{{\mathfrak {S}}_n}(S^{[n]}\times S^n)$ its analogue with respect to the permutation action of ![]() ${\mathfrak {S}}_n$ on the factor
${\mathfrak {S}}_n$ on the factor ![]() $S^n$ and the trivial action on the factor
$S^n$ and the trivial action on the factor ![]() $S^{[n]}$. Let
$S^{[n]}$. Let ![]() $\rho$ be the natural
$\rho$ be the natural ![]() ${\mathfrak {S}}_n$-linearization of
${\mathfrak {S}}_n$-linearization of ![]() ${\mathcal {O}}_{\Gamma _S}$. The object
${\mathcal {O}}_{\Gamma _S}$. The object ![]() $({\mathcal {O}}_{\Gamma _S},\rho )$ of
$({\mathcal {O}}_{\Gamma _S},\rho )$ of ![]() $D^b_{{\mathfrak {S}}_n}(S^{[n]}\times S^n)$ is the Fourier–Mukai kernel of an equivalence of derived categories
$D^b_{{\mathfrak {S}}_n}(S^{[n]}\times S^n)$ is the Fourier–Mukai kernel of an equivalence of derived categories
given by the composition ![]() $Rq_*^{{\mathfrak {S}}_n}Lb^*$ of the functors
$Rq_*^{{\mathfrak {S}}_n}Lb^*$ of the functors ![]() $Lb^*:D^b_{{\mathfrak {S}}_n}(S^n)\rightarrow D^b_{{\mathfrak {S}}_n}(\Gamma _S)$ and
$Lb^*:D^b_{{\mathfrak {S}}_n}(S^n)\rightarrow D^b_{{\mathfrak {S}}_n}(\Gamma _S)$ and ![]() $Rq_*^{{\mathfrak {S}}_n}:D^b_{{\mathfrak {S}}_n}(\Gamma _S)\rightarrow D^b(S^{[n]})$, by [Reference Bridgeland, King and ReidBKR01].
$Rq_*^{{\mathfrak {S}}_n}:D^b_{{\mathfrak {S}}_n}(\Gamma _S)\rightarrow D^b(S^{[n]})$, by [Reference Bridgeland, King and ReidBKR01].
7. A universal bundle over  $M^{[n]}\times S^{[n]}$ from a universal bundle over
$M^{[n]}\times S^{[n]}$ from a universal bundle over  $M\times S$
$M\times S$
In § 7.1 we recall the construction of a locally free Fourier–Mukai kernel of an equivalence of the derived categories of the Hilbert schemes ![]() $S^{[n]}$ and
$S^{[n]}$ and ![]() $M^{[n]}$, where
$M^{[n]}$, where ![]() $M$ is a two-dimensional smooth and projective moduli space of vector bundles on a
$M$ is a two-dimensional smooth and projective moduli space of vector bundles on a ![]() $K3$ surface
$K3$ surface ![]() $S$. In § 7.2 we construct a functor
$S$. In § 7.2 we construct a functor ![]() $\widetilde {\Theta }_n:{\mathcal {G}}^{[1]}\rightarrow {\mathcal {G}}^{[n]}$, which sends a morphism associated to an equivalence
$\widetilde {\Theta }_n:{\mathcal {G}}^{[1]}\rightarrow {\mathcal {G}}^{[n]}$, which sends a morphism associated to an equivalence ![]() $\Phi$ of derived categories of
$\Phi$ of derived categories of ![]() $K3$ surfaces to a morphism associated to the equivalence of the derived categories of their Hilbert schemes, which is the BKR conjugate of the cartesian power
$K3$ surfaces to a morphism associated to the equivalence of the derived categories of their Hilbert schemes, which is the BKR conjugate of the cartesian power ![]() $\Phi ^n$. In § 7.3 we normalize
$\Phi ^n$. In § 7.3 we normalize ![]() $\widetilde {\Theta }_n$ to obtain the functor
$\widetilde {\Theta }_n$ to obtain the functor ![]() $\Theta _n:{\mathcal {G}}^{[1]}\rightarrow {\mathcal {G}}^{[n]}$, mentioned in the introduction in (1.8), which maps
$\Theta _n:{\mathcal {G}}^{[1]}\rightarrow {\mathcal {G}}^{[n]}$, mentioned in the introduction in (1.8), which maps ![]() ${\mathcal {G}}^{[1]}_{an}$ to
${\mathcal {G}}^{[1]}_{an}$ to ![]() ${\mathcal {G}}^{[n]}_{an}$. The functor
${\mathcal {G}}^{[n]}_{an}$. The functor ![]() $\Theta _n$ sends a parallel-transport operator between two
$\Theta _n$ sends a parallel-transport operator between two ![]() $K3$ surfaces
$K3$ surfaces ![]() $S_1$ and
$S_1$ and ![]() $S_2$ to the associated parallel-transport operator between their Hilbert schemes
$S_2$ to the associated parallel-transport operator between their Hilbert schemes ![]() $S_1^{[n]}$ and
$S_1^{[n]}$ and ![]() $S_2^{[n]}$. If
$S_2^{[n]}$. If ![]() $\phi \in {\rm Hom}_{{\mathcal {G}}_{an}^{[1]}}(S_1,S_2)$ is induced by the class
$\phi \in {\rm Hom}_{{\mathcal {G}}_{an}^{[1]}}(S_1,S_2)$ is induced by the class ![]() $\kappa ({\mathcal {U}})\sqrt {td_{S_1\times S_2}}$ of the Fourier–Mukai kernel
$\kappa ({\mathcal {U}})\sqrt {td_{S_1\times S_2}}$ of the Fourier–Mukai kernel ![]() ${\mathcal {U}}$ of an equivalence
${\mathcal {U}}$ of an equivalence ![]() $\Phi _{\mathcal {U}}:D^b(S_1)\rightarrow D^b(S_2)$, then
$\Phi _{\mathcal {U}}:D^b(S_1)\rightarrow D^b(S_2)$, then ![]() $\Theta _n(\phi )$ is induced by the analogous class associated to the BKR conjugate of the
$\Theta _n(\phi )$ is induced by the analogous class associated to the BKR conjugate of the ![]() $n$th cartesian power of
$n$th cartesian power of ![]() $\Phi _{\mathcal {U}}$. In Corollary 7.4 we show that
$\Phi _{\mathcal {U}}$. In Corollary 7.4 we show that ![]() $\widetilde {H}(\Theta _n(\phi )):\widetilde {H}(S_1^{[n]},{\mathbb {Q}})\rightarrow \widetilde {H}(S_2^{[n]},{\mathbb {Q}})$ is the naive extension of
$\widetilde {H}(\Theta _n(\phi )):\widetilde {H}(S_1^{[n]},{\mathbb {Q}})\rightarrow \widetilde {H}(S_2^{[n]},{\mathbb {Q}})$ is the naive extension of ![]() $\widetilde {H}(\phi ):\widetilde {H}(S_1,{\mathbb {Q}})\rightarrow \widetilde {H}(S_2,{\mathbb {Q}})$.
$\widetilde {H}(\phi ):\widetilde {H}(S_1,{\mathbb {Q}})\rightarrow \widetilde {H}(S_2,{\mathbb {Q}})$.
7.1 A universal bundle over  $M^{[n]}\times S^{[n]}$
$M^{[n]}\times S^{[n]}$
Assume that ![]() $S$ is a
$S$ is a ![]() $K3$ surface,
$K3$ surface, ![]() $v=(r,\lambda,s)\in \widetilde {H}(S,{\mathbb {Z}})$ is a primitive and isotropic Mukai vector of rank
$v=(r,\lambda,s)\in \widetilde {H}(S,{\mathbb {Z}})$ is a primitive and isotropic Mukai vector of rank ![]() $r\geq 2$, and
$r\geq 2$, and ![]() $H$ is a
$H$ is a ![]() $v$-generic polarization. Then every
$v$-generic polarization. Then every ![]() $H$-slope-semistable sheaf on
$H$-slope-semistable sheaf on ![]() $S$ is
$S$ is ![]() $H$-slope-stable and locally free. Let
$H$-slope-stable and locally free. Let ![]() $M$ be the moduli space of
$M$ be the moduli space of ![]() $H$-slope-stable sheaves on
$H$-slope-stable sheaves on ![]() $S$ with Mukai vector
$S$ with Mukai vector ![]() $v$. Then
$v$. Then ![]() $M$ is a
$M$ is a ![]() $K3$ surface, by [Reference MukaiMuk87]. Assume that a universal sheaf
$K3$ surface, by [Reference MukaiMuk87]. Assume that a universal sheaf ![]() ${\mathcal {U}}$ exists over
${\mathcal {U}}$ exists over ![]() $M\times S$. Then
$M\times S$. Then ![]() ${\mathcal {U}}$ is the Fourier–Mukai kernel of an equivalence
${\mathcal {U}}$ is the Fourier–Mukai kernel of an equivalence
(see [Reference HuybrechtsHuy06, Proposition 10.25]). We get the equivalence
and its conjugate
Let ![]() ${\mathfrak {S}}_{n,\Delta }$ be the diagonal subgroup of
${\mathfrak {S}}_{n,\Delta }$ be the diagonal subgroup of ![]() ${\mathfrak {S}}_n\times {\mathfrak {S}}_n$. Let
${\mathfrak {S}}_n\times {\mathfrak {S}}_n$. Let ![]() ${\mathcal {U}}^{\boxtimes n}:={\mathcal {U}}\boxtimes \cdots \boxtimes {\mathcal {U}}$ be the exterior tensor power of
${\mathcal {U}}^{\boxtimes n}:={\mathcal {U}}\boxtimes \cdots \boxtimes {\mathcal {U}}$ be the exterior tensor power of ![]() ${\mathcal {U}}$ over
${\mathcal {U}}$ over ![]() $M^n\times S^n$. Then
$M^n\times S^n$. Then ![]() ${\mathcal {U}}^{\boxtimes n}$ admits the permutation
${\mathcal {U}}^{\boxtimes n}$ admits the permutation ![]() ${\mathfrak {S}}_{n,\Delta }$-linearization
${\mathfrak {S}}_{n,\Delta }$-linearization ![]() $\rho _\boxtimes$. Denote by
$\rho _\boxtimes$. Denote by ![]() $\chi$ the sign character of
$\chi$ the sign character of ![]() ${\mathfrak {S}}_{n,\Delta }$. We get the object
${\mathfrak {S}}_{n,\Delta }$. We get the object ![]() $({\mathcal {U}}^{\boxtimes n},\rho _\boxtimes \otimes \chi )$ in
$({\mathcal {U}}^{\boxtimes n},\rho _\boxtimes \otimes \chi )$ in ![]() $D^b_{{\mathfrak {S}}_{n,\Delta }}(M^n\times S^n)$.
$D^b_{{\mathfrak {S}}_{n,\Delta }}(M^n\times S^n)$.
We use the same notation for the morphisms ![]() $M^n\stackrel {b}{\leftarrow }\Gamma _M\stackrel {q}{\rightarrow } M^{[n]}$ from the isospectral Hilbert scheme of
$M^n\stackrel {b}{\leftarrow }\Gamma _M\stackrel {q}{\rightarrow } M^{[n]}$ from the isospectral Hilbert scheme of ![]() $M$. We get the product morphisms
$M$. We get the product morphisms
Lemma 7.1 The equivalence ![]() $\Phi _{\mathcal {U}}^{[n]}$ has the rank
$\Phi _{\mathcal {U}}^{[n]}$ has the rank ![]() $n!r^n$ locally free Fourier–Mukai kernel
$n!r^n$ locally free Fourier–Mukai kernel
Proof. The statement is proved in [Reference MarkmanMar21a, § 11.1.2, (11.6)]
7.2 The functor  $\widetilde {\Theta }_n:{\mathcal {G}}^{[1]}\rightarrow {\mathcal {G}}^{[n]}$
$\widetilde {\Theta }_n:{\mathcal {G}}^{[1]}\rightarrow {\mathcal {G}}^{[n]}$
In the remainder of § 7 we will keep the assumption that the rank of the object ![]() ${\mathcal {U}}\in D^b(S\times M)$ is non-zero, but drop the assumption that
${\mathcal {U}}\in D^b(S\times M)$ is non-zero, but drop the assumption that ![]() ${\mathcal {U}}$ is represented by a coherent sheaf. Let
${\mathcal {U}}$ is represented by a coherent sheaf. Let ![]() ${\mathcal {G}}^{[n]}$ be the subgroupoid of the groupoid
${\mathcal {G}}^{[n]}$ be the subgroupoid of the groupoid ![]() ${\mathcal {G}}$ given in (1.1) whose objects are of
${\mathcal {G}}$ given in (1.1) whose objects are of ![]() $K3^{[n]}$ type. We define next the functor
$K3^{[n]}$ type. We define next the functor ![]() $\widetilde {\Theta }_n:{\mathcal {G}}^{[1]}\rightarrow {\mathcal {G}}^{[n]}$. Define
$\widetilde {\Theta }_n:{\mathcal {G}}^{[1]}\rightarrow {\mathcal {G}}^{[n]}$. Define ![]() $\widetilde {\Theta }_n(X,\epsilon )=(X^{[n]},\epsilon ^{[n]})$, where the orientation
$\widetilde {\Theta }_n(X,\epsilon )=(X^{[n]},\epsilon ^{[n]})$, where the orientation ![]() $\epsilon ^{[n]}$ of
$\epsilon ^{[n]}$ of ![]() $H^2(X^{[n]},{\mathbb {Q}})$ is such that the class
$H^2(X^{[n]},{\mathbb {Q}})$ is such that the class ![]() $\delta$ extends a basis compatible with the orientation
$\delta$ extends a basis compatible with the orientation ![]() $\epsilon$ to one compatible with
$\epsilon$ to one compatible with ![]() $\epsilon ^{[n]}$.
$\epsilon ^{[n]}$.
(1) The functor ![]() $\widetilde {\Theta }_n$ maps a parallel-transport operator, associated to two fibers over two points
$\widetilde {\Theta }_n$ maps a parallel-transport operator, associated to two fibers over two points ![]() $b_0$ and
$b_0$ and ![]() $b_1$ in the base of a family
$b_1$ in the base of a family ![]() ${\mathcal {X}}\rightarrow B$ of
${\mathcal {X}}\rightarrow B$ of ![]() $K3$ surfaces and a path
$K3$ surfaces and a path ![]() $\gamma$ from
$\gamma$ from ![]() $b_0$ to
$b_0$ to ![]() $b_1$, to the parallel-transport operator associated to the same path and the relative Hilbert scheme
$b_1$, to the parallel-transport operator associated to the same path and the relative Hilbert scheme ![]() ${\mathcal {X}}^{[n]}\rightarrow B$. Denote by
${\mathcal {X}}^{[n]}\rightarrow B$. Denote by
the composition of the isomorphism ![]() $H^2(S,{\mathbb {Z}})\cong H^2(S^{(n)},{\mathbb {Z}})$ with the pullback
$H^2(S,{\mathbb {Z}})\cong H^2(S^{(n)},{\mathbb {Z}})$ with the pullback ![]() $H^2(S^{(n)},{\mathbb {Z}})\rightarrow H^2(S^{[n]},{\mathbb {Z}})$ via the Hilbert–Chow morphism.
$H^2(S^{(n)},{\mathbb {Z}})\rightarrow H^2(S^{[n]},{\mathbb {Z}})$ via the Hilbert–Chow morphism.
(2) The functor ![]() $\widetilde {\Theta }_n$ sends the cup product with
$\widetilde {\Theta }_n$ sends the cup product with ![]() $\exp (\lambda )$,
$\exp (\lambda )$, ![]() $\lambda \in H^2(X,{\mathbb {Q}})$, to the cup product with
$\lambda \in H^2(X,{\mathbb {Q}})$, to the cup product with ![]() $\exp (\theta (\lambda ))$.
$\exp (\theta (\lambda ))$.
(3) The functor ![]() $\widetilde {\Theta }_n$ sends the isometry
$\widetilde {\Theta }_n$ sends the isometry ![]() $\phi _{\mathcal {P}}:H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ induced by the correspondence
$\phi _{\mathcal {P}}:H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ induced by the correspondence ![]() $\sqrt {td_{X\times Y}}ch({\mathcal {P}})$, where
$\sqrt {td_{X\times Y}}ch({\mathcal {P}})$, where ![]() ${\mathcal {P}}\in D^b(X\times Y)$ is the Fourier–Mukai kernel of an equivalence
${\mathcal {P}}\in D^b(X\times Y)$ is the Fourier–Mukai kernel of an equivalence ![]() $\Phi _{\mathcal {P}}:D^b(X)\rightarrow D^b(Y)$, to the isometry induced by the correspondence
$\Phi _{\mathcal {P}}:D^b(X)\rightarrow D^b(Y)$, to the isometry induced by the correspondence ![]() $\sqrt {td_{X^{[n]}\times Y^{[n]}}}ch({\mathcal {P}}^{[n]})$, where
$\sqrt {td_{X^{[n]}\times Y^{[n]}}}ch({\mathcal {P}}^{[n]})$, where ![]() ${\mathcal {P}}^{[n]}$ is the Fourier–Mukai kernel in (7.2) of the BKR-conjugate of
${\mathcal {P}}^{[n]}$ is the Fourier–Mukai kernel in (7.2) of the BKR-conjugate of ![]() $\Phi _{\mathcal {P}}^{\boxtimes n}$ as in (7.1).
$\Phi _{\mathcal {P}}^{\boxtimes n}$ as in (7.1).
The image of morphisms under the functor ![]() $\widetilde {\Theta }_n$ was defined above separately for the three types of morphisms. Let
$\widetilde {\Theta }_n$ was defined above separately for the three types of morphisms. Let ![]() $[{\mathcal {O}}_{\Gamma _S}]$ be the class of
$[{\mathcal {O}}_{\Gamma _S}]$ be the class of ![]() ${\mathcal {O}}_{\Gamma _S}$, with its natural linearization, in the topological
${\mathcal {O}}_{\Gamma _S}$, with its natural linearization, in the topological ![]() ${\mathfrak {S}}_n$-equivariant
${\mathfrak {S}}_n$-equivariant ![]() $K$-ring
$K$-ring ![]() $K_{{\mathfrak {S}}_n}(S^n\times S^{[n]})$. We get the correspondence
$K_{{\mathfrak {S}}_n}(S^n\times S^{[n]})$. We get the correspondence ![]() $[{\mathcal {O}}_{\Gamma _S}]_*:K_{{\mathfrak {S}}_n}(S^n)\rightarrow K(S^{[n]})$ on the level of topological
$[{\mathcal {O}}_{\Gamma _S}]_*:K_{{\mathfrak {S}}_n}(S^n)\rightarrow K(S^{[n]})$ on the level of topological ![]() $K$-rings. The inverse is induced by a class in
$K$-rings. The inverse is induced by a class in ![]() $K_{{\mathfrak {S}}_n}(S^n\times S^{[n]})$ as well. The value of
$K_{{\mathfrak {S}}_n}(S^n\times S^{[n]})$ as well. The value of ![]() $\widetilde {\Theta }_n$ on a morphism in
$\widetilde {\Theta }_n$ on a morphism in ![]() ${\mathcal {G}}^{[1]}$ of type (3) associated to an equivalence
${\mathcal {G}}^{[1]}$ of type (3) associated to an equivalence ![]() $\Phi _{\mathcal {U}}$ with Fourier–Mukai kernel
$\Phi _{\mathcal {U}}$ with Fourier–Mukai kernel ![]() ${\mathcal {U}}$ involves first composing the correspondence
${\mathcal {U}}$ involves first composing the correspondence ![]() $[{\mathcal {U}}^{\boxtimes n},\rho _\boxtimes ]_*: K_{{\mathfrak {S}}_n}(M^n)\rightarrow K_{{\mathfrak {S}}_n}(S^n)$ with
$[{\mathcal {U}}^{\boxtimes n},\rho _\boxtimes ]_*: K_{{\mathfrak {S}}_n}(M^n)\rightarrow K_{{\mathfrak {S}}_n}(S^n)$ with ![]() $[{\mathcal {O}}_{\Gamma _S}]_*$ and the inverse of
$[{\mathcal {O}}_{\Gamma _S}]_*$ and the inverse of ![]() $[{\mathcal {O}}_{\Gamma _M}]_*$, to obtain the correspondence from
$[{\mathcal {O}}_{\Gamma _M}]_*$, to obtain the correspondence from ![]() $K(M^{[n]})$ to
$K(M^{[n]})$ to ![]() $K(S^{[n]})$, and then using the Chern character isomorphism and its inverse to obtain the cohomological morphism in
$K(S^{[n]})$, and then using the Chern character isomorphism and its inverse to obtain the cohomological morphism in ![]() ${\rm Hom}_{{\mathcal {G}}^{[n]}}(M^{[n]},S^{[n]})$ (see [Reference Bridgeland, King and ReidBKR01, § 10.1]). The value of
${\rm Hom}_{{\mathcal {G}}^{[n]}}(M^{[n]},S^{[n]})$ (see [Reference Bridgeland, King and ReidBKR01, § 10.1]). The value of ![]() $\widetilde {\Theta }_n$ on morphisms of types (1) and (2) may be obtained by first conjugating via the Chern character their cartesian powers to lift these morphisms to correspondences from
$\widetilde {\Theta }_n$ on morphisms of types (1) and (2) may be obtained by first conjugating via the Chern character their cartesian powers to lift these morphisms to correspondences from ![]() $K_{{\mathfrak {S}}_n}(M^n)$ to
$K_{{\mathfrak {S}}_n}(M^n)$ to ![]() $K_{{\mathfrak {S}}_n}(S^n)$. The check that
$K_{{\mathfrak {S}}_n}(S^n)$. The check that ![]() $\widetilde {\Theta }_n$ maps compositions of morphisms to compositions reduces to showing that its value on (1) morphisms that are parallel-transport operators or (2) morphisms that are multiplication by
$\widetilde {\Theta }_n$ maps compositions of morphisms to compositions reduces to showing that its value on (1) morphisms that are parallel-transport operators or (2) morphisms that are multiplication by ![]() $\exp (\lambda )$,
$\exp (\lambda )$, ![]() $\lambda \in H^2(X,{\mathbb {Q}})$, is induced by composing the correspondences from
$\lambda \in H^2(X,{\mathbb {Q}})$, is induced by composing the correspondences from ![]() $K_{{\mathfrak {S}}_n}(M^n)$ to
$K_{{\mathfrak {S}}_n}(M^n)$ to ![]() $K_{{\mathfrak {S}}_n}(S^n)$ with the same correspondences,
$K_{{\mathfrak {S}}_n}(S^n)$ with the same correspondences, ![]() $[{\mathcal {O}}_{\Gamma _S}]_*$ and the inverse of
$[{\mathcal {O}}_{\Gamma _S}]_*$ and the inverse of ![]() $[{\mathcal {O}}_{\Gamma _M}]_*$, used for morphisms of type (3). For parallel-transport operators this is the case, since the class
$[{\mathcal {O}}_{\Gamma _M}]_*$, used for morphisms of type (3). For parallel-transport operators this is the case, since the class ![]() $[{\mathcal {O}}_{\Gamma _S}]$ in
$[{\mathcal {O}}_{\Gamma _S}]$ in ![]() $K_{{\mathfrak {S}}_n}(S^n\times S^{[n]})$ is a global class in the corresponding local system of
$K_{{\mathfrak {S}}_n}(S^n\times S^{[n]})$ is a global class in the corresponding local system of ![]() $K$-rings over the base of every family of
$K$-rings over the base of every family of ![]() $K3$ surfaces, hence the correspondences
$K3$ surfaces, hence the correspondences ![]() $[{\mathcal {O}}_{\Gamma _S}]$ and
$[{\mathcal {O}}_{\Gamma _S}]$ and ![]() $[{\mathcal {O}}_{\Gamma _M}]$ intertwine parallel-transport operators associated to paths in the base of such families. The check for multiplication by
$[{\mathcal {O}}_{\Gamma _M}]$ intertwine parallel-transport operators associated to paths in the base of such families. The check for multiplication by ![]() $\exp (\lambda )$,
$\exp (\lambda )$, ![]() $\lambda \in H^2(X,{\mathbb {Q}})$, reduces to checking for integral classes, as the correspondences are all linear. In this case the action corresponds to tensorization by topological line bundles on the level of
$\lambda \in H^2(X,{\mathbb {Q}})$, reduces to checking for integral classes, as the correspondences are all linear. In this case the action corresponds to tensorization by topological line bundles on the level of ![]() $K$-rings. The correspondence
$K$-rings. The correspondence ![]() $[{\mathcal {O}}_{\Gamma _S}]_*$ intertwines tensorization in
$[{\mathcal {O}}_{\Gamma _S}]_*$ intertwines tensorization in ![]() $K_{{\mathfrak {S}}_n}(S^n)$ by the cartesian power
$K_{{\mathfrak {S}}_n}(S^n)$ by the cartesian power ![]() $L^{\boxtimes n}$ of a line bundle on
$L^{\boxtimes n}$ of a line bundle on ![]() $S$ and by the line bundle
$S$ and by the line bundle ![]() $\tilde {L}$ on
$\tilde {L}$ on ![]() $S^{[n]}$ with
$S^{[n]}$ with ![]() $c_1(\tilde {L})=\theta (c_1(L))$, since
$c_1(\tilde {L})=\theta (c_1(L))$, since ![]() $\theta (c_1(L))$ is defined as the pullback of the class associated to
$\theta (c_1(L))$ is defined as the pullback of the class associated to ![]() $c_1(L)$ in the symmetric product
$c_1(L)$ in the symmetric product ![]() $S^{(n)}$, and the isospectral Hilbert scheme is a reduced fiber product of
$S^{(n)}$, and the isospectral Hilbert scheme is a reduced fiber product of ![]() $S^n$ and
$S^n$ and ![]() $S^{[n]}$ over
$S^{[n]}$ over ![]() $S^{(n)}$. Hence, the projection formula yields that
$S^{(n)}$. Hence, the projection formula yields that ![]() $[{\mathcal {O}}_{\Gamma _S}]_*$ indeed intertwines the two tensorizations.
$[{\mathcal {O}}_{\Gamma _S}]_*$ indeed intertwines the two tensorizations.
7.3 The functor  $\Theta _n:{\mathcal {G}}^{[1]}\rightarrow {\mathcal {G}}^{[n]}$
$\Theta _n:{\mathcal {G}}^{[1]}\rightarrow {\mathcal {G}}^{[n]}$
Let ![]() $\phi :\widetilde {H}(M,{\mathbb {Z}})\rightarrow \widetilde {H}(S,{\mathbb {Z}})$ be the isometry induced by the correspondence
$\phi :\widetilde {H}(M,{\mathbb {Z}})\rightarrow \widetilde {H}(S,{\mathbb {Z}})$ be the isometry induced by the correspondence ![]() $ch({\mathcal {U}})\sqrt {td_{M\times S}}$. The morphism
$ch({\mathcal {U}})\sqrt {td_{M\times S}}$. The morphism ![]() $\widetilde {\Theta }_n(\phi ):H^*(M^{[n]},{\mathbb {Q}})\rightarrow H^*(S^{[n]},{\mathbb {Q}})$ is induced by the correspondence
$\widetilde {\Theta }_n(\phi ):H^*(M^{[n]},{\mathbb {Q}})\rightarrow H^*(S^{[n]},{\mathbb {Q}})$ is induced by the correspondence
where ![]() $E$ is given in terms of
$E$ is given in terms of ![]() ${\mathcal {U}}$ in (7.2). We recall next the relationship between
${\mathcal {U}}$ in (7.2). We recall next the relationship between ![]() $\phi$ and
$\phi$ and ![]() $\widetilde {H}(\widetilde {\Theta }_n(\phi )):\widetilde {H}(M^{[n]},{\mathbb {Q}})\rightarrow \widetilde {H}(S^{[n]},{\mathbb {Q}})$. Let
$\widetilde {H}(\widetilde {\Theta }_n(\phi )):\widetilde {H}(M^{[n]},{\mathbb {Q}})\rightarrow \widetilde {H}(S^{[n]},{\mathbb {Q}})$. Let
be the extension of ![]() $\theta :H^2(S,{\mathbb {Z}})\rightarrow H^2(S^{[n]},{\mathbb {Z}})$, given in (7.3), mapping
$\theta :H^2(S,{\mathbb {Z}})\rightarrow H^2(S^{[n]},{\mathbb {Z}})$, given in (7.3), mapping ![]() $\alpha$ to
$\alpha$ to ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ to
$\beta$ to ![]() $\beta$. Let
$\beta$. Let
be the embedding given by ![]() $\tilde {\iota }_g(\tilde {\theta }(x))=\tilde {\theta }(g(x))$ and
$\tilde {\iota }_g(\tilde {\theta }(x))=\tilde {\theta }(g(x))$ and ![]() $\tilde {\iota }_g$ acts as the identity on the one-dimensional subspace orthogonal to the image of
$\tilde {\iota }_g$ acts as the identity on the one-dimensional subspace orthogonal to the image of ![]() $\tilde {\theta }$. Given an isometry
$\tilde {\theta }$. Given an isometry ![]() $g:\widetilde {H}(M,{\mathbb {Q}})\rightarrow \widetilde {H}(S,{\mathbb {Q}})$ we denote by
$g:\widetilde {H}(M,{\mathbb {Q}})\rightarrow \widetilde {H}(S,{\mathbb {Q}})$ we denote by ![]() $\tilde {\iota }_g:\widetilde {H}(M^{[n]},{\mathbb {Q}})\rightarrow \widetilde {H}(S^{[n]},{\mathbb {Q}})$ the isometry satisfying
$\tilde {\iota }_g:\widetilde {H}(M^{[n]},{\mathbb {Q}})\rightarrow \widetilde {H}(S^{[n]},{\mathbb {Q}})$ the isometry satisfying ![]() $\tilde {\iota }_g(\tilde {\theta }(x))=\tilde {\theta }(g(x))$ and mapping
$\tilde {\iota }_g(\tilde {\theta }(x))=\tilde {\theta }(g(x))$ and mapping ![]() $\delta \in H^2(M^{[n]},{\mathbb {Q}})$ to
$\delta \in H^2(M^{[n]},{\mathbb {Q}})$ to ![]() $\delta \in H^2(S^{[n]},{\mathbb {Q}})$.
$\delta \in H^2(S^{[n]},{\mathbb {Q}})$.
Choose markings ![]() $\eta _S:H^2(S,{\mathbb {Z}})\rightarrow \Lambda _{K3}$ and
$\eta _S:H^2(S,{\mathbb {Z}})\rightarrow \Lambda _{K3}$ and ![]() $\eta _M:H^2(M,{\mathbb {Z}})\rightarrow \Lambda _{K3}$, where
$\eta _M:H^2(M,{\mathbb {Z}})\rightarrow \Lambda _{K3}$, where ![]() $\Lambda _{K3}$ is the
$\Lambda _{K3}$ is the ![]() $K3$ lattice, and let
$K3$ lattice, and let ![]() $\Lambda$ be the orthogonal direct sum
$\Lambda$ be the orthogonal direct sum
where ![]() $(\delta _0,\delta _0)=2-2n$,
$(\delta _0,\delta _0)=2-2n$, ![]() $n\geq 2$. Let
$n\geq 2$. Let
be the embedding, where ![]() $\iota _g$ is the extension of
$\iota _g$ is the extension of ![]() $g$ satisfying
$g$ satisfying ![]() $\iota _g(\delta _0)=\delta _0$. Choose an orientation of
$\iota _g(\delta _0)=\delta _0$. Choose an orientation of ![]() $\Lambda _{K3}$ and an orientation of
$\Lambda _{K3}$ and an orientation of ![]() $\Lambda$, so that
$\Lambda$, so that ![]() $\delta _0$ extends a basis compatible with the orientation of the former to one compatible with that of the latter. Set
$\delta _0$ extends a basis compatible with the orientation of the former to one compatible with that of the latter. Set ![]() $\det (\phi ):=\det (\eta _S\circ \phi \circ \eta _M^{-1})$. Extend the marking
$\det (\phi ):=\det (\eta _S\circ \phi \circ \eta _M^{-1})$. Extend the marking ![]() $\eta _S$ to a marking
$\eta _S$ to a marking
sending ![]() $\delta$ to
$\delta$ to ![]() $\delta _0$, where
$\delta _0$, where ![]() $\delta$ is half the class of the divisor of non-reduced subschemes. Define
$\delta$ is half the class of the divisor of non-reduced subschemes. Define ![]() $\eta _{M^{[n]}}$ similarly. Define
$\eta _{M^{[n]}}$ similarly. Define ![]() $\widetilde {H}(\widetilde {\Theta }_n(\phi ))$ using Convention 5.16.
$\widetilde {H}(\widetilde {\Theta }_n(\phi ))$ using Convention 5.16.
Lemma 7.2 We have ![]() $\widetilde {H}(\widetilde {\Theta }_n(\phi ))=\det (\phi )^{n+1}(B_{-\delta /2}\circ \tilde {\iota }_\phi \circ B_{\delta /2}).$
$\widetilde {H}(\widetilde {\Theta }_n(\phi ))=\det (\phi )^{n+1}(B_{-\delta /2}\circ \tilde {\iota }_\phi \circ B_{\delta /2}).$
Proof. Let ![]() $\zeta :H^*(M,{\mathbb {Q}})\rightarrow H^*(S,{\mathbb {Q}})$ be a parallel-transport operator such that
$\zeta :H^*(M,{\mathbb {Q}})\rightarrow H^*(S,{\mathbb {Q}})$ be a parallel-transport operator such that ![]() $\det (\eta _S\circ \bar {\zeta }\circ \eta _M^{-1})=1,$ where
$\det (\eta _S\circ \bar {\zeta }\circ \eta _M^{-1})=1,$ where ![]() $\bar {\zeta }$ is the restriction of
$\bar {\zeta }$ is the restriction of ![]() $\zeta$ to
$\zeta$ to ![]() $H^2(M,{\mathbb {Q}})$. Then
$H^2(M,{\mathbb {Q}})$. Then ![]() $\zeta$ lifts to a parallel-transport operator
$\zeta$ lifts to a parallel-transport operator ![]() $\zeta ^{[n]}:H^*(M^{[n]},{\mathbb {Q}})\rightarrow H^*(S^{[n]},{\mathbb {Q}})$, since associated to a family of
$\zeta ^{[n]}:H^*(M^{[n]},{\mathbb {Q}})\rightarrow H^*(S^{[n]},{\mathbb {Q}})$, since associated to a family of ![]() $K3$ surfaces is a canonical family of relative Douady spaces. Let
$K3$ surfaces is a canonical family of relative Douady spaces. Let ![]() $\bar {\zeta }^{[n]}$ be the restriction of
$\bar {\zeta }^{[n]}$ be the restriction of ![]() $\zeta ^{[n]}$ to
$\zeta ^{[n]}$ to ![]() $H^2(M^{[n]},{\mathbb {Q}})$. Then
$H^2(M^{[n]},{\mathbb {Q}})$. Then ![]() $\det (\eta _{S^{[n]}}\circ \bar {\zeta }^{[n]}\circ \eta _{M^{[n]}}^{-1})=1$. We get
$\det (\eta _{S^{[n]}}\circ \bar {\zeta }^{[n]}\circ \eta _{M^{[n]}}^{-1})=1$. We get ![]() $\widetilde {H}(\zeta ^{[n]})=\tilde {\iota }_{\zeta }=B_{-\delta /2}\circ \tilde {\iota }_\zeta \circ B_{\delta /2}$, where the first equality is by Remark 5.18. The composition
$\widetilde {H}(\zeta ^{[n]})=\tilde {\iota }_{\zeta }=B_{-\delta /2}\circ \tilde {\iota }_\zeta \circ B_{\delta /2}$, where the first equality is by Remark 5.18. The composition ![]() $\phi _1:=\zeta \circ \phi$ is an element of
$\phi _1:=\zeta \circ \phi$ is an element of ![]() ${\rm Aut}_{{\mathcal {G}}^{[1]}}(S)$. We conclude that the equality in the statement of the lemma is equivalent to the equality
${\rm Aut}_{{\mathcal {G}}^{[1]}}(S)$. We conclude that the equality in the statement of the lemma is equivalent to the equality
The latter equality holds for all elements in ![]() ${\rm Aut}_{{\mathcal {G}}^{[1]}}(S)$ by [Reference MarkmanMar21a, Theorem 12.2] (see also [Reference BeckmannBec23, Theorem 7.4] and in case
${\rm Aut}_{{\mathcal {G}}^{[1]}}(S)$ by [Reference MarkmanMar21a, Theorem 12.2] (see also [Reference BeckmannBec23, Theorem 7.4] and in case ![]() $n=2$ Taelman's earlier result [Reference TaelmanTae23, Theorem 9.4]).
$n=2$ Taelman's earlier result [Reference TaelmanTae23, Theorem 9.4]).
Let ![]() $\varphi :\widetilde {H}(M,{\mathbb {Q}})\rightarrow \widetilde {H}(S,{\mathbb {Q}})$ be the isometry induced by
$\varphi :\widetilde {H}(M,{\mathbb {Q}})\rightarrow \widetilde {H}(S,{\mathbb {Q}})$ be the isometry induced by ![]() $\kappa ({\mathcal {U}})\sqrt {td_{M\times S}}$. Let
$\kappa ({\mathcal {U}})\sqrt {td_{M\times S}}$. Let
be the isometry induced by the correspondence ![]() $\kappa (E)\sqrt {td_{M^{[n]}\times S^{[n]}}}$. Again,
$\kappa (E)\sqrt {td_{M^{[n]}\times S^{[n]}}}$. Again, ![]() $\varphi ^{[n]}$ is a morphism in
$\varphi ^{[n]}$ is a morphism in ![]() ${\rm Hom}_{{\mathcal {G}}^{[n]}}(M^{[n]},S^{[n]})$. As previously, we denote by
${\rm Hom}_{{\mathcal {G}}^{[n]}}(M^{[n]},S^{[n]})$. As previously, we denote by ![]() $\widetilde {H}(\varphi )_0$ the restriction of
$\widetilde {H}(\varphi )_0$ the restriction of ![]() $\varphi$ to
$\varphi$ to ![]() $H^2(M,{\mathbb {Q}})$ and set
$H^2(M,{\mathbb {Q}})$ and set ![]() $\psi _{\mathcal {U}}:=\widetilde {H}_0(\varphi )$, where
$\psi _{\mathcal {U}}:=\widetilde {H}_0(\varphi )$, where ![]() $\widetilde {H}_0(\varphi ):=\nu (\widetilde {H}(\varphi )_0)\widetilde {H}(\varphi )_0$ as in (5.8). We define
$\widetilde {H}_0(\varphi ):=\nu (\widetilde {H}(\varphi )_0)\widetilde {H}(\varphi )_0$ as in (5.8). We define ![]() $\widetilde {H}(\varphi ^{[n]})_0$ as the restriction of
$\widetilde {H}(\varphi ^{[n]})_0$ as the restriction of ![]() $\widetilde {H}(\varphi ^{[n]})$ to
$\widetilde {H}(\varphi ^{[n]})$ to ![]() $H^2(M^{[n]},{\mathbb {Q}})$ and set
$H^2(M^{[n]},{\mathbb {Q}})$ and set ![]() $\psi _E:=\widetilde {H}_0(\varphi ^{[n]})$, where
$\psi _E:=\widetilde {H}_0(\varphi ^{[n]})$, where ![]() $\widetilde {H}_0(\varphi ^{[n]}):=\nu (\widetilde {H}(\varphi ^{[n]})_0)\widetilde {H}(\varphi ^{[n]})_0$.
$\widetilde {H}_0(\varphi ^{[n]}):=\nu (\widetilde {H}(\varphi ^{[n]})_0)\widetilde {H}(\varphi ^{[n]})_0$.
Corollary 7.3 We have
Consequently, ![]() $\psi _E\circ \theta =\theta \circ \psi _{\mathcal {U}}$ and
$\psi _E\circ \theta =\theta \circ \psi _{\mathcal {U}}$ and ![]() $\psi _E(\delta )=\delta$.
$\psi _E(\delta )=\delta$.
Proof. Let ![]() $a_1\in H^2(M,{\mathbb {Z}})$ and
$a_1\in H^2(M,{\mathbb {Z}})$ and ![]() $a_2\in H^2(S,{\mathbb {Z}})$ be the classes satisfying
$a_2\in H^2(S,{\mathbb {Z}})$ be the classes satisfying ![]() $c_1({\mathcal {U}})=\pi _M^*(a_1)+\pi _S^*(a_2)$. Let
$c_1({\mathcal {U}})=\pi _M^*(a_1)+\pi _S^*(a_2)$. Let ![]() $e_1\in H^2(M^{[n]},{\mathbb {Z}})$ and
$e_1\in H^2(M^{[n]},{\mathbb {Z}})$ and ![]() $e_2\in H^2(S^{[n]},{\mathbb {Z}})$ be the classes satisfying
$e_2\in H^2(S^{[n]},{\mathbb {Z}})$ be the classes satisfying ![]() $c_1(E)=\pi _{M^{[n]}}^*(e_1)+\pi _{S^{[n]}}^*(e_2)$. Set
$c_1(E)=\pi _{M^{[n]}}^*(e_1)+\pi _{S^{[n]}}^*(e_2)$. Set ![]() $R:=n!r^n$. We have
$R:=n!r^n$. We have
 \begin{align*} \widetilde{H}(\varphi^{[n]})&=B_{-e_2/R}\circ \widetilde{H}(\widetilde{\Theta}_n(\phi))\circ B_{-e_1/R}\\ &=\det(\phi)^{n+1}B_{-(\delta/2+e_2/R)}\circ \tilde{\iota}_\phi\circ B_{\delta/2-e_1/R}\\ &=\det(\phi)^{n+1}B_{(\theta(a_2)/r-\delta/2-e_2/R)}\circ \iota_\varphi\circ B_{(\theta(a_1)/r+\delta/2-e_1/R)}\\ &= \det(\phi)^{n+1}B_{\lambda_2}\circ \iota_\varphi\circ B_{\lambda_1}, \end{align*}
\begin{align*} \widetilde{H}(\varphi^{[n]})&=B_{-e_2/R}\circ \widetilde{H}(\widetilde{\Theta}_n(\phi))\circ B_{-e_1/R}\\ &=\det(\phi)^{n+1}B_{-(\delta/2+e_2/R)}\circ \tilde{\iota}_\phi\circ B_{\delta/2-e_1/R}\\ &=\det(\phi)^{n+1}B_{(\theta(a_2)/r-\delta/2-e_2/R)}\circ \iota_\varphi\circ B_{(\theta(a_1)/r+\delta/2-e_1/R)}\\ &= \det(\phi)^{n+1}B_{\lambda_2}\circ \iota_\varphi\circ B_{\lambda_1}, \end{align*}
where ![]() $\lambda _1=\theta (a_1)/r+\delta /2-e_1/R$ and
$\lambda _1=\theta (a_1)/r+\delta /2-e_1/R$ and ![]() $\lambda _2=\theta (a_2)/r-\delta /2-e_2/R$. The first equality follows from the definition of
$\lambda _2=\theta (a_2)/r-\delta /2-e_2/R$. The first equality follows from the definition of ![]() $\kappa (E)$, the second from Lemma 7.2, the third from the definition of
$\kappa (E)$, the second from Lemma 7.2, the third from the definition of ![]() $\kappa ({\mathcal {U}})$, and the fourth is obvious. Note that
$\kappa ({\mathcal {U}})$, and the fourth is obvious. Note that ![]() $\det (\phi )=\det (\varphi )$. In order to establish (7.9) it remains to prove that
$\det (\phi )=\det (\varphi )$. In order to establish (7.9) it remains to prove that ![]() $\lambda _i=0$,
$\lambda _i=0$, ![]() $i=1,2$, or, equivalently,
$i=1,2$, or, equivalently,
Both ![]() $\varphi$ and
$\varphi$ and ![]() $\varphi ^{[n]}$ are degree reversing, by Lemma 4.1. Hence, both
$\varphi ^{[n]}$ are degree reversing, by Lemma 4.1. Hence, both ![]() $\widetilde {H}(\varphi ^{[n]})$ and
$\widetilde {H}(\varphi ^{[n]})$ and ![]() $\iota _\varphi$ are degree reversing, the first by Lemma 3.4. If
$\iota _\varphi$ are degree reversing, the first by Lemma 3.4. If ![]() $\lambda _1\neq 0$, then
$\lambda _1\neq 0$, then ![]() $(\lambda _1,\lambda '_1)\neq 0$, for some
$(\lambda _1,\lambda '_1)\neq 0$, for some ![]() $\lambda _1'\in H^2(M^{[n]},{\mathbb {Z}})$ and the coefficient of
$\lambda _1'\in H^2(M^{[n]},{\mathbb {Z}})$ and the coefficient of ![]() $\beta$ in
$\beta$ in ![]() $B_{\lambda _1}(\lambda '_1)$ is non-zero, which implies that the coefficient of
$B_{\lambda _1}(\lambda '_1)$ is non-zero, which implies that the coefficient of ![]() $\alpha$ in
$\alpha$ in ![]() $\iota _{\varphi }(B_{\lambda _1}(\lambda '_1))$ is non-zero, and hence so is the coefficient of
$\iota _{\varphi }(B_{\lambda _1}(\lambda '_1))$ is non-zero, and hence so is the coefficient of ![]() $\alpha$ in
$\alpha$ in ![]() $\widetilde {H}(\varphi ^{[n]})(\lambda _1')$. This contradicts the fact that
$\widetilde {H}(\varphi ^{[n]})(\lambda _1')$. This contradicts the fact that ![]() $\widetilde {H}(\varphi ^{[n]})$ maps
$\widetilde {H}(\varphi ^{[n]})$ maps ![]() $H^2(M^{[n]},{\mathbb {Q}})$ to
$H^2(M^{[n]},{\mathbb {Q}})$ to ![]() $H^2(S^{[n]},{\mathbb {Q}})$. Hence,
$H^2(S^{[n]},{\mathbb {Q}})$. Hence, ![]() $\lambda _1=0$.
$\lambda _1=0$.
If ![]() $\lambda _2\neq 0$, then
$\lambda _2\neq 0$, then ![]() $(\lambda _2,\lambda '_2)\neq 0$, for some
$(\lambda _2,\lambda '_2)\neq 0$, for some ![]() $\lambda _2'\in H^2(S^{[n]},{\mathbb {Z}})$ and the coefficient of
$\lambda _2'\in H^2(S^{[n]},{\mathbb {Z}})$ and the coefficient of ![]() $\beta$ in
$\beta$ in ![]() $B_{\lambda _2}(\lambda '_2)$ is non-zero. There exists a class
$B_{\lambda _2}(\lambda '_2)$ is non-zero. There exists a class ![]() $\lambda _1'\in H^2(M^{[n]},{\mathbb {Q}})$, such that
$\lambda _1'\in H^2(M^{[n]},{\mathbb {Q}})$, such that ![]() $\iota _\varphi (\lambda _1')=\lambda _2'$, as
$\iota _\varphi (\lambda _1')=\lambda _2'$, as ![]() $\iota _\varphi$ is an isometry. Hence, the coefficient of
$\iota _\varphi$ is an isometry. Hence, the coefficient of ![]() $\beta$ in
$\beta$ in ![]() $\widetilde {H}(\varphi ^{[n]})(\lambda _1')$ does not vanish. A contradiction. We conclude that
$\widetilde {H}(\varphi ^{[n]})(\lambda _1')$ does not vanish. A contradiction. We conclude that ![]() $\lambda _2=0$.
$\lambda _2=0$.
Equality (7.9) implies that ![]() $\nu (\widetilde {H}(\varphi ^{[n]})_0)=\det (\varphi )^{n+1}\nu (\widetilde {H}(\varphi )_0)$. Hence,
$\nu (\widetilde {H}(\varphi ^{[n]})_0)=\det (\varphi )^{n+1}\nu (\widetilde {H}(\varphi )_0)$. Hence, ![]() $\psi _E$ is the extension of
$\psi _E$ is the extension of ![]() $\psi _{\mathcal {U}}$ mapping
$\psi _{\mathcal {U}}$ mapping ![]() $\delta \in H^2(M^{[n]},{\mathbb {Q}})$ to
$\delta \in H^2(M^{[n]},{\mathbb {Q}})$ to ![]() $\delta \in H^2(S^{[n]},{\mathbb {Q}})$.
$\delta \in H^2(S^{[n]},{\mathbb {Q}})$.
Let ![]() ${\mathcal {G}}^{[n]}$ be the subgroupoid of the groupoid
${\mathcal {G}}^{[n]}$ be the subgroupoid of the groupoid ![]() ${\mathcal {G}}$ given in (1.1) whose objects are of
${\mathcal {G}}$ given in (1.1) whose objects are of ![]() $K3^{[n]}$ type. Let
$K3^{[n]}$ type. Let
be the following normalization of the functor ![]() $\widetilde {\Theta }_n$ defined in § 7.2. The functor
$\widetilde {\Theta }_n$ defined in § 7.2. The functor ![]() $\Theta _n$ sends an object of
$\Theta _n$ sends an object of ![]() ${\mathcal {G}}^{[1]}$ to the same object that
${\mathcal {G}}^{[1]}$ to the same object that ![]() $\widetilde {\Theta }_n$ does. Given a morphism
$\widetilde {\Theta }_n$ does. Given a morphism ![]() $\phi \in {\rm Hom}_{{\mathcal {G}}^{[1]}}((X,\epsilon ),(Y,\epsilon '))$, we define
$\phi \in {\rm Hom}_{{\mathcal {G}}^{[1]}}((X,\epsilon ),(Y,\epsilon '))$, we define
where we denote by ![]() $\delta$ half the class of the divisor of non-reduced subschemes in both
$\delta$ half the class of the divisor of non-reduced subschemes in both ![]() $X^{[n]}$ and
$X^{[n]}$ and ![]() $Y^{[n]}$ and
$Y^{[n]}$ and ![]() $B_{\lambda }$ is the cup product with
$B_{\lambda }$ is the cup product with ![]() $\exp (\lambda )$. Note that if
$\exp (\lambda )$. Note that if ![]() $\phi$ is
$\phi$ is ![]() $B_\lambda \in {\rm Aut}(X,\epsilon )$,
$B_\lambda \in {\rm Aut}(X,\epsilon )$, ![]() $\lambda \in H^2(X,{\mathbb {Q}})$, or if
$\lambda \in H^2(X,{\mathbb {Q}})$, or if ![]() $\phi$ is a parallel-transport operator, then
$\phi$ is a parallel-transport operator, then ![]() $\Theta _n(\phi )=\widetilde {\Theta }_n(\phi )$.
$\Theta _n(\phi )=\widetilde {\Theta }_n(\phi )$.
Corollary 7.4 The functor ![]() $\Theta _n$ maps
$\Theta _n$ maps ![]() ${\mathcal {G}}^{[1]}_{an}$ to
${\mathcal {G}}^{[1]}_{an}$ to ![]() ${\mathcal {G}}^{[n]}_{an}$. Furthermore,
${\mathcal {G}}^{[n]}_{an}$. Furthermore, ![]() $\Theta _n(\varphi )=\varphi ^{[n]},$ where
$\Theta _n(\varphi )=\varphi ^{[n]},$ where ![]() $\varphi$ and
$\varphi$ and ![]() $\varphi ^{[n]}$ are the morphisms in Corollary 7.3.
$\varphi ^{[n]}$ are the morphisms in Corollary 7.3.
Proof. The statement is clear for parallel-transport operators. Hence, it suffices to prove the equality ![]() $\Theta _n(\varphi )=\varphi ^{[n]}$. Keep the notation of the proof of Corollary 7.3. The second equality below follows from (7.10) and (7.11):
$\Theta _n(\varphi )=\varphi ^{[n]}$. Keep the notation of the proof of Corollary 7.3. The second equality below follows from (7.10) and (7.11):
 \begin{align*} \varphi^{[n]}&=B_{-(e_2/R)}\circ \widetilde{\Theta}_n(\phi)\circ B_{-(e_1/R)}= B_{-(\theta(a_2/r))}\circ B_{\delta/2}\circ \widetilde{\Theta}_n(\phi)\circ B_{-\delta/2}\circ B_{-(\theta(a_1)/r)}\\ &=\Theta_n(B_{-a_2/r})\circ \Theta_n(\phi)\circ \Theta_n(B_{-a_1/r}) =\Theta_n(B_{-a_2/r}\circ\phi\circ B_{-a_1/r})=\Theta_n(\varphi). \end{align*}
\begin{align*} \varphi^{[n]}&=B_{-(e_2/R)}\circ \widetilde{\Theta}_n(\phi)\circ B_{-(e_1/R)}= B_{-(\theta(a_2/r))}\circ B_{\delta/2}\circ \widetilde{\Theta}_n(\phi)\circ B_{-\delta/2}\circ B_{-(\theta(a_1)/r)}\\ &=\Theta_n(B_{-a_2/r})\circ \Theta_n(\phi)\circ \Theta_n(B_{-a_1/r}) =\Theta_n(B_{-a_2/r}\circ\phi\circ B_{-a_1/r})=\Theta_n(\varphi). \end{align*}
The equality ![]() $\Theta _n(\varphi )=\varphi ^{[n]}$ follows.
$\Theta _n(\varphi )=\varphi ^{[n]}$ follows.
8. Deforming the universal vector bundle over  $M^{[n]}\times S^{[n]}$
$M^{[n]}\times S^{[n]}$
We consider in this section a sequence of examples of two-dimensional moduli spaces ![]() $M$ of stable vector bundles over a
$M$ of stable vector bundles over a ![]() $K3$ surface
$K3$ surface ![]() $S$, such that the vector bundle
$S$, such that the vector bundle ![]() $E$ over
$E$ over ![]() $M^{[n]}\times S^{[n]}$, given in (7.2) as the Fourier–Mukai kernel of an equivalence of derived categories, can be deformed with
$M^{[n]}\times S^{[n]}$, given in (7.2) as the Fourier–Mukai kernel of an equivalence of derived categories, can be deformed with ![]() $M^{[n]}\times S^{[n]}$ over the whole connected component
$M^{[n]}\times S^{[n]}$ over the whole connected component ![]() ${\mathfrak {M}}_\psi ^0$ of a moduli space of rational Hodge isometries introduced in § 5.2.
${\mathfrak {M}}_\psi ^0$ of a moduli space of rational Hodge isometries introduced in § 5.2.
Keep the notation of § 7. Assume that ![]() ${\rm Pic}(S)$ is cyclic, generated by the class
${\rm Pic}(S)$ is cyclic, generated by the class ![]() $h:=c_1(H)$ of an ample line bundle
$h:=c_1(H)$ of an ample line bundle ![]() $H$ with
$H$ with ![]() $(h,h)=2rs$, where
$(h,h)=2rs$, where ![]() $r$ and
$r$ and ![]() $s$ are positive integers and
$s$ are positive integers and ![]() $\gcd (r,s)=1$. The Mukai vector
$\gcd (r,s)=1$. The Mukai vector ![]() $v:=(r,h,s)$ is then isotropic. The following properties of the moduli space
$v:=(r,h,s)$ is then isotropic. The following properties of the moduli space ![]() $M$ of
$M$ of ![]() $H$-stable sheaves with Mukai vector
$H$-stable sheaves with Mukai vector ![]() $v$ are proved in [Reference MukaiMuk99]. Here
$v$ are proved in [Reference MukaiMuk99]. Here ![]() $M$ is a
$M$ is a ![]() $K3$ surface with a cyclic Picard group generated by an ample line bundle
$K3$ surface with a cyclic Picard group generated by an ample line bundle ![]() $\hat {H}$ with class
$\hat {H}$ with class ![]() $\hat {h}:=c_1(\hat {H})$ satisfying
$\hat {h}:=c_1(\hat {H})$ satisfying ![]() $(\hat {h},\hat {h})=(h,h)$;
$(\hat {h},\hat {h})=(h,h)$; ![]() $M$ parametrizes locally free
$M$ parametrizes locally free ![]() $H$-slope-stable sheaves. For each integer
$H$-slope-stable sheaves. For each integer ![]() $k$, such that
$k$, such that ![]() $ks\equiv 1$ (mod
$ks\equiv 1$ (mod ![]() $r$) there exists over
$r$) there exists over ![]() $M\times S$ a universal vector bundle
$M\times S$ a universal vector bundle ![]() ${\mathcal {U}}$ with
${\mathcal {U}}$ with ![]() $c_1({\mathcal {U}})=\pi _M^*(k\hat {h})+\pi _S^*(h)$. The universal vector bundle
$c_1({\mathcal {U}})=\pi _M^*(k\hat {h})+\pi _S^*(h)$. The universal vector bundle ![]() ${\mathcal {U}}$ restricts to an
${\mathcal {U}}$ restricts to an ![]() $\hat {H}$-slope-stable vector bundle on
$\hat {H}$-slope-stable vector bundle on ![]() $M\times \{x\}$ of Mukai vector
$M\times \{x\}$ of Mukai vector ![]() $\hat {v}:=(r,k\hat {h},k^2s)$, for each point
$\hat {v}:=(r,k\hat {h},k^2s)$, for each point ![]() $x\in S$, and the classification morphism induces an isomorphism between
$x\in S$, and the classification morphism induces an isomorphism between ![]() $S$ and the moduli space
$S$ and the moduli space ![]() $M_{\hat {H}}(\hat {v})$ of
$M_{\hat {H}}(\hat {v})$ of ![]() $\hat {H}$-stable sheaves on
$\hat {H}$-stable sheaves on ![]() $M$, by [Reference MukaiMuk99, Theorem 1.2].
$M$, by [Reference MukaiMuk99, Theorem 1.2].
Proposition 8.1 [Reference BuskinBus19, Proposition 4.19]Footnote 13
The class ![]() $-\kappa ({\mathcal {U}})\sqrt {td_{M\times S}}$ induces a degree-reversing rational Hodge isometry
$-\kappa ({\mathcal {U}})\sqrt {td_{M\times S}}$ induces a degree-reversing rational Hodge isometry ![]() $\phi _{\mathcal {U}}:\widetilde {H}(M,{\mathbb {Q}})\rightarrow \widetilde {H}(S,{\mathbb {Q}})$, which restricts to a rational Hodge isometry
$\phi _{\mathcal {U}}:\widetilde {H}(M,{\mathbb {Q}})\rightarrow \widetilde {H}(S,{\mathbb {Q}})$, which restricts to a rational Hodge isometry ![]() $\psi _{\mathcal {U}}:H^2(M,{\mathbb {Q}})\rightarrow H^2(S,{\mathbb {Q}})$ satisfying
$\psi _{\mathcal {U}}:H^2(M,{\mathbb {Q}})\rightarrow H^2(S,{\mathbb {Q}})$ satisfying ![]() $\psi _{\mathcal {U}}(\hat {h})=h$, such that
$\psi _{\mathcal {U}}(\hat {h})=h$, such that ![]() $\eta _S\circ \psi _{\mathcal {U}}\circ \eta _M^{-1}$ belongs to the double orbit
$\eta _S\circ \psi _{\mathcal {U}}\circ \eta _M^{-1}$ belongs to the double orbit ![]() $O(\Lambda _{K3})\rho _u O(\Lambda _{K3})$ of a reflection
$O(\Lambda _{K3})\rho _u O(\Lambda _{K3})$ of a reflection ![]() $\rho _u$ in the co-rank-
$\rho _u$ in the co-rank-![]() $1$ lattice
$1$ lattice ![]() $u^\perp \subset \Lambda _{K3}$ of a primitive class
$u^\perp \subset \Lambda _{K3}$ of a primitive class ![]() $u$ with
$u$ with ![]() $(u,u)=2r$.
$(u,u)=2r$.
We claim that ![]() ${\mathcal {U}}$ is slope-stable with respect to every Kähler class on
${\mathcal {U}}$ is slope-stable with respect to every Kähler class on ![]() $M\times S$. It suffices to show it for every ample class, i.e. for
$M\times S$. It suffices to show it for every ample class, i.e. for ![]() $\omega :=a\pi _S^*(h)+b\pi _M^*(\hat {h})$, for all
$\omega :=a\pi _S^*(h)+b\pi _M^*(\hat {h})$, for all ![]() $a>0$ and
$a>0$ and ![]() $b>0$. Let
$b>0$. Let ![]() ${\mathcal {W}}$ be a saturated non-zero proper subsheaf of
${\mathcal {W}}$ be a saturated non-zero proper subsheaf of ![]() ${\mathcal {U}}$. Then
${\mathcal {U}}$. Then ![]() ${\mathcal {W}}$ is reflexive, hence it is locally free away from a closed subvariety of dimension at most
${\mathcal {W}}$ is reflexive, hence it is locally free away from a closed subvariety of dimension at most ![]() $1$. It follows that the restriction of
$1$. It follows that the restriction of ![]() ${\mathcal {W}}$ to the generic fiber of
${\mathcal {W}}$ to the generic fiber of ![]() $\pi _S$ and of
$\pi _S$ and of ![]() $\pi _M$ is locally free. Let
$\pi _M$ is locally free. Let ![]() $W_x$ (respectively,
$W_x$ (respectively, ![]() $W_m$) be such a restriction to the fiber over
$W_m$) be such a restriction to the fiber over ![]() $x\in S$ (respectively,
$x\in S$ (respectively, ![]() $m\in M$). Define
$m\in M$). Define ![]() $U_x$ and
$U_x$ and ![]() $U_m$ similarly in terms of
$U_m$ similarly in terms of ![]() ${\mathcal {U}}$. Then
${\mathcal {U}}$. Then ![]() $c_1({\mathcal {W}})=\pi _M^*c_1(W_x)+\pi _S^*c_1(W_m)$ and
$c_1({\mathcal {W}})=\pi _M^*c_1(W_x)+\pi _S^*c_1(W_m)$ and ![]() $\omega ^3=a^2bh^2\hat {h}+ab^2h\hat {h}^2$. Set
$\omega ^3=a^2bh^2\hat {h}+ab^2h\hat {h}^2$. Set ![]() $\rho :={\rm rank}({\mathcal {W}})$. We have
$\rho :={\rm rank}({\mathcal {W}})$. We have
 \begin{align*} \mu_\omega({\mathcal{W}}) &= \frac{1}{\rho}c_1({\mathcal{W}})\omega^3= a^2b(h,h)\mu_{\hat{h}}(W_m)+ab^2(\hat{h},\hat{h})\mu_h(W_x)\\ &< a^2b(h,h)\mu_{\hat{h}}(U_m)+ab^2(\hat{h},\hat{h})\mu_h(U_x)=\mu_\omega({\mathcal{U}}). \end{align*}
\begin{align*} \mu_\omega({\mathcal{W}}) &= \frac{1}{\rho}c_1({\mathcal{W}})\omega^3= a^2b(h,h)\mu_{\hat{h}}(W_m)+ab^2(\hat{h},\hat{h})\mu_h(W_x)\\ &< a^2b(h,h)\mu_{\hat{h}}(U_m)+ab^2(\hat{h},\hat{h})\mu_h(U_x)=\mu_\omega({\mathcal{U}}). \end{align*}
Hence, ![]() ${\mathcal {U}}$ is slope-stable with respect to every Kähler class on
${\mathcal {U}}$ is slope-stable with respect to every Kähler class on ![]() $M\times S$. The universal vector bundle
$M\times S$. The universal vector bundle ![]() ${\mathcal {U}}$ thus satisfies the assumptions of Proposition 5.22 (namely Assumption 5.19 stated for
${\mathcal {U}}$ thus satisfies the assumptions of Proposition 5.22 (namely Assumption 5.19 stated for ![]() $E$). Set
$E$). Set ![]() $\psi :=\eta _S\circ \psi _{\mathcal {U}}\circ \eta _M^{-1}$. Let
$\psi :=\eta _S\circ \psi _{\mathcal {U}}\circ \eta _M^{-1}$. Let ![]() ${\mathfrak {M}}_\psi ^0$ be the connected component of
${\mathfrak {M}}_\psi ^0$ be the connected component of ![]() ${\mathfrak {M}}_\psi$ through
${\mathfrak {M}}_\psi$ through ![]() $q_0:=(M,\eta _M,S,\eta _S)$.
$q_0:=(M,\eta _M,S,\eta _S)$.
Choose a generic twistor line ![]() $Q$ in
$Q$ in ![]() ${\mathfrak {M}}_\psi ^0$ through
${\mathfrak {M}}_\psi ^0$ through ![]() $q_0$ and let
$q_0$ and let ![]() $(S',\eta _{S'},M',\eta _{M'})$ be a quadruple in this line with
$(S',\eta _{S'},M',\eta _{M'})$ be a quadruple in this line with ![]() ${\rm Pic}(S')=0$. There exists classes
${\rm Pic}(S')=0$. There exists classes ![]() $\zeta _{S'}\in H^2(S',{\mathcal {O}}_{S'}^*)$ and
$\zeta _{S'}\in H^2(S',{\mathcal {O}}_{S'}^*)$ and ![]() $\zeta _{M'}\in H^2(M',{\mathcal {O}}_{M'}^*)$ and a
$\zeta _{M'}\in H^2(M',{\mathcal {O}}_{M'}^*)$ and a ![]() $\zeta$-twisted locally free sheaf
$\zeta$-twisted locally free sheaf ![]() ${\mathcal {U}}'$ over
${\mathcal {U}}'$ over ![]() $M'\times S'$, with
$M'\times S'$, with ![]() $\zeta :=\pi _{S'}^*(\zeta _{S'})\pi _{M'}^*(\zeta _{M'})$, such that
$\zeta :=\pi _{S'}^*(\zeta _{S'})\pi _{M'}^*(\zeta _{M'})$, such that ![]() $(M'\times S',{\mathcal {E}}nd({\mathcal {U}}'))$ is deformation equivalent to
$(M'\times S',{\mathcal {E}}nd({\mathcal {U}}'))$ is deformation equivalent to ![]() $(M\times S,{\mathcal {E}}nd({\mathcal {U}}))$, by Proposition 5.22. Moreover,
$(M\times S,{\mathcal {E}}nd({\mathcal {U}}))$, by Proposition 5.22. Moreover, ![]() ${\mathcal {U}}'$ is
${\mathcal {U}}'$ is ![]() $\omega$-slope-stable with respect to some Kähler class on
$\omega$-slope-stable with respect to some Kähler class on ![]() $S'\times M'$, by Proposition 5.15. We note that the existence of such
$S'\times M'$, by Proposition 5.15. We note that the existence of such ![]() ${\mathcal {U}}'$ follows already from [Reference BuskinBus19, Theorem 5.1] in this case where
${\mathcal {U}}'$ follows already from [Reference BuskinBus19, Theorem 5.1] in this case where ![]() $n=1$. It follows that
$n=1$. It follows that ![]() ${\mathcal {U}}'$ does not have any non-zero proper saturated subsheaf, since
${\mathcal {U}}'$ does not have any non-zero proper saturated subsheaf, since ![]() ${\rm Pic}(M'\times S')$ is trivial. Indeed, for every proper non-zero saturated
${\rm Pic}(M'\times S')$ is trivial. Indeed, for every proper non-zero saturated ![]() $\zeta$-twisted subsheaf
$\zeta$-twisted subsheaf ![]() $F$ of
$F$ of ![]() ${\mathcal {U}}'$ the untwisted sheaf
${\mathcal {U}}'$ the untwisted sheaf ![]() ${\mathcal {H}}om({\mathcal {U}}',F)$ would have slope zero, since
${\mathcal {H}}om({\mathcal {U}}',F)$ would have slope zero, since ![]() ${\rm Pic}(M'\times S')$ is trivial, and so
${\rm Pic}(M'\times S')$ is trivial, and so ![]() $F$ would slope-destabilize
$F$ would slope-destabilize ![]() ${\mathcal {U}}'$ (Definition 5.14).
${\mathcal {U}}'$ (Definition 5.14).
The construction of the sheaf ![]() $E$ over
$E$ over ![]() $M^{[n]}\times S^{[n]}$, given in (7.2), has a natural relative extension over the chosen twistor line
$M^{[n]}\times S^{[n]}$, given in (7.2), has a natural relative extension over the chosen twistor line ![]() $Q$ in
$Q$ in ![]() ${\mathfrak {M}}^0_\psi$ through
${\mathfrak {M}}^0_\psi$ through ![]() $q_0$ resulting in the twisted sheaf
$q_0$ resulting in the twisted sheaf ![]() $E'$ over
$E'$ over ![]() $M'^{[n]}\times S'^{[n]}$ given by substituting
$M'^{[n]}\times S'^{[n]}$ given by substituting ![]() ${\mathcal {U}}'$ for
${\mathcal {U}}'$ for ![]() ${\mathcal {U}}$ in (7.2). The check that (7.2) is still meaningful in the twisted setting reduces to checking that
${\mathcal {U}}$ in (7.2). The check that (7.2) is still meaningful in the twisted setting reduces to checking that ![]() $(q\times q)_*^{{\mathfrak {S}}_{n,\Delta }}$ is well defined. This is the case, since
$(q\times q)_*^{{\mathfrak {S}}_{n,\Delta }}$ is well defined. This is the case, since ![]() ${\mathcal {U}}'^{\boxtimes n}$ is
${\mathcal {U}}'^{\boxtimes n}$ is ![]() $\zeta ^{\boxtimes n}$-twisted, and
$\zeta ^{\boxtimes n}$-twisted, and ![]() $(b\times b)^*(\zeta ^{\boxtimes n})$ is the pullback via
$(b\times b)^*(\zeta ^{\boxtimes n})$ is the pullback via ![]() $q\times q$ of a Brauer class on
$q\times q$ of a Brauer class on ![]() $M'^{[n]}\times S'^{[n]}$ (which is itself the pullback of a Brauer class on
$M'^{[n]}\times S'^{[n]}$ (which is itself the pullback of a Brauer class on ![]() $M'^{(n)}\times S'^{(n)}$), as explained in [Reference MarkmanMar21a, § 10, Proof of Theorem 1.4].
$M'^{(n)}\times S'^{(n)}$), as explained in [Reference MarkmanMar21a, § 10, Proof of Theorem 1.4].
Let ![]() $\psi _{{\mathcal {U}}'}:H^2(M',{\mathbb {Q}})\rightarrow H^2(S',{\mathbb {Q}})$ and
$\psi _{{\mathcal {U}}'}:H^2(M',{\mathbb {Q}})\rightarrow H^2(S',{\mathbb {Q}})$ and ![]() $\psi _{E'}:H^2(M'^{[n]},{\mathbb {Q}})\rightarrow H^2(S'^{[n]},{\mathbb {Q}})$ be the parallel transports of
$\psi _{E'}:H^2(M'^{[n]},{\mathbb {Q}})\rightarrow H^2(S'^{[n]},{\mathbb {Q}})$ be the parallel transports of ![]() $\psi _{\mathcal {U}}$ and
$\psi _{\mathcal {U}}$ and ![]() $\psi _{\mathcal {E}}$ in the relevant local systems over the chosen twistor line
$\psi _{\mathcal {E}}$ in the relevant local systems over the chosen twistor line ![]() $Q$.
$Q$.
Lemma 8.2 The isometry ![]() $\psi _{E'}$ maps some Kähler class
$\psi _{E'}$ maps some Kähler class ![]() $\omega _1$ on
$\omega _1$ on ![]() $M'^{[n]}$ to a Kähler class on
$M'^{[n]}$ to a Kähler class on ![]() $S'^{[n]}$.
$S'^{[n]}$.
Proof. The isometry ![]() $\psi _{{\mathcal {U}}'}$ maps some Kähler class
$\psi _{{\mathcal {U}}'}$ maps some Kähler class ![]() $\omega _{M'}$ to a Kähler class
$\omega _{M'}$ to a Kähler class ![]() $\omega _{S'}$, as
$\omega _{S'}$, as ![]() $(S',\eta _{S'},M',\eta _{M'})$ is a point of
$(S',\eta _{S'},M',\eta _{M'})$ is a point of ![]() ${\mathfrak {M}}_\psi$. The equalities
${\mathfrak {M}}_\psi$. The equalities ![]() $\psi _{E'}\circ \theta =\theta \circ \psi _{{\mathcal {U}}'}$ and
$\psi _{E'}\circ \theta =\theta \circ \psi _{{\mathcal {U}}'}$ and ![]() $\psi _{E'}(\delta )=\delta$ follow from Corollary 7.3. The Picard groups of both Douady spaces
$\psi _{E'}(\delta )=\delta$ follow from Corollary 7.3. The Picard groups of both Douady spaces ![]() $M'^{[n]}$ and
$M'^{[n]}$ and ![]() $S'^{[n]}$ are cyclic generated by the classes
$S'^{[n]}$ are cyclic generated by the classes ![]() $\delta$ and their cones of effective curves are thus rays spanned by the class
$\delta$ and their cones of effective curves are thus rays spanned by the class ![]() $\delta ^\vee := {2(\delta,\bullet )}{n-1}$ in
$\delta ^\vee := {2(\delta,\bullet )}{n-1}$ in ![]() $H^2(M'^{[n]},{\mathbb {Q}})^*$ (were we identify
$H^2(M'^{[n]},{\mathbb {Q}})^*$ (were we identify ![]() $H_2(M'^{[n]},{\mathbb {Q}})$ with
$H_2(M'^{[n]},{\mathbb {Q}})$ with ![]() $H^2(M'^{[n]},{\mathbb {Q}})^*$), by [Reference MarkmanMar13, Corollary 3.6]. Choose a sufficiently large real number
$H^2(M'^{[n]},{\mathbb {Q}})^*$), by [Reference MarkmanMar13, Corollary 3.6]. Choose a sufficiently large real number ![]() $t$, such that
$t$, such that ![]() $(t\theta (\omega _{M'})-\delta,t\theta (\omega _{M'})-\delta )>0$. Then
$(t\theta (\omega _{M'})-\delta,t\theta (\omega _{M'})-\delta )>0$. Then ![]() $\omega _1:=t\theta (\omega _{M'})-\delta$ is a class in the connected component of the positive cone in
$\omega _1:=t\theta (\omega _{M'})-\delta$ is a class in the connected component of the positive cone in ![]() $H^{1,1}(M'^{[n]},{\mathbb {R}})$, which contains the Kähler cone, as it pairs positively with
$H^{1,1}(M'^{[n]},{\mathbb {R}})$, which contains the Kähler cone, as it pairs positively with ![]() $\theta (\omega _{M'})$, and
$\theta (\omega _{M'})$, and ![]() $\omega _1$ pairs positively with the class of every effective curve. Hence,
$\omega _1$ pairs positively with the class of every effective curve. Hence, ![]() $\omega _1$ is a Kähler class, by [Reference HuybrechtsHuy03b, Corollary 3.4]. Now,
$\omega _1$ is a Kähler class, by [Reference HuybrechtsHuy03b, Corollary 3.4]. Now, ![]() $\psi _{E'}(\omega _1)=t\theta (\omega _{S'})-\delta$ is a Kähler class, by the same reason.
$\psi _{E'}(\omega _1)=t\theta (\omega _{S'})-\delta$ is a Kähler class, by the same reason.
Let ![]() $\eta _{S'^{[n]}}$ be the marking of
$\eta _{S'^{[n]}}$ be the marking of ![]() $S'^{[n]}$ induced by extending the marking
$S'^{[n]}$ induced by extending the marking ![]() $\eta _{S^{[n]}}$ given in (7.8) to a trivialization of the local system over the chosen twistor path
$\eta _{S^{[n]}}$ given in (7.8) to a trivialization of the local system over the chosen twistor path ![]() $Q$. Define
$Q$. Define ![]() $\eta _{M'^{[n]}}$ similarly in terms of
$\eta _{M'^{[n]}}$ similarly in terms of ![]() $\eta _{M^{[n]}}$. Set
$\eta _{M^{[n]}}$. Set ![]() $\psi ^{[n]}:=\eta _{S'^{[n]}}^{-1}\psi _{E'}\eta _{M'^{[n]}}$. Let
$\psi ^{[n]}:=\eta _{S'^{[n]}}^{-1}\psi _{E'}\eta _{M'^{[n]}}$. Let
be the connected component of ![]() ${\mathfrak {M}}_{\psi ^{[n]}}$ containing the quadruple
${\mathfrak {M}}_{\psi ^{[n]}}$ containing the quadruple ![]() $(M'^{[n]},\eta _{M'^{[n]}},S'^{[n]},\eta _{S'^{[n]}})$.
$(M'^{[n]},\eta _{M'^{[n]}},S'^{[n]},\eta _{S'^{[n]}})$.
Lemma 8.3 The twisted vector bundle ![]() $E'$ is slope-stable with respect to every Kähler class on
$E'$ is slope-stable with respect to every Kähler class on ![]() $M'^{[n]}\times S'^{[n]}$.
$M'^{[n]}\times S'^{[n]}$.
Proof. We have already noted that ![]() ${\mathcal {U}}'$ does not have any non-zero proper saturated subsheaf. Here and in the following, by a subsheaf of a twisted sheaf we mean a twisted subsheaf with respect to the same co-cycle representing the Brauer class. Hence,
${\mathcal {U}}'$ does not have any non-zero proper saturated subsheaf. Here and in the following, by a subsheaf of a twisted sheaf we mean a twisted subsheaf with respect to the same co-cycle representing the Brauer class. Hence, ![]() ${\mathcal {U}}'^{\boxtimes n}$ does not have any non-zero proper saturated subsheaves, by [Reference MarkmanMar21a, Proposition 10.1]. Given
${\mathcal {U}}'^{\boxtimes n}$ does not have any non-zero proper saturated subsheaves, by [Reference MarkmanMar21a, Proposition 10.1]. Given ![]() $\sigma \in {\mathfrak {S}}_n$, let
$\sigma \in {\mathfrak {S}}_n$, let ![]() $(1\times \sigma ):M^n\times S^n\rightarrow M^n\times S^n$ act as the identity on
$(1\times \sigma ):M^n\times S^n\rightarrow M^n\times S^n$ act as the identity on ![]() $M^n$ and via
$M^n$ and via ![]() $\sigma$ on
$\sigma$ on ![]() $S^n$. The vector bundles
$S^n$. The vector bundles ![]() ${\mathcal {U}}^{\boxtimes n}$ and
${\mathcal {U}}^{\boxtimes n}$ and ![]() $(1\times \sigma )^*{\mathcal {U}}^{\boxtimes n}$ are non-isomorphic, for every
$(1\times \sigma )^*{\mathcal {U}}^{\boxtimes n}$ are non-isomorphic, for every ![]() $\sigma \in {\mathfrak {S}}_n$,
$\sigma \in {\mathfrak {S}}_n$, ![]() $\sigma \neq 1$. Furthermore,
$\sigma \neq 1$. Furthermore, ![]() ${\rm Hom}({\mathcal {U}}^{\boxtimes n},(1\times \sigma )^*{\mathcal {U}}^{\boxtimes n})=0,$ for such
${\rm Hom}({\mathcal {U}}^{\boxtimes n},(1\times \sigma )^*{\mathcal {U}}^{\boxtimes n})=0,$ for such ![]() $\sigma$. Now the dimensions of
$\sigma$. Now the dimensions of ![]() ${\rm Hom}({\mathcal {U}}^{\boxtimes n},(1\times \sigma )^*{\mathcal {U}}^{\boxtimes n})$ and
${\rm Hom}({\mathcal {U}}^{\boxtimes n},(1\times \sigma )^*{\mathcal {U}}^{\boxtimes n})$ and ![]() ${\rm Hom}({\mathcal {U}}'^{\boxtimes n},(1\times \sigma )^*{\mathcal {U}}'^{\boxtimes n})$ are equal, by the invariance of the dimension of sheaf cohomologies of hyperholomorphic sheaves under twistor deformations [Reference VerbitskyVer99b, § 3.5]. Hence,
${\rm Hom}({\mathcal {U}}'^{\boxtimes n},(1\times \sigma )^*{\mathcal {U}}'^{\boxtimes n})$ are equal, by the invariance of the dimension of sheaf cohomologies of hyperholomorphic sheaves under twistor deformations [Reference VerbitskyVer99b, § 3.5]. Hence,
does not have any non-zero proper saturated ![]() ${\mathfrak {S}}_n$-invariant subsheaf, by [Reference MarkmanMar21a, Lemma 11.5]. The same is true for
${\mathfrak {S}}_n$-invariant subsheaf, by [Reference MarkmanMar21a, Lemma 11.5]. The same is true for ![]() $(b\times b)^*{\mathcal {U}}'^{\boxtimes n}$, as
$(b\times b)^*{\mathcal {U}}'^{\boxtimes n}$, as ![]() $b\times b$ is a birational morphism.
$b\times b$ is a birational morphism.
Consider the following commutative diagram.

Here ![]() $e$ is the natural injective homomorphism from the
$e$ is the natural injective homomorphism from the ![]() ${\mathfrak {S}}_{n,\Delta }$-invariant subsheaf with respect to the linearization
${\mathfrak {S}}_{n,\Delta }$-invariant subsheaf with respect to the linearization ![]() $\chi \otimes \rho _\boxtimes$ of
$\chi \otimes \rho _\boxtimes$ of ![]() ${\mathcal {U}}'^{\boxtimes n}$. The right arrow
${\mathcal {U}}'^{\boxtimes n}$. The right arrow ![]() $p$ is the projection on the subset of direct summands. For each
$p$ is the projection on the subset of direct summands. For each ![]() $(\sigma,\tau )\in {\mathfrak {S}}_n\times {\mathfrak {S}}_n$ we have the evaluation homomorphism from the bottom left vector bundle to the corresponding direct summand of the bottom right vector bundle due to the equality
$(\sigma,\tau )\in {\mathfrak {S}}_n\times {\mathfrak {S}}_n$ we have the evaluation homomorphism from the bottom left vector bundle to the corresponding direct summand of the bottom right vector bundle due to the equality ![]() $(q\times q)\circ (\sigma \times \tau )=(q\times q)$. The homomorphism
$(q\times q)\circ (\sigma \times \tau )=(q\times q)$. The homomorphism ![]() $ev$ is the resulting diagonal homomorphism. The homomorphism
$ev$ is the resulting diagonal homomorphism. The homomorphism ![]() $ev$ restricts to an isomorphism over the complement of the ramification divisor of
$ev$ restricts to an isomorphism over the complement of the ramification divisor of ![]() $q\times q$.
$q\times q$.
The homomorphism ![]() $e$ is
$e$ is ![]() ${\mathfrak {S}}_{n,\Delta }$-equivariant. The homomorphism
${\mathfrak {S}}_{n,\Delta }$-equivariant. The homomorphism ![]() $ev$ is
$ev$ is ![]() ${\mathfrak {S}}_n\times {\mathfrak {S}}_n$-equivariant. The homomorphism
${\mathfrak {S}}_n\times {\mathfrak {S}}_n$-equivariant. The homomorphism ![]() $p$ is
$p$ is ![]() ${\mathfrak {S}}_n\times {\mathfrak {S}}_n$-equivariant, where the latter group acts on the top right vector bundle via the projection
${\mathfrak {S}}_n\times {\mathfrak {S}}_n$-equivariant, where the latter group acts on the top right vector bundle via the projection ![]() ${\mathfrak {S}}_n\times {\mathfrak {S}}_n\rightarrow {\mathfrak {S}}_n$ onto the second factor. It follows that the homomorphism
${\mathfrak {S}}_n\times {\mathfrak {S}}_n\rightarrow {\mathfrak {S}}_n$ onto the second factor. It follows that the homomorphism ![]() $p\circ ev\circ e$ is
$p\circ ev\circ e$ is ![]() ${\mathfrak {S}}_{n,\Delta }$-equivariant, where the latter group acts via the isomorphism
${\mathfrak {S}}_{n,\Delta }$-equivariant, where the latter group acts via the isomorphism ![]() ${\mathfrak {S}}_{n,\Delta }\rightarrow {\mathfrak {S}}_n$, given by
${\mathfrak {S}}_{n,\Delta }\rightarrow {\mathfrak {S}}_n$, given by ![]() $(\sigma,\sigma )\mapsto \sigma$ on the top right vector bundle.
$(\sigma,\sigma )\mapsto \sigma$ on the top right vector bundle.
The homomorphism ![]() $p\circ ev\circ e$ restricts to an isomorphism over the complement of the ramification divisor of
$p\circ ev\circ e$ restricts to an isomorphism over the complement of the ramification divisor of ![]() $q\times q$. Hence, the pullback via
$q\times q$. Hence, the pullback via ![]() $q\times q$ of any saturated non-zero proper subsheaf of
$q\times q$ of any saturated non-zero proper subsheaf of ![]() $(q\times q)_*^{{\mathfrak {S}}_{n,\Delta }}(b\times b)^*{\mathcal {U}}'^{\boxtimes n}$ maps via
$(q\times q)_*^{{\mathfrak {S}}_{n,\Delta }}(b\times b)^*{\mathcal {U}}'^{\boxtimes n}$ maps via ![]() $p\circ ev\circ e$ to an
$p\circ ev\circ e$ to an ![]() ${\mathfrak {S}}_n$-invariant non-zero subsheaf of the top right vector bundle, whose saturation is a proper subsheaf. We have seen that such a subsheaf does not exist. It follows that
${\mathfrak {S}}_n$-invariant non-zero subsheaf of the top right vector bundle, whose saturation is a proper subsheaf. We have seen that such a subsheaf does not exist. It follows that ![]() $(q\times q)_*^{{\mathfrak {S}}_{n,\Delta }}(b\times b)^*{\mathcal {U}}'^{\boxtimes n}$ does not have any saturated non-zero proper subsheaf. Hence, neither does
$(q\times q)_*^{{\mathfrak {S}}_{n,\Delta }}(b\times b)^*{\mathcal {U}}'^{\boxtimes n}$ does not have any saturated non-zero proper subsheaf. Hence, neither does ![]() $E'$, as the latter is the tensor product of the former with a line bundle.
$E'$, as the latter is the tensor product of the former with a line bundle.
Theorem 8.4 Every quadruple ![]() $(X_1,\eta _1,X_2,\eta _2)$ in the component
$(X_1,\eta _1,X_2,\eta _2)$ in the component ![]() ${\mathfrak {M}}_{\psi ^{[n]}}^0$, given in (8.1), supports a compatible vector bundle (Definition 5.21).
${\mathfrak {M}}_{\psi ^{[n]}}^0$, given in (8.1), supports a compatible vector bundle (Definition 5.21).
Proof. Lemma 8.2 verifies Assumption 5.19(2) for the locally free sheaf ![]() $E'$ supported by the quadruple
$E'$ supported by the quadruple ![]() $(M'^{[n]},\eta _{M'^{[n]}},S'^{[n]},\eta _{S'^{[n]}})$ in the component
$(M'^{[n]},\eta _{M'^{[n]}},S'^{[n]},\eta _{S'^{[n]}})$ in the component ![]() ${\mathfrak {M}}^0_{\psi ^{[n]}}$. Lemma 8.3 verifies the stability condition in Assumption 5.19(3) for
${\mathfrak {M}}^0_{\psi ^{[n]}}$. Lemma 8.3 verifies the stability condition in Assumption 5.19(3) for ![]() $E'$. The statement thus follows from Proposition 5.22.
$E'$. The statement thus follows from Proposition 5.22.
Let ![]() $\Lambda _{K3}$ be the
$\Lambda _{K3}$ be the ![]() $K3$ lattice,
$K3$ lattice, ![]() $\Lambda$ the lattice given in (7.6), and
$\Lambda$ the lattice given in (7.6), and ![]() $\iota :O(\Lambda _{K3})\rightarrow O(\Lambda )$ the inclusion (7.7). Let
$\iota :O(\Lambda _{K3})\rightarrow O(\Lambda )$ the inclusion (7.7). Let ![]() $u\in \Lambda _{K3}$ be a primitive element with
$u\in \Lambda _{K3}$ be a primitive element with ![]() $(u,u)>0$. Let
$(u,u)>0$. Let ![]() $\rho _u$ be the reflection in the co-rank-
$\rho _u$ be the reflection in the co-rank-![]() $1$ sublattice
$1$ sublattice ![]() $u^\perp \subset \Lambda _{K3}$. Let
$u^\perp \subset \Lambda _{K3}$. Let ![]() ${\rm Mon}(\Lambda )\subset O^+(\Lambda )$ be the subgroup which acts on the discriminant group
${\rm Mon}(\Lambda )\subset O^+(\Lambda )$ be the subgroup which acts on the discriminant group ![]() $\Lambda ^*/\Lambda$ via
$\Lambda ^*/\Lambda$ via ![]() $\pm 1$.
$\pm 1$.
Let ![]() ${\mathfrak {M}}_\Lambda ^0$ be the connected component of the moduli space
${\mathfrak {M}}_\Lambda ^0$ be the connected component of the moduli space ![]() ${\mathfrak {M}}_\Lambda$ of marked pairs
${\mathfrak {M}}_\Lambda$ of marked pairs ![]() $(X,\eta )$, with
$(X,\eta )$, with ![]() $X$ of
$X$ of ![]() $K3^{[n]}$ type, containing the marked pair
$K3^{[n]}$ type, containing the marked pair ![]() $(S^{[n]},\eta _{S^{[n]}})$, given in (7.8).
$(S^{[n]},\eta _{S^{[n]}})$, given in (7.8).
Corollary 8.5 Let ![]() $\tilde {\psi }\in O^+(\Lambda _{\mathbb {Q}})$ be an isometry in the double orbit
$\tilde {\psi }\in O^+(\Lambda _{\mathbb {Q}})$ be an isometry in the double orbit ![]() ${\rm Mon}(\Lambda )(-\iota (\rho _u)){\rm Mon}(\Lambda )$. There exists a non-empty connected component
${\rm Mon}(\Lambda )(-\iota (\rho _u)){\rm Mon}(\Lambda )$. There exists a non-empty connected component ![]() ${\mathfrak {M}}_{\tilde {\psi }}^0$ of
${\mathfrak {M}}_{\tilde {\psi }}^0$ of ![]() ${\mathfrak {M}}_{\tilde {\psi }}$ parametrizing quadruples
${\mathfrak {M}}_{\tilde {\psi }}$ parametrizing quadruples ![]() $(X_1,\eta _1,X_2,\eta _2)$, with
$(X_1,\eta _1,X_2,\eta _2)$, with ![]() $(X_1,\eta _1)$ and
$(X_1,\eta _1)$ and ![]() $(X_2,\eta _2)$ in
$(X_2,\eta _2)$ in ![]() ${\mathfrak {M}}_\Lambda ^0$, such that each quadruple in
${\mathfrak {M}}_\Lambda ^0$, such that each quadruple in ![]() ${\mathfrak {M}}_{\tilde {\psi }}^0$ supports a compatible vector bundle (Definition 5.21).
${\mathfrak {M}}_{\tilde {\psi }}^0$ supports a compatible vector bundle (Definition 5.21).
Proof. The double orbit ![]() $O^+(\Lambda _{K3})(-\rho _u) O^+(\Lambda _{K3})$ depends only on
$O^+(\Lambda _{K3})(-\rho _u) O^+(\Lambda _{K3})$ depends only on ![]() $(u,u)$, by [Reference BuskinBus19, Proposition 3.3]. Hence, the double orbit
$(u,u)$, by [Reference BuskinBus19, Proposition 3.3]. Hence, the double orbit ![]() ${\rm Mon}(\Lambda )(-\iota (\rho _u)){\rm Mon}(\Lambda )$ depends only on
${\rm Mon}(\Lambda )(-\iota (\rho _u)){\rm Mon}(\Lambda )$ depends only on ![]() $(u,u)$, and so we may assume that
$(u,u)$, and so we may assume that ![]() $\tilde {\psi }=\gamma _1\iota (\eta _S\psi _{\mathcal {U}}\eta _M^{-1})\gamma _0$, for some
$\tilde {\psi }=\gamma _1\iota (\eta _S\psi _{\mathcal {U}}\eta _M^{-1})\gamma _0$, for some ![]() $\gamma _1,\gamma _2\in {\rm Mon}(\Lambda )$, where
$\gamma _1,\gamma _2\in {\rm Mon}(\Lambda )$, where ![]() $\psi _{\mathcal {U}}$ is the isometry in Proposition 8.1. Set
$\psi _{\mathcal {U}}$ is the isometry in Proposition 8.1. Set ![]() $\psi :=\eta _S\psi _{\mathcal {U}}\eta _M^{-1}$. The isometry
$\psi :=\eta _S\psi _{\mathcal {U}}\eta _M^{-1}$. The isometry ![]() $\psi ^{[n]}$, given in (8.1), is equal to
$\psi ^{[n]}$, given in (8.1), is equal to ![]() $\iota (\psi )$, by Corollary 7.3, and so
$\iota (\psi )$, by Corollary 7.3, and so ![]() $\tilde {\psi }=\gamma _2\psi ^{[n]}\gamma _1$. We get the isomorphism
$\tilde {\psi }=\gamma _2\psi ^{[n]}\gamma _1$. We get the isomorphism ![]() $f:{\mathfrak {M}}_{\psi ^{[n]}}\rightarrow {\mathfrak {M}}_{\tilde {\psi }}$ given by
$f:{\mathfrak {M}}_{\psi ^{[n]}}\rightarrow {\mathfrak {M}}_{\tilde {\psi }}$ given by
which maps connected components to connected components, since ![]() $\eta _i^{-1}{\rm Mon}(\Lambda )\eta _i$ is the monodromy group
$\eta _i^{-1}{\rm Mon}(\Lambda )\eta _i$ is the monodromy group ![]() ${\rm Mon}^2(X_i)$ of
${\rm Mon}^2(X_i)$ of ![]() $X_i$,
$X_i$, ![]() $i=1,2$, by [Reference MarkmanMar08, Theorem 1.6 and Lemma 4.10]. Furthermore, the marked pair
$i=1,2$, by [Reference MarkmanMar08, Theorem 1.6 and Lemma 4.10]. Furthermore, the marked pair ![]() $(X_1,\gamma _1^{-1}\eta _1)$ belongs to the connected component
$(X_1,\gamma _1^{-1}\eta _1)$ belongs to the connected component ![]() ${\mathfrak {M}}_\Lambda ^0$ of
${\mathfrak {M}}_\Lambda ^0$ of ![]() $(X_1,\eta _1)$, since
$(X_1,\eta _1)$, since ![]() $\gamma _1^{-1}$ belongs to
$\gamma _1^{-1}$ belongs to ![]() ${\rm Mon}(\Lambda )$ and
${\rm Mon}(\Lambda )$ and ![]() ${\rm Mon}(\Lambda )=\eta _1{\rm Mon}^2(X_1)\eta _1^{-1}$. Similarly,
${\rm Mon}(\Lambda )=\eta _1{\rm Mon}^2(X_1)\eta _1^{-1}$. Similarly, ![]() $(X_2,\gamma _2\eta _2)$ belongs to the same connected component
$(X_2,\gamma _2\eta _2)$ belongs to the same connected component ![]() ${\mathfrak {M}}_\Lambda ^0$ of
${\mathfrak {M}}_\Lambda ^0$ of ![]() $(X_2,\eta _2)$. Clearly, if
$(X_2,\eta _2)$. Clearly, if ![]() $q\in {\mathfrak {M}}_{\psi ^{[n]}}$ supports a compatible vector bundle, then
$q\in {\mathfrak {M}}_{\psi ^{[n]}}$ supports a compatible vector bundle, then ![]() $f(q)$ supports (the same) compatible vector bundle. The statement now follows from Theorem 8.4.
$f(q)$ supports (the same) compatible vector bundle. The statement now follows from Theorem 8.4.
9. Algebraicity of a rational Hodge isometry
We prove Theorems 1.1 and 1.4 in this section. Let ![]() ${\mathcal {G}}_{an}$ be the subgroupoid of
${\mathcal {G}}_{an}$ be the subgroupoid of ![]() ${\mathcal {G}}$ given in (1.2). Note that morphisms in
${\mathcal {G}}$ given in (1.2). Note that morphisms in ![]() ${\rm Hom}_{{\mathcal {G}}_{an}}((X,\epsilon ),(Y,\epsilon '))$ are induced by analytic correspondences in
${\rm Hom}_{{\mathcal {G}}_{an}}((X,\epsilon ),(Y,\epsilon '))$ are induced by analytic correspondences in ![]() $X\times Y$ and are degree preserving up to sign.
$X\times Y$ and are degree preserving up to sign.
Theorem 9.1 Let ![]() $X$ and
$X$ and ![]() $Y$ be IHSMs of
$Y$ be IHSMs of ![]() $K3^{[n]}$ type and let
$K3^{[n]}$ type and let ![]() $f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ be a rational Hodge isometry. For every pair of orientations
$f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ be a rational Hodge isometry. For every pair of orientations ![]() $\epsilon$ and
$\epsilon$ and ![]() $\epsilon '$ there exists a morphism
$\epsilon '$ there exists a morphism ![]() $\phi$ in
$\phi$ in ![]() ${\rm Hom}_{{\mathcal {G}}_{an}}((X,\epsilon ),(Y,\epsilon '))$, such that
${\rm Hom}_{{\mathcal {G}}_{an}}((X,\epsilon ),(Y,\epsilon '))$, such that ![]() $\widetilde {H}_0(\phi )$ is equal to
$\widetilde {H}_0(\phi )$ is equal to ![]() $f$ or
$f$ or ![]() $-f$.
$-f$.
Proof. The set ![]() ${\rm Hom}_{{\mathcal {G}}_{an}}((X,\epsilon ),(Y,\epsilon '))$ is independent of the orientations as is the functor
${\rm Hom}_{{\mathcal {G}}_{an}}((X,\epsilon ),(Y,\epsilon '))$ is independent of the orientations as is the functor ![]() $\widetilde {H}_0$, so the existence of
$\widetilde {H}_0$, so the existence of ![]() $\phi$ is independent of the orientations. We may assume that
$\phi$ is independent of the orientations. We may assume that ![]() $\nu (f)=1$, possibly after replacing
$\nu (f)=1$, possibly after replacing ![]() $f$ by
$f$ by ![]() $-f$. Choose markings
$-f$. Choose markings ![]() $\eta _X$ and
$\eta _X$ and ![]() $\eta _Y$, such that
$\eta _Y$, such that ![]() $(X,\eta _X)$ and
$(X,\eta _X)$ and ![]() $(Y,\eta _Y)$ belong to the same connected component
$(Y,\eta _Y)$ belong to the same connected component ![]() ${\mathfrak {M}}^0_\Lambda$ of
${\mathfrak {M}}^0_\Lambda$ of ![]() ${\mathfrak {M}}_\Lambda$. Choose an orientation of
${\mathfrak {M}}_\Lambda$. Choose an orientation of ![]() $\Lambda$ and endow
$\Lambda$ and endow ![]() $H^2(X,{\mathbb {Z}})$ and
$H^2(X,{\mathbb {Z}})$ and ![]() $H^2(Y,{\mathbb {Z}})$ with the orientations
$H^2(Y,{\mathbb {Z}})$ with the orientations ![]() $\epsilon$ and
$\epsilon$ and ![]() $\epsilon '$, so that
$\epsilon '$, so that ![]() $\eta _X$ and
$\eta _X$ and ![]() $\eta _Y$ are orientation preserving. We write
$\eta _Y$ are orientation preserving. We write ![]() ${\rm Hom}_{{\mathcal {G}}_{an}}(X,Y)$ instead of
${\rm Hom}_{{\mathcal {G}}_{an}}(X,Y)$ instead of ![]() ${\rm Hom}_{{\mathcal {G}}_{an}}((X,\epsilon ),(Y,\epsilon '))$, as in Convention 5.16, and we will continue to use the convention in the following argument. Set
${\rm Hom}_{{\mathcal {G}}_{an}}((X,\epsilon ),(Y,\epsilon '))$, as in Convention 5.16, and we will continue to use the convention in the following argument. Set ![]() $\psi :=\eta _Y\circ f\circ \eta _X^{-1}$. Then
$\psi :=\eta _Y\circ f\circ \eta _X^{-1}$. Then ![]() $\psi$ belongs to
$\psi$ belongs to ![]() $O^+(\Lambda _{\mathbb {Q}})$ and so it decomposes as
$O^+(\Lambda _{\mathbb {Q}})$ and so it decomposes as
where each ![]() $\psi _i$ belongs to the double orbit
$\psi _i$ belongs to the double orbit ![]() ${\rm Mon}(\Lambda )\iota (-\rho _u){\rm Mon}(\Lambda )$, for some element
${\rm Mon}(\Lambda )\iota (-\rho _u){\rm Mon}(\Lambda )$, for some element ![]() $u\in \Lambda _{K3}$ with
$u\in \Lambda _{K3}$ with ![]() $(u,u)>0$, by Corollary 2.5. The proof proceeds by induction on
$(u,u)>0$, by Corollary 2.5. The proof proceeds by induction on ![]() $k$.
$k$.
Case ![]() $k=0$. In this case
$k=0$. In this case ![]() $\psi =id$ and
$\psi =id$ and ![]() $f=\eta _Y^{-1}\eta _X$ is a Hodge isometry. There exists a parallel-transport operator
$f=\eta _Y^{-1}\eta _X$ is a Hodge isometry. There exists a parallel-transport operator ![]() $\phi :H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$, which is a morphism in
$\phi :H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$, which is a morphism in ![]() ${\rm Hom}_{{\mathcal {G}}_{an}}(X,Y)$, and such that
${\rm Hom}_{{\mathcal {G}}_{an}}(X,Y)$, and such that ![]() $\phi$ restricts to
$\phi$ restricts to ![]() $H^2(X,{\mathbb {Q}})$ as
$H^2(X,{\mathbb {Q}})$ as ![]() $f$, by Theorem 5.2. In this case
$f$, by Theorem 5.2. In this case ![]() $\widetilde {H}_0(\phi )$ is also equal to the restriction of
$\widetilde {H}_0(\phi )$ is also equal to the restriction of ![]() $\phi$ to
$\phi$ to ![]() $H^2(X,{\mathbb {Q}})$, by Remark 5.18.
$H^2(X,{\mathbb {Q}})$, by Remark 5.18.
Assume that ![]() $k\geq 1$ and that the statement holds for
$k\geq 1$ and that the statement holds for ![]() $k-1$. Set
$k-1$. Set ![]() $\psi '=\psi _{k-1}\circ \cdots \circ \psi _1$, so that
$\psi '=\psi _{k-1}\circ \cdots \circ \psi _1$, so that ![]() $\psi =\psi _k\psi '$. Set
$\psi =\psi _k\psi '$. Set ![]() $\ell _0:=P(X,\eta _X)$,
$\ell _0:=P(X,\eta _X)$, ![]() $\ell _{k-1}:=\psi '(\ell _0)$, and
$\ell _{k-1}:=\psi '(\ell _0)$, and ![]() $\ell _k=\psi (\ell _0)$. Note that
$\ell _k=\psi (\ell _0)$. Note that ![]() $\ell _k=P(Y,\eta _Y)$. Let
$\ell _k=P(Y,\eta _Y)$. Let ![]() $(X_{k-1},\eta _{k-1})$ be a marked pair in
$(X_{k-1},\eta _{k-1})$ be a marked pair in ![]() ${\mathfrak {M}}_\Lambda ^0$, such that
${\mathfrak {M}}_\Lambda ^0$, such that ![]() $P(X_{k-1},\eta _{k-1})=\ell _{k-1}$. Such a marked pair exists, by the surjectivity of the period map [Reference HuybrechtsHuy99]. Set
$P(X_{k-1},\eta _{k-1})=\ell _{k-1}$. Such a marked pair exists, by the surjectivity of the period map [Reference HuybrechtsHuy99]. Set ![]() $f':=\eta _{k-1}^{-1}\circ \psi '\circ \eta _X$. There exists a morphism
$f':=\eta _{k-1}^{-1}\circ \psi '\circ \eta _X$. There exists a morphism ![]() $\phi '\in {\rm Hom}_{{\mathcal {G}}_{an}}(X,X_{k-1})$, such that
$\phi '\in {\rm Hom}_{{\mathcal {G}}_{an}}(X,X_{k-1})$, such that ![]() $\widetilde {H}_0(\phi ')=f'$, by the induction hypothesis. The quadruple
$\widetilde {H}_0(\phi ')=f'$, by the induction hypothesis. The quadruple ![]() $(X_{k-1},\eta _{k-1},Y,\eta _Y)$ satisfies the condition that
$(X_{k-1},\eta _{k-1},Y,\eta _Y)$ satisfies the condition that ![]() $\eta _Y^{-1}\psi _k\eta _{k-1}$ is a Hodge isometry, since
$\eta _Y^{-1}\psi _k\eta _{k-1}$ is a Hodge isometry, since
but it may not belong to ![]() ${\mathfrak {M}}_{\psi _k}$, since
${\mathfrak {M}}_{\psi _k}$, since ![]() $\eta _Y^{-1}\psi _k\eta _{k-1}$ need not map a Kähler class to a Kähler class.
$\eta _Y^{-1}\psi _k\eta _{k-1}$ need not map a Kähler class to a Kähler class.
There exists a connected component ![]() ${\mathfrak {M}}^0_{\psi _k}$ of
${\mathfrak {M}}^0_{\psi _k}$ of ![]() ${\mathfrak {M}}_{\psi _k}$ in which every quadruple supports a compatible vector bundle, and such that
${\mathfrak {M}}_{\psi _k}$ in which every quadruple supports a compatible vector bundle, and such that ![]() $\Pi _i:{\mathfrak {M}}^0_{\psi _k}\rightarrow {\mathfrak {M}}_\Lambda$ has image in the connected component
$\Pi _i:{\mathfrak {M}}^0_{\psi _k}\rightarrow {\mathfrak {M}}_\Lambda$ has image in the connected component ![]() ${\mathfrak {M}}^0_\Lambda$, for
${\mathfrak {M}}^0_\Lambda$, for ![]() $i=1,2$, by Corollary 8.5. Extend the pair
$i=1,2$, by Corollary 8.5. Extend the pair ![]() $(X_{k-1},\eta _{k-1})$ to a quadruple
$(X_{k-1},\eta _{k-1})$ to a quadruple ![]() $q:=(X_{k-1},\eta _{k-1},Y',\eta _{Y'})$ in
$q:=(X_{k-1},\eta _{k-1},Y',\eta _{Y'})$ in ![]() ${\mathfrak {M}}^0_{\psi _k}$. Such a point
${\mathfrak {M}}^0_{\psi _k}$. Such a point ![]() $q$ exists, by the surjectivity lemma (Lemma 5.7). Let
$q$ exists, by the surjectivity lemma (Lemma 5.7). Let ![]() $F_q$ be the compatible vector bundle supported by
$F_q$ be the compatible vector bundle supported by ![]() $q$. Set
$q$. Set ![]() $\phi _k':=\left [\kappa (F_q)\sqrt {td_{X_{k-1}\times Y'}}\right ]_*:H^*(X_{k-1},{\mathbb {Q}})\rightarrow H^*(Y',{\mathbb {Q}})$. Then
$\phi _k':=\left [\kappa (F_q)\sqrt {td_{X_{k-1}\times Y'}}\right ]_*:H^*(X_{k-1},{\mathbb {Q}})\rightarrow H^*(Y',{\mathbb {Q}})$. Then ![]() $\widetilde {H}_0\big (\phi _k'\big )=\eta _{Y'}^{-1}\circ \psi _k\circ \eta _{k-1},$ by Definition 5.21 of the compatibility of
$\widetilde {H}_0\big (\phi _k'\big )=\eta _{Y'}^{-1}\circ \psi _k\circ \eta _{k-1},$ by Definition 5.21 of the compatibility of ![]() $F_q$. We have
$F_q$. We have ![]() $P(Y',\eta _{Y'})=\psi _k(P(X_{k-1},\eta _{k-1}))=P(Y,\eta _Y)$, where the first equality is by Lemma 5.4. Hence, there exists a morphism
$P(Y',\eta _{Y'})=\psi _k(P(X_{k-1},\eta _{k-1}))=P(Y,\eta _Y)$, where the first equality is by Lemma 5.4. Hence, there exists a morphism ![]() $\phi _k\in {\rm Hom}_{{\mathcal {G}}_{an}}(Y',Y)$, such that
$\phi _k\in {\rm Hom}_{{\mathcal {G}}_{an}}(Y',Y)$, such that ![]() $\widetilde {H}_0(\phi _k)=\eta _Y^{-1}\eta _{Y'}$, by the case
$\widetilde {H}_0(\phi _k)=\eta _Y^{-1}\eta _{Y'}$, by the case ![]() $k=0$ of the statement. We conclude that
$k=0$ of the statement. We conclude that ![]() $\phi :=\phi _k\circ \phi _k'\circ \phi '$ is a morphism in
$\phi :=\phi _k\circ \phi _k'\circ \phi '$ is a morphism in ![]() ${\rm Hom}_{{\mathcal {G}}_{an}}(X,Y)$, and
${\rm Hom}_{{\mathcal {G}}_{an}}(X,Y)$, and ![]() $\widetilde {H}_0(\phi )=f$.
$\widetilde {H}_0(\phi )=f$.
Proof Proof of Theorem 1.1
Let ![]() $f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ be a Hodge isometry. We may assume that
$f:H^2(X,{\mathbb {Q}})\rightarrow H^2(Y,{\mathbb {Q}})$ be a Hodge isometry. We may assume that ![]() $\nu (f)=1$, possibly after replacing
$\nu (f)=1$, possibly after replacing ![]() $f$ by
$f$ by ![]() $-f$ (and
$-f$ (and ![]() $\tilde {f}$ by
$\tilde {f}$ by ![]() $-\tilde {f}$ in the statement of the theorem). There exist orientations
$-\tilde {f}$ in the statement of the theorem). There exist orientations ![]() $\epsilon$ and
$\epsilon$ and ![]() $\epsilon '$ and a morphism
$\epsilon '$ and a morphism ![]() $\phi \in {\rm Hom}_{{\mathcal {G}}_{an}}((X,\epsilon ),(Y,\epsilon '))$, such that
$\phi \in {\rm Hom}_{{\mathcal {G}}_{an}}((X,\epsilon ),(Y,\epsilon '))$, such that ![]() $\widetilde {H}_0(\phi )=f$, by Theorem 9.1. Morphisms of
$\widetilde {H}_0(\phi )=f$, by Theorem 9.1. Morphisms of ![]() ${\mathcal {G}}_{an}$ are induced by analytic correspondences, as already noted in the paragraph following (1.2) defining this groupoid. If
${\mathcal {G}}_{an}$ are induced by analytic correspondences, as already noted in the paragraph following (1.2) defining this groupoid. If ![]() $\phi$ is degree preserving, then
$\phi$ is degree preserving, then ![]() $\widetilde {H}_0(\phi )$ is a rational scalar multiple of the restriction of
$\widetilde {H}_0(\phi )$ is a rational scalar multiple of the restriction of ![]() $\phi$ to
$\phi$ to ![]() $H^2(X,{\mathbb {Q}})$, by Lemma 3.6, and so we choose
$H^2(X,{\mathbb {Q}})$, by Lemma 3.6, and so we choose ![]() $\tilde {f}$ to be the appropriate scalar multiple of
$\tilde {f}$ to be the appropriate scalar multiple of ![]() $\phi$. If
$\phi$. If ![]() $\phi$ is degree reversing, then setting
$\phi$ is degree reversing, then setting ![]() $\tilde {f}=\phi$ we get an analytic correspondence with the desired properties, by Lemma 3.7.
$\tilde {f}=\phi$ we get an analytic correspondence with the desired properties, by Lemma 3.7.
10. The Pontryagin product on the cohomology of IHSMs of  $K3^{[n]}$ type
$K3^{[n]}$ type
In § 10.1 we introduce the Pontryagin product on the cohomology of an IHSM with vanishing odd cohomology. The results still apply to the even cohomology if the odd cohomology does not vanish. In § 10.2 we prove Conjecture 1.8 for morphisms in the image of the functor ![]() $\Theta _n:{\mathcal {G}}^{[1]}_{an}\rightarrow {\mathcal {G}}^{[n]}_{an}$, given in (7.12). In particular, morphisms in the image of
$\Theta _n:{\mathcal {G}}^{[1]}_{an}\rightarrow {\mathcal {G}}^{[n]}_{an}$, given in (7.12). In particular, morphisms in the image of ![]() $\Theta _n$, once normalized as in Conjecture 1.8, conjugate the cup product to itself, if they are degree preserving, and to the Pontryagin product if they are degree reversing.
$\Theta _n$, once normalized as in Conjecture 1.8, conjugate the cup product to itself, if they are degree preserving, and to the Pontryagin product if they are degree reversing.
10.1 The Pontryagin product for an IHSM with vanishing odd cohomology
Let ![]() $X$ be an IHSM, let
$X$ be an IHSM, let ![]() ${\mathfrak g}\subset {\mathfrak sl}(H^*(X,{\mathbb {Q}}))$ be its LLV algebra, and let
${\mathfrak g}\subset {\mathfrak sl}(H^*(X,{\mathbb {Q}}))$ be its LLV algebra, and let ![]() $h\in {\mathfrak g}$ be the grading operator given in (3.1). The commutator of
$h\in {\mathfrak g}$ be the grading operator given in (3.1). The commutator of ![]() $h$ in
$h$ in ![]() ${\mathfrak g}$ is
${\mathfrak g}$ is ![]() $\bar {{\mathfrak g}}\oplus {\mathbb {Q}} \cdot h$ and composing the isomorphism
$\bar {{\mathfrak g}}\oplus {\mathbb {Q}} \cdot h$ and composing the isomorphism ![]() $\dot {\rho }^{-1}:{\mathfrak g}\cong {\mathfrak so}(\widetilde {H}(X,{\mathbb {Q}}))$, given in (3.2), with restriction to
$\dot {\rho }^{-1}:{\mathfrak g}\cong {\mathfrak so}(\widetilde {H}(X,{\mathbb {Q}}))$, given in (3.2), with restriction to ![]() $H^2(X,{\mathbb {Q}})$ yields an isomorphism
$H^2(X,{\mathbb {Q}})$ yields an isomorphism ![]() $\bar {{\mathfrak g}}\cong {\mathfrak so}(H^2(X,{\mathbb {Q}}))$, by Lemma 3.5. Assume that the odd cohomology of
$\bar {{\mathfrak g}}\cong {\mathfrak so}(H^2(X,{\mathbb {Q}}))$, by Lemma 3.5. Assume that the odd cohomology of ![]() $X$ vanishes. If the second Betti number
$X$ vanishes. If the second Betti number ![]() $b_2(X)$ of
$b_2(X)$ of ![]() $X$ is even, assume that the monodromy group of
$X$ is even, assume that the monodromy group of ![]() $X$ contains reflections and
$X$ contains reflections and ![]() ${\rm dim}(X)=2n$ for odd
${\rm dim}(X)=2n$ for odd ![]() $n$. The latter assumption holds true for all currently known examples of IHSMs with even
$n$. The latter assumption holds true for all currently known examples of IHSMs with even ![]() $b_2(X)$ (
$b_2(X)$ (![]() $K3$ surfaces and IHSMs of O'Grady
$K3$ surfaces and IHSMs of O'Grady ![]() $6$ deformation type). The
$6$ deformation type). The ![]() ${\mathfrak g}$ action on
${\mathfrak g}$ action on ![]() $H^*(X,{\mathbb {C}})$ integrates to an action of
$H^*(X,{\mathbb {C}})$ integrates to an action of ![]() $SO(\widetilde {H}(X,{\mathbb {C}}))$ and the commutator of
$SO(\widetilde {H}(X,{\mathbb {C}}))$ and the commutator of ![]() $h$ is
$h$ is ![]() ${\mathbb {C}}^\times \times SO(H^2(X,{\mathbb {C}}))$, where an element
${\mathbb {C}}^\times \times SO(H^2(X,{\mathbb {C}}))$, where an element ![]() $t$ of the first factor
$t$ of the first factor ![]() ${\mathbb {C}}^\times$ maps
${\mathbb {C}}^\times$ maps ![]() $\alpha$ to
$\alpha$ to ![]() $t\alpha$ and
$t\alpha$ and ![]() $\beta$ to
$\beta$ to ![]() $({1}/{t})\beta$. The image of the second factor
$({1}/{t})\beta$. The image of the second factor ![]() $SO(H^2(X,{\mathbb {C}}))$ in
$SO(H^2(X,{\mathbb {C}}))$ in ![]() $GL(H^*(X,{\mathbb {C}}))$ acts on
$GL(H^*(X,{\mathbb {C}}))$ acts on ![]() $H^*(X,{\mathbb {C}})$ via ring automorphisms, by [Reference Looijenga and LuntsLL97, Proposition 4.5(ii)]. The coset
$H^*(X,{\mathbb {C}})$ via ring automorphisms, by [Reference Looijenga and LuntsLL97, Proposition 4.5(ii)]. The coset ![]() $\{g\in SO(\widetilde {H}(X,{\mathbb {C}})) : ghg^{-1}=-h\}$ of the commutator is the product of the component of
$\{g\in SO(\widetilde {H}(X,{\mathbb {C}})) : ghg^{-1}=-h\}$ of the commutator is the product of the component of ![]() $O({\mathbb {C}}\alpha \oplus {\mathbb {C}}\beta )$ with determinant
$O({\mathbb {C}}\alpha \oplus {\mathbb {C}}\beta )$ with determinant ![]() $-1$ with the component of
$-1$ with the component of ![]() $O(H^2(X,{\mathbb {C}}))$ with determinant
$O(H^2(X,{\mathbb {C}}))$ with determinant ![]() $-1$. If the monodromy group contains an element
$-1$. If the monodromy group contains an element ![]() $R$ of order
$R$ of order ![]() $2$ acting as a reflection on
$2$ acting as a reflection on ![]() $H^2(X,{\mathbb {C}})$, then the factor
$H^2(X,{\mathbb {C}})$, then the factor ![]() $O(H^2(X,{\mathbb {C}}))$ acts on
$O(H^2(X,{\mathbb {C}}))$ acts on ![]() $H^*(X,{\mathbb {C}})$ via ring automorphisms. Such a monodromy operator
$H^*(X,{\mathbb {C}})$ via ring automorphisms. Such a monodromy operator ![]() $R$ acts on
$R$ acts on ![]() $\widetilde {H}(X,{\mathbb {Q}})$ via the operator
$\widetilde {H}(X,{\mathbb {Q}})$ via the operator ![]() $\widetilde {H}(R)$ stabilizing both
$\widetilde {H}(R)$ stabilizing both ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ and restricting to
$\beta$ and restricting to ![]() $H^2(X,{\mathbb {Q}})$ as the monodromy reflection. A choice of such an element
$H^2(X,{\mathbb {Q}})$ as the monodromy reflection. A choice of such an element ![]() $R\in {\rm Mon}(X)$ yields an action of
$R\in {\rm Mon}(X)$ yields an action of ![]() $O(\widetilde {H}(X,{\mathbb {C}}))$ on
$O(\widetilde {H}(X,{\mathbb {C}}))$ on ![]() $H^*(X,{\mathbb {C}})$
$H^*(X,{\mathbb {C}})$
extending the above homomorphism ![]() $\rho :SO(\widetilde {H}(X,{\mathbb {C}}))\rightarrow GL(H^*(X,{\mathbb {C}}))$ and satisfying
$\rho :SO(\widetilde {H}(X,{\mathbb {C}}))\rightarrow GL(H^*(X,{\mathbb {C}}))$ and satisfying ![]() $\rho (\widetilde {H}(R))=R$.
$\rho (\widetilde {H}(R))=R$.
Let ![]() $\tau$ be the element of
$\tau$ be the element of ![]() $O(\widetilde {H}(X,{\mathbb {Q}}))$ interchanging
$O(\widetilde {H}(X,{\mathbb {Q}}))$ interchanging ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ and acting on
$\beta$ and acting on ![]() $H^2(X,{\mathbb {C}})$ via multiplication by
$H^2(X,{\mathbb {C}})$ via multiplication by ![]() $-1$. If
$-1$. If ![]() $b_2(X)$ is odd, then
$b_2(X)$ is odd, then ![]() $\tau$ belongs to
$\tau$ belongs to ![]() $SO(\widetilde {H}(X,{\mathbb {Q}}))$ and
$SO(\widetilde {H}(X,{\mathbb {Q}}))$ and ![]() $\rho _\tau$ is well defined, and if
$\rho _\tau$ is well defined, and if ![]() $b_2(X)$ is even we define
$b_2(X)$ is even we define ![]() $\rho _\tau$ via (10.1). Define the Pontryagin product
$\rho _\tau$ via (10.1). Define the Pontryagin product ![]() $\star$ on
$\star$ on ![]() $H^*(X,{\mathbb {Q}})$ by
$H^*(X,{\mathbb {Q}})$ by
Remark 10.1 The subring ![]() $SH^*(X,{\mathbb {C}})$ of
$SH^*(X,{\mathbb {C}})$ of ![]() $H^*(X,{\mathbb {C}})$ generated by
$H^*(X,{\mathbb {C}})$ generated by ![]() $H^2(X,{\mathbb {C}})$ is invariant under monodromy operators and it is an LLV subrepresentation, hence it is invariant under elements in the image of
$H^2(X,{\mathbb {C}})$ is invariant under monodromy operators and it is an LLV subrepresentation, hence it is invariant under elements in the image of ![]() $\rho$. The defining (10.2) implies that
$\rho$. The defining (10.2) implies that ![]() $SH^*(X,{\mathbb {C}})$ is a subring with respect to the Pontryagin product.
$SH^*(X,{\mathbb {C}})$ is a subring with respect to the Pontryagin product.
The values of the representation ![]() $\rho$ on the connected component with determinant
$\rho$ on the connected component with determinant ![]() $-1$ depends on our choice of the monodromy reflection
$-1$ depends on our choice of the monodromy reflection ![]() $R$ (see [Reference MarkmanMar08, Lemma 4.13]). Thus, if
$R$ (see [Reference MarkmanMar08, Lemma 4.13]). Thus, if ![]() $b_2(X)$ is even, then
$b_2(X)$ is even, then ![]() $\rho _\tau$ depends on the choice of
$\rho _\tau$ depends on the choice of ![]() $R$. Nevertheless, the Pontryagin product does not depend on this choice as we show next (and generalize in Remark 10.5).
$R$. Nevertheless, the Pontryagin product does not depend on this choice as we show next (and generalize in Remark 10.5).
Lemma 10.2
(1) The Pontryagin product
 $\star$ is independent of the choice of the monodromy reflection
$\star$ is independent of the choice of the monodromy reflection  $R$.
$R$.(2) Parallel-transport operators are isomorphisms of the Pontryagin rings.
(3) The unit with respect to
 $\star$ is
$\star$ is  $\rho _\tau (1)$ and is independent of the choice of
$\rho _\tau (1)$ and is independent of the choice of  $R$.
$R$.
Proof. (1) The statement is clear if ![]() $b_2(X)$ is odd. Assume that
$b_2(X)$ is odd. Assume that ![]() $b_2(X)$ is even. Let
$b_2(X)$ is even. Let ![]() $R'\in {\rm Mon}(X)$ be another monodromy reflection and let
$R'\in {\rm Mon}(X)$ be another monodromy reflection and let ![]() $\rho ':O(\widetilde {H}(X,{\mathbb {C}}))\rightarrow GL(H^*(X,{\mathbb {C}}))$ be the resulting representation. Let
$\rho ':O(\widetilde {H}(X,{\mathbb {C}}))\rightarrow GL(H^*(X,{\mathbb {C}}))$ be the resulting representation. Let ![]() $f,f'\in SO(\widetilde {H}(X,{\mathbb {C}}))$ be the elements satisfying
$f,f'\in SO(\widetilde {H}(X,{\mathbb {C}}))$ be the elements satisfying ![]() $\tau =f\widetilde {H}(R)=f'\widetilde {H}(R')$. Then
$\tau =f\widetilde {H}(R)=f'\widetilde {H}(R')$. Then ![]() $\rho _{f'}=\rho '_{f'}$, as the restrictions of
$\rho _{f'}=\rho '_{f'}$, as the restrictions of ![]() $\rho$ and
$\rho$ and ![]() $\rho '$ to
$\rho '$ to ![]() $SO(\widetilde {H}(X,{\mathbb {C}}))$ are equal. Now,
$SO(\widetilde {H}(X,{\mathbb {C}}))$ are equal. Now, ![]() $f'=f\widetilde {H}(R)\widetilde {H}(R')=f\widetilde {H}(RR')$. Thus,
$f'=f\widetilde {H}(R)\widetilde {H}(R')=f\widetilde {H}(RR')$. Thus,
Set ![]() $g:=R\rho _{\widetilde {H}(RR')}R'$. Then
$g:=R\rho _{\widetilde {H}(RR')}R'$. Then ![]() $\rho '_\tau =\rho _\tau g$, and
$\rho '_\tau =\rho _\tau g$, and ![]() $g$ is an automorphism of
$g$ is an automorphism of ![]() $H^*(X,{\mathbb {C}})$ with respect to cup product, since each of
$H^*(X,{\mathbb {C}})$ with respect to cup product, since each of ![]() $R$,
$R$, ![]() $\rho _{\widetilde {H}(RR')}$, and
$\rho _{\widetilde {H}(RR')}$, and ![]() $R'$ is. Furthermore,
$R'$ is. Furthermore, ![]() $\rho _\tau g\rho _\tau g=(\rho '_\tau )^2=id$, so
$\rho _\tau g\rho _\tau g=(\rho '_\tau )^2=id$, so ![]() $g\rho _\tau g=\rho _\tau$. Now compute
$g\rho _\tau g=\rho _\tau$. Now compute
(2) Let ![]() $f:H^*(X,{\mathbb {C}})\rightarrow H^*(Y,{\mathbb {C}})$ be a parallel-transport operator. We get the commutative diagram
$f:H^*(X,{\mathbb {C}})\rightarrow H^*(Y,{\mathbb {C}})$ be a parallel-transport operator. We get the commutative diagram

where the horizontal arrows are the integration of the infinitesimal LLV Lie algebras actions. Clearly, ![]() $\widetilde {H}(f)$ conjugates
$\widetilde {H}(f)$ conjugates ![]() $\tau$ to
$\tau$ to ![]() $\tau$. Parallel-transport operators conjugate a monodromy reflection to such, and so the representation
$\tau$. Parallel-transport operators conjugate a monodromy reflection to such, and so the representation ![]() $\rho$, given in (10.1), get conjugated via the pair
$\rho$, given in (10.1), get conjugated via the pair ![]() $f$ and
$f$ and ![]() $\widetilde {H}(f)$ to
$\widetilde {H}(f)$ to ![]() $\rho ':O(\widetilde {H}(Y,{\mathbb {C}}))\rightarrow GL(H^*(Y,{\mathbb {C}}))$, as in part (1), and so
$\rho ':O(\widetilde {H}(Y,{\mathbb {C}}))\rightarrow GL(H^*(Y,{\mathbb {C}}))$, as in part (1), and so ![]() $f$ conjugates
$f$ conjugates ![]() $\rho _\tau$ to
$\rho _\tau$ to ![]() $\rho '_\tau$. The statement of part (2) now follows from part (1).
$\rho '_\tau$. The statement of part (2) now follows from part (1).
(3) The unit of a ring is unique, and so ![]() $\rho _\tau (1)$ is independent of
$\rho _\tau (1)$ is independent of ![]() $R$, by part (1).
$R$, by part (1).
We calculate the unit explicitly next.
Lemma 10.3 The unit of ![]() $H^*(X,{\mathbb {Q}})$ with respect to the
$H^*(X,{\mathbb {Q}})$ with respect to the ![]() $\star$ product is
$\star$ product is ![]() $c_X[pt]/n!$, where
$c_X[pt]/n!$, where ![]() $\dim (X)=2n$ and
$\dim (X)=2n$ and ![]() $c_X$ is the Fujiki constant.
$c_X$ is the Fujiki constant.
Proof. Consider the ![]() $SO(\widetilde {H}(X,{\mathbb {Q}}))$-equivariant embedding
$SO(\widetilde {H}(X,{\mathbb {Q}}))$-equivariant embedding
given in (3.3), where ![]() $SO(\widetilde {H}(X,{\mathbb {Q}}))$ acts on
$SO(\widetilde {H}(X,{\mathbb {Q}}))$ acts on ![]() $SH^*(X,{\mathbb {Q}})$ via the representation
$SH^*(X,{\mathbb {Q}})$ via the representation ![]() $\rho$ integrating the infinitesimal LLV action and via the natural representation on
$\rho$ integrating the infinitesimal LLV action and via the natural representation on ![]() ${\rm Sym}^n(\widetilde {H}(X,{\mathbb {Q}}))$. If
${\rm Sym}^n(\widetilde {H}(X,{\mathbb {Q}}))$. If ![]() $b_2(X)$ is odd, then
$b_2(X)$ is odd, then ![]() $\tau$ belongs to
$\tau$ belongs to ![]() $SO(\widetilde {H}(X,{\mathbb {C}}))$. If
$SO(\widetilde {H}(X,{\mathbb {C}}))$. If ![]() $b_2(X)$ is even, then
$b_2(X)$ is even, then ![]() $X$ admits monodromy reflections, by assumptions, and
$X$ admits monodromy reflections, by assumptions, and ![]() $\Psi$ is equivariant with respect to those as well, and so
$\Psi$ is equivariant with respect to those as well, and so ![]() $\Psi$ is equivariant with respect to the
$\Psi$ is equivariant with respect to the ![]() $\rho _\tau$ action on its domain and the
$\rho _\tau$ action on its domain and the ![]() $\tau$ action of its codomain. The element
$\tau$ action of its codomain. The element ![]() $1$ belongs to
$1$ belongs to ![]() $SH^*(X,{\mathbb {C}})$ and
$SH^*(X,{\mathbb {C}})$ and ![]() $\Psi (1)=\alpha ^n/n!$, by [Reference TaelmanTae23, Proposition 3.5]. Now,
$\Psi (1)=\alpha ^n/n!$, by [Reference TaelmanTae23, Proposition 3.5]. Now, ![]() $\tau (\alpha )=\beta$ and so
$\tau (\alpha )=\beta$ and so ![]() $\Psi (\rho _\tau (1))=\rho _\tau (\Psi (1))=\beta ^n/n!=\Psi (c_X[pt]/n!)$, where the last equality follows from [Reference TaelmanTae23, Lemma 3.6]. Hence,
$\Psi (\rho _\tau (1))=\rho _\tau (\Psi (1))=\beta ^n/n!=\Psi (c_X[pt]/n!)$, where the last equality follows from [Reference TaelmanTae23, Lemma 3.6]. Hence, ![]() $\rho _\tau (1)=c_X[pt]/n!$.
$\rho _\tau (1)=c_X[pt]/n!$.
Let ![]() $\mu _t$ be the element of
$\mu _t$ be the element of ![]() $SO({\mathbb {C}}\alpha \oplus {\mathbb {C}}\beta )$, given by
$SO({\mathbb {C}}\alpha \oplus {\mathbb {C}}\beta )$, given by ![]() $\mu _t(\alpha )=t^{-1}\alpha$ and
$\mu _t(\alpha )=t^{-1}\alpha$ and ![]() $\mu _t(\beta )=t\beta$, and
$\mu _t(\beta )=t\beta$, and ![]() $\mu _t$ restricts to
$\mu _t$ restricts to ![]() $H^2(X,{\mathbb {C}})$ as the identity. Then
$H^2(X,{\mathbb {C}})$ as the identity. Then ![]() $\rho _{\mu _t}$ acts on
$\rho _{\mu _t}$ acts on ![]() $H^{2k}(X,{\mathbb {C}})[2n]$ via multiplication by
$H^{2k}(X,{\mathbb {C}})[2n]$ via multiplication by ![]() $t^k$.
$t^k$.
Lemma 10.4 Let ![]() $g$ be an element of
$g$ be an element of ![]() $O(\widetilde {H}(X,{\mathbb {C}}))$.
$O(\widetilde {H}(X,{\mathbb {C}}))$.
(1) If
 $ghg^{-1}=h$, then
$ghg^{-1}=h$, then  $g(\alpha )=t\alpha$, for some
$g(\alpha )=t\alpha$, for some  $t\in {\mathbb {C}}^\times$, and
$t\in {\mathbb {C}}^\times$, and  $\rho _{\mu _t g}$ is an automorphism of the cohomology ring
$\rho _{\mu _t g}$ is an automorphism of the cohomology ring  $H^*(X,{\mathbb {C}})$ with respect to the usual cup product.
$H^*(X,{\mathbb {C}})$ with respect to the usual cup product.(2) If
 $ghg^{-1}=-h$, then
$ghg^{-1}=-h$, then  $g(\alpha )=t^{-1}\beta$, for some
$g(\alpha )=t^{-1}\beta$, for some  $t\in {\mathbb {C}}^\times$, and
for all
$t\in {\mathbb {C}}^\times$, and
for all \[ \rho_{\mu_t g}(\gamma\cup\delta) = \rho_{\mu_t g}(\gamma)\star\rho_{\mu_t g}(\delta), \]
\[ \rho_{\mu_t g}(\gamma\cup\delta) = \rho_{\mu_t g}(\gamma)\star\rho_{\mu_t g}(\delta), \]
 $\gamma, \delta \in H^*(X,{\mathbb {C}})$.
$\gamma, \delta \in H^*(X,{\mathbb {C}})$.
Proof. (1) If ![]() $ghg^{-1}=h$ and
$ghg^{-1}=h$ and ![]() $g(\alpha )=t\alpha$, then
$g(\alpha )=t\alpha$, then ![]() $\mu _t g$ belongs to the factor
$\mu _t g$ belongs to the factor ![]() $OH^2(X,{\mathbb {C}})$ of the commutator of
$OH^2(X,{\mathbb {C}})$ of the commutator of ![]() $h$, and so
$h$, and so ![]() $\rho _{\mu _t g}$ acts by ring automorphisms.
$\rho _{\mu _t g}$ acts by ring automorphisms.
(2) If ![]() $ghg^{-1}=-h$ and
$ghg^{-1}=-h$ and ![]() $g(\alpha )=t^{-1}\beta$, then
$g(\alpha )=t^{-1}\beta$, then ![]() $f:=\tau \mu _t g$ commutes with
$f:=\tau \mu _t g$ commutes with ![]() $h$ and the second equality below follows from part (1):
$h$ and the second equality below follows from part (1):
Remark 10.5 Lemma 10.4(2) equivalently states that the same Pontryagin product can be defined in terms of any degree-reversing isometry ![]() $g\in O(\widetilde {H}(X,{\mathbb {Q}}))$, by
$g\in O(\widetilde {H}(X,{\mathbb {Q}}))$, by
10.2 The Pontryagin product for an IHSM of  $K3^{[n]}$ type
$K3^{[n]}$ type
Assume from now on that ![]() $X$ is of
$X$ is of ![]() $K3^{[n]}$ type. The following lemma states that the functor
$K3^{[n]}$ type. The following lemma states that the functor ![]() $\Theta _n$, given in (7.12), integrates the infinitesimal LLV Lie algebra action when restricted to automorphisms of determinant
$\Theta _n$, given in (7.12), integrates the infinitesimal LLV Lie algebra action when restricted to automorphisms of determinant ![]() $1$.
$1$.
Lemma 10.6 The restriction of ![]() $\Theta _n$ to the subgroup
$\Theta _n$ to the subgroup ![]() $S{\rm Aut}_{{\mathcal {G}}^{[1]}}(S,\epsilon )$, of elements of
$S{\rm Aut}_{{\mathcal {G}}^{[1]}}(S,\epsilon )$, of elements of ![]() ${\rm Aut}_{{\mathcal {G}}^{[1]}}(S,\epsilon )$ of determinant
${\rm Aut}_{{\mathcal {G}}^{[1]}}(S,\epsilon )$ of determinant ![]() $1$, is equal to the restriction of the composition of
$1$, is equal to the restriction of the composition of ![]() $\tilde {\iota }:SO(\widetilde {H}(S,{\mathbb {C}}))\rightarrow SO(\widetilde {H}(S^{[n]},{\mathbb {C}}))$, given in (7.5), with the representation
$\tilde {\iota }:SO(\widetilde {H}(S,{\mathbb {C}}))\rightarrow SO(\widetilde {H}(S^{[n]},{\mathbb {C}}))$, given in (7.5), with the representation ![]() $\rho$ given in (10.1).
$\rho$ given in (10.1).
Proof. The infinitesimal LLV action ![]() $\dot {\rho }$, given in (3.2), sends
$\dot {\rho }$, given in (3.2), sends ![]() $e_{\theta (\lambda )}\in {\mathfrak so}(\widetilde {H}(S^{[n]},{\mathbb {Q}}))$ to cup product with
$e_{\theta (\lambda )}\in {\mathfrak so}(\widetilde {H}(S^{[n]},{\mathbb {Q}}))$ to cup product with ![]() $\theta (\lambda )$, by the
$\theta (\lambda )$, by the ![]() ${\mathfrak so}(\widetilde {H}(S^{[n]},{\mathbb {Q}}))$-equivariance of
${\mathfrak so}(\widetilde {H}(S^{[n]},{\mathbb {Q}}))$-equivariance of ![]() $\Psi$ in (3.3). Thus, the equality
$\Psi$ in (3.3). Thus, the equality ![]() $\Theta _n(\phi )=\rho _{\tilde {\iota }(\phi )}$ holds, when
$\Theta _n(\phi )=\rho _{\tilde {\iota }(\phi )}$ holds, when ![]() $\phi$ is cup product with
$\phi$ is cup product with ![]() $\exp (e_\lambda )$,
$\exp (e_\lambda )$, ![]() $\lambda \in H^2(S,{\mathbb {Q}})$, by the definition of
$\lambda \in H^2(S,{\mathbb {Q}})$, by the definition of ![]() $\Theta _n$. The map
$\Theta _n$. The map ![]() $\Theta _n:{\rm Aut}_{{\mathcal {G}}^{[1]}}(S,\epsilon )\rightarrow {\rm Aut}_{{\mathcal {G}}^{[1]}}(S^{[n]},\epsilon ^{[n]})$ is induced by an algebraic map, due to its topological nature via Grothendieck–Riemann–Roch, and so extends to the Zariski closure
$\Theta _n:{\rm Aut}_{{\mathcal {G}}^{[1]}}(S,\epsilon )\rightarrow {\rm Aut}_{{\mathcal {G}}^{[1]}}(S^{[n]},\epsilon ^{[n]})$ is induced by an algebraic map, due to its topological nature via Grothendieck–Riemann–Roch, and so extends to the Zariski closure ![]() $O(\widetilde {H}(S,{\mathbb {C}}))$ of
$O(\widetilde {H}(S,{\mathbb {C}}))$ of ![]() ${\rm Aut}_{{\mathcal {G}}^{[1]}}(S,\epsilon )$. The statement thus reduces to the equality of the differentials of
${\rm Aut}_{{\mathcal {G}}^{[1]}}(S,\epsilon )$. The statement thus reduces to the equality of the differentials of ![]() $\Theta _n$ and
$\Theta _n$ and ![]() $\rho \circ \tilde {\iota }$. We already established the equality
$\rho \circ \tilde {\iota }$. We already established the equality ![]() $d\Theta _n(e_\lambda )=\dot {\rho }(d\tilde {\iota }(e_\lambda ))=\dot {\rho }(e_{\theta (\lambda )})$. We denote
$d\Theta _n(e_\lambda )=\dot {\rho }(d\tilde {\iota }(e_\lambda ))=\dot {\rho }(e_{\theta (\lambda )})$. We denote ![]() $\dot {\rho }(e_{\theta (\lambda )})$ by
$\dot {\rho }(e_{\theta (\lambda )})$ by ![]() $e_{\theta (\lambda )}$ as well, so that the latter equality becomes
$e_{\theta (\lambda )}$ as well, so that the latter equality becomes
Choose ![]() $(M,\epsilon ')$ and
$(M,\epsilon ')$ and ![]() $\phi \in {\rm Hom}_{{\mathcal {G}}^{[1]}}((S,\epsilon ),(M,\epsilon '))$, so that
$\phi \in {\rm Hom}_{{\mathcal {G}}^{[1]}}((S,\epsilon ),(M,\epsilon '))$, so that ![]() $\phi$ is degree reversing. We can choose, for example,
$\phi$ is degree reversing. We can choose, for example, ![]() $(M,\epsilon ')=(S,\epsilon )$ and
$(M,\epsilon ')=(S,\epsilon )$ and ![]() $\phi :=[ch({\mathcal {I}}_{\Delta })\sqrt {td_{S\times S}}]_*$, where
$\phi :=[ch({\mathcal {I}}_{\Delta })\sqrt {td_{S\times S}}]_*$, where ![]() ${\mathcal {I}}_{\Delta }$ is the ideal sheaf of the diagonal. Note that
${\mathcal {I}}_{\Delta }$ is the ideal sheaf of the diagonal. Note that ![]() $\phi =\widetilde {H}(\phi )$, as
$\phi =\widetilde {H}(\phi )$, as ![]() $H^*(S,{\mathbb {Q}})=\widetilde {H}(S,{\mathbb {Q}})$ and similarly for
$H^*(S,{\mathbb {Q}})=\widetilde {H}(S,{\mathbb {Q}})$ and similarly for ![]() $M$. Let
$M$. Let ![]() $t\in {\mathbb {Q}}$, so that
$t\in {\mathbb {Q}}$, so that ![]() $\phi (\beta )=t\alpha$. Let
$\phi (\beta )=t\alpha$. Let ![]() $\lambda \in H^2(S,{\mathbb {Q}})$ be an element with
$\lambda \in H^2(S,{\mathbb {Q}})$ be an element with ![]() $(\lambda,\lambda )\neq 0$. Then
$(\lambda,\lambda )\neq 0$. Then
by Lemma 1.6. Here ![]() $e_\lambda ^\vee$ is the dual Lefschetz operator with respect to the grading operator of the LLV algebra
$e_\lambda ^\vee$ is the dual Lefschetz operator with respect to the grading operator of the LLV algebra ![]() ${\mathfrak g}_S$ of
${\mathfrak g}_S$ of ![]() $S$. The morphism
$S$. The morphism ![]() $\widetilde {H}(\Theta _n(\phi ))$ is degree reversing as well, by Corollaries 7.3 and 7.4. Hence, so is
$\widetilde {H}(\Theta _n(\phi ))$ is degree reversing as well, by Corollaries 7.3 and 7.4. Hence, so is ![]() $\Theta _n(\phi )$, by Lemma 3.4. Say
$\Theta _n(\phi )$, by Lemma 3.4. Say ![]() $(\widetilde {H}(\Theta _n(\phi )))(\beta )=t'\alpha$. Then
$(\widetilde {H}(\Theta _n(\phi )))(\beta )=t'\alpha$. Then
by Lemma 1.6. Here ![]() $e_{\theta (\lambda )}^\vee$ is the dual Lefschetz operator with respect to the grading operator of the LLV algebra
$e_{\theta (\lambda )}^\vee$ is the dual Lefschetz operator with respect to the grading operator of the LLV algebra ![]() ${\mathfrak g}_{S^{[n]}}$ of
${\mathfrak g}_{S^{[n]}}$ of ![]() $S^{[n]}$ given in (3.1). Note that
$S^{[n]}$ given in (3.1). Note that ![]() $t'=\det (\phi )^{n+1}t$ and
$t'=\det (\phi )^{n+1}t$ and ![]() $\widetilde {H}(\Theta _n(\phi ))=\det (\phi )^{n+1}\tilde {\iota }_\phi,$ by Corollary 7.3. The second equality below follows (using also that
$\widetilde {H}(\Theta _n(\phi ))=\det (\phi )^{n+1}\tilde {\iota }_\phi,$ by Corollary 7.3. The second equality below follows (using also that ![]() $e_{\tilde {\iota }_\phi (\theta (\lambda ))}=e_{\theta (\phi (\lambda ))})$:
$e_{\tilde {\iota }_\phi (\theta (\lambda ))}=e_{\theta (\phi (\lambda ))})$:
Given a morphism ![]() $\phi \in {\rm Hom}_{{\mathcal {G}}^{[1]}}((S,\epsilon ),(M,\epsilon '))$, we have
$\phi \in {\rm Hom}_{{\mathcal {G}}^{[1]}}((S,\epsilon ),(M,\epsilon '))$, we have
since ![]() $\Theta _n(\phi \psi \phi ^{-1})=\Theta _n(\phi )\Theta _n(\psi )\Theta _n(\phi )^{-1}$. We conclude that
$\Theta _n(\phi \psi \phi ^{-1})=\Theta _n(\phi )\Theta _n(\psi )\Theta _n(\phi )^{-1}$. We conclude that
The left-hand side is ![]() $d\Theta _n\big ( ({t(\lambda,\lambda )}/{2})e_\lambda ^\vee \big )$, by (10.4). Hence,
$d\Theta _n\big ( ({t(\lambda,\lambda )}/{2})e_\lambda ^\vee \big )$, by (10.4). Hence, ![]() $d\Theta _n(e_\lambda ^\vee )=e_{\theta (\lambda )}^\vee$. Now
$d\Theta _n(e_\lambda ^\vee )=e_{\theta (\lambda )}^\vee$. Now ![]() $\dot {\rho }:{\mathfrak so}(\widetilde {H}(S^{[n]},{\mathbb {Q}}))\rightarrow {\mathfrak g}_{S^{[n]}}$ maps the grading operator of
$\dot {\rho }:{\mathfrak so}(\widetilde {H}(S^{[n]},{\mathbb {Q}}))\rightarrow {\mathfrak g}_{S^{[n]}}$ maps the grading operator of ![]() ${\mathfrak so}(\widetilde {H}(S^{[n]},{\mathbb {Q}}))$ to that of
${\mathfrak so}(\widetilde {H}(S^{[n]},{\mathbb {Q}}))$ to that of ![]() ${\mathfrak g}_{S^{[n]}}$ and the differential of
${\mathfrak g}_{S^{[n]}}$ and the differential of ![]() $\tilde {\iota }$ sends the grading operator of
$\tilde {\iota }$ sends the grading operator of ![]() ${\mathfrak g}_S$ to that of
${\mathfrak g}_S$ to that of ![]() ${\mathfrak so}(\widetilde {H}(S^{[n]},{\mathbb {Q}}))$. Hence, the differential of
${\mathfrak so}(\widetilde {H}(S^{[n]},{\mathbb {Q}}))$. Hence, the differential of ![]() $\rho \circ \tilde {\iota }$ sends
$\rho \circ \tilde {\iota }$ sends ![]() $e_\lambda ^\vee$ to
$e_\lambda ^\vee$ to ![]() $e_{\theta (\lambda )}^\vee$ and we get the equality
$e_{\theta (\lambda )}^\vee$ and we get the equality
The statement follows, since ![]() ${\mathfrak so}(H^*(S,{\mathbb {Q}}))$ is generated by the pairs
${\mathfrak so}(H^*(S,{\mathbb {Q}}))$ is generated by the pairs ![]() $(e_\lambda,e^\vee _\lambda )$, as
$(e_\lambda,e^\vee _\lambda )$, as ![]() $\lambda$ varies over elements of
$\lambda$ varies over elements of ![]() $H^2(S,{\mathbb {Q}})$ with
$H^2(S,{\mathbb {Q}})$ with ![]() $(\lambda,\lambda )\neq 0$.
$(\lambda,\lambda )\neq 0$.
Let ![]() ${\mathcal {R}}^{[n]}_{an}$ be the subgroupoid of
${\mathcal {R}}^{[n]}_{an}$ be the subgroupoid of ![]() ${\mathcal {G}}_{an}^{[n]}$ given in (1.6).
${\mathcal {G}}_{an}^{[n]}$ given in (1.6).
Proposition 10.7 The restriction of the functor ![]() $\widetilde {H}_0$ to the subgroupoid
$\widetilde {H}_0$ to the subgroupoid ![]() ${\mathcal {R}}^{[n]}_{an}$ remains full.
${\mathcal {R}}^{[n]}_{an}$ remains full.
Proof. It suffices to prove that all morphisms of ![]() ${\mathcal {G}}^{[n]}_{an}$, which were used in the proof of Theorem 1.4 to prove the fullness of
${\mathcal {G}}^{[n]}_{an}$, which were used in the proof of Theorem 1.4 to prove the fullness of ![]() $\widetilde {H}_0$, are already morphisms of
$\widetilde {H}_0$, are already morphisms of ![]() ${\mathcal {R}}^{[n]}_{an}$. Parallel-transport operators, which are Hodge isometries, are morphisms in
${\mathcal {R}}^{[n]}_{an}$. Parallel-transport operators, which are Hodge isometries, are morphisms in ![]() ${\mathcal {R}}^{[n]}_{an}$. The morphisms other than parallel-transport operators where all deformations of those that appear in Corollary 7.4, hence conjugates of those that appear in Corollary 7.4 via parallel-transport operators. It suffices to prove that the morphism
${\mathcal {R}}^{[n]}_{an}$. The morphisms other than parallel-transport operators where all deformations of those that appear in Corollary 7.4, hence conjugates of those that appear in Corollary 7.4 via parallel-transport operators. It suffices to prove that the morphism ![]() $\Theta _n(\varphi )$ of
$\Theta _n(\varphi )$ of ![]() ${\mathcal {G}}^{[n]}_{an}$ that appears in Corollary 7.4 belongs to
${\mathcal {G}}^{[n]}_{an}$ that appears in Corollary 7.4 belongs to ![]() ${\mathcal {R}}^{[n]}_{an}$, in other words, that
${\mathcal {R}}^{[n]}_{an}$, in other words, that ![]() $\mu _{\chi (\Theta _n(\varphi ))}\Theta _n(\varphi )$ conjugates the cup product of
$\mu _{\chi (\Theta _n(\varphi ))}\Theta _n(\varphi )$ conjugates the cup product of ![]() $H^*(S^{[n]},{\mathbb {Q}})$ to the Pontryagin product.
$H^*(S^{[n]},{\mathbb {Q}})$ to the Pontryagin product.
Let ![]() $f:H^*(S,{\mathbb {Z}})\rightarrow H^*(M,{\mathbb {Z}})$ be a parallel-transport operator. Then
$f:H^*(S,{\mathbb {Z}})\rightarrow H^*(M,{\mathbb {Z}})$ be a parallel-transport operator. Then ![]() $f\circ \varphi$ belongs to
$f\circ \varphi$ belongs to ![]() ${\rm Aut}_{{\mathcal {G}}^{[1]}}(M)$,
${\rm Aut}_{{\mathcal {G}}^{[1]}}(M)$, ![]() $\mu _{\chi (\Theta _n(f\circ \varphi ))}=\mu _{\chi (\Theta _n(\varphi ))}$ and
$\mu _{\chi (\Theta _n(f\circ \varphi ))}=\mu _{\chi (\Theta _n(\varphi ))}$ and ![]() $\mu _{\chi (\Theta _n(\varphi ))}\Theta _n(\varphi )$ conjugates the cup product of
$\mu _{\chi (\Theta _n(\varphi ))}\Theta _n(\varphi )$ conjugates the cup product of ![]() $H^*(M^{[n]},{\mathbb {Q}})$ to the Pontryagin product, if and only if
$H^*(M^{[n]},{\mathbb {Q}})$ to the Pontryagin product, if and only if ![]() $\mu _{\chi (\Theta _n(f\circ \varphi ))}\Theta _n(f\circ \varphi )$ does, by Lemma 10.2(2). Hence, it suffices to prove the statement of the Proposition for automorphisms in the image of
$\mu _{\chi (\Theta _n(f\circ \varphi ))}\Theta _n(f\circ \varphi )$ does, by Lemma 10.2(2). Hence, it suffices to prove the statement of the Proposition for automorphisms in the image of ![]() $\Theta _n$.
$\Theta _n$.
The restriction of ![]() $\Theta _n$ to the subgroup
$\Theta _n$ to the subgroup ![]() $S{\rm Aut}_{{\mathcal {G}}^{[1]}}(S,\epsilon )$ of elements of
$S{\rm Aut}_{{\mathcal {G}}^{[1]}}(S,\epsilon )$ of elements of ![]() ${\rm Aut}_{{\mathcal {G}}^{[1]}}(S,\epsilon )$ of determinant
${\rm Aut}_{{\mathcal {G}}^{[1]}}(S,\epsilon )$ of determinant ![]() $1$ is equal to the restriction of the composition of
$1$ is equal to the restriction of the composition of ![]() $\tilde {\iota }:SO(\widetilde {H}(S,{\mathbb {C}}))\rightarrow SO(\widetilde {H}(S^{[n]},{\mathbb {C}}))$ with the representation
$\tilde {\iota }:SO(\widetilde {H}(S,{\mathbb {C}}))\rightarrow SO(\widetilde {H}(S^{[n]},{\mathbb {C}}))$ with the representation ![]() $\rho$ given in (10.1), by Lemma 10.6. The two agree on the whole of
$\rho$ given in (10.1), by Lemma 10.6. The two agree on the whole of ![]() ${\rm Aut}_{{\mathcal {G}}^{[1]}}(S,\epsilon )$ if we choose the reflection
${\rm Aut}_{{\mathcal {G}}^{[1]}}(S,\epsilon )$ if we choose the reflection ![]() $R$ in the definition of
$R$ in the definition of ![]() $\rho$ to be the image of a monodromy reflection of
$\rho$ to be the image of a monodromy reflection of ![]() $S$. Hence, if
$S$. Hence, if ![]() $\varphi \in {\rm Aut}_{{\mathcal {G}}^{[1]}}(S,\epsilon )$ conjugates
$\varphi \in {\rm Aut}_{{\mathcal {G}}^{[1]}}(S,\epsilon )$ conjugates ![]() $h$ to
$h$ to ![]() $-h$, then
$-h$, then ![]() $\mu _{\chi (\Theta _n(\varphi ))}\Theta _n(\varphi )=\rho (\mu _{\chi (\varphi )}\varphi )$ conjugates the cup product to the Pontryagin product and if
$\mu _{\chi (\Theta _n(\varphi ))}\Theta _n(\varphi )=\rho (\mu _{\chi (\varphi )}\varphi )$ conjugates the cup product to the Pontryagin product and if ![]() $\varphi$ commutes with
$\varphi$ commutes with ![]() $h$, then
$h$, then ![]() $\mu _{\chi (\Theta _n(\varphi ))}\Theta _n(\varphi )$ is a ring automorphism with respect to the cup product, by Lemmas 10.2 and 10.4.
$\mu _{\chi (\Theta _n(\varphi ))}\Theta _n(\varphi )$ is a ring automorphism with respect to the cup product, by Lemmas 10.2 and 10.4.
Proof Proof of Corollary 1.10
Choose an IHSM ![]() $X$ and a twisted vector bundle
$X$ and a twisted vector bundle ![]() $E$ over
$E$ over ![]() $X\times Y$ as in Theorem 1.5. There exists a rational number
$X\times Y$ as in Theorem 1.5. There exists a rational number ![]() $t$, such that the isomorphism
$t$, such that the isomorphism ![]() $\phi :=\mu _t\circ [\kappa (E)\sqrt {td_{X\times Y}}]_*:H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ satisfies (1.7), by the proof of Proposition 10.7. Given classes
$\phi :=\mu _t\circ [\kappa (E)\sqrt {td_{X\times Y}}]_*:H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ satisfies (1.7), by the proof of Proposition 10.7. Given classes ![]() $\gamma _1, \gamma _2\in H^*(Y,{\mathbb {Q}})$, we thus have
$\gamma _1, \gamma _2\in H^*(Y,{\mathbb {Q}})$, we thus have
The isomorphism ![]() $\mu _t$ is algebraic, since the Lefschetz standard conjecture holds for
$\mu _t$ is algebraic, since the Lefschetz standard conjecture holds for ![]() $Y$, by [Reference Charles and MarkmanCM13], and so the Künneth factors of the diagonal in
$Y$, by [Reference Charles and MarkmanCM13], and so the Künneth factors of the diagonal in ![]() $H^i(Y,{\mathbb {Q}})\otimes H^{4n-i}(Y,{\mathbb {Q}})$,
$H^i(Y,{\mathbb {Q}})\otimes H^{4n-i}(Y,{\mathbb {Q}})$, ![]() $0\leq i\leq 4n$, are algebraic, by [Reference KleimanKle68, Proposition 1.4.4]. Hence, the isomorphism
$0\leq i\leq 4n$, are algebraic, by [Reference KleimanKle68, Proposition 1.4.4]. Hence, the isomorphism ![]() $\phi$ is induced by an algebraic correspondence. Now
$\phi$ is induced by an algebraic correspondence. Now ![]() $\phi ^{-1}:H^*(Y,{\mathbb {Q}})\rightarrow H^*(X,{\mathbb {Q}})$ is equal to
$\phi ^{-1}:H^*(Y,{\mathbb {Q}})\rightarrow H^*(X,{\mathbb {Q}})$ is equal to ![]() $[\kappa (E^*)\sqrt {td_{Y\times X}}]_*\circ \mu _{t^{-1}}$ and is algebraic as well. Denote by
$[\kappa (E^*)\sqrt {td_{Y\times X}}]_*\circ \mu _{t^{-1}}$ and is algebraic as well. Denote by ![]() $(\phi ^{-1})^t:H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ the isomorphism induce by the class in
$(\phi ^{-1})^t:H^*(X,{\mathbb {Q}})\rightarrow H^*(Y,{\mathbb {Q}})$ the isomorphism induce by the class in ![]() $H^*(X\times Y,{\mathbb {Q}})$, which is the transpose of the class in
$H^*(X\times Y,{\mathbb {Q}})$, which is the transpose of the class in ![]() $H^*(Y\times X,{\mathbb {Q}})$ inducing
$H^*(Y\times X,{\mathbb {Q}})$ inducing ![]() $\phi ^{-1}$. Then
$\phi ^{-1}$. Then ![]() $(\phi ^{-1})^t\times (\phi ^{-1})^t\times \phi : H^*(X^3,{\mathbb {Q}})\rightarrow H^*(Y^3,{\mathbb {Q}})$ is an algebraic correspondence taking the class
$(\phi ^{-1})^t\times (\phi ^{-1})^t\times \phi : H^*(X^3,{\mathbb {Q}})\rightarrow H^*(Y^3,{\mathbb {Q}})$ is an algebraic correspondence taking the class ![]() $[\Delta ]$ of the diagonal to an algebraic class
$[\Delta ]$ of the diagonal to an algebraic class ![]() ${\rm Pont}$ inducing the Pontryagin product. The latter statement is equivalent to the equality
${\rm Pont}$ inducing the Pontryagin product. The latter statement is equivalent to the equality
by (10.5). The above equation is verified as follows (let ![]() $a, b, c$ be classes in
$a, b, c$ be classes in ![]() $H^*(X,{\mathbb {Q}})$):
$H^*(X,{\mathbb {Q}})$):
 \begin{align*} &\phi\big(\pi_{3,*}\big( \pi_1^*[\phi^{-1}(\gamma_1)\cup a]\cup \pi_2^*[\phi^{-1}(\gamma_2)\cup b]\cup \pi_3^*c \big)\big)\\ &\quad=\bigg(\int_X\phi^{-1}(\gamma_1)\cup a\bigg) \bigg(\int_X\phi^{-1}(\gamma_2)\cup b\bigg)\phi(c)\\ &\quad= \bigg(\int_X\gamma_1\cup (\phi^{-1})^t(a)\bigg) \bigg(\int_X\gamma_2\cup (\phi^{-1})^t(b)\bigg)\phi(c)\\ &\quad= \pi_{3,*}\big( \pi_1^*(\gamma_1)\cup\pi_2^*(\gamma_2)\cup \big((\phi^{-1})^t\otimes (\phi^{-1})^t\otimes \phi \big)(\pi_1^*(a)\cup \pi_2^*(b)\cup \pi_3^*(c)) \big). \end{align*}
\begin{align*} &\phi\big(\pi_{3,*}\big( \pi_1^*[\phi^{-1}(\gamma_1)\cup a]\cup \pi_2^*[\phi^{-1}(\gamma_2)\cup b]\cup \pi_3^*c \big)\big)\\ &\quad=\bigg(\int_X\phi^{-1}(\gamma_1)\cup a\bigg) \bigg(\int_X\phi^{-1}(\gamma_2)\cup b\bigg)\phi(c)\\ &\quad= \bigg(\int_X\gamma_1\cup (\phi^{-1})^t(a)\bigg) \bigg(\int_X\gamma_2\cup (\phi^{-1})^t(b)\bigg)\phi(c)\\ &\quad= \pi_{3,*}\big( \pi_1^*(\gamma_1)\cup\pi_2^*(\gamma_2)\cup \big((\phi^{-1})^t\otimes (\phi^{-1})^t\otimes \phi \big)(\pi_1^*(a)\cup \pi_2^*(b)\cup \pi_3^*(c)) \big). \end{align*}
Finally, we observe that ![]() $[\kappa (E^*)\sqrt {td_{Y\times X}}]_*\circ \mu _{t^{-1}}=\mu _t\circ [\kappa (E^*)\sqrt {td_{Y\times X}}]_*,$ as
$[\kappa (E^*)\sqrt {td_{Y\times X}}]_*\circ \mu _{t^{-1}}=\mu _t\circ [\kappa (E^*)\sqrt {td_{Y\times X}}]_*,$ as ![]() $[\kappa (E^*)\sqrt {td_{Y\times X}}]_*$ is degree reversing, and
$[\kappa (E^*)\sqrt {td_{Y\times X}}]_*$ is degree reversing, and ![]() $\kappa (E^*)=\kappa (E)$, by Corollary 4.2. Hence,
$\kappa (E^*)=\kappa (E)$, by Corollary 4.2. Hence, ![]() $\phi = (\phi ^{-1})^t$.
$\phi = (\phi ^{-1})^t$.
Acknowledgements
This work was partially supported by a grant from the Simons Foundation (#427110). Part of this work was carried out while the author was visiting the Mathematics Institute at Bonn University. I thank Daniel Huybrechts for the invitation, his hospitality, and for stimulating conversations. I thank Georg Oberdieck for his comments on an earlier draft of this paper. I thank Chenyu Bai for pointing out the need for Lemma 5.3. I thank the referee for his careful reading and insightful comments.
Conflicts of Interest
None.