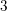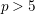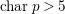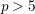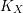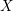1 Introduction
Lots of progress have been made recently on the log minimal model program for ![]() $3$-folds in characteristic
$3$-folds in characteristic ![]() $p>5$, see [Reference Birkar3, Reference Birkar and Waldron6, Reference Hacon and Xu12, Reference Waldron21]. One of the things that is not treated in these papers is the finiteness of the number of log minimal models. A partial answer was given in [Reference Birkar and Waldron6, Theorem 1.4]. Here we show that a stronger finiteness result (Theorem 1.2) analogous to [Reference Birkar, Cascini, Hacon and McKernan5, Corollary 1.1.5] holds on
$p>5$, see [Reference Birkar3, Reference Birkar and Waldron6, Reference Hacon and Xu12, Reference Waldron21]. One of the things that is not treated in these papers is the finiteness of the number of log minimal models. A partial answer was given in [Reference Birkar and Waldron6, Theorem 1.4]. Here we show that a stronger finiteness result (Theorem 1.2) analogous to [Reference Birkar, Cascini, Hacon and McKernan5, Corollary 1.1.5] holds on ![]() $3$-folds in
$3$-folds in ![]() $\operatorname{char}p>5$. We then give some applications of this result (Corollary 1.3).
$\operatorname{char}p>5$. We then give some applications of this result (Corollary 1.3).
On the second part of the paper we work with the nef and movable cone of curves and pseudo-effective divisors. First we verify that a famous theorem [Reference Boucksom, Demailly, Păun and Peternell7, Theorem 2.2] on the duality of strongly movable curves and pseudo-effective divisors hold in positive characteristic in arbitrary dimension (Theorem 1.4). We then give some applications of this result (Theorem 1.6 and Corollary 1.7). Finally we focus our attention to Batyrev’s conjecture on the structure of nef cone of curves.
Conjecture 1.1. [Reference Batyrev2, Conjecture 4.4]
Let ![]() $(X,\unicode[STIX]{x1D6E5})$ be a projective KLT pair. Then there are countably many
$(X,\unicode[STIX]{x1D6E5})$ be a projective KLT pair. Then there are countably many ![]() $(K_{X}+\unicode[STIX]{x1D6E5})$-negative movable curves
$(K_{X}+\unicode[STIX]{x1D6E5})$-negative movable curves ![]() $C_{i}$ such that
$C_{i}$ such that
The rays ![]() $\mathbb{R}_{{\geqslant}0}[C_{i}]$ only accumulate along the hyperplane
$\mathbb{R}_{{\geqslant}0}[C_{i}]$ only accumulate along the hyperplane ![]() $(K_{X}+\unicode[STIX]{x1D6E5})^{\bot }$.
$(K_{X}+\unicode[STIX]{x1D6E5})^{\bot }$.
This conjecture is one of the main outstanding conjecture in this direction. We prove a version of this conjecture on ![]() $3$-folds in
$3$-folds in ![]() $\operatorname{char}p>5$ (Theorem 1.8). We also give a proof of this conjecture in full generality over the field of complex numbers (Theorem 1.9). Batyrev proved this conjecture for terminal
$\operatorname{char}p>5$ (Theorem 1.8). We also give a proof of this conjecture in full generality over the field of complex numbers (Theorem 1.9). Batyrev proved this conjecture for terminal ![]() $3$-folds defined over
$3$-folds defined over ![]() $\mathbb{C}$. However, his proof contained an error which was later rectified by Araujo in [Reference Araujo1]. Using sophisticated tools from [Reference Birkar, Cascini, Hacon and McKernan5] she laid down a clear path toward the proof of the higher dimensional version of the conjecture. Her results were then sharpened later by Lehmann in [Reference Lehmann17] again using the tools from [Reference Birkar, Cascini, Hacon and McKernan5]. We follow the general strategy as in [Reference Lehmann17] in proving this conjecture in positive characteristic, and the finiteness of log minimal models (Theorem 1.2) becomes indispensable in this process.
$\mathbb{C}$. However, his proof contained an error which was later rectified by Araujo in [Reference Araujo1]. Using sophisticated tools from [Reference Birkar, Cascini, Hacon and McKernan5] she laid down a clear path toward the proof of the higher dimensional version of the conjecture. Her results were then sharpened later by Lehmann in [Reference Lehmann17] again using the tools from [Reference Birkar, Cascini, Hacon and McKernan5]. We follow the general strategy as in [Reference Lehmann17] in proving this conjecture in positive characteristic, and the finiteness of log minimal models (Theorem 1.2) becomes indispensable in this process.
The following theorem is the positive characteristic (![]() $\operatorname{char}p>5$) analog of [Reference Birkar, Cascini, Hacon and McKernan5, Corollary 1.1.5] on
$\operatorname{char}p>5$) analog of [Reference Birkar, Cascini, Hacon and McKernan5, Corollary 1.1.5] on ![]() $3$-folds. This result is interesting on its own and should be useful in the future.
$3$-folds. This result is interesting on its own and should be useful in the future.
Theorem 1.2. (Finiteness of log minimal models)
Let ![]() $\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective contraction between two normal projective varieties with
$\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective contraction between two normal projective varieties with ![]() $\operatorname{dim}X=3$ and
$\operatorname{dim}X=3$ and ![]() $\operatorname{char}p>5$. Let
$\operatorname{char}p>5$. Let ![]() $V$ be a finite dimensional affine subspace of
$V$ be a finite dimensional affine subspace of ![]() $\operatorname{WDiv}_{\mathbb{R}}(X)$ which is defined over the rationals. Suppose that there is a divisor
$\operatorname{WDiv}_{\mathbb{R}}(X)$ which is defined over the rationals. Suppose that there is a divisor ![]() $0\leqslant \unicode[STIX]{x1D6E5}_{0}\in V$ such that
$0\leqslant \unicode[STIX]{x1D6E5}_{0}\in V$ such that ![]() $K_{X}+\unicode[STIX]{x1D6E5}_{0}$ is KLT. Let
$K_{X}+\unicode[STIX]{x1D6E5}_{0}$ is KLT. Let ![]() $A$ be a general ample
$A$ be a general ample ![]() $\mathbb{Q}$-divisor over
$\mathbb{Q}$-divisor over ![]() $U$, which has no components in common with any element of
$U$, which has no components in common with any element of ![]() $V$. Then the following hold:
$V$. Then the following hold:
(1) There are finitely many birational contractions
 $\unicode[STIX]{x1D719}_{i}:X{\dashrightarrow}Y_{i}$ over
$\unicode[STIX]{x1D719}_{i}:X{\dashrightarrow}Y_{i}$ over  $U$,
$U$,  $1\leqslant i\leqslant m$ such that where each
$1\leqslant i\leqslant m$ such that where each $$\begin{eqnarray}{\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)=\mathop{\bigcup }_{i=1}^{m}{\mathcal{W}}_{i},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)=\mathop{\bigcup }_{i=1}^{m}{\mathcal{W}}_{i},\end{eqnarray}$$ ${\mathcal{W}}_{i}={\mathcal{W}}_{\unicode[STIX]{x1D719}_{i},A,\unicode[STIX]{x1D70B}}(V)$ is a rational polytope. Moreover, if
${\mathcal{W}}_{i}={\mathcal{W}}_{\unicode[STIX]{x1D719}_{i},A,\unicode[STIX]{x1D70B}}(V)$ is a rational polytope. Moreover, if  $\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ is a log minimal model of
$\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ is a log minimal model of  $(X,\unicode[STIX]{x1D6E5})$ over
$(X,\unicode[STIX]{x1D6E5})$ over  $U$, for some
$U$, for some  $\unicode[STIX]{x1D6E5}\in {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$, then
$\unicode[STIX]{x1D6E5}\in {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$, then  $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}_{i}$, for some
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}_{i}$, for some  $1\leqslant i\leqslant m$.
$1\leqslant i\leqslant m$.(2) There are finitely many rational maps
 $\unicode[STIX]{x1D713}_{j}:X{\dashrightarrow}Z_{j}$ over
$\unicode[STIX]{x1D713}_{j}:X{\dashrightarrow}Z_{j}$ over  $U$,
$U$,  $1\leqslant j\leqslant n$ which partition
$1\leqslant j\leqslant n$ which partition  ${\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$ into the subsets
${\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$ into the subsets  ${\mathcal{A}}_{j}={\mathcal{A}}_{\unicode[STIX]{x1D713}_{j},A,\unicode[STIX]{x1D70B}}(V)$.
${\mathcal{A}}_{j}={\mathcal{A}}_{\unicode[STIX]{x1D713}_{j},A,\unicode[STIX]{x1D70B}}(V)$.(3) For every
 $1\leqslant i\leqslant m$ there is a
$1\leqslant i\leqslant m$ there is a  $1\leqslant j\leqslant n$ and a morphism
$1\leqslant j\leqslant n$ and a morphism  $f_{i,j}:Y_{i}\rightarrow Z_{j}$ such that
$f_{i,j}:Y_{i}\rightarrow Z_{j}$ such that  ${\mathcal{W}}_{i}\subseteq \bar{{\mathcal{A}}_{j}}$.
${\mathcal{W}}_{i}\subseteq \bar{{\mathcal{A}}_{j}}$.(4) In particular,
 ${\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$ is a rational polytope and each
${\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$ is a rational polytope and each  $\bar{{\mathcal{A}}_{j}}$ is a finite union of rational polytopes.
$\bar{{\mathcal{A}}_{j}}$ is a finite union of rational polytopes.
A direct consequence of Theorem 1.2 is that the ring of adjoint divisors is finitely generated:
Corollary 1.3. Let ![]() $\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective contraction between two normal projective varieties with
$\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective contraction between two normal projective varieties with ![]() $\operatorname{dim}X=3$ and
$\operatorname{dim}X=3$ and ![]() $\operatorname{char}p>5$. Fix an ample
$\operatorname{char}p>5$. Fix an ample![]() $/U$
$/U$![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() $A\geqslant 0$ on
$A\geqslant 0$ on ![]() $X$. Let
$X$. Let ![]() $\unicode[STIX]{x1D6E5}_{i}=A+B_{i}$ for some
$\unicode[STIX]{x1D6E5}_{i}=A+B_{i}$ for some ![]() $\mathbb{Q}$-divisors
$\mathbb{Q}$-divisors ![]() $B_{1},B_{2},\ldots ,B_{k}\geqslant 0$. Assume that
$B_{1},B_{2},\ldots ,B_{k}\geqslant 0$. Assume that ![]() $D_{i}=K_{X}+\unicode[STIX]{x1D6E5}_{i}$ is DLT and
$D_{i}=K_{X}+\unicode[STIX]{x1D6E5}_{i}$ is DLT and ![]() $\mathbb{Q}$-Cartier for all
$\mathbb{Q}$-Cartier for all ![]() $1\leqslant i\leqslant k$. Then the adjoint ring
$1\leqslant i\leqslant k$. Then the adjoint ring
is a finitely generated ![]() ${\mathcal{O}}_{U}$-algebra.
${\mathcal{O}}_{U}$-algebra.
Next we verify that a positive characteristic analog of [Reference Boucksom, Demailly, Păun and Peternell7, Theorem 2.2] holds in arbitrary dimension.
Theorem 1.4. Let ![]() $X$ be a projective variety defined over an algebraically closed field of arbitrary characteristic. Then the cone
$X$ be a projective variety defined over an algebraically closed field of arbitrary characteristic. Then the cone ![]() $\overline{\operatorname{Eff}}(X)$ of pseudo-effective divisors is dual to the cone
$\overline{\operatorname{Eff}}(X)$ of pseudo-effective divisors is dual to the cone ![]() $\overline{\operatorname{SNM}}(X)$ of strongly movable curves.
$\overline{\operatorname{SNM}}(X)$ of strongly movable curves.
Remark 1.5. We note that this theorem is believed to be known among the experts, while the actual proof in full generality (the ![]() $\operatorname{char}p>0$ version) never appeared in any literature as far as we know. In the case when
$\operatorname{char}p>0$ version) never appeared in any literature as far as we know. In the case when ![]() $X$ is a smooth projective variety in characteristic
$X$ is a smooth projective variety in characteristic ![]() $p>0$, the proof of Theorem 1.4 is outlined by Fulger and Lehmann in [Reference Fulger and Lehmann11, Theorem 2.22] based on the proof of [Reference Boucksom, Demailly, Păun and Peternell7]. So if we assume the existence of resolution of singularities in characteristic
$p>0$, the proof of Theorem 1.4 is outlined by Fulger and Lehmann in [Reference Fulger and Lehmann11, Theorem 2.22] based on the proof of [Reference Boucksom, Demailly, Păun and Peternell7]. So if we assume the existence of resolution of singularities in characteristic ![]() $p>0$, then Theorem 1.4 will be a formal consequence of [Reference Fulger and Lehmann11, Theorem 2.22]. In particular, when
$p>0$, then Theorem 1.4 will be a formal consequence of [Reference Fulger and Lehmann11, Theorem 2.22]. In particular, when ![]() $\operatorname{dim}X\leqslant 3$, Theorem 1.4 follows from Fulger and Lehmann’s result.
$\operatorname{dim}X\leqslant 3$, Theorem 1.4 follows from Fulger and Lehmann’s result.
In our proof we verify that the proof presented in [Reference Lazarsfeld16, Theorem 11.4.19] (which does not assume resolution of singularities) works in positive characteristic with the help of Takagi’s Fujita approximation theorem [Reference Takagi19] in characteristic ![]() $p>0$.
$p>0$.
As an application of Theorem 1.4 we give a criterion for the pseudo-effectiveness of ![]() $K_{X}$ in terms of the existence of an algebraic family of rational curves on
$K_{X}$ in terms of the existence of an algebraic family of rational curves on ![]() $X$. This answers partially a question of Campana [Reference Campana8, Question 12.1] in arbitrary characteristic.
$X$. This answers partially a question of Campana [Reference Campana8, Question 12.1] in arbitrary characteristic.
Theorem 1.6. Let ![]() $X$ be a smooth projective variety defined over an algebraically closed field of arbitrary characteristic. Then
$X$ be a smooth projective variety defined over an algebraically closed field of arbitrary characteristic. Then ![]() $K_{X}$ is not pseudo-effective if and only if there exists an algebraic family of
$K_{X}$ is not pseudo-effective if and only if there exists an algebraic family of ![]() $K_{X}$-negative rational curves covering a dense subset of
$K_{X}$-negative rational curves covering a dense subset of ![]() $X$.
$X$.
An immediate corollary of this result is the following sufficient condition for uniruledness in positive characteristic.
Corollary 1.7. Let ![]() $X$ be a smooth projective variety defined over an algebraically closed field of arbitrary characteristic. If
$X$ be a smooth projective variety defined over an algebraically closed field of arbitrary characteristic. If ![]() $K_{X}$ is not pseudo-effective, then
$K_{X}$ is not pseudo-effective, then ![]() $X$ is uniruled.
$X$ is uniruled.
Note that the converse of this statement is true in ![]() $\operatorname{char}0$ and false in
$\operatorname{char}0$ and false in ![]() $\operatorname{char}p>0$.
$\operatorname{char}p>0$.
We then prove a version of Batyrev’s conjecture on the structure of nef cone of curves on ![]() $3$-folds in characteristic
$3$-folds in characteristic ![]() $p>5$.
$p>5$.
Theorem 1.8. Let ![]() $(X,\unicode[STIX]{x1D6E5})$ be a projective DLT pair of dimension
$(X,\unicode[STIX]{x1D6E5})$ be a projective DLT pair of dimension ![]() $3$ in char
$3$ in char ![]() $p>5$. Then there are countably many
$p>5$. Then there are countably many ![]() $(K_{X}+\unicode[STIX]{x1D6E5})$-negative movable curves
$(K_{X}+\unicode[STIX]{x1D6E5})$-negative movable curves ![]() $C_{i}$ such that
$C_{i}$ such that
The rays ![]() $\mathbb{R}_{{\geqslant}0}[C_{i}]$ only accumulate along the hyperplanes which support both
$\mathbb{R}_{{\geqslant}0}[C_{i}]$ only accumulate along the hyperplanes which support both ![]() $\overline{\operatorname{NM}}(X)$ and
$\overline{\operatorname{NM}}(X)$ and ![]() $\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}$.
$\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}$.
Finally we prove the finiteness of coextremal rays of the nef cone of curves for varieties of arbitrary dimension over ![]() $\mathbb{C}$. We use Kollár’s effective base-point free theorem and the boundedness of
$\mathbb{C}$. We use Kollár’s effective base-point free theorem and the boundedness of ![]() $\unicode[STIX]{x1D700}$-log canonical log Fano varieties (formerly known as the “BAB Conjecture”) recently proved by Birkar [Reference Birkar4]. This gives a complete proof of Batyrev’s conjecture in full generality in characteristic
$\unicode[STIX]{x1D700}$-log canonical log Fano varieties (formerly known as the “BAB Conjecture”) recently proved by Birkar [Reference Birkar4]. This gives a complete proof of Batyrev’s conjecture in full generality in characteristic ![]() $0$. We note that the finiteness of coextremal rays was proved in [Reference Araujo1] for terminal
$0$. We note that the finiteness of coextremal rays was proved in [Reference Araujo1] for terminal ![]() $3$-folds over
$3$-folds over ![]() $\mathbb{C}$, and a weaker version of it is also proved in [Reference Lehmann17] on arbitrary dimensions over
$\mathbb{C}$, and a weaker version of it is also proved in [Reference Lehmann17] on arbitrary dimensions over ![]() $\mathbb{C}$.
$\mathbb{C}$.
Theorem 1.9. Let ![]() $(X,\unicode[STIX]{x1D6E5}\geqslant 0)$ be a projective KLT pair over
$(X,\unicode[STIX]{x1D6E5}\geqslant 0)$ be a projective KLT pair over ![]() $\mathbb{C}$.
$\mathbb{C}$.
(1) There are countably many
 $(K_{X}+\unicode[STIX]{x1D6E5})$-negative movable curves
$(K_{X}+\unicode[STIX]{x1D6E5})$-negative movable curves  $C_{i}$ such that
$C_{i}$ such that  $$\begin{eqnarray}\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+\overline{\operatorname{NM}}(X)=\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+\sum \mathbb{R}_{{\geqslant}0}[C_{i}].\end{eqnarray}$$
$$\begin{eqnarray}\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+\overline{\operatorname{NM}}(X)=\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+\sum \mathbb{R}_{{\geqslant}0}[C_{i}].\end{eqnarray}$$(2) For any ample
 $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $H\geqslant 0$
$H\geqslant 0$ $$\begin{eqnarray}\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+\overline{\operatorname{NM}}(X)=\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}+H\geqslant 0}+\mathop{\sum }_{i=1}^{N}\mathbb{R}_{{\geqslant}0}[C_{i}].\end{eqnarray}$$
$$\begin{eqnarray}\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+\overline{\operatorname{NM}}(X)=\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}+H\geqslant 0}+\mathop{\sum }_{i=1}^{N}\mathbb{R}_{{\geqslant}0}[C_{i}].\end{eqnarray}$$
Some remarks about the paper. In writing this paper we have tried to give as much detail as possible even if the arguments are very similar to the characteristic ![]() $0$ case. This is for convenience, future reference, and to avoid any unpleasant surprises having to do with positive characteristic. The paper is organized in the following manner: 1.1 and 1.2 are proved in Section 4; 1.3, 1.5 and 1.6 are in Section 5; 1.7 is in Section 6, and finally we prove 1.8 in Section 7. In Sections 4 and 6 we work over a field of
$0$ case. This is for convenience, future reference, and to avoid any unpleasant surprises having to do with positive characteristic. The paper is organized in the following manner: 1.1 and 1.2 are proved in Section 4; 1.3, 1.5 and 1.6 are in Section 5; 1.7 is in Section 6, and finally we prove 1.8 in Section 7. In Sections 4 and 6 we work over a field of ![]() $\operatorname{char}p>5$, in Section 5 we work over fields of arbitrary characteristic, and in Section 7 we work in
$\operatorname{char}p>5$, in Section 5 we work over fields of arbitrary characteristic, and in Section 7 we work in ![]() $\operatorname{char}0$.
$\operatorname{char}0$.
2 Preliminaries
We work with ![]() $\mathbb{R}$-Cartier divisors and use standard notations and terminologies from [Reference Kollár and Mori14]. We abbreviate Kawamata log terminal (resp. purely log terminal, divisorially log terminal, and log canonical) as KLT (resp. PLT, DLT and LC). By abuse of language we also say that
$\mathbb{R}$-Cartier divisors and use standard notations and terminologies from [Reference Kollár and Mori14]. We abbreviate Kawamata log terminal (resp. purely log terminal, divisorially log terminal, and log canonical) as KLT (resp. PLT, DLT and LC). By abuse of language we also say that ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ is KLT (resp. PLT, DLT and LC). A birational map
$K_{X}+\unicode[STIX]{x1D6E5}$ is KLT (resp. PLT, DLT and LC). A birational map ![]() $\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ is called a birational contraction if
$\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ is called a birational contraction if ![]() $\unicode[STIX]{x1D719}$ does not extract any divisor, that is,
$\unicode[STIX]{x1D719}$ does not extract any divisor, that is, ![]() $\unicode[STIX]{x1D719}^{-1}:Y{\dashrightarrow}X$ does not contract any divisor. A projective morphism
$\unicode[STIX]{x1D719}^{-1}:Y{\dashrightarrow}X$ does not contract any divisor. A projective morphism ![]() $\unicode[STIX]{x1D70B}:X\rightarrow U$ is called a projective contraction if
$\unicode[STIX]{x1D70B}:X\rightarrow U$ is called a projective contraction if ![]() $f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{U}$. Throughout the whole paper we assume that our ground field
$f_{\ast }{\mathcal{O}}_{X}={\mathcal{O}}_{U}$. Throughout the whole paper we assume that our ground field ![]() $k$ is algebraically closed.
$k$ is algebraically closed.
Definition 2.1. Let ![]() $\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ be a birational contraction of normal quasiprojective varieties. Let
$\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ be a birational contraction of normal quasiprojective varieties. Let ![]() $D$ be a
$D$ be a ![]() $\mathbb{R}$-Cartier divisor on
$\mathbb{R}$-Cartier divisor on ![]() $X$ such that
$X$ such that ![]() $D^{\prime }=\unicode[STIX]{x1D719}_{\ast }D$ is also
$D^{\prime }=\unicode[STIX]{x1D719}_{\ast }D$ is also ![]() $\mathbb{R}$-Cartier. We say
$\mathbb{R}$-Cartier. We say ![]() $\unicode[STIX]{x1D719}$ is
$\unicode[STIX]{x1D719}$ is ![]() $D$-non-positive (respectively
$D$-non-positive (respectively ![]() $D$-negative) if for some common resolution
$D$-negative) if for some common resolution ![]() $p:W\rightarrow X$ and
$p:W\rightarrow X$ and ![]() $q:W\rightarrow Y$, we can write
$q:W\rightarrow Y$, we can write
where ![]() $E\geqslant 0$ is
$E\geqslant 0$ is ![]() $q$-exceptional (respectively
$q$-exceptional (respectively ![]() $E\geqslant 0$ is
$E\geqslant 0$ is ![]() $q$-exceptional and the support of
$q$-exceptional and the support of ![]() $E$ contains the strict transform of the
$E$ contains the strict transform of the ![]() $\unicode[STIX]{x1D719}$-exceptional divisors).
$\unicode[STIX]{x1D719}$-exceptional divisors).
Definition 2.2. Let ![]() $\unicode[STIX]{x1D70B}\,:\,X\,\rightarrow \,U$ be a projective morphism between normal quasiprojective varieties. Suppose that
$\unicode[STIX]{x1D70B}\,:\,X\,\rightarrow \,U$ be a projective morphism between normal quasiprojective varieties. Suppose that ![]() $K_{X}\,+\,\unicode[STIX]{x1D6E5}$ is LC and
$K_{X}\,+\,\unicode[STIX]{x1D6E5}$ is LC and ![]() $\unicode[STIX]{x1D719}\,:\,X{\dashrightarrow}Y$ is a birational contraction of normal quasiprojective varieties over
$\unicode[STIX]{x1D719}\,:\,X{\dashrightarrow}Y$ is a birational contraction of normal quasiprojective varieties over ![]() $U$ and
$U$ and ![]() $Y$ is projective over
$Y$ is projective over ![]() $U$. Set
$U$. Set ![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}$.
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}$.
(1) Y is a weak log canonical model for
 $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over  $U$ if
$U$ if  $\unicode[STIX]{x1D719}$ is
$\unicode[STIX]{x1D719}$ is  $(K_{X}+\unicode[STIX]{x1D6E5})$-non-positive and
$(K_{X}+\unicode[STIX]{x1D6E5})$-non-positive and  $K_{Y}+\unicode[STIX]{x1D6E4}$ is nef over
$K_{Y}+\unicode[STIX]{x1D6E4}$ is nef over  $U$.
$U$.(2)
 $Y$ is a log minimal model for
$Y$ is a log minimal model for  $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over  $U$ if
$U$ if  $\unicode[STIX]{x1D719}$ is
$\unicode[STIX]{x1D719}$ is  $(K_{X}+\unicode[STIX]{x1D6E5})$-negative,
$(K_{X}+\unicode[STIX]{x1D6E5})$-negative,  $K_{Y}+\unicode[STIX]{x1D6E4}$ is DLT and nef over
$K_{Y}+\unicode[STIX]{x1D6E4}$ is DLT and nef over  $U$, and
$U$, and  $Y$ is
$Y$ is  $\mathbb{Q}$-factorial.
$\mathbb{Q}$-factorial.
Remark 2.3. Note that our definition of log minimal model is same as the log terminal model in [Reference Birkar, Cascini, Hacon and McKernan5, Definition 3.6.7].
Definition 2.4. Let ![]() $\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective morphism of normal quasiprojective varieties and let
$\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective morphism of normal quasiprojective varieties and let ![]() $D$ be an
$D$ be an ![]() $\mathbb{R}$-Cartier divisor on
$\mathbb{R}$-Cartier divisor on ![]() $X$.
$X$.
(1) We say that a birational contraction
 $f:X{\dashrightarrow}Y$ over
$f:X{\dashrightarrow}Y$ over  $U$ is a semi-ample model of
$U$ is a semi-ample model of  $D$ over
$D$ over  $U$ if
$U$ if  $f$ is
$f$ is  $D$-non-positive,
$D$-non-positive,  $Y$ is normal and projective over
$Y$ is normal and projective over  $U$ and
$U$ and  $H=f_{\ast }D$ is semi-ample over
$H=f_{\ast }D$ is semi-ample over  $U$.
$U$.(2) We say that a rational map
 $g:X{\dashrightarrow}Z$ over
$g:X{\dashrightarrow}Z$ over  $U$ is the ample model for
$U$ is the ample model for  $D$ over
$D$ over  $U$ if
$U$ if  $Z$ is normal and projective over
$Z$ is normal and projective over  $U$ and there is an ample divisor
$U$ and there is an ample divisor  $H$ over
$H$ over  $U$ on
$U$ on  $Z$ such that if
$Z$ such that if  $p:W\rightarrow X$ and
$p:W\rightarrow X$ and  $q:W\rightarrow Z$ resolve
$q:W\rightarrow Z$ resolve  $g$, then
$g$, then  $q$ is a contraction morphism and we may write
$q$ is a contraction morphism and we may write  $p^{\ast }D{\sim}_{\mathbb{R},U}q^{\ast }H+E$, where
$p^{\ast }D{\sim}_{\mathbb{R},U}q^{\ast }H+E$, where  $E\geqslant 0$ and for every
$E\geqslant 0$ and for every  $B\in |p^{\ast }D/U|_{\mathbb{R}}$, then
$B\in |p^{\ast }D/U|_{\mathbb{R}}$, then  $B\geqslant E$.
$B\geqslant E$.
Definition 2.5. Let ![]() $\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective morphism between two normal quasiprojective varieties. Let
$\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective morphism between two normal quasiprojective varieties. Let ![]() $V$ be a finite dimensional affine subspace of the real vector space
$V$ be a finite dimensional affine subspace of the real vector space ![]() $\operatorname{WDiv}_{\mathbb{R}}(X)$ of Weil divisors of
$\operatorname{WDiv}_{\mathbb{R}}(X)$ of Weil divisors of ![]() $X$. Fix an
$X$. Fix an ![]() $\mathbb{R}$-divisor
$\mathbb{R}$-divisor ![]() $A\geqslant 0$ and define
$A\geqslant 0$ and define
 $$\begin{eqnarray}\displaystyle & \displaystyle V_{A}=\{\unicode[STIX]{x1D6E5}:\unicode[STIX]{x1D6E5}=A+B,B\in V\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle {\mathcal{L}}_{A}(V)=\{\unicode[STIX]{x1D6E5}=A+B\in V_{A}:K_{X}+\unicode[STIX]{x1D6E5}\text{ is LC and }B\geqslant 0\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)=\{\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{A}(V):K_{X}+\unicode[STIX]{x1D6E5}\text{ is pseudo-effective over }U\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle {\mathcal{N}}_{A,\unicode[STIX]{x1D70B}}(V)=\{\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{A}(V):K_{X}+\unicode[STIX]{x1D6E5}\text{ is nef over }U\}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle V_{A}=\{\unicode[STIX]{x1D6E5}:\unicode[STIX]{x1D6E5}=A+B,B\in V\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle {\mathcal{L}}_{A}(V)=\{\unicode[STIX]{x1D6E5}=A+B\in V_{A}:K_{X}+\unicode[STIX]{x1D6E5}\text{ is LC and }B\geqslant 0\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)=\{\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{A}(V):K_{X}+\unicode[STIX]{x1D6E5}\text{ is pseudo-effective over }U\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle {\mathcal{N}}_{A,\unicode[STIX]{x1D70B}}(V)=\{\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{A}(V):K_{X}+\unicode[STIX]{x1D6E5}\text{ is nef over }U\}. & \displaystyle \nonumber\end{eqnarray}$$ Given a birational contraction ![]() $\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ over
$\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ over ![]() $U$, define
$U$, define
and given a rational map ![]() $\unicode[STIX]{x1D713}:X{\dashrightarrow}Z$ over
$\unicode[STIX]{x1D713}:X{\dashrightarrow}Z$ over ![]() $U$, define
$U$, define
3 Tanaka’s Bertini-type theorem
Following is a generalization of Tanaka’s result on Bertini-type theorems in positive characteristic [Reference Tanaka20, Theorem 1]. The proof presented here is suggested by Tanaka.
Theorem 3.1. Fix ![]() $\mathbb{K}\in \{\mathbb{Q},\mathbb{R}\}$. Let
$\mathbb{K}\in \{\mathbb{Q},\mathbb{R}\}$. Let ![]() $X$ be a projective variety over a field
$X$ be a projective variety over a field ![]() $k$ containing an infinite perfect subfield
$k$ containing an infinite perfect subfield ![]() $k_{0}$ of characteristic
$k_{0}$ of characteristic ![]() $p>0$. We assume that log resolution exists. Let
$p>0$. We assume that log resolution exists. Let ![]() $D$ be a semi-ample
$D$ be a semi-ample ![]() $\mathbb{K}$-Cartier
$\mathbb{K}$-Cartier ![]() $\mathbb{K}$-divisor on
$\mathbb{K}$-divisor on ![]() $X$ and
$X$ and ![]() $Z_{1},Z_{2},\ldots ,Z_{l}$ are finitely many closed subsets of
$Z_{1},Z_{2},\ldots ,Z_{l}$ are finitely many closed subsets of ![]() $X$. Then the following hold:
$X$. Then the following hold:
(1) If
 $(X,\unicode[STIX]{x1D6E5}_{1}\geqslant 0),(X,\unicode[STIX]{x1D6E5}_{2}\geqslant 0),\ldots ,(X,\unicode[STIX]{x1D6E5}_{m}\geqslant 0)$ are all KLT pairs, then there exists an effective
$(X,\unicode[STIX]{x1D6E5}_{1}\geqslant 0),(X,\unicode[STIX]{x1D6E5}_{2}\geqslant 0),\ldots ,(X,\unicode[STIX]{x1D6E5}_{m}\geqslant 0)$ are all KLT pairs, then there exists an effective  $\mathbb{K}$-Carter
$\mathbb{K}$-Carter  $\mathbb{K}$-divisor
$\mathbb{K}$-divisor  $0\leqslant D^{\prime }{\sim}_{\mathbb{K}}D$ not containing any
$0\leqslant D^{\prime }{\sim}_{\mathbb{K}}D$ not containing any  $Z_{j},1\leqslant j\leqslant l$ in its support such that
$Z_{j},1\leqslant j\leqslant l$ in its support such that  $(X,\unicode[STIX]{x1D6E5}_{1}+D^{\prime }),(X,\unicode[STIX]{x1D6E5}_{2}+D^{\prime }),\ldots ,(X,\unicode[STIX]{x1D6E5}_{m}+D^{\prime })$ are all KLT.
$(X,\unicode[STIX]{x1D6E5}_{1}+D^{\prime }),(X,\unicode[STIX]{x1D6E5}_{2}+D^{\prime }),\ldots ,(X,\unicode[STIX]{x1D6E5}_{m}+D^{\prime })$ are all KLT.(2) If
 $(X,\unicode[STIX]{x1D6E5}_{1}\geqslant 0),(X,\unicode[STIX]{x1D6E5}_{2}\geqslant 0),\ldots ,(X,\unicode[STIX]{x1D6E5}_{m}\geqslant 0)$ are all LC pairs, then there exists an effective
$(X,\unicode[STIX]{x1D6E5}_{1}\geqslant 0),(X,\unicode[STIX]{x1D6E5}_{2}\geqslant 0),\ldots ,(X,\unicode[STIX]{x1D6E5}_{m}\geqslant 0)$ are all LC pairs, then there exists an effective  $\mathbb{K}$-Carter
$\mathbb{K}$-Carter  $\mathbb{K}$-divisor
$\mathbb{K}$-divisor  $0\leqslant D^{\prime }{\sim}_{\mathbb{K}}D$ not containing any
$0\leqslant D^{\prime }{\sim}_{\mathbb{K}}D$ not containing any  $Z_{j},1\leqslant j\leqslant l$ in its support such that
$Z_{j},1\leqslant j\leqslant l$ in its support such that  $(X,\unicode[STIX]{x1D6E5}_{1}+D^{\prime }),(X,\unicode[STIX]{x1D6E5}_{2}+D^{\prime }),\ldots ,(X,\unicode[STIX]{x1D6E5}_{m}+D^{\prime })$ are all LC.
$(X,\unicode[STIX]{x1D6E5}_{1}+D^{\prime }),(X,\unicode[STIX]{x1D6E5}_{2}+D^{\prime }),\ldots ,(X,\unicode[STIX]{x1D6E5}_{m}+D^{\prime })$ are all LC.
Proof. Let ![]() $f:Y\rightarrow X$ be a log resolution of the pairs
$f:Y\rightarrow X$ be a log resolution of the pairs ![]() $(X,\unicode[STIX]{x1D6E5}_{i}\geqslant 0)$ for all
$(X,\unicode[STIX]{x1D6E5}_{i}\geqslant 0)$ for all ![]() $i=1,2,\ldots ,m$ and
$i=1,2,\ldots ,m$ and
where ![]() $\unicode[STIX]{x1D6E4}_{i}\geqslant 0$ and
$\unicode[STIX]{x1D6E4}_{i}\geqslant 0$ and ![]() $F_{i}\geqslant 0$ do not share any common component and
$F_{i}\geqslant 0$ do not share any common component and ![]() $f_{\ast }\unicode[STIX]{x1D6E4}_{i}=\unicode[STIX]{x1D6E5}_{i}$ and
$f_{\ast }\unicode[STIX]{x1D6E4}_{i}=\unicode[STIX]{x1D6E5}_{i}$ and ![]() $f_{\ast }F_{i}=0$, for all
$f_{\ast }F_{i}=0$, for all ![]() $i=1,2,\ldots ,m$.
$i=1,2,\ldots ,m$.
First we deal with the log canonical case. Define a divisor ![]() $\unicode[STIX]{x1D6E5}_{Y}$ on
$\unicode[STIX]{x1D6E5}_{Y}$ on ![]() $Y$ as
$Y$ as ![]() $\unicode[STIX]{x1D6E5}_{Y}:=(f_{\ast }^{-1}(\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2}+\cdots +\unicode[STIX]{x1D6E5}_{m}))_{\text{red}}+E$, where
$\unicode[STIX]{x1D6E5}_{Y}:=(f_{\ast }^{-1}(\unicode[STIX]{x1D6E5}_{1}+\unicode[STIX]{x1D6E5}_{2}+\cdots +\unicode[STIX]{x1D6E5}_{m}))_{\text{red}}+E$, where ![]() $E$ is the reduced
$E$ is the reduced ![]() $f$-exceptional divisor with
$f$-exceptional divisor with ![]() $\operatorname{Supp}E=\operatorname{Ex}(f)$. Then
$\operatorname{Supp}E=\operatorname{Ex}(f)$. Then ![]() $(Y,\unicode[STIX]{x1D6E5}_{Y}\geqslant 0)$ is a LC pair. By [Reference Tanaka20, Theorem 1] and its proof it follows that there exists an effective
$(Y,\unicode[STIX]{x1D6E5}_{Y}\geqslant 0)$ is a LC pair. By [Reference Tanaka20, Theorem 1] and its proof it follows that there exists an effective ![]() $\mathbb{K}$-divisor
$\mathbb{K}$-divisor ![]() $0\leqslant D^{\prime }{\sim}_{\mathbb{K}}D$ not containing any
$0\leqslant D^{\prime }{\sim}_{\mathbb{K}}D$ not containing any ![]() $Z_{j},1\leqslant j\leqslant l$ in its support such that
$Z_{j},1\leqslant j\leqslant l$ in its support such that ![]() $(Y,\unicode[STIX]{x1D6E5}_{Y}+f^{\ast }D^{\prime })$ is LC. From (3.1) we see that
$(Y,\unicode[STIX]{x1D6E5}_{Y}+f^{\ast }D^{\prime })$ is LC. From (3.1) we see that ![]() $\unicode[STIX]{x1D6E4}_{i}+f^{\ast }D^{\prime }\leqslant \unicode[STIX]{x1D6E5}_{Y}$ and thus
$\unicode[STIX]{x1D6E4}_{i}+f^{\ast }D^{\prime }\leqslant \unicode[STIX]{x1D6E5}_{Y}$ and thus ![]() $(Y,\unicode[STIX]{x1D6E4}_{i}+f^{\ast }D^{\prime })$ is LC, for all
$(Y,\unicode[STIX]{x1D6E4}_{i}+f^{\ast }D^{\prime })$ is LC, for all ![]() $i=1,2,\ldots ,m$. It then follows that
$i=1,2,\ldots ,m$. It then follows that ![]() $(X,\unicode[STIX]{x1D6E5}_{i}+D^{\prime })$ is LC for all
$(X,\unicode[STIX]{x1D6E5}_{i}+D^{\prime })$ is LC for all ![]() $i=1,2,\ldots ,m$.
$i=1,2,\ldots ,m$.
We now work with the KLT case. The divisor ![]() $mD$ is semi-ample
$mD$ is semi-ample ![]() $\mathbb{K}$-Cartier
$\mathbb{K}$-Cartier ![]() $\mathbb{K}$-divisor on
$\mathbb{K}$-divisor on ![]() $X$. Then by the log canonical case there exists an effective
$X$. Then by the log canonical case there exists an effective ![]() $\mathbb{K}$-divisor
$\mathbb{K}$-divisor ![]() $0\leqslant D^{\prime \prime }{\sim}_{\mathbb{K}}mD$ not containing any
$0\leqslant D^{\prime \prime }{\sim}_{\mathbb{K}}mD$ not containing any ![]() $Z_{j},1\leqslant j\leqslant l$ in its support such that
$Z_{j},1\leqslant j\leqslant l$ in its support such that ![]() $(X,\unicode[STIX]{x1D6E5}_{i}+D^{\prime \prime })$ is LC for all
$(X,\unicode[STIX]{x1D6E5}_{i}+D^{\prime \prime })$ is LC for all ![]() $i=1,2,\ldots ,m$. Set
$i=1,2,\ldots ,m$. Set ![]() $D^{\prime }:=(1/m)D^{\prime \prime }{\sim}_{\mathbb{K}}D$. We claim that
$D^{\prime }:=(1/m)D^{\prime \prime }{\sim}_{\mathbb{K}}D$. We claim that ![]() $(X,\unicode[STIX]{x1D6E5}_{i}+D^{\prime })$ is KLT for all
$(X,\unicode[STIX]{x1D6E5}_{i}+D^{\prime })$ is KLT for all ![]() $i=1,2,\ldots ,m$. Since
$i=1,2,\ldots ,m$. Since ![]() $(X,\unicode[STIX]{x1D6E5}_{i})$ is KLT, if
$(X,\unicode[STIX]{x1D6E5}_{i})$ is KLT, if ![]() $(X,\unicode[STIX]{x1D6E5}_{i}+D^{\prime })$ is not KLT then this will implies that
$(X,\unicode[STIX]{x1D6E5}_{i}+D^{\prime })$ is not KLT then this will implies that ![]() $(X,\unicode[STIX]{x1D6E5}_{i}+D^{\prime \prime })$ is not LC (for
$(X,\unicode[STIX]{x1D6E5}_{i}+D^{\prime \prime })$ is not LC (for ![]() $m\geqslant 2$), a contradiction. Therefore,
$m\geqslant 2$), a contradiction. Therefore, ![]() $(X,\unicode[STIX]{x1D6E5}_{i}+D^{\prime })$ is KLT for all
$(X,\unicode[STIX]{x1D6E5}_{i}+D^{\prime })$ is KLT for all ![]() $i=1,2,\ldots ,m$.◻
$i=1,2,\ldots ,m$.◻
4 Finiteness of log minimal models
In this section, we prove the finiteness of log minimal models, namely Theorem 1.2. The ideas and techniques used here are based on the paper [Reference Birkar, Cascini, Hacon and McKernan5].
Lemma 4.1. Let ![]() $\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective morphism of normal projective varieties with
$\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective morphism of normal projective varieties with ![]() $\operatorname{dim}X=3$ and
$\operatorname{dim}X=3$ and ![]() $\operatorname{char}p>5$. Suppose that
$\operatorname{char}p>5$. Suppose that ![]() $(X,\unicode[STIX]{x1D6E5})$ is a KLT pair, where
$(X,\unicode[STIX]{x1D6E5})$ is a KLT pair, where ![]() $\unicode[STIX]{x1D6E5}$ is big over
$\unicode[STIX]{x1D6E5}$ is big over ![]() $U$.
$U$.
If ![]() $\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ is a weak log canonical model of
$\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ is a weak log canonical model of ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over ![]() $U$, then
$U$, then
(1)
 $\unicode[STIX]{x1D719}$ is a semi-ample model over
$\unicode[STIX]{x1D719}$ is a semi-ample model over  $U$.
$U$.(2) the ample model
 $\unicode[STIX]{x1D713}:X{\dashrightarrow}Z$ of
$\unicode[STIX]{x1D713}:X{\dashrightarrow}Z$ of  $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over  $U$ exists, and
$U$ exists, and(3) there is a projective contraction
 $h:Y\rightarrow Z$ such that
$h:Y\rightarrow Z$ such that  $K_{Y}+\unicode[STIX]{x1D6E4}{\sim}_{\mathbb{R},U}h^{\ast }H$, for some ample
$K_{Y}+\unicode[STIX]{x1D6E4}{\sim}_{\mathbb{R},U}h^{\ast }H$, for some ample  $\mathbb{R}$-divisor
$\mathbb{R}$-divisor  $H$ over
$H$ over  $U$, where
$U$, where  $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}$.
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}$.
Proof. Since ![]() $K_{Y}+\unicode[STIX]{x1D6E4}$ is KLT and
$K_{Y}+\unicode[STIX]{x1D6E4}$ is KLT and ![]() $\unicode[STIX]{x1D6E4}$ is big, it follows from [Reference Birkar and Waldron6, Theorem 1.2] that
$\unicode[STIX]{x1D6E4}$ is big, it follows from [Reference Birkar and Waldron6, Theorem 1.2] that ![]() $K_{Y}+\unicode[STIX]{x1D6E4}$ is semi-ample. Part
$K_{Y}+\unicode[STIX]{x1D6E4}$ is semi-ample. Part ![]() $(2)$ and
$(2)$ and ![]() $(3)$ then follow from [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.6.6(3)].◻
$(3)$ then follow from [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.6.6(3)].◻
Lemma 4.2. Let ![]() $(X,\unicode[STIX]{x1D6E5}\,\geqslant \,0)$ be a
$(X,\unicode[STIX]{x1D6E5}\,\geqslant \,0)$ be a ![]() $3$-fold projective DLT pair in
$3$-fold projective DLT pair in ![]() $\operatorname{char}p\,>\,5$. Then there exists a small birational morphism
$\operatorname{char}p\,>\,5$. Then there exists a small birational morphism ![]() $\unicode[STIX]{x1D70B}:Y\rightarrow X$ from a
$\unicode[STIX]{x1D70B}:Y\rightarrow X$ from a ![]() $\mathbb{Q}$-factorial normal projective
$\mathbb{Q}$-factorial normal projective ![]() $3$-fold
$3$-fold ![]() $Y$ such that
$Y$ such that
and ![]() $(Y,\unicode[STIX]{x1D6E5}_{Y}\geqslant 0)$ is DLT.
$(Y,\unicode[STIX]{x1D6E5}_{Y}\geqslant 0)$ is DLT.
Proof. Since ![]() $(X,\unicode[STIX]{x1D6E5})$ is DLT, there exists a log resolution
$(X,\unicode[STIX]{x1D6E5})$ is DLT, there exists a log resolution ![]() $f:X^{\prime }\rightarrow X$ of
$f:X^{\prime }\rightarrow X$ of ![]() $(X,\unicode[STIX]{x1D6E5})$ such that
$(X,\unicode[STIX]{x1D6E5})$ such that ![]() $a(E_{i},X,\unicode[STIX]{x1D6E5})>-1$ for every
$a(E_{i},X,\unicode[STIX]{x1D6E5})>-1$ for every ![]() $f$-exceptional divisor
$f$-exceptional divisor ![]() $E_{i}$. We can write
$E_{i}$. We can write
where ![]() $\unicode[STIX]{x1D6E4}\geqslant 0$ and
$\unicode[STIX]{x1D6E4}\geqslant 0$ and ![]() $E\geqslant 0$ do not share any common component, and
$E\geqslant 0$ do not share any common component, and ![]() $f_{\ast }\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E5},f_{\ast }E=0$.
$f_{\ast }\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E5},f_{\ast }E=0$.
Let ![]() $F\geqslant 0$ be a reduced divisor with
$F\geqslant 0$ be a reduced divisor with ![]() $\operatorname{Supp}F=\operatorname{Ex}(f)$. Then
$\operatorname{Supp}F=\operatorname{Ex}(f)$. Then ![]() $(X^{\prime },\unicode[STIX]{x1D6E4}+\unicode[STIX]{x1D700}F)$ is DLT for
$(X^{\prime },\unicode[STIX]{x1D6E4}+\unicode[STIX]{x1D700}F)$ is DLT for ![]() $0<\unicode[STIX]{x1D700}\ll 1$. Furthermore, we have
$0<\unicode[STIX]{x1D700}\ll 1$. Furthermore, we have
By [Reference Waldron21, Corollary 1.8] we can run a terminating ![]() $(K_{X^{\prime }}+\unicode[STIX]{x1D6E4}+\unicode[STIX]{x1D700}F)$-MMP over
$(K_{X^{\prime }}+\unicode[STIX]{x1D6E4}+\unicode[STIX]{x1D700}F)$-MMP over ![]() $X$. Let
$X$. Let ![]() $\unicode[STIX]{x1D719}:X^{\prime }{\dashrightarrow}Y$ be the corresponding minimal model over
$\unicode[STIX]{x1D719}:X^{\prime }{\dashrightarrow}Y$ be the corresponding minimal model over ![]() $X$, that is,
$X$, that is, ![]() $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D719}_{\ast }F$ is nef over
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D719}_{\ast }F$ is nef over ![]() $X$, where
$X$, where ![]() $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D719}_{\ast }F=\unicode[STIX]{x1D719}_{\ast }(K_{X^{\prime }}+\unicode[STIX]{x1D6E4}+\unicode[STIX]{x1D700}F)$. It is easy to see from the Negativity lemma that
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D719}_{\ast }F=\unicode[STIX]{x1D719}_{\ast }(K_{X^{\prime }}+\unicode[STIX]{x1D6E4}+\unicode[STIX]{x1D700}F)$. It is easy to see from the Negativity lemma that ![]() $\unicode[STIX]{x1D719}$ contracts all
$\unicode[STIX]{x1D719}$ contracts all ![]() $f$-exceptional divisors, that is,
$f$-exceptional divisors, that is, ![]() $\unicode[STIX]{x1D719}_{\ast }F=0$; in particular, if
$\unicode[STIX]{x1D719}_{\ast }F=0$; in particular, if ![]() $\unicode[STIX]{x1D70B}:Y\rightarrow X$ is the structure morphism, then
$\unicode[STIX]{x1D70B}:Y\rightarrow X$ is the structure morphism, then ![]() $\unicode[STIX]{x1D70B}$ is a small birational morphism,
$\unicode[STIX]{x1D70B}$ is a small birational morphism, ![]() $Y$ is
$Y$ is ![]() $\mathbb{Q}$-factorial,
$\mathbb{Q}$-factorial, ![]() $(Y,\unicode[STIX]{x1D6E5}_{Y}\geqslant 0)$ is DLT and
$(Y,\unicode[STIX]{x1D6E5}_{Y}\geqslant 0)$ is DLT and
Remark 4.3. In the proof of the following results we use [Reference Birkar, Cascini, Hacon and McKernan5, Lemmas 3.6.12, 3.7.2, 3.7.3, 3.7.4 and 3.7.5]. Proofs of these lemmas depend on the Bertini’s theorem for base-point free linear system in characteristic ![]() $0$. However, their proofs use Bertini’s theorem in one specific way, namely, given an ample
$0$. However, their proofs use Bertini’s theorem in one specific way, namely, given an ample![]() $/U$
$/U$![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() $A\geqslant 0$ and finitely many LC pairs
$A\geqslant 0$ and finitely many LC pairs ![]() $(X,\unicode[STIX]{x1D6E5}_{i}\geqslant 0),i=1,2,\ldots ,m$, there exists an effective divisor
$(X,\unicode[STIX]{x1D6E5}_{i}\geqslant 0),i=1,2,\ldots ,m$, there exists an effective divisor ![]() $0\leqslant A^{\prime }{\sim}_{\mathbb{Q},U}A$ such that
$0\leqslant A^{\prime }{\sim}_{\mathbb{Q},U}A$ such that ![]() $(X,\unicode[STIX]{x1D6E5}_{i}+A^{\prime })$ is LC for all
$(X,\unicode[STIX]{x1D6E5}_{i}+A^{\prime })$ is LC for all ![]() $i=1,2,\ldots ,m$. We note that in the following results in characteristic
$i=1,2,\ldots ,m$. We note that in the following results in characteristic ![]() $p>0$ our set up is:
$p>0$ our set up is: ![]() $\unicode[STIX]{x1D70B}:X\rightarrow U$ is a projective morphism and
$\unicode[STIX]{x1D70B}:X\rightarrow U$ is a projective morphism and ![]() $X$ and
$X$ and ![]() $U$ are both projective varieties. So for an ample
$U$ are both projective varieties. So for an ample![]() $/U$
$/U$![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() $A\geqslant 0$ there exists an effective divisor
$A\geqslant 0$ there exists an effective divisor ![]() $0\leqslant A^{\prime }=A+l\unicode[STIX]{x1D70B}^{\ast }H{\sim}_{\mathbb{Q},U}A,l\gg 0$ such that
$0\leqslant A^{\prime }=A+l\unicode[STIX]{x1D70B}^{\ast }H{\sim}_{\mathbb{Q},U}A,l\gg 0$ such that ![]() $(X,\unicode[STIX]{x1D6E5}_{i}+A^{\prime })$ is LC for all
$(X,\unicode[STIX]{x1D6E5}_{i}+A^{\prime })$ is LC for all ![]() $i$ by Theorem 3.1, where
$i$ by Theorem 3.1, where ![]() $H$ is an ample divisor on
$H$ is an ample divisor on ![]() $U$. In particular, the proofs of those lemmas from [Reference Birkar, Cascini, Hacon and McKernan5] hold in our settings. In the following Lemma 4.4 we give a sketch of the proof of [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.7.4] in our settings explaining the use of Theorem 3.1 in place of Bertini’s theorem.
$U$. In particular, the proofs of those lemmas from [Reference Birkar, Cascini, Hacon and McKernan5] hold in our settings. In the following Lemma 4.4 we give a sketch of the proof of [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.7.4] in our settings explaining the use of Theorem 3.1 in place of Bertini’s theorem.
Lemma 4.4. Let ![]() $\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective morphism between two normal projective varieties. Assume that log resolution exists. Let
$\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective morphism between two normal projective varieties. Assume that log resolution exists. Let ![]() $V$ be a finite dimensional affine subspace of
$V$ be a finite dimensional affine subspace of ![]() $\operatorname{WDiv}_{\mathbb{R}}(X)$, which is defined over the rationals, and let
$\operatorname{WDiv}_{\mathbb{R}}(X)$, which is defined over the rationals, and let ![]() $A$ be a general ample
$A$ be a general ample ![]() $\mathbb{Q}$-divisor over
$\mathbb{Q}$-divisor over ![]() $U$. Let
$U$. Let ![]() $S$ be a sum of prime divisors. Suppose that there is a DLT pair
$S$ be a sum of prime divisors. Suppose that there is a DLT pair ![]() $(X,\unicode[STIX]{x1D6E5}_{0})$, where
$(X,\unicode[STIX]{x1D6E5}_{0})$, where ![]() $S=\lfloor \unicode[STIX]{x1D6E5}_{0}\rfloor$, and let
$S=\lfloor \unicode[STIX]{x1D6E5}_{0}\rfloor$, and let ![]() $G\geqslant 0$ be any divisor whose support does not contain any LC centers of
$G\geqslant 0$ be any divisor whose support does not contain any LC centers of ![]() $(X,\unicode[STIX]{x1D6E5}_{0})$.
$(X,\unicode[STIX]{x1D6E5}_{0})$.
Then we may find a general ample ![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() $A^{\prime }\geqslant 0$ over
$A^{\prime }\geqslant 0$ over ![]() $U$, an affine subspace
$U$, an affine subspace ![]() $V^{\prime }$ of
$V^{\prime }$ of ![]() $\operatorname{WDiv}_{\mathbb{R}}(X)$, which is defined over the rationals, and a rational affine linear isomorphism
$\operatorname{WDiv}_{\mathbb{R}}(X)$, which is defined over the rationals, and a rational affine linear isomorphism
so that:
(1)
 $L$ preserves
$L$ preserves  $\mathbb{Q}$-linear equivalence over
$\mathbb{Q}$-linear equivalence over  $U$;
$U$;(2)
 $L({\mathcal{L}}_{S+A}(V))$ is contained in the interior of
$L({\mathcal{L}}_{S+A}(V))$ is contained in the interior of  ${\mathcal{L}}_{S+A^{\prime }}(V^{\prime })$;
${\mathcal{L}}_{S+A^{\prime }}(V^{\prime })$;(3) for any
 $\unicode[STIX]{x1D6E5}\in L({\mathcal{L}}_{S+A}(V))$,
$\unicode[STIX]{x1D6E5}\in L({\mathcal{L}}_{S+A}(V))$,  $K_{X}+\unicode[STIX]{x1D6E5}$ is DLT and
$K_{X}+\unicode[STIX]{x1D6E5}$ is DLT and  $\lfloor \unicode[STIX]{x1D6E5}\rfloor =S$; and
$\lfloor \unicode[STIX]{x1D6E5}\rfloor =S$; and(4) for any
 $\unicode[STIX]{x1D6E5}\in L({\mathcal{L}}_{S+A}(V))$, the support of
$\unicode[STIX]{x1D6E5}\in L({\mathcal{L}}_{S+A}(V))$, the support of  $\unicode[STIX]{x1D6E5}$ contains the support of
$\unicode[STIX]{x1D6E5}$ contains the support of  $G$.
$G$.
Sketch of the proof.
We only explain the part where Bertini’s theorem is used in the proof of [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.7.4], which is basically the second paragraph in [Reference Birkar, Cascini, Hacon and McKernan5, page 436]. All other arguments in the rest of the proof of [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.7.4] holds in our settings here without any change.
We basically show that we can choose ample divisors ![]() $A_{i}$ and
$A_{i}$ and ![]() $A^{\prime }$ as in the proof of [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.7.4] such that
$A^{\prime }$ as in the proof of [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.7.4] such that ![]() $(X,\unicode[STIX]{x1D6E5}+A^{\prime }-A)$ is LC,
$(X,\unicode[STIX]{x1D6E5}+A^{\prime }-A)$ is LC, ![]() $(X,\unicode[STIX]{x1D6E5}+4/3A_{i}+A^{\prime }-A)$ is LC for all
$(X,\unicode[STIX]{x1D6E5}+4/3A_{i}+A^{\prime }-A)$ is LC for all ![]() $1\leqslant i\leqslant l$ and for all
$1\leqslant i\leqslant l$ and for all ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{S+A}(V)$, and
$\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{S+A}(V)$, and ![]() $(X,A^{\prime }+\unicode[STIX]{x1D6E5}_{0})$ is DLT.
$(X,A^{\prime }+\unicode[STIX]{x1D6E5}_{0})$ is DLT.
To that end, let ![]() $\unicode[STIX]{x1D6E4}_{1},\unicode[STIX]{x1D6E4}_{2},\ldots ,\unicode[STIX]{x1D6E4}_{m}$ be the vertices of the rational polytope
$\unicode[STIX]{x1D6E4}_{1},\unicode[STIX]{x1D6E4}_{2},\ldots ,\unicode[STIX]{x1D6E4}_{m}$ be the vertices of the rational polytope ![]() ${\mathcal{L}}_{S+A}(V)$. Since
${\mathcal{L}}_{S+A}(V)$. Since ![]() $(X,\unicode[STIX]{x1D6E4}_{i})$ is LC for all
$(X,\unicode[STIX]{x1D6E4}_{i})$ is LC for all ![]() $1\leqslant j\leqslant m$ and
$1\leqslant j\leqslant m$ and ![]() $(X,\unicode[STIX]{x1D6E5}_{0})$ is DLT, by Theorem 3.1 there exists a divisor
$(X,\unicode[STIX]{x1D6E5}_{0})$ is DLT, by Theorem 3.1 there exists a divisor ![]() $0\leqslant A^{\prime \prime }{\sim}_{\mathbb{Q}}A$ such that
$0\leqslant A^{\prime \prime }{\sim}_{\mathbb{Q}}A$ such that ![]() $(X,\unicode[STIX]{x1D6E4}_{j}+A^{\prime \prime })$ is LC for all
$(X,\unicode[STIX]{x1D6E4}_{j}+A^{\prime \prime })$ is LC for all ![]() $1\leqslant j\leqslant m$ and the support of
$1\leqslant j\leqslant m$ and the support of ![]() $A^{\prime \prime }$ does not contain any LC center of
$A^{\prime \prime }$ does not contain any LC center of ![]() $(X,\unicode[STIX]{x1D6E5}_{0})$. Set
$(X,\unicode[STIX]{x1D6E5}_{0})$. Set ![]() $A^{\prime }=\unicode[STIX]{x1D700}A^{\prime \prime }$ for a rational number
$A^{\prime }=\unicode[STIX]{x1D700}A^{\prime \prime }$ for a rational number ![]() $\unicode[STIX]{x1D700}\in (0,1/4]$. For
$\unicode[STIX]{x1D700}\in (0,1/4]$. For ![]() $0<\unicode[STIX]{x1D700}\ll 1/4$ we see that
$0<\unicode[STIX]{x1D700}\ll 1/4$ we see that ![]() $(X,\unicode[STIX]{x1D6E4}_{j}+A^{\prime })$ is LC for all
$(X,\unicode[STIX]{x1D6E4}_{j}+A^{\prime })$ is LC for all ![]() $1\leqslant j\leqslant m$ and
$1\leqslant j\leqslant m$ and ![]() $(X,\unicode[STIX]{x1D6E5}_{0}+A^{\prime })$ is DLT. Furthermore, since
$(X,\unicode[STIX]{x1D6E5}_{0}+A^{\prime })$ is DLT. Furthermore, since ![]() $A_{i}$’s are general ample
$A_{i}$’s are general ample ![]() $\mathbb{Q}$-divisors and
$\mathbb{Q}$-divisors and ![]() $0<\unicode[STIX]{x1D700}\ll 1/4$, it again follows from Theorem 3.1 that
$0<\unicode[STIX]{x1D700}\ll 1/4$, it again follows from Theorem 3.1 that ![]() $(X,\unicode[STIX]{x1D6E4}_{j}+4/3A_{i}+A^{\prime })$ is LC for all
$(X,\unicode[STIX]{x1D6E4}_{j}+4/3A_{i}+A^{\prime })$ is LC for all ![]() $1\leqslant j\leqslant m$ and
$1\leqslant j\leqslant m$ and ![]() $1\leqslant i\leqslant l$. Now for any
$1\leqslant i\leqslant l$. Now for any ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{S+A}(V)$ we can write
$\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{S+A}(V)$ we can write ![]() $\unicode[STIX]{x1D6E5}=\sum _{j=1}^{m}\unicode[STIX]{x1D706}_{j}\unicode[STIX]{x1D6E4}_{j}$ for some
$\unicode[STIX]{x1D6E5}=\sum _{j=1}^{m}\unicode[STIX]{x1D706}_{j}\unicode[STIX]{x1D6E4}_{j}$ for some ![]() $\unicode[STIX]{x1D706}_{j}\geqslant 0$ such that
$\unicode[STIX]{x1D706}_{j}\geqslant 0$ such that ![]() $\sum _{j=1}^{m}\unicode[STIX]{x1D706}_{j}=1$. It is easy to see that convex sum of finitely many LC divisors are LC. It then follows that
$\sum _{j=1}^{m}\unicode[STIX]{x1D706}_{j}=1$. It is easy to see that convex sum of finitely many LC divisors are LC. It then follows that ![]() $(X,\unicode[STIX]{x1D6E5}+A^{\prime })$ and
$(X,\unicode[STIX]{x1D6E5}+A^{\prime })$ and ![]() $(X,\unicode[STIX]{x1D6E5}+4/3A_{i}+A^{\prime })$ are both LC for all
$(X,\unicode[STIX]{x1D6E5}+4/3A_{i}+A^{\prime })$ are both LC for all ![]() $1\leqslant i\leqslant l$ and for all
$1\leqslant i\leqslant l$ and for all ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{S+A}(V)$. In particular, we finally have
$\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{S+A}(V)$. In particular, we finally have ![]() $(X,\unicode[STIX]{x1D6E5}+A^{\prime }-A)$ is LC,
$(X,\unicode[STIX]{x1D6E5}+A^{\prime }-A)$ is LC, ![]() $(X,\unicode[STIX]{x1D6E5}+4/3A_{i}+A^{\prime }-A)$ is LC for all
$(X,\unicode[STIX]{x1D6E5}+4/3A_{i}+A^{\prime }-A)$ is LC for all ![]() $1\leqslant i\leqslant l$ and for all
$1\leqslant i\leqslant l$ and for all ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{S+A}(V)$, and
$\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{S+A}(V)$, and ![]() $(X,A^{\prime }+\unicode[STIX]{x1D6E5}_{0})$ is DLT. ◻
$(X,A^{\prime }+\unicode[STIX]{x1D6E5}_{0})$ is DLT. ◻
Definition 4.5. Given an extremal ray ![]() $R\subseteq \overline{\operatorname{NE}}(X)$, we define a hyperplane
$R\subseteq \overline{\operatorname{NE}}(X)$, we define a hyperplane
Theorem 4.6. Let ![]() $\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective contraction between two normal projective varieties with
$\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective contraction between two normal projective varieties with ![]() $\operatorname{dim}X=3$ and
$\operatorname{dim}X=3$ and ![]() $\operatorname{char}p>5$. Let
$\operatorname{char}p>5$. Let ![]() $V$ be a finite dimensional affine subspace of
$V$ be a finite dimensional affine subspace of ![]() $\operatorname{WDiv}_{\mathbb{R}}(X)$ which is defined over the rationals. Fix a general ample
$\operatorname{WDiv}_{\mathbb{R}}(X)$ which is defined over the rationals. Fix a general ample![]() $/U$
$/U$![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() $A$ on
$A$ on ![]() $X$. Suppose that there is a divisor
$X$. Suppose that there is a divisor ![]() $\unicode[STIX]{x1D6E5}_{0}\geqslant 0$ such that
$\unicode[STIX]{x1D6E5}_{0}\geqslant 0$ such that ![]() $K_{X}+\unicode[STIX]{x1D6E5}_{0}$ is KLT.
$K_{X}+\unicode[STIX]{x1D6E5}_{0}$ is KLT.
Then the set of hyperplanes ![]() $R^{\bot }$ is finite in
$R^{\bot }$ is finite in ![]() ${\mathcal{L}}_{A}(V)$, as
${\mathcal{L}}_{A}(V)$, as ![]() $R$ ranges over the set of all extremal rays of
$R$ ranges over the set of all extremal rays of ![]() $\overline{\operatorname{NE}}(X/U)$. In particular,
$\overline{\operatorname{NE}}(X/U)$. In particular, ![]() ${\mathcal{N}}_{A,\unicode[STIX]{x1D70B}}(V)$ is a rational polytope.
${\mathcal{N}}_{A,\unicode[STIX]{x1D70B}}(V)$ is a rational polytope.
Proof. This result corresponds to [Reference Birkar, Cascini, Hacon and McKernan5, Theorem 3.11.1].
Since ![]() ${\mathcal{L}}_{A}(V)$ is compact, it is enough to prove the finiteness of
${\mathcal{L}}_{A}(V)$ is compact, it is enough to prove the finiteness of ![]() $R^{\bot }$ locally in a neighborhood of a point
$R^{\bot }$ locally in a neighborhood of a point ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{A}(V)$. Now since there is a boundary divisor
$\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{A}(V)$. Now since there is a boundary divisor ![]() $\unicode[STIX]{x1D6E5}_{0}$ such that
$\unicode[STIX]{x1D6E5}_{0}$ such that ![]() $(X,\unicode[STIX]{x1D6E5}_{0})$ is KLT and the image of a hyperplane under linear isomorphism of affine spaces is again a hyperplane, by Lemma 4.4 we may assume that
$(X,\unicode[STIX]{x1D6E5}_{0})$ is KLT and the image of a hyperplane under linear isomorphism of affine spaces is again a hyperplane, by Lemma 4.4 we may assume that ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ is KLT. Fix
$K_{X}+\unicode[STIX]{x1D6E5}$ is KLT. Fix ![]() $\unicode[STIX]{x1D700}>0$ such that if
$\unicode[STIX]{x1D700}>0$ such that if ![]() $\unicode[STIX]{x1D6E5}^{\prime }\in {\mathcal{L}}_{A}(V)$ and
$\unicode[STIX]{x1D6E5}^{\prime }\in {\mathcal{L}}_{A}(V)$ and ![]() $\Vert \unicode[STIX]{x1D6E5}^{\prime }-\unicode[STIX]{x1D6E5}\Vert <\unicode[STIX]{x1D700}$, then
$\Vert \unicode[STIX]{x1D6E5}^{\prime }-\unicode[STIX]{x1D6E5}\Vert <\unicode[STIX]{x1D700}$, then ![]() $\unicode[STIX]{x1D6E5}^{\prime }-\unicode[STIX]{x1D6E5}+A/2$ is ample over
$\unicode[STIX]{x1D6E5}^{\prime }-\unicode[STIX]{x1D6E5}+A/2$ is ample over ![]() $U$. Let
$U$. Let ![]() $R$ be an extremal ray over
$R$ be an extremal ray over ![]() $U$ such that
$U$ such that ![]() $(K_{X}+\unicode[STIX]{x1D6E5}^{\prime })\cdot R=0$ for some
$(K_{X}+\unicode[STIX]{x1D6E5}^{\prime })\cdot R=0$ for some ![]() $\unicode[STIX]{x1D6E5}^{\prime }\in {\mathcal{L}}_{A}(V)$ with
$\unicode[STIX]{x1D6E5}^{\prime }\in {\mathcal{L}}_{A}(V)$ with ![]() $\Vert \unicode[STIX]{x1D6E5}^{\prime }-\unicode[STIX]{x1D6E5}\Vert <\unicode[STIX]{x1D700}$. Then we have
$\Vert \unicode[STIX]{x1D6E5}^{\prime }-\unicode[STIX]{x1D6E5}\Vert <\unicode[STIX]{x1D700}$. Then we have
Write ![]() $\unicode[STIX]{x1D6E5}=A+B$. Then
$\unicode[STIX]{x1D6E5}=A+B$. Then ![]() $K_{X}+\unicode[STIX]{x1D6E5}-A/2=K_{X}+B+A/2$. By [Reference Waldron21, Theorem 1.7(3)] there are only finitely many extremal rays
$K_{X}+\unicode[STIX]{x1D6E5}-A/2=K_{X}+B+A/2$. By [Reference Waldron21, Theorem 1.7(3)] there are only finitely many extremal rays ![]() $R$ satisfying these properties.
$R$ satisfying these properties.
Now ![]() ${\mathcal{N}}_{A,\unicode[STIX]{x1D70B}}(V)$ is clearly a closed subset of
${\mathcal{N}}_{A,\unicode[STIX]{x1D70B}}(V)$ is clearly a closed subset of ![]() ${\mathcal{L}}_{A}(V)$. Let
${\mathcal{L}}_{A}(V)$. Let ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{A}(V)$. If
$\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{A}(V)$. If ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ is not nef
$K_{X}+\unicode[STIX]{x1D6E5}$ is not nef![]() $/U$, then again by [Reference Waldron21, Theorem 1.7] there exists an extremal ray
$/U$, then again by [Reference Waldron21, Theorem 1.7] there exists an extremal ray ![]() $R$ of
$R$ of ![]() $\overline{\operatorname{NE}}(X/U)$ generated by a rational curve
$\overline{\operatorname{NE}}(X/U)$ generated by a rational curve ![]() $\unicode[STIX]{x1D6F4}$ such that
$\unicode[STIX]{x1D6F4}$ such that ![]() $(K_{X}+\unicode[STIX]{x1D6E5})\cdot \unicode[STIX]{x1D6F4}<0$. In particular,
$(K_{X}+\unicode[STIX]{x1D6E5})\cdot \unicode[STIX]{x1D6F4}<0$. In particular, ![]() ${\mathcal{N}}_{A,\unicode[STIX]{x1D70B}}(V)$ is contained in the half-spaces
${\mathcal{N}}_{A,\unicode[STIX]{x1D70B}}(V)$ is contained in the half-spaces ![]() $R^{{\geqslant}0}=\{\unicode[STIX]{x1D6E4}\in {\mathcal{L}}_{A}(V):(K_{X}+\unicode[STIX]{x1D6E4})\cdot R\geqslant 0\}$ of the hyperplanes
$R^{{\geqslant}0}=\{\unicode[STIX]{x1D6E4}\in {\mathcal{L}}_{A}(V):(K_{X}+\unicode[STIX]{x1D6E4})\cdot R\geqslant 0\}$ of the hyperplanes ![]() $R^{\bot }$. Then by the previous part, there exists finitely many extremal rays
$R^{\bot }$. Then by the previous part, there exists finitely many extremal rays ![]() $R_{1},R_{2},\ldots ,R_{n}$ of
$R_{1},R_{2},\ldots ,R_{n}$ of ![]() $\overline{\operatorname{NE}}(X/U)$ such that
$\overline{\operatorname{NE}}(X/U)$ such that ![]() ${\mathcal{N}}_{A,\unicode[STIX]{x1D70B}}(V)=\bigcap _{i=1}^{n}R_{i}^{{\geqslant}0}$. Since
${\mathcal{N}}_{A,\unicode[STIX]{x1D70B}}(V)=\bigcap _{i=1}^{n}R_{i}^{{\geqslant}0}$. Since ![]() $R_{i}$’s are generated by irreducible curves, the hyperplanes
$R_{i}$’s are generated by irreducible curves, the hyperplanes ![]() $R_{i}^{\bot }$’s are all rational hyperplanes, in particular,
$R_{i}^{\bot }$’s are all rational hyperplanes, in particular, ![]() ${\mathcal{N}}_{A}(V)$ is a rational polytope.◻
${\mathcal{N}}_{A}(V)$ is a rational polytope.◻
Corollary 4.7. Let ![]() $\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective contraction between two normal projective varieties with
$\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective contraction between two normal projective varieties with ![]() $\operatorname{dim}X=3$ and
$\operatorname{dim}X=3$ and ![]() $\operatorname{char}p>5$. Let
$\operatorname{char}p>5$. Let ![]() $V$ be a finite dimensional affine subspace of
$V$ be a finite dimensional affine subspace of ![]() $\operatorname{WDiv}_{\mathbb{R}}(X)$ which is defined over the rationals. Fix a general ample
$\operatorname{WDiv}_{\mathbb{R}}(X)$ which is defined over the rationals. Fix a general ample![]() $/U$
$/U$![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() $A$ on
$A$ on ![]() $X$. Suppose that there is a divisor
$X$. Suppose that there is a divisor ![]() $\unicode[STIX]{x1D6E5}_{0}\geqslant 0$ such that
$\unicode[STIX]{x1D6E5}_{0}\geqslant 0$ such that ![]() $K_{X}+\unicode[STIX]{x1D6E5}_{0}$ is KLT. Let
$K_{X}+\unicode[STIX]{x1D6E5}_{0}$ is KLT. Let ![]() $\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ be a birational contraction over
$\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ be a birational contraction over ![]() $U$.
$U$.
Then ![]() ${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ is a rational polytope. Moreover, there are finitely many morphisms
${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ is a rational polytope. Moreover, there are finitely many morphisms ![]() $f_{i}:Y\rightarrow Z_{i}$ over
$f_{i}:Y\rightarrow Z_{i}$ over ![]() $U$,
$U$, ![]() $1\leqslant i\leqslant k$, such that if
$1\leqslant i\leqslant k$, such that if ![]() $f:Y\rightarrow Z$ is any contraction over
$f:Y\rightarrow Z$ is any contraction over ![]() $U$ and there is an
$U$ and there is an ![]() $\mathbb{R}$-divisor
$\mathbb{R}$-divisor ![]() $D$ on
$D$ on ![]() $Z$, which is ample over
$Z$, which is ample over ![]() $U$, such that
$U$, such that ![]() $K_{Y}+\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }(K_{X}+\unicode[STIX]{x1D6E5}){\sim}_{\mathbb{R},U}f^{\ast }D$ for some
$K_{Y}+\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }(K_{X}+\unicode[STIX]{x1D6E5}){\sim}_{\mathbb{R},U}f^{\ast }D$ for some ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$, then there is an index
$\unicode[STIX]{x1D6E5}\in {\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$, then there is an index ![]() $1\leqslant i\leqslant k$ and an isomorphism
$1\leqslant i\leqslant k$ and an isomorphism ![]() $\unicode[STIX]{x1D702}:Z_{i}\rightarrow Z$ such that
$\unicode[STIX]{x1D702}:Z_{i}\rightarrow Z$ such that ![]() $f=\unicode[STIX]{x1D702}\circ f_{i}$.
$f=\unicode[STIX]{x1D702}\circ f_{i}$.
Proof. This result corresponds to [Reference Birkar, Cascini, Hacon and McKernan5, Corollary 3.11.2].
Replacing ![]() $V_{A}$ by the span of
$V_{A}$ by the span of ![]() ${\mathcal{L}}_{A}(V)$ if necessary we may assume that
${\mathcal{L}}_{A}(V)$ if necessary we may assume that ![]() ${\mathcal{L}}_{A}(V)$ spans
${\mathcal{L}}_{A}(V)$ spans ![]() $V_{A}$. By compactness, to prove that
$V_{A}$. By compactness, to prove that ![]() ${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ is a rational polytope, we may work locally about a divisor
${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ is a rational polytope, we may work locally about a divisor ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$. By [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.7.4] we may assume that
$\unicode[STIX]{x1D6E5}\in {\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$. By [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.7.4] we may assume that ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ is KLT. Then
$K_{X}+\unicode[STIX]{x1D6E5}$ is KLT. Then ![]() $K_{Y}+\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$ is KLT as well. Let
$K_{Y}+\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$ is KLT as well. Let ![]() $C=\unicode[STIX]{x1D719}_{\ast }A$ and
$C=\unicode[STIX]{x1D719}_{\ast }A$ and ![]() $W=\unicode[STIX]{x1D719}_{\ast }(V)$. Then
$W=\unicode[STIX]{x1D719}_{\ast }(V)$. Then ![]() $C$ is a big
$C$ is a big![]() $/U$
$/U$![]() $\mathbb{Q}$-divisor on
$\mathbb{Q}$-divisor on ![]() $Y$. By [Reference Birkar, Cascini, Hacon and McKernan5, Lemmas 3.7.3 and 3.7.4] there exists a rational affine linear isomorphism
$Y$. By [Reference Birkar, Cascini, Hacon and McKernan5, Lemmas 3.7.3 and 3.7.4] there exists a rational affine linear isomorphism ![]() $L:W\rightarrow W^{\prime }$ and an ample
$L:W\rightarrow W^{\prime }$ and an ample![]() $/U$
$/U$![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() $C^{\prime }$ such that
$C^{\prime }$ such that ![]() $L(\unicode[STIX]{x1D6E4})$ is contained in the interior of
$L(\unicode[STIX]{x1D6E4})$ is contained in the interior of ![]() ${\mathcal{L}}_{C^{\prime }}(W^{\prime })$ and
${\mathcal{L}}_{C^{\prime }}(W^{\prime })$ and ![]() $L(\unicode[STIX]{x1D6F9}){\sim}_{\mathbb{Q},U}\unicode[STIX]{x1D6F9}$ for every
$L(\unicode[STIX]{x1D6F9}){\sim}_{\mathbb{Q},U}\unicode[STIX]{x1D6F9}$ for every ![]() $\unicode[STIX]{x1D6F9}\in W$. Then by Theorem 4.6,
$\unicode[STIX]{x1D6F9}\in W$. Then by Theorem 4.6, ![]() ${\mathcal{N}}_{C^{\prime },\unicode[STIX]{x1D713}}(W^{\prime })$ is a nonempty rational polytope containing
${\mathcal{N}}_{C^{\prime },\unicode[STIX]{x1D713}}(W^{\prime })$ is a nonempty rational polytope containing ![]() $L(\unicode[STIX]{x1D6E4})$, where
$L(\unicode[STIX]{x1D6E4})$, where ![]() $\unicode[STIX]{x1D713}:Y\rightarrow U$ is the structure morphism. Therefore,
$\unicode[STIX]{x1D713}:Y\rightarrow U$ is the structure morphism. Therefore, ![]() ${\mathcal{N}}_{C,\unicode[STIX]{x1D713}}(W)$ is a rational polytope locally around
${\mathcal{N}}_{C,\unicode[STIX]{x1D713}}(W)$ is a rational polytope locally around ![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}$.
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}$.
Consider the following resolution of ![]() $\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ which is also a log resolution of
$\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ which is also a log resolution of ![]() $(X,\unicode[STIX]{x1D6E5})$.
$(X,\unicode[STIX]{x1D6E5})$.

Then we have
Note that ![]() $\unicode[STIX]{x1D6E5}\,\in \,{\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ if and only if
$\unicode[STIX]{x1D6E5}\,\in \,{\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ if and only if ![]() $\unicode[STIX]{x1D6E4}\,=\,\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}\,\in \,{\mathcal{N}}_{C,\unicode[STIX]{x1D713}}(W)$ and
$\unicode[STIX]{x1D6E4}\,=\,\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}\,\in \,{\mathcal{N}}_{C,\unicode[STIX]{x1D713}}(W)$ and ![]() $\unicode[STIX]{x1D6F9}\,-\,\unicode[STIX]{x1D6F7}\,\geqslant \,0$. Since the map
$\unicode[STIX]{x1D6F9}\,-\,\unicode[STIX]{x1D6F7}\,\geqslant \,0$. Since the map ![]() $L:V\rightarrow W$ given by
$L:V\rightarrow W$ given by ![]() $\unicode[STIX]{x1D6E5}\rightarrow \unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}$ is rational and linear, in a neighborhood of
$\unicode[STIX]{x1D6E5}\rightarrow \unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}$ is rational and linear, in a neighborhood of ![]() $\unicode[STIX]{x1D6E5}$,
$\unicode[STIX]{x1D6E5}$, ![]() ${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ is cut out from
${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ is cut out from ![]() ${\mathcal{L}}_{A}(V)$ by finitely many half-spaces generated by affine rational hyperplanes. Therefore, by compactness,
${\mathcal{L}}_{A}(V)$ by finitely many half-spaces generated by affine rational hyperplanes. Therefore, by compactness, ![]() ${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ is a rational polytope.
${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ is a rational polytope.
Now for any ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ we have
$\unicode[STIX]{x1D6E5}\in {\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ we have ![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}=A^{\prime }+B^{\prime }$, where
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}=A^{\prime }+B^{\prime }$, where ![]() $A^{\prime }\geqslant 0$ is a big divisor on
$A^{\prime }\geqslant 0$ is a big divisor on ![]() $Y$. Therefore, by perturbing
$Y$. Therefore, by perturbing ![]() $\unicode[STIX]{x1D6E4}$, from the base-point free theorem [Reference Birkar and Waldron6, Theorem 1.2] it follows that there is a contraction
$\unicode[STIX]{x1D6E4}$, from the base-point free theorem [Reference Birkar and Waldron6, Theorem 1.2] it follows that there is a contraction ![]() $g:Y\rightarrow Z$ satisfying the required conditions. The rational map
$g:Y\rightarrow Z$ satisfying the required conditions. The rational map ![]() $g\circ \unicode[STIX]{x1D719}:X{\dashrightarrow}Z$ is the ample model of
$g\circ \unicode[STIX]{x1D719}:X{\dashrightarrow}Z$ is the ample model of ![]() $K_{X}+\unicode[STIX]{x1D6E5}$. Next we prove that there are only finitely many such contractions
$K_{X}+\unicode[STIX]{x1D6E5}$. Next we prove that there are only finitely many such contractions ![]() $g:Y\rightarrow Z$ corresponding to all
$g:Y\rightarrow Z$ corresponding to all ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$.
$\unicode[STIX]{x1D6E5}\in {\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$.
For two contractions ![]() $f:Y\rightarrow Z,f_{\ast }{\mathcal{O}}_{Y}={\mathcal{O}}_{Z}$ and
$f:Y\rightarrow Z,f_{\ast }{\mathcal{O}}_{Y}={\mathcal{O}}_{Z}$ and ![]() $f^{\prime }:Y\rightarrow Z^{\prime },f_{\ast }^{\prime }{\mathcal{O}}_{Y}={\mathcal{O}}_{Z^{\prime }}$ over
$f^{\prime }:Y\rightarrow Z^{\prime },f_{\ast }^{\prime }{\mathcal{O}}_{Y}={\mathcal{O}}_{Z^{\prime }}$ over ![]() $U$, there exists an isomorphism
$U$, there exists an isomorphism ![]() $\unicode[STIX]{x1D702}:Z\rightarrow Z^{\prime }$ satisfying
$\unicode[STIX]{x1D702}:Z\rightarrow Z^{\prime }$ satisfying ![]() $f^{\prime }=\unicode[STIX]{x1D702}\circ f$ if and only if
$f^{\prime }=\unicode[STIX]{x1D702}\circ f$ if and only if ![]() $f$ and
$f$ and ![]() $f^{\prime }$ contracts exactly same curves, that is,
$f^{\prime }$ contracts exactly same curves, that is, ![]() $f(C)=\operatorname{pt}$ if and only if
$f(C)=\operatorname{pt}$ if and only if ![]() $f^{\prime }(C)=\operatorname{pt}$ for irreducible curves
$f^{\prime }(C)=\operatorname{pt}$ for irreducible curves ![]() $C\subseteq X$ (see [Reference Debarre9, Proposition 1.14 and Lemma 1.15]). Let
$C\subseteq X$ (see [Reference Debarre9, Proposition 1.14 and Lemma 1.15]). Let ![]() $f:Y\rightarrow Z$ be a contraction over
$f:Y\rightarrow Z$ be a contraction over ![]() $U$ such that
$U$ such that
where ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ and
$\unicode[STIX]{x1D6E5}\in {\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ and ![]() $D$ is an ample
$D$ is an ample![]() $/U$
$/U$![]() $\mathbb{R}$-divisor on
$\mathbb{R}$-divisor on ![]() $Z$.
$Z$. ![]() $\unicode[STIX]{x1D6E4}$ belongs to the interior of a unique face
$\unicode[STIX]{x1D6E4}$ belongs to the interior of a unique face ![]() $G$ of
$G$ of ![]() ${\mathcal{N}}_{C,\unicode[STIX]{x1D713}}(W)$. Let
${\mathcal{N}}_{C,\unicode[STIX]{x1D713}}(W)$. Let ![]() $\unicode[STIX]{x1D6E4}_{1},\unicode[STIX]{x1D6E4}_{2},\ldots ,\unicode[STIX]{x1D6E4}_{k}$ be the vertices of the
$\unicode[STIX]{x1D6E4}_{1},\unicode[STIX]{x1D6E4}_{2},\ldots ,\unicode[STIX]{x1D6E4}_{k}$ be the vertices of the ![]() $G$. Write
$G$. Write ![]() $\unicode[STIX]{x1D6E4}=\sum _{j=1}^{k}\unicode[STIX]{x1D706}_{j}\unicode[STIX]{x1D6E4}_{j}$, where
$\unicode[STIX]{x1D6E4}=\sum _{j=1}^{k}\unicode[STIX]{x1D706}_{j}\unicode[STIX]{x1D6E4}_{j}$, where ![]() $\sum _{j=1}^{k}\unicode[STIX]{x1D706}_{j}=1$ and
$\sum _{j=1}^{k}\unicode[STIX]{x1D706}_{j}=1$ and ![]() $\unicode[STIX]{x1D706}_{j}\geqslant 0$ for all
$\unicode[STIX]{x1D706}_{j}\geqslant 0$ for all ![]() $j=1,2,\ldots ,k$. Since
$j=1,2,\ldots ,k$. Since ![]() $\unicode[STIX]{x1D6E4}$ is contained in the interior of
$\unicode[STIX]{x1D6E4}$ is contained in the interior of ![]() $G$, for any given (fixed) index
$G$, for any given (fixed) index ![]() $i$, we can choose
$i$, we can choose ![]() $\unicode[STIX]{x1D706}_{i}>0$ in
$\unicode[STIX]{x1D706}_{i}>0$ in ![]() $\unicode[STIX]{x1D6E4}=\sum _{j=1}^{k}\unicode[STIX]{x1D706}_{j}\unicode[STIX]{x1D6E4}_{j}$. Let
$\unicode[STIX]{x1D6E4}=\sum _{j=1}^{k}\unicode[STIX]{x1D706}_{j}\unicode[STIX]{x1D6E4}_{j}$. Let ![]() $C\subseteq Y$ be a curve contracted by
$C\subseteq Y$ be a curve contracted by ![]() $f$, then
$f$, then ![]() $0=(K_{Y}+\unicode[STIX]{x1D6E4})\cdot C=\sum _{j=1}^{k}\unicode[STIX]{x1D706}_{j}(K_{Y}+\unicode[STIX]{x1D6E4}_{j})\cdot C\geqslant 0$. This implies that
$0=(K_{Y}+\unicode[STIX]{x1D6E4})\cdot C=\sum _{j=1}^{k}\unicode[STIX]{x1D706}_{j}(K_{Y}+\unicode[STIX]{x1D6E4}_{j})\cdot C\geqslant 0$. This implies that ![]() $\unicode[STIX]{x1D706}_{i}(K_{Y}+\unicode[STIX]{x1D6E4}_{i})\cdot C=0$, that is,
$\unicode[STIX]{x1D706}_{i}(K_{Y}+\unicode[STIX]{x1D6E4}_{i})\cdot C=0$, that is, ![]() $(K_{Y}+\unicode[STIX]{x1D6E4}_{i})\cdot C=0$, since
$(K_{Y}+\unicode[STIX]{x1D6E4}_{i})\cdot C=0$, since ![]() $\unicode[STIX]{x1D706}_{i}\neq 0$. Therefore, if
$\unicode[STIX]{x1D706}_{i}\neq 0$. Therefore, if ![]() $C$ is contracted by
$C$ is contracted by ![]() $f$, then
$f$, then ![]() $(K_{Y}+\unicode[STIX]{x1D6E4}_{j})\cdot C=0$ for all
$(K_{Y}+\unicode[STIX]{x1D6E4}_{j})\cdot C=0$ for all ![]() $j=1,2,\ldots ,k$. Conversely, if
$j=1,2,\ldots ,k$. Conversely, if ![]() $C$ is a curve on
$C$ is a curve on ![]() $Y$ such that
$Y$ such that ![]() $(K_{Y}+\unicode[STIX]{x1D6E4}_{j})\cdot C=0$ for all
$(K_{Y}+\unicode[STIX]{x1D6E4}_{j})\cdot C=0$ for all ![]() $j=1,2,\ldots ,k$, then clearly
$j=1,2,\ldots ,k$, then clearly ![]() $(K_{Y}+\unicode[STIX]{x1D6E4})\cdot C=0$, and hence
$(K_{Y}+\unicode[STIX]{x1D6E4})\cdot C=0$, and hence ![]() $C$ is contracted by
$C$ is contracted by ![]() $f$. Therefore, the curves contacted by
$f$. Therefore, the curves contacted by ![]() $f$ are uniquely determined by
$f$ are uniquely determined by ![]() $G$. Now
$G$. Now ![]() $\unicode[STIX]{x1D6E5}$ is contained in the interior of a unique face
$\unicode[STIX]{x1D6E5}$ is contained in the interior of a unique face ![]() $F$ of
$F$ of ![]() ${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ and
${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ and ![]() $G$ is determined by
$G$ is determined by ![]() $F$. But since
$F$. But since ![]() ${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ is a rational polytope it has only finitely many faces.◻
${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ is a rational polytope it has only finitely many faces.◻
Corollary 4.8. Let ![]() $\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective contraction between two normal projective varieties with
$\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective contraction between two normal projective varieties with ![]() $\operatorname{dim}X=3$ and
$\operatorname{dim}X=3$ and ![]() $\operatorname{char}p>5$. Let
$\operatorname{char}p>5$. Let ![]() $V$ be a finite dimensional affine subspace of
$V$ be a finite dimensional affine subspace of ![]() $\operatorname{WDiv}_{\mathbb{R}}(X)$ which is defined over the rationals. Fix a general ample
$\operatorname{WDiv}_{\mathbb{R}}(X)$ which is defined over the rationals. Fix a general ample![]() $/U$
$/U$![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() $A\geqslant 0$ on
$A\geqslant 0$ on ![]() $X$. Suppose that there is a divisor
$X$. Suppose that there is a divisor ![]() $\unicode[STIX]{x1D6E5}_{0}\geqslant 0$ such that
$\unicode[STIX]{x1D6E5}_{0}\geqslant 0$ such that ![]() $K_{X}+\unicode[STIX]{x1D6E5}_{0}$ is KLT. Let
$K_{X}+\unicode[STIX]{x1D6E5}_{0}$ is KLT. Let ![]() $f:X\rightarrow Z$ be a morphism over
$f:X\rightarrow Z$ be a morphism over ![]() $U$ such that
$U$ such that ![]() $\unicode[STIX]{x1D6E5}_{0}\in {\mathcal{L}}_{A}(V)$ and
$\unicode[STIX]{x1D6E5}_{0}\in {\mathcal{L}}_{A}(V)$ and ![]() $K_{X}+\unicode[STIX]{x1D6E5}_{0}{\sim}_{\mathbb{R},U}f^{\ast }H$, where
$K_{X}+\unicode[STIX]{x1D6E5}_{0}{\sim}_{\mathbb{R},U}f^{\ast }H$, where ![]() $H$ is an ample divisor over
$H$ is an ample divisor over ![]() $U$. Let
$U$. Let ![]() $\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ be a birational contraction over
$\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ be a birational contraction over ![]() $Z$.
$Z$.
Then there is a neighborhood ![]() $P_{0}$ of
$P_{0}$ of ![]() $\unicode[STIX]{x1D6E5}_{0}$ in
$\unicode[STIX]{x1D6E5}_{0}$ in ![]() ${\mathcal{L}}_{A}(\unicode[STIX]{x1D6E5})$ such that for all
${\mathcal{L}}_{A}(\unicode[STIX]{x1D6E5})$ such that for all ![]() $\unicode[STIX]{x1D6E5}\in P_{0}$,
$\unicode[STIX]{x1D6E5}\in P_{0}$, ![]() $\unicode[STIX]{x1D719}$ is a log minimal model for
$\unicode[STIX]{x1D719}$ is a log minimal model for ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over ![]() $Z$ if and only if
$Z$ if and only if ![]() $\unicode[STIX]{x1D719}$ is a log minimal model for
$\unicode[STIX]{x1D719}$ is a log minimal model for ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over ![]() $U$.
$U$.
Proof. This result corresponds to [Reference Birkar, Cascini, Hacon and McKernan5, Corollary 3.11.3].
By Theorem 4.6 there exists finitely many extremal rays ![]() $R_{1},R_{2},\ldots ,R_{k}$ of
$R_{1},R_{2},\ldots ,R_{k}$ of ![]() $\overline{\operatorname{NE}}(Y/U)$ such that if
$\overline{\operatorname{NE}}(Y/U)$ such that if ![]() $K_{Y}+\unicode[STIX]{x1D6E4}=K_{Y}+\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}$ is not nef over
$K_{Y}+\unicode[STIX]{x1D6E4}=K_{Y}+\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}$ is not nef over ![]() $U$ for some
$U$ for some ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{A}(V)$, then it is negative on one of these rays. If
$\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{A}(V)$, then it is negative on one of these rays. If ![]() $\unicode[STIX]{x1D6E4}_{0}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}_{0}$, then we may write
$\unicode[STIX]{x1D6E4}_{0}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}_{0}$, then we may write
where ![]() $g:Y\rightarrow Z$ is the structure morphism.
$g:Y\rightarrow Z$ is the structure morphism.
Claim. If ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{A}(V)$ is sufficiently close to
$\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{A}(V)$ is sufficiently close to ![]() $\unicode[STIX]{x1D6E5}_{0}$ and
$\unicode[STIX]{x1D6E5}_{0}$ and ![]() $(K_{Y}+\unicode[STIX]{x1D6E4})\cdot R_{i_{0}}=\unicode[STIX]{x1D719}_{\ast }(K_{X}+\unicode[STIX]{x1D6E5})\cdot R_{i_{0}}<0$ for some
$(K_{Y}+\unicode[STIX]{x1D6E4})\cdot R_{i_{0}}=\unicode[STIX]{x1D719}_{\ast }(K_{X}+\unicode[STIX]{x1D6E5})\cdot R_{i_{0}}<0$ for some ![]() $i_{0}\in \{1,2,\ldots ,k\}$, then
$i_{0}\in \{1,2,\ldots ,k\}$, then ![]() $(K_{Y}+\unicode[STIX]{x1D6E4}_{0})\cdot R_{i_{0}}=\unicode[STIX]{x1D719}_{\ast }(K_{X}+\unicode[STIX]{x1D6E5}_{0})\cdot R_{i_{0}}=0$.
$(K_{Y}+\unicode[STIX]{x1D6E4}_{0})\cdot R_{i_{0}}=\unicode[STIX]{x1D719}_{\ast }(K_{X}+\unicode[STIX]{x1D6E5}_{0})\cdot R_{i_{0}}=0$.
Proof of the claim.
On the contrary assume that ![]() $(K_{Y}+\unicode[STIX]{x1D6E4}_{0})\cdot R_{i_{0}}>0$. Let
$(K_{Y}+\unicode[STIX]{x1D6E4}_{0})\cdot R_{i_{0}}>0$. Let ![]() $\unicode[STIX]{x1D6FC}=\frac{1}{2}(K_{Y}+\unicode[STIX]{x1D6E4}_{0})\cdot R_{i_{0}}>0$. Then
$\unicode[STIX]{x1D6FC}=\frac{1}{2}(K_{Y}+\unicode[STIX]{x1D6E4}_{0})\cdot R_{i_{0}}>0$. Then ![]() $(K_{Y}+\unicode[STIX]{x1D6E4}_{0})\cdot R_{i_{0}}>\unicode[STIX]{x1D6FC}$. Let
$(K_{Y}+\unicode[STIX]{x1D6E4}_{0})\cdot R_{i_{0}}>\unicode[STIX]{x1D6FC}$. Let ![]() $\unicode[STIX]{x1D6E4}^{\prime }=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}^{\prime }$ for some
$\unicode[STIX]{x1D6E4}^{\prime }=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}^{\prime }$ for some ![]() $\unicode[STIX]{x1D6E5}^{\prime }\in {\mathcal{L}}_{A}(V)$ such that
$\unicode[STIX]{x1D6E5}^{\prime }\in {\mathcal{L}}_{A}(V)$ such that ![]() $K_{Y}+\unicode[STIX]{x1D6E4}^{\prime }$ is LC. Then by [Reference Waldron21, Theorem 1.7] we have
$K_{Y}+\unicode[STIX]{x1D6E4}^{\prime }$ is LC. Then by [Reference Waldron21, Theorem 1.7] we have ![]() $(K_{Y}+\unicode[STIX]{x1D6E4}^{\prime })\cdot R_{i_{0}}\geqslant -6$. Choose
$(K_{Y}+\unicode[STIX]{x1D6E4}^{\prime })\cdot R_{i_{0}}\geqslant -6$. Choose ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{A}(V)$ such that
$\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{A}(V)$ such that ![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}$ lies on the line segment joining
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}$ lies on the line segment joining ![]() $\unicode[STIX]{x1D6E4}_{0}$ and
$\unicode[STIX]{x1D6E4}_{0}$ and ![]() $\unicode[STIX]{x1D6E4}^{\prime }$, that is,
$\unicode[STIX]{x1D6E4}^{\prime }$, that is, ![]() $\unicode[STIX]{x1D6E4}=r\unicode[STIX]{x1D6E4}_{0}+s\unicode[STIX]{x1D6E4}^{\prime }$ for some
$\unicode[STIX]{x1D6E4}=r\unicode[STIX]{x1D6E4}_{0}+s\unicode[STIX]{x1D6E4}^{\prime }$ for some ![]() $r\geqslant 0$ and
$r\geqslant 0$ and ![]() $s>0$ satisfying
$s>0$ satisfying ![]() $r+s=1$. Then
$r+s=1$. Then
 $$\begin{eqnarray}\displaystyle (K_{Y}+\unicode[STIX]{x1D6E4})\cdot R_{i_{0}} & = & \displaystyle r(K_{Y}+\unicode[STIX]{x1D6E4}_{0})\cdot R_{i_{0}}\nonumber\\ \displaystyle & & \displaystyle +\,s(K_{Y}+\unicode[STIX]{x1D6E4}^{\prime })\cdot R_{i_{0}}>2r\unicode[STIX]{x1D6FC}-6s>0\quad \text{if }r>\frac{3s}{\unicode[STIX]{x1D6FC}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (K_{Y}+\unicode[STIX]{x1D6E4})\cdot R_{i_{0}} & = & \displaystyle r(K_{Y}+\unicode[STIX]{x1D6E4}_{0})\cdot R_{i_{0}}\nonumber\\ \displaystyle & & \displaystyle +\,s(K_{Y}+\unicode[STIX]{x1D6E4}^{\prime })\cdot R_{i_{0}}>2r\unicode[STIX]{x1D6FC}-6s>0\quad \text{if }r>\frac{3s}{\unicode[STIX]{x1D6FC}}.\nonumber\end{eqnarray}$$ This is a contradiction. Therefore, if ![]() $\unicode[STIX]{x1D6E5}$ is sufficiently close to
$\unicode[STIX]{x1D6E5}$ is sufficiently close to ![]() $\unicode[STIX]{x1D6E5}_{0}$ then
$\unicode[STIX]{x1D6E5}_{0}$ then ![]() $(K_{Y}+\unicode[STIX]{x1D6E4})\cdot R_{i_{0}}<0$ implies that
$(K_{Y}+\unicode[STIX]{x1D6E4})\cdot R_{i_{0}}<0$ implies that ![]() $(K_{Y}+\unicode[STIX]{x1D6E4}_{0})\cdot R_{i_{0}}=0$.◻
$(K_{Y}+\unicode[STIX]{x1D6E4}_{0})\cdot R_{i_{0}}=0$.◻
In other words, there exists a neighborhood ![]() $P_{0}$ of
$P_{0}$ of ![]() $\unicode[STIX]{x1D6E5}_{0}$ in
$\unicode[STIX]{x1D6E5}_{0}$ in ![]() ${\mathcal{L}}_{A}(V)$ such that if
${\mathcal{L}}_{A}(V)$ such that if ![]() $\unicode[STIX]{x1D6E5}\in P_{0}$ and
$\unicode[STIX]{x1D6E5}\in P_{0}$ and ![]() $K_{Y}+\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$ is not nef over
$K_{Y}+\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$ is not nef over ![]() $U$, then
$U$, then ![]() $(K_{Y}+\unicode[STIX]{x1D6E4})\cdot R_{i_{0}}<0$ for some
$(K_{Y}+\unicode[STIX]{x1D6E4})\cdot R_{i_{0}}<0$ for some ![]() $i_{0}\in \{1,2,\ldots ,k\}$ and
$i_{0}\in \{1,2,\ldots ,k\}$ and ![]() $R_{i_{0}}$ is extremal over
$R_{i_{0}}$ is extremal over ![]() $Z$ (otherwise
$Z$ (otherwise ![]() $(K_{Y}+\unicode[STIX]{x1D6E4}_{0})\cdot R_{i_{0}}>0$), and consequently
$(K_{Y}+\unicode[STIX]{x1D6E4}_{0})\cdot R_{i_{0}}>0$), and consequently ![]() $K_{Y}+\unicode[STIX]{x1D6E4}$ is not nef over
$K_{Y}+\unicode[STIX]{x1D6E4}$ is not nef over ![]() $Z$. Contra-positively, if
$Z$. Contra-positively, if ![]() $\unicode[STIX]{x1D719}$ is a log minimal model of
$\unicode[STIX]{x1D719}$ is a log minimal model of ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over ![]() $Z$, then it is a log minimal model over
$Z$, then it is a log minimal model over ![]() $U$. The other direction is obvious.◻
$U$. The other direction is obvious.◻
Proposition 4.9. Let ![]() $\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective contraction between two normal projective varieties with
$\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective contraction between two normal projective varieties with ![]() $\operatorname{dim}X=3$ and
$\operatorname{dim}X=3$ and ![]() $\operatorname{char}p>5$. Let
$\operatorname{char}p>5$. Let ![]() $V$ be a finite dimensional affine subspace of
$V$ be a finite dimensional affine subspace of ![]() $\operatorname{WDiv}_{\mathbb{R}}(X)$ which is defined over the rationals. Fix a general ample
$\operatorname{WDiv}_{\mathbb{R}}(X)$ which is defined over the rationals. Fix a general ample![]() $/U$
$/U$![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() $A$ on
$A$ on ![]() $X$. Let
$X$. Let ![]() ${\mathcal{C}}\subseteq {\mathcal{L}}_{A}(V)$ be a rational polytope such that if
${\mathcal{C}}\subseteq {\mathcal{L}}_{A}(V)$ be a rational polytope such that if ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{C}}$, then
$\unicode[STIX]{x1D6E5}\in {\mathcal{C}}$, then ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ is KLT.
$K_{X}+\unicode[STIX]{x1D6E5}$ is KLT.
Then there are finitely many rational maps ![]() $\unicode[STIX]{x1D719}_{i}\,:\,X{\dashrightarrow}X_{i}$ over
$\unicode[STIX]{x1D719}_{i}\,:\,X{\dashrightarrow}X_{i}$ over ![]() $U\!$,
$U\!$, ![]() $1\,\leqslant \,i\,\leqslant \,k$, with the property that if
$1\,\leqslant \,i\,\leqslant \,k$, with the property that if ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{C}}\cap {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$, then there is an index
$\unicode[STIX]{x1D6E5}\in {\mathcal{C}}\cap {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$, then there is an index ![]() $1\leqslant j\leqslant k$ such that
$1\leqslant j\leqslant k$ such that ![]() $\unicode[STIX]{x1D719}_{j}$ is a log minimal model of
$\unicode[STIX]{x1D719}_{j}$ is a log minimal model of ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over ![]() $U$.
$U$.
Remark 4.10. This proposition is proved in [Reference Birkar and Waldron6, Theorem 1.4] with the additional hypothesis that ![]() $X$ is
$X$ is ![]() $\mathbb{Q}$-factorial. One can conceivably prove the above statement using [Reference Birkar and Waldron6, Theorem 1.4] by going to a
$\mathbb{Q}$-factorial. One can conceivably prove the above statement using [Reference Birkar and Waldron6, Theorem 1.4] by going to a ![]() $\mathbb{Q}$-factorization of
$\mathbb{Q}$-factorization of ![]() $X$. However, we take a different approach here, we use the techniques of [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 7.1] which fits better with rest of the paper.
$X$. However, we take a different approach here, we use the techniques of [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 7.1] which fits better with rest of the paper.
Proof of Proposition 4.9.
Replacing ![]() $V_{A}$ by the span of
$V_{A}$ by the span of ![]() ${\mathcal{C}}$ if necessary we may assume that
${\mathcal{C}}$ if necessary we may assume that ![]() ${\mathcal{C}}$ spans
${\mathcal{C}}$ spans ![]() $V_{A}$. We proceed by induction on the dimension of
$V_{A}$. We proceed by induction on the dimension of ![]() ${\mathcal{C}}$.
${\mathcal{C}}$.
First assume that ![]() $\operatorname{dim}{\mathcal{C}}=0$. Then
$\operatorname{dim}{\mathcal{C}}=0$. Then ![]() ${\mathcal{C}}=\{\unicode[STIX]{x1D6E5}_{0}\}$ for some
${\mathcal{C}}=\{\unicode[STIX]{x1D6E5}_{0}\}$ for some ![]() $\unicode[STIX]{x1D6E5}_{0}\in {\mathcal{L}}_{A}(V)$. If
$\unicode[STIX]{x1D6E5}_{0}\in {\mathcal{L}}_{A}(V)$. If ![]() $\unicode[STIX]{x1D6E5}_{0}\in {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$, then by [Reference Birkar3, Theorem 1.2] there exists a log minimal model
$\unicode[STIX]{x1D6E5}_{0}\in {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$, then by [Reference Birkar3, Theorem 1.2] there exists a log minimal model ![]() $\unicode[STIX]{x1D719}:X{\dashrightarrow}Y/U$ for
$\unicode[STIX]{x1D719}:X{\dashrightarrow}Y/U$ for ![]() $K_{X}+\unicode[STIX]{x1D6E5}_{0}$. By induction assume that the statement is true for any such rational polytope
$K_{X}+\unicode[STIX]{x1D6E5}_{0}$. By induction assume that the statement is true for any such rational polytope ![]() ${\mathcal{C}}^{\prime }$ with
${\mathcal{C}}^{\prime }$ with ![]() $\operatorname{dim}{\mathcal{C}}^{\prime }<\operatorname{dim}{\mathcal{C}}$.
$\operatorname{dim}{\mathcal{C}}^{\prime }<\operatorname{dim}{\mathcal{C}}$.
Now we prove the statement assuming that there is a divisor ![]() $\unicode[STIX]{x1D6E5}_{0}\in {\mathcal{C}}$ such that
$\unicode[STIX]{x1D6E5}_{0}\in {\mathcal{C}}$ such that ![]() $K_{X}+\unicode[STIX]{x1D6E5}_{0}{\sim}_{\mathbb{R},U}0$. Let
$K_{X}+\unicode[STIX]{x1D6E5}_{0}{\sim}_{\mathbb{R},U}0$. Let ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{C}}$ be a divisor such that
$\unicode[STIX]{x1D6E5}\in {\mathcal{C}}$ be a divisor such that ![]() $\unicode[STIX]{x1D6E5}\neq \unicode[STIX]{x1D6E5}_{0}$. Then there exists a divisor
$\unicode[STIX]{x1D6E5}\neq \unicode[STIX]{x1D6E5}_{0}$. Then there exists a divisor ![]() $\unicode[STIX]{x1D6E5}^{\prime }$ on one of the faces of
$\unicode[STIX]{x1D6E5}^{\prime }$ on one of the faces of ![]() ${\mathcal{C}}$ such that
${\mathcal{C}}$ such that
for some ![]() $0<\unicode[STIX]{x1D706}\leqslant 1$.
$0<\unicode[STIX]{x1D706}\leqslant 1$.
We have
Therefore, ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$ if and only if
$\unicode[STIX]{x1D6E5}\in {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$ if and only if ![]() $\unicode[STIX]{x1D6E5}^{\prime }\in {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$, and by [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.6.9]
$\unicode[STIX]{x1D6E5}^{\prime }\in {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$, and by [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.6.9] ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ and
$K_{X}+\unicode[STIX]{x1D6E5}$ and ![]() $K_{X}+\unicode[STIX]{x1D6E5}^{\prime }$ have same log minimal models over
$K_{X}+\unicode[STIX]{x1D6E5}^{\prime }$ have same log minimal models over ![]() $U$. Since
$U$. Since ![]() ${\mathcal{C}}$ is a rational polytope, it has finitely many faces each of which are rational polytope themselves; therefore, by induction we are done.
${\mathcal{C}}$ is a rational polytope, it has finitely many faces each of which are rational polytope themselves; therefore, by induction we are done.
Now we prove the general case. Applying [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.7.4] we may assume that ![]() ${\mathcal{C}}$ is contained in the interior of
${\mathcal{C}}$ is contained in the interior of ![]() ${\mathcal{L}}_{A}(V)$. Note that
${\mathcal{L}}_{A}(V)$. Note that ![]() ${\mathcal{C}}\cap {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$ is compact (as
${\mathcal{C}}\cap {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$ is compact (as ![]() ${\mathcal{L}}_{A}(V)$ is compact and
${\mathcal{L}}_{A}(V)$ is compact and ![]() ${\mathcal{C}}\cap {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}$ is closed). So it is sufficient to prove the statement locally in a neighborhood of a divisor
${\mathcal{C}}\cap {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}$ is closed). So it is sufficient to prove the statement locally in a neighborhood of a divisor ![]() $\unicode[STIX]{x1D6E5}_{0}\in {\mathcal{C}}\cap {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$.
$\unicode[STIX]{x1D6E5}_{0}\in {\mathcal{C}}\cap {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$.
Let ![]() $\unicode[STIX]{x1D719}:X{\dashrightarrow}Y/U$ be a log minimal model for
$\unicode[STIX]{x1D719}:X{\dashrightarrow}Y/U$ be a log minimal model for ![]() $K_{X}+\unicode[STIX]{x1D6E5}_{0}$ and
$K_{X}+\unicode[STIX]{x1D6E5}_{0}$ and ![]() $\unicode[STIX]{x1D6E4}_{0}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}_{0}$. Let
$\unicode[STIX]{x1D6E4}_{0}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}_{0}$. Let ![]() ${\mathcal{C}}_{0}\subseteq {\mathcal{L}}_{A}(V)$ be a neighborhood around
${\mathcal{C}}_{0}\subseteq {\mathcal{L}}_{A}(V)$ be a neighborhood around ![]() $\unicode[STIX]{x1D6E5}$, which is also a rational polytope. Since
$\unicode[STIX]{x1D6E5}$, which is also a rational polytope. Since ![]() $\unicode[STIX]{x1D719}$ is
$\unicode[STIX]{x1D719}$ is ![]() $(K_{X}+\unicode[STIX]{x1D6E5}_{0})$-negative, by shirking
$(K_{X}+\unicode[STIX]{x1D6E5}_{0})$-negative, by shirking ![]() ${\mathcal{C}}_{0}$ (without changing its dimension) around
${\mathcal{C}}_{0}$ (without changing its dimension) around ![]() $\unicode[STIX]{x1D6E5}_{0}$ we may assume that
$\unicode[STIX]{x1D6E5}_{0}$ we may assume that ![]() $a(F,K_{X}+\unicode[STIX]{x1D6E5})<a(F,K_{Y}+\unicode[STIX]{x1D6E5})$ for all
$a(F,K_{X}+\unicode[STIX]{x1D6E5})<a(F,K_{Y}+\unicode[STIX]{x1D6E5})$ for all ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{C}}_{0}$ and for all
$\unicode[STIX]{x1D6E5}\in {\mathcal{C}}_{0}$ and for all ![]() $\unicode[STIX]{x1D719}$-exceptional divisors
$\unicode[STIX]{x1D719}$-exceptional divisors ![]() $F$. Note that
$F$. Note that ![]() $K_{Y}+\unicode[STIX]{x1D6E4}_{0}$ is KLT and
$K_{Y}+\unicode[STIX]{x1D6E4}_{0}$ is KLT and ![]() $Y$ is
$Y$ is ![]() $\mathbb{Q}$-factorial. Since KLT is an open condition, all nearby divisors of
$\mathbb{Q}$-factorial. Since KLT is an open condition, all nearby divisors of ![]() $\unicode[STIX]{x1D6E4}_{0}$ in
$\unicode[STIX]{x1D6E4}_{0}$ in ![]() $Y$ are also KLT. Therefore, by shrinking
$Y$ are also KLT. Therefore, by shrinking ![]() ${\mathcal{C}}_{0}$ further around
${\mathcal{C}}_{0}$ further around ![]() $\unicode[STIX]{x1D6E5}_{0}$ we may assume that
$\unicode[STIX]{x1D6E5}_{0}$ we may assume that ![]() $K_{Y}+\unicode[STIX]{x1D6E4}$ is KLT for all
$K_{Y}+\unicode[STIX]{x1D6E4}$ is KLT for all ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{C}}_{0}$, where
$\unicode[STIX]{x1D6E5}\in {\mathcal{C}}_{0}$, where ![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}$.
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}$.
Replacing ![]() ${\mathcal{C}}$ by
${\mathcal{C}}$ by ![]() ${\mathcal{C}}_{0}$ we may assume that the rational polytope
${\mathcal{C}}_{0}$ we may assume that the rational polytope ![]() ${\mathcal{C}}^{\prime }=\unicode[STIX]{x1D719}_{\ast }({\mathcal{C}})$ is contained in
${\mathcal{C}}^{\prime }=\unicode[STIX]{x1D719}_{\ast }({\mathcal{C}})$ is contained in ![]() ${\mathcal{L}}_{\unicode[STIX]{x1D719}_{\ast }A}(W)$, where
${\mathcal{L}}_{\unicode[STIX]{x1D719}_{\ast }A}(W)$, where ![]() $W=\unicode[STIX]{x1D719}_{\ast }V$. Note that
$W=\unicode[STIX]{x1D719}_{\ast }V$. Note that ![]() $\unicode[STIX]{x1D719}_{\ast }A$ is not an ample divisor, however it is a big
$\unicode[STIX]{x1D719}_{\ast }A$ is not an ample divisor, however it is a big ![]() $\mathbb{Q}$-divisor on
$\mathbb{Q}$-divisor on ![]() $Y$. By [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.7.3] there exists a rational affine linear isomorphism
$Y$. By [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.7.3] there exists a rational affine linear isomorphism ![]() $L:W\rightarrow V^{\prime }$ on
$L:W\rightarrow V^{\prime }$ on ![]() $Y$ and a general ample
$Y$ and a general ample![]() $/U$
$/U$![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() $A^{\prime }$ on
$A^{\prime }$ on ![]() $Y$ such that
$Y$ such that ![]() $L({\mathcal{C}}^{\prime })\subseteq {\mathcal{L}}_{A^{\prime }}(V^{\prime })$,
$L({\mathcal{C}}^{\prime })\subseteq {\mathcal{L}}_{A^{\prime }}(V^{\prime })$, ![]() $L(\unicode[STIX]{x1D6E4}){\sim}_{\mathbb{Q},U}\unicode[STIX]{x1D6E4}$ for all
$L(\unicode[STIX]{x1D6E4}){\sim}_{\mathbb{Q},U}\unicode[STIX]{x1D6E4}$ for all ![]() $\unicode[STIX]{x1D6E4}\in {\mathcal{C}}^{\prime }$ and
$\unicode[STIX]{x1D6E4}\in {\mathcal{C}}^{\prime }$ and ![]() $K_{Y}+\unicode[STIX]{x1D6E4}$ is KLT for any
$K_{Y}+\unicode[STIX]{x1D6E4}$ is KLT for any ![]() $\unicode[STIX]{x1D6E4}\in L({\mathcal{C}}^{\prime })$.
$\unicode[STIX]{x1D6E4}\in L({\mathcal{C}}^{\prime })$.
By [Reference Birkar, Cascini, Hacon and McKernan5, Lemmas 3.6.9 and 3.6.10], any log minimal model of ![]() $(Y,L(\unicode[STIX]{x1D6E4}))$ over
$(Y,L(\unicode[STIX]{x1D6E4}))$ over ![]() $U$ is also a log minimal model of
$U$ is also a log minimal model of ![]() $(X,\unicode[STIX]{x1D6E5})$ over
$(X,\unicode[STIX]{x1D6E5})$ over ![]() $U$ for every
$U$ for every ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{C}}$. Thus replacing
$\unicode[STIX]{x1D6E5}\in {\mathcal{C}}$. Thus replacing ![]() $X$ by
$X$ by ![]() $Y$ and
$Y$ and ![]() ${\mathcal{C}}$ by
${\mathcal{C}}$ by ![]() $L({\mathcal{C}}^{\prime })$ we may assume that
$L({\mathcal{C}}^{\prime })$ we may assume that ![]() $X$ is
$X$ is ![]() $\mathbb{Q}$-factorial and
$\mathbb{Q}$-factorial and ![]() $K_{X}+\unicode[STIX]{x1D6E5}_{0}$ is
$K_{X}+\unicode[STIX]{x1D6E5}_{0}$ is ![]() $\unicode[STIX]{x1D70B}$-nef. Since
$\unicode[STIX]{x1D70B}$-nef. Since ![]() $\unicode[STIX]{x1D6E5}_{0}$ is a big divisor, by the base-point free theorem [Reference Birkar and Waldron6, Theorem 1.2]
$\unicode[STIX]{x1D6E5}_{0}$ is a big divisor, by the base-point free theorem [Reference Birkar and Waldron6, Theorem 1.2] ![]() $K_{X}+\unicode[STIX]{x1D6E5}_{0}$ has an ample model
$K_{X}+\unicode[STIX]{x1D6E5}_{0}$ has an ample model ![]() $\unicode[STIX]{x1D713}:X\rightarrow Z$. In particular,
$\unicode[STIX]{x1D713}:X\rightarrow Z$. In particular, ![]() $K_{X}+\unicode[STIX]{x1D6E5}_{0}{\sim}_{\mathbb{R},Z}0$. By the case we have already proved, there exist finitely many birational maps
$K_{X}+\unicode[STIX]{x1D6E5}_{0}{\sim}_{\mathbb{R},Z}0$. By the case we have already proved, there exist finitely many birational maps ![]() $\unicode[STIX]{x1D719}_{i}:X{\dashrightarrow}Y_{i}$ over
$\unicode[STIX]{x1D719}_{i}:X{\dashrightarrow}Y_{i}$ over ![]() $Z$,
$Z$, ![]() $1\leqslant i\leqslant k$, such that for any
$1\leqslant i\leqslant k$, such that for any ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{C}}\cap {\mathcal{E}}_{A,\unicode[STIX]{x1D713}}(V)$, there is an index
$\unicode[STIX]{x1D6E5}\in {\mathcal{C}}\cap {\mathcal{E}}_{A,\unicode[STIX]{x1D713}}(V)$, there is an index ![]() $i$ such that
$i$ such that ![]() $\unicode[STIX]{x1D719}_{i}$ is a log minimal model of
$\unicode[STIX]{x1D719}_{i}$ is a log minimal model of ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over ![]() $Z$. Since there are only finitely many indices
$Z$. Since there are only finitely many indices ![]() $1\leqslant i\leqslant k$, by shrinking
$1\leqslant i\leqslant k$, by shrinking ![]() ${\mathcal{C}}$ (without changing its dimension) if necessary, it follows from Corollary 4.8 that if
${\mathcal{C}}$ (without changing its dimension) if necessary, it follows from Corollary 4.8 that if ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{C}}$, then
$\unicode[STIX]{x1D6E5}\in {\mathcal{C}}$, then ![]() $\unicode[STIX]{x1D719}_{i}$ is a log minimal model for
$\unicode[STIX]{x1D719}_{i}$ is a log minimal model for ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over ![]() $Z$ if and only if it is a log minimal model for
$Z$ if and only if it is a log minimal model for ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over ![]() $U$.
$U$.
Let ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{C}}\cap {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$. Then
$\unicode[STIX]{x1D6E5}\in {\mathcal{C}}\cap {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$. Then ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{C}}\cap {\mathcal{E}}_{A,\unicode[STIX]{x1D713}}(V)$, and there exists an index
$\unicode[STIX]{x1D6E5}\in {\mathcal{C}}\cap {\mathcal{E}}_{A,\unicode[STIX]{x1D713}}(V)$, and there exists an index ![]() $1\leqslant j\leqslant k$ such that
$1\leqslant j\leqslant k$ such that ![]() $\unicode[STIX]{x1D719}_{j}$ is a log minimal model for
$\unicode[STIX]{x1D719}_{j}$ is a log minimal model for ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over ![]() $Z$. But then
$Z$. But then ![]() $\unicode[STIX]{x1D719}_{j}$ is a log minimal model for
$\unicode[STIX]{x1D719}_{j}$ is a log minimal model for ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over ![]() $U$.◻
$U$.◻
Theorem 4.11. Let ![]() $\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective contraction between two normal projective varieties with
$\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective contraction between two normal projective varieties with ![]() $\operatorname{dim}X=3$ and
$\operatorname{dim}X=3$ and ![]() $\operatorname{char}p>5$. Suppose that there is a KLT pair
$\operatorname{char}p>5$. Suppose that there is a KLT pair ![]() $(X,\unicode[STIX]{x1D6E5}_{0}\geqslant 0)$. Fix
$(X,\unicode[STIX]{x1D6E5}_{0}\geqslant 0)$. Fix ![]() $A\geqslant 0$, a general ample
$A\geqslant 0$, a general ample![]() $/U$
$/U$![]() $\mathbb{Q}$-divisor. Let
$\mathbb{Q}$-divisor. Let ![]() $V$ be a finite dimensional affine subspace of
$V$ be a finite dimensional affine subspace of ![]() $\operatorname{WDiv}_{\mathbb{R}}(X)$ which is defined over the rationals. Let
$\operatorname{WDiv}_{\mathbb{R}}(X)$ which is defined over the rationals. Let ![]() ${\mathcal{C}}\subseteq {\mathcal{L}}_{A}(V)$ be a rational polytope.
${\mathcal{C}}\subseteq {\mathcal{L}}_{A}(V)$ be a rational polytope.
Then there are finitely many birational maps ![]() $\unicode[STIX]{x1D713}_{j}:X{\dashrightarrow}Z_{j}$ over
$\unicode[STIX]{x1D713}_{j}:X{\dashrightarrow}Z_{j}$ over ![]() $U$,
$U$, ![]() $1\leqslant j\leqslant l$ such that if
$1\leqslant j\leqslant l$ such that if ![]() $\unicode[STIX]{x1D713}:X{\dashrightarrow}Z$ is a weak log canonical model of
$\unicode[STIX]{x1D713}:X{\dashrightarrow}Z$ is a weak log canonical model of ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over ![]() $U$, for some
$U$, for some ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{C}}$, then there is an index
$\unicode[STIX]{x1D6E5}\in {\mathcal{C}}$, then there is an index ![]() $1\leqslant j\leqslant l$ and an isomorphism
$1\leqslant j\leqslant l$ and an isomorphism ![]() $\unicode[STIX]{x1D709}:Z_{j}\rightarrow Z$ such that
$\unicode[STIX]{x1D709}:Z_{j}\rightarrow Z$ such that ![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D709}\circ \unicode[STIX]{x1D713}_{j}$.
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D709}\circ \unicode[STIX]{x1D713}_{j}$.
Proof. This result corresponds to [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 7.2].
By [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.7.4] for every ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{C}}$ there exists a
$\unicode[STIX]{x1D6E5}\in {\mathcal{C}}$ there exists a ![]() $\unicode[STIX]{x1D6E5}^{\prime }\geqslant 0$ such that
$\unicode[STIX]{x1D6E5}^{\prime }\geqslant 0$ such that ![]() $K_{X}+\unicode[STIX]{x1D6E5}^{\prime }$ is KLT and
$K_{X}+\unicode[STIX]{x1D6E5}^{\prime }$ is KLT and ![]() $K_{X}+\unicode[STIX]{x1D6E5}^{\prime }{\sim}_{\mathbb{R},U}K_{X}+\unicode[STIX]{x1D6E5}$. Then by [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.6.9]
$K_{X}+\unicode[STIX]{x1D6E5}^{\prime }{\sim}_{\mathbb{R},U}K_{X}+\unicode[STIX]{x1D6E5}$. Then by [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.6.9] ![]() $\unicode[STIX]{x1D713}:X{\dashrightarrow}Z$ is a weak log canonical model of
$\unicode[STIX]{x1D713}:X{\dashrightarrow}Z$ is a weak log canonical model of ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over ![]() $U$ if and only if
$U$ if and only if ![]() $\unicode[STIX]{x1D713}^{\prime }$ is a weak log canonical model of
$\unicode[STIX]{x1D713}^{\prime }$ is a weak log canonical model of ![]() $K_{X}+\unicode[STIX]{x1D6E5}^{\prime }$ of over
$K_{X}+\unicode[STIX]{x1D6E5}^{\prime }$ of over ![]() $U$. Therefore, by [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.7.4] we may assume that
$U$. Therefore, by [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.7.4] we may assume that ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ is KLT for every
$K_{X}+\unicode[STIX]{x1D6E5}$ is KLT for every ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{C}}$.
$\unicode[STIX]{x1D6E5}\in {\mathcal{C}}$.
Let ![]() $G\geqslant 0$ be a divisor such that it contains the support of every divisor in
$G\geqslant 0$ be a divisor such that it contains the support of every divisor in ![]() $V$ and
$V$ and ![]() $f:Y\rightarrow X$ a log resolution of
$f:Y\rightarrow X$ a log resolution of ![]() $(X,G)$. For a
$(X,G)$. For a ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{A}(V)$ we can write
$\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{A}(V)$ we can write
where ![]() $\unicode[STIX]{x1D6E4}\geqslant 0$ and
$\unicode[STIX]{x1D6E4}\geqslant 0$ and ![]() $E\geqslant 0$ have no common components,
$E\geqslant 0$ have no common components, ![]() $f_{\ast }\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E5}$ and
$f_{\ast }\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E5}$ and ![]() $f_{\ast }E=0$.
$f_{\ast }E=0$.
If ![]() $\unicode[STIX]{x1D713}:X{\dashrightarrow}Z$ is a weak log canonical model of
$\unicode[STIX]{x1D713}:X{\dashrightarrow}Z$ is a weak log canonical model of ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over ![]() $U$, then
$U$, then ![]() $\unicode[STIX]{x1D713}\circ f:Y{\dashrightarrow}Z$ is a weak log canonical model of
$\unicode[STIX]{x1D713}\circ f:Y{\dashrightarrow}Z$ is a weak log canonical model of ![]() $K_{Y}+\unicode[STIX]{x1D6E4}$ over
$K_{Y}+\unicode[STIX]{x1D6E4}$ over ![]() $U$. Let
$U$. Let ![]() ${\mathcal{C}}^{\prime }$ be the image of
${\mathcal{C}}^{\prime }$ be the image of ![]() ${\mathcal{C}}$ under the map
${\mathcal{C}}$ under the map ![]() $\unicode[STIX]{x1D6E5}\rightarrow \unicode[STIX]{x1D6E4}$. Then
$\unicode[STIX]{x1D6E5}\rightarrow \unicode[STIX]{x1D6E4}$. Then ![]() ${\mathcal{C}}^{\prime }$ is a rational polytope and
${\mathcal{C}}^{\prime }$ is a rational polytope and ![]() $K_{Y}+\unicode[STIX]{x1D6E4}$ is KLT for all
$K_{Y}+\unicode[STIX]{x1D6E4}$ is KLT for all ![]() $\unicode[STIX]{x1D6E4}\in {\mathcal{C}}^{\prime }$. In particular,
$\unicode[STIX]{x1D6E4}\in {\mathcal{C}}^{\prime }$. In particular, ![]() $\mathbf{B}_{+}(f^{\ast }A/U)$ does not contain any LC centers of
$\mathbf{B}_{+}(f^{\ast }A/U)$ does not contain any LC centers of ![]() $K_{Y}+\unicode[STIX]{x1D6E4}$ for any
$K_{Y}+\unicode[STIX]{x1D6E4}$ for any ![]() $\unicode[STIX]{x1D6E4}\in {\mathcal{C}}^{\prime }$. Let
$\unicode[STIX]{x1D6E4}\in {\mathcal{C}}^{\prime }$. Let ![]() $W$ be the subspace of
$W$ be the subspace of ![]() $\operatorname{WDiv}_{\mathbb{R}}(Y)$ spanned by the strict transforms of the components of
$\operatorname{WDiv}_{\mathbb{R}}(Y)$ spanned by the strict transforms of the components of ![]() $G$ and the exceptional divisors of
$G$ and the exceptional divisors of ![]() $f$. Then by [Reference Birkar, Cascini, Hacon and McKernan5, Lemmas 3.7.3 and 3.6.9] we may assume that there exists a general ample
$f$. Then by [Reference Birkar, Cascini, Hacon and McKernan5, Lemmas 3.7.3 and 3.6.9] we may assume that there exists a general ample![]() $/U$
$/U$![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() $A^{\prime }$ on
$A^{\prime }$ on ![]() $Y$ such that
$Y$ such that ![]() ${\mathcal{C}}^{\prime }\subseteq {\mathcal{L}}_{A^{\prime }}(W)$. Replacing
${\mathcal{C}}^{\prime }\subseteq {\mathcal{L}}_{A^{\prime }}(W)$. Replacing ![]() $X$ by
$X$ by ![]() $Y$ and
$Y$ and ![]() ${\mathcal{C}}$ by
${\mathcal{C}}$ by ![]() ${\mathcal{C}}^{\prime }$ we assume that
${\mathcal{C}}^{\prime }$ we assume that ![]() $X$ is smooth.
$X$ is smooth.
Let ![]() $H_{1}\geqslant 0,H_{2}\geqslant 0,\ldots ,H_{q}\geqslant 0$ be general ample
$H_{1}\geqslant 0,H_{2}\geqslant 0,\ldots ,H_{q}\geqslant 0$ be general ample![]() $/U$
$/U$![]() $\mathbb{Q}$-Cartier divisor on
$\mathbb{Q}$-Cartier divisor on ![]() $X$ such that they generate
$X$ such that they generate ![]() $\operatorname{WDiv}_{\mathbb{R}}(X)$ modulo numerical equivalence over
$\operatorname{WDiv}_{\mathbb{R}}(X)$ modulo numerical equivalence over ![]() $U$. Let
$U$. Let ![]() $H=H_{1}+H_{2}+\cdots +H_{q}$. By [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.7.4] we may assume that if
$H=H_{1}+H_{2}+\cdots +H_{q}$. By [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.7.4] we may assume that if ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{C}}$, then
$\unicode[STIX]{x1D6E5}\in {\mathcal{C}}$, then ![]() $\unicode[STIX]{x1D6E5}$ contains the support of
$\unicode[STIX]{x1D6E5}$ contains the support of ![]() $H$. Let
$H$. Let ![]() $W$ be the affine subspace of
$W$ be the affine subspace of ![]() $\operatorname{WDiv}_{\mathbb{R}}(X)$ spanned by
$\operatorname{WDiv}_{\mathbb{R}}(X)$ spanned by ![]() $V$ and the support of
$V$ and the support of ![]() $H$. Let
$H$. Let ![]() ${\mathcal{C}}^{\prime }$ be a rational polytope in
${\mathcal{C}}^{\prime }$ be a rational polytope in ![]() ${\mathcal{L}}_{A}(W)$ containing
${\mathcal{L}}_{A}(W)$ containing ![]() ${\mathcal{C}}$ in its interior such that
${\mathcal{C}}$ in its interior such that ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ is KLT for all
$K_{X}+\unicode[STIX]{x1D6E5}$ is KLT for all ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{C}}^{\prime }$.
$\unicode[STIX]{x1D6E5}\in {\mathcal{C}}^{\prime }$.
Then by Proposition 4.9 there are finitely many rational maps ![]() $\unicode[STIX]{x1D719}_{i}:X{\dashrightarrow}Y_{i},\;1\leqslant i\leqslant k$ over
$\unicode[STIX]{x1D719}_{i}:X{\dashrightarrow}Y_{i},\;1\leqslant i\leqslant k$ over ![]() $U$, such that for any
$U$, such that for any ![]() $\unicode[STIX]{x1D6E5}^{\prime }\in {\mathcal{C}}^{\prime }\cap {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(W)$ there exists an index
$\unicode[STIX]{x1D6E5}^{\prime }\in {\mathcal{C}}^{\prime }\cap {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(W)$ there exists an index ![]() $1\leqslant j\leqslant k$ such that
$1\leqslant j\leqslant k$ such that ![]() $\unicode[STIX]{x1D719}_{j}$ is a log minimal model of
$\unicode[STIX]{x1D719}_{j}$ is a log minimal model of ![]() $K_{X}+\unicode[STIX]{x1D6E5}^{\prime }$ over
$K_{X}+\unicode[STIX]{x1D6E5}^{\prime }$ over ![]() $U$. By Corollary 4.7 for each index
$U$. By Corollary 4.7 for each index ![]() $1\leqslant i\leqslant k$ there are finitely many projective contractions
$1\leqslant i\leqslant k$ there are finitely many projective contractions ![]() $f_{i,m}:Y_{i}\rightarrow Z_{i,m}$ over
$f_{i,m}:Y_{i}\rightarrow Z_{i,m}$ over ![]() $U$ such that if
$U$ such that if ![]() $\unicode[STIX]{x1D6E5}^{\prime }\in {\mathcal{W}}_{\unicode[STIX]{x1D719}_{i},A,\unicode[STIX]{x1D70B}}(W)$ and there is a contraction
$\unicode[STIX]{x1D6E5}^{\prime }\in {\mathcal{W}}_{\unicode[STIX]{x1D719}_{i},A,\unicode[STIX]{x1D70B}}(W)$ and there is a contraction ![]() $f:Y_{i}\rightarrow Z$ over
$f:Y_{i}\rightarrow Z$ over ![]() $U$, with
$U$, with
for some ample![]() $/U$
$/U$![]() $\mathbb{R}$-divisor
$\mathbb{R}$-divisor ![]() $D$ on
$D$ on ![]() $Z$, then there is an index
$Z$, then there is an index ![]() $(i,m)$ and an isomorphism
$(i,m)$ and an isomorphism ![]() $\unicode[STIX]{x1D709}:Z_{i,m}\rightarrow Z$ such that
$\unicode[STIX]{x1D709}:Z_{i,m}\rightarrow Z$ such that ![]() $f=\unicode[STIX]{x1D709}\circ f_{i,m}$. Let
$f=\unicode[STIX]{x1D709}\circ f_{i,m}$. Let ![]() $\unicode[STIX]{x1D713}_{j}:X{\dashrightarrow}Z_{j}$,
$\unicode[STIX]{x1D713}_{j}:X{\dashrightarrow}Z_{j}$, ![]() $1\leqslant j\leqslant l$ be the finitely many rational maps obtained by composing every
$1\leqslant j\leqslant l$ be the finitely many rational maps obtained by composing every ![]() $\unicode[STIX]{x1D719}_{i}$ with every
$\unicode[STIX]{x1D719}_{i}$ with every ![]() $f_{i,j}$. Pick
$f_{i,j}$. Pick ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{C}}$ and let
$\unicode[STIX]{x1D6E5}\in {\mathcal{C}}$ and let ![]() $\unicode[STIX]{x1D713}:X{\dashrightarrow}Z$ be a weak log canonical model of
$\unicode[STIX]{x1D713}:X{\dashrightarrow}Z$ be a weak log canonical model of ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over ![]() $U$. Then
$U$. Then ![]() $K_{Z}+\unicode[STIX]{x1D6E9}$ is KLT and nef over
$K_{Z}+\unicode[STIX]{x1D6E9}$ is KLT and nef over ![]() $U$, where
$U$, where ![]() $\unicode[STIX]{x1D6E9}=\unicode[STIX]{x1D713}_{\ast }\unicode[STIX]{x1D6E5}$. Since
$\unicode[STIX]{x1D6E9}=\unicode[STIX]{x1D713}_{\ast }\unicode[STIX]{x1D6E5}$. Since ![]() $K_{Z}+\unicode[STIX]{x1D6E9}$ is KLT, by [Reference Birkar3, Theorem 1.6]
$K_{Z}+\unicode[STIX]{x1D6E9}$ is KLT, by [Reference Birkar3, Theorem 1.6] ![]() $Z$ has a
$Z$ has a ![]() $\mathbb{Q}$-factorization
$\mathbb{Q}$-factorization ![]() $\unicode[STIX]{x1D702}:Y^{\prime }\rightarrow Z$, where
$\unicode[STIX]{x1D702}:Y^{\prime }\rightarrow Z$, where ![]() $\unicode[STIX]{x1D702}$ is a small birational morphism and
$\unicode[STIX]{x1D702}$ is a small birational morphism and ![]() $Y^{\prime }$ is
$Y^{\prime }$ is ![]() $\mathbb{Q}$-factorial. Then by [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.6.12] we may find
$\mathbb{Q}$-factorial. Then by [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.6.12] we may find ![]() $\unicode[STIX]{x1D6E5}^{\prime }\in {\mathcal{C}}^{\prime }\cap {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(W)$ such that
$\unicode[STIX]{x1D6E5}^{\prime }\in {\mathcal{C}}^{\prime }\cap {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(W)$ such that ![]() $\unicode[STIX]{x1D713}$ is an ample model of
$\unicode[STIX]{x1D713}$ is an ample model of ![]() $K_{X}+\unicode[STIX]{x1D6E5}^{\prime }$ over
$K_{X}+\unicode[STIX]{x1D6E5}^{\prime }$ over ![]() $U$. Pick an index
$U$. Pick an index ![]() $1\leqslant i\leqslant k$ such that
$1\leqslant i\leqslant k$ such that ![]() $\unicode[STIX]{x1D719}_{i}$ is a log minimal model of
$\unicode[STIX]{x1D719}_{i}$ is a log minimal model of ![]() $K_{X}+\unicode[STIX]{x1D6E5}^{\prime }$ over
$K_{X}+\unicode[STIX]{x1D6E5}^{\prime }$ over ![]() $U$. By [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.6.6(4)] there exists a contraction
$U$. By [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.6.6(4)] there exists a contraction ![]() $f:Y_{i}\rightarrow Z$ such that
$f:Y_{i}\rightarrow Z$ such that
where ![]() $\unicode[STIX]{x1D6E4}_{i}=\unicode[STIX]{x1D719}_{i\ast }\unicode[STIX]{x1D6E5}^{\prime }$ and
$\unicode[STIX]{x1D6E4}_{i}=\unicode[STIX]{x1D719}_{i\ast }\unicode[STIX]{x1D6E5}^{\prime }$ and ![]() $\unicode[STIX]{x1D6E9}^{\prime }=\unicode[STIX]{x1D713}_{\ast }\unicode[STIX]{x1D6E5}^{\prime }$. As
$\unicode[STIX]{x1D6E9}^{\prime }=\unicode[STIX]{x1D713}_{\ast }\unicode[STIX]{x1D6E5}^{\prime }$. As ![]() $K_{Z}+\unicode[STIX]{x1D6E9}^{\prime }$ is ample over
$K_{Z}+\unicode[STIX]{x1D6E9}^{\prime }$ is ample over ![]() $U$, it follows that there is an index
$U$, it follows that there is an index ![]() $m$ and isomorphism
$m$ and isomorphism ![]() $\unicode[STIX]{x1D709}:Z_{i,m}\rightarrow Z$ such that
$\unicode[STIX]{x1D709}:Z_{i,m}\rightarrow Z$ such that ![]() $f=\unicode[STIX]{x1D709}\circ f_{i,m}$. But then
$f=\unicode[STIX]{x1D709}\circ f_{i,m}$. But then
for some index ![]() $1\leqslant j\leqslant l$.◻
$1\leqslant j\leqslant l$.◻
Corollary 4.12. (Finiteness of weak log conical models)
Let ![]() $\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective contraction between two normal projective varieties with
$\unicode[STIX]{x1D70B}:X\rightarrow U$ be a projective contraction between two normal projective varieties with ![]() $\operatorname{dim}X=3$ and
$\operatorname{dim}X=3$ and ![]() $\operatorname{char}p>5$. Fix a general ample
$\operatorname{char}p>5$. Fix a general ample![]() $/U$
$/U$![]() $\mathbb{Q}$-divisor
$\mathbb{Q}$-divisor ![]() $A\geqslant 0$. Let
$A\geqslant 0$. Let ![]() $V$ be a finite dimensional affine subspace of
$V$ be a finite dimensional affine subspace of ![]() $\operatorname{WDiv}_{\mathbb{R}}(X)$ which is defined over the rationals. Suppose that there is a KLT pair
$\operatorname{WDiv}_{\mathbb{R}}(X)$ which is defined over the rationals. Suppose that there is a KLT pair ![]() $(X,\unicode[STIX]{x1D6E5}_{0})$.
$(X,\unicode[STIX]{x1D6E5}_{0})$.
Then there are finitely many birational maps ![]() $\unicode[STIX]{x1D713}_{j}:X{\dashrightarrow}Z_{j}$ over
$\unicode[STIX]{x1D713}_{j}:X{\dashrightarrow}Z_{j}$ over ![]() $U$,
$U$, ![]() $1\leqslant j\leqslant l$ such that if
$1\leqslant j\leqslant l$ such that if ![]() $\unicode[STIX]{x1D713}:X{\dashrightarrow}Z$ is a weak log canonical model of
$\unicode[STIX]{x1D713}:X{\dashrightarrow}Z$ is a weak log canonical model of ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over ![]() $U$, for some
$U$, for some ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{A}(V)$, then there is an index
$\unicode[STIX]{x1D6E5}\in {\mathcal{L}}_{A}(V)$, then there is an index ![]() $1\leqslant j\leqslant l$ and an isomorphism
$1\leqslant j\leqslant l$ and an isomorphism ![]() $\unicode[STIX]{x1D709}:Z_{j}\rightarrow Z$ such that
$\unicode[STIX]{x1D709}:Z_{j}\rightarrow Z$ such that ![]() $\unicode[STIX]{x1D713}=\unicode[STIX]{x1D709}\circ \unicode[STIX]{x1D713}_{j}$.
$\unicode[STIX]{x1D713}=\unicode[STIX]{x1D709}\circ \unicode[STIX]{x1D713}_{j}$.
Proof. This result corresponds to [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 7.3].
Since ![]() ${\mathcal{L}}_{A}(V)$ is a rational polytope, the statement follows from Theorem 4.11.◻
${\mathcal{L}}_{A}(V)$ is a rational polytope, the statement follows from Theorem 4.11.◻
Proof of Theorem 1.2.
First we prove ![]() $(1)$ and
$(1)$ and ![]() $(2)$. Since ample models are unique by [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.6.6(1)], by Corollaries 4.12 and 4.7 it suffices to prove that if
$(2)$. Since ample models are unique by [Reference Birkar, Cascini, Hacon and McKernan5, Lemma 3.6.6(1)], by Corollaries 4.12 and 4.7 it suffices to prove that if ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$, then
$\unicode[STIX]{x1D6E5}\in {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$, then ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ has both a log minimal model over
$K_{X}+\unicode[STIX]{x1D6E5}$ has both a log minimal model over ![]() $U$ and an ample model over
$U$ and an ample model over ![]() $U$.
$U$.
By [Reference Birkar, Cascini, Hacon and McKernan5, Lemmas 3.7.5 and 3.6.9] we may assume that ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ is KLT. Then [Reference Birkar3, Theorem 1.2] gives the existence of a log minimal model of
$K_{X}+\unicode[STIX]{x1D6E5}$ is KLT. Then [Reference Birkar3, Theorem 1.2] gives the existence of a log minimal model of ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over ![]() $U$, and the existence of the ample model follows from Lemma 4.1.
$U$, and the existence of the ample model follows from Lemma 4.1.
Part ![]() $(3)$ follows as in the proof of Corollary 4.7. Indeed if
$(3)$ follows as in the proof of Corollary 4.7. Indeed if ![]() $\unicode[STIX]{x1D6E5}_{1},\unicode[STIX]{x1D6E5}_{2},\ldots ,\unicode[STIX]{x1D6E5}_{k}$ are the vertices of
$\unicode[STIX]{x1D6E5}_{1},\unicode[STIX]{x1D6E5}_{2},\ldots ,\unicode[STIX]{x1D6E5}_{k}$ are the vertices of ![]() ${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ for a birational contraction
${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ for a birational contraction ![]() $\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$, and
$\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$, and ![]() $\unicode[STIX]{x1D6E5}$ and
$\unicode[STIX]{x1D6E5}$ and ![]() $\unicode[STIX]{x1D6E5}^{\prime }$ are two divisors lying in the interior of
$\unicode[STIX]{x1D6E5}^{\prime }$ are two divisors lying in the interior of ![]() ${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$, then for a given (fixed)
${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$, then for a given (fixed) ![]() $0\leqslant l\leqslant k$ we can write
$0\leqslant l\leqslant k$ we can write ![]() $\unicode[STIX]{x1D6E5}=\sum \unicode[STIX]{x1D707}_{j}\unicode[STIX]{x1D6E5}_{j}$ and
$\unicode[STIX]{x1D6E5}=\sum \unicode[STIX]{x1D707}_{j}\unicode[STIX]{x1D6E5}_{j}$ and ![]() $\unicode[STIX]{x1D6E5}^{\prime }=\sum \unicode[STIX]{x1D707}_{j}^{\prime }\unicode[STIX]{x1D6E5}_{j}$ for some
$\unicode[STIX]{x1D6E5}^{\prime }=\sum \unicode[STIX]{x1D707}_{j}^{\prime }\unicode[STIX]{x1D6E5}_{j}$ for some ![]() $\unicode[STIX]{x1D707}_{l}>0$. Therefore, from the base-point free theorem [Reference Birkar and Waldron6, Theorem 1.2] it follows that a curve
$\unicode[STIX]{x1D707}_{l}>0$. Therefore, from the base-point free theorem [Reference Birkar and Waldron6, Theorem 1.2] it follows that a curve ![]() $C$ is contracted by
$C$ is contracted by ![]() $K_{Y}+\unicode[STIX]{x1D6E4}=K_{Y}+\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}$ if and only if it is contracted by
$K_{Y}+\unicode[STIX]{x1D6E4}=K_{Y}+\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}$ if and only if it is contracted by ![]() $K_{Y}+\unicode[STIX]{x1D6E4}^{\prime }=K_{Y}+\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}^{\prime }$. In particular, the interior of
$K_{Y}+\unicode[STIX]{x1D6E4}^{\prime }=K_{Y}+\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}^{\prime }$. In particular, the interior of ![]() ${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ is contained in a single ample model
${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$ is contained in a single ample model ![]() ${\mathcal{A}}_{\unicode[STIX]{x1D713},A,\unicode[STIX]{x1D70B}}(V)$ for some projective contraction
${\mathcal{A}}_{\unicode[STIX]{x1D713},A,\unicode[STIX]{x1D70B}}(V)$ for some projective contraction ![]() $\unicode[STIX]{x1D713}:Y\rightarrow Z$. Therefore,
$\unicode[STIX]{x1D713}:Y\rightarrow Z$. Therefore, ![]() ${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)\subseteq \bar{{\mathcal{A}}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$.
${\mathcal{W}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)\subseteq \bar{{\mathcal{A}}}_{\unicode[STIX]{x1D719},A,\unicode[STIX]{x1D70B}}(V)$.
Part ![]() $(4)$ follows combining Part
$(4)$ follows combining Part ![]() $(1),(2)$ and
$(1),(2)$ and ![]() $(3)$.◻
$(3)$.◻
Proof of Corollary 1.3.
Let ![]() $V$ be the finite dimensional affine subspace of
$V$ be the finite dimensional affine subspace of ![]() $\operatorname{WDiv}(X)_{\mathbb{R}}$ generated by the irreducible components of
$\operatorname{WDiv}(X)_{\mathbb{R}}$ generated by the irreducible components of ![]() $\unicode[STIX]{x1D6E5}_{1},\unicode[STIX]{x1D6E5}_{2},\ldots ,\unicode[STIX]{x1D6E5}_{k}$. Then by Theorem 1.2 there exist finitely many rational maps
$\unicode[STIX]{x1D6E5}_{1},\unicode[STIX]{x1D6E5}_{2},\ldots ,\unicode[STIX]{x1D6E5}_{k}$. Then by Theorem 1.2 there exist finitely many rational maps ![]() $\unicode[STIX]{x1D719}_{i}:X{\dashrightarrow}Y_{i}$ over
$\unicode[STIX]{x1D719}_{i}:X{\dashrightarrow}Y_{i}$ over ![]() $U$,
$U$, ![]() $1\leqslant i\leqslant q$, such that for every
$1\leqslant i\leqslant q$, such that for every ![]() $\unicode[STIX]{x1D6E5}\in {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$ there is an index
$\unicode[STIX]{x1D6E5}\in {\mathcal{E}}_{A,\unicode[STIX]{x1D70B}}(V)$ there is an index ![]() $1\leqslant j\leqslant q$ such that
$1\leqslant j\leqslant q$ such that ![]() $\unicode[STIX]{x1D719}_{j}$ is a log minimal model of
$\unicode[STIX]{x1D719}_{j}$ is a log minimal model of ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ over
$K_{X}+\unicode[STIX]{x1D6E5}$ over ![]() $U$. Let
$U$. Let ![]() ${\mathcal{C}}\subseteq {\mathcal{L}}_{A}(V)$ be the (rational) polytope spanned by
${\mathcal{C}}\subseteq {\mathcal{L}}_{A}(V)$ be the (rational) polytope spanned by ![]() $\unicode[STIX]{x1D6E5}_{1},\unicode[STIX]{x1D6E5}_{2},\ldots ,\unicode[STIX]{x1D6E5}_{k}$ and let
$\unicode[STIX]{x1D6E5}_{1},\unicode[STIX]{x1D6E5}_{2},\ldots ,\unicode[STIX]{x1D6E5}_{k}$ and let
Then ![]() ${\mathcal{C}}_{j}$ is a rational polytope. Note that the ring
${\mathcal{C}}_{j}$ is a rational polytope. Note that the ring ![]() ${\mathcal{R}}(\unicode[STIX]{x1D70B},D^{\bullet })$ is finitely generated if and only if the rings corresponding to the (rational) polytope
${\mathcal{R}}(\unicode[STIX]{x1D70B},D^{\bullet })$ is finitely generated if and only if the rings corresponding to the (rational) polytope ![]() ${\mathcal{C}}_{j}$ are finitely generated for all
${\mathcal{C}}_{j}$ are finitely generated for all ![]() $j=1,2,\ldots ,q$. Therefore, replacing
$j=1,2,\ldots ,q$. Therefore, replacing ![]() $\unicode[STIX]{x1D6E5}_{1},\unicode[STIX]{x1D6E5}_{2},\ldots ,\unicode[STIX]{x1D6E5}_{k}$ by the vertices of
$\unicode[STIX]{x1D6E5}_{1},\unicode[STIX]{x1D6E5}_{2},\ldots ,\unicode[STIX]{x1D6E5}_{k}$ by the vertices of ![]() ${\mathcal{C}}_{j}$ we may assume that
${\mathcal{C}}_{j}$ we may assume that ![]() ${\mathcal{C}}={\mathcal{C}}_{j}$ and
${\mathcal{C}}={\mathcal{C}}_{j}$ and ![]() $\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ is a log minimal model for all
$\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ is a log minimal model for all ![]() $\unicode[STIX]{x1D6E5}_{1},\unicode[STIX]{x1D6E5}_{2},\ldots ,\unicode[STIX]{x1D6E5}_{k}$. Let
$\unicode[STIX]{x1D6E5}_{1},\unicode[STIX]{x1D6E5}_{2},\ldots ,\unicode[STIX]{x1D6E5}_{k}$. Let ![]() $\unicode[STIX]{x1D70B}^{\prime }:Y\rightarrow U$ be the induced morphism. Let
$\unicode[STIX]{x1D70B}^{\prime }:Y\rightarrow U$ be the induced morphism. Let ![]() $\unicode[STIX]{x1D6E4}_{i}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}_{i}$ for all
$\unicode[STIX]{x1D6E4}_{i}=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}_{i}$ for all ![]() $1\leqslant i\leqslant k$. Let
$1\leqslant i\leqslant k$. Let ![]() $g:W\rightarrow X$ and
$g:W\rightarrow X$ and ![]() $h:W\rightarrow Y$ be a resolution of the graph of
$h:W\rightarrow Y$ be a resolution of the graph of ![]() $\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$.
$\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$.

Then we have
for ![]() $1\leqslant i\leqslant k$.
$1\leqslant i\leqslant k$.
Note that ![]() $F_{i}\geqslant 0$ is an effective
$F_{i}\geqslant 0$ is an effective ![]() $h$-exceptional divisor, since
$h$-exceptional divisor, since ![]() $\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ is a log minimal model
$\unicode[STIX]{x1D719}:X{\dashrightarrow}Y$ is a log minimal model![]() $/U$ for
$/U$ for ![]() $\unicode[STIX]{x1D6E5}_{i}$,
$\unicode[STIX]{x1D6E5}_{i}$, ![]() $1\leqslant i\leqslant k$. Let
$1\leqslant i\leqslant k$. Let ![]() $m>0$ be positive integer such that
$m>0$ be positive integer such that ![]() $G_{i}=m(K_{Y}+\unicode[STIX]{x1D6E4}_{i})$ and
$G_{i}=m(K_{Y}+\unicode[STIX]{x1D6E4}_{i})$ and ![]() $D_{i}=m(K_{X}+\unicode[STIX]{x1D6E5}_{i})$ are both Cartier for all
$D_{i}=m(K_{X}+\unicode[STIX]{x1D6E5}_{i})$ are both Cartier for all ![]() $1\leqslant i\leqslant k$. Then from the projection formula it follows that
$1\leqslant i\leqslant k$. Then from the projection formula it follows that
Therefore, replacing ![]() $X$ by
$X$ by ![]() $Y$ we may assume that
$Y$ we may assume that ![]() $X$ is
$X$ is ![]() $\mathbb{Q}$-factorial and
$\mathbb{Q}$-factorial and ![]() $K_{X}+\unicode[STIX]{x1D6E5}_{i}$ is KLT and nef over
$K_{X}+\unicode[STIX]{x1D6E5}_{i}$ is KLT and nef over ![]() $U$ for all
$U$ for all ![]() $1\leqslant i\leqslant k$. Since
$1\leqslant i\leqslant k$. Since ![]() $\unicode[STIX]{x1D6E5}_{i}$ is big for all
$\unicode[STIX]{x1D6E5}_{i}$ is big for all ![]() $1\leqslant i\leqslant k$, by [Reference Birkar and Waldron6, Theorem 1.2]
$1\leqslant i\leqslant k$, by [Reference Birkar and Waldron6, Theorem 1.2] ![]() $K_{X}+\unicode[STIX]{x1D6E5}_{i}$ is semi-ample for all
$K_{X}+\unicode[STIX]{x1D6E5}_{i}$ is semi-ample for all ![]() $1\leqslant i\leqslant k$. Therefore, it follows that the ring
$1\leqslant i\leqslant k$. Therefore, it follows that the ring ![]() ${\mathcal{R}}(\unicode[STIX]{x1D70B},D^{\bullet })$ is finitely generated.◻
${\mathcal{R}}(\unicode[STIX]{x1D70B},D^{\bullet })$ is finitely generated.◻
5 The duality of pseudo-effective divisors and movable curves
In this section, we work on projective varieties of arbitrary dimension and over an algebraically closed ground field ![]() $k=\overline{k}$ of arbitrary characteristic. We prove Theorems 1.4 and 1.6 here.
$k=\overline{k}$ of arbitrary characteristic. We prove Theorems 1.4 and 1.6 here.
Definition 5.1. (Movable curves, strongly movable curves and nef curves)
Let ![]() $X$ be a projective variety. An irreducible curve
$X$ be a projective variety. An irreducible curve ![]() $C$ is called movable if there exists an algebraic family of irreducible curves
$C$ is called movable if there exists an algebraic family of irreducible curves ![]() $\{C_{t}\}\text{}_{t\in T}$ such that
$\{C_{t}\}\text{}_{t\in T}$ such that ![]() $C=C_{t_{0}}$ for some
$C=C_{t_{0}}$ for some ![]() $t_{0}\in T$ and
$t_{0}\in T$ and ![]() $\bigcup _{t\in T}C_{t}\subseteq X$ is dense in
$\bigcup _{t\in T}C_{t}\subseteq X$ is dense in ![]() $X$.
$X$.
A class ![]() $\unicode[STIX]{x1D6FE}\in N_{1}(X)_{\mathbb{R}}$ is called movable if there exists a movable curve
$\unicode[STIX]{x1D6FE}\in N_{1}(X)_{\mathbb{R}}$ is called movable if there exists a movable curve ![]() $C$ such that
$C$ such that ![]() $\unicode[STIX]{x1D6FE}=[C]$ in
$\unicode[STIX]{x1D6FE}=[C]$ in ![]() $N_{1}(X)_{\mathbb{R}}$.
$N_{1}(X)_{\mathbb{R}}$.
An irreducible curve ![]() $C$ is called strongly movable if there exists a projective birational morphism
$C$ is called strongly movable if there exists a projective birational morphism ![]() $f:X^{\prime }\rightarrow X$ and ample divisors
$f:X^{\prime }\rightarrow X$ and ample divisors ![]() $H_{1}^{\prime },H_{2}^{\prime },\ldots ,H_{n-1}^{\prime }$ on
$H_{1}^{\prime },H_{2}^{\prime },\ldots ,H_{n-1}^{\prime }$ on ![]() $X^{\prime }$ such that
$X^{\prime }$ such that ![]() $C=f_{\ast }(H_{1}^{\prime }\cap H_{2}^{\prime }\cap \ldots \cap H_{n-1}^{\prime })$, where
$C=f_{\ast }(H_{1}^{\prime }\cap H_{2}^{\prime }\cap \ldots \cap H_{n-1}^{\prime })$, where ![]() $n=\operatorname{dim}X=\operatorname{dim}X^{\prime }$.
$n=\operatorname{dim}X=\operatorname{dim}X^{\prime }$.
A class ![]() $\unicode[STIX]{x1D6FE}\in N_{1}(X)_{\mathbb{R}}$ is called strongly movable if there exists a strongly movable curve
$\unicode[STIX]{x1D6FE}\in N_{1}(X)_{\mathbb{R}}$ is called strongly movable if there exists a strongly movable curve ![]() $C$ such that
$C$ such that ![]() $\unicode[STIX]{x1D6FE}=[C]$ in
$\unicode[STIX]{x1D6FE}=[C]$ in ![]() $N_{1}(X)_{\mathbb{R}}$.
$N_{1}(X)_{\mathbb{R}}$.
An irreducible curve ![]() $C$ is called a nef curve if
$C$ is called a nef curve if ![]() $D\cdot C\geqslant 0$ for every effective Cartier divisor
$D\cdot C\geqslant 0$ for every effective Cartier divisor ![]() $D\geqslant 0$. A class
$D\geqslant 0$. A class ![]() $\unicode[STIX]{x1D6FE}\in N_{1}(X)_{\mathbb{R}}$ is called nef is there exists a nef curve
$\unicode[STIX]{x1D6FE}\in N_{1}(X)_{\mathbb{R}}$ is called nef is there exists a nef curve ![]() $C$ such that
$C$ such that ![]() $\unicode[STIX]{x1D6FE}=[C]$.
$\unicode[STIX]{x1D6FE}=[C]$.
Definition 5.2. (Cone of movable, strongly movable and nef curves)
Let ![]() $X$ be a projective variety. The closure in
$X$ be a projective variety. The closure in ![]() $N_{1}(X)_{\mathbb{R}}$ of the cone of effective classes of movable curves
$N_{1}(X)_{\mathbb{R}}$ of the cone of effective classes of movable curves
is called the cone of movable curves.
The closure in ![]() $N_{1}(X)_{\mathbb{R}}$ of the cone of effective classes of strongly movable curves
$N_{1}(X)_{\mathbb{R}}$ of the cone of effective classes of strongly movable curves
is called the cone of strongly movable curves.
The closure in ![]() $N_{1}(X)_{\mathbb{R}}$ of the cone of effective classes of nef curves
$N_{1}(X)_{\mathbb{R}}$ of the cone of effective classes of nef curves
is called the cone of nef curves.
The following theorem of Takagi on the existence of Fujita approximation in arbitrary characteristic is one of the main ingredient of our proof.
Theorem 5.3. (Fujita’s approximation theorem [Reference Takagi19, Corollary 2.16])
Let ![]() $X$ be a projective variety defined over an algebraically closed field
$X$ be a projective variety defined over an algebraically closed field ![]() $k$ of arbitrary characteristic. Let
$k$ of arbitrary characteristic. Let ![]() $\unicode[STIX]{x1D709}\in N^{1}(X)_{\mathbb{R}}$ be a big divisor class. Then for any real number
$\unicode[STIX]{x1D709}\in N^{1}(X)_{\mathbb{R}}$ be a big divisor class. Then for any real number ![]() $\unicode[STIX]{x1D700}>0$ there exists a birational morphism
$\unicode[STIX]{x1D700}>0$ there exists a birational morphism ![]() $\unicode[STIX]{x1D707}:X^{\prime }\rightarrow X$ from a projective variety
$\unicode[STIX]{x1D707}:X^{\prime }\rightarrow X$ from a projective variety ![]() $X^{\prime }$ and a decomposition
$X^{\prime }$ and a decomposition
in ![]() $N^{1}(X^{\prime })_{\mathbb{R}}$ such that:
$N^{1}(X^{\prime })_{\mathbb{R}}$ such that:
(1)
 $a$ is an ample class and
$a$ is an ample class and  $e$ is effective; and
$e$ is effective; and(2)
 $\operatorname{vol}_{X^{\prime }}(a)>\operatorname{vol}_{X}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D700}$.
$\operatorname{vol}_{X^{\prime }}(a)>\operatorname{vol}_{X}(\unicode[STIX]{x1D709})-\unicode[STIX]{x1D700}$.
Theorem 5.4. Let ![]() $X$ be a projective variety of dimension
$X$ be a projective variety of dimension ![]() $n$ over an algebraically closed field
$n$ over an algebraically closed field ![]() $k$ of arbitrary characteristic. Let
$k$ of arbitrary characteristic. Let ![]() $\unicode[STIX]{x1D709}\in N^{1}(X)_{\mathbb{R}}$ be a big divisor class. Consider a Fujita approximation of
$\unicode[STIX]{x1D709}\in N^{1}(X)_{\mathbb{R}}$ be a big divisor class. Consider a Fujita approximation of ![]() $\unicode[STIX]{x1D709}$:
$\unicode[STIX]{x1D709}$:
Let ![]() $h\in N^{1}(X)_{\mathbb{R}}$ be an ample class such that
$h\in N^{1}(X)_{\mathbb{R}}$ be an ample class such that ![]() $h\pm \unicode[STIX]{x1D709}$ are both ample. Then
$h\pm \unicode[STIX]{x1D709}$ are both ample. Then
Proof. This is [Reference Lazarsfeld15, Theorem 11.4.21]. The main ingredients of the proof of [Reference Lazarsfeld16, Theorem 11.4.21] are the Fujita’s approximation theorem, Hodge type inequalities [Reference Lazarsfeld15, Corollary 1.6.3, Lemma 11.4.22], and the continuity of volume [Reference Lazarsfeld15, Theorem 2.2.44, Example 2.2.47]. The Fujita’s approximation theorem is known in positive characteristic due to [Reference Takagi19] and the other two results are also known to hold in positive characteristic (their proofs in [Reference Lazarsfeld15] work in arbitrary characteristic). As a result, the proof of [Reference Lazarsfeld16, Theorem 11.4.21] holds in arbitrary characteristic. ◻
Proof of the Theorem 1.4.
It is well known that ![]() $\overline{\operatorname{Eff}}(X)\subseteq \overline{\operatorname{SNM}}(X)^{\ast }$. By contradiction, assume that the inclusion
$\overline{\operatorname{Eff}}(X)\subseteq \overline{\operatorname{SNM}}(X)^{\ast }$. By contradiction, assume that the inclusion ![]() $\overline{\operatorname{Eff}}(X)\subsetneq \overline{\operatorname{SNM}}(X)^{\ast }$ is strict. Then there exists a class
$\overline{\operatorname{Eff}}(X)\subsetneq \overline{\operatorname{SNM}}(X)^{\ast }$ is strict. Then there exists a class ![]() $\unicode[STIX]{x1D709}\in N^{1}(X)_{\mathbb{R}}$ such that
$\unicode[STIX]{x1D709}\in N^{1}(X)_{\mathbb{R}}$ such that
Fix an ample class ![]() $h$ such that
$h$ such that ![]() $h\pm 2\unicode[STIX]{x1D709}$ is ample. Since
$h\pm 2\unicode[STIX]{x1D709}$ is ample. Since ![]() $\unicode[STIX]{x1D709}$ lies in the interior of
$\unicode[STIX]{x1D709}$ lies in the interior of ![]() $\overline{\operatorname{SNM}}(X)^{\ast }$, there exists
$\overline{\operatorname{SNM}}(X)^{\ast }$, there exists ![]() $\unicode[STIX]{x1D700}>0$ such that
$\unicode[STIX]{x1D700}>0$ such that ![]() $\unicode[STIX]{x1D709}-\unicode[STIX]{x1D700}h\in \overline{\operatorname{SNM}}(X)^{\ast }$. In particular,
$\unicode[STIX]{x1D709}-\unicode[STIX]{x1D700}h\in \overline{\operatorname{SNM}}(X)^{\ast }$. In particular,
for every strongly movable class ![]() $\unicode[STIX]{x1D6FE}$ on
$\unicode[STIX]{x1D6FE}$ on ![]() $X$. Now consider the class
$X$. Now consider the class
Since ![]() $\unicode[STIX]{x1D709}$ is pseudo-effective,
$\unicode[STIX]{x1D709}$ is pseudo-effective, ![]() $\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FF}}$ is big for all
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FF}}$ is big for all ![]() $\unicode[STIX]{x1D6FF}>0$. For small
$\unicode[STIX]{x1D6FF}>0$. For small ![]() $\unicode[STIX]{x1D6FF}>0$ consider a Fujita approximation (by Theorem 5.3)
$\unicode[STIX]{x1D6FF}>0$ consider a Fujita approximation (by Theorem 5.3)
such that
Since ![]() $\unicode[STIX]{x1D6FF}^{2n}$ is a polynomial of degree
$\unicode[STIX]{x1D6FF}^{2n}$ is a polynomial of degree ![]() $2n$ in
$2n$ in ![]() $\unicode[STIX]{x1D6FF}$ and
$\unicode[STIX]{x1D6FF}$ and ![]() $\operatorname{vol}_{X}(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FF}})=(\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FF}h)^{n}$ is a polynomial of degree
$\operatorname{vol}_{X}(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FF}})=(\unicode[STIX]{x1D709}+\unicode[STIX]{x1D6FF}h)^{n}$ is a polynomial of degree ![]() $n$ in
$n$ in ![]() $\unicode[STIX]{x1D6FF}$ and
$\unicode[STIX]{x1D6FF}$ and ![]() $(h^{n})>0$, for
$(h^{n})>0$, for ![]() $\unicode[STIX]{x1D6FF}>0$ sufficiently small we may assume that
$\unicode[STIX]{x1D6FF}>0$ sufficiently small we may assume that ![]() $0<\unicode[STIX]{x1D6FF}^{2n}<\frac{1}{2}\operatorname{vol}_{X}(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FF}})$. In particular,
$0<\unicode[STIX]{x1D6FF}^{2n}<\frac{1}{2}\operatorname{vol}_{X}(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FF}})$. In particular,
Consider the strongly movable class
Then by the projection formula and [Reference Lazarsfeld15, Corollary 1.6.3(ii)], we get
 $$\begin{eqnarray}\displaystyle (h\cdot \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FF}})_{X} & = & \displaystyle (\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FF}}^{\ast }(h)\cdot a_{\unicode[STIX]{x1D6FF}}^{n-1})_{X_{\unicode[STIX]{x1D6FF}}^{\prime }}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle (h^{n})_{X}^{1/n}\cdot (a_{\unicode[STIX]{x1D6FF}}^{n})_{X_{\unicode[STIX]{x1D6FF}}^{\prime }}^{(n-1)/n}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (h\cdot \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FF}})_{X} & = & \displaystyle (\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FF}}^{\ast }(h)\cdot a_{\unicode[STIX]{x1D6FF}}^{n-1})_{X_{\unicode[STIX]{x1D6FF}}^{\prime }}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle (h^{n})_{X}^{1/n}\cdot (a_{\unicode[STIX]{x1D6FF}}^{n})_{X_{\unicode[STIX]{x1D6FF}}^{\prime }}^{(n-1)/n}.\end{eqnarray}$$On the other hand,
 $$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D709}\cdot \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FF}})_{X} & {\leqslant} & \displaystyle (\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FF}}\cdot \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FF}})_{X}\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FF}}^{\ast }(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FF}})\cdot a_{\unicode[STIX]{x1D6FF}}^{n-1})_{X_{\unicode[STIX]{x1D6FF}}^{\prime }}\nonumber\\ \displaystyle & = & \displaystyle (a_{\unicode[STIX]{x1D6FF}}^{n})_{X_{\unicode[STIX]{x1D6FF}}^{\prime }}+(e_{\unicode[STIX]{x1D6FF}}\cdot a_{\unicode[STIX]{x1D6FF}}^{n-1})_{X_{\unicode[STIX]{x1D6FF}}^{\prime }}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (\unicode[STIX]{x1D709}\cdot \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FF}})_{X} & {\leqslant} & \displaystyle (\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FF}}\cdot \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FF}})_{X}\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D6FF}}^{\ast }(\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FF}})\cdot a_{\unicode[STIX]{x1D6FF}}^{n-1})_{X_{\unicode[STIX]{x1D6FF}}^{\prime }}\nonumber\\ \displaystyle & = & \displaystyle (a_{\unicode[STIX]{x1D6FF}}^{n})_{X_{\unicode[STIX]{x1D6FF}}^{\prime }}+(e_{\unicode[STIX]{x1D6FF}}\cdot a_{\unicode[STIX]{x1D6FF}}^{n-1})_{X_{\unicode[STIX]{x1D6FF}}^{\prime }}.\end{eqnarray}$$ Now ![]() $h\pm \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FF}}$ is ample provided that
$h\pm \unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FF}}$ is ample provided that ![]() $\unicode[STIX]{x1D6FF}<\frac{1}{2}$. Therefore, by Theorem 5.4 and (5.2) we get,
$\unicode[STIX]{x1D6FF}<\frac{1}{2}$. Therefore, by Theorem 5.4 and (5.2) we get,
where ![]() $C_{1}=20\cdot (h^{n})_{X}>0$ is independent of
$C_{1}=20\cdot (h^{n})_{X}>0$ is independent of ![]() $\unicode[STIX]{x1D6FF}$.
$\unicode[STIX]{x1D6FF}$.
Now from (5.3), (5.4), (5.5) and (5.6) we get
 $$\begin{eqnarray}\displaystyle 0\leqslant \frac{(\unicode[STIX]{x1D709}\cdot \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FF}})}{(h\cdot \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FF}})} & {\leqslant} & \displaystyle \frac{(a_{\unicode[STIX]{x1D6FF}}^{n})_{X_{\unicode[STIX]{x1D6FF}}^{\prime }}+C_{1}\cdot \unicode[STIX]{x1D6FF}^{n}}{(h^{n})_{X}^{1/n}\cdot (a_{\unicode[STIX]{x1D6FF}}^{n})_{X_{\unicode[STIX]{x1D6FF}}^{\prime }}^{(n-1)/n}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1}{(h^{n})_{X}^{1/n}}\cdot (a_{\unicode[STIX]{x1D6FF}}^{n})_{X_{\unicode[STIX]{x1D6FF}}^{\prime }}^{1/n}+\frac{C_{1}\cdot \unicode[STIX]{x1D6FF}^{n}}{(h^{n})_{X}^{1/n}}\cdot \frac{2^{(n-1)/n}}{\unicode[STIX]{x1D6FF}^{n-1}\cdot (h^{n})_{X}^{(n-1)/n}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C_{2}\cdot (a_{\unicode[STIX]{x1D6FF}}^{n})_{X_{\unicode[STIX]{x1D6FF}}^{\prime }}^{1/n}+C_{3}\cdot \unicode[STIX]{x1D6FF},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\leqslant \frac{(\unicode[STIX]{x1D709}\cdot \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FF}})}{(h\cdot \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FF}})} & {\leqslant} & \displaystyle \frac{(a_{\unicode[STIX]{x1D6FF}}^{n})_{X_{\unicode[STIX]{x1D6FF}}^{\prime }}+C_{1}\cdot \unicode[STIX]{x1D6FF}^{n}}{(h^{n})_{X}^{1/n}\cdot (a_{\unicode[STIX]{x1D6FF}}^{n})_{X_{\unicode[STIX]{x1D6FF}}^{\prime }}^{(n-1)/n}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1}{(h^{n})_{X}^{1/n}}\cdot (a_{\unicode[STIX]{x1D6FF}}^{n})_{X_{\unicode[STIX]{x1D6FF}}^{\prime }}^{1/n}+\frac{C_{1}\cdot \unicode[STIX]{x1D6FF}^{n}}{(h^{n})_{X}^{1/n}}\cdot \frac{2^{(n-1)/n}}{\unicode[STIX]{x1D6FF}^{n-1}\cdot (h^{n})_{X}^{(n-1)/n}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle C_{2}\cdot (a_{\unicode[STIX]{x1D6FF}}^{n})_{X_{\unicode[STIX]{x1D6FF}}^{\prime }}^{1/n}+C_{3}\cdot \unicode[STIX]{x1D6FF},\end{eqnarray}$$ where ![]() $C_{2}$ and
$C_{2}$ and ![]() $C_{3}$ are constants independent of
$C_{3}$ are constants independent of ![]() $\unicode[STIX]{x1D6FF}$.
$\unicode[STIX]{x1D6FF}$.
Now recall that ![]() $\unicode[STIX]{x1D709}$ lies on the boundary of the big cone. Therefore, by the continuity of volume [Reference Lazarsfeld15, Theorem 2.2.44]
$\unicode[STIX]{x1D709}$ lies on the boundary of the big cone. Therefore, by the continuity of volume [Reference Lazarsfeld15, Theorem 2.2.44]
and hence also
Thus from (5.7) we see that ![]() $(\unicode[STIX]{x1D709}\cdot \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FF}})/(h\cdot \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FF}})\rightarrow 0$ as
$(\unicode[STIX]{x1D709}\cdot \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FF}})/(h\cdot \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D6FF}})\rightarrow 0$ as ![]() $\unicode[STIX]{x1D6FF}\rightarrow 0^{+}$. But this contradicts (5.1), and completes the proof.◻
$\unicode[STIX]{x1D6FF}\rightarrow 0^{+}$. But this contradicts (5.1), and completes the proof.◻
Corollary 5.5. Let ![]() $X$ be a projective variety defined over an algebraically closed field of arbitrary characteristic. Then the cone of movable curves, the strongly movable curves and the cone of nef curves all coincide, that is,
$X$ be a projective variety defined over an algebraically closed field of arbitrary characteristic. Then the cone of movable curves, the strongly movable curves and the cone of nef curves all coincide, that is, ![]() $\overline{\operatorname{NM}}(X)=\overline{\operatorname{SNM}}(X)=\overline{\operatorname{NF}}(X)$.
$\overline{\operatorname{NM}}(X)=\overline{\operatorname{SNM}}(X)=\overline{\operatorname{NF}}(X)$.
Proof. From the definition of nef curves it is clear that ![]() $\overline{\operatorname{NF}}(X)=\overline{\operatorname{Eff}}(X)^{\ast }$, and
$\overline{\operatorname{NF}}(X)=\overline{\operatorname{Eff}}(X)^{\ast }$, and ![]() $\overline{\operatorname{Eff}}(X)^{\ast }=\overline{\operatorname{SNM}}(X)$ by Theorem 1.4. Thus we only need to prove that
$\overline{\operatorname{Eff}}(X)^{\ast }=\overline{\operatorname{SNM}}(X)$ by Theorem 1.4. Thus we only need to prove that ![]() $\overline{\operatorname{NM}}(X)=\overline{\operatorname{SNM}}(X)$. The inclusion
$\overline{\operatorname{NM}}(X)=\overline{\operatorname{SNM}}(X)$. The inclusion ![]() $\overline{\operatorname{SNM}}(X)\subseteq \overline{\operatorname{NM}}(X)$ is clear. We prove the other inclusion. Let
$\overline{\operatorname{SNM}}(X)\subseteq \overline{\operatorname{NM}}(X)$ is clear. We prove the other inclusion. Let ![]() $\unicode[STIX]{x1D6FE}\in \overline{\operatorname{NM}}(X)$. Then there exists a movable curve
$\unicode[STIX]{x1D6FE}\in \overline{\operatorname{NM}}(X)$. Then there exists a movable curve ![]() $C$ such that
$C$ such that ![]() $\unicode[STIX]{x1D6FE}=[C]$. By Theorem 1.4 it is enough to show that
$\unicode[STIX]{x1D6FE}=[C]$. By Theorem 1.4 it is enough to show that ![]() $D\cdot \unicode[STIX]{x1D6FE}\geqslant 0$ for all effective Cartier divisors. Since
$D\cdot \unicode[STIX]{x1D6FE}\geqslant 0$ for all effective Cartier divisors. Since ![]() $C$ belongs to an algebraic family of curves
$C$ belongs to an algebraic family of curves ![]() $\{C_{t}\}\text{}_{t\in T}$ such that
$\{C_{t}\}\text{}_{t\in T}$ such that ![]() $\bigcup _{t\in T}C_{t}$ covers a dense subset of
$\bigcup _{t\in T}C_{t}$ covers a dense subset of ![]() $X$, we can find a curve
$X$, we can find a curve ![]() $C_{t_{1}}$ in this family such that
$C_{t_{1}}$ in this family such that ![]() $C_{t_{1}}\nsubseteq \operatorname{Supp}(D)$. Thus
$C_{t_{1}}\nsubseteq \operatorname{Supp}(D)$. Thus ![]() $D\cdot \unicode[STIX]{x1D6FE}=D\cdot C_{t_{1}}\geqslant 0$, that is
$D\cdot \unicode[STIX]{x1D6FE}=D\cdot C_{t_{1}}\geqslant 0$, that is ![]() $\unicode[STIX]{x1D6FE}\in \overline{\operatorname{Eff}}(X)^{\ast }=\overline{\operatorname{SNM}}(X)$.◻
$\unicode[STIX]{x1D6FE}\in \overline{\operatorname{Eff}}(X)^{\ast }=\overline{\operatorname{SNM}}(X)$.◻
Proof of Theorem 1.6.
If there exists an algebraic family of ![]() $K_{X}$-negative rational curves covering a dense subset of
$K_{X}$-negative rational curves covering a dense subset of ![]() $X$, then from Theorem 1.4 and Corollary 5.5 it follows that
$X$, then from Theorem 1.4 and Corollary 5.5 it follows that ![]() $K_{X}$ it not pseudo-effective.
$K_{X}$ it not pseudo-effective.
Now assume that ![]() $K_{X}$ is not pseudo-effective. Then by Theorem 1.4 and Corollary 5.5, there exist a movable class
$K_{X}$ is not pseudo-effective. Then by Theorem 1.4 and Corollary 5.5, there exist a movable class ![]() $\unicode[STIX]{x1D6FE}\in \overline{\operatorname{NM}}(X)$ and an algebraic family of irreducible curves
$\unicode[STIX]{x1D6FE}\in \overline{\operatorname{NM}}(X)$ and an algebraic family of irreducible curves ![]() $\{C_{t}\}\text{}_{t\in T}$ representing
$\{C_{t}\}\text{}_{t\in T}$ representing ![]() $\unicode[STIX]{x1D6FE}$ such that
$\unicode[STIX]{x1D6FE}$ such that ![]() $K_{X}\cdot C_{t}<0$ for all
$K_{X}\cdot C_{t}<0$ for all ![]() $t\in T$ and
$t\in T$ and ![]() $\bigcup _{t\in T}C_{t}\subseteq X$ is dense in
$\bigcup _{t\in T}C_{t}\subseteq X$ is dense in ![]() $X$. We fix a very ample divisor
$X$. We fix a very ample divisor ![]() $H$ in
$H$ in ![]() $X$. Then by [Reference Miyaoka18, Theorem 1.1] there exist rational curves
$X$. Then by [Reference Miyaoka18, Theorem 1.1] there exist rational curves ![]() $\{C_{s}^{\prime }\}\text{}_{s\in S}$ of bounded degree through every point of
$\{C_{s}^{\prime }\}\text{}_{s\in S}$ of bounded degree through every point of ![]() $\bigcup _{t\in T}C_{t}\subseteq X$ such that
$\bigcup _{t\in T}C_{t}\subseteq X$ such that
 $$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle H\cdot C_{s}^{\prime }\leqslant \frac{2\operatorname{dim}X\cdot (H\cdot \unicode[STIX]{x1D6FE})}{-K_{X}\cdot \unicode[STIX]{x1D6FE}}\qquad \text{and}\\ \displaystyle 0<-(K_{X}\cdot C_{s}^{\prime })\leqslant \operatorname{dim}X+1\quad \text{ for all }s\in S.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\displaystyle H\cdot C_{s}^{\prime }\leqslant \frac{2\operatorname{dim}X\cdot (H\cdot \unicode[STIX]{x1D6FE})}{-K_{X}\cdot \unicode[STIX]{x1D6FE}}\qquad \text{and}\\ \displaystyle 0<-(K_{X}\cdot C_{s}^{\prime })\leqslant \operatorname{dim}X+1\quad \text{ for all }s\in S.\end{array}\end{eqnarray}$$ By [Reference Kollár and Mori14, Corollary 1.19(3)] there are finitely many subclasses of these rational curves, say ![]() $\{C_{s}^{\prime }\}\text{}_{s\in S_{i}}$,
$\{C_{s}^{\prime }\}\text{}_{s\in S_{i}}$, ![]() $1\leqslant i\leqslant n,S_{i}\subseteq S\text{ and }\coprod _{i=1}^{n}S_{i}=S$, such that for each fixed
$1\leqslant i\leqslant n,S_{i}\subseteq S\text{ and }\coprod _{i=1}^{n}S_{i}=S$, such that for each fixed ![]() $i$, any two curves in
$i$, any two curves in ![]() $\{C_{s}^{\prime }\}\text{}_{s\in S_{i}}$ are numerically equivalent. Now since
$\{C_{s}^{\prime }\}\text{}_{s\in S_{i}}$ are numerically equivalent. Now since ![]() $\bigcup _{s\in S}C_{s}^{\prime }\subseteq X$ is dense in
$\bigcup _{s\in S}C_{s}^{\prime }\subseteq X$ is dense in ![]() $X$, it follows that one of these subclasses, say
$X$, it follows that one of these subclasses, say ![]() $\{C_{\unicode[STIX]{x1D706}}^{\prime }\}\text{}_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}$,
$\{C_{\unicode[STIX]{x1D706}}^{\prime }\}\text{}_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}$, ![]() $\unicode[STIX]{x1D6EC}=S_{i_{k}}$ for some
$\unicode[STIX]{x1D6EC}=S_{i_{k}}$ for some ![]() $i_{k}\in \{1,2,\ldots ,n\}$ has the property that
$i_{k}\in \{1,2,\ldots ,n\}$ has the property that ![]() $\bigcup _{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}C_{\unicode[STIX]{x1D706}}^{\prime }\subseteq X$ is dense in
$\bigcup _{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}C_{\unicode[STIX]{x1D706}}^{\prime }\subseteq X$ is dense in ![]() $X$. Let
$X$. Let ![]() $d:=H\cdot C_{\unicode[STIX]{x1D706}}^{\prime }$. Then the curves
$d:=H\cdot C_{\unicode[STIX]{x1D706}}^{\prime }$. Then the curves ![]() $\{C_{\unicode[STIX]{x1D706}}^{\prime }\}\text{}_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}$ belong to the family
$\{C_{\unicode[STIX]{x1D706}}^{\prime }\}\text{}_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}$ belong to the family ![]() $\operatorname{Univ}_{d}(\mathbb{P}^{1},X)\rightarrow \operatorname{Hom}_{d}(\mathbb{P}^{1},X)$, where
$\operatorname{Univ}_{d}(\mathbb{P}^{1},X)\rightarrow \operatorname{Hom}_{d}(\mathbb{P}^{1},X)$, where ![]() $\operatorname{Hom}_{d}(\mathbb{P}^{1},X)$ is the scheme of degree
$\operatorname{Hom}_{d}(\mathbb{P}^{1},X)$ is the scheme of degree ![]() $d$ morphisms
$d$ morphisms ![]() $\mathbb{P}^{1}\rightarrow X$. Let
$\mathbb{P}^{1}\rightarrow X$. Let ![]() $V^{\prime }\subseteq \operatorname{Hom}_{d}(\mathbb{P}^{1},X)$ be the connected component of
$V^{\prime }\subseteq \operatorname{Hom}_{d}(\mathbb{P}^{1},X)$ be the connected component of ![]() $\operatorname{Hom}_{d}(\mathbb{P}^{1},X)$ which contains all the points corresponding to the curves
$\operatorname{Hom}_{d}(\mathbb{P}^{1},X)$ which contains all the points corresponding to the curves ![]() $\{C_{\unicode[STIX]{x1D706}}^{\prime }\}\text{}_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}$ (since all
$\{C_{\unicode[STIX]{x1D706}}^{\prime }\}\text{}_{\unicode[STIX]{x1D706}\in \unicode[STIX]{x1D6EC}}$ (since all ![]() $C_{\unicode[STIX]{x1D706}}^{\prime }$’s are numerically equivalent, they are contained in a connected component). Let
$C_{\unicode[STIX]{x1D706}}^{\prime }$’s are numerically equivalent, they are contained in a connected component). Let ![]() ${\mathcal{U}}^{\prime }=V^{\prime }\times _{\operatorname{Hom}_{d}(\mathbb{P}^{1},X)}\operatorname{Univ}_{d}(\mathbb{P}^{1},X)$. Then
${\mathcal{U}}^{\prime }=V^{\prime }\times _{\operatorname{Hom}_{d}(\mathbb{P}^{1},X)}\operatorname{Univ}_{d}(\mathbb{P}^{1},X)$. Then ![]() ${\mathcal{U}}^{\prime }\rightarrow V^{\prime }$ is a (flat) family of rational curves
${\mathcal{U}}^{\prime }\rightarrow V^{\prime }$ is a (flat) family of rational curves ![]() $\unicode[STIX]{x1D6E4}_{t}$ such that
$\unicode[STIX]{x1D6E4}_{t}$ such that ![]() $K_{X}\cdot \unicode[STIX]{x1D6E4}_{t}<0$ and
$K_{X}\cdot \unicode[STIX]{x1D6E4}_{t}<0$ and ![]() $\bigcup _{t\in V^{\prime }}\unicode[STIX]{x1D6E4}_{t}\subseteq X$ is dense in
$\bigcup _{t\in V^{\prime }}\unicode[STIX]{x1D6E4}_{t}\subseteq X$ is dense in ![]() $X$. Finally, let
$X$. Finally, let ![]() $V$ be an irreducible component of
$V$ be an irreducible component of ![]() $V^{\prime }$ such that
$V^{\prime }$ such that ![]() $\bigcup _{t\in V}\unicode[STIX]{x1D6E4}_{t}\subseteq X$ is dense in
$\bigcup _{t\in V}\unicode[STIX]{x1D6E4}_{t}\subseteq X$ is dense in ![]() $X$. Set
$X$. Set ![]() ${\mathcal{U}}=V\times _{V^{\prime }}{\mathcal{U}}^{\prime }=V\times _{\operatorname{Hom}_{d}(\mathbb{P}^{1},X)}\operatorname{Univ}_{d}(\mathbb{P}^{1},X)$. Then
${\mathcal{U}}=V\times _{V^{\prime }}{\mathcal{U}}^{\prime }=V\times _{\operatorname{Hom}_{d}(\mathbb{P}^{1},X)}\operatorname{Univ}_{d}(\mathbb{P}^{1},X)$. Then ![]() ${\mathcal{U}}\rightarrow V$ is a (flat) algebraic family of rational curves satisfying the required conditions.◻
${\mathcal{U}}\rightarrow V$ is a (flat) algebraic family of rational curves satisfying the required conditions.◻
Proof of Corollary 1.7.
Following the notations as in the proof of Theorem 1.6 we see that the evaluation map ![]() $\operatorname{ev}:\mathbb{P}^{1}\times _{k}V\rightarrow X$ is a dominant morphism, where
$\operatorname{ev}:\mathbb{P}^{1}\times _{k}V\rightarrow X$ is a dominant morphism, where ![]() $V$ is an irreducible variety. Thus by [Reference Debarre9, Remark 4.2(2)]
$V$ is an irreducible variety. Thus by [Reference Debarre9, Remark 4.2(2)] ![]() $X$ is uniruled.◻
$X$ is uniruled.◻
6 The structure of the nef cone of curves
In this section, we prove the structure theorem for nef cone of curves. It gives a partial answer to Batyrev’s Conjecture 1.1 in positive characteristic.
We define coextremal rays and bounding divisors as in [Reference Lehmann17].
Definition 6.1. Let ![]() $\unicode[STIX]{x1D6FC}$ be a class in
$\unicode[STIX]{x1D6FC}$ be a class in ![]() $\overline{\operatorname{NM}}(X)$. A coextremal ray
$\overline{\operatorname{NM}}(X)$. A coextremal ray ![]() $\mathbb{R}_{{\geqslant}0}\unicode[STIX]{x1D6FC}\subseteq N_{1}(X)$ is a
$\mathbb{R}_{{\geqslant}0}\unicode[STIX]{x1D6FC}\subseteq N_{1}(X)$ is a ![]() $(K_{X}+\unicode[STIX]{x1D6E5})$-negative ray of
$(K_{X}+\unicode[STIX]{x1D6E5})$-negative ray of ![]() $\overline{\operatorname{NM}}(X)$ which is extremal for
$\overline{\operatorname{NM}}(X)$ which is extremal for ![]() $\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+\overline{\operatorname{NM}}(X)$; equivalently it satisfies the following properties:
$\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+\overline{\operatorname{NM}}(X)$; equivalently it satisfies the following properties:
(1)
 $(K_{X}+\unicode[STIX]{x1D6E5})\cdot \unicode[STIX]{x1D6FC}<0$.
$(K_{X}+\unicode[STIX]{x1D6E5})\cdot \unicode[STIX]{x1D6FC}<0$.(2) If
 $\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2}\in \overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+\overline{\operatorname{NM}}(X)$ and
$\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2}\in \overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+\overline{\operatorname{NM}}(X)$ and  $\unicode[STIX]{x1D6FD}_{1}+\unicode[STIX]{x1D6FD}_{2}\in \mathbb{R}_{{\geqslant}0}\unicode[STIX]{x1D6FC}$, then
$\unicode[STIX]{x1D6FD}_{1}+\unicode[STIX]{x1D6FD}_{2}\in \mathbb{R}_{{\geqslant}0}\unicode[STIX]{x1D6FC}$, then  $\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2}\in \mathbb{R}_{{\geqslant}0}\unicode[STIX]{x1D6FC}$.
$\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2}\in \mathbb{R}_{{\geqslant}0}\unicode[STIX]{x1D6FC}$.
Definition 6.2. A nonzero ![]() $\mathbb{R}$-Cartier divisor
$\mathbb{R}$-Cartier divisor ![]() $D$ is called a bounding divisor if it satisfies the following properties:
$D$ is called a bounding divisor if it satisfies the following properties:
(1)
 $D\cdot \unicode[STIX]{x1D6FC}\geqslant 0$ for every class
$D\cdot \unicode[STIX]{x1D6FC}\geqslant 0$ for every class  $\unicode[STIX]{x1D6FC}$ in
$\unicode[STIX]{x1D6FC}$ in  $\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+\overline{\operatorname{NM}}(X)$.
$\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+\overline{\operatorname{NM}}(X)$.(2)
 $D^{\bot }$ contains some coextremal ray.
$D^{\bot }$ contains some coextremal ray.
For a subset ![]() $V\subseteq N_{1}(X)$, a bounding divisor
$V\subseteq N_{1}(X)$, a bounding divisor ![]() $D$ is called a
$D$ is called a ![]() $V$-bounding divisor if
$V$-bounding divisor if ![]() $D\cdot \unicode[STIX]{x1D6FC}\geqslant 0$ for all
$D\cdot \unicode[STIX]{x1D6FC}\geqslant 0$ for all ![]() $\unicode[STIX]{x1D6FC}\in V$.
$\unicode[STIX]{x1D6FC}\in V$.
We need the following results first.
Lemma 6.3. Let ![]() $(X,\unicode[STIX]{x1D6E5}\geqslant 0)$ be a
$(X,\unicode[STIX]{x1D6E5}\geqslant 0)$ be a ![]() $\mathbb{Q}$-factorial projective KLT pair of dimension
$\mathbb{Q}$-factorial projective KLT pair of dimension ![]() $3$ and
$3$ and ![]() $\operatorname{char}p>5$. Suppose that
$\operatorname{char}p>5$. Suppose that ![]() $\unicode[STIX]{x1D6E5}$ is a big
$\unicode[STIX]{x1D6E5}$ is a big ![]() $\mathbb{R}$-divisor. If
$\mathbb{R}$-divisor. If ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ lies on the boundary of
$K_{X}+\unicode[STIX]{x1D6E5}$ lies on the boundary of ![]() $\overline{\operatorname{Eff}}(X)$, then there exists a birational contraction
$\overline{\operatorname{Eff}}(X)$, then there exists a birational contraction ![]() $\unicode[STIX]{x1D719}:X{\dashrightarrow}X^{\prime }$, a projective morphism
$\unicode[STIX]{x1D719}:X{\dashrightarrow}X^{\prime }$, a projective morphism ![]() $f:X^{\prime }\rightarrow Y$ and an ample
$f:X^{\prime }\rightarrow Y$ and an ample ![]() $\mathbb{R}$-divisor
$\mathbb{R}$-divisor ![]() $L$ on
$L$ on ![]() $Y$ such that
$Y$ such that ![]() $K_{X^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime }{\sim}_{\mathbb{R}}f^{\ast }L$ and
$K_{X^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime }{\sim}_{\mathbb{R}}f^{\ast }L$ and ![]() $-(K_{X^{\prime }}+G^{\prime })$ is
$-(K_{X^{\prime }}+G^{\prime })$ is ![]() $f$-ample for some KLT pair
$f$-ample for some KLT pair ![]() $(X^{\prime },G^{\prime })$, where
$(X^{\prime },G^{\prime })$, where ![]() $K_{X^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime }=\unicode[STIX]{x1D719}_{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$.
$K_{X^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime }=\unicode[STIX]{x1D719}_{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$.
Proof. Let ![]() $H\geqslant 0$ be an ample
$H\geqslant 0$ be an ample ![]() $\mathbb{R}$-divisor on
$\mathbb{R}$-divisor on ![]() $X$ such that
$X$ such that ![]() $K_{X}+\unicode[STIX]{x1D6E5}+H$ is KLT and nef (using Theorem 3.1). Since
$K_{X}+\unicode[STIX]{x1D6E5}+H$ is KLT and nef (using Theorem 3.1). Since ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ is pseudo-effective, by [Reference Birkar and Waldron6, Theorem 1.6]
$K_{X}+\unicode[STIX]{x1D6E5}$ is pseudo-effective, by [Reference Birkar and Waldron6, Theorem 1.6] ![]() $(K_{X}+\unicode[STIX]{x1D6E5})$-MMP with the scaling of
$(K_{X}+\unicode[STIX]{x1D6E5})$-MMP with the scaling of ![]() $H$ terminates with a log minimal model
$H$ terminates with a log minimal model ![]() $\unicode[STIX]{x1D719}^{\prime }:X{\dashrightarrow}X^{\prime }$ such that
$\unicode[STIX]{x1D719}^{\prime }:X{\dashrightarrow}X^{\prime }$ such that ![]() $K_{X^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime }=\unicode[STIX]{x1D719}_{\ast }^{\prime }(K_{X}+\unicode[STIX]{x1D6E5})$ is nef. Since
$K_{X^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime }=\unicode[STIX]{x1D719}_{\ast }^{\prime }(K_{X}+\unicode[STIX]{x1D6E5})$ is nef. Since ![]() $\unicode[STIX]{x1D6E5}^{\prime }$ is a big divisor, by perturbing
$\unicode[STIX]{x1D6E5}^{\prime }$ is a big divisor, by perturbing ![]() $\unicode[STIX]{x1D6E5}^{\prime }$, from the base-point free theorem [Reference Birkar and Waldron6, Theorem 1.2] it follows that
$\unicode[STIX]{x1D6E5}^{\prime }$, from the base-point free theorem [Reference Birkar and Waldron6, Theorem 1.2] it follows that ![]() $K_{X^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime }$ is semi-ample. Therefore, there exists a projective morphism
$K_{X^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime }$ is semi-ample. Therefore, there exists a projective morphism ![]() $f:X^{\prime }\rightarrow Y$ and an ample
$f:X^{\prime }\rightarrow Y$ and an ample ![]() $\mathbb{R}$-divisor
$\mathbb{R}$-divisor ![]() $L$ on
$L$ on ![]() $Y$ such that
$Y$ such that ![]() $K_{X^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime }{\sim}_{\mathbb{R}}f^{\ast }L$ (see [Reference Fujino10, Lemma 4.13]). Write
$K_{X^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime }{\sim}_{\mathbb{R}}f^{\ast }L$ (see [Reference Fujino10, Lemma 4.13]). Write ![]() $\unicode[STIX]{x1D6E5}^{\prime }=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}\equiv A^{\prime }+B^{\prime }$, where
$\unicode[STIX]{x1D6E5}^{\prime }=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}\equiv A^{\prime }+B^{\prime }$, where ![]() $A^{\prime }$ is an ample
$A^{\prime }$ is an ample ![]() $\mathbb{R}$-divisor. Then
$\mathbb{R}$-divisor. Then ![]() $(X^{\prime },\unicode[STIX]{x1D6E5}^{\prime }+\unicode[STIX]{x1D700}B^{\prime })$ is KLT for
$(X^{\prime },\unicode[STIX]{x1D6E5}^{\prime }+\unicode[STIX]{x1D700}B^{\prime })$ is KLT for ![]() $0<\unicode[STIX]{x1D700}\ll 1$. In particular,
$0<\unicode[STIX]{x1D700}\ll 1$. In particular, ![]() $(X^{\prime },(1-\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}^{\prime }+\unicode[STIX]{x1D700}B^{\prime })$ is KLT. Let
$(X^{\prime },(1-\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}^{\prime }+\unicode[STIX]{x1D700}B^{\prime })$ is KLT. Let ![]() $G^{\prime }=(1-\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}^{\prime }+\unicode[STIX]{x1D700}B^{\prime }\geqslant 0$. Then
$G^{\prime }=(1-\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}^{\prime }+\unicode[STIX]{x1D700}B^{\prime }\geqslant 0$. Then ![]() $(X^{\prime },G^{\prime })$ is KLT and
$(X^{\prime },G^{\prime })$ is KLT and ![]() $K_{X^{\prime }}+G^{\prime }\equiv _{f}-\unicode[STIX]{x1D700}A^{\prime }$.◻
$K_{X^{\prime }}+G^{\prime }\equiv _{f}-\unicode[STIX]{x1D700}A^{\prime }$.◻
Remark 6.4. Note that the variety ![]() $Y$ in the lemma above is uniquely determined by
$Y$ in the lemma above is uniquely determined by ![]() $K_{X}+\unicode[STIX]{x1D6E5}$, since it is the ample model of
$K_{X}+\unicode[STIX]{x1D6E5}$, since it is the ample model of ![]() $(X,\unicode[STIX]{x1D6E5})$.
$(X,\unicode[STIX]{x1D6E5})$.
Proposition 6.5. Let ![]() $(X,\unicode[STIX]{x1D6E5}\geqslant 0)$ be a
$(X,\unicode[STIX]{x1D6E5}\geqslant 0)$ be a ![]() $\mathbb{Q}$-factorial projective KLT pair with
$\mathbb{Q}$-factorial projective KLT pair with ![]() $\operatorname{dim}X=3$ and
$\operatorname{dim}X=3$ and ![]() $\operatorname{char}p>5$. Suppose that
$\operatorname{char}p>5$. Suppose that ![]() $A\geqslant 0$ is a general ample
$A\geqslant 0$ is a general ample ![]() $\mathbb{Q}$-divisor on
$\mathbb{Q}$-divisor on ![]() $X$. Let
$X$. Let ![]() $V$ be a finite dimensional subspace of
$V$ be a finite dimensional subspace of ![]() $\operatorname{WDiv}_{\mathbb{R}}(X)$. Define
$\operatorname{WDiv}_{\mathbb{R}}(X)$. Define
Then there are finitely many birational contractions ![]() $\unicode[STIX]{x1D719}_{i}:X{\dashrightarrow}X_{i}$ for
$\unicode[STIX]{x1D719}_{i}:X{\dashrightarrow}X_{i}$ for ![]() $1\leqslant i\leqslant k$ such that for every
$1\leqslant i\leqslant k$ such that for every ![]() $\unicode[STIX]{x1D6E4}\in {\mathcal{E}}_{A}$ satisfying the property that
$\unicode[STIX]{x1D6E4}\in {\mathcal{E}}_{A}$ satisfying the property that ![]() $K_{X}+\unicode[STIX]{x1D6E5}+A+\unicode[STIX]{x1D6E4}$ lies on the boundary of
$K_{X}+\unicode[STIX]{x1D6E5}+A+\unicode[STIX]{x1D6E4}$ lies on the boundary of ![]() $\overline{\operatorname{Eff}}(X)$, there exists an index
$\overline{\operatorname{Eff}}(X)$, there exists an index ![]() $1\leqslant j\leqslant k$ such that
$1\leqslant j\leqslant k$ such that ![]() $\unicode[STIX]{x1D719}_{j}$ is a log minimal model of
$\unicode[STIX]{x1D719}_{j}$ is a log minimal model of ![]() $K_{X}+\unicode[STIX]{x1D6E5}+A+\unicode[STIX]{x1D6E4}$. Furthermore, corresponding to each
$K_{X}+\unicode[STIX]{x1D6E5}+A+\unicode[STIX]{x1D6E4}$. Furthermore, corresponding to each ![]() $\unicode[STIX]{x1D719}_{i}$, there exists a unique log Fano fibration
$\unicode[STIX]{x1D719}_{i}$, there exists a unique log Fano fibration ![]() $g_{i}:X_{i}\rightarrow Y_{i}$ such that
$g_{i}:X_{i}\rightarrow Y_{i}$ such that ![]() $K_{X_{i}}+{\unicode[STIX]{x1D719}_{i}}_{\ast }(\unicode[STIX]{x1D6E5}+A+\unicode[STIX]{x1D6E4}){\sim}_{\mathbb{R}}g_{i}^{\ast }L_{i}$, where
$K_{X_{i}}+{\unicode[STIX]{x1D719}_{i}}_{\ast }(\unicode[STIX]{x1D6E5}+A+\unicode[STIX]{x1D6E4}){\sim}_{\mathbb{R}}g_{i}^{\ast }L_{i}$, where ![]() $L_{i}$ is an ample
$L_{i}$ is an ample ![]() $\mathbb{R}$-divisor on
$\mathbb{R}$-divisor on ![]() $Y_{i}$.
$Y_{i}$.
Proof. This result corresponds to [Reference Lehmann17, Theorem 3.2].
For a given ![]() $\unicode[STIX]{x1D6E4}\in {\mathcal{E}}_{A}$ the existence of
$\unicode[STIX]{x1D6E4}\in {\mathcal{E}}_{A}$ the existence of ![]() $\unicode[STIX]{x1D719}_{i}$ and
$\unicode[STIX]{x1D719}_{i}$ and ![]() $g_{i}$ is clear from Lemma 6.3. Then from Theorem 1.2 and Remark 6.4 it follows that there are only finitely many such
$g_{i}$ is clear from Lemma 6.3. Then from Theorem 1.2 and Remark 6.4 it follows that there are only finitely many such ![]() $\unicode[STIX]{x1D719}_{i}$ and
$\unicode[STIX]{x1D719}_{i}$ and ![]() $g_{i}$ for all
$g_{i}$ for all ![]() $\unicode[STIX]{x1D6E4}\in {\mathcal{E}}_{A}$.◻
$\unicode[STIX]{x1D6E4}\in {\mathcal{E}}_{A}$.◻
Proposition 6.6. Let ![]() $(X,\unicode[STIX]{x1D6E5})$ be a
$(X,\unicode[STIX]{x1D6E5})$ be a ![]() $\mathbb{Q}$-factorial projective KLT pair with
$\mathbb{Q}$-factorial projective KLT pair with ![]() $\operatorname{dim}X=3$ and
$\operatorname{dim}X=3$ and ![]() $\operatorname{char}p>5$. Suppose that
$\operatorname{char}p>5$. Suppose that ![]() $B\geqslant 0$ is a big
$B\geqslant 0$ is a big ![]() $\mathbb{R}$-divisor such that
$\mathbb{R}$-divisor such that ![]() $(X,\unicode[STIX]{x1D6E5}+B)$ is KLT. Then there exist an open neighborhood
$(X,\unicode[STIX]{x1D6E5}+B)$ is KLT. Then there exist an open neighborhood ![]() $U\subseteq N^{1}(X)$ of
$U\subseteq N^{1}(X)$ of ![]() $[K_{X}+\unicode[STIX]{x1D6E5}+B]\in N^{1}(X)$ and a finite set of movable curves
$[K_{X}+\unicode[STIX]{x1D6E5}+B]\in N^{1}(X)$ and a finite set of movable curves ![]() $\{C_{i}\}\text{}_{i=1}^{N}$ on
$\{C_{i}\}\text{}_{i=1}^{N}$ on ![]() $X$ such that for every class
$X$ such that for every class ![]() $\unicode[STIX]{x1D6FC}\in U$ which lies on the boundary of
$\unicode[STIX]{x1D6FC}\in U$ which lies on the boundary of ![]() $\overline{\operatorname{Eff}}(X)$ we have
$\overline{\operatorname{Eff}}(X)$ we have ![]() $\unicode[STIX]{x1D6FC}\cdot C_{i}=0$ for some
$\unicode[STIX]{x1D6FC}\cdot C_{i}=0$ for some ![]() $i\in \{1,2,\ldots ,N\}$.
$i\in \{1,2,\ldots ,N\}$.
Proof. This result corresponds to [Reference Lehmann17, Proposition 3.3].
Since ![]() $B$ is a big
$B$ is a big ![]() $\mathbb{R}$-divisor,
$\mathbb{R}$-divisor, ![]() $B\equiv H+E$ for some ample
$B\equiv H+E$ for some ample ![]() $\mathbb{R}$-divisor
$\mathbb{R}$-divisor ![]() $H\geqslant 0$ and an effective
$H\geqslant 0$ and an effective ![]() $\mathbb{R}$-divisor
$\mathbb{R}$-divisor ![]() $E$. Then
$E$. Then ![]() $K_{X}+\unicode[STIX]{x1D6E5}+B+\unicode[STIX]{x1D700}E$ is KLT for
$K_{X}+\unicode[STIX]{x1D6E5}+B+\unicode[STIX]{x1D700}E$ is KLT for ![]() $0<\unicode[STIX]{x1D700}\ll 1$. In particular,
$0<\unicode[STIX]{x1D700}\ll 1$. In particular, ![]() $K_{X}+\unicode[STIX]{x1D6E5}+(1-\unicode[STIX]{x1D700})B+\unicode[STIX]{x1D700}E$ is KLT. Let
$K_{X}+\unicode[STIX]{x1D6E5}+(1-\unicode[STIX]{x1D700})B+\unicode[STIX]{x1D700}E$ is KLT. Let ![]() $A\geqslant 0$ be an ample
$A\geqslant 0$ be an ample ![]() $\mathbb{Q}$-divisor such that
$\mathbb{Q}$-divisor such that ![]() $\unicode[STIX]{x1D700}H-A$ is ample and
$\unicode[STIX]{x1D700}H-A$ is ample and ![]() $K_{X}+\unicode[STIX]{x1D6E5}+A+(1-\unicode[STIX]{x1D700})B+\unicode[STIX]{x1D700}E$ is KLT, by Theorem 3.1. Let
$K_{X}+\unicode[STIX]{x1D6E5}+A+(1-\unicode[STIX]{x1D700})B+\unicode[STIX]{x1D700}E$ is KLT, by Theorem 3.1. Let ![]() $\{H_{j}\geqslant 0\}\text{}_{j=1}^{m}$ be a finite set of ample
$\{H_{j}\geqslant 0\}\text{}_{j=1}^{m}$ be a finite set of ample ![]() $\mathbb{Q}$-divisors such that the convex hull of the classes
$\mathbb{Q}$-divisors such that the convex hull of the classes ![]() $[H_{j}]$’s contains an open set around
$[H_{j}]$’s contains an open set around ![]() $[\unicode[STIX]{x1D700}H-A]$ in
$[\unicode[STIX]{x1D700}H-A]$ in ![]() $N^{1}(X)$. Let
$N^{1}(X)$. Let ![]() $U^{\prime }$ be an open neighborhood of
$U^{\prime }$ be an open neighborhood of ![]() $[B-A]$ contained in the convex hull of
$[B-A]$ contained in the convex hull of ![]() $[B-\unicode[STIX]{x1D700}H+H_{j}]$’s. We apply [Reference Lehmann17, Lemma 3.1] to
$[B-\unicode[STIX]{x1D700}H+H_{j}]$’s. We apply [Reference Lehmann17, Lemma 3.1] to ![]() $K_{X}+\unicode[STIX]{x1D6E5}+A+(1-\unicode[STIX]{x1D700})B+\unicode[STIX]{x1D700}E$ and
$K_{X}+\unicode[STIX]{x1D6E5}+A+(1-\unicode[STIX]{x1D700})B+\unicode[STIX]{x1D700}E$ and ![]() $H_{j}$’s to obtain finitely many ample
$H_{j}$’s to obtain finitely many ample ![]() $\mathbb{Q}$-divisors
$\mathbb{Q}$-divisors ![]() $0\leqslant W_{j}{\sim}_{\mathbb{Q}}H_{j}$. Let
$0\leqslant W_{j}{\sim}_{\mathbb{Q}}H_{j}$. Let ![]() $V$ be the vector space of
$V$ be the vector space of ![]() $\mathbb{R}$-divisors spanned by the irreducible components of
$\mathbb{R}$-divisors spanned by the irreducible components of ![]() $(1-\unicode[STIX]{x1D700})B+\unicode[STIX]{x1D700}E$ and of the
$(1-\unicode[STIX]{x1D700})B+\unicode[STIX]{x1D700}E$ and of the ![]() $W_{j}$’s. Therefore,
$W_{j}$’s. Therefore, ![]() $V$ is a finite dimensional subspace of
$V$ is a finite dimensional subspace of ![]() $\operatorname{WDiv}(X)_{\mathbb{R}}$ such that every class in
$\operatorname{WDiv}(X)_{\mathbb{R}}$ such that every class in ![]() $U^{\prime }$ has an effective representative
$U^{\prime }$ has an effective representative ![]() $\unicode[STIX]{x1D6E4}\in V$ with
$\unicode[STIX]{x1D6E4}\in V$ with ![]() $(X,\unicode[STIX]{x1D6E5}+A+\unicode[STIX]{x1D6E4})$ KLT.
$(X,\unicode[STIX]{x1D6E5}+A+\unicode[STIX]{x1D6E4})$ KLT.
Let ![]() $\unicode[STIX]{x1D6E4}\in V$ be a representative of a class in
$\unicode[STIX]{x1D6E4}\in V$ be a representative of a class in ![]() $U^{\prime }$ such that
$U^{\prime }$ such that ![]() $D=K_{X}+\unicode[STIX]{x1D6E5}+A+\unicode[STIX]{x1D6E4}$ is KLT. We can run the
$D=K_{X}+\unicode[STIX]{x1D6E5}+A+\unicode[STIX]{x1D6E4}$ is KLT. We can run the ![]() $D$-MMP with the scaling of an ample divisor. If
$D$-MMP with the scaling of an ample divisor. If ![]() $D$ lies on the boundary of
$D$ lies on the boundary of ![]() $\overline{\operatorname{Eff}}(X)$, then by Proposition 6.5 there exists a birational contraction
$\overline{\operatorname{Eff}}(X)$, then by Proposition 6.5 there exists a birational contraction ![]() $\unicode[STIX]{x1D719}_{i}:X{\dashrightarrow}X_{i}$ and a log Fano fibration
$\unicode[STIX]{x1D719}_{i}:X{\dashrightarrow}X_{i}$ and a log Fano fibration ![]() $g_{i}:X_{i}\rightarrow Z_{i}$ such that
$g_{i}:X_{i}\rightarrow Z_{i}$ such that ![]() $K_{X_{i}}+{\unicode[STIX]{x1D719}_{i}}_{\ast }(\unicode[STIX]{x1D6E5}+A+\unicode[STIX]{x1D6E4}){\sim}_{\mathbb{R}}f^{\ast }L_{i}$ for some ample
$K_{X_{i}}+{\unicode[STIX]{x1D719}_{i}}_{\ast }(\unicode[STIX]{x1D6E5}+A+\unicode[STIX]{x1D6E4}){\sim}_{\mathbb{R}}f^{\ast }L_{i}$ for some ample ![]() $\mathbb{R}$-divisor
$\mathbb{R}$-divisor ![]() $L_{i}$ on
$L_{i}$ on ![]() $Z_{i}$. Let
$Z_{i}$. Let ![]() $C_{i}^{\prime }$ be a curve on a general fiber of
$C_{i}^{\prime }$ be a curve on a general fiber of ![]() $g_{i}$. Note that the exceptional locus
$g_{i}$. Note that the exceptional locus ![]() $\operatorname{Ex}(\unicode[STIX]{x1D719}_{i}^{-1})$ where
$\operatorname{Ex}(\unicode[STIX]{x1D719}_{i}^{-1})$ where ![]() $\unicode[STIX]{x1D719}_{i}^{-1}:X_{i}{\dashrightarrow}X$ is not an isomorphism intersects the general fiber of
$\unicode[STIX]{x1D719}_{i}^{-1}:X_{i}{\dashrightarrow}X$ is not an isomorphism intersects the general fiber of ![]() $g_{i}$ along at least codimension
$g_{i}$ along at least codimension ![]() $2$ subsets (see [Reference Birkar and Waldron6, Lemma 2.4]). Therefore, by choosing
$2$ subsets (see [Reference Birkar and Waldron6, Lemma 2.4]). Therefore, by choosing ![]() $C_{i}^{\prime }$ sufficiently general we see that
$C_{i}^{\prime }$ sufficiently general we see that ![]() $\unicode[STIX]{x1D719}_{i}:X_{i}{\dashrightarrow}X$ is an isomorphism in a neighborhood of
$\unicode[STIX]{x1D719}_{i}:X_{i}{\dashrightarrow}X$ is an isomorphism in a neighborhood of ![]() $C_{i}^{\prime }$ and
$C_{i}^{\prime }$ and ![]() $C_{i}^{\prime }$ belongs to a family of curves dominating
$C_{i}^{\prime }$ belongs to a family of curves dominating ![]() $X_{i}$. Let
$X_{i}$. Let ![]() $C_{i}$ be the image of
$C_{i}$ be the image of ![]() $C_{i}^{\prime }$ under
$C_{i}^{\prime }$ under ![]() $\unicode[STIX]{x1D719}_{i}^{-1}$. Then
$\unicode[STIX]{x1D719}_{i}^{-1}$. Then ![]() $C_{i}$ is a movable curve on
$C_{i}$ is a movable curve on ![]() $X$ and
$X$ and ![]() $D\cdot C_{i}=(K_{X_{i}}+{\unicode[STIX]{x1D719}_{i}}_{\ast }(\unicode[STIX]{x1D6E5}+A+\unicode[STIX]{x1D6E4}))\cdot C_{i}^{\prime }=f^{\ast }L_{i}\cdot C_{i}^{\prime }=0$.
$D\cdot C_{i}=(K_{X_{i}}+{\unicode[STIX]{x1D719}_{i}}_{\ast }(\unicode[STIX]{x1D6E5}+A+\unicode[STIX]{x1D6E4}))\cdot C_{i}^{\prime }=f^{\ast }L_{i}\cdot C_{i}^{\prime }=0$.
Now by Proposition 6.5 there are finitely many log Fano fibrations ![]() $g_{i}:X_{i}\rightarrow Z_{i}$ for all
$g_{i}:X_{i}\rightarrow Z_{i}$ for all ![]() $\unicode[STIX]{x1D6E4}\in V$. Therefore, there are finitely many movable curves
$\unicode[STIX]{x1D6E4}\in V$. Therefore, there are finitely many movable curves ![]() $\{C_{i}\}$ on
$\{C_{i}\}$ on ![]() $X$ satisfying the properties as in the previous paragraph. Set
$X$ satisfying the properties as in the previous paragraph. Set ![]() $U=U^{\prime }+[K_{X}+\unicode[STIX]{x1D6E5}+A]$. Then
$U=U^{\prime }+[K_{X}+\unicode[STIX]{x1D6E5}+A]$. Then ![]() $U$ is an open neighborhood of
$U$ is an open neighborhood of ![]() $[K_{X}+\unicode[STIX]{x1D6E5}+A]$ and the curves
$[K_{X}+\unicode[STIX]{x1D6E5}+A]$ and the curves ![]() $C_{i}$’s have the required properties.◻
$C_{i}$’s have the required properties.◻
Corollary 6.7. Let ![]() $(X,\unicode[STIX]{x1D6E5})$ be a
$(X,\unicode[STIX]{x1D6E5})$ be a ![]() $\mathbb{Q}$-factorial projective KLT pair with
$\mathbb{Q}$-factorial projective KLT pair with ![]() $\operatorname{dim}X=3$ and
$\operatorname{dim}X=3$ and ![]() $\operatorname{char}p>5$. Suppose that
$\operatorname{char}p>5$. Suppose that ![]() ${\mathcal{S}}\subseteq \overline{\operatorname{Eff}}(X)$ is a set of divisor classes satisfying the following properties:
${\mathcal{S}}\subseteq \overline{\operatorname{Eff}}(X)$ is a set of divisor classes satisfying the following properties:
(1)
 ${\mathcal{S}}$ is closed.
${\mathcal{S}}$ is closed.(2) For each element
 $\unicode[STIX]{x1D6FD}\in {\mathcal{S}}$, there is some big effective divisor
$\unicode[STIX]{x1D6FD}\in {\mathcal{S}}$, there is some big effective divisor  $B$ such that
$B$ such that  $(X,\unicode[STIX]{x1D6E5}+B)$ is KLT and
$(X,\unicode[STIX]{x1D6E5}+B)$ is KLT and  $[K_{X}+\unicode[STIX]{x1D6E5}+B]=c\unicode[STIX]{x1D6FD}$ for some
$[K_{X}+\unicode[STIX]{x1D6E5}+B]=c\unicode[STIX]{x1D6FD}$ for some  $c>0$.
$c>0$.
Then there are finitely many movable curves ![]() $\{C_{i}\}$ such that every class
$\{C_{i}\}$ such that every class ![]() $\unicode[STIX]{x1D6FC}$ which lies on the boundary of
$\unicode[STIX]{x1D6FC}$ which lies on the boundary of ![]() $\overline{\operatorname{Eff}}(X)$ satisfies
$\overline{\operatorname{Eff}}(X)$ satisfies ![]() $\unicode[STIX]{x1D6FC}\cdot C_{i}=0$ for some
$\unicode[STIX]{x1D6FC}\cdot C_{i}=0$ for some ![]() $i$.
$i$.
Proof. With the help of Proposition 6.6, the same proof as in [Reference Lehmann17, Corollary 3.5] works. ◻
Proposition 6.8. Let ![]() $(X,\unicode[STIX]{x1D6E5})$ be a
$(X,\unicode[STIX]{x1D6E5})$ be a ![]() $\mathbb{Q}$-factorial projective KLT pair with
$\mathbb{Q}$-factorial projective KLT pair with ![]() $\operatorname{dim}X=3$ and
$\operatorname{dim}X=3$ and ![]() $\operatorname{char}p>5$. Let
$\operatorname{char}p>5$. Let ![]() $V$ be a closed convex cone containing
$V$ be a closed convex cone containing ![]() $\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}=0}-\{0\}$ in its interior. Then there is a finite set of movable curves
$\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}=0}-\{0\}$ in its interior. Then there is a finite set of movable curves ![]() $\{C_{i}\}$ such that for any
$\{C_{i}\}$ such that for any ![]() $V$-bounding divisor
$V$-bounding divisor ![]() $D$ there is some
$D$ there is some ![]() $C_{i}$ for which
$C_{i}$ for which ![]() $D\cdot C_{i}=0$.
$D\cdot C_{i}=0$.
Proof. This result corresponds to [Reference Lehmann17, Proposition 4.4].
Let ![]() ${\mathcal{S}}$ be the set of all
${\mathcal{S}}$ be the set of all ![]() $V$-bounding divisors. We may assume that
$V$-bounding divisors. We may assume that ![]() ${\mathcal{S}}$ is nonempty, otherwise there is nothing to prove. Note that a nonzero
${\mathcal{S}}$ is nonempty, otherwise there is nothing to prove. Note that a nonzero ![]() $\mathbb{R}$-Cartier divisor
$\mathbb{R}$-Cartier divisor ![]() $D$ is
$D$ is ![]() $V$-bounding if and only if
$V$-bounding if and only if ![]() $D$ lies on the boundary of
$D$ lies on the boundary of ![]() $\overline{\operatorname{Eff}}(X)$ and satisfies the closed condition
$\overline{\operatorname{Eff}}(X)$ and satisfies the closed condition
Now by [Reference Lehmann17, Lemma 4.3] there exists an ample ![]() $\mathbb{R}$-Cartier divisor
$\mathbb{R}$-Cartier divisor ![]() $A_{D}\geqslant 0$ and a positive real number
$A_{D}\geqslant 0$ and a positive real number ![]() $\unicode[STIX]{x1D6FF}_{D}>0$ such that
$\unicode[STIX]{x1D6FF}_{D}>0$ such that
Let ![]() $A^{\prime }\geqslant 0$ be an ample
$A^{\prime }\geqslant 0$ be an ample ![]() $\mathbb{R}$-divisor such that
$\mathbb{R}$-divisor such that ![]() $A^{\prime }{\sim}_{\mathbb{R}}(1/\unicode[STIX]{x1D6FF}_{D})A_{D}$ and
$A^{\prime }{\sim}_{\mathbb{R}}(1/\unicode[STIX]{x1D6FF}_{D})A_{D}$ and ![]() $(X,\unicode[STIX]{x1D6E5}+A^{\prime })$ is KLT (see Theorem 3.1). Then we have
$(X,\unicode[STIX]{x1D6E5}+A^{\prime })$ is KLT (see Theorem 3.1). Then we have
Therefore, by Corollary 6.7 there exists finitely many movable curves ![]() $\{C_{i}\}$ satisfying the required conditions.◻
$\{C_{i}\}$ satisfying the required conditions.◻
Theorem 6.9. Let ![]() $(X,\unicode[STIX]{x1D6E5})$ be a
$(X,\unicode[STIX]{x1D6E5})$ be a ![]() $\mathbb{Q}$-factorial projective DLT pair with
$\mathbb{Q}$-factorial projective DLT pair with ![]() $\operatorname{dim}X=3$ and
$\operatorname{dim}X=3$ and ![]() $\operatorname{char}p>5$. Let
$\operatorname{char}p>5$. Let ![]() $V$ be a closed convex cone containing
$V$ be a closed convex cone containing ![]() $\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}=0}-\{0\}$ in its interior. Then there exist finitely many movable curves
$\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}=0}-\{0\}$ in its interior. Then there exist finitely many movable curves ![]() $C_{i}$ such that
$C_{i}$ such that
Proof. This result is a variant of [Reference Lehmann17, Corollary 4.5].
Without loss of generality we may assume by shrinking ![]() $V$ if necessary that
$V$ if necessary that ![]() $\overline{\operatorname{NE}}(X)+V$ does not contain any
$\overline{\operatorname{NE}}(X)+V$ does not contain any ![]() $1$-dimensional subspace of
$1$-dimensional subspace of ![]() $N_{1}(X)$. Then there exists an ample divisor
$N_{1}(X)$. Then there exists an ample divisor ![]() $A$ which is positive on
$A$ which is positive on ![]() $V-\{0\}$.
$V-\{0\}$.
First we reduce the problem to the KLT case. Let ![]() $H\geqslant 0$ be an ample
$H\geqslant 0$ be an ample ![]() $\mathbb{Q}$-divisor on
$\mathbb{Q}$-divisor on ![]() $X$. Since
$X$. Since ![]() $X$ is
$X$ is ![]() $\mathbb{Q}$-factorial,
$\mathbb{Q}$-factorial, ![]() $H+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6E5}$ is ample for
$H+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6E5}$ is ample for ![]() $0<\unicode[STIX]{x1D700}\ll 1$. Let
$0<\unicode[STIX]{x1D700}\ll 1$. Let ![]() $0\leqslant A{\sim}_{\mathbb{R}}H+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6E5}$ be an ample divisor which avoids all DLT centers of
$0\leqslant A{\sim}_{\mathbb{R}}H+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6E5}$ be an ample divisor which avoids all DLT centers of ![]() $(X,\unicode[STIX]{x1D6E5})$ as well as all irreducible components of
$(X,\unicode[STIX]{x1D6E5})$ as well as all irreducible components of ![]() $\unicode[STIX]{x1D6E5}$. Then
$\unicode[STIX]{x1D6E5}$. Then ![]() $(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}A)$ is DLT for
$(X,\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}A)$ is DLT for ![]() $1<\unicode[STIX]{x1D6FF}\ll 1$. In particular,
$1<\unicode[STIX]{x1D6FF}\ll 1$. In particular, ![]() $(X,(1-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}A)$ is KLT and
$(X,(1-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}A)$ is KLT and ![]() $K_{X}+(1-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}A{\sim}_{\mathbb{R}}K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}H$. Choose
$K_{X}+(1-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}A{\sim}_{\mathbb{R}}K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}H$. Choose ![]() $\unicode[STIX]{x1D6FF}>0$ sufficiently small such that
$\unicode[STIX]{x1D6FF}>0$ sufficiently small such that ![]() $\overline{\operatorname{NE}}(X)_{K_{X}+(1-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}A=0}$ is contained in the interior of the cone
$\overline{\operatorname{NE}}(X)_{K_{X}+(1-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}A=0}$ is contained in the interior of the cone ![]() $V$. We show that if we assume the statement for
$V$. We show that if we assume the statement for ![]() $((1-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}A,V)$, then it holds for
$((1-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}A,V)$, then it holds for ![]() $(\unicode[STIX]{x1D6E5},V)$.
$(\unicode[STIX]{x1D6E5},V)$.
Let ![]() $\unicode[STIX]{x1D6FC}\in \overline{\operatorname{NM}}(X)$. If
$\unicode[STIX]{x1D6FC}\in \overline{\operatorname{NM}}(X)$. If ![]() $\unicode[STIX]{x1D6FC}\in \overline{\operatorname{NE}}(X)_{K_{X}+(1-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}A\geqslant 0}+V+\sum \mathbb{R}_{{\geqslant}0}[C_{i}]$, then
$\unicode[STIX]{x1D6FC}\in \overline{\operatorname{NE}}(X)_{K_{X}+(1-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}A\geqslant 0}+V+\sum \mathbb{R}_{{\geqslant}0}[C_{i}]$, then ![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE}+\sum a_{i}[C_{i}]$, where
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}+\unicode[STIX]{x1D6FE}+\sum a_{i}[C_{i}]$, where ![]() $\unicode[STIX]{x1D6FD}\in \overline{\operatorname{NE}}(X)_{K_{X}+(1-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}A\geqslant 0},\unicode[STIX]{x1D6FE}\in V$ and
$\unicode[STIX]{x1D6FD}\in \overline{\operatorname{NE}}(X)_{K_{X}+(1-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}A\geqslant 0},\unicode[STIX]{x1D6FE}\in V$ and ![]() $a_{i}\geqslant 0$ for all
$a_{i}\geqslant 0$ for all ![]() $i$. Note that
$i$. Note that ![]() $(K_{X}+(1-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}A)\cdot \unicode[STIX]{x1D6FD}\geqslant 0$ implies that
$(K_{X}+(1-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}A)\cdot \unicode[STIX]{x1D6FD}\geqslant 0$ implies that ![]() $(K_{X}+\unicode[STIX]{x1D6E5})\cdot \unicode[STIX]{x1D6FD}\geqslant 0$ by letting
$(K_{X}+\unicode[STIX]{x1D6E5})\cdot \unicode[STIX]{x1D6FD}\geqslant 0$ by letting ![]() $\unicode[STIX]{x1D6FF}\rightarrow 0^{+}$. Therefore, by replacing
$\unicode[STIX]{x1D6FF}\rightarrow 0^{+}$. Therefore, by replacing ![]() $(X,\unicode[STIX]{x1D6E5})$ by
$(X,\unicode[STIX]{x1D6E5})$ by ![]() $(X,(1-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}A)$ we may assume that
$(X,(1-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D700})\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D6FF}A)$ we may assume that ![]() $(X,\unicode[STIX]{x1D6E5}\geqslant 0)$ is KLT.
$(X,\unicode[STIX]{x1D6E5}\geqslant 0)$ is KLT.
Let ![]() $\{C_{i}\}\text{}_{i=1}^{N}$ be the finite set of curves obtained in Proposition 6.8. It is obvious that the right hand side of (6.1) is contained in the left hand side. We show the other inclusion. Let
$\{C_{i}\}\text{}_{i=1}^{N}$ be the finite set of curves obtained in Proposition 6.8. It is obvious that the right hand side of (6.1) is contained in the left hand side. We show the other inclusion. Let ![]() $\unicode[STIX]{x1D6FC}\in \overline{\operatorname{NM}}(X)$ such that it is not contained in
$\unicode[STIX]{x1D6FC}\in \overline{\operatorname{NM}}(X)$ such that it is not contained in ![]() $\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+V+\sum \mathbb{R}_{{\geqslant}0}[C_{i}]$. Then there exists a
$\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+V+\sum \mathbb{R}_{{\geqslant}0}[C_{i}]$. Then there exists a ![]() $\mathbb{R}$-divisor
$\mathbb{R}$-divisor ![]() $B$ such that
$B$ such that ![]() $B\cdot \unicode[STIX]{x1D6FE}\geqslant 0$ for all
$B\cdot \unicode[STIX]{x1D6FE}\geqslant 0$ for all ![]() $\unicode[STIX]{x1D6FE}\in \overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+V+\sum \mathbb{R}_{{\geqslant}0}[C_{i}]$ but
$\unicode[STIX]{x1D6FE}\in \overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+V+\sum \mathbb{R}_{{\geqslant}0}[C_{i}]$ but ![]() $B\cdot \unicode[STIX]{x1D6FC}<0$.
$B\cdot \unicode[STIX]{x1D6FC}<0$.
Let ![]() $A$ be an ample divisor which is positive on
$A$ be an ample divisor which is positive on ![]() $V-\{0\}$. Set
$V-\{0\}$. Set ![]() $\unicode[STIX]{x1D700}=\operatorname{max}\{t>0:A+tB\text{ is pseudo-effective }\}$. Then
$\unicode[STIX]{x1D700}=\operatorname{max}\{t>0:A+tB\text{ is pseudo-effective }\}$. Then ![]() $\unicode[STIX]{x1D700}>0$. Furthermore, from the discussion in the proof of the Proposition 6.8 it follows that
$\unicode[STIX]{x1D700}>0$. Furthermore, from the discussion in the proof of the Proposition 6.8 it follows that ![]() $A+\unicode[STIX]{x1D700}B$ is a
$A+\unicode[STIX]{x1D700}B$ is a ![]() $V$-bounding divisor. However,
$V$-bounding divisor. However, ![]() $(A+\unicode[STIX]{x1D700}B)\cdot C_{i}>0$ for all
$(A+\unicode[STIX]{x1D700}B)\cdot C_{i}>0$ for all ![]() $i\in \{1,2,\ldots ,N\}$, a contradiction to the Proposition 6.8.◻
$i\in \{1,2,\ldots ,N\}$, a contradiction to the Proposition 6.8.◻
Theorem 6.10. Let ![]() $(X,\unicode[STIX]{x1D6E5})$ be a projective DLT pair with
$(X,\unicode[STIX]{x1D6E5})$ be a projective DLT pair with ![]() $\operatorname{dim}X=3$ and
$\operatorname{dim}X=3$ and ![]() $\operatorname{char}p>5$. Let
$\operatorname{char}p>5$. Let ![]() $V$ be a closed convex cone containing
$V$ be a closed convex cone containing ![]() $\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}=0}-\{0\}$ in its interior. Then there are finitely many movable curves
$\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}=0}-\{0\}$ in its interior. Then there are finitely many movable curves ![]() $C_{i}$ such that
$C_{i}$ such that
Proof. This result corresponds to [Reference Lehmann17, Theorem 4.7].
The statement is vacuously true if ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ is pseudo-effective. So we may assume that
$K_{X}+\unicode[STIX]{x1D6E5}$ is pseudo-effective. So we may assume that ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ is not pseudo-effective. We complete the proof in two steps.
$K_{X}+\unicode[STIX]{x1D6E5}$ is not pseudo-effective. We complete the proof in two steps.
First we reduce the problem to a ![]() $\mathbb{Q}$-factorial DLT pair. By Lemma 4.2 there exists a small birational morphism
$\mathbb{Q}$-factorial DLT pair. By Lemma 4.2 there exists a small birational morphism ![]() $\unicode[STIX]{x1D70B}:Y\rightarrow X$ and a
$\unicode[STIX]{x1D70B}:Y\rightarrow X$ and a ![]() $\mathbb{Q}$-factorial DLT pair
$\mathbb{Q}$-factorial DLT pair ![]() $(Y,\unicode[STIX]{x1D6E4}\geqslant 0)$ such that
$(Y,\unicode[STIX]{x1D6E4}\geqslant 0)$ such that
Since the map ![]() $\unicode[STIX]{x1D70B}_{\ast }:N_{1}(Y)\rightarrow N_{1}(X)$ is linear,
$\unicode[STIX]{x1D70B}_{\ast }:N_{1}(Y)\rightarrow N_{1}(X)$ is linear, ![]() $\unicode[STIX]{x1D70B}_{\ast }^{-1}V$ is closed and convex. Furthermore,
$\unicode[STIX]{x1D70B}_{\ast }^{-1}V$ is closed and convex. Furthermore, ![]() $\overline{\operatorname{NE}}(Y)_{K_{Y}+\unicode[STIX]{x1D6E4}=0}$ is contained in the interior of
$\overline{\operatorname{NE}}(Y)_{K_{Y}+\unicode[STIX]{x1D6E4}=0}$ is contained in the interior of ![]() $\unicode[STIX]{x1D70B}_{\ast }^{-1}V$, since
$\unicode[STIX]{x1D70B}_{\ast }^{-1}V$, since ![]() $\unicode[STIX]{x1D70B}_{\ast }$ on curves is dual to
$\unicode[STIX]{x1D70B}_{\ast }$ on curves is dual to ![]() $\unicode[STIX]{x1D70B}^{\ast }$ on divisors. Then by Theorem 6.9 we have
$\unicode[STIX]{x1D70B}^{\ast }$ on divisors. Then by Theorem 6.9 we have
where ![]() $\{C_{i}^{\prime }\}$ are movable curves on
$\{C_{i}^{\prime }\}$ are movable curves on ![]() $Y$.
$Y$.
By [Reference Lehmann17, Lemma 2.1] pushing forward the above relation by ![]() $\unicode[STIX]{x1D70B}_{\ast }$ we get
$\unicode[STIX]{x1D70B}_{\ast }$ we get
where ![]() $C_{i}=\unicode[STIX]{x1D70B}_{\ast }C_{i}^{\prime }$.
$C_{i}=\unicode[STIX]{x1D70B}_{\ast }C_{i}^{\prime }$.
Since birational push-forward of a movable curve is again movable, this completes the proof. ◻
Proof of Theorem 1.8.
Let ![]() $\{V_{j}\}$ be a countable collection of nested closed convex cones containing
$\{V_{j}\}$ be a countable collection of nested closed convex cones containing ![]() $\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}=0}-\{0\}$ in their interiors such that
$\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}=0}-\{0\}$ in their interiors such that
Let ![]() ${\mathcal{C}}_{j}$ be the finite set of movable curves corresponding to
${\mathcal{C}}_{j}$ be the finite set of movable curves corresponding to ![]() $V_{j}$ obtained in Theorem 6.10. Note that all the curves in
$V_{j}$ obtained in Theorem 6.10. Note that all the curves in ![]() ${\mathcal{C}}_{j}^{\prime }$ lie on the boundary of
${\mathcal{C}}_{j}^{\prime }$ lie on the boundary of ![]() $\overline{\operatorname{NM}}(X)$, but not all of them generate extremal rays of
$\overline{\operatorname{NM}}(X)$, but not all of them generate extremal rays of ![]() $\overline{\operatorname{NM}}(X)$. By removing those redundant curves we may assume that each curve in
$\overline{\operatorname{NM}}(X)$. By removing those redundant curves we may assume that each curve in ![]() ${\mathcal{C}}_{j}$ generates a coextremal ray. Define
${\mathcal{C}}_{j}$ generates a coextremal ray. Define ![]() ${\mathcal{C}}=\bigcup _{j}{\mathcal{C}}_{j}$. Then
${\mathcal{C}}=\bigcup _{j}{\mathcal{C}}_{j}$. Then ![]() ${\mathcal{C}}$ is at most countable.
${\mathcal{C}}$ is at most countable.
By contradiction assume that ![]() $\unicode[STIX]{x1D6FC}\in \overline{\operatorname{NM}}(X)$ but
$\unicode[STIX]{x1D6FC}\in \overline{\operatorname{NM}}(X)$ but
Since this cone is closed and convex, there is a convex open neighborhood ![]() $U$ of the cone which does not contain
$U$ of the cone which does not contain ![]() $\unicode[STIX]{x1D6FC}$. Then from our construction it follows that
$\unicode[STIX]{x1D6FC}$. Then from our construction it follows that ![]() $V_{j}\subseteq U$ for
$V_{j}\subseteq U$ for ![]() $j$ sufficiently large. In particular,
$j$ sufficiently large. In particular,
But this is a contradiction to Theorem 6.10. This completes the proof of the first part of the theorem.
Let ![]() $\unicode[STIX]{x1D6FC}$ be a curve class which lies on the
$\unicode[STIX]{x1D6FC}$ be a curve class which lies on the ![]() $(K_{X}+\unicode[STIX]{x1D6E5})$-negative portion of the boundary of
$(K_{X}+\unicode[STIX]{x1D6E5})$-negative portion of the boundary of ![]() $\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+\overline{\operatorname{NM}}(X)$ and that
$\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+\overline{\operatorname{NM}}(X)$ and that ![]() $\unicode[STIX]{x1D6FC}$ does not lie on a hyperplane supporting both
$\unicode[STIX]{x1D6FC}$ does not lie on a hyperplane supporting both ![]() $\overline{\operatorname{NM}}(X)$ and
$\overline{\operatorname{NM}}(X)$ and ![]() $\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}$. For a sufficiently small open neighborhood
$\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}$. For a sufficiently small open neighborhood ![]() $U$ of
$U$ of ![]() $\unicode[STIX]{x1D6FC}$ the points of
$\unicode[STIX]{x1D6FC}$ the points of ![]() $\overline{U}$ still do not lie on such a hyperplane. We may also assume that
$\overline{U}$ still do not lie on such a hyperplane. We may also assume that ![]() $\overline{U}$ is disjoint from
$\overline{U}$ is disjoint from ![]() $\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}$. We define
$\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}$. We define
Fix a compact slice ![]() ${\mathcal{S}}$ of
${\mathcal{S}}$ of ![]() $\overline{\operatorname{Eff}}(X)$ and let
$\overline{\operatorname{Eff}}(X)$ and let ![]() ${\mathcal{D}}$ denote the bounding divisors contained in
${\mathcal{D}}$ denote the bounding divisors contained in ![]() ${\mathcal{S}}$ which have vanishing intersection with some elements of
${\mathcal{S}}$ which have vanishing intersection with some elements of ![]() ${\mathcal{P}}$. By construction
${\mathcal{P}}$. By construction ![]() ${\mathcal{D}}$ is positive on
${\mathcal{D}}$ is positive on ![]() $\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}-\{0\}$. By passing to a compact slice, say
$\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}-\{0\}$. By passing to a compact slice, say ![]() ${\mathcal{T}}$, it is easy to see that
${\mathcal{T}}$, it is easy to see that ![]() ${\mathcal{D}}$ is also positive on
${\mathcal{D}}$ is also positive on ![]() $V_{j}-\{0\}$ for
$V_{j}-\{0\}$ for ![]() $j\gg 0$. In other words, every element of
$j\gg 0$. In other words, every element of ![]() ${\mathcal{P}}$ is on the boundary of
${\mathcal{P}}$ is on the boundary of ![]() $\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+V_{j}+\overline{\operatorname{NM}}(X)$. By Theorem 6.10 there are only finitely many coextremal rays that lie on this cone, and thus there are only finitely many coextremal rays contained in
$\overline{\operatorname{NE}}(X)_{K_{X}+\unicode[STIX]{x1D6E5}\geqslant 0}+V_{j}+\overline{\operatorname{NM}}(X)$. By Theorem 6.10 there are only finitely many coextremal rays that lie on this cone, and thus there are only finitely many coextremal rays contained in ![]() $U$. Therefore,
$U$. Therefore, ![]() $\unicode[STIX]{x1D6FC}$ cannot be an accumulation point.◻
$\unicode[STIX]{x1D6FC}$ cannot be an accumulation point.◻
7 Finiteness of coextremal rays in characteristic  $0$
$0$
In this section, we prove the Batyrev’ Conjecture 1.1 over the filed of complex numbers ![]() $\mathbb{C}$. We follow the same strategy as in the proof of [Reference Araujo1, Theorem 1.3]. For a given
$\mathbb{C}$. We follow the same strategy as in the proof of [Reference Araujo1, Theorem 1.3]. For a given ![]() $\unicode[STIX]{x1D700}>0$, a pair
$\unicode[STIX]{x1D700}>0$, a pair ![]() $(X,\unicode[STIX]{x1D6E5})$ is called a
$(X,\unicode[STIX]{x1D6E5})$ is called a ![]() $\unicode[STIX]{x1D700}$-log canonical pair if for every divisor
$\unicode[STIX]{x1D700}$-log canonical pair if for every divisor ![]() $E$ over
$E$ over ![]() $X$ the discrepancies
$X$ the discrepancies ![]() $a(E;X,\unicode[STIX]{x1D6E5})\geqslant -1+\unicode[STIX]{x1D700}$.
$a(E;X,\unicode[STIX]{x1D6E5})\geqslant -1+\unicode[STIX]{x1D700}$.
Proposition 7.1. Fix a real number ![]() $\unicode[STIX]{x1D700}>0$ and an integer
$\unicode[STIX]{x1D700}>0$ and an integer ![]() $n>0$. Then there exists a constant
$n>0$. Then there exists a constant ![]() $G=G(n,\unicode[STIX]{x1D700})>0$ depending only on
$G=G(n,\unicode[STIX]{x1D700})>0$ depending only on ![]() $n$ and
$n$ and ![]() $\unicode[STIX]{x1D700}$ and satisfying the following properties:
$\unicode[STIX]{x1D700}$ and satisfying the following properties:
If ![]() $(X,\unicode[STIX]{x1D6E5})$ is a
$(X,\unicode[STIX]{x1D6E5})$ is a ![]() $\mathbb{Q}$-factorial projective
$\mathbb{Q}$-factorial projective ![]() $\unicode[STIX]{x1D700}$-log canonical pair of dimension
$\unicode[STIX]{x1D700}$-log canonical pair of dimension ![]() $n$ and
$n$ and ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ is not pseudo-effective, then for every Mori fiber space
$K_{X}+\unicode[STIX]{x1D6E5}$ is not pseudo-effective, then for every Mori fiber space ![]() $\unicode[STIX]{x1D719}:X{\dashrightarrow}X^{\prime }$,
$\unicode[STIX]{x1D719}:X{\dashrightarrow}X^{\prime }$, ![]() $f^{\prime }:X^{\prime }\rightarrow Y^{\prime }$, obtained via a
$f^{\prime }:X^{\prime }\rightarrow Y^{\prime }$, obtained via a ![]() $(K_{X}+\unicode[STIX]{x1D6E5})$-MMP, there exists a projective movable curve
$(K_{X}+\unicode[STIX]{x1D6E5})$-MMP, there exists a projective movable curve ![]() $C\subseteq X$ isomorphic (under
$C\subseteq X$ isomorphic (under ![]() $\unicode[STIX]{x1D719}$) to a movable curve
$\unicode[STIX]{x1D719}$) to a movable curve ![]() $C^{\prime }$ lying on the general fiber of
$C^{\prime }$ lying on the general fiber of ![]() $f^{\prime }$ such that
$f^{\prime }$ such that ![]() $-(K_{X}+\unicode[STIX]{x1D6E5})\cdot C\leqslant G$.
$-(K_{X}+\unicode[STIX]{x1D6E5})\cdot C\leqslant G$.
Proof. Since ![]() $K_{X}+\unicode[STIX]{x1D6E5}$ is not pseudo-effective, by running a
$K_{X}+\unicode[STIX]{x1D6E5}$ is not pseudo-effective, by running a ![]() $(K_{X}+\unicode[STIX]{x1D6E5})$-MMP as in [Reference Birkar, Cascini, Hacon and McKernan5, Corollary 1.3.3] we end up with a Mori fiber space
$(K_{X}+\unicode[STIX]{x1D6E5})$-MMP as in [Reference Birkar, Cascini, Hacon and McKernan5, Corollary 1.3.3] we end up with a Mori fiber space ![]() $f^{\prime }:X^{\prime }\rightarrow Y^{\prime }$ such that
$f^{\prime }:X^{\prime }\rightarrow Y^{\prime }$ such that ![]() $-(K_{X^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime })$ is
$-(K_{X^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime })$ is ![]() $f^{\prime }$-ample, where
$f^{\prime }$-ample, where ![]() $\unicode[STIX]{x1D719}:X{\dashrightarrow}X^{\prime }$ is a birational contraction and
$\unicode[STIX]{x1D719}:X{\dashrightarrow}X^{\prime }$ is a birational contraction and ![]() $\unicode[STIX]{x1D6E5}^{\prime }=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}$. Note that
$\unicode[STIX]{x1D6E5}^{\prime }=\unicode[STIX]{x1D719}_{\ast }\unicode[STIX]{x1D6E5}$. Note that ![]() $(X^{\prime },\unicode[STIX]{x1D6E5}^{\prime })$ is a
$(X^{\prime },\unicode[STIX]{x1D6E5}^{\prime })$ is a ![]() $\mathbb{Q}$-factorial projective
$\mathbb{Q}$-factorial projective ![]() $\unicode[STIX]{x1D700}$-log canonical pair and
$\unicode[STIX]{x1D700}$-log canonical pair and ![]() $\unicode[STIX]{x1D70C}(X^{\prime }/Y^{\prime })=1$.
$\unicode[STIX]{x1D70C}(X^{\prime }/Y^{\prime })=1$.
Let ![]() $F$ be a general fiber of
$F$ be a general fiber of ![]() $f^{\prime }$. Then
$f^{\prime }$. Then ![]() $(F,\unicode[STIX]{x1D6E5}_{F})$ is
$(F,\unicode[STIX]{x1D6E5}_{F})$ is ![]() $\unicode[STIX]{x1D700}$-log canonical and
$\unicode[STIX]{x1D700}$-log canonical and ![]() $-(K_{F}+\unicode[STIX]{x1D6E5}_{F})$ is ample, where
$-(K_{F}+\unicode[STIX]{x1D6E5}_{F})$ is ample, where ![]() $K_{F}+\unicode[STIX]{x1D6E5}_{F}=(K_{X^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime })|_{F}$. Note that
$K_{F}+\unicode[STIX]{x1D6E5}_{F}=(K_{X^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime })|_{F}$. Note that ![]() $-K_{X}=-(K_{X}+\unicode[STIX]{x1D6E5})+\unicode[STIX]{x1D6E5}$ is
$-K_{X}=-(K_{X}+\unicode[STIX]{x1D6E5})+\unicode[STIX]{x1D6E5}$ is ![]() $f^{\prime }$-ample, since
$f^{\prime }$-ample, since ![]() $\unicode[STIX]{x1D70C}(X^{\prime }/Y^{\prime })=1$. In particular,
$\unicode[STIX]{x1D70C}(X^{\prime }/Y^{\prime })=1$. In particular, ![]() $-K_{F}{\sim}_{\mathbb{Q}}-K_{X}|_{F}$ is ample. By the boundedness of
$-K_{F}{\sim}_{\mathbb{Q}}-K_{X}|_{F}$ is ample. By the boundedness of ![]() $\unicode[STIX]{x1D700}$-log canonical log Fano varieties [Reference Birkar4, Theorem 1.1], there exist an integer
$\unicode[STIX]{x1D700}$-log canonical log Fano varieties [Reference Birkar4, Theorem 1.1], there exist an integer ![]() $M=M(d,\unicode[STIX]{x1D700})>0$ and a real number
$M=M(d,\unicode[STIX]{x1D700})>0$ and a real number ![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}(d,\unicode[STIX]{x1D700})>0$ depending only on
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}(d,\unicode[STIX]{x1D700})>0$ depending only on ![]() $\operatorname{dim}F=d$ and
$\operatorname{dim}F=d$ and ![]() $\unicode[STIX]{x1D700}$ such that
$\unicode[STIX]{x1D700}$ such that ![]() $-MK_{F}$ is an ample Cartier divisor and
$-MK_{F}$ is an ample Cartier divisor and ![]() $(-K_{F})^{d}\leqslant \unicode[STIX]{x1D706}$. Then
$(-K_{F})^{d}\leqslant \unicode[STIX]{x1D706}$. Then ![]() $-MK_{F}-(K_{F}+\unicode[STIX]{x1D6E5}_{F})$ is ample. Thus by Kollár’s effective base-point free theorem [Reference Kollár13, Theorem 1.1], there exists an integer
$-MK_{F}-(K_{F}+\unicode[STIX]{x1D6E5}_{F})$ is ample. Thus by Kollár’s effective base-point free theorem [Reference Kollár13, Theorem 1.1], there exists an integer ![]() $N=N(M,d)>0$ such that
$N=N(M,d)>0$ such that ![]() $-NK_{F}$ is base-point free.
$-NK_{F}$ is base-point free.
Now let ![]() $Z^{\prime }\subseteq X^{\prime }$ be the exceptional locus of
$Z^{\prime }\subseteq X^{\prime }$ be the exceptional locus of ![]() $\unicode[STIX]{x1D719}^{-1}:X^{\prime }{\dashrightarrow}X$. Then
$\unicode[STIX]{x1D719}^{-1}:X^{\prime }{\dashrightarrow}X$. Then ![]() $\operatorname{codim}_{X^{\prime }}Z^{\prime }\geqslant 2$. Let
$\operatorname{codim}_{X^{\prime }}Z^{\prime }\geqslant 2$. Let ![]() $C^{\prime }$ be a general curve contained in
$C^{\prime }$ be a general curve contained in ![]() $F$ obtained by intersecting
$F$ obtained by intersecting ![]() $(d-1)$ general members of the linear system
$(d-1)$ general members of the linear system ![]() $|-NK_{F}|$. Then
$|-NK_{F}|$. Then ![]() $C^{\prime }$ belongs to a moving family of curves dominating
$C^{\prime }$ belongs to a moving family of curves dominating ![]() $X$, that is,
$X$, that is, ![]() $C^{\prime }$ is a movable curve, and
$C^{\prime }$ is a movable curve, and ![]() $C^{\prime }$ does not intersect
$C^{\prime }$ does not intersect ![]() $F\cap Z$, since
$F\cap Z$, since ![]() $\operatorname{codim}_{F}(F\cap Z)\geqslant 2$. In particular,
$\operatorname{codim}_{F}(F\cap Z)\geqslant 2$. In particular, ![]() $C^{\prime }$ can be lifted isomorphically to
$C^{\prime }$ can be lifted isomorphically to ![]() $X$, we denote the lift by
$X$, we denote the lift by ![]() $C$. Then
$C$. Then ![]() $C$ is a movable curve on
$C$ is a movable curve on ![]() $X$, and
$X$, and ![]() $-(K_{X}+\unicode[STIX]{x1D6E5})\cdot C=-(K_{X^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime })\cdot C^{\prime }=-(K_{F}+\unicode[STIX]{x1D6E5}_{F})\cdot C^{\prime }\leqslant -K_{F}\cdot C^{\prime }=(-K_{F})\cdot (-NK_{F})^{d-1}=N^{d-1}(-K_{F})^{d}\leqslant N^{d-1}\unicode[STIX]{x1D706}$. Set
$-(K_{X}+\unicode[STIX]{x1D6E5})\cdot C=-(K_{X^{\prime }}+\unicode[STIX]{x1D6E5}^{\prime })\cdot C^{\prime }=-(K_{F}+\unicode[STIX]{x1D6E5}_{F})\cdot C^{\prime }\leqslant -K_{F}\cdot C^{\prime }=(-K_{F})\cdot (-NK_{F})^{d-1}=N^{d-1}(-K_{F})^{d}\leqslant N^{d-1}\unicode[STIX]{x1D706}$. Set ![]() $G:=\unicode[STIX]{x1D706}N^{d-1}$ and we are done.◻
$G:=\unicode[STIX]{x1D706}N^{d-1}$ and we are done.◻
Proof of Theorem 1.9.
The first part of the theorem follows either from [Reference Araujo1, Theorem 1.1] or [Reference Lehmann17, Theorem 1.3].
Next we reduce the problem to the ![]() $\mathbb{Q}$-factorial case. Since
$\mathbb{Q}$-factorial case. Since ![]() $(X,\unicode[STIX]{x1D6E5}\geqslant 0)$ is KLT, there exists a small birational morphism
$(X,\unicode[STIX]{x1D6E5}\geqslant 0)$ is KLT, there exists a small birational morphism ![]() $f:Y\rightarrow X$ such that
$f:Y\rightarrow X$ such that ![]() $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$, and
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5})$, and ![]() $(Y,\unicode[STIX]{x1D6E5}_{Y}\geqslant 0)$ is a
$(Y,\unicode[STIX]{x1D6E5}_{Y}\geqslant 0)$ is a ![]() $\mathbb{Q}$-factorial terminal pair. Assume that the finiteness of coextremal rays is known on
$\mathbb{Q}$-factorial terminal pair. Assume that the finiteness of coextremal rays is known on ![]() $\mathbb{Q}$-factorial KLT pairs. Now
$\mathbb{Q}$-factorial KLT pairs. Now ![]() $K_{Y}+\unicode[STIX]{x1D6E5}_{Y}+f^{\ast }H$ is KLT for
$K_{Y}+\unicode[STIX]{x1D6E5}_{Y}+f^{\ast }H$ is KLT for ![]() $H$ general ample divisor. Write
$H$ general ample divisor. Write ![]() $\unicode[STIX]{x1D6E5}_{Y}+f^{\ast }H\equiv A+E$ for some ample
$\unicode[STIX]{x1D6E5}_{Y}+f^{\ast }H\equiv A+E$ for some ample ![]() $\mathbb{R}$-divisor
$\mathbb{R}$-divisor ![]() $A\geqslant 0$ and effective
$A\geqslant 0$ and effective ![]() $\mathbb{R}$-Cartier divisor
$\mathbb{R}$-Cartier divisor ![]() $E$. Then
$E$. Then ![]() $(Y,\unicode[STIX]{x1D6E5}_{Y}+f^{\ast }H+\unicode[STIX]{x1D700}(A+E))$ is KLT for all
$(Y,\unicode[STIX]{x1D6E5}_{Y}+f^{\ast }H+\unicode[STIX]{x1D700}(A+E))$ is KLT for all ![]() $0<\unicode[STIX]{x1D700}\ll 1$. Then
$0<\unicode[STIX]{x1D700}\ll 1$. Then ![]() $(Y,(1-\unicode[STIX]{x1D700})(\unicode[STIX]{x1D6E5}_{Y}+f^{\ast }H)+\unicode[STIX]{x1D700}(A+E))$ is KLT. Note that
$(Y,(1-\unicode[STIX]{x1D700})(\unicode[STIX]{x1D6E5}_{Y}+f^{\ast }H)+\unicode[STIX]{x1D700}(A+E))$ is KLT. Note that ![]() $K_{Y}+(1-\unicode[STIX]{x1D700})(\unicode[STIX]{x1D6E5}_{Y}+f^{\ast }H)+\unicode[STIX]{x1D700}(A+E)\equiv K_{Y}+\unicode[STIX]{x1D6E5}_{Y}+f^{\ast }H$. Set
$K_{Y}+(1-\unicode[STIX]{x1D700})(\unicode[STIX]{x1D6E5}_{Y}+f^{\ast }H)+\unicode[STIX]{x1D700}(A+E)\equiv K_{Y}+\unicode[STIX]{x1D6E5}_{Y}+f^{\ast }H$. Set ![]() $\unicode[STIX]{x1D6E5}^{\prime }=(1-\unicode[STIX]{x1D700})(\unicode[STIX]{x1D6E5}_{Y}+f^{\ast }H)+\unicode[STIX]{x1D700}E$. Then
$\unicode[STIX]{x1D6E5}^{\prime }=(1-\unicode[STIX]{x1D700})(\unicode[STIX]{x1D6E5}_{Y}+f^{\ast }H)+\unicode[STIX]{x1D700}E$. Then ![]() $(Y,\unicode[STIX]{x1D6E5}^{\prime })$ is KLT and
$(Y,\unicode[STIX]{x1D6E5}^{\prime })$ is KLT and ![]() $K_{Y}+\unicode[STIX]{x1D6E5}^{\prime }+\unicode[STIX]{x1D700}A\equiv K_{Y}+\unicode[STIX]{x1D6E5}_{Y}+f^{\ast }H=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5}+H)$. Therefore, by assumption we have
$K_{Y}+\unicode[STIX]{x1D6E5}^{\prime }+\unicode[STIX]{x1D700}A\equiv K_{Y}+\unicode[STIX]{x1D6E5}_{Y}+f^{\ast }H=f^{\ast }(K_{X}+\unicode[STIX]{x1D6E5}+H)$. Therefore, by assumption we have
Pushing forward these cones by ![]() $f_{\ast }$ we get the finiteness result on
$f_{\ast }$ we get the finiteness result on ![]() $X$. Therefore, replacing
$X$. Therefore, replacing ![]() $X$ by
$X$ by ![]() $Y$ we may assume that
$Y$ we may assume that ![]() $X$ is a
$X$ is a ![]() $\mathbb{Q}$-factorial KLT pair. Let
$\mathbb{Q}$-factorial KLT pair. Let ![]() $\unicode[STIX]{x1D6F4}$ be the set of all
$\unicode[STIX]{x1D6F4}$ be the set of all ![]() $(K_{X}+\unicode[STIX]{x1D6E5})$-negative movable curves classes
$(K_{X}+\unicode[STIX]{x1D6E5})$-negative movable curves classes ![]() $[C_{i}]$ as in Part
$[C_{i}]$ as in Part ![]() $(1)$. Let
$(1)$. Let ![]() $\unicode[STIX]{x1D6F4}_{H}\subseteq \unicode[STIX]{x1D6F4}$ be the set consisting of the classes
$\unicode[STIX]{x1D6F4}_{H}\subseteq \unicode[STIX]{x1D6F4}$ be the set consisting of the classes ![]() $[C]\in \unicode[STIX]{x1D6F4}$ such that
$[C]\in \unicode[STIX]{x1D6F4}$ such that ![]() $(K_{X}+\unicode[STIX]{x1D6E5}+H)\cdot C<0$. Then by [Reference Araujo1, Theorem 1.1]
$(K_{X}+\unicode[STIX]{x1D6E5}+H)\cdot C<0$. Then by [Reference Araujo1, Theorem 1.1]
We show that the set of rays ![]() $\{\mathbb{R}_{{\geqslant}0}[C]:[C]\in \unicode[STIX]{x1D6F4}_{H}\}$ is finite.
$\{\mathbb{R}_{{\geqslant}0}[C]:[C]\in \unicode[STIX]{x1D6F4}_{H}\}$ is finite.
Let ![]() $\unicode[STIX]{x1D700}>0$ be the minimum log discrepancy of
$\unicode[STIX]{x1D700}>0$ be the minimum log discrepancy of ![]() $(X,\unicode[STIX]{x1D6E5})$. Then
$(X,\unicode[STIX]{x1D6E5})$. Then ![]() $(X,\unicode[STIX]{x1D6E5})$ is
$(X,\unicode[STIX]{x1D6E5})$ is ![]() $\unicode[STIX]{x1D700}$-log canonical. From the statement of [Reference Araujo1, Theorem 1.1] and Proposition 7.1 we see that the movable curves
$\unicode[STIX]{x1D700}$-log canonical. From the statement of [Reference Araujo1, Theorem 1.1] and Proposition 7.1 we see that the movable curves ![]() $C$ in
$C$ in ![]() $\unicode[STIX]{x1D6F4}_{H}$ satisfy the conclusion of the Proposition 7.1. In particular,
$\unicode[STIX]{x1D6F4}_{H}$ satisfy the conclusion of the Proposition 7.1. In particular, ![]() $0<-(K_{X}+\unicode[STIX]{x1D6E5})\cdot C\leqslant G$ for all
$0<-(K_{X}+\unicode[STIX]{x1D6E5})\cdot C\leqslant G$ for all ![]() $[C]\in \sum _{H}$. We also have
$[C]\in \sum _{H}$. We also have ![]() $(K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D716}H)\cdot C<0$. Therefore,
$(K_{X}+\unicode[STIX]{x1D6E5}+\unicode[STIX]{x1D716}H)\cdot C<0$. Therefore, ![]() $\unicode[STIX]{x1D716}H\cdot C\leqslant G$ for all
$\unicode[STIX]{x1D716}H\cdot C\leqslant G$ for all ![]() $[C]\in \unicode[STIX]{x1D6F4}_{H}$. In particular, the curves corresponding to the classes
$[C]\in \unicode[STIX]{x1D6F4}_{H}$. In particular, the curves corresponding to the classes ![]() $\{\mathbb{R}_{{\geqslant}0}[C]:[C]\in \unicode[STIX]{x1D6F4}_{H}\}$ belong a bounded family, and hence they correspond to only finitely many different numerical equivalence classes.◻
$\{\mathbb{R}_{{\geqslant}0}[C]:[C]\in \unicode[STIX]{x1D6F4}_{H}\}$ belong a bounded family, and hence they correspond to only finitely many different numerical equivalence classes.◻
Acknowledgments
This paper originated in a conversation with Professor Burt Totaro. I would like to thank him for our fruitful discussions. I am also grateful to him for answering my questions, reading an early draft and giving valuable suggestion to improve the presentation of the paper. My sincerest gratitude goes to Professor Christopher Hacon for answering several questions, carefully reading some parts of an early draft and point out few errors. I would also like to thank Hiromu Tanaka for suggesting a quicker proof of the Theorem 3.1. I would like to thank Joe Waldron for lot of useful discussions and the referee(s) for pointing out typos and giving valuable suggestions.