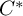Introduction and main results
Over the last decades étale groupoids and their homological and K-theoretical invariants have played an increasingly important role in the fields of operator algebras, noncommutative geometry and topological dynamics. Kumjian and Renault showed that
![]() $C^*$
-algebras associated with groupoids provide versatile models for large classes of
$C^*$
-algebras associated with groupoids provide versatile models for large classes of
![]() $C^*$
-algebras [Reference Kumjian27, Reference Renault54]. More recently, Li showed that every classifiable
$C^*$
-algebras [Reference Kumjian27, Reference Renault54]. More recently, Li showed that every classifiable
![]() $C^*$
-algebra admits a (twisted) groupoid model [Reference Li33]. One of the biggest open questions in the field concerns the universal coefficient theorem (UCT) and work of Barlak and Li [Reference Barlak and Li3] showed that the UCT problem can be translated to the question whether every nuclear
$C^*$
-algebra admits a (twisted) groupoid model [Reference Li33]. One of the biggest open questions in the field concerns the universal coefficient theorem (UCT) and work of Barlak and Li [Reference Barlak and Li3] showed that the UCT problem can be translated to the question whether every nuclear
![]() $C^*$
-algebra admits a groupoid model.
$C^*$
-algebra admits a groupoid model.
In another direction, Matui’s works [Reference Matui35, Reference Matui36] have kickstarted a fruitful line of research in topological dynamics using étale groupoids at its heart (see also [Reference Li32]). In this area, it turns out that many invariants for topological dynamical systems can most naturally been defined in the framework of groupoid homology or the K-theory of groupoid
![]() $C^*$
-algebras. Consequently, there is a great deal of interest around the homology and K-theory of étale groupoids and their interaction. Examples of recent research in this direction are the HK conjecture of Matui [Reference Matui35]a, or the relation between the homology theory of Smale spaces and the K-theory of their corresponding
$C^*$
-algebras. Consequently, there is a great deal of interest around the homology and K-theory of étale groupoids and their interaction. Examples of recent research in this direction are the HK conjecture of Matui [Reference Matui35]a, or the relation between the homology theory of Smale spaces and the K-theory of their corresponding
![]() $C^*$
-algebras [Reference Putnam52]. In this latter example, a special case of the methods developed here (i.e., when the groupoid is torsion-free and ample) has already been applied with great success and lead to many interesting results in topological dynamics, as is demonstrated by the papers [Reference Bönicke, Dell’Aiera, Gabe and Willett9, Reference Proietti and Yamashita49, Reference Proietti and Yamashita51, Reference Proietti and Yamashita50].
$C^*$
-algebras [Reference Putnam52]. In this latter example, a special case of the methods developed here (i.e., when the groupoid is torsion-free and ample) has already been applied with great success and lead to many interesting results in topological dynamics, as is demonstrated by the papers [Reference Bönicke, Dell’Aiera, Gabe and Willett9, Reference Proietti and Yamashita49, Reference Proietti and Yamashita51, Reference Proietti and Yamashita50].
Motivated by these developments we set out to develop the category-theory based approach to the Baum–Connes conjecture for the class of étale groupoids in full generality. This approach is very suitable for formulating and proving general statements about the Baum–Connes conjecture and for obtaining functorial properties of the assembly map and K-theoretic duality type results [Reference Emerson and Meyer21, Reference Nishikawa and Proietti46]. As already observed by Meyer and Nest [Reference Meyer and Nest40], many permanence results of the Baum–Connes conjecture become quite accessible in this setup. Besides this, several results obtained by the first named author [Reference Bönicke10, Reference Bönicke11] and C. Dell’Aiera [Reference Bönicke and Dell’Aiera12] are generalized to all étale groupoids.
The following statement summarizes a selection of applications that we are able to obtain through this approach. Some statements are deliberately vague to spare the reader the technical details at this stage, we refer to the final section of this article (Section 4) for the definitions and more precise statements.
Theorem A. Let G be an étale groupoid which is second countable, locally compact and Hausdorff.
-
1. Suppose
 $\Sigma $
is a twist over G. If G satisfies the strong Baum–Connes conjecture, then
$\Sigma $
is a twist over G. If G satisfies the strong Baum–Connes conjecture, then
 $C_r^*(G,\Sigma )$
satisfies the UCT.
$C_r^*(G,\Sigma )$
satisfies the UCT. -
2. The K-theory of
 $C_r^*(G,\Sigma )$
only depends on the homotopy class of
$C_r^*(G,\Sigma )$
only depends on the homotopy class of
 $\Sigma $
.
$\Sigma $
. -
3. If G is strongly amenable at infinity, then there is a dual Dirac morphism for G. In particular, the Baum–Connes assembly map is split-injective.
-
4. The (strong) Baum–Connes conjecture enjoys many permanence properties both with respect to the involved groupoid (it passes to subgroupoids, direct products, increasing unions) and the coefficient algebra (inductive limits, tensor products).
The results in Theorem A should be compared to another line of research, which uses quantitative K-theory methods to obtain many interesting related results on the UCT, the Baum–Connes conjecture and its permanence properties [Reference Guentner, Willett and Yu23, Reference Oyono-Oyono47, Reference Willett and Yu63].
In [Reference Meyer and Nest40], R. Meyer and R. Nest established the category theoretic framework we are after in the setting of locally compact groups and more generally for transformation groups. To this end, they leverage the triangulated structure of the equivariant bivariant Kasparov category and in particular the notion of complementary subcategories and localization. This paper extends these methods to include étale groupoids.
A related approach is described in [Reference Davis and Lück18], where the authors give a unified approach to various isomorphism conjectures, including the Baum–Connes conjecture by means of the orbit category and the homotopy theory of spectra. In both approaches, the role of weakly contractible objects, defined in terms of a certain family of subgroups of a given group G, is in a certain sense fundamental. For the Baum–Connes conjecture associated to a discrete group, this family is given by the finite subgroups of G. Analogously, when G is locally compact, the family is given by the compact subgroups.
Thus, the first task when attempting to generalise this approach is the identification of a suitable class of subgroupoids of a given étale groupoid G. Associated to this class is a homological ideal in the Kasparov category
![]() $\operatorname {\mathrm {KK}}^G$
, which is the starting point for several notions of relative homological algebra, for example, the notion of projective object. In the words of Meyer and Nest [Reference Meyer and Nest40, page 215], ‘it is not so clear what should correspond to compact subgroups’ in the case of the Baum–Connes conjecture for groupoids.
$\operatorname {\mathrm {KK}}^G$
, which is the starting point for several notions of relative homological algebra, for example, the notion of projective object. In the words of Meyer and Nest [Reference Meyer and Nest40, page 215], ‘it is not so clear what should correspond to compact subgroups’ in the case of the Baum–Connes conjecture for groupoids.
A partial solution to this question was offered in [Reference Emerson and Meyer21], where the authors show a relation of complementarity between the subcategory of proper objects and the objects
![]() $A\in \operatorname {\mathrm {KK}}^G$
such that
$A\in \operatorname {\mathrm {KK}}^G$
such that
![]() $p^*(A)$
is contractible in
$p^*(A)$
is contractible in
![]() $\operatorname {\mathrm {KK}}^{G\ltimes \underline {E} G}$
. Here,
$\operatorname {\mathrm {KK}}^{G\ltimes \underline {E} G}$
. Here,
![]() $p^*$
is the pullback functor associated to the projection
$p^*$
is the pullback functor associated to the projection
![]() $p\colon G\ltimes \underline {E} G\to G$
, where
$p\colon G\ltimes \underline {E} G\to G$
, where
![]() $\underline {E} G$
denotes the universal example for proper actions (which is well defined for groupoids; see, for example, [Reference Tu59]). This approach is based on the fact that
$\underline {E} G$
denotes the universal example for proper actions (which is well defined for groupoids; see, for example, [Reference Tu59]). This approach is based on the fact that
![]() $p^*$
is, effectively speaking, the localization functor which we seek (see Theorem 3.12). However, this is not completely satisfactory because (a) it relies on the existence of a Kasparov dual [Reference Emerson and Meyer21, Theorem 4.37], and (b) it does not present the projective objects in terms of a simpler class of ‘building blocks’ constructed via induction on a suitable family of subgroupoids.
$p^*$
is, effectively speaking, the localization functor which we seek (see Theorem 3.12). However, this is not completely satisfactory because (a) it relies on the existence of a Kasparov dual [Reference Emerson and Meyer21, Theorem 4.37], and (b) it does not present the projective objects in terms of a simpler class of ‘building blocks’ constructed via induction on a suitable family of subgroupoids.
This paper remedies these shortcomings by using a ‘slice theorem’ (see Proposition 3.2 below and compare with [Reference Tu60, Proposition 2.42]) for étale groupoids acting properly on a space, which allows us to identify a family of subgroupoids that we call ‘compact actions’, as they are isomorphic to action groupoids for finite groups sitting inside the isotropy of G. On a first approximation, we can say that the family of compact subgroups is replaced in our case by the family of proper subgroupoids of G (see Lemma 3.16 for more details on this statement).
Having this, most of the machinery from [Reference Meyer and Nest40] can be reproduced in the groupoid context in a straightforward fashion, as it is mostly formal and inherited from the more general theory of triangulated categories. We say ‘most’ because we encountered another technical difficulty along the way, which we now briefly explain. Having defined projective objects as retracts of (direct sums of) ‘compactly induced’ objects, we were facing the issue of identifying the localizing subcategory of proper objects with the one induced by projectives. Indeed, a result of this kind is highly desirable because not only it would match up nicely with the statement in [Reference Emerson and Meyer21], but more importantly it allows to rephrase the main result of [Reference Tu58], on the Baum–Connes conjecture for a groupoid G satisfying the Haagerup property, as a proof that the category
![]() $\operatorname {\mathrm {KK}}^G$
is generated by projective objects as defined by us.
$\operatorname {\mathrm {KK}}^G$
is generated by projective objects as defined by us.
A blueprint for this result ought to be found in [Reference Meyer and Nest40], and indeed [Reference Meyer and Nest40, Theorem 7.1] and its applications correspond to the statement we need. Nevertheless, we were not able to simply generalize the proof therein, essentially because (a) our compact actions are open subgroupoids, and (b) the excisive properties of
![]() $\operatorname {\mathrm {RKK}}^G(-\,;A, B)$
are not entirely clear (at least to us) in general, even in simple cases such as homotopy pushouts. Nevertheless, by briefly passing to E-theory (which has long exact sequences without extra hypotheses) and using the fact that localizing subcategories are closed under direct summands, we are able to find an alternative proof of the identification of localizing subcategories of (respectively) compactly induced and proper objects.
$\operatorname {\mathrm {RKK}}^G(-\,;A, B)$
are not entirely clear (at least to us) in general, even in simple cases such as homotopy pushouts. Nevertheless, by briefly passing to E-theory (which has long exact sequences without extra hypotheses) and using the fact that localizing subcategories are closed under direct summands, we are able to find an alternative proof of the identification of localizing subcategories of (respectively) compactly induced and proper objects.
Before passing to the organization of the paper, we present two of the core results which should serve as a brief summary of this work. For more details on definitions and applications, the reader should consult Sections 1 and 4.
Theorem B. Let
![]() $\mathcal {N}\subseteq \operatorname {\mathrm {KK}}^G$
be the subcategory of G-
$\mathcal {N}\subseteq \operatorname {\mathrm {KK}}^G$
be the subcategory of G-
![]() $C^*$
-algebras A such that
$C^*$
-algebras A such that
![]() $\operatorname {\mathrm {Res}}^G_H(A)\cong 0$
for any proper open subgroupoid
$\operatorname {\mathrm {Res}}^G_H(A)\cong 0$
for any proper open subgroupoid
![]() $H\subseteq G$
. Let
$H\subseteq G$
. Let
![]() $\mathcal {P}\subseteq \operatorname {\mathrm {KK}}^G$
be the smallest localizing triangulated subcategory containing proper G-
$\mathcal {P}\subseteq \operatorname {\mathrm {KK}}^G$
be the smallest localizing triangulated subcategory containing proper G-
![]() $C^*$
-algebras. Then
$C^*$
-algebras. Then
![]() $(\mathcal {P},\mathcal {N})$
is a pair of complementary subcategories and
$(\mathcal {P},\mathcal {N})$
is a pair of complementary subcategories and
![]() $\mathcal {P}$
is generated by ‘compactly induced’ objects (see Theorem 3.4 for details).
$\mathcal {P}$
is generated by ‘compactly induced’ objects (see Theorem 3.4 for details).
The previous result implies that, for any
![]() $A\in \operatorname {\mathrm {KK}}^G$
, there is an exact triangle, functorial in A and unique up to isomorphism such that
$A\in \operatorname {\mathrm {KK}}^G$
, there is an exact triangle, functorial in A and unique up to isomorphism such that
![]() $P(A)\in \mathcal {P}$
and
$P(A)\in \mathcal {P}$
and
![]() $N(A)\in \mathcal {N}$
,
$N(A)\in \mathcal {N}$
,
Following [Reference Meyer39], the object
![]() $P(A)$
is called the cellular approximation of A. We should point out that if
$P(A)$
is called the cellular approximation of A. We should point out that if
![]() $P(C_0(G^0))$
is a proper G-
$P(C_0(G^0))$
is a proper G-
![]() $C^*$
-algebra, then any
$C^*$
-algebra, then any
![]() $A\in \mathcal {P}$
is
$A\in \mathcal {P}$
is
![]() $\operatorname {\mathrm {KK}}^G$
-equivalent to a proper
$\operatorname {\mathrm {KK}}^G$
-equivalent to a proper
![]() $C^*$
-algebra (see Remark 3.11).
$C^*$
-algebra (see Remark 3.11).
The next result gives a more familiar presentation of the localization
![]() $\operatorname {\mathrm {KK}}^G/\mathcal {N}$
, and expresses the ordinary Baum–Connes conjecture in terms of the natural morphism
$\operatorname {\mathrm {KK}}^G/\mathcal {N}$
, and expresses the ordinary Baum–Connes conjecture in terms of the natural morphism
![]() $D_A\colon P(A)\to A$
introduced above. We can view this theorem as a bridge between the somewhat abstract notions arising via the triangulated category approach and more classical objects, such as the
$D_A\colon P(A)\to A$
introduced above. We can view this theorem as a bridge between the somewhat abstract notions arising via the triangulated category approach and more classical objects, such as the
![]() $\operatorname {\mathrm {RKK}}$
-group and the ‘topological’ K-theory group appearing at the left-hand side of the Baum–Connes conjecture.
$\operatorname {\mathrm {RKK}}$
-group and the ‘topological’ K-theory group appearing at the left-hand side of the Baum–Connes conjecture.
Theorem C. Let
![]() $p\colon \underline {E} G\to G^{0}$
be the structure map of the G-action. The pullback functor descends to an isomorphism of categories
$p\colon \underline {E} G\to G^{0}$
be the structure map of the G-action. The pullback functor descends to an isomorphism of categories
![]() $p^*\colon \operatorname {\mathrm {KK}}^G/\mathcal {N}\to \operatorname {\mathrm {RKK}}(\underline {E} G)$
. The induced map
$p^*\colon \operatorname {\mathrm {KK}}^G/\mathcal {N}\to \operatorname {\mathrm {RKK}}(\underline {E} G)$
. The induced map
![]() $(D_A\rtimes _r G)_*\colon K_*(P(A)\rtimes _r G) \to K_*(A\rtimes _r G)$
corresponds to the assembly map under the natural identification
$(D_A\rtimes _r G)_*\colon K_*(P(A)\rtimes _r G) \to K_*(A\rtimes _r G)$
corresponds to the assembly map under the natural identification
![]() $K_*^{\mathrm {top}}(G;A)\cong K_*(P(A)\rtimes _r G)$
.
$K_*^{\mathrm {top}}(G;A)\cong K_*(P(A)\rtimes _r G)$
.
The paper is organized as follows. In Section 1, we lay out the fundamental definitions and conventions which we use throughout the paper. We define groupoid crossed products, pass on to discussing the triangulated structure of the equivariant
![]() $\operatorname {\mathrm {KK}}$
- and E-categories and finish with some basic results on complementary subcategories and homotopy direct limits. Section 2 is entirely dedicated to the main technical result of the paper, that is, an adjunction between the functors
$\operatorname {\mathrm {KK}}$
- and E-categories and finish with some basic results on complementary subcategories and homotopy direct limits. Section 2 is entirely dedicated to the main technical result of the paper, that is, an adjunction between the functors
![]() $\operatorname {\mathrm {Ind}}_H^G\colon \operatorname {\mathrm {KK}}^H\rightleftarrows \operatorname {\mathrm {KK}}^G\colon \operatorname {\mathrm {Res}}_G^H$
.
$\operatorname {\mathrm {Ind}}_H^G\colon \operatorname {\mathrm {KK}}^H\rightleftarrows \operatorname {\mathrm {KK}}^G\colon \operatorname {\mathrm {Res}}_G^H$
.
This adjoint situation is the technical foundation for the main results of the paper. Its proof is fairly complicated in terms of bookkeeping of variables, but it does not require particularly new conceptual ideas. In fact, the definition for unit and counit are very intuitive in terms of the open inclusion
![]() $H\subseteq G$
. The model for the induction functor is perhaps a minor point of novelty, as it is based on the crossed product construction rather than on (generalized) fixed-point algebras. This is especially useful as an open subgroupoid
$H\subseteq G$
. The model for the induction functor is perhaps a minor point of novelty, as it is based on the crossed product construction rather than on (generalized) fixed-point algebras. This is especially useful as an open subgroupoid
![]() $H\subseteq G$
need not act on G properly (see Remark 2.1).
$H\subseteq G$
need not act on G properly (see Remark 2.1).
Section 3 is entirely dedicated to proving Theorems B and C above, along with some other auxiliary results. The excisive properties of E-theory are used in this section.
Section 4 discusses several applications of the main results of the paper. In particular, we give the precise statements and proofs of the results mentioned in Theorem A.
1 Preliminaries
Let G be a second countable, locally compact, Hausdorff groupoid with unit space
![]() $G^{0}$
. We let
$G^{0}$
. We let
![]() $s,r\colon G\to G^0$
denote, respectively, the source and range maps. In addition, we use the notation
$s,r\colon G\to G^0$
denote, respectively, the source and range maps. In addition, we use the notation
![]() $G_x=s^{-1}(x)$
,
$G_x=s^{-1}(x)$
,
![]() $G^x=r^{-1}(x)$
, and for a subset
$G^x=r^{-1}(x)$
, and for a subset
![]() $A \subset G^{0}$
, we write
$A \subset G^{0}$
, we write
![]() $G_A = \bigcup _{x \in A} G_x$
,
$G_A = \bigcup _{x \in A} G_x$
,
![]() $G^A = \bigcup _{x \in A} G^x$
, and
$G^A = \bigcup _{x \in A} G^x$
, and
![]() $G|_A = G^A \cap G_A$
. Throughout this paper, we assume the existence of a (left) Haar system
$G|_A = G^A \cap G_A$
. Throughout this paper, we assume the existence of a (left) Haar system
![]() $\{\lambda ^x\}_{x\in G^0}$
on G [Reference Renault53].
$\{\lambda ^x\}_{x\in G^0}$
on G [Reference Renault53].
Let X be second countable, locally compact, Hausdorff space. A
![]() $C_0(X)$
-algebra is a
$C_0(X)$
-algebra is a
![]() $C^*$
-algebra A endowed with a nondegenerate
$C^*$
-algebra A endowed with a nondegenerate
![]() $*$
-homomorphism from
$*$
-homomorphism from
![]() $C_0(X)$
to the center of the multiplier algebra
$C_0(X)$
to the center of the multiplier algebra
![]() $\mathcal {M}(A)$
. For an open set
$\mathcal {M}(A)$
. For an open set
![]() $U \subset X$
, we define
$U \subset X$
, we define
![]() $A_U = C_0(U) A $
. For a locally closed subset
$A_U = C_0(U) A $
. For a locally closed subset
![]() $Y \subset X$
(i.e.,
$Y \subset X$
(i.e.,
![]() $Y = U \smallsetminus V$
for some open sets
$Y = U \smallsetminus V$
for some open sets
![]() $U, V \subset X$
), we set
$U, V \subset X$
), we set
![]() $A_Y = A_U / A_{U \cap V}$
, and we put
$A_Y = A_U / A_{U \cap V}$
, and we put
![]() $A_x = A_{\{x\}} = A / A C_0(X \setminus \{x\})$
for
$A_x = A_{\{x\}} = A / A C_0(X \setminus \{x\})$
for
![]() $x \in X$
. More on
$x \in X$
. More on
![]() $C_0(X)$
-algebras can be found in [Reference Blanchard7].
$C_0(X)$
-algebras can be found in [Reference Blanchard7].
Let us fix our preliminary conventions on tensor products. A more in-depth discussion is provided after Definition 1.6. If A and B are
![]() $C_0(X)$
-algebras, their maximal tensor product
$C_0(X)$
-algebras, their maximal tensor product
![]() $A\otimes B$
is naturally equipped with a
$A\otimes B$
is naturally equipped with a
![]() $C_0(X\times X)$
-structure, and we define the (maximal) balanced tensor product
$C_0(X\times X)$
-structure, and we define the (maximal) balanced tensor product
![]() $A\otimes _X B$
as the
$A\otimes _X B$
as the
![]() $C_0(X)$
-algebra
$C_0(X)$
-algebra
![]() $(A\otimes B)_{\Delta _X}$
, where
$(A\otimes B)_{\Delta _X}$
, where
![]() $\Delta _X\subseteq X\times X$
is the diagonal subspace.
$\Delta _X\subseteq X\times X$
is the diagonal subspace.
Note that if
![]() $f \colon Y \to X$
is a continuous map, then
$f \colon Y \to X$
is a continuous map, then
![]() $C_0(Y)$
is a
$C_0(Y)$
is a
![]() $C_0(X)$
-algebra. It is a continuous field if and only if f is open [Reference Blanchard and Kirchberg8]. In particular, this applies to the situation
$C_0(X)$
-algebra. It is a continuous field if and only if f is open [Reference Blanchard and Kirchberg8]. In particular, this applies to the situation
![]() $Y = G$
and
$Y = G$
and
![]() $f = s$
because the source and range maps are open when a Haar system exists [Reference Renault53, Proposition 2.4]. The map f defines a ‘forgetful’ functor, sending a
$f = s$
because the source and range maps are open when a Haar system exists [Reference Renault53, Proposition 2.4]. The map f defines a ‘forgetful’ functor, sending a
![]() $C_0(Y)$
-algebra A to a
$C_0(Y)$
-algebra A to a
![]() $C_0(X)$
-algebra
$C_0(X)$
-algebra
![]() $f_*(A)$
, by way of the composition
$f_*(A)$
, by way of the composition
![]() $C_0(X)\to \mathcal {M}(C_0(Y))\to Z\mathcal {M}(A)$
. In addition, for a
$C_0(X)\to \mathcal {M}(C_0(Y))\to Z\mathcal {M}(A)$
. In addition, for a
![]() $C_0(X)$
-algebra B, a continuous function like f above also induces a pullback functor
$C_0(X)$
-algebra B, a continuous function like f above also induces a pullback functor
![]() $f^*B = C_0(Y) \otimes _{X} B$
from the category of
$f^*B = C_0(Y) \otimes _{X} B$
from the category of
![]() $C_0(X)$
-algebras to that of
$C_0(X)$
-algebras to that of
![]() $C_0(Y)$
-algebras.
$C_0(Y)$
-algebras.
We are ready to define the notion of groupoid action on
![]() $C^*$
-algebras.
$C^*$
-algebras.
Definition 1.1. Let G be a second countable locally compact Hausdorff groupoid, and put
![]() $G^{0} = X$
. A continuous action of G on a
$G^{0} = X$
. A continuous action of G on a
![]() $C_0(X)$
-algebra A (with structure map
$C_0(X)$
-algebra A (with structure map
![]() $\rho $
) is given by an isomorphism of
$\rho $
) is given by an isomorphism of
![]() $C_0(G)$
-algebras
$C_0(G)$
-algebras
such that the induced homomorphisms
![]() $\alpha _g \colon A_{s(g)} \to A_{r(g)}$
for
$\alpha _g \colon A_{s(g)} \to A_{r(g)}$
for
![]() $g \in G$
satisfy
$g \in G$
satisfy
![]() $\alpha _{g h} = \alpha _g \alpha _h$
. In this case, we say that A is a G-
$\alpha _{g h} = \alpha _g \alpha _h$
. In this case, we say that A is a G-
![]() $C^*$
-algebra.
$C^*$
-algebra.
If A is a commutative
![]() $C^*$
-algebra, say
$C^*$
-algebra, say
![]() $A\cong C_0(Z)$
, then we view the moment map as a continuous function
$A\cong C_0(Z)$
, then we view the moment map as a continuous function
![]() $\rho \colon Z\to X$
. In this case, the action
$\rho \colon Z\to X$
. In this case, the action
![]() $\alpha $
can be given as a continuous map making the following diagram commute,
$\alpha $
can be given as a continuous map making the following diagram commute,

(above, we are slightly abusing notation by writing r for the map
![]() $(g,z)\mapsto r(g)$
). The action groupoid obtained this way will be denoted
$(g,z)\mapsto r(g)$
). The action groupoid obtained this way will be denoted
![]() $G\ltimes Z$
, it has unit space Z and its generic arrow is determined by a pair
$G\ltimes Z$
, it has unit space Z and its generic arrow is determined by a pair
![]() $(g,z)\in G\times Z$
with range z and source
$(g,z)\in G\times Z$
with range z and source
![]() $\alpha (g^{-1},z)$
.
$\alpha (g^{-1},z)$
.
Details on the construction of groupoid crossed product
![]() $C^*$
-algebras can be found in [Reference Khoshkam and Skandalis25, Reference Muhly and Williams44]. We are going to only briefly recap the definitions here. Given a G-algebra A, define the auxiliary algebra
$C^*$
-algebras can be found in [Reference Khoshkam and Skandalis25, Reference Muhly and Williams44]. We are going to only briefly recap the definitions here. Given a G-algebra A, define the auxiliary algebra
![]() $A_0=C_c(G)\cdot r^*A$
and the
$A_0=C_c(G)\cdot r^*A$
and the
![]() $\ast $
-algebra structure
$\ast $
-algebra structure
 $$ \begin{align*} (f\star g)(\gamma)&=\int f(\eta)\alpha_\eta(g(\eta^{-1}\gamma))\,d\lambda^{r(\gamma)}(\eta)\\ f^*(\gamma)&=\alpha_\gamma(f(\gamma^{-1})^*) \end{align*} $$
$$ \begin{align*} (f\star g)(\gamma)&=\int f(\eta)\alpha_\eta(g(\eta^{-1}\gamma))\,d\lambda^{r(\gamma)}(\eta)\\ f^*(\gamma)&=\alpha_\gamma(f(\gamma^{-1})^*) \end{align*} $$
for
![]() $f,g\in A_0$
. For
$f,g\in A_0$
. For
![]() $f\in A_0$
, we also define
$f\in A_0$
, we also define
![]() $\lVert f \rVert _1$
to be the supremum, over
$\lVert f \rVert _1$
to be the supremum, over
![]() $x\in X$
, of the quantity
$x\in X$
, of the quantity
![]() $\max \{\int \lVert f(\gamma ) \rVert \,d\lambda _x(\gamma ), \int \lVert f(\gamma ) \rVert \,d\lambda ^x(\gamma )\}$
, where
$\max \{\int \lVert f(\gamma ) \rVert \,d\lambda _x(\gamma ), \int \lVert f(\gamma ) \rVert \,d\lambda ^x(\gamma )\}$
, where
![]() $\lambda _x(\gamma )=\lambda ^x(\gamma ^{-1})$
. The enveloping
$\lambda _x(\gamma )=\lambda ^x(\gamma ^{-1})$
. The enveloping
![]() $C^*$
-algebra of the Banach
$C^*$
-algebra of the Banach
![]() $\ast $
-algebra obtained by completing
$\ast $
-algebra obtained by completing
![]() $A_0$
with respect to
$A_0$
with respect to
![]() $\lVert \cdot \rVert _1$
is called the full crossed product of A by G.
$\lVert \cdot \rVert _1$
is called the full crossed product of A by G.
In this paper, unless otherwise stated, we are going to consider the reduced crossed product
![]() $C^*$
-algebra of A by G, denoted
$C^*$
-algebra of A by G, denoted
![]() $A\rtimes _r G$
(at times we might drop the subscript ‘r’), which is obtained as a quotient of the full crossed product as follows. For
$A\rtimes _r G$
(at times we might drop the subscript ‘r’), which is obtained as a quotient of the full crossed product as follows. For
![]() $x\in X$
, consider the
$x\in X$
, consider the
![]() $A_x$
-Hilbert module
$A_x$
-Hilbert module
![]() $L^2(G^x,\lambda ^x)\otimes A_x$
. The formula
$L^2(G^x,\lambda ^x)\otimes A_x$
. The formula
![]() $\Lambda _x(f)g=f\star g$
defines an adjointable operator and extends to a
$\Lambda _x(f)g=f\star g$
defines an adjointable operator and extends to a
![]() $\ast $
-representation of the full crossed product.
$\ast $
-representation of the full crossed product.
Definition 1.2. The reduced crossed product
![]() $A\rtimes _r G$
is defined as the quotient of the full crossed product by the joint kernel of the family
$A\rtimes _r G$
is defined as the quotient of the full crossed product by the joint kernel of the family
![]() $(\Lambda _x)_{x\in X}$
of representations.
$(\Lambda _x)_{x\in X}$
of representations.
Let us consider the G-equivariant Kasparov category
![]() $\operatorname {\mathrm {KK}}^G$
whose objects are separable and trivially graded
$\operatorname {\mathrm {KK}}^G$
whose objects are separable and trivially graded
![]() $C^*$
-algebras equipped with an action of G and whose set of morphisms
$C^*$
-algebras equipped with an action of G and whose set of morphisms
![]() $A\rightarrow B$
is Le Gall’s groupoid equivariant Kasparov group
$A\rightarrow B$
is Le Gall’s groupoid equivariant Kasparov group
![]() $\operatorname {\mathrm {KK}}^G(A,B)$
(see [Reference Le Gall30]); the composition in this category is the Kasparov product. We can view
$\operatorname {\mathrm {KK}}^G(A,B)$
(see [Reference Le Gall30]); the composition in this category is the Kasparov product. We can view
![]() $\operatorname {\mathrm {KK}}^G$
as a functor from the category of (separable) G-
$\operatorname {\mathrm {KK}}^G$
as a functor from the category of (separable) G-
![]() $C^*$
-algebras sending equivariant
$C^*$
-algebras sending equivariant
![]() $*$
-homomorphisms
$*$
-homomorphisms
![]() $A\to B$
to their respective class in the abelian group
$A\to B$
to their respective class in the abelian group
![]() $\operatorname {\mathrm {KK}}^G(A,B)$
. When viewed in this way, the functor
$\operatorname {\mathrm {KK}}^G(A,B)$
. When viewed in this way, the functor
![]() $\operatorname {\mathrm {KK}}^G$
enjoys an important property: It is the universal split-exact,
$\operatorname {\mathrm {KK}}^G$
enjoys an important property: It is the universal split-exact,
![]() $C^*$
-stable and homotopy invariant functor (see [Reference Meyer37, Reference Proietti and Yamashita49, Reference Thomsen56] for more details).
$C^*$
-stable and homotopy invariant functor (see [Reference Meyer37, Reference Proietti and Yamashita49, Reference Thomsen56] for more details).
Given a G-action on a space Z with moment map
![]() $p_Z\colon Z \to G^{0}$
, we have introduced above the pullback functor
$p_Z\colon Z \to G^{0}$
, we have introduced above the pullback functor
![]() $p^*_Z$
sending G-
$p^*_Z$
sending G-
![]() $C^*$
-algebras to
$C^*$
-algebras to
![]() $G\ltimes Z$
-
$G\ltimes Z$
-
![]() $C^*$
-algebras. Thanks to the universal property discussed above, we can promote this functor to a functor between equivariant Kasparov categories
$C^*$
-algebras. Thanks to the universal property discussed above, we can promote this functor to a functor between equivariant Kasparov categories
![]() $p^*_{Z}\colon \operatorname {\mathrm {KK}}^G\to \operatorname {\mathrm {KK}}^{G\ltimes Z}$
. This will be particularly useful when we take Z to be a model for the classifying space for proper actions of G (and in this case we may use the notation
$p^*_{Z}\colon \operatorname {\mathrm {KK}}^G\to \operatorname {\mathrm {KK}}^{G\ltimes Z}$
. This will be particularly useful when we take Z to be a model for the classifying space for proper actions of G (and in this case we may use the notation
![]() $Z=\underline {E} G$
) [Reference Tu59, Proposition 6.15].
$Z=\underline {E} G$
) [Reference Tu59, Proposition 6.15].
Moreover, given a map
![]() $f\colon G\to G\ltimes Z$
, the universal property ensures
$f\colon G\to G\ltimes Z$
, the universal property ensures
![]() $f_*$
yields well-defined functor between the corresponding
$f_*$
yields well-defined functor between the corresponding
![]() $\operatorname {\mathrm {KK}}$
-categories. Furthermore, when
$\operatorname {\mathrm {KK}}$
-categories. Furthermore, when
![]() $f\colon X\to Z$
is proper, we have a standard adjunction (see [Reference Meyer and Nest40])
$f\colon X\to Z$
is proper, we have a standard adjunction (see [Reference Meyer and Nest40])
Finally, let us define the category
![]() $\operatorname {\mathrm {RKK}}(Z)$
as follows.
$\operatorname {\mathrm {RKK}}(Z)$
as follows.
Definition 1.3. The category
![]() $\operatorname {\mathrm {RKK}}^G(Z)$
has the same objects as
$\operatorname {\mathrm {RKK}}^G(Z)$
has the same objects as
![]() $\operatorname {\mathrm {KK}}^G$
, and its
$\operatorname {\mathrm {KK}}^G$
, and its
![]() $\operatorname {\mathrm {Hom}}$
-sets
$\operatorname {\mathrm {Hom}}$
-sets
![]() $\operatorname {\mathrm {Hom}}(A,B)$
are given by the abelian groups
$\operatorname {\mathrm {Hom}}(A,B)$
are given by the abelian groups
![]() $\operatorname {\mathrm {KK}}^{G\ltimes Z}(p_Z^*A,p_Z^*B)$
.
$\operatorname {\mathrm {KK}}^{G\ltimes Z}(p_Z^*A,p_Z^*B)$
.
For a map f as above (not necessarily proper), the functor
![]() $f^*\colon \operatorname {\mathrm {KK}}^{G\ltimes Z}\to \operatorname {\mathrm {KK}}^{G\ltimes X}$
induces natural maps (slightly abusing notation)
$f^*\colon \operatorname {\mathrm {KK}}^{G\ltimes Z}\to \operatorname {\mathrm {KK}}^{G\ltimes X}$
induces natural maps (slightly abusing notation)
whenever the factorization
![]() $p_Z\circ f = p_Y$
holds. In this sense, for fixed A and B,
$p_Z\circ f = p_Y$
holds. In this sense, for fixed A and B,
![]() $\operatorname {\mathrm {RKK}}^G$
is a contravariant functor. It is also homotopy invariant, that is,
$\operatorname {\mathrm {RKK}}^G$
is a contravariant functor. It is also homotopy invariant, that is,
![]() $f_1^*=f_2^*$
if the maps
$f_1^*=f_2^*$
if the maps
![]() $f_1, f_2$
are G-homotopic. In order to see this, note that we have an isomorphism
$f_1, f_2$
are G-homotopic. In order to see this, note that we have an isomorphism
induced by Equation (1), hence the claim follows from the homotopy invariance of
![]() $\operatorname {\mathrm {KK}}^G(A,B)$
in the second variable B.
$\operatorname {\mathrm {KK}}^G(A,B)$
in the second variable B.
1.1 Triangulated structure and comparison with E-theory
Let us start by fixing some standard conventions. For a
![]() $C^*$
-algebra A, we have a suspension functor
$C^*$
-algebra A, we have a suspension functor
![]() $\Sigma A$
defined as
$\Sigma A$
defined as
![]() $\Sigma A =C_0(\mathbb {R})\otimes A$
. For an equivariant
$\Sigma A =C_0(\mathbb {R})\otimes A$
. For an equivariant
![]() $*$
-homomorphism of G-C
$*$
-homomorphism of G-C
![]() $^*$
-algebras
$^*$
-algebras
![]() $f \colon A \to B$
, we define its associated mapping cone by
$f \colon A \to B$
, we define its associated mapping cone by
This inherits a structure of G-C
![]() $^*$
-algebra from A and B.
$^*$
-algebra from A and B.
An exact triangle in
![]() $\operatorname {\mathrm {KK}}^G$
is the data of a diagram of the form
$\operatorname {\mathrm {KK}}^G$
is the data of a diagram of the form
and a
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $f\colon A' \to B'$
of G-C
$f\colon A' \to B'$
of G-C
![]() $^*$
-algebras, together with a commutative diagram
$^*$
-algebras, together with a commutative diagram

where the vertical arrows are equivalences in
![]() $\operatorname {\mathrm {KK}}^G$
, and the rightmost downward arrow is equal to the leftmost downward arrow, up to applying
$\operatorname {\mathrm {KK}}^G$
, and the rightmost downward arrow is equal to the leftmost downward arrow, up to applying
![]() $\Sigma $
and the Bott periodicity isomorphism
$\Sigma $
and the Bott periodicity isomorphism
![]() $\Sigma ^2 B' \simeq B'$
in
$\Sigma ^2 B' \simeq B'$
in
![]() $\operatorname {\mathrm {KK}}^G$
.
$\operatorname {\mathrm {KK}}^G$
.
As we see from above, the most natural triangulated structure lives on the opposite category
![]() $(\operatorname {\mathrm {KK}}^G)^{\text {op}}$
. The opposite category of a triangulated category inherits a canonical triangulated category structure, which has ‘the same’ exact triangles. The passage to opposite categories exchanges suspensions and desuspensions and modifies some sign conventions. Thus, the functor
$(\operatorname {\mathrm {KK}}^G)^{\text {op}}$
. The opposite category of a triangulated category inherits a canonical triangulated category structure, which has ‘the same’ exact triangles. The passage to opposite categories exchanges suspensions and desuspensions and modifies some sign conventions. Thus, the functor
![]() $\Sigma $
becomes in principle a desuspension functor in
$\Sigma $
becomes in principle a desuspension functor in
![]() $\operatorname {\mathrm {KK}}^G$
, but due to Bott periodicity
$\operatorname {\mathrm {KK}}^G$
, but due to Bott periodicity
![]() $\Sigma $
and
$\Sigma $
and
![]() $\Sigma ^{-1}$
agree so that we can safely overlook this fact. Moreover, depending on the definition of triangulated category, one may want the suspension to be an equivalence or an isomorphism of categories. In the latter case,
$\Sigma ^{-1}$
agree so that we can safely overlook this fact. Moreover, depending on the definition of triangulated category, one may want the suspension to be an equivalence or an isomorphism of categories. In the latter case,
![]() $\operatorname {\mathrm {KK}}^G$
should be replaced by an equivalent category (see [Reference Meyer and Nest40, Section 2.1]). This is not terribly important and will be ignored in the sequel.
$\operatorname {\mathrm {KK}}^G$
should be replaced by an equivalent category (see [Reference Meyer and Nest40, Section 2.1]). This is not terribly important and will be ignored in the sequel.
The triangulated category axioms are discussed in greater detail in [Reference Neeman45, Reference Verdier and Maltsiniotis62]. Most of them amount to formal properties of mapping cones and mapping cylinders, which can be shown in analogy with classical topology. The fundamental axiom requires that any morphism
![]() $A \to B$
should be part of an exact triangle. In our setting, this can be proved as a consequence of the generalization of [Reference Meyer37] to groupoid-equivariant
$A \to B$
should be part of an exact triangle. In our setting, this can be proved as a consequence of the generalization of [Reference Meyer37] to groupoid-equivariant
![]() $\operatorname {\mathrm {KK}}$
-theory (see also [Reference Lafforgue29, Lemma A.3.2]). Having done that, the rest of the proof follows the same outline of [Reference Meyer and Nest40, Appendix A], where the triangulated structure is established in the case of action groupoids.
$\operatorname {\mathrm {KK}}$
-theory (see also [Reference Lafforgue29, Lemma A.3.2]). Having done that, the rest of the proof follows the same outline of [Reference Meyer and Nest40, Appendix A], where the triangulated structure is established in the case of action groupoids.
There is an alternative, perhaps more conceptual path which consists in defining the Kasparov category as a certain localization of the Spanier–Whitehead category associated to the standard tensor category of G-
![]() $C^*$
-algebras and
$C^*$
-algebras and
![]() $*$
-homomorphisms [Reference Dell’Ambrogio20]. The triangulated structure of the Spanier–Whithead category is proved in [Reference Dell’Ambrogio20, Theorem A.5.3]. The argument given there can be directly used to show that
$*$
-homomorphisms [Reference Dell’Ambrogio20]. The triangulated structure of the Spanier–Whithead category is proved in [Reference Dell’Ambrogio20, Theorem A.5.3]. The argument given there can be directly used to show that
![]() $\operatorname {\mathrm {KK}}^G$
is triangulated, because it makes use of only two facts, which we prove below.
$\operatorname {\mathrm {KK}}^G$
is triangulated, because it makes use of only two facts, which we prove below.
Proposition 1.4. Let C be the standard tensor category of separable G-
![]() $C^*$
-algebras (with
$C^*$
-algebras (with
![]() $\otimes _X$
) and
$\otimes _X$
) and
![]() $*$
-homomorphisms. Denote by F the canonical functor from C to
$*$
-homomorphisms. Denote by F the canonical functor from C to
![]() $\operatorname {\mathrm {KK}}^G$
. The following hold:
$\operatorname {\mathrm {KK}}^G$
. The following hold:
-
– up to an isomorphism of morphisms in
 $\operatorname {\mathrm {KK}}^G$
, each morphism of
$\operatorname {\mathrm {KK}}^G$
, each morphism of
 $\operatorname {\mathrm {KK}}^G$
is in the image of F;
$\operatorname {\mathrm {KK}}^G$
is in the image of F; -
– up to an isomorphism of diagrams
 $Q\to K\to D$
in
$Q\to K\to D$
in
 $\operatorname {\mathrm {KK}}^G$
, each composable pair of morphisms of
$\operatorname {\mathrm {KK}}^G$
, each composable pair of morphisms of
 $\operatorname {\mathrm {KK}}^G$
is in the image of F.
$\operatorname {\mathrm {KK}}^G$
is in the image of F.
Proof. In order to show the lifting properties above we make use of ‘extension triangles’. Let
![]() $f\in \operatorname {\mathrm {KK}}_{0}^{G}(Q,K)$
be a morphism and denote by
$f\in \operatorname {\mathrm {KK}}_{0}^{G}(Q,K)$
be a morphism and denote by
![]() $\tilde {f}$
the corresponding element
$\tilde {f}$
the corresponding element
![]() $\tilde {f}\in \operatorname {\mathrm {KK}}_{1}^{G}({\Sigma Q, K})$
. By applying [Reference Lafforgue29, Lemma A.3.4], we can represent
$\tilde {f}\in \operatorname {\mathrm {KK}}_{1}^{G}({\Sigma Q, K})$
. By applying [Reference Lafforgue29, Lemma A.3.4], we can represent
![]() $\tilde {f}$
by a Kasparov module where the operator T is G-equivariant. Then the proof of [Reference Lafforgue29, Lemma A.3.2] gives that
$\tilde {f}$
by a Kasparov module where the operator T is G-equivariant. Then the proof of [Reference Lafforgue29, Lemma A.3.2] gives that
![]() $\tilde {f}$
is represented by an equivariant (semi-)split extension which fits a diagram as follows (see [Reference Meyer and Nest40, Section 2.3]):
$\tilde {f}$
is represented by an equivariant (semi-)split extension which fits a diagram as follows (see [Reference Meyer and Nest40, Section 2.3]):

where
![]() $\beta _Q$
is the Bott isomorphism and
$\beta _Q$
is the Bott isomorphism and
![]() $\epsilon _K$
is an equivalence. Hence, we have that
$\epsilon _K$
is an equivalence. Hence, we have that
![]() $F(\iota _f)\cong f$
. Notice how this argument automatically shows that f is contained in an exact triangle (up to equivalence).
$F(\iota _f)\cong f$
. Notice how this argument automatically shows that f is contained in an exact triangle (up to equivalence).
Now, given
![]() $g\in \operatorname {\mathrm {KK}}_{0}^{G}(K,D)$
, set
$g\in \operatorname {\mathrm {KK}}_{0}^{G}(K,D)$
, set
![]() $h=g\circ \epsilon _K^{-1},C_f=\operatorname {\mathrm {Cone}}(p_f)$
and consider the diagram
$h=g\circ \epsilon _K^{-1},C_f=\operatorname {\mathrm {Cone}}(p_f)$
and consider the diagram

This shows that the pair
![]() $(f,g)$
can be lifted to a composable pair
$(f,g)$
can be lifted to a composable pair
![]() $(\Sigma ^2\iota _f,\iota _h)$
.
$(\Sigma ^2\iota _f,\iota _h)$
.
Remark 1.5. The proof above depends on the fact that extensions with an equivariant, contractive, completely positive section can be shown to be isomorphic to mapping cone triangles. From an abstract standpoint, we may express this by saying that
![]() $\operatorname {\mathrm {KK}}^G$
is the result of the Verdier quotient [Reference Krause26, Reference Neeman45] of the Spanier–Whitehead category of G-
$\operatorname {\mathrm {KK}}^G$
is the result of the Verdier quotient [Reference Krause26, Reference Neeman45] of the Spanier–Whitehead category of G-
![]() $C^*$
-algebras [Reference Dell’Ambrogio20] by the thick tensor ideal of objects
$C^*$
-algebras [Reference Dell’Ambrogio20] by the thick tensor ideal of objects
![]() $\operatorname {\mathrm {Cone}}(\epsilon _K)$
, for all canonical comparison maps
$\operatorname {\mathrm {Cone}}(\epsilon _K)$
, for all canonical comparison maps
![]() $\epsilon _K$
associated to equivariant semisplit extensions (to be precise, we need to take into account yet another class of morphisms, to ensure that
$\epsilon _K$
associated to equivariant semisplit extensions (to be precise, we need to take into account yet another class of morphisms, to ensure that
![]() $\operatorname {\mathrm {KK}}^G$
is a stable functor; see [Reference Dell’Ambrogio20, Section A6.1] and Definition 1.6 below).
$\operatorname {\mathrm {KK}}^G$
is a stable functor; see [Reference Dell’Ambrogio20, Section A6.1] and Definition 1.6 below).
Definition 1.6. Let
![]() $\mathrm {SW}(C)$
be the Spanier–Whitehead category of the standard category of G-
$\mathrm {SW}(C)$
be the Spanier–Whitehead category of the standard category of G-
![]() $C^*$
-algebras, and let
$C^*$
-algebras, and let
![]() $\mathcal {I}\subseteq \mathrm {SW}(C)$
be the thick tensor ideal generated by the mapping cones of morphisms:
$\mathcal {I}\subseteq \mathrm {SW}(C)$
be the thick tensor ideal generated by the mapping cones of morphisms:
-
–
 $\epsilon _K$
for any extension
$\epsilon _K$
for any extension
 $K\hookrightarrow E \twoheadrightarrow Q$
in C;
$K\hookrightarrow E \twoheadrightarrow Q$
in C; -
–
 $\mathcal {K}(H_1)\to \mathcal {K}(H_1\oplus H_2)$
for any two nonzero G-Hilbert spaces
$\mathcal {K}(H_1)\to \mathcal {K}(H_1\oplus H_2)$
for any two nonzero G-Hilbert spaces
 $H_1,H_2$
, where the map is induced by the canonical inclusion in the first factor.
$H_1,H_2$
, where the map is induced by the canonical inclusion in the first factor.
The equivariant E-theory category is defined as the Verdier quotient
![]() $E_G=\mathrm {SW}(C)/\mathcal {I}$
.
$E_G=\mathrm {SW}(C)/\mathcal {I}$
.
It should be clear from the definition above that
![]() $E_G$
, viewed as functor from the category of separable G-
$E_G$
, viewed as functor from the category of separable G-
![]() $C^*$
-algebras is the universal half-exact,
$C^*$
-algebras is the universal half-exact,
![]() $C^*$
-stable, and homotopy invariant functor. In this sense, we can understand E-theory as the universal ‘correction’ of
$C^*$
-stable, and homotopy invariant functor. In this sense, we can understand E-theory as the universal ‘correction’ of
![]() $\operatorname {\mathrm {KK}}$
-theory in terms of excision properties. The universal property implies in particular that any functor between ‘concrete’ categories of
$\operatorname {\mathrm {KK}}$
-theory in terms of excision properties. The universal property implies in particular that any functor between ‘concrete’ categories of
![]() $C^*$
-algebras such as
$C^*$
-algebras such as
![]() $f_*$
and
$f_*$
and
![]() $f^*$
extends to E-theory the same way it does for
$f^*$
extends to E-theory the same way it does for
![]() $\operatorname {\mathrm {KK}}$
-theory.
$\operatorname {\mathrm {KK}}$
-theory.
By the same token, for a separable G-
![]() $C^*$
-algebra B we can define a functor
$C^*$
-algebra B we can define a functor
![]() $\sigma _B$
which is given by
$\sigma _B$
which is given by
![]() $\sigma _B(A)=A\otimes _X B$
on objects and
$\sigma _B(A)=A\otimes _X B$
on objects and
![]() $\sigma _B(\phi )=\phi \otimes \mathrm {1}_B$
on morphisms. It is important to discuss whether or not
$\sigma _B(\phi )=\phi \otimes \mathrm {1}_B$
on morphisms. It is important to discuss whether or not
![]() $\sigma _B$
is a triangulated functor on our K-theory categories
$\sigma _B$
is a triangulated functor on our K-theory categories
![]() $\operatorname {\mathrm {KK}}^G$
and
$\operatorname {\mathrm {KK}}^G$
and
![]() $E_G$
. By this, we mean whether or not
$E_G$
. By this, we mean whether or not
![]() $\sigma _A$
preserves exact triangles. Since we are adopting the convention of using the maximal tensor product, the preservation of exact triangles is a simple consequence of the fact that
$\sigma _A$
preserves exact triangles. Since we are adopting the convention of using the maximal tensor product, the preservation of exact triangles is a simple consequence of the fact that
![]() $-\otimes B$
is an exact functor, and clearly it preserves semisplit extensions.
$-\otimes B$
is an exact functor, and clearly it preserves semisplit extensions.
When B is
![]() $C_0(X)$
-nuclear, that is, a continuous field over X with nuclear fibers [Reference Bauval4], we have an isomorphism
$C_0(X)$
-nuclear, that is, a continuous field over X with nuclear fibers [Reference Bauval4], we have an isomorphism
![]() $A\otimes _X B\cong (A\otimes ^{\text {min}} B)_{\Delta _X}$
[Reference Blanchard7]. Note that this applies in particular to the pullback functor
$A\otimes _X B\cong (A\otimes ^{\text {min}} B)_{\Delta _X}$
[Reference Blanchard7]. Note that this applies in particular to the pullback functor
![]() $f^*$
associated to an open map
$f^*$
associated to an open map
![]() $f\colon Y\to X$
, such as the range and source maps
$f\colon Y\to X$
, such as the range and source maps
![]() $r,s\colon G\to G^{0}=X$
. Thus, if B is exact or
$r,s\colon G\to G^{0}=X$
. Thus, if B is exact or
![]() $C_0(X)$
-nuclear the functor
$C_0(X)$
-nuclear the functor
![]() $\sigma _B$
is triangulated, regardless of the specific choice of tensor product.
$\sigma _B$
is triangulated, regardless of the specific choice of tensor product.
The property of being
![]() $C_0(X)$
-nuclear, or rather its K-theoretic counterpart called
$C_0(X)$
-nuclear, or rather its K-theoretic counterpart called
![]() $\operatorname {\mathrm {KK}}^X$
-nuclearity, is important to establish a useful identification between
$\operatorname {\mathrm {KK}}^X$
-nuclearity, is important to establish a useful identification between
![]() $\operatorname {\mathrm {KK}}$
- and E-theory groups as follows. More information on
$\operatorname {\mathrm {KK}}$
- and E-theory groups as follows. More information on
![]() $\operatorname {\mathrm {KK}}^X$
-nuclearity can be found in [Reference Bauval4]; here, we limit ourselves to record the following simple fact, which is proved in [Reference Tu58, Proposition 5.1 & Corollary 5.2] (see Definition 3.1 for proper groupoids).
$\operatorname {\mathrm {KK}}^X$
-nuclearity can be found in [Reference Bauval4]; here, we limit ourselves to record the following simple fact, which is proved in [Reference Tu58, Proposition 5.1 & Corollary 5.2] (see Definition 3.1 for proper groupoids).
Proposition 1.7. Suppose G is proper. If A is
![]() $\operatorname {\mathrm {KK}}^{G^0}$
-nuclear, for example, A is a continuous field over the unit space of G with nuclear fibers, then the functor
$\operatorname {\mathrm {KK}}^{G^0}$
-nuclear, for example, A is a continuous field over the unit space of G with nuclear fibers, then the functor
![]() $B\mapsto \operatorname {\mathrm {KK}}^G(A,B)$
is half-exact.
$B\mapsto \operatorname {\mathrm {KK}}^G(A,B)$
is half-exact.
Having this, the following is a simple consequence of the universal properties.
Corollary 1.8 [Reference Park and Trout48].
If G is proper and A is a
![]() $\operatorname {\mathrm {KK}}^G$
-nuclear
$\operatorname {\mathrm {KK}}^G$
-nuclear
![]() $C^*$
-algebra, there is a natural isomorphism
$C^*$
-algebra, there is a natural isomorphism
![]() $\operatorname {\mathrm {KK}}^G(A,B)\cong E_G(A,B)$
for any separable G-
$\operatorname {\mathrm {KK}}^G(A,B)\cong E_G(A,B)$
for any separable G-
![]() $C^*$
-algebra B.
$C^*$
-algebra B.
Proof. Denote by F the standard
![]() $\operatorname {\mathrm {KK}}$
-functor from the category of separable
$\operatorname {\mathrm {KK}}$
-functor from the category of separable
![]() $C^*$
-algebras. The universal property of
$C^*$
-algebras. The universal property of
![]() $\operatorname {\mathrm {KK}}$
-theory gives us a map
$\operatorname {\mathrm {KK}}$
-theory gives us a map
![]() $\Phi _{C,B}\colon \operatorname {\mathrm {KK}}^G(C,B)\to E_G(C,B)$
. Let
$\Phi _{C,B}\colon \operatorname {\mathrm {KK}}^G(C,B)\to E_G(C,B)$
. Let
![]() $F^\prime $
be the functor (from separable
$F^\prime $
be the functor (from separable
![]() $C^*$
-algebras) given by
$C^*$
-algebras) given by
![]() $F^\prime (B)=\operatorname {\mathrm {KK}}^G(A,B)$
and
$F^\prime (B)=\operatorname {\mathrm {KK}}^G(A,B)$
and
![]() $F^\prime (f\colon C\to B)$
induced by Kasparov product with
$F^\prime (f\colon C\to B)$
induced by Kasparov product with
![]() $F(f)$
. Since
$F(f)$
. Since
![]() $\operatorname {\mathrm {KK}}^G(A,-)$
is half-exact, the universal property of E-theory yields a map
$\operatorname {\mathrm {KK}}^G(A,-)$
is half-exact, the universal property of E-theory yields a map
![]() $\Psi _{C,B}\colon \operatorname {\mathrm {KK}}^G(A,C)\times E_G(C,B)\to \operatorname {\mathrm {KK}}^G(A,B)$
. It is clear that
$\Psi _{C,B}\colon \operatorname {\mathrm {KK}}^G(A,C)\times E_G(C,B)\to \operatorname {\mathrm {KK}}^G(A,B)$
. It is clear that
![]() $\Psi (-\,,\Phi \circ F)=F^\prime $
. In particular, for
$\Psi (-\,,\Phi \circ F)=F^\prime $
. In particular, for
![]() $f\colon A\to B$
, we have
$f\colon A\to B$
, we have
which implies that
![]() $\Psi _{A,B}(1_A,-)$
is a left inverse for
$\Psi _{A,B}(1_A,-)$
is a left inverse for
![]() $\Phi _{A,B}$
. The argument for showing it is a right inverse is analogous.
$\Phi _{A,B}$
. The argument for showing it is a right inverse is analogous.
1.2 Complementary subcategories and cellular approximation
In this subsection, we recall some facts about complementary subcategories, homotopy colimits in triangulated categories and the fundamental notion of cellular approximation. The material in this section is summarized from [Reference Meyer38, Reference Meyer39, Reference Meyer and Nest40, Reference Meyer and Nest41].
Let
![]() $F\colon \mathcal {T} \to \mathcal {S}$
be an exact functor between triangulated categories. This means that F intertwines suspensions and preserves exact triangles. The kernel of F (on morphisms), denoted
$F\colon \mathcal {T} \to \mathcal {S}$
be an exact functor between triangulated categories. This means that F intertwines suspensions and preserves exact triangles. The kernel of F (on morphisms), denoted
![]() $\mathcal {I}=\ker F$
, will be called a homological ideal (see [Reference Meyer and Nest41, Remark 19]). We say that
$\mathcal {I}=\ker F$
, will be called a homological ideal (see [Reference Meyer and Nest41, Remark 19]). We say that
![]() $\mathcal {I}$
is compatible with direct sums if F commutes with countable direct sums (see [Reference Meyer39, Proposition 3.14]). Note that triangulated categories involving
$\mathcal {I}$
is compatible with direct sums if F commutes with countable direct sums (see [Reference Meyer39, Proposition 3.14]). Note that triangulated categories involving
![]() $\operatorname {\mathrm {KK}}$
-theory have no more than countable direct sums because separability assumptions are needed for certain analytical results in the background.
$\operatorname {\mathrm {KK}}$
-theory have no more than countable direct sums because separability assumptions are needed for certain analytical results in the background.
An object
![]() $P\in \mathcal {T}$
is called
$P\in \mathcal {T}$
is called
![]() $\mathcal {I}$
-projective if
$\mathcal {I}$
-projective if
![]() $\mathcal {I}(P,A)=0$
for all objects
$\mathcal {I}(P,A)=0$
for all objects
![]() $A\in \mathcal {T}$
. An object
$A\in \mathcal {T}$
. An object
![]() $N\in \mathcal {T}$
is called
$N\in \mathcal {T}$
is called
![]() $\mathcal {I}$
-contractible if
$\mathcal {I}$
-contractible if
![]() $\mathrm {id}_N$
belongs to
$\mathrm {id}_N$
belongs to
![]() $\mathcal {I}(N,N)$
. Reference to
$\mathcal {I}(N,N)$
. Reference to
![]() $\mathcal {I}$
is often omitted in the sequel. Let
$\mathcal {I}$
is often omitted in the sequel. Let
![]() $P_{\mathcal {I}}, N_{\mathcal {I}} \subseteq \mathcal {T}$
be the full subcategories of projective and contractible objects, respectively.
$P_{\mathcal {I}}, N_{\mathcal {I}} \subseteq \mathcal {T}$
be the full subcategories of projective and contractible objects, respectively.
We denote by
![]() $\langle {P_{\mathcal {I}}}\rangle $
the localizing subcategory generated by the projective objects, that is, the smallest triangulated subcategory that is closed under countable direct sums and contains
$\langle {P_{\mathcal {I}}}\rangle $
the localizing subcategory generated by the projective objects, that is, the smallest triangulated subcategory that is closed under countable direct sums and contains
![]() $P_{\mathcal {I}}$
. In particular,
$P_{\mathcal {I}}$
. In particular,
![]() $\langle P_{\mathcal {I}}\rangle $
is closed under isomorphisms, suspensions, and if
$\langle P_{\mathcal {I}}\rangle $
is closed under isomorphisms, suspensions, and if
is an exact triangle in
![]() $\mathcal {T}$
where any two of the objects
$\mathcal {T}$
where any two of the objects
![]() $A,B,C$
are in
$A,B,C$
are in
![]() $\langle P_{\mathcal {I}}\rangle $
, so is the third. Note that
$\langle P_{\mathcal {I}}\rangle $
, so is the third. Note that
![]() $N_{\mathcal {I}}$
is localizing, and any localizing subcategory is thick, that is, closed under direct summands (see [Reference Neeman45]).
$N_{\mathcal {I}}$
is localizing, and any localizing subcategory is thick, that is, closed under direct summands (see [Reference Neeman45]).
Definition 1.9. Given an object
![]() $A\in \mathcal {T}$
and a chain complex
$A\in \mathcal {T}$
and a chain complex
we say that Equation (3) is a projective resolution of A if
-
– all the
 $P_n$
’s are projective;
$P_n$
’s are projective; -
– the chain complex below is split exact

We say that
![]() $\mathcal {T}$
has enough projectives if any object admits a projective resolution.
$\mathcal {T}$
has enough projectives if any object admits a projective resolution.
Proposition 1.10 [Reference Meyer and Nest41, Proposition 44].
The construction of projective resolutions yields a functor
![]() $\mathcal {T} \to \mathrm {Ho}(\mathcal {T})$
. In particular, two projective resolutions of the same object are chain homotopy equivalent.
$\mathcal {T} \to \mathrm {Ho}(\mathcal {T})$
. In particular, two projective resolutions of the same object are chain homotopy equivalent.
Definition 1.11. We call two thick triangulated subcategories
![]() $\mathcal {P},\mathcal {N}$
of
$\mathcal {P},\mathcal {N}$
of
![]() $\mathcal {T}$
complementary if
$\mathcal {T}$
complementary if
![]() $\mathcal {T}(P,N)=0$
for all
$\mathcal {T}(P,N)=0$
for all
![]() $P\in \mathcal {P},N\in \mathcal {N}$
and, for any
$P\in \mathcal {P},N\in \mathcal {N}$
and, for any
![]() $A\in \mathcal {T}$
, there is an exact triangle
$A\in \mathcal {T}$
, there is an exact triangle
where
![]() $P\in \mathcal {P}$
and
$P\in \mathcal {P}$
and
![]() $N\in \mathcal {N}$
.
$N\in \mathcal {N}$
.
Proposition 1.12 [Reference Meyer and Nest40, Proposition 2.9].
Let
![]() $(\mathcal {P},\mathcal {N})$
be a pair of complementary subcategories of
$(\mathcal {P},\mathcal {N})$
be a pair of complementary subcategories of
![]() $\mathcal {T}$
.
$\mathcal {T}$
.
-
– We have
 $N\in \mathcal {N}$
if and only if
$N\in \mathcal {N}$
if and only if
 $\mathcal {T}(P,N)=0$
for all
$\mathcal {T}(P,N)=0$
for all
 $P\in \mathcal {P}$
. Analogously, we have
$P\in \mathcal {P}$
. Analogously, we have
 $P\in \mathcal {P}$
if and only if
$P\in \mathcal {P}$
if and only if
 $\mathcal {T}(P,N)=0$
for all
$\mathcal {T}(P,N)=0$
for all
 $N\in \mathcal {N}$
.
$N\in \mathcal {N}$
. -
– The exact triangle
 $P \to A \to N \to \Sigma P$
with
$P \to A \to N \to \Sigma P$
with
 $P\in \mathcal {P}$
and
$P\in \mathcal {P}$
and
 $N\in \mathcal {N}$
is uniquely determined up to isomorphism and depends functorially on A. In particular, its entries define functors
$N\in \mathcal {N}$
is uniquely determined up to isomorphism and depends functorially on A. In particular, its entries define functors  $$ \begin{align*} P\colon \mathcal{T} & \to \mathcal{P} & N\colon \mathcal{T} & \to \mathcal{N}\\ A &\mapsto P & A &\mapsto N. \end{align*} $$
$$ \begin{align*} P\colon \mathcal{T} & \to \mathcal{P} & N\colon \mathcal{T} & \to \mathcal{N}\\ A &\mapsto P & A &\mapsto N. \end{align*} $$
-
– The functors P and N are respectively left adjoint to the embedding functor
 $\mathcal {P}\to \mathcal {T}$
and right adjoint to the embedding functor
$\mathcal {P}\to \mathcal {T}$
and right adjoint to the embedding functor
 $\mathcal {N} \to \mathcal {T}$
.
$\mathcal {N} \to \mathcal {T}$
. -
– The localizations
 $\mathcal {T}/\mathcal {N}$
and
$\mathcal {T}/\mathcal {N}$
and
 $\mathcal {T}/\mathcal {P}$
exist and the compositions are equivalences of triangulated categories (see [Reference Krause26] for localization).
$\mathcal {T}/\mathcal {P}$
exist and the compositions are equivalences of triangulated categories (see [Reference Krause26] for localization). $$ \begin{align*} \mathcal{P} &\longrightarrow \mathcal{T} \longrightarrow \mathcal{T}/\mathcal{N} \\ \mathcal{N} &\longrightarrow \mathcal{T} \longrightarrow \mathcal{T}/\mathcal{P} \end{align*} $$
$$ \begin{align*} \mathcal{P} &\longrightarrow \mathcal{T} \longrightarrow \mathcal{T}/\mathcal{N} \\ \mathcal{N} &\longrightarrow \mathcal{T} \longrightarrow \mathcal{T}/\mathcal{P} \end{align*} $$
-
– If
 $K\colon \mathcal {T} \to \mathcal {C}$
is a covariant functor, then its localization with respect to
$K\colon \mathcal {T} \to \mathcal {C}$
is a covariant functor, then its localization with respect to
 $\mathcal {N}$
is defined by
$\mathcal {N}$
is defined by
 $\mathbb {L}K=K\circ P$
and the natural maps
$\mathbb {L}K=K\circ P$
and the natural maps
 $P(A)\to A$
provide a natural transformation
$P(A)\to A$
provide a natural transformation
 $\mathbb {L}K \Rightarrow K$
.
$\mathbb {L}K \Rightarrow K$
.
The following result will be very important for us.
Theorem 1.13 [Reference Meyer39, Theorem 3.16].
Let
![]() $\mathcal {T}$
be a triangulated category with countable direct sums, and let
$\mathcal {T}$
be a triangulated category with countable direct sums, and let
![]() $\mathcal {I}$
be a homological ideal with enough projective objects. Suppose that
$\mathcal {I}$
be a homological ideal with enough projective objects. Suppose that
![]() $\mathcal {I}$
is compatible with countable direct sums. Then the pair of localizing subcategories
$\mathcal {I}$
is compatible with countable direct sums. Then the pair of localizing subcategories
![]() $(\langle P_{\mathcal {I}}\rangle ,N_{\mathcal {I}})$
in
$(\langle P_{\mathcal {I}}\rangle ,N_{\mathcal {I}})$
in
![]() $\mathcal {T}$
is complementary.
$\mathcal {T}$
is complementary.
A pair of complementary subcategories helps clarify the degree to which a projective resolution ‘computes’ a homological functor into the category of abelian groups. The object
![]() $P(A)$
resulting from Proposition 1.12 is called the
$P(A)$
resulting from Proposition 1.12 is called the
![]() $P_{\mathcal {I}}$
-cellular approximation of A (it is called simiplicial approximation in [Reference Meyer and Nest40]).
$P_{\mathcal {I}}$
-cellular approximation of A (it is called simiplicial approximation in [Reference Meyer and Nest40]).
Definition 1.14. In general, the homotopy direct limit of a countable inductive system
![]() $(A_n,\alpha _m^n)$
is defined as the object
$(A_n,\alpha _m^n)$
is defined as the object
![]() $A^h_\infty $
fitting into the exact triangle below:
$A^h_\infty $
fitting into the exact triangle below:
where
![]() $S|_{A_n}\colon A_n\to A_{n+1}$
is just the connecting map
$S|_{A_n}\colon A_n\to A_{n+1}$
is just the connecting map
![]() $\alpha _n^{n+1}$
. We write
$\alpha _n^{n+1}$
. We write
![]() $\text {ho-lim}(A_n,\alpha _m^n)=A^h_\infty $
, or simply
$\text {ho-lim}(A_n,\alpha _m^n)=A^h_\infty $
, or simply
![]() $\text {ho-lim}\, A_n$
when the connecting maps are clear from context.
$\text {ho-lim}\, A_n$
when the connecting maps are clear from context.
Remark 1.15. The object
![]() $P(A)$
can be computed as the homotopy limit of an inductive system
$P(A)$
can be computed as the homotopy limit of an inductive system
![]() $(P_n,\phi _n)$
with
$(P_n,\phi _n)$
with
![]() $P_n \in P_{\mathcal {I}}$
(in fact,
$P_n \in P_{\mathcal {I}}$
(in fact,
![]() $P_n$
belongs to a subclass of objects in
$P_n$
belongs to a subclass of objects in
![]() $P_{\mathcal {I}}$
, see [Reference Meyer39, Proposition 3.18] for more details).
$P_{\mathcal {I}}$
, see [Reference Meyer39, Proposition 3.18] for more details).
We mention a few more properties of this limit that will be useful for our later arguments. First of all, the last map in the triangle above is equivalent to a sequence of maps
![]() $\alpha _n^\infty \colon A_n \to A^h_\infty $
with the compatibility relation
$\alpha _n^\infty \colon A_n \to A^h_\infty $
with the compatibility relation
![]() $\alpha _n^\infty \circ \alpha _m^n=\alpha _m^\infty $
when
$\alpha _n^\infty \circ \alpha _m^n=\alpha _m^\infty $
when
![]() $m\leq n$
.
$m\leq n$
.
Lemma 1.16 [Reference Neeman45].
Suppose F is a (co)homological functor, that is, it sends exact triangles to long exact sequences of abelian groups.
-
– (homological case): If
 $F(\bigoplus A_n)\cong \bigoplus F(A_n)$
, then the maps
$F(\bigoplus A_n)\cong \bigoplus F(A_n)$
, then the maps
 $\alpha _n^\infty $
give an isomorphism
$\alpha _n^\infty $
give an isomorphism
 $\varinjlim F_k(A_n)\cong F_k(A^h_\infty ).$
$\varinjlim F_k(A_n)\cong F_k(A^h_\infty ).$
-
– (cohomological case): If
 $F(\bigoplus A_n)\cong \prod F(A_n)$
, there is a short exact sequence where the last map is induced by
$F(\bigoplus A_n)\cong \prod F(A_n)$
, there is a short exact sequence where the last map is induced by $$\begin{align*}0\longrightarrow \varprojlim{}^1F^{k-1}(A_n) \longrightarrow F^k(A^h_\infty) \longrightarrow \varprojlim F^k(A_n)\longrightarrow 0, \end{align*}$$
$$\begin{align*}0\longrightarrow \varprojlim{}^1F^{k-1}(A_n) \longrightarrow F^k(A^h_\infty) \longrightarrow \varprojlim F^k(A_n)\longrightarrow 0, \end{align*}$$
 $(\alpha _n^\infty )_{n\in \mathbb {N}}$
.
$(\alpha _n^\infty )_{n\in \mathbb {N}}$
.
Let us consider the ordinary inductive limit of
![]() $C^*$
-algebras
$C^*$
-algebras
![]() $A_\infty $
associated to the system
$A_\infty $
associated to the system
![]() $(A_n,\alpha _m^n)$
, where the maps
$(A_n,\alpha _m^n)$
, where the maps
![]() $\alpha _m^n$
are equivariant
$\alpha _m^n$
are equivariant
![]() $\ast $
-homomorphisms. We keep using
$\ast $
-homomorphisms. We keep using
![]() $\alpha _n^\infty $
for the canonical maps
$\alpha _n^\infty $
for the canonical maps
![]() $A_n\to A_\infty $
. The relation between
$A_n\to A_\infty $
. The relation between
![]() $A^h_\infty $
and
$A^h_\infty $
and
![]() $A_\infty $
, as discussed in [Reference Meyer and Nest40, Section 2.4], is based on the notion of an admissible system in
$A_\infty $
, as discussed in [Reference Meyer and Nest40, Section 2.4], is based on the notion of an admissible system in
![]() $\operatorname {\mathrm {KK}}^G$
. We do not need this definition here, but we recall a sufficient condition: The system
$\operatorname {\mathrm {KK}}^G$
. We do not need this definition here, but we recall a sufficient condition: The system
![]() $(A_n,\alpha _m^n)$
is admissible if there exist equivariant completely positive contractions
$(A_n,\alpha _m^n)$
is admissible if there exist equivariant completely positive contractions
![]() $\phi _n\colon A_\infty \to A_n$
such that
$\phi _n\colon A_\infty \to A_n$
such that
![]() $\alpha _n^\infty \circ \phi _n\colon A_\infty \to A_\infty $
converges to the identity in the point norm topology [Reference Meyer and Nest40, Lemma 2.7]. The situation is simpler in
$\alpha _n^\infty \circ \phi _n\colon A_\infty \to A_\infty $
converges to the identity in the point norm topology [Reference Meyer and Nest40, Lemma 2.7]. The situation is simpler in
![]() $E_G$
-theory: By Definition 1.6, since all extensions in
$E_G$
-theory: By Definition 1.6, since all extensions in
![]() $E_G$
-theory are admissible, all inductive systems are admissible too.
$E_G$
-theory are admissible, all inductive systems are admissible too.
Proposition 1.17. We have
![]() $A^h_\infty \cong A_\infty $
in the category
$A^h_\infty \cong A_\infty $
in the category
![]() $E_G$
. If the inductive system
$E_G$
. If the inductive system
![]() $(A_n,\alpha _m^n)$
is admissible, we have
$(A_n,\alpha _m^n)$
is admissible, we have
![]() $A^h_\infty \cong A_\infty $
in the category
$A^h_\infty \cong A_\infty $
in the category
![]() $\operatorname {\mathrm {KK}}^G$
.
$\operatorname {\mathrm {KK}}^G$
.
1.3 Crossed products of Hilbert modules and descent
In this section, we recall the notion of crossed product of Hilbert modules and define the Kasparov descent morphism in the context of groupoids. We will focus on reduced crossed products. To this end, we start by recasting
![]() $C_0(X)$
-algebras under the perspective of
$C_0(X)$
-algebras under the perspective of
![]() $C^*$
-bundles. If A is a
$C^*$
-bundles. If A is a
![]() $C_0(X)$
-algebra, there exists a topology on
$C_0(X)$
-algebra, there exists a topology on
![]() $\mathcal {A}=\bigsqcup _{x\in X} A_x$
making the natural map
$\mathcal {A}=\bigsqcup _{x\in X} A_x$
making the natural map
![]() $\mathcal {A}\to X$
an upper-semicontinuous
$\mathcal {A}\to X$
an upper-semicontinuous
![]() $C^*$
-bundle. The associated algebra of sections vanishing at infinity, denoted
$C^*$
-bundle. The associated algebra of sections vanishing at infinity, denoted
![]() $\Gamma _0(X,\mathcal {A})$
, admits a
$\Gamma _0(X,\mathcal {A})$
, admits a
![]() $C_0(X)$
-linear isomorphism onto A. The correspondence
$C_0(X)$
-linear isomorphism onto A. The correspondence
![]() $A\mapsto \mathcal {A}$
sends
$A\mapsto \mathcal {A}$
sends
![]() $C_0(X)$
-linear morphisms to
$C_0(X)$
-linear morphisms to
![]() $C^*$
-bundles morphisms.
$C^*$
-bundles morphisms.
If
![]() $f\colon Y \to X$
is a continuous map, the pullback
$f\colon Y \to X$
is a continuous map, the pullback
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $f^*A$
can also be defined by first constructing the pullback bundle
$f^*A$
can also be defined by first constructing the pullback bundle
![]() $f^*\mathcal {A}$
, then setting
$f^*\mathcal {A}$
, then setting
![]() $f^*A=\Gamma _0(Y,f^*\mathcal {A})$
. A G-action on A can be given by defining a functor from G (viewed as a category) to the category of
$f^*A=\Gamma _0(Y,f^*\mathcal {A})$
. A G-action on A can be given by defining a functor from G (viewed as a category) to the category of
![]() $C^*$
-algebras, sending
$C^*$
-algebras, sending
![]() $x\in X$
to
$x\in X$
to
![]() $A_x$
, then imposing continuity on the resulting G-action on the topological space
$A_x$
, then imposing continuity on the resulting G-action on the topological space
![]() $\mathcal {A}$
. The definition of
$\mathcal {A}$
. The definition of
![]() $A\rtimes G$
can then be reframed by endowing the compactly supported sections
$A\rtimes G$
can then be reframed by endowing the compactly supported sections
![]() $\Gamma _c(G,r^*\mathcal {A})$
with a
$\Gamma _c(G,r^*\mathcal {A})$
with a
![]() $\ast $
-algebra structure and completing in the appropriate norm as explained previously.
$\ast $
-algebra structure and completing in the appropriate norm as explained previously.
Given a G-algebra
![]() $(A,\alpha )$
and a Hilbert A-module
$(A,\alpha )$
and a Hilbert A-module
![]() $\mathcal {E}$
, for each
$\mathcal {E}$
, for each
![]() $x\in X$
one defines the Hilbert
$x\in X$
one defines the Hilbert
![]() $A_{x}$
-module
$A_{x}$
-module
![]() $\mathfrak {E}_{x}$
to be the balanced tensor product
$\mathfrak {E}_{x}$
to be the balanced tensor product
![]() $\mathcal {E}\otimes _{A}A_{x}$
. The space
$\mathcal {E}\otimes _{A}A_{x}$
. The space
![]() $\mathfrak {E}:=\bigsqcup _{x\in X}\mathfrak {E}_{x}$
may be topologized to obtain an upper-semicontinuous Hilbert
$\mathfrak {E}:=\bigsqcup _{x\in X}\mathfrak {E}_{x}$
may be topologized to obtain an upper-semicontinuous Hilbert
![]() $\mathcal {A}$
-module bundle
$\mathcal {A}$
-module bundle
![]() $p_{\mathfrak {E}}:\mathfrak {E}\longrightarrow X$
. The space of sections
$p_{\mathfrak {E}}:\mathfrak {E}\longrightarrow X$
. The space of sections
![]() $\Gamma _{0}(X;\mathfrak {E})$
is equipped with pointwise operations to furnish a Hilbert
$\Gamma _{0}(X;\mathfrak {E})$
is equipped with pointwise operations to furnish a Hilbert
![]() $\Gamma _{0}(X;\mathcal {A})$
-module, to which
$\Gamma _{0}(X;\mathcal {A})$
-module, to which
![]() $\mathcal {E}$
is canonically isomorphic as a Hilbert A-module. We will identify
$\mathcal {E}$
is canonically isomorphic as a Hilbert A-module. We will identify
![]() $\mathcal {E}$
with its associated section space
$\mathcal {E}$
with its associated section space
![]() $\Gamma _{0}(X;\mathfrak {E})$
. We have associated bundles of
$\Gamma _{0}(X;\mathfrak {E})$
. We have associated bundles of
![]() $C^{*}$
-algebras
$C^{*}$
-algebras
![]() $\mathcal {K}(\mathfrak {E})$
and
$\mathcal {K}(\mathfrak {E})$
and
![]() $\mathcal {L}(\mathfrak {E})$
, whose fibres over
$\mathcal {L}(\mathfrak {E})$
, whose fibres over
![]() $x\in X$
are
$x\in X$
are
![]() $\mathcal {K}(\mathfrak {E}_{x})$
and
$\mathcal {K}(\mathfrak {E}_{x})$
and
![]() $\mathcal {L}(\mathfrak {E}_{x})$
, respectively (the former bundle is upper-semicontinuous). By the identification
$\mathcal {L}(\mathfrak {E}_{x})$
, respectively (the former bundle is upper-semicontinuous). By the identification
![]() $\mathcal {E} = \Gamma _{0}(X;\mathfrak {E})$
, we then also have
$\mathcal {E} = \Gamma _{0}(X;\mathfrak {E})$
, we then also have
![]() $\mathcal {K}(\mathcal {E}) = \Gamma _{0}(X;\mathcal {K}(\mathfrak {E}))$
and
$\mathcal {K}(\mathcal {E}) = \Gamma _{0}(X;\mathcal {K}(\mathfrak {E}))$
and
![]() $\mathcal {L}(\mathcal {E}) = \Gamma _{b}(X;\mathcal {L}(\mathfrak {E}))$
(strictly continuous bounded sections).
$\mathcal {L}(\mathcal {E}) = \Gamma _{b}(X;\mathcal {L}(\mathfrak {E}))$
(strictly continuous bounded sections).
A G-action
![]() $\mathcal {E} = \Gamma _{0}(X;\mathfrak {E})$
consists of a family
$\mathcal {E} = \Gamma _{0}(X;\mathfrak {E})$
consists of a family
![]() $\{W_{\gamma }\}_{\gamma \in G}$
such that:
$\{W_{\gamma }\}_{\gamma \in G}$
such that:
-
– for each
 $\gamma \in G$
,
$\gamma \in G$
,
 $W_{\gamma }:\mathfrak {E}_{s(\gamma )}\longrightarrow \mathfrak {E}_{r(\gamma )}$
is an isometric isomorphism of Banach spaces such that
$W_{\gamma }:\mathfrak {E}_{s(\gamma )}\longrightarrow \mathfrak {E}_{r(\gamma )}$
is an isometric isomorphism of Banach spaces such that
 $\langle W_{\gamma }e, W_{\gamma }f\rangle _{r(\gamma )} = \alpha _{\gamma }(\langle e,f\rangle _{s(\gamma )})$
for all
$\langle W_{\gamma }e, W_{\gamma }f\rangle _{r(\gamma )} = \alpha _{\gamma }(\langle e,f\rangle _{s(\gamma )})$
for all
 $e,f\in \mathfrak {E}_{s(\gamma )}$
;
$e,f\in \mathfrak {E}_{s(\gamma )}$
; -
– the map
 $G{}_s{\times }{_{p_{\mathfrak {E}}}}\mathfrak {E}\longrightarrow \mathfrak {E}$
,
$G{}_s{\times }{_{p_{\mathfrak {E}}}}\mathfrak {E}\longrightarrow \mathfrak {E}$
,
 $(\gamma ,e)\mapsto W_{\gamma }e$
defines a continuous action of G on
$(\gamma ,e)\mapsto W_{\gamma }e$
defines a continuous action of G on
 $\mathfrak {E}$
.
$\mathfrak {E}$
.
Conjugation by W gives rise to a strictly continuous action
![]() $\varepsilon :G{}_s{\times }{_{p_{\mathfrak {E}}}}\mathcal {L}(\mathfrak {E})\longrightarrow \mathcal {L}(\mathfrak {E})$
of G on the upper-semicontinuous bundle
$\varepsilon :G{}_s{\times }{_{p_{\mathfrak {E}}}}\mathcal {L}(\mathfrak {E})\longrightarrow \mathcal {L}(\mathfrak {E})$
of G on the upper-semicontinuous bundle
![]() $\mathcal {L}(\mathfrak {E})$
(the restriction of
$\mathcal {L}(\mathfrak {E})$
(the restriction of
![]() $\varepsilon $
to the compact operators is continuous in the usual sense).
$\varepsilon $
to the compact operators is continuous in the usual sense).
If
![]() $(B, \beta ) $
is a G-algebra and
$(B, \beta ) $
is a G-algebra and
![]() $\pi \colon B\to \mathcal {L}(\mathcal {E})$
a
$\pi \colon B\to \mathcal {L}(\mathcal {E})$
a
![]() $C_0(X)$
-linear representation, we define a G-representation by requiring equivariance, namely for all
$C_0(X)$
-linear representation, we define a G-representation by requiring equivariance, namely for all
![]() $\gamma \in G$
we have
$\gamma \in G$
we have
Given a Kasparov module
![]() $(\pi ,\mathcal {E},T)$
representing a class in
$(\pi ,\mathcal {E},T)$
representing a class in
![]() $\operatorname {\mathrm {KK}}^G(B,A)$
, let us consider the
$\operatorname {\mathrm {KK}}^G(B,A)$
, let us consider the
![]() $B\rtimes _r G$
-
$B\rtimes _r G$
-
![]() $A\rtimes _r G$
-module
$A\rtimes _r G$
-module
![]() $(\tilde {\pi },\mathcal {E}\widehat {\otimes }_A (A\rtimes _r G), T\widehat {\otimes } 1)$
, where
$(\tilde {\pi },\mathcal {E}\widehat {\otimes }_A (A\rtimes _r G), T\widehat {\otimes } 1)$
, where
![]() $\tilde {\pi }$
is a representation of
$\tilde {\pi }$
is a representation of
![]() $B\rtimes _r G$
induced by
$B\rtimes _r G$
induced by
![]() $\pi $
as follows. First of all, note that
$\pi $
as follows. First of all, note that
![]() $\mathcal {E}\widehat {\otimes }_A (A\rtimes _r G)$
is isomorphic to the completion of
$\mathcal {E}\widehat {\otimes }_A (A\rtimes _r G)$
is isomorphic to the completion of
![]() $\Gamma _c(G,r^*\mathfrak {E})$
with respect to the
$\Gamma _c(G,r^*\mathfrak {E})$
with respect to the
![]() $\Gamma _{c}(G;r^{*}\mathcal {A})$
-valued inner product
$\Gamma _{c}(G;r^{*}\mathcal {A})$
-valued inner product
for
![]() $\xi ,\xi '\in \Gamma _{c}(G;r^{*}\mathfrak {E})$
and
$\xi ,\xi '\in \Gamma _{c}(G;r^{*}\mathfrak {E})$
and
![]() $\gamma \in G$
. We denote this completion
$\gamma \in G$
. We denote this completion
![]() $\mathcal {E}\rtimes G$
. Consider the formula below, defined for
$\mathcal {E}\rtimes G$
. Consider the formula below, defined for
![]() $f\in \Gamma _{c}(G;r^{*}\mathcal {A})$
,
$f\in \Gamma _{c}(G;r^{*}\mathcal {A})$
,
![]() $\xi \in \Gamma _{c}(G;r^{*}\mathfrak {E})$
, and
$\xi \in \Gamma _{c}(G;r^{*}\mathfrak {E})$
, and
![]() $\gamma \in G$
,
$\gamma \in G$
,
This determines a bounded representation
![]() $\tilde {\pi }=\pi \rtimes G :A\rtimes _rG\longrightarrow \mathcal {L}(\mathcal {E}\rtimes G)$
(see, for example, [Reference MacDonald34, Prop. 7.6]).
$\tilde {\pi }=\pi \rtimes G :A\rtimes _rG\longrightarrow \mathcal {L}(\mathcal {E}\rtimes G)$
(see, for example, [Reference MacDonald34, Prop. 7.6]).
Definition 1.18. We define the Kasparov descent morphism to be the homomorphism of abelian groups
which sends the class of
![]() $(\pi ,\mathcal {E}, T)$
to the class of
$(\pi ,\mathcal {E}, T)$
to the class of
![]() $(\tilde {\pi },\mathcal {E}\widehat {\otimes }_A (A\rtimes _r G),T\widehat {\otimes } 1)$
.
$(\tilde {\pi },\mathcal {E}\widehat {\otimes }_A (A\rtimes _r G),T\widehat {\otimes } 1)$
.
It can be checked that
![]() $\jmath ^G$
is compatible with the product in
$\jmath ^G$
is compatible with the product in
![]() $\operatorname {\mathrm {KK}}^G$
, meaning that
$\operatorname {\mathrm {KK}}^G$
, meaning that
![]() $\jmath ^G(x\,\widehat {\otimes }_D\, y)=\jmath ^G(x)\,\widehat {\otimes }_{D\rtimes _r G}\, \jmath ^G(y)$
, giving us a well-defined functor [Reference Le Gall31, Theorem 3.4].
$\jmath ^G(x\,\widehat {\otimes }_D\, y)=\jmath ^G(x)\,\widehat {\otimes }_{D\rtimes _r G}\, \jmath ^G(y)$
, giving us a well-defined functor [Reference Le Gall31, Theorem 3.4].
2 Induction-restriction adjunction
Consider a subgroupoid
![]() $H\subseteq G$
. The inclusion map
$H\subseteq G$
. The inclusion map
![]() $H\hookrightarrow G$
induces a natural restriction functor
$H\hookrightarrow G$
induces a natural restriction functor
![]() $\operatorname {\mathrm {Res}}_G^H\colon \operatorname {\mathrm {KK}}^G\to \operatorname {\mathrm {KK}}^H$
. In this section, we will construct a functor in the other direction, called the induction functor, and prove that these two functors are adjoint when
$\operatorname {\mathrm {Res}}_G^H\colon \operatorname {\mathrm {KK}}^G\to \operatorname {\mathrm {KK}}^H$
. In this section, we will construct a functor in the other direction, called the induction functor, and prove that these two functors are adjoint when
![]() $H\subseteq G$
is open. This generalizes earlier results for transformation groups [Reference Meyer and Nest40] and ample groupoids [Reference Bönicke10].
$H\subseteq G$
is open. This generalizes earlier results for transformation groups [Reference Meyer and Nest40] and ample groupoids [Reference Bönicke10].
2.1 The induction functor
Let
![]() $(B,\beta )\in \operatorname {\mathrm {KK}}^H$
with moment map
$(B,\beta )\in \operatorname {\mathrm {KK}}^H$
with moment map
![]() $\rho \colon C_0(H^{0})\to Z(\mathcal {M}(B))$
. In this subsection, it is sufficient to assume H is locally closed in G. Recall
$\rho \colon C_0(H^{0})\to Z(\mathcal {M}(B))$
. In this subsection, it is sufficient to assume H is locally closed in G. Recall
![]() $G_{H^{0}}$
is the subspace of G consisting of arrows with source in
$G_{H^{0}}$
is the subspace of G consisting of arrows with source in
![]() $H^{0}$
. We consider the restriction of the source map
$H^{0}$
. We consider the restriction of the source map
![]() $\phi = s|_{ G_{H^0}}:G_{H^{0}}\rightarrow H^{0}$
and construct the pullback algebra
$\phi = s|_{ G_{H^0}}:G_{H^{0}}\rightarrow H^{0}$
and construct the pullback algebra
This balanced tensor product is then a
![]() $C_0(H^{0})$
-algebra in its own right and can be equipped with the diagonal action
$C_0(H^{0})$
-algebra in its own right and can be equipped with the diagonal action
![]() $\text {rt}\otimes \beta $
of H, where
$\text {rt}\otimes \beta $
of H, where
![]() $\text {rt}$
denotes the action of H on
$\text {rt}$
denotes the action of H on
![]() $C_0(G_{H^{0}})$
induced by right translation. We define the induced algebra as the corresponding reduced crossed product
$C_0(G_{H^{0}})$
induced by right translation. We define the induced algebra as the corresponding reduced crossed product
To define a G-action on
![]() $\operatorname {\mathrm {Ind}}_H^G B$
, notice that G also acts on the balanced tensor product
$\operatorname {\mathrm {Ind}}_H^G B$
, notice that G also acts on the balanced tensor product
![]() $C_0(G_{H^{0}}) \otimes _{H^{0}} B$
by
$C_0(G_{H^{0}}) \otimes _{H^{0}} B$
by
![]() $\mathrm {lt}\otimes \mathrm {id}_B$
, where
$\mathrm {lt}\otimes \mathrm {id}_B$
, where
![]() $\mathrm {lt}$
denotes the action of G on
$\mathrm {lt}$
denotes the action of G on
![]() $C_0(G_{H^{0}})$
induced by left translation. A straightforward computation reveals that the actions
$C_0(G_{H^{0}})$
induced by left translation. A straightforward computation reveals that the actions
![]() $\mathrm {rt}\otimes \beta $
and
$\mathrm {rt}\otimes \beta $
and
![]() $\mathrm {lt}\otimes \mathrm {id}_B$
commute and therefore the left translation action of G descends to an action on the crossed product
$\mathrm {lt}\otimes \mathrm {id}_B$
commute and therefore the left translation action of G descends to an action on the crossed product
![]() $(C_0(G_{H^{0}}) \otimes _{H^{0}}B)\rtimes _{\text {rt}\otimes \beta } H.$
$(C_0(G_{H^{0}}) \otimes _{H^{0}}B)\rtimes _{\text {rt}\otimes \beta } H.$
Having defined
![]() $\operatorname {\mathrm {Ind}}_H^G$
on objects, let us consider the case of morphisms. Consider a right Hilbert B-module
$\operatorname {\mathrm {Ind}}_H^G$
on objects, let us consider the case of morphisms. Consider a right Hilbert B-module
![]() $\mathcal {E}$
. Considering the canonical action
$\mathcal {E}$
. Considering the canonical action
![]() $B\longrightarrow \mathcal {M}(C_0(G_{H^{0}})\otimes _{H^{0}} B)$
given by multiplication in the second factor, we can form the
$B\longrightarrow \mathcal {M}(C_0(G_{H^{0}})\otimes _{H^{0}} B)$
given by multiplication in the second factor, we can form the
![]() $\phi ^*B$
-module
$\phi ^*B$
-module
Note the module above corresponds to the space of section of the pullback bundle
![]() $\phi ^*\mathfrak {E}$
. Assume now that
$\phi ^*\mathfrak {E}$
. Assume now that
![]() $\mathcal {E}$
carries an action of H (call it
$\mathcal {E}$
carries an action of H (call it
![]() $\epsilon $
) along with a nondegenerate equivariant representation
$\epsilon $
) along with a nondegenerate equivariant representation
![]() $\pi \colon A\to \mathcal {L}(\mathcal {E})$
of an H-algebra A. First of all, we note that
$\pi \colon A\to \mathcal {L}(\mathcal {E})$
of an H-algebra A. First of all, we note that
![]() $\epsilon \otimes (\mathrm {rt}\otimes \beta )$
defines an H-action on
$\epsilon \otimes (\mathrm {rt}\otimes \beta )$
defines an H-action on
![]() $\phi ^*\mathcal {E}$
. Then we define a representation of
$\phi ^*\mathcal {E}$
. Then we define a representation of
![]() $\phi ^*A$
on
$\phi ^*A$
on
![]() $\mathcal {\phi ^*\mathcal {E}}$
by considering elements
$\mathcal {\phi ^*\mathcal {E}}$
by considering elements
![]() $f\otimes a$
, with
$f\otimes a$
, with
![]() $f\in C_c(G_{H^{0}})$
and
$f\in C_c(G_{H^{0}})$
and
![]() $a\in A$
, whose linear span is dense in
$a\in A$
, whose linear span is dense in
![]() $\Gamma _c(G_{H^{0}},\phi ^*\mathcal {A})\subseteq \phi ^*A$
and setting
$\Gamma _c(G_{H^{0}},\phi ^*\mathcal {A})\subseteq \phi ^*A$
and setting
![]() $\phi ^*\pi (f\otimes a) = \pi (a)\otimes (f\,\cdot )$
.
$\phi ^*\pi (f\otimes a) = \pi (a)\otimes (f\,\cdot )$
.
Now, if
![]() $(\pi ,\mathcal {E},T)$
is an A-B-Kasparov module, then
$(\pi ,\mathcal {E},T)$
is an A-B-Kasparov module, then
![]() $(\phi ^*{\pi },\phi ^*\mathcal {E},T\widehat {\otimes } 1)$
is a
$(\phi ^*{\pi },\phi ^*\mathcal {E},T\widehat {\otimes } 1)$
is a
![]() $\phi ^*A$
-
$\phi ^*A$
-
![]() $\phi ^*B$
-module equipped with an action of H, and we can define the induction functor by means of the descent morphism defined above, as follows:
$\phi ^*B$
-module equipped with an action of H, and we can define the induction functor by means of the descent morphism defined above, as follows:
To complete the description of
![]() $\operatorname {\mathrm {Ind}}_H^G$
, we need two more observations. The
$\operatorname {\mathrm {Ind}}_H^G$
, we need two more observations. The
![]() $\phi ^*B$
-module
$\phi ^*B$
-module
![]() $\mathcal {E}\otimes _B (C_0(G_{H^{0}})\otimes _{H^{0}} B)$
admits a G-action induced by left translation on
$\mathcal {E}\otimes _B (C_0(G_{H^{0}})\otimes _{H^{0}} B)$
admits a G-action induced by left translation on
![]() $C_0(G_{H^{0}})$
. Notice this action is defined by fibreing over the range map. Clearly
$C_0(G_{H^{0}})$
. Notice this action is defined by fibreing over the range map. Clearly
![]() $T\widehat {\otimes } 1$
is equivariant with respect to this translation. To check the equivariance of
$T\widehat {\otimes } 1$
is equivariant with respect to this translation. To check the equivariance of
![]() $\phi ^*\pi $
, by definition it is sufficient to consider
$\phi ^*\pi $
, by definition it is sufficient to consider
![]() $\gamma \in G$
and
$\gamma \in G$
and
![]() $f\in C_c(G_{H^{0}})$
, and write
$f\in C_c(G_{H^{0}})$
, and write
with
![]() $g\in C_0(G_{H^{0}})$
,
$g\in C_0(G_{H^{0}})$
,
![]() $\eta \in G_{H^{0}}$
with
$\eta \in G_{H^{0}}$
with
![]() $r(\eta )=s(\gamma )$
. This ensures the G-action commutes with the H-action on
$r(\eta )=s(\gamma )$
. This ensures the G-action commutes with the H-action on
![]() $(\phi ^*{\pi },\phi ^*\mathcal {E},T\widehat {\otimes } 1)$
, hence
$(\phi ^*{\pi },\phi ^*\mathcal {E},T\widehat {\otimes } 1)$
, hence
![]() $\jmath _H(\phi ^*{\pi },\phi ^*\mathcal {E},T\widehat {\otimes } 1)\in \operatorname {\mathrm {KK}}^G(A,B)$
. Finally, as
$\jmath _H(\phi ^*{\pi },\phi ^*\mathcal {E},T\widehat {\otimes } 1)\in \operatorname {\mathrm {KK}}^G(A,B)$
. Finally, as
![]() $\operatorname {\mathrm {Ind}}_H^G$
is defined as a composition of the pullback functor
$\operatorname {\mathrm {Ind}}_H^G$
is defined as a composition of the pullback functor
![]() $\phi ^*$
with the descent functor
$\phi ^*$
with the descent functor
![]() $\jmath ^G$
, it is indeed a functor
$\jmath ^G$
, it is indeed a functor
![]() $\operatorname {\mathrm {Ind}}_H^G\colon \operatorname {\mathrm {KK}}^H\to \operatorname {\mathrm {KK}}^G$
.
$\operatorname {\mathrm {Ind}}_H^G\colon \operatorname {\mathrm {KK}}^H\to \operatorname {\mathrm {KK}}^G$
.
Remark 2.1. Both the descent functor
![]() $\jmath _G:\operatorname {\mathrm {KK}}^G\rightarrow \operatorname {\mathrm {KK}}$
and the induction functor
$\jmath _G:\operatorname {\mathrm {KK}}^G\rightarrow \operatorname {\mathrm {KK}}$
and the induction functor
![]() $\operatorname {\mathrm {Ind}}_H^G:\operatorname {\mathrm {KK}}^H\rightarrow \operatorname {\mathrm {KK}}^G$
can be abstractly constructed using the universal property of equivariant
$\operatorname {\mathrm {Ind}}_H^G:\operatorname {\mathrm {KK}}^H\rightarrow \operatorname {\mathrm {KK}}^G$
can be abstractly constructed using the universal property of equivariant
![]() $\operatorname {\mathrm {KK}}$
-theory, by observing that the respective constructions on the
$\operatorname {\mathrm {KK}}$
-theory, by observing that the respective constructions on the
![]() $C^*$
-level are compatible with split-exact sequences, stabilisations and homotopies (compare [Reference Meyer and Nest41]). In many applications, however, it is useful to have a concrete model at hand. This is certainly the case for the adjunction result in Theorem 2.3 below but has also proven to be a useful construction in [Reference Proietti and Yamashita49, Reference Bönicke, Dell’Aiera, Gabe and Willett9].
$C^*$
-level are compatible with split-exact sequences, stabilisations and homotopies (compare [Reference Meyer and Nest41]). In many applications, however, it is useful to have a concrete model at hand. This is certainly the case for the adjunction result in Theorem 2.3 below but has also proven to be a useful construction in [Reference Proietti and Yamashita49, Reference Bönicke, Dell’Aiera, Gabe and Willett9].
The model for the induction functor in [Reference Bönicke10] is different from the one employed here. Given an H-
![]() $C^*$
-algebra A, the construction of
$C^*$
-algebra A, the construction of
![]() $\operatorname {\mathrm {Ind}}_H^G(A)$
in [Reference Bönicke10] prescribes constructing the pullback algebra
$\operatorname {\mathrm {Ind}}_H^G(A)$
in [Reference Bönicke10] prescribes constructing the pullback algebra
![]() $\phi ^*A= C_0(G_{H^0}){}_s{\otimes }{_\rho } A$
as above, but then considers the (generalized) fixed-point algebra
$\phi ^*A= C_0(G_{H^0}){}_s{\otimes }{_\rho } A$
as above, but then considers the (generalized) fixed-point algebra
![]() $\phi ^*A^H$
associated to the diagonal H-action. If H is acting properly on G, then the main result in [Reference Brown13] implies that
$\phi ^*A^H$
associated to the diagonal H-action. If H is acting properly on G, then the main result in [Reference Brown13] implies that
![]() $\phi ^*A^H$
is strongly Morita equivalent to
$\phi ^*A^H$
is strongly Morita equivalent to
![]() $\operatorname {\mathrm {Ind}}_H^G(A)$
. It is not hard to see that the imprimitivity bimodule witnessing this equivalence gives a G-equivariant
$\operatorname {\mathrm {Ind}}_H^G(A)$
. It is not hard to see that the imprimitivity bimodule witnessing this equivalence gives a G-equivariant
![]() $\operatorname {\mathrm {KK}}$
-equivalence.
$\operatorname {\mathrm {KK}}$
-equivalence.
It should be noted that, when
![]() $H\subseteq G$
is closed (hence
$H\subseteq G$
is closed (hence
![]() $G\rtimes H$
is proper), then the spectrum of
$G\rtimes H$
is proper), then the spectrum of
![]() $\phi ^*C_0(Z)^H$
is homeomorphic to the ordinary induction space
$\phi ^*C_0(Z)^H$
is homeomorphic to the ordinary induction space
![]() $G\times _H Z$
(see [Reference Bönicke10, Proposition 3.22]). However, if
$G\times _H Z$
(see [Reference Bönicke10, Proposition 3.22]). However, if
![]() $H\subseteq G$
is open, then it need not act properly on G, and it is well known that quotients by nonproper actions can lead to pathological topological spaces (e.g., non-Hausdorff, nonlocally compact). It is for this reason that in this paper, where induction from open subgroupoids is considered, we have taken the approach of defining induction via crossed products.
$H\subseteq G$
is open, then it need not act properly on G, and it is well known that quotients by nonproper actions can lead to pathological topological spaces (e.g., non-Hausdorff, nonlocally compact). It is for this reason that in this paper, where induction from open subgroupoids is considered, we have taken the approach of defining induction via crossed products.
2.2 Proof of the adjunction
Recall that if G acts freely and properly on a second countable, locally compact, Hausdorff space Y, then
![]() $G\ltimes Y$
is Morita equivalent as a groupoid to
$G\ltimes Y$
is Morita equivalent as a groupoid to
![]() $Y/G$
and hence the groupoid
$Y/G$
and hence the groupoid
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C_0(Y)\rtimes G\cong C^*(G\ltimes Y)$
is strongly Morita equivalent to
$C_0(Y)\rtimes G\cong C^*(G\ltimes Y)$
is strongly Morita equivalent to
![]() $C_0(Y/G)$
[Reference Brown13]. Note that
$C_0(Y/G)$
[Reference Brown13]. Note that
![]() $G\ltimes Y$
is an amenable groupoid, so the reduced and full crossed products are isomorphic; see, for example, [Reference Anantharaman-Delaroche and Renault1, Corollary 2.1.17 & Proposition 6.1.10]).
$G\ltimes Y$
is an amenable groupoid, so the reduced and full crossed products are isomorphic; see, for example, [Reference Anantharaman-Delaroche and Renault1, Corollary 2.1.17 & Proposition 6.1.10]).
In particular, when Y equals G itself and the action is given by right translation, the associated imprimitivity bimodule
![]() $X^G$
gives a
$X^G$
gives a
![]() $*$
-isomorphism
$*$
-isomorphism
![]() $C_0(G)\rtimes _{\text {rt}} G\cong \mathcal {K}(L^2(G))$
, where
$C_0(G)\rtimes _{\text {rt}} G\cong \mathcal {K}(L^2(G))$
, where
![]() $L^2(G)$
is the standard continuous field of Hilbert spaces associated to G. The
$L^2(G)$
is the standard continuous field of Hilbert spaces associated to G. The
![]() $\operatorname {\mathrm {KK}}$
-class induced by
$\operatorname {\mathrm {KK}}$
-class induced by
![]() $X^G$
will be important in a moment.
$X^G$
will be important in a moment.
If
![]() $(A,G,\alpha )$
is a groupoid dynamical system, then the pushforward along the source map
$(A,G,\alpha )$
is a groupoid dynamical system, then the pushforward along the source map
![]() $s_*\alpha $
is an isomorphism of
$s_*\alpha $
is an isomorphism of
![]() $C^*$
-dynamical systems:
$C^*$
-dynamical systems:
where the intertwining map is given precisely by
![]() $\alpha $
[Reference Le Gall30]. As a consequence, we have the following.
$\alpha $
[Reference Le Gall30]. As a consequence, we have the following.
Lemma 2.2. If
![]() $H\subseteq G$
is a locally closed subgroupoid and A is a G-algebra, then we have a canonical isomorphism
$H\subseteq G$
is a locally closed subgroupoid and A is a G-algebra, then we have a canonical isomorphism
After
![]() $\Phi $
, the G-action on the right-hand side is given by
$\Phi $
, the G-action on the right-hand side is given by
![]() $\text {lt}\otimes \alpha $
, that is, left translation on
$\text {lt}\otimes \alpha $
, that is, left translation on
![]() $C_0(G_{H^{0}})\rtimes _{\mathrm {rt}} H$
, tensorized with the original action
$C_0(G_{H^{0}})\rtimes _{\mathrm {rt}} H$
, tensorized with the original action
![]() $\alpha $
on A.
$\alpha $
on A.
Proof. Let
![]() $\alpha :s^*A\longrightarrow r^*A$
denote the
$\alpha :s^*A\longrightarrow r^*A$
denote the
![]() $C_0(G)$
-linear isomorphism implementing the action of G on A. Now, we can consider the pushforward along the source maps to obtain a
$C_0(G)$
-linear isomorphism implementing the action of G on A. Now, we can consider the pushforward along the source maps to obtain a
![]() $C_0(G^{0})$
-linear isomorphism
$C_0(G^{0})$
-linear isomorphism
![]() $\alpha =s_*\alpha :s_*s^*A\longrightarrow s_*r^*A$
. Now,
$\alpha =s_*\alpha :s_*s^*A\longrightarrow s_*r^*A$
. Now,
![]() $s_*s^*A$
is just the balanced tensor product
$s_*s^*A$
is just the balanced tensor product
![]() $C_0(G)\otimes _{G^{0}}A$
with the canonical
$C_0(G)\otimes _{G^{0}}A$
with the canonical
![]() $C_0(G^{0})$
-algebra structure, while
$C_0(G^{0})$
-algebra structure, while
![]() $s_*r^*A= \Gamma _0(G,r^*\mathcal {A})$
is equipped with the
$s_*r^*A= \Gamma _0(G,r^*\mathcal {A})$
is equipped with the
![]() $C_0(G^{0})$
-algebra structure obtained by the formula
$C_0(G^{0})$
-algebra structure obtained by the formula
![]() $(\varphi \cdot f)(g)=\varphi (s(g))f(g)$
for
$(\varphi \cdot f)(g)=\varphi (s(g))f(g)$
for
![]() $\varphi \in C_0(G^{0})$
and
$\varphi \in C_0(G^{0})$
and
![]() $f\in \Gamma _0(G,r^*\mathcal {A})$
. Note that this differs from the canonical structure it obtains as a balanced tensor product! With the structure defined above we can identify the fibre over a point
$f\in \Gamma _0(G,r^*\mathcal {A})$
. Note that this differs from the canonical structure it obtains as a balanced tensor product! With the structure defined above we can identify the fibre over a point
![]() $x\in G^{0}$
as
$x\in G^{0}$
as
![]() $\Gamma _0(G,r^*\mathcal {A})_x=\Gamma _0(G_x,r^*\mathcal {A})$
and it makes sense to consider the action
$\Gamma _0(G,r^*\mathcal {A})_x=\Gamma _0(G_x,r^*\mathcal {A})$
and it makes sense to consider the action
![]() $\mathrm {rt}\otimes \mathrm {id}_A$
defined by
$\mathrm {rt}\otimes \mathrm {id}_A$
defined by
Summing up the discussion, we see that
![]() $\alpha $
implements an isomorphism of groupoid dynamical systems
$\alpha $
implements an isomorphism of groupoid dynamical systems
Now, if we restrict these systems to the subgroupoid H we obtain an isomorphism
In particular, we obtain an isomorphism between the crossed products and hence conclude
 $$ \begin{align*} \operatorname{\mathrm{Ind}}_H^G \operatorname{\mathrm{Res}}_G^H A & = (C_0(G_{H^{0}}) {\mathbin{\mathop{{}_{s}{\otimes}{_{\rho}}}{}_{{H^{0}}}}} \operatorname{\mathrm{Res}}_G^H A)\rtimes_{r,\text{rt}\otimes \alpha} H\\ &\cong (C_0(G_{H^{0}}) {\mathbin{\mathop{{}_{r}{\otimes}{_{\rho}}}{}_{{G^{0}}}}} A)\rtimes_{r,\text{rt}\otimes \mathrm{id}_A} H\\ &\cong (C_0(G_{H^{0}})\rtimes_{\mathrm{rt}}H)\otimes_{G^{0}} A.\\[-37pt] \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Ind}}_H^G \operatorname{\mathrm{Res}}_G^H A & = (C_0(G_{H^{0}}) {\mathbin{\mathop{{}_{s}{\otimes}{_{\rho}}}{}_{{H^{0}}}}} \operatorname{\mathrm{Res}}_G^H A)\rtimes_{r,\text{rt}\otimes \alpha} H\\ &\cong (C_0(G_{H^{0}}) {\mathbin{\mathop{{}_{r}{\otimes}{_{\rho}}}{}_{{G^{0}}}}} A)\rtimes_{r,\text{rt}\otimes \mathrm{id}_A} H\\ &\cong (C_0(G_{H^{0}})\rtimes_{\mathrm{rt}}H)\otimes_{G^{0}} A.\\[-37pt] \end{align*} $$
Choosing
![]() $H=G$
in the result above yields an isomorphism
$H=G$
in the result above yields an isomorphism
We now prepare to prove the adjunction by defining some auxiliary maps. From now on, we assume
![]() $H\subseteq G$
to be an open subgroupoid. We get an induced embedding
$H\subseteq G$
to be an open subgroupoid. We get an induced embedding
and hence, using the previous lemma, an embedding
We can promote
![]() $X^G$
to a
$X^G$
to a
![]() $\operatorname {\mathrm {KK}}^G$
-equivalence
$\operatorname {\mathrm {KK}}^G$
-equivalence
given by the right A-module
![]() $L^2(G)_r{\otimes }{_\rho } A$
, where A acts pointwise as ‘constant functions’. The representation of the crossed product
$L^2(G)_r{\otimes }{_\rho } A$
, where A acts pointwise as ‘constant functions’. The representation of the crossed product
![]() $r^*A\rtimes G\cong \operatorname {\mathrm {Ind}}_G^G\operatorname {\mathrm {Res}}_G^G(A)$
is the integrated form of the covariant pair given by the right regular representation of G, and pointwise multiplication of functions in
$r^*A\rtimes G\cong \operatorname {\mathrm {Ind}}_G^G\operatorname {\mathrm {Res}}_G^G(A)$
is the integrated form of the covariant pair given by the right regular representation of G, and pointwise multiplication of functions in
![]() $r^*A$
. We will denote this by
$r^*A$
. We will denote this by
![]() $M_A\rtimes R_G$
.
$M_A\rtimes R_G$
.
Now, let
![]() $B\in \operatorname {\mathrm {KK}}^H$
and recall that
$B\in \operatorname {\mathrm {KK}}^H$
and recall that
Then the inclusion
![]() $C_0(H)\subseteq C_0(G|_{ H^{0}})$
induces a map
$C_0(H)\subseteq C_0(G|_{ H^{0}})$
induces a map
Theorem 2.3. Let G be a locally compact Hausdorff groupoid with Haar system. For every open subgroupoid
![]() $H\subseteq G$
, there is an adjunction
$H\subseteq G$
, there is an adjunction
with counit and unit
 $$ \begin{align*} \epsilon\colon \operatorname{\mathrm{Ind}}_H^G\operatorname{\mathrm{Res}}_G^H&\to 1_{\operatorname{\mathrm{KK}}^G}\\ \eta\colon 1_{\operatorname{\mathrm{KK}}^H} &\to \operatorname{\mathrm{Res}}_G^H\operatorname{\mathrm{Ind}}_H^G \end{align*} $$
$$ \begin{align*} \epsilon\colon \operatorname{\mathrm{Ind}}_H^G\operatorname{\mathrm{Res}}_G^H&\to 1_{\operatorname{\mathrm{KK}}^G}\\ \eta\colon 1_{\operatorname{\mathrm{KK}}^H} &\to \operatorname{\mathrm{Res}}_G^H\operatorname{\mathrm{Ind}}_H^G \end{align*} $$
described as follows:
 $$ \begin{align*} \epsilon_A &= X^G_A\circ \kappa \\ \eta_B &=\iota \circ \bigl(X^{H}_B\bigr)^{\text{op}}. \end{align*} $$
$$ \begin{align*} \epsilon_A &= X^G_A\circ \kappa \\ \eta_B &=\iota \circ \bigl(X^{H}_B\bigr)^{\text{op}}. \end{align*} $$
Here below we isolate a couple of technical lemmas which will be useful in the proof of the adjunction. The first lemma is just an observation on the compatibility of the canonical element
![]() $X_A^G$
with restriction and induction.
$X_A^G$
with restriction and induction.
Lemma 2.4. Let
![]() $H\subseteq G$
be an open subgroupoid and
$H\subseteq G$
be an open subgroupoid and
![]() $A\in \operatorname {\mathrm {KK}}^G$
. Then we have
$A\in \operatorname {\mathrm {KK}}^G$
. Then we have
![]() $X^H_{\operatorname {\mathrm {Res}}_G^H A}=\sigma _{\operatorname {\mathrm {Res}}^H_G A}(X_{C_0(H^{0})}^H)$
and
$X^H_{\operatorname {\mathrm {Res}}_G^H A}=\sigma _{\operatorname {\mathrm {Res}}^H_G A}(X_{C_0(H^{0})}^H)$
and
![]() $\operatorname {\mathrm {Res}}_G^H(X_A^G)=\sigma _{\operatorname {\mathrm {Res}}_G^H A}(\operatorname {\mathrm {Res}}_G^H(X_{C_0(G^{0})}^G))$
.
$\operatorname {\mathrm {Res}}_G^H(X_A^G)=\sigma _{\operatorname {\mathrm {Res}}_G^H A}(\operatorname {\mathrm {Res}}_G^H(X_{C_0(G^{0})}^G))$
.
Proof. The first equality is immediate from the definition of
![]() $X_A^G$
and the isomorphism
$X_A^G$
and the isomorphism
![]() $\operatorname {\mathrm {Ind}}_G^G\operatorname {\mathrm {Res}}_G^G(A)\cong \mathcal {K}(L^2(G))\otimes _{G^{0}} A$
explained above. The second equality follows from the first and the fact that restriction and tensorization commute.
$\operatorname {\mathrm {Ind}}_G^G\operatorname {\mathrm {Res}}_G^G(A)\cong \mathcal {K}(L^2(G))\otimes _{G^{0}} A$
explained above. The second equality follows from the first and the fact that restriction and tensorization commute.
Let
![]() $L^2(G,B)$
denote the completion of
$L^2(G,B)$
denote the completion of
![]() $\Gamma _c(G,r^*\mathcal {B})$
with respect to the B-valued inner product
$\Gamma _c(G,r^*\mathcal {B})$
with respect to the B-valued inner product
![]() $\langle \xi _1,\xi _2\rangle (x)=\int _{G^x} \xi _1(g)^*\xi _2(g)\,d\lambda ^x(g)$
. Note that
$\langle \xi _1,\xi _2\rangle (x)=\int _{G^x} \xi _1(g)^*\xi _2(g)\,d\lambda ^x(g)$
. Note that
![]() $L^2(G,B)$
is canonically isomorphic to the B-module
$L^2(G,B)$
is canonically isomorphic to the B-module
![]() $L^2(G)\otimes _{G^{0}} B$
introduced above.
$L^2(G)\otimes _{G^{0}} B$
introduced above.
Let us make a point on notation before continuing the proof. So far, we have used A and
![]() $\mathcal {A}$
to denote a
$\mathcal {A}$
to denote a
![]() $C_0(X)$
-
$C_0(X)$
-
![]() $C^*$
-algebra and its corresponding
$C^*$
-algebra and its corresponding
![]() $C^*$
-bundle. However, this difference in font is not very convenient when A is replaced by a more complicated algebra, for example,
$C^*$
-bundle. However, this difference in font is not very convenient when A is replaced by a more complicated algebra, for example,
![]() $A=C_0(G)\rtimes H$
. In the sequel, we suppress this notational distinction, as the context suffices to disambiguate the usage.
$A=C_0(G)\rtimes H$
. In the sequel, we suppress this notational distinction, as the context suffices to disambiguate the usage.
Lemma 2.5. Let
![]() $H\subseteq G$
be an open subgroupoid and
$H\subseteq G$
be an open subgroupoid and
![]() $B\in \operatorname {\mathrm {KK}}^H$
. Then there is an isometric G-equivariant homomorphism
$B\in \operatorname {\mathrm {KK}}^H$
. Then there is an isometric G-equivariant homomorphism
of Hilbert
![]() $\operatorname {\mathrm {Ind}}_H^G B$
-modules.
$\operatorname {\mathrm {Ind}}_H^G B$
-modules.
Proof. Let us first describe the module
![]() $\operatorname {\mathrm {Ind}}_H^G L^2(H,B)$
more concretely. We have a canonical isomorphism
$\operatorname {\mathrm {Ind}}_H^G L^2(H,B)$
more concretely. We have a canonical isomorphism
![]() $L^2(H,B)\otimes _B (C_0(G_{H^{0}})\otimes _{H^{0}} B)\cong L^2(H,C_0(G_{H^{0}})\otimes _{H^{0}} B)$
given by
$L^2(H,B)\otimes _B (C_0(G_{H^{0}})\otimes _{H^{0}} B)\cong L^2(H,C_0(G_{H^{0}})\otimes _{H^{0}} B)$
given by
![]() $\xi \otimes f\mapsto [h\mapsto \xi (h)f]$
. Hence, we can write
$\xi \otimes f\mapsto [h\mapsto \xi (h)f]$
. Hence, we can write
![]() $\operatorname {\mathrm {Ind}}_H^G L^2(H,B)$
as
$\operatorname {\mathrm {Ind}}_H^G L^2(H,B)$
as
![]() $L^2(H,C_0(G_{H^{0}})\otimes _{H^{0}} B)\rtimes H$
. So for a function
$L^2(H,C_0(G_{H^{0}})\otimes _{H^{0}} B)\rtimes H$
. So for a function
![]() $\xi \in \Gamma _c(H,r^*L^2(H,C_0(G_{H^{0}})\otimes _{H^{0}} B))$
, we define
$\xi \in \Gamma _c(H,r^*L^2(H,C_0(G_{H^{0}})\otimes _{H^{0}} B))$
, we define
![]() $\Phi (\xi )\in L^2(G,\operatorname {\mathrm {Ind}}_H^G B)$
as
$\Phi (\xi )\in L^2(G,\operatorname {\mathrm {Ind}}_H^G B)$
as
 $$ \begin{align*}\Phi(\xi)(g,h,x)=\left\{\begin{array}{ll} \beta_{x^{-1}g}(\xi(g^{-1}xh,g^{-1}x,g)), & g^{-1}x\in H \\ 0 ,& \text{otherwise} \end{array}\right\},\end{align*} $$
$$ \begin{align*}\Phi(\xi)(g,h,x)=\left\{\begin{array}{ll} \beta_{x^{-1}g}(\xi(g^{-1}xh,g^{-1}x,g)), & g^{-1}x\in H \\ 0 ,& \text{otherwise} \end{array}\right\},\end{align*} $$
where
![]() $g\in G$
,
$g\in G$
,
![]() $h\in H$
and
$h\in H$
and
![]() $x\in G_{r(h)}^{r(g)}$
.
$x\in G_{r(h)}^{r(g)}$
.
Given
![]() $\xi _1,\xi _2 \in \Gamma _c(H,r^*L^2(H,C_0(G_{H^{0}})\otimes _{H^{0}} B))$
, we compute (for
$\xi _1,\xi _2 \in \Gamma _c(H,r^*L^2(H,C_0(G_{H^{0}})\otimes _{H^{0}} B))$
, we compute (for
![]() $h\in H$
and
$h\in H$
and
![]() $x\in G_{r(h)}$
) that
$x\in G_{r(h)}$
) that
![]() $\langle \Phi (\xi _1),\Phi (\xi _2)\rangle (h,x)$
equals
$\langle \Phi (\xi _1),\Phi (\xi _2)\rangle (h,x)$
equals
 $$ \begin{align*} &\int\limits_{G}\left[\Phi(\xi_1)(g)^\ast\Phi(\xi_2)(g)\right](h,x)\,d\lambda^{r(x)}(g)\\ = &\int\limits_{G} \int\limits_{H}(\mathrm{rt}\otimes\beta)_{\tilde{h}}(\Phi(\xi_1)(g,\tilde{h}^{-1})^*\Phi(\xi_2)(g,\tilde{h}^{-1}h))(x)\,d\lambda^{r(h)}(\tilde{h})\,d\lambda^{r(x)}(g)\\ = &\int\limits_{G} \int\limits_{H}\beta_{\tilde{h}}(\Phi(\xi_1)(g,\tilde{h}^{-1},x\tilde{h})^*\Phi(\xi_2)(g,\tilde{h}^{-1}h,x\tilde{h}))\,d\lambda^{r(h)}(\tilde{h})\,d\lambda^{r(x)}(g)\\ =& \int\limits_{xH} \int\limits_{H}\beta_{x^{-1}g}(\xi_1(g^{-1}x,g^{-1}x\tilde{h},g)^*\xi_2(g^{-1}xh,g^{-1}x\tilde{h},g))\,d\lambda^{r(h)}(\tilde{h})\,d\lambda^{r(x)}(g).\end{align*} $$
$$ \begin{align*} &\int\limits_{G}\left[\Phi(\xi_1)(g)^\ast\Phi(\xi_2)(g)\right](h,x)\,d\lambda^{r(x)}(g)\\ = &\int\limits_{G} \int\limits_{H}(\mathrm{rt}\otimes\beta)_{\tilde{h}}(\Phi(\xi_1)(g,\tilde{h}^{-1})^*\Phi(\xi_2)(g,\tilde{h}^{-1}h))(x)\,d\lambda^{r(h)}(\tilde{h})\,d\lambda^{r(x)}(g)\\ = &\int\limits_{G} \int\limits_{H}\beta_{\tilde{h}}(\Phi(\xi_1)(g,\tilde{h}^{-1},x\tilde{h})^*\Phi(\xi_2)(g,\tilde{h}^{-1}h,x\tilde{h}))\,d\lambda^{r(h)}(\tilde{h})\,d\lambda^{r(x)}(g)\\ =& \int\limits_{xH} \int\limits_{H}\beta_{x^{-1}g}(\xi_1(g^{-1}x,g^{-1}x\tilde{h},g)^*\xi_2(g^{-1}xh,g^{-1}x\tilde{h},g))\,d\lambda^{r(h)}(\tilde{h})\,d\lambda^{r(x)}(g).\end{align*} $$
At this point, we perform two change of variables and keep computing:
 $$ \begin{align*} &\stackrel{g\mapsto xg}{=}\int\limits_{H}\int\limits_{H}\beta_g(\xi_1(g^{-1},g^{-1}\tilde{h},xg)^*\xi_2(g^{-1}h,g^{-1}\tilde{h},xg))\,d\lambda^{r(h)}(\tilde{h})\,d\lambda^{s(x)}(g)\\ & \stackrel{\tilde{h}\mapsto g\tilde{h}}{=}\int\limits_{H}\int\limits_{H}\beta_g(\xi_1(g^{-1},\tilde{h},xg)^*\xi_2(g^{-1}h,\tilde{h},xg))\,d\lambda^{s(g)}(\tilde{h})\,d\lambda^{s(x)}(g)\\ & = \int\limits_{H}\int\limits_{H}\beta_{g^{-1}}(\xi_1(g,\tilde{h},xg^{-1})^*\xi_2(gh,\tilde{h},xg^{-1}))\,d\lambda^{r(g)}(\tilde{h})\,d\lambda_{s(x)}(g)\\ & = \int\limits_{H} (\mathrm{rt}\otimes \beta)_{g^{-1}}(\langle \xi_1(g),\xi_2(gh)\rangle(x)\,d\lambda_{r(h)}(g)\\ & = \langle \xi_1,\xi_2\rangle (h,x). \end{align*} $$
$$ \begin{align*} &\stackrel{g\mapsto xg}{=}\int\limits_{H}\int\limits_{H}\beta_g(\xi_1(g^{-1},g^{-1}\tilde{h},xg)^*\xi_2(g^{-1}h,g^{-1}\tilde{h},xg))\,d\lambda^{r(h)}(\tilde{h})\,d\lambda^{s(x)}(g)\\ & \stackrel{\tilde{h}\mapsto g\tilde{h}}{=}\int\limits_{H}\int\limits_{H}\beta_g(\xi_1(g^{-1},\tilde{h},xg)^*\xi_2(g^{-1}h,\tilde{h},xg))\,d\lambda^{s(g)}(\tilde{h})\,d\lambda^{s(x)}(g)\\ & = \int\limits_{H}\int\limits_{H}\beta_{g^{-1}}(\xi_1(g,\tilde{h},xg^{-1})^*\xi_2(gh,\tilde{h},xg^{-1}))\,d\lambda^{r(g)}(\tilde{h})\,d\lambda_{s(x)}(g)\\ & = \int\limits_{H} (\mathrm{rt}\otimes \beta)_{g^{-1}}(\langle \xi_1(g),\xi_2(gh)\rangle(x)\,d\lambda_{r(h)}(g)\\ & = \langle \xi_1,\xi_2\rangle (h,x). \end{align*} $$
This verifies that
![]() $\Phi $
extends to an isometry. Now, we proceed to checking that
$\Phi $
extends to an isometry. Now, we proceed to checking that
![]() $\Phi $
is a right module map. Below, we have
$\Phi $
is a right module map. Below, we have
![]() $\xi \in \Gamma _c(H,r^*L^2(H,C_0(G_{H^{0}})\otimes _{H^{0}} B))$
as before, and the element f belongs to
$\xi \in \Gamma _c(H,r^*L^2(H,C_0(G_{H^{0}})\otimes _{H^{0}} B))$
as before, and the element f belongs to
![]() $\Gamma _c(H,r^*(C_0(G_{H^{0}}){}_s{\otimes }{_\rho }B))$
.
$\Gamma _c(H,r^*(C_0(G_{H^{0}}){}_s{\otimes }{_\rho }B))$
.
 $$ \begin{align*} (\Phi(\xi)f)(g,h,x) &= \Phi(\xi)(g,h,x)f(h,x)\\ &=\int_{H^{r(g)}} \Phi(\xi)(g,\tilde{h},x)\beta_{\tilde{h}}(f(\tilde{h}^{-1}h,x\tilde{h}))\,d\lambda^{r(h)}(\tilde{h})\\ & = \int_{H^{r(g)}} \beta_{x^{-1}g}(\xi(g^{-1}x\tilde{h},g^{-1}x,g))\beta_{\tilde{h}}(f(\tilde{h}^{-1}h,x\tilde{h}))\,d\lambda^{r(h)}(\tilde{h})\\ & \stackrel{\tilde{h}\mapsto x^{-1}g\tilde{h}}{=} \int_{H^{s(g)}} \beta_{x^{-1}g}(\xi(\tilde{h},g^{-1}x,g)\beta_{\tilde{h}}(f(\tilde{h}^{-1}g^{-1}xh,g\tilde{h})))\,d\lambda^{s(g)}(\tilde{h})\\ & = \beta_{x^{-1}g}((\xi f)(g^{-1}xh,g^{-1}x,g))\\ & = \Phi(\xi f)(g,h,x). \end{align*} $$
$$ \begin{align*} (\Phi(\xi)f)(g,h,x) &= \Phi(\xi)(g,h,x)f(h,x)\\ &=\int_{H^{r(g)}} \Phi(\xi)(g,\tilde{h},x)\beta_{\tilde{h}}(f(\tilde{h}^{-1}h,x\tilde{h}))\,d\lambda^{r(h)}(\tilde{h})\\ & = \int_{H^{r(g)}} \beta_{x^{-1}g}(\xi(g^{-1}x\tilde{h},g^{-1}x,g))\beta_{\tilde{h}}(f(\tilde{h}^{-1}h,x\tilde{h}))\,d\lambda^{r(h)}(\tilde{h})\\ & \stackrel{\tilde{h}\mapsto x^{-1}g\tilde{h}}{=} \int_{H^{s(g)}} \beta_{x^{-1}g}(\xi(\tilde{h},g^{-1}x,g)\beta_{\tilde{h}}(f(\tilde{h}^{-1}g^{-1}xh,g\tilde{h})))\,d\lambda^{s(g)}(\tilde{h})\\ & = \beta_{x^{-1}g}((\xi f)(g^{-1}xh,g^{-1}x,g))\\ & = \Phi(\xi f)(g,h,x). \end{align*} $$
To complete the argument, we show that the left action of G commutes with
![]() $\Phi $
. Let us take
$\Phi $
. Let us take
![]() $g'\in G$
with
$g'\in G$
with
![]() $r(g')=r(g)$
, and compute
$r(g')=r(g)$
, and compute
 $$ \begin{align*} (g'\Phi(\xi))(g,h,x)&=\Phi(\xi)(g^{\prime-1}g,h,g^{\prime-1}x)\\ &=\beta_{x^{-1}g} (\xi(g^{-1}xh,g^{-1}x,g^{\prime-1}g))\\ &=\beta_{x^{-1}g}((g' \xi)(g^{-1}xh,g^{-1}x,g))\\ &=\Phi(g'\xi)(g,h,x). \end{align*} $$
$$ \begin{align*} (g'\Phi(\xi))(g,h,x)&=\Phi(\xi)(g^{\prime-1}g,h,g^{\prime-1}x)\\ &=\beta_{x^{-1}g} (\xi(g^{-1}xh,g^{-1}x,g^{\prime-1}g))\\ &=\beta_{x^{-1}g}((g' \xi)(g^{-1}xh,g^{-1}x,g))\\ &=\Phi(g'\xi)(g,h,x). \end{align*} $$
The proof is complete.
Proof of Theorem 2.3.
We need to verify the counit-unit equations. We start by proving that for every
![]() $A\in \operatorname {\mathrm {KK}}^G$
the composition
$A\in \operatorname {\mathrm {KK}}^G$
the composition
equals the identity in
![]() $\operatorname {\mathrm {KK}}^H(\operatorname {\mathrm {Res}}_G^HA,\operatorname {\mathrm {Res}}_G^HA)$
: Expanding the definitions of counit and unit in this case, we have
$\operatorname {\mathrm {KK}}^H(\operatorname {\mathrm {Res}}_G^HA,\operatorname {\mathrm {Res}}_G^HA)$
: Expanding the definitions of counit and unit in this case, we have
![]() $\operatorname {\mathrm {Res}}_G^H(\epsilon _A)\circ \eta _{\operatorname {\mathrm {Res}}_G^H A} = \operatorname {\mathrm {Res}} (X_A^G)\circ \operatorname {\mathrm {Res}}(\kappa )\circ \iota \circ (X_{\operatorname {\mathrm {Res}}_G^H A}^H)^{\text {op}}$
. Following the definitions, it is then easily seen that after identifying
$\operatorname {\mathrm {Res}}_G^H(\epsilon _A)\circ \eta _{\operatorname {\mathrm {Res}}_G^H A} = \operatorname {\mathrm {Res}} (X_A^G)\circ \operatorname {\mathrm {Res}}(\kappa )\circ \iota \circ (X_{\operatorname {\mathrm {Res}}_G^H A}^H)^{\text {op}}$
. Following the definitions, it is then easily seen that after identifying
 $$ \begin{gather*} \operatorname{\mathrm{Ind}}_H^H(\operatorname{\mathrm{Res}}_G^H A)=(C_0(H)\rtimes_{\mathrm{rt}}H)\otimes \operatorname{\mathrm{Res}}_G^HA\\ \operatorname{\mathrm{Res}}_G^H(\operatorname{\mathrm{Ind}}_G^G A)\cong \operatorname{\mathrm{Res}}_G^H((C_0(G)\rtimes_{\mathrm{rt}}G)\otimes_{G^{0}} A)\cong (C_0(G^{H^{0}})\rtimes_{\mathrm{rt}}G)\otimes_{H^{0}}\operatorname{\mathrm{Res}}_G^H A, \end{gather*} $$
$$ \begin{gather*} \operatorname{\mathrm{Ind}}_H^H(\operatorname{\mathrm{Res}}_G^H A)=(C_0(H)\rtimes_{\mathrm{rt}}H)\otimes \operatorname{\mathrm{Res}}_G^HA\\ \operatorname{\mathrm{Res}}_G^H(\operatorname{\mathrm{Ind}}_G^G A)\cong \operatorname{\mathrm{Res}}_G^H((C_0(G)\rtimes_{\mathrm{rt}}G)\otimes_{G^{0}} A)\cong (C_0(G^{H^{0}})\rtimes_{\mathrm{rt}}G)\otimes_{H^{0}}\operatorname{\mathrm{Res}}_G^H A, \end{gather*} $$
the composition
![]() $\operatorname {\mathrm {Res}}(\kappa )\circ \iota $
is just given by
$\operatorname {\mathrm {Res}}(\kappa )\circ \iota $
is just given by
 $$ \begin{align} (C_0(H)\rtimes H)\otimes_{H^{0}} \operatorname{\mathrm{Res}}_G^H A\stackrel{j\otimes \mathrm{id}}{\longrightarrow}(C_0(G^{H^{0}})\rtimes G)\otimes_{H^{0}} \operatorname{\mathrm{Res}}_G^H A, \end{align} $$
$$ \begin{align} (C_0(H)\rtimes H)\otimes_{H^{0}} \operatorname{\mathrm{Res}}_G^H A\stackrel{j\otimes \mathrm{id}}{\longrightarrow}(C_0(G^{H^{0}})\rtimes G)\otimes_{H^{0}} \operatorname{\mathrm{Res}}_G^H A, \end{align} $$
where
![]() $j:C_0(H)\rtimes H\longrightarrow C_0(G^{H^{0}})\rtimes G$
is induced by the inclusion of H as an open subgroupoid. Using Lemma 2.4, we have
$j:C_0(H)\rtimes H\longrightarrow C_0(G^{H^{0}})\rtimes G$
is induced by the inclusion of H as an open subgroupoid. Using Lemma 2.4, we have
 $$ \begin{align*} \operatorname{\mathrm{Res}}_G^H(\epsilon_A)\circ\eta_{\operatorname{\mathrm{Res}}_G^H A} &= \operatorname{\mathrm{Res}} (X_A^G)\circ \operatorname{\mathrm{Res}}(\kappa)\circ \iota\circ (X_{\operatorname{\mathrm{Res}}_G^H A}^H)^{\text{op}}\\ &=\sigma_{\operatorname{\mathrm{Res}}_G^H A}(\operatorname{\mathrm{Res}}_G^H(X_{C_0(G^{0})}^G) \circ \sigma_{\operatorname{\mathrm{Res}}_G^H A}(j)\circ \sigma_{\operatorname{\mathrm{Res}}_H^G A}((X_{C_0(H^{0})}^H)^{\text{op}})\\ &= \sigma_{\operatorname{\mathrm{Res}}_G^H A}\left(\operatorname{\mathrm{Res}}_G^H(X_{C_0(G^{0})}^G)\circ j\circ (X_{C_0(H^{0})}^H)^{\text{op}}\right). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Res}}_G^H(\epsilon_A)\circ\eta_{\operatorname{\mathrm{Res}}_G^H A} &= \operatorname{\mathrm{Res}} (X_A^G)\circ \operatorname{\mathrm{Res}}(\kappa)\circ \iota\circ (X_{\operatorname{\mathrm{Res}}_G^H A}^H)^{\text{op}}\\ &=\sigma_{\operatorname{\mathrm{Res}}_G^H A}(\operatorname{\mathrm{Res}}_G^H(X_{C_0(G^{0})}^G) \circ \sigma_{\operatorname{\mathrm{Res}}_G^H A}(j)\circ \sigma_{\operatorname{\mathrm{Res}}_H^G A}((X_{C_0(H^{0})}^H)^{\text{op}})\\ &= \sigma_{\operatorname{\mathrm{Res}}_G^H A}\left(\operatorname{\mathrm{Res}}_G^H(X_{C_0(G^{0})}^G)\circ j\circ (X_{C_0(H^{0})}^H)^{\text{op}}\right). \end{align*} $$
Hence, it is enough to show that the conclusion holds for
![]() $A=C_0(G^{0})$
. In this case, we can further use the isomorphisms
$A=C_0(G^{0})$
. In this case, we can further use the isomorphisms
![]() $C_0(H)\rtimes _{\mathrm {rt}} H\cong \mathcal {K}(L^2(H))$
and
$C_0(H)\rtimes _{\mathrm {rt}} H\cong \mathcal {K}(L^2(H))$
and
![]() $C_0(G^{H^{0}})\rtimes _{\mathrm {rt}} G\cong \mathcal {K}(L^2(G^{H^{0}}))$
to replace the map in Equation (4) by the canonical map
$C_0(G^{H^{0}})\rtimes _{\mathrm {rt}} G\cong \mathcal {K}(L^2(G^{H^{0}}))$
to replace the map in Equation (4) by the canonical map
and the required verification is easily seen to be reduced to showing that the (interior) Kasparov product
equals the class of identity
![]() $id_{C_0(H^0)}$
in
$id_{C_0(H^0)}$
in
![]() $\operatorname {\mathrm {KK}}^H(C_0(H^{0}),C_0(H^{0}))$
.
$\operatorname {\mathrm {KK}}^H(C_0(H^{0}),C_0(H^{0}))$
.
The element
![]() $\operatorname {\mathrm {Res}}_G^H(X_{C_0(G^{0})}^G)\in \operatorname {\mathrm {KK}}^H(\mathcal {K}(L^2(G^{H^{0}})),C_0(H^{0}))$
can be represented by the triple
$\operatorname {\mathrm {Res}}_G^H(X_{C_0(G^{0})}^G)\in \operatorname {\mathrm {KK}}^H(\mathcal {K}(L^2(G^{H^{0}})),C_0(H^{0}))$
can be represented by the triple
![]() $(L^2(G^{H^{0}}),\Phi ,0)$
, where
$(L^2(G^{H^{0}}),\Phi ,0)$
, where
![]() $\Phi $
is the canonical action. Consequently,
$\Phi $
is the canonical action. Consequently,
![]() $i^*[\operatorname {\mathrm {Res}}_G^H(X^G_{C_0(G^{0})})$
is represented by
$i^*[\operatorname {\mathrm {Res}}_G^H(X^G_{C_0(G^{0})})$
is represented by
![]() $(L^2(G^{H^{0}}),\Phi \circ i,0)$
. The representation
$(L^2(G^{H^{0}}),\Phi \circ i,0)$
. The representation
![]() $\Phi \circ i$
fails to be nondegenerate, but we can replace
$\Phi \circ i$
fails to be nondegenerate, but we can replace
![]() $L^2(G^{H^{0}})$
by its ‘nondegenerate closure’
$L^2(G^{H^{0}})$
by its ‘nondegenerate closure’
![]() $\overline {\Phi \circ i(\mathcal {K}(L_s^2(H)))L^2(G^{H^{0}})}$
without changing its
$\overline {\Phi \circ i(\mathcal {K}(L_s^2(H)))L^2(G^{H^{0}})}$
without changing its
![]() $\operatorname {\mathrm {KK}}^H$
-class (see [Reference Blackadar6, Proposition 18.3.6]). This module is easily seen to be (isomorphic to)
$\operatorname {\mathrm {KK}}^H$
-class (see [Reference Blackadar6, Proposition 18.3.6]). This module is easily seen to be (isomorphic to)
![]() $L^2(H)$
. Therefore,
$L^2(H)$
. Therefore,
![]() $i^*[\operatorname {\mathrm {Res}}_G^H(X^G_{C_0(G^{0})})]=[X^H_{C_0(H^{0})}]$
and the desired equality follows from
$i^*[\operatorname {\mathrm {Res}}_G^H(X^G_{C_0(G^{0})})]=[X^H_{C_0(H^{0})}]$
and the desired equality follows from
The next verification in order regards the composition
The map
![]() $\kappa \circ \operatorname {\mathrm {Ind}}_H^G(\iota )$
gives an inclusion
$\kappa \circ \operatorname {\mathrm {Ind}}_H^G(\iota )$
gives an inclusion

By using the isomorphisms introduced in Lemma 2.2 above, we can replace the previous inclusion into the more convenient map

Above, the Greek letters indicate our choice of notation for the variable on the given groupoid. These will be useful in a moment.
Recall the action on A is denoted by
![]() $\alpha $
. Suppressing notation for the inclusions
$\alpha $
. Suppressing notation for the inclusions
![]() $H\subseteq G$
and
$H\subseteq G$
and
![]() $C_0(H)\subseteq C_0(G)$
, the map i can be understood by
$C_0(H)\subseteq C_0(G)$
, the map i can be understood by
where f is in
![]() $\Gamma _c(H,r^*(C_0(G_{H^{0}}){}_s{\otimes }{_{r\otimes \rho }}(C_0(H)_r{\otimes }{_\rho }A)\rtimes _{\text {rt}\otimes \text {id}} H))$
. Note that the right-hand side is zero unless
$\Gamma _c(H,r^*(C_0(G_{H^{0}}){}_s{\otimes }{_{r\otimes \rho }}(C_0(H)_r{\otimes }{_\rho }A)\rtimes _{\text {rt}\otimes \text {id}} H))$
. Note that the right-hand side is zero unless
![]() $\gamma ^{-1}\nu \in H$
and
$\gamma ^{-1}\nu \in H$
and
![]() $\eta \in H$
(note
$\eta \in H$
(note
![]() $\gamma \in G_{H^{0}}$
follows). The composition in Equation (5) can be computed via the Kasparov product (over the domain of i)
$\gamma \in G_{H^{0}}$
follows). The composition in Equation (5) can be computed via the Kasparov product (over the domain of i)
We claim that
The class
![]() $i^*[X^G_{\operatorname {\mathrm {Ind}}_H^G A}]$
is represented by the Kasparov triple
$i^*[X^G_{\operatorname {\mathrm {Ind}}_H^G A}]$
is represented by the Kasparov triple
while the class
![]() $\operatorname {\mathrm {Ind}}_H^G(X_A^H)$
is represented by
$\operatorname {\mathrm {Ind}}_H^G(X_A^H)$
is represented by
Consider the isometric embedding
from Lemma 2.5. We first verify that
![]() $\Phi $
intertwines the left actions of
$\Phi $
intertwines the left actions of
![]() $\operatorname {\mathrm {Ind}}_H^G \operatorname {\mathrm {Ind}}_H^H A$
. To this end, recall that for
$\operatorname {\mathrm {Ind}}_H^G \operatorname {\mathrm {Ind}}_H^H A$
. To this end, recall that for
![]() $f\in \Gamma _c(H,r^*(C_0(G_{H^{0}})\otimes _{G^{0}}\operatorname {\mathrm {Ind}}_H^H A))$
, we have that
$f\in \Gamma _c(H,r^*(C_0(G_{H^{0}})\otimes _{G^{0}}\operatorname {\mathrm {Ind}}_H^H A))$
, we have that
![]() $(\operatorname {\mathrm {Ind}}_H^G(M_A\rtimes R_H)(f)\xi )(g,h,x)$
equals
$(\operatorname {\mathrm {Ind}}_H^G(M_A\rtimes R_H)(f)\xi )(g,h,x)$
equals
 $$\begin{align*}\int\limits_H\int\limits_H f(h_1,x,h_2,h)\alpha_{h_1}(\xi(h_1^{-1}g,h_1^{-1}hh_2,xh_1))\,d\lambda^{s(h)}(h_2)\,d\lambda^{s(x)}(h_1). \end{align*}$$
$$\begin{align*}\int\limits_H\int\limits_H f(h_1,x,h_2,h)\alpha_{h_1}(\xi(h_1^{-1}g,h_1^{-1}hh_2,xh_1))\,d\lambda^{s(h)}(h_2)\,d\lambda^{s(x)}(h_1). \end{align*}$$
Hence, considering elements
![]() $\xi \in \Gamma _c(H,r^*L^2(H,C_0(G_{H^{0}})\otimes _{H^{0}} B))$
and
$\xi \in \Gamma _c(H,r^*L^2(H,C_0(G_{H^{0}})\otimes _{H^{0}} B))$
and
![]() $f\in \Gamma _c(H,r^* (C_0(G){}_s{\otimes }{_{r}}(C_0(H){}_s{\otimes }{_\rho }A)\rtimes H))$
, we compute
$f\in \Gamma _c(H,r^* (C_0(G){}_s{\otimes }{_{r}}(C_0(H){}_s{\otimes }{_\rho }A)\rtimes H))$
, we compute
 $$ \begin{align*} &\Phi(\operatorname{\mathrm{Ind}}_H^G(M_A\rtimes R_H)(f)\xi)(g,h,x) =\alpha_{x^{-1}g}((\operatorname{\mathrm{Ind}}_H^G(M_A\rtimes R_H)(f)\xi)(g^{-1}xh,g^{-1}x,g))\\& \quad = \int\limits_H\int\limits_H\alpha_{x^{-1}g}(f(h_1,g,h_2,g^{-1}x)\alpha_{h_1}(\xi(h_1^{-1}g^{-1}xh,h_1^{-1}g^{-1}xh_2,gh_1)))\,d\lambda^{s(x)}(h_2)\,d\lambda^{s(g)}(h_1)\\& \quad = \int\limits_H \int\limits_H i(f)(h_1,g,h_2,x)\alpha_{h_2}(\Phi(\xi)(gh_1,h_2^{-1}h,xh_2))\,d\lambda^{s(x)}(h_2)\,d\lambda^{s(g)}(h_1)\\& \quad = \left((M_{\operatorname{\mathrm{Ind}}_H^G A}\rtimes R_G)(i(f))\Phi(\xi)\right)(g,h,x). \end{align*} $$
$$ \begin{align*} &\Phi(\operatorname{\mathrm{Ind}}_H^G(M_A\rtimes R_H)(f)\xi)(g,h,x) =\alpha_{x^{-1}g}((\operatorname{\mathrm{Ind}}_H^G(M_A\rtimes R_H)(f)\xi)(g^{-1}xh,g^{-1}x,g))\\& \quad = \int\limits_H\int\limits_H\alpha_{x^{-1}g}(f(h_1,g,h_2,g^{-1}x)\alpha_{h_1}(\xi(h_1^{-1}g^{-1}xh,h_1^{-1}g^{-1}xh_2,gh_1)))\,d\lambda^{s(x)}(h_2)\,d\lambda^{s(g)}(h_1)\\& \quad = \int\limits_H \int\limits_H i(f)(h_1,g,h_2,x)\alpha_{h_2}(\Phi(\xi)(gh_1,h_2^{-1}h,xh_2))\,d\lambda^{s(x)}(h_2)\,d\lambda^{s(g)}(h_1)\\& \quad = \left((M_{\operatorname{\mathrm{Ind}}_H^G A}\rtimes R_G)(i(f))\Phi(\xi)\right)(g,h,x). \end{align*} $$
Since the representation
![]() $\operatorname {\mathrm {Ind}}_H^G(M_A\rtimes R_H)$
is nondegenerate, it follows immediately that
$\operatorname {\mathrm {Ind}}_H^G(M_A\rtimes R_H)$
is nondegenerate, it follows immediately that
![]() $\text {Img}(\Phi )\subseteq \overline {((M_{\operatorname {\mathrm {Ind}}_H^G A}\rtimes R_G)\circ i)L^2(G,\operatorname {\mathrm {Ind}}_H^G A)}$
. In fact, since
$\text {Img}(\Phi )\subseteq \overline {((M_{\operatorname {\mathrm {Ind}}_H^G A}\rtimes R_G)\circ i)L^2(G,\operatorname {\mathrm {Ind}}_H^G A)}$
. In fact, since
![]() $\text {Img}(\Phi )$
is closed, in order to have equality it suffices to show the image is dense. From the definition of i in Equation (6), we see that
$\text {Img}(\Phi )$
is closed, in order to have equality it suffices to show the image is dense. From the definition of i in Equation (6), we see that
where F is spanned by those
![]() $L^2$
-functions such that
$L^2$
-functions such that
![]() $f(g,h,x)=0$
unless
$f(g,h,x)=0$
unless
![]() $g^{-1}x\in H$
(notation from Lemma 2.5). With this, the surjectivity is clear from the formula for
$g^{-1}x\in H$
(notation from Lemma 2.5). With this, the surjectivity is clear from the formula for
![]() $\Phi $
in Lemma 2.5. Since the element
$\Phi $
in Lemma 2.5. Since the element
![]() $i^*[X_{\operatorname {\mathrm {Ind}}_H^G A}^G]$
can equally well be represented by the submodule
$i^*[X_{\operatorname {\mathrm {Ind}}_H^G A}^G]$
can equally well be represented by the submodule
![]() $\overline {((M_{\operatorname {\mathrm {Ind}}_H^G A}\rtimes R_G)\circ i)L^2(G,\operatorname {\mathrm {Ind}}_H^G A)}$
(see [Reference Blackadar6, Proposition 18.3.6]), we conclude that
$\overline {((M_{\operatorname {\mathrm {Ind}}_H^G A}\rtimes R_G)\circ i)L^2(G,\operatorname {\mathrm {Ind}}_H^G A)}$
(see [Reference Blackadar6, Proposition 18.3.6]), we conclude that
![]() $i^*[X_{\operatorname {\mathrm {Ind}}_H^G B}^G]=\operatorname {\mathrm {Ind}}_H^G X_A^H$
and hence
$i^*[X_{\operatorname {\mathrm {Ind}}_H^G B}^G]=\operatorname {\mathrm {Ind}}_H^G X_A^H$
and hence
as desired.
2.3 Compatibility with other functors
Let
![]() $f\colon Y\to X$
be a continuous map, and A and B be
$f\colon Y\to X$
be a continuous map, and A and B be
![]() $C_0(X)$
-algebras. There is a natural isomorphism
$C_0(X)$
-algebras. There is a natural isomorphism
![]() $f^*(A\otimes _X B)=f^*(A)\otimes _Y f^*(B)$
because both algebras are naturally isomorphic to restrictions of
$f^*(A\otimes _X B)=f^*(A)\otimes _Y f^*(B)$
because both algebras are naturally isomorphic to restrictions of
![]() $C_0(Y\times Y)\otimes A \otimes B $
to the same copy of
$C_0(Y\times Y)\otimes A \otimes B $
to the same copy of
![]() $Y\times X$
in the topological space
$Y\times X$
in the topological space
![]() $Y\times Y\times X\times X$
(cf. [Reference Bönicke and Dell’Aiera12, Lemma 6.4])
$Y\times Y\times X\times X$
(cf. [Reference Bönicke and Dell’Aiera12, Lemma 6.4])
Lemma 2.6. There is a natural isomorphism
In particular,
![]() $\operatorname {\mathrm {Ind}}_H^G\circ f^* \cong f^*\circ \operatorname {\mathrm {Ind}}_H^G $
.
$\operatorname {\mathrm {Ind}}_H^G\circ f^* \cong f^*\circ \operatorname {\mathrm {Ind}}_H^G $
.
Proof. Let
![]() $\phi $
be the restriction of the source map to
$\phi $
be the restriction of the source map to
![]() $G_{H^{0}}$
. We have
$G_{H^{0}}$
. We have
by the observation above. Now, pushing forward along
![]() $\phi $
again we obtain an isomorphism of H-
$\phi $
again we obtain an isomorphism of H-
![]() $C^*$
-algebras
$C^*$
-algebras
Now, when we take crossed products by H for the leftmost system, we get
![]() $\operatorname {\mathrm {Ind}}_H^G (A\otimes _{H^0} \operatorname {\mathrm {Res}}_G^H(B))$
by definition. The rightmost system is just
$\operatorname {\mathrm {Ind}}_H^G (A\otimes _{H^0} \operatorname {\mathrm {Res}}_G^H(B))$
by definition. The rightmost system is just
![]() $C_0(G_{H^0})\otimes _{H^0}A\otimes _{H^0} \operatorname {\mathrm {Res}}_G^H B$
with the diagonal H-action
$C_0(G_{H^0})\otimes _{H^0}A\otimes _{H^0} \operatorname {\mathrm {Res}}_G^H B$
with the diagonal H-action
![]() $\mathrm {rt}\otimes \alpha \otimes \operatorname {\mathrm {Res}}_G^H(\beta )$
. So upon using commutativity of the tensor product and applying Lemma 2.2, we may replace it by the action
$\mathrm {rt}\otimes \alpha \otimes \operatorname {\mathrm {Res}}_G^H(\beta )$
. So upon using commutativity of the tensor product and applying Lemma 2.2, we may replace it by the action
![]() $\mathrm {rt}\otimes \alpha \otimes \mathrm {id}_{B}$
.
$\mathrm {rt}\otimes \alpha \otimes \mathrm {id}_{B}$
.
Summing up, after taking crossed products by H we arrive at the desired conclusion:
where
![]() $\phi _*\phi ^*A\rtimes H=\operatorname {\mathrm {Ind}}_H^G(A)$
by definition.
$\phi _*\phi ^*A\rtimes H=\operatorname {\mathrm {Ind}}_H^G(A)$
by definition.
We conclude this section by listing other compatibility relations, which are straightforward as each of them involves a forgetful functor.
 $$ \begin{gather*} \operatorname{\mathrm{Res}}_G^H(A\otimes_X B)\cong \operatorname{\mathrm{Res}}_G^H(A)\otimes_X \operatorname{\mathrm{Res}}_G^H(B)\\ \operatorname{\mathrm{Ind}}_H^G\circ f_* \cong f_*\circ \operatorname{\mathrm{Ind}}_H^G\qquad \operatorname{\mathrm{Res}}_G^H\circ f_* \cong f_*\circ \operatorname{\mathrm{Res}}_G^H\qquad \operatorname{\mathrm{Res}}_G^H\circ f^* \cong f^*\circ \operatorname{\mathrm{Res}}_G^H. \end{gather*} $$
$$ \begin{gather*} \operatorname{\mathrm{Res}}_G^H(A\otimes_X B)\cong \operatorname{\mathrm{Res}}_G^H(A)\otimes_X \operatorname{\mathrm{Res}}_G^H(B)\\ \operatorname{\mathrm{Ind}}_H^G\circ f_* \cong f_*\circ \operatorname{\mathrm{Ind}}_H^G\qquad \operatorname{\mathrm{Res}}_G^H\circ f_* \cong f_*\circ \operatorname{\mathrm{Res}}_G^H\qquad \operatorname{\mathrm{Res}}_G^H\circ f^* \cong f^*\circ \operatorname{\mathrm{Res}}_G^H. \end{gather*} $$
3 The strong Baum–Connes conjecture
In this section, we formulate the strong Baum–Connes conjecture for étale groupoids by using the framework developed in the previous section.
As a start, a natural idea is identifying a ‘probing’ class of objects
![]() $\mathcal {P}r\subseteq \operatorname {\mathrm {KK}}^G$
, that we understand somewhat better than a generic object of
$\mathcal {P}r\subseteq \operatorname {\mathrm {KK}}^G$
, that we understand somewhat better than a generic object of
![]() $\operatorname {\mathrm {KK}}^G$
, and for which we can prove the equality of categories
$\operatorname {\mathrm {KK}}^G$
, and for which we can prove the equality of categories
![]() $\langle \mathcal {P} r\rangle = \operatorname {\mathrm {KK}}^G$
.
$\langle \mathcal {P} r\rangle = \operatorname {\mathrm {KK}}^G$
.
Definition 3.1. We say that G is proper if the anchor map
![]() $(r,s)\colon G \to X\times X$
is proper. Furthermore, if Z is a a second countable, locally compact, Hausdorff G-space, we say that G acts properly on Z if
$(r,s)\colon G \to X\times X$
is proper. Furthermore, if Z is a a second countable, locally compact, Hausdorff G-space, we say that G acts properly on Z if
![]() $Z\rtimes G$
is proper. A G-algebra A is called proper if there is a proper G-space Z such that A is a
$Z\rtimes G$
is proper. A G-algebra A is called proper if there is a proper G-space Z such that A is a
![]() $Z\rtimes G$
-algebra.
$Z\rtimes G$
-algebra.
We let
![]() $\mathcal {P}r$
denote the class of proper objects in
$\mathcal {P}r$
denote the class of proper objects in
![]() $\operatorname {\mathrm {KK}}^G$
.
$\operatorname {\mathrm {KK}}^G$
.
Evidently, a commutative G-
![]() $C^*$
-algebra is proper if and only if its spectrum is a proper G-space.
$C^*$
-algebra is proper if and only if its spectrum is a proper G-space.
Recall that G is called étale if its source and range maps are local homeomorphisms. A bisection is an open
![]() $W\subseteq G$
such that
$W\subseteq G$
such that
![]() $s|_W,r|_W$
are homeomorphisms onto an open in X. Hereafter, it is assumed that G is étale.
$s|_W,r|_W$
are homeomorphisms onto an open in X. Hereafter, it is assumed that G is étale.
Recall that a map
![]() $f:X \to Y$
is proper at
$f:X \to Y$
is proper at
![]() $y \in Y$
if
$y \in Y$
if
-
– the fiber at y is compact,
-
– any open containing the fiber also contains a tube (a tube is the preimage of an open neighborhood of y).
A map is proper if and only if it is proper at each point. The proposition below clarifies the local picture of proper actions (cf. [Reference Moerdijk and Pronk42, Theorem 4.1.1] and [Reference Tu60, Proposition 2.42]).
Proposition 3.2. Suppose G acts properly on Z and denote by
![]() $\rho \colon Z \to X$
the moment map. Then for each
$\rho \colon Z \to X$
the moment map. Then for each
![]() $z\in Z$
there are open neighborhoods
$z\in Z$
there are open neighborhoods
![]() $U^\rho ,U$
, respectively, of
$U^\rho ,U$
, respectively, of
![]() $z\in Z$
and
$z\in Z$
and
![]() $\rho (z)\in X$
, satisfying:
$\rho (z)\in X$
, satisfying:
-
– The fixgroup
 $\Gamma _z:=\{g\in G\mid g z=z\}$
acts on U;
$\Gamma _z:=\{g\in G\mid g z=z\}$
acts on U; -
– There exists an isomorphism from
 $\Gamma _z \ltimes U$
onto an open subgroupoid
$\Gamma _z \ltimes U$
onto an open subgroupoid
 $H_z$
of
$H_z$
of
 $G|_U$
;
$G|_U$
; -
– The G-action restricted to
 $U^\rho $
is induced from
$U^\rho $
is induced from
 $\Gamma _z \ltimes U$
; in other words, the groupoid
$\Gamma _z \ltimes U$
; in other words, the groupoid
 $(G\ltimes Z)|_{U^\rho }$
equals
$(G\ltimes Z)|_{U^\rho }$
equals
 $(\Gamma _z \ltimes U)\ltimes U^{\rho }$
.
$(\Gamma _z \ltimes U)\ltimes U^{\rho }$
.
Proof. Since the G-action on Z is proper,
![]() $\Gamma _z$
is a finite subgroup of the isotropy group
$\Gamma _z$
is a finite subgroup of the isotropy group
![]() $G_{\rho (z)}^{\rho (z)}$
. For each
$G_{\rho (z)}^{\rho (z)}$
. For each
![]() $g\in \Gamma _z$
, choose an open bisection
$g\in \Gamma _z$
, choose an open bisection
![]() $W_g$
around g. Since G is Hausdorff and
$W_g$
around g. Since G is Hausdorff and
![]() $\Gamma _z$
is finite, we may assume that the
$\Gamma _z$
is finite, we may assume that the
![]() $W_g$
are pairwise disjoint. For any two
$W_g$
are pairwise disjoint. For any two
![]() $g,h\in \Gamma _z$
, there is an open neighborhood V of
$g,h\in \Gamma _z$
, there is an open neighborhood V of
![]() $\rho (z)$
such that
$\rho (z)$
such that
![]() $W_{gh}\cap G|_V$
and
$W_{gh}\cap G|_V$
and
![]() $(W_g W_h)\cap G|_V$
are nonempty and equal because both are bisections containing
$(W_g W_h)\cap G|_V$
are nonempty and equal because both are bisections containing
![]() $gh$
. Likewise, for each g in
$gh$
. Likewise, for each g in
![]() $\Gamma _z$
there is an open neighborhood V of
$\Gamma _z$
there is an open neighborhood V of
![]() $\rho (z)$
, where
$\rho (z)$
, where
![]() $W_{g^{-1}}\cap G|_{V}$
and
$W_{g^{-1}}\cap G|_{V}$
and
![]() $(W_g)^{-1}\cap G|_{V}$
are nonempty and equal. Ranging over the group
$(W_g)^{-1}\cap G|_{V}$
are nonempty and equal. Ranging over the group
![]() $\Gamma _z$
, we collect a finite number of V’s whose intersection we denote by U. Notice U is an open neighborhood of
$\Gamma _z$
, we collect a finite number of V’s whose intersection we denote by U. Notice U is an open neighborhood of
![]() $\rho (z)$
. We now replace all the
$\rho (z)$
. We now replace all the
![]() $W_g$
’s by
$W_g$
’s by
![]() $W_g\cap r^{-1}(U)\cap s^{-1}(U)$
. Then we can define an action of
$W_g\cap r^{-1}(U)\cap s^{-1}(U)$
. Then we can define an action of
![]() $\Gamma _z$
on U by setting
$\Gamma _z$
on U by setting
![]() $g\cdot x:=r(s_{|W_g}^{-1}(x))$
, that is, g acts by the partial homeomorphism
$g\cdot x:=r(s_{|W_g}^{-1}(x))$
, that is, g acts by the partial homeomorphism
![]() $U\rightarrow U$
associated with the bisection
$U\rightarrow U$
associated with the bisection
![]() $W_g$
. This is then indeed a well-defined action by the construction of the
$W_g$
. This is then indeed a well-defined action by the construction of the
![]() $W_g$
above. We have a canonical continuous groupoid homomorphism
$W_g$
above. We have a canonical continuous groupoid homomorphism
Since the
![]() $W_g$
were chosen pairwise disjoint this is in fact an isomorphism of topological groupoids onto the union
$W_g$
were chosen pairwise disjoint this is in fact an isomorphism of topological groupoids onto the union
![]() $H:=\bigsqcup _{g\in \Gamma _z}W_g$
.
$H:=\bigsqcup _{g\in \Gamma _z}W_g$
.
Define
![]() $U^\prime :=\rho ^{-1}(U)$
. Because G acts on Z, and H is a subgroupoid of G, the notation
$U^\prime :=\rho ^{-1}(U)$
. Because G acts on Z, and H is a subgroupoid of G, the notation
![]() $U^\prime \rtimes H$
makes sense, and it indicates an open subgroupoid of the restriction
$U^\prime \rtimes H$
makes sense, and it indicates an open subgroupoid of the restriction
![]() $(Z\rtimes G)|_{U^\prime }$
. The action of G on Z is proper; in particular, the anchor map of the groupoid
$(Z\rtimes G)|_{U^\prime }$
. The action of G on Z is proper; in particular, the anchor map of the groupoid
![]() $Z\rtimes G$
is proper at z. Now,
$Z\rtimes G$
is proper at z. Now,
![]() $U^\prime \rtimes H$
is an open containing the fiber of the anchor map at z; therefore, it contains a tube. In other words, there is an open neighborhood of z, say
$U^\prime \rtimes H$
is an open containing the fiber of the anchor map at z; therefore, it contains a tube. In other words, there is an open neighborhood of z, say
![]() $U^\rho $
(we may assume it is also contained in
$U^\rho $
(we may assume it is also contained in
![]() $U^\prime $
), such that the restriction
$U^\prime $
), such that the restriction
![]() $(Z\rtimes G)|_{U^\rho }$
(i.e., the tube at
$(Z\rtimes G)|_{U^\rho }$
(i.e., the tube at
![]() $U^\rho $
) is contained in
$U^\rho $
) is contained in
![]() $U^\prime \rtimes H$
. This means that the groupoid that G induces on
$U^\prime \rtimes H$
. This means that the groupoid that G induces on
![]() $U^\rho $
only involves arrows belonging to H (recall that H is isomorphic to
$U^\rho $
only involves arrows belonging to H (recall that H is isomorphic to
![]() $U\rtimes \Gamma $
).
$U\rtimes \Gamma $
).
Remark 3.3. As a simple corollary of Proposition 3.2, the range map
![]() $r\colon s^{-1}(U^\rho )\to Z$
descends to a G-equivariant homeomorphism
$r\colon s^{-1}(U^\rho )\to Z$
descends to a G-equivariant homeomorphism
Moreover, the space
![]() $s^{-1}(U^\rho )$
provides a principal bibundle implementing an equivalence between
$s^{-1}(U^\rho )$
provides a principal bibundle implementing an equivalence between
![]() $(G\rtimes Z)|_{U^\rho }$
and
$(G\rtimes Z)|_{U^\rho }$
and
![]() $(G\rtimes Z)|_{V}$
in the sense of [Reference Muhly, Renault and Williams43] (cf. [Reference del Hoyo19]). Hence, the induction functor
$(G\rtimes Z)|_{V}$
in the sense of [Reference Muhly, Renault and Williams43] (cf. [Reference del Hoyo19]). Hence, the induction functor
![]() $\operatorname {\mathrm {KK}}^{(G\rtimes Z)|_{U^\rho }}\to \operatorname {\mathrm {KK}}^{(G\rtimes Z)|_{V}}$
is essentially surjective [Reference Le Gall30], that is, if A is a G-algebra over Z, then
$\operatorname {\mathrm {KK}}^{(G\rtimes Z)|_{U^\rho }}\to \operatorname {\mathrm {KK}}^{(G\rtimes Z)|_{V}}$
is essentially surjective [Reference Le Gall30], that is, if A is a G-algebra over Z, then
![]() $A|_{V}$
is isomorphic to
$A|_{V}$
is isomorphic to
![]() $\operatorname {\mathrm {Ind}}_{(G\rtimes Z)|_{U^\rho }}^{(G\rtimes Z)|_{V}}(A|_{U^{\rho }})$
. We can forget the
$\operatorname {\mathrm {Ind}}_{(G\rtimes Z)|_{U^\rho }}^{(G\rtimes Z)|_{V}}(A|_{U^{\rho }})$
. We can forget the
![]() $C_0(Z)$
-structure and obtain
$C_0(Z)$
-structure and obtain
![]() $A|_{V}\cong \operatorname {\mathrm {Ind}}_{H}^G(A|_{U^{\rho }})$
in
$A|_{V}\cong \operatorname {\mathrm {Ind}}_{H}^G(A|_{U^{\rho }})$
in
![]() $\operatorname {\mathrm {KK}}^G$
.
$\operatorname {\mathrm {KK}}^G$
.
In Definition 3.1 for a proper G-algebra, we can always assume Z to be a realization of
![]() $\underline{E}G$
, the classifying space for proper actions of G. Indeed, if
$\underline{E}G$
, the classifying space for proper actions of G. Indeed, if
![]() $\phi \colon Z\to \underline{E}G$
is a G-equivariant continuous map, then
$\phi \colon Z\to \underline{E}G$
is a G-equivariant continuous map, then
![]() $\phi ^*\colon C_0(\underline{E}G) \to M(C_0(Z))$
can be precomposed with the structure map
$\phi ^*\colon C_0(\underline{E}G) \to M(C_0(Z))$
can be precomposed with the structure map
![]() $C_0(Z) \to ZM(A)$
, making A into an
$C_0(Z) \to ZM(A)$
, making A into an
![]() $\underline{E}G\rtimes G$
-algebra.
$\underline{E}G\rtimes G$
-algebra.
Note that if G is locally compact,
![]() $\sigma $
-compact, Hausdorff
$\sigma $
-compact, Hausdorff
![]() $\underline{E}G$
always exists and is locally compact,
$\underline{E}G$
always exists and is locally compact,
![]() $\sigma $
-compact, and Hausdorff; in our case, G is second countable, hence
$\sigma $
-compact, and Hausdorff; in our case, G is second countable, hence
![]() $\underline{E}G$
is too [Reference Tu59, Proposition 6.15].
$\underline{E}G$
is too [Reference Tu59, Proposition 6.15].
A subgroupoid of the form
![]() $\Phi (\Gamma _z \ltimes U )\subseteq G$
, as in Proposition 3.2, will be called a compact action around
$\Phi (\Gamma _z \ltimes U )\subseteq G$
, as in Proposition 3.2, will be called a compact action around
![]() $\rho (z)$
. Given a proper G-algebra over
$\rho (z)$
. Given a proper G-algebra over
![]() $Z=\underline{E}G$
, for any
$Z=\underline{E}G$
, for any
![]() $z\in Z$
we can find an open neighborhood as in Equation (7). These open cover Z, and we can extract a countable subcover
$z\in Z$
we can find an open neighborhood as in Equation (7). These open cover Z, and we can extract a countable subcover
![]() $\mathcal {V}$
(being second countable, Z is a Lindelöf space). Corresponding to this subcover, we get a countable collection of compact actions which we denote by
$\mathcal {V}$
(being second countable, Z is a Lindelöf space). Corresponding to this subcover, we get a countable collection of compact actions which we denote by
![]() $\mathcal {F}$
. Define the full subcategory of compactly induced objects,
$\mathcal {F}$
. Define the full subcategory of compactly induced objects,
We define a homological ideal
![]() $\mathcal {I}$
as the kernel of a single functor
$\mathcal {I}$
as the kernel of a single functor
 $$ \begin{align} F\colon \operatorname{\mathrm{KK}}^G&\to \prod_{Q\in \mathcal{F}}\operatorname{\mathrm{KK}}^Q\\\notag A&\mapsto (\operatorname{\mathrm{Res}}_G^Q(A))_{Q\in \mathcal{F}}. \end{align} $$
$$ \begin{align} F\colon \operatorname{\mathrm{KK}}^G&\to \prod_{Q\in \mathcal{F}}\operatorname{\mathrm{KK}}^Q\\\notag A&\mapsto (\operatorname{\mathrm{Res}}_G^Q(A))_{Q\in \mathcal{F}}. \end{align} $$
The functor F commutes with direct sums because each restriction functor clearly does. Hence,
![]() $\mathcal {I}$
is compatible with countable direct sums. The proof below follows the blueprint in [Reference Meyer39, Theorem 7.3], we reproduce it here for completeness.
$\mathcal {I}$
is compatible with countable direct sums. The proof below follows the blueprint in [Reference Meyer39, Theorem 7.3], we reproduce it here for completeness.
Theorem 3.4. The projective objects for
![]() $\mathcal {I}$
are the retracts of direct sums of objects in
$\mathcal {I}$
are the retracts of direct sums of objects in
![]() $\mathcal {C}\mathcal {I}$
and the ideal
$\mathcal {C}\mathcal {I}$
and the ideal
![]() $\mathcal {I}$
has enough projective objects. Therefore, the subcategories in
$\mathcal {I}$
has enough projective objects. Therefore, the subcategories in
![]() $(\langle \mathcal {C}\mathcal {I}\rangle ,N_{\mathcal {I}})$
form a pair of complementary subcategories.
$(\langle \mathcal {C}\mathcal {I}\rangle ,N_{\mathcal {I}})$
form a pair of complementary subcategories.
Proof. According to [Reference Meyer39, Theorem 3.22], we need to study the (possibly) partially defined left adjoint of the functor F defined in Equation (8). Since each compact action
![]() $Q\in \mathcal {F}$
is open in G, the functor
$Q\in \mathcal {F}$
is open in G, the functor
![]() $\operatorname {\mathrm {Ind}}_Q^G$
is left adjoint to
$\operatorname {\mathrm {Ind}}_Q^G$
is left adjoint to
![]() $\operatorname {\mathrm {Res}}_G^Q$
. Thus, we may take the globally defined adjoint
$\operatorname {\mathrm {Res}}_G^Q$
. Thus, we may take the globally defined adjoint
Since
![]() $\mathcal {F}$
is countable and F is compatible with countable direct sums, this definition is legitimate. It follows that
$\mathcal {F}$
is countable and F is compatible with countable direct sums, this definition is legitimate. It follows that
![]() $\mathcal {I}$
has enough projective objects which are retracts as described. Indeed,
$\mathcal {I}$
has enough projective objects which are retracts as described. Indeed,
![]() $F^\dagger F(A)$
is projective because the isomorphism
$F^\dagger F(A)$
is projective because the isomorphism
is given by
![]() $f\mapsto \operatorname {\mathrm {Res}}_G^Q(f)\circ \eta _{\operatorname {\mathrm {Res}}_G^Q(A)}$
, where
$f\mapsto \operatorname {\mathrm {Res}}_G^Q(f)\circ \eta _{\operatorname {\mathrm {Res}}_G^Q(A)}$
, where
![]() $\eta $
is the unit of the adjunction. We then see that if
$\eta $
is the unit of the adjunction. We then see that if
![]() $f\in \mathcal {I}$
, then we must have
$f\in \mathcal {I}$
, then we must have
![]() $f=0$
. Similarly, the counits of the adjunctions yield an
$f=0$
. Similarly, the counits of the adjunctions yield an
![]() $\mathcal {I}$
-epic morphism
$\mathcal {I}$
-epic morphism
![]() $\delta : F^\dagger F(A)\to A$
[Reference Meyer and Nest41, Definition 21]. In particular, if A is already projective, then
$\delta : F^\dagger F(A)\to A$
[Reference Meyer and Nest41, Definition 21]. In particular, if A is already projective, then
![]() $\delta $
can be embedded in a split triangle. Split triangles are isomorphic to direct sum triangles [Reference Neeman45, Corollary 1.2.7].
$\delta $
can be embedded in a split triangle. Split triangles are isomorphic to direct sum triangles [Reference Neeman45, Corollary 1.2.7].
Using notation from Section 1.2 and applying the result above, we have
![]() $\mathcal {P}=\langle \mathcal {C}\mathcal {I}\rangle =\langle P_{\mathcal {I}}\rangle $
and
$\mathcal {P}=\langle \mathcal {C}\mathcal {I}\rangle =\langle P_{\mathcal {I}}\rangle $
and
![]() $\mathcal {N}=N_{\mathcal {I}}$
. Since we will only be dealing with the homological ideal
$\mathcal {N}=N_{\mathcal {I}}$
. Since we will only be dealing with the homological ideal
![]() $\ker (F)$
just described, we will drop the
$\ker (F)$
just described, we will drop the
![]() $\mathcal {I}$
from our notation and just write
$\mathcal {I}$
from our notation and just write
![]() $\mathcal {N}$
instead of
$\mathcal {N}$
instead of
![]() $N_{\mathcal {I}}$
. The objects in
$N_{\mathcal {I}}$
. The objects in
![]() $\mathcal {N}\subseteq \operatorname {\mathrm {KK}}^G$
are also referred to as weakly contractible. We denote by
$\mathcal {N}\subseteq \operatorname {\mathrm {KK}}^G$
are also referred to as weakly contractible. We denote by
![]() $P(A)$
the
$P(A)$
the
![]() $\mathcal {C}\mathcal {I}$
-cellular approximation of A. Note
$\mathcal {C}\mathcal {I}$
-cellular approximation of A. Note
![]() $P(A)$
belongs to
$P(A)$
belongs to
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
Corollary 3.5. We have the following equivalences,
Proof. We have already explained that tensorization via the maximal balanced tensor product functor gives a triangulated functor. Hence, it maps the canonical exact triangle
![]() $P(C_0(G^0))\longrightarrow C_0(G^0)\longrightarrow N(C_0(G^0))$
to an exact triangle
$P(C_0(G^0))\longrightarrow C_0(G^0)\longrightarrow N(C_0(G^0))$
to an exact triangle
If we can show that
![]() $-\, \otimes ^{\text {}}_{G^0} A$
leaves the subcategories
$-\, \otimes ^{\text {}}_{G^0} A$
leaves the subcategories
![]() $\langle \mathcal {C}\mathcal {I}\rangle $
and
$\langle \mathcal {C}\mathcal {I}\rangle $
and
![]() $\mathcal {N}$
invariant, the result follows from the uniqueness statement in Proposition 1.12. Let us begin with the contractible objects: For
$\mathcal {N}$
invariant, the result follows from the uniqueness statement in Proposition 1.12. Let us begin with the contractible objects: For
![]() $B\in \mathcal {N}$
, since the restriction functor behaves well with respect to the maximal balanced tensor product, we compute
$B\in \mathcal {N}$
, since the restriction functor behaves well with respect to the maximal balanced tensor product, we compute
and hence
![]() $B\otimes _{G^0}^{\text {max}} A\in \mathcal {N}$
.
$B\otimes _{G^0}^{\text {max}} A\in \mathcal {N}$
.
On the other hand, for every
![]() $Q\in \mathcal {F}$
and
$Q\in \mathcal {F}$
and
![]() $B\in \operatorname {\mathrm {KK}}^Q$
, Lemma 2.6 provides
$B\in \operatorname {\mathrm {KK}}^Q$
, Lemma 2.6 provides
![]() $\operatorname {\mathrm {KK}}^G$
-equivalences
$\operatorname {\mathrm {KK}}^G$
-equivalences
Definition 3.6. We say that G satisfies the strong Baum–Connes conjecture (with coefficients in A) if the natural map
![]() $P(A)\rtimes _r G \to A\rtimes _r G$
is a
$P(A)\rtimes _r G \to A\rtimes _r G$
is a
![]() $\operatorname {\mathrm {KK}}$
-equivalence.
$\operatorname {\mathrm {KK}}$
-equivalence.
A stronger variant of the formulation above is requiring
![]() $P(A)\to A$
to be an isomorphism in
$P(A)\to A$
to be an isomorphism in
![]() $\operatorname {\mathrm {KK}}^G$
. However, it is known that even the ordinary (weaker) form of the conjecture admits counterexamples [Reference Higson, Lafforgue and Skandalis24].
$\operatorname {\mathrm {KK}}^G$
. However, it is known that even the ordinary (weaker) form of the conjecture admits counterexamples [Reference Higson, Lafforgue and Skandalis24].
We will need the following deep result proved by J.-L. Tu.
Theorem 3.7 [Reference Tu58].
Suppose G is a second countable, locally compact, Hausdorff groupoid. If G acts properly on a continuous field of affine Euclidean spaces, then there exists a proper G-
![]() $C^*$
-algebra P such that
$C^*$
-algebra P such that
![]() $P\cong C_0(G^0)$
in
$P\cong C_0(G^0)$
in
![]() $\operatorname {\mathrm {KK}}^G$
.
$\operatorname {\mathrm {KK}}^G$
.
This result has the following immediate consequence:
Corollary 3.8. Suppose G is a second countable, locally compact, Hausdorff groupoid. If G admits a proper action on a continuous field of affine Euclidean spaces, then we have the equality of categories
![]() $\langle \mathcal {P} r\rangle =\operatorname {\mathrm {KK}}^G$
.
$\langle \mathcal {P} r\rangle =\operatorname {\mathrm {KK}}^G$
.
Proof. If
![]() $A\in \operatorname {\mathrm {KK}}^G$
is any G-
$A\in \operatorname {\mathrm {KK}}^G$
is any G-
![]() $C^*$
-algebra, we have that
$C^*$
-algebra, we have that
![]() $A\otimes _{G^0} P$
is proper and
$A\otimes _{G^0} P$
is proper and
![]() $\operatorname {\mathrm {KK}}^G$
-equivalent to A.
$\operatorname {\mathrm {KK}}^G$
-equivalent to A.
Our next goal is to show that
![]() $\langle \mathcal {C}\mathcal {I}\rangle =\langle \mathcal {P} r\rangle $
. Let us first treat the proper case:
$\langle \mathcal {C}\mathcal {I}\rangle =\langle \mathcal {P} r\rangle $
. Let us first treat the proper case:
Lemma 3.9. Let G be a proper étale groupoid. Then
![]() $C_0(G^{0})\in \langle \mathcal {C}\mathcal {I}\rangle \subseteq \operatorname {\mathrm {KK}}^G$
.
$C_0(G^{0})\in \langle \mathcal {C}\mathcal {I}\rangle \subseteq \operatorname {\mathrm {KK}}^G$
.
Proof. We have to show that
![]() $\operatorname {\mathrm {KK}}^G(C_0(G^{0}),N)=0$
for every
$\operatorname {\mathrm {KK}}^G(C_0(G^{0}),N)=0$
for every
![]() $\mathcal {I}$
-contractible object
$\mathcal {I}$
-contractible object
![]() $N\in \operatorname {\mathrm {KK}}^G$
. Since
$N\in \operatorname {\mathrm {KK}}^G$
. Since
![]() $C_0(G^{0})$
is clearly
$C_0(G^{0})$
is clearly
![]() $C_0(G^{0})$
-nuclear, we have an isomorphism
$C_0(G^{0})$
-nuclear, we have an isomorphism
by Corollary 1.8. Consequently, we can work in the setting of G-equivariant E-theory instead. The upshot is that E-theory satisfies excision. In particular, since G is proper, it is locally induced by compact actions as is explained in Proposition 3.2, that is, we have a countable cover
![]() $\mathcal {V}$
of
$\mathcal {V}$
of
![]() $G^{0}$
by G-invariant sets with
$G^{0}$
by G-invariant sets with
As a first step, we aim to replace
![]() $\mathcal {V}$
by an increasing sequence. In order to arrange this, we need to show that given
$\mathcal {V}$
by an increasing sequence. In order to arrange this, we need to show that given
![]() $V_0,V_1\in \mathcal {V}$
we have
$V_0,V_1\in \mathcal {V}$
we have
Let us first observe that
![]() $\operatorname {\mathrm {KK}}^G(C_0(V_0\cap V_1),N)=0$
. Following Proposition 3.2, we can write
$\operatorname {\mathrm {KK}}^G(C_0(V_0\cap V_1),N)=0$
. Following Proposition 3.2, we can write
![]() $V_i=GU_i$
such that there exist
$V_i=GU_i$
such that there exist
![]() $H_i\in \mathcal {F}$
with
$H_i\in \mathcal {F}$
with
![]() $G\times _{H_i}U_i\cong GU_i=V_i$
. Observe that we have
$G\times _{H_i}U_i\cong GU_i=V_i$
. Observe that we have
![]() $V_0\cap V_1=G(U_0\cap GU_1)$
and that if
$V_0\cap V_1=G(U_0\cap GU_1)$
and that if
![]() $g\in G$
satisfies
$g\in G$
satisfies
![]() $g(U_0\cap GU_1)\cap (U_0\cap GU_1)\neq \emptyset $
, then also
$g(U_0\cap GU_1)\cap (U_0\cap GU_1)\neq \emptyset $
, then also
![]() $gU_0\cap U_0\neq \emptyset $
and hence by the construction of
$gU_0\cap U_0\neq \emptyset $
and hence by the construction of
![]() $H_0$
,
$H_0$
,
![]() $g\in H_0$
. Thus, the canonical map
$g\in H_0$
. Thus, the canonical map
is a homeomorphism as it is the restriction of the homeomorphism
![]() $G\times _{H_0} U_0\cong GU_0$
. It follows that
$G\times _{H_0} U_0\cong GU_0$
. It follows that
![]() $C_0(V_0\cap V_1)\cong C_0(G\times _{H_0} H_0(U_0\cap GU_1))=\operatorname {\mathrm {Ind}}_{H_0}^G(C_0(H_0(U_0\cap GU_1))\in \mathcal {CI},$
and hence
$C_0(V_0\cap V_1)\cong C_0(G\times _{H_0} H_0(U_0\cap GU_1))=\operatorname {\mathrm {Ind}}_{H_0}^G(C_0(H_0(U_0\cap GU_1))\in \mathcal {CI},$
and hence
![]() $E_G(C_0(V_0\cap V_1),N)\cong \operatorname {\mathrm {KK}}^G(C_0(V_0\cap V_1),N)=0$
.
$E_G(C_0(V_0\cap V_1),N)\cong \operatorname {\mathrm {KK}}^G(C_0(V_0\cap V_1),N)=0$
.
The corresponding statement for the union
![]() $V_0\cup V_1$
now follows easily from the long exact sequences in
$V_0\cup V_1$
now follows easily from the long exact sequences in
![]() $E_G$
-theory associated with the short exact sequences:
$E_G$
-theory associated with the short exact sequences:
 $$ \begin{align*} &0\longrightarrow C_0(V_0\cap V_1)\longrightarrow C_0(V_1)\longrightarrow C_0(V_1\smallsetminus V_0)\longrightarrow 0,\\ &0\longrightarrow C_0(V_0)\longrightarrow C_0(V_0\cup V_1)\longrightarrow C_0(V_1\smallsetminus V_0)\longrightarrow 0. \end{align*} $$
$$ \begin{align*} &0\longrightarrow C_0(V_0\cap V_1)\longrightarrow C_0(V_1)\longrightarrow C_0(V_1\smallsetminus V_0)\longrightarrow 0,\\ &0\longrightarrow C_0(V_0)\longrightarrow C_0(V_0\cup V_1)\longrightarrow C_0(V_1\smallsetminus V_0)\longrightarrow 0. \end{align*} $$
In each sequence, two out of three groups in the induced long exact sequence vanish and hence so does the third. Replacing
![]() $V_n$
by
$V_n$
by
![]() $\bigcup _{i=1}^n V_i$
, we can assume that
$\bigcup _{i=1}^n V_i$
, we can assume that
![]() $\mathcal {V}=(V_n)_{n\in \mathbb {N}}$
is an increasing sequence. We clearly have
$\mathcal {V}=(V_n)_{n\in \mathbb {N}}$
is an increasing sequence. We clearly have
![]() $C_0(G^{0})=\varinjlim _n C_0(V_n)$
, and since E-theory has countable direct sums we have a Milnor
$C_0(G^{0})=\varinjlim _n C_0(V_n)$
, and since E-theory has countable direct sums we have a Milnor
![]() $\lim ^1$
-sequence (see Lemma 1.16)
$\lim ^1$
-sequence (see Lemma 1.16)
Since the left and right terms are both zero, this concludes the proof.
In the argument above, we can replace
![]() $C_0(G^{0})$
by any
$C_0(G^{0})$
by any
![]() $\operatorname {\mathrm {KK}}^G$
-nuclear G-algebra A.
$\operatorname {\mathrm {KK}}^G$
-nuclear G-algebra A.
Theorem 3.10. The localizing subcategory of
![]() $\operatorname {\mathrm {KK}}^G$
generated by compactly induced objects equals the one generated by proper objects, that is,
$\operatorname {\mathrm {KK}}^G$
generated by compactly induced objects equals the one generated by proper objects, that is,
![]() $\langle \mathcal {C}\mathcal {I}\rangle =\langle \mathcal {P} r\rangle $
.
$\langle \mathcal {C}\mathcal {I}\rangle =\langle \mathcal {P} r\rangle $
.
Proof. Consider the canonical triangle
and let
![]() $p:G\ltimes \underline {E} G\rightarrow G$
denote the projection homomorphism. The associated functor
$p:G\ltimes \underline {E} G\rightarrow G$
denote the projection homomorphism. The associated functor
![]() $p^*:\operatorname {\mathrm {KK}}^G\rightarrow \operatorname {\mathrm {KK}}^{G\ltimes \underline {E} G}$
maps contractible objects to contractible objects. Indeed, since
$p^*:\operatorname {\mathrm {KK}}^G\rightarrow \operatorname {\mathrm {KK}}^{G\ltimes \underline {E} G}$
maps contractible objects to contractible objects. Indeed, since
![]() $\underline {E} G$
is a proper G-space, a compact action for
$\underline {E} G$
is a proper G-space, a compact action for
![]() $G\ltimes \underline {E} G$
is just given by the restriction to one of the sets
$G\ltimes \underline {E} G$
is just given by the restriction to one of the sets
![]() $U^\rho $
as in Proposition 3.2. Continuing to use the notation from that proposition, let Q be the open copy of
$U^\rho $
as in Proposition 3.2. Continuing to use the notation from that proposition, let Q be the open copy of
![]() $\Gamma _z\ltimes U$
inside G, a compact action for G! Then the compositions of groupoid homomorphisms
$\Gamma _z\ltimes U$
inside G, a compact action for G! Then the compositions of groupoid homomorphisms
![]() $(G\ltimes \underline {E} G)|_{U^\rho }\hookrightarrow G\ltimes \underline {E} G\stackrel {p}{\rightarrow }G$
and
$(G\ltimes \underline {E} G)|_{U^\rho }\hookrightarrow G\ltimes \underline {E} G\stackrel {p}{\rightarrow }G$
and
![]() $(G\ltimes \underline {E} G)|_{U^\rho }\cong (\Gamma _z\ltimes U)\ltimes U^\rho \stackrel {p}{\rightarrow }\Gamma _z\ltimes U\cong Q\hookrightarrow G$
coincide. The resulting commutative diagram of
$(G\ltimes \underline {E} G)|_{U^\rho }\cong (\Gamma _z\ltimes U)\ltimes U^\rho \stackrel {p}{\rightarrow }\Gamma _z\ltimes U\cong Q\hookrightarrow G$
coincide. The resulting commutative diagram of
![]() $\operatorname {\mathrm {KK}}$
groups gives
$\operatorname {\mathrm {KK}}$
groups gives
![]() $\operatorname {\mathrm {Res}}_{(G\ltimes \underline {E} G)|_{U^\rho }}(\mathrm {id}_{p^*N})=\operatorname {\mathrm {Res}}_{(G\ltimes \underline {E} G)|_{U^\rho }}(p^*(\mathrm {id}_N))=p^*(\operatorname {\mathrm {Res}}_Q(\mathrm {id}_N))=0$
for any contractible object
$\operatorname {\mathrm {Res}}_{(G\ltimes \underline {E} G)|_{U^\rho }}(\mathrm {id}_{p^*N})=\operatorname {\mathrm {Res}}_{(G\ltimes \underline {E} G)|_{U^\rho }}(p^*(\mathrm {id}_N))=p^*(\operatorname {\mathrm {Res}}_Q(\mathrm {id}_N))=0$
for any contractible object
![]() $N\in \operatorname {\mathrm {KK}}^G$
.
$N\in \operatorname {\mathrm {KK}}^G$
.
Combining this with Lemma 3.9, we can use the fact that
![]() $\langle \mathcal {C}\mathcal {I}\rangle $
and
$\langle \mathcal {C}\mathcal {I}\rangle $
and
![]() $\mathcal {N}$
are complementary to conclude that
$\mathcal {N}$
are complementary to conclude that
![]() $p^*(\eta )\in \operatorname {\mathrm {KK}}^{G\ltimes \underline {E} G}({C_0(\underline {E} G)},{p^*N})=0$
.
$p^*(\eta )\in \operatorname {\mathrm {KK}}^{G\ltimes \underline {E} G}({C_0(\underline {E} G)},{p^*N})=0$
.
Now, let
![]() $A\in \operatorname {\mathrm {KK}}^G$
be an arbitrary proper G-algebra. As explained before, we may assume that A is a
$A\in \operatorname {\mathrm {KK}}^G$
be an arbitrary proper G-algebra. As explained before, we may assume that A is a
![]() $C_0(\underline {E} G)$
-algebra. From our observation above, it follows that
$C_0(\underline {E} G)$
-algebra. From our observation above, it follows that
![]() $p^*(\eta )\otimes _{\underline {E} G} 1_A=0$
. Since the functors
$p^*(\eta )\otimes _{\underline {E} G} 1_A=0$
. Since the functors
![]() $p^*$
and
$p^*$
and
![]() $\sigma _A$
are both triangulated, we can apply them in this order to obtain a triangle
$\sigma _A$
are both triangulated, we can apply them in this order to obtain a triangle
Note that
![]() $C_0(\underline {E} G)\otimes _{\underline {E} G}A\cong A$
. Rotating this triangle gives the triangle
$C_0(\underline {E} G)\otimes _{\underline {E} G}A\cong A$
. Rotating this triangle gives the triangle
in which the last morphism is zero as indicated. Thus, [Reference Neeman45, Corollary 1.2.7] implies that the latter triangle splits, namely
![]() $\Sigma (p^*P\otimes _{\underline {E} G}A)\cong (p^*N\otimes _{\underline {E} G}A)\oplus \Sigma A$
.
$\Sigma (p^*P\otimes _{\underline {E} G}A)\cong (p^*N\otimes _{\underline {E} G}A)\oplus \Sigma A$
.
In particular, after suspending once more we obtain a retraction
![]() $A\longrightarrow p^*P\otimes _{\underline {E} G}A$
, that is, a right inverse of
$A\longrightarrow p^*P\otimes _{\underline {E} G}A$
, that is, a right inverse of
![]() $p^*D\otimes _{\underline {E} G} 1_A:p^*P\otimes _{\underline {E} G}A\longrightarrow A$
. Now, applying the forgetful functor
$p^*D\otimes _{\underline {E} G} 1_A:p^*P\otimes _{\underline {E} G}A\longrightarrow A$
. Now, applying the forgetful functor
![]() $p_{*}$
gives a retraction
$p_{*}$
gives a retraction
![]() $A\longrightarrow p_{*}(p^*P\otimes _{\underline {E} G}A)\cong P\otimes _{G^0} A\cong P(A)$
. Since
$A\longrightarrow p_{*}(p^*P\otimes _{\underline {E} G}A)\cong P\otimes _{G^0} A\cong P(A)$
. Since
![]() $\langle \mathcal {C}\mathcal {I}\rangle $
is a thick subcategory of
$\langle \mathcal {C}\mathcal {I}\rangle $
is a thick subcategory of
![]() $\operatorname {\mathrm {KK}}^G$
it follows that
$\operatorname {\mathrm {KK}}^G$
it follows that
![]() $A\in \langle \mathcal {C}\mathcal {I}\rangle $
.
$A\in \langle \mathcal {C}\mathcal {I}\rangle $
.
Remark 3.11. In general, we do not know if any object in
![]() $\langle \mathcal {C}\mathcal {I}\rangle $
is equivalent in
$\langle \mathcal {C}\mathcal {I}\rangle $
is equivalent in
![]() $\operatorname {\mathrm {KK}}^G$
to a proper G-
$\operatorname {\mathrm {KK}}^G$
to a proper G-
![]() $C^*$
-algebra. However, if the cellular approximation
$C^*$
-algebra. However, if the cellular approximation
![]() $P=P(C_0(G^0))$
happens to be proper (e.g., in the setting of Theorem 3.7), then the previous statement clearly holds, because for any
$P=P(C_0(G^0))$
happens to be proper (e.g., in the setting of Theorem 3.7), then the previous statement clearly holds, because for any
![]() $A\in \langle \mathcal {C}\mathcal {I}\rangle $
, we have that
$A\in \langle \mathcal {C}\mathcal {I}\rangle $
, we have that
![]() $P\otimes _{G^0} A\cong A$
is a proper G-
$P\otimes _{G^0} A\cong A$
is a proper G-
![]() $C^*$
-algebra (cf. [Reference Emerson and Meyer21, Corollary 4.37] and [Reference Meyer and Nest41, Section 7].)
$C^*$
-algebra (cf. [Reference Emerson and Meyer21, Corollary 4.37] and [Reference Meyer and Nest41, Section 7].)
The corollary below identifies the localization category in terms of the more classical
![]() $\operatorname {\mathrm {RKK}}^G$
-functor. Recall a morphism
$\operatorname {\mathrm {RKK}}^G$
-functor. Recall a morphism
![]() $f\colon A\to B$
in
$f\colon A\to B$
in
![]() $\operatorname {\mathrm {KK}}^G$
is called a weak equivalence if
$\operatorname {\mathrm {KK}}^G$
is called a weak equivalence if
![]() $F(f)$
is an isomorphism, where F is the functor in Equation (8). For instance, the natural map
$F(f)$
is an isomorphism, where F is the functor in Equation (8). For instance, the natural map
![]() $D_A\colon P(A)\to A$
is a weak equivalence.
$D_A\colon P(A)\to A$
is a weak equivalence.
Theorem 3.12. Let
![]() $p\colon \underline {E} G\to G^{0}$
be the moment map underlying the G-action. The functor
$p\colon \underline {E} G\to G^{0}$
be the moment map underlying the G-action. The functor
![]() $p^*:\operatorname {\mathrm {KK}}^G\to \operatorname {\mathrm {RKK}}^G(\underline {E} G)$
is an isomorphism of categories up to localization at
$p^*:\operatorname {\mathrm {KK}}^G\to \operatorname {\mathrm {RKK}}^G(\underline {E} G)$
is an isomorphism of categories up to localization at
![]() $N_{\mathcal {I}}$
. More precisely, the indicated maps in the following commutative diagram are isomorphisms.
$N_{\mathcal {I}}$
. More precisely, the indicated maps in the following commutative diagram are isomorphisms.

Proof. Let us first consider the bottom map. Since
![]() $\operatorname {\mathrm {RKK}}^G(\underline {E} G; -\,,B)$
is a cohomological functor, the claim follows from the inclusion
$\operatorname {\mathrm {RKK}}^G(\underline {E} G; -\,,B)$
is a cohomological functor, the claim follows from the inclusion
![]() $N_{\mathcal {I}} \subseteq \mathrm {ker}(p^*)$
. If A is weakly contractible, then
$N_{\mathcal {I}} \subseteq \mathrm {ker}(p^*)$
. If A is weakly contractible, then
![]() $p^*(A)$
is both weakly contractible and proper, hence
$p^*(A)$
is both weakly contractible and proper, hence
![]() $\operatorname {\mathrm {KK}}^{G\ltimes \underline {E} G}(p^*A,p^*A)=0$
by Proposition 1.12. Thus,
$\operatorname {\mathrm {KK}}^{G\ltimes \underline {E} G}(p^*A,p^*A)=0$
by Proposition 1.12. Thus,
![]() $p^*(A)=0$
.
$p^*(A)=0$
.
Secondly, let us turn to the vertical map. Both the top and the bottom groups are functorial in the first slot and compatible with direct sums, hence the class of objects for which
![]() $p^*$
is an isomorphism is localizing. Thus, we can assume
$p^*$
is an isomorphism is localizing. Thus, we can assume
![]() $P(A)=\operatorname {\mathrm {Ind}}_H^G(D)$
for some compact action
$P(A)=\operatorname {\mathrm {Ind}}_H^G(D)$
for some compact action
![]() $H\subseteq G$
. Then, by using the induction-restriction adjunction and exchanging
$H\subseteq G$
. Then, by using the induction-restriction adjunction and exchanging
![]() $p^*$
and
$p^*$
and
![]() $\operatorname {\mathrm {Ind}}_H^G$
, we can reduce ourselves to proving that
$\operatorname {\mathrm {Ind}}_H^G$
, we can reduce ourselves to proving that
is an isomorphism (we are using notation from Equation (7)). The subgroupoid H is a compact action and it satisfies a strong form of the Baum–Connes conjecture; in particular it admits a Dirac-dual-Dirac triple as in [Reference Emerson and Meyer21, Definition 4.38]. Then [Reference Emerson and Meyer21, Theorem 4.34 & 4.39] imply that Equation (10) is an isomorphism. More concretely, if
![]() $P^\prime $
a proper
$P^\prime $
a proper
![]() $C^*$
-algebra which is also the cellular approximation of
$C^*$
-algebra which is also the cellular approximation of
![]() $C(H^{(0)})$
, then the inverse map is given by
$C(H^{(0)})$
, then the inverse map is given by
![]() $[x]\mapsto p_*(P^\prime \otimes _{U^\rho } [x])$
(cf. [Reference Emerson and Meyer21, Lemma 4.31]).
$[x]\mapsto p_*(P^\prime \otimes _{U^\rho } [x])$
(cf. [Reference Emerson and Meyer21, Lemma 4.31]).
Remark 3.13. The second part of the proof above should be viewed as a statement about the H-equivariant ‘contractibility’ of
![]() $\underline {E} G$
(cf. [Reference Meyer and Nest40, Theorem 7.1] and [Reference Tu58, Theorem 11.3]). Concerning the map in Equation (10), if the G-cellular approximation P was
$\underline {E} G$
(cf. [Reference Meyer and Nest40, Theorem 7.1] and [Reference Tu58, Theorem 11.3]). Concerning the map in Equation (10), if the G-cellular approximation P was
![]() $\operatorname {\mathrm {KK}}^G$
-equivalent to a proper
$\operatorname {\mathrm {KK}}^G$
-equivalent to a proper
![]() $C^*$
-algebra, then the map
$C^*$
-algebra, then the map
![]() $[x]\mapsto p_*(P\otimes _{\underline {E} G} [x])$
would provide an inverse already in
$[x]\mapsto p_*(P\otimes _{\underline {E} G} [x])$
would provide an inverse already in
![]() $\operatorname {\mathrm {KK}}^G$
. This holds for many groupoids, as is shown by Theorem 3.7; however, by passing to H via the adjunction, we do not need to assume that P is proper in the theorem above.
$\operatorname {\mathrm {KK}}^G$
. This holds for many groupoids, as is shown by Theorem 3.7; however, by passing to H via the adjunction, we do not need to assume that P is proper in the theorem above.
The relation to the ordinary Baum–Connes conjecture is explained by means of the following result (compare with [Reference Emerson and Meyer21, Theorem 6.12]; see also [Reference Meyer and Nest40] for action groupoids). The left-hand side of the Baum–Connes assembly map (with coefficients in A) is often denoted
![]() $K_*^{\mathrm {top}}(G;A)$
and is defined as
$K_*^{\mathrm {top}}(G;A)$
and is defined as
![]() $\varinjlim _{Y \subseteq \underline {E} G} \operatorname {\mathrm {KK}}^G(C_0(Y),A)$
, the limit ranging over the directed set of G-invariant G-compact subspaces of
$\varinjlim _{Y \subseteq \underline {E} G} \operatorname {\mathrm {KK}}^G(C_0(Y),A)$
, the limit ranging over the directed set of G-invariant G-compact subspaces of
![]() $\underline {E} G$
.
$\underline {E} G$
.
Theorem 3.14. Let
![]() $A\in \operatorname {\mathrm {KK}}^G$
be a G-
$A\in \operatorname {\mathrm {KK}}^G$
be a G-
![]() $C^*$
-algebra, and denote by
$C^*$
-algebra, and denote by
![]() $\mu ^G_A$
the associated assembly map. Let
$\mu ^G_A$
the associated assembly map. Let
![]() $D_A\colon P(A)\to A$
be the natural
$D_A\colon P(A)\to A$
be the natural
![]() $\operatorname {\mathrm {KK}}^G$
-morphism. The indicated maps in the following commuting diagram are isomorphisms.
$\operatorname {\mathrm {KK}}^G$
-morphism. The indicated maps in the following commuting diagram are isomorphisms.

Proof. The functor
![]() $K_*^{\mathrm {top}}(G;\,-)$
is homological, it commutes with direct sums and by the vertical isomorphism in Theorem 3.12, it is functorial for maps in
$K_*^{\mathrm {top}}(G;\,-)$
is homological, it commutes with direct sums and by the vertical isomorphism in Theorem 3.12, it is functorial for maps in
![]() $\operatorname {\mathrm {RKK}}^G(\underline {E} G; A,B)$
. The same theorem also implies
$\operatorname {\mathrm {RKK}}^G(\underline {E} G; A,B)$
. The same theorem also implies
![]() $p^*(D_A)$
is invertible, thus the left map in the diagram above is an isomorphism. Now,
$p^*(D_A)$
is invertible, thus the left map in the diagram above is an isomorphism. Now,
![]() $\mu ^G_{P(A)}$
is an isomorphism if the Baum–Connes conjecture holds for compactly induced coefficient algebras. This is proved in [Reference Chabert and Echterhoff14] (see also [Reference Chabert, Echterhoff and Oyono-Oyono16] and [Reference Emerson and Meyer21, Theorem 4.48]).
$\mu ^G_{P(A)}$
is an isomorphism if the Baum–Connes conjecture holds for compactly induced coefficient algebras. This is proved in [Reference Chabert and Echterhoff14] (see also [Reference Chabert, Echterhoff and Oyono-Oyono16] and [Reference Emerson and Meyer21, Theorem 4.48]).
Combining
![]() $\langle \mathcal {C}\mathcal {I}\rangle =\langle \mathcal {P} r\rangle $
and Tu’s Theorem 3.7, we obtain the following.
$\langle \mathcal {C}\mathcal {I}\rangle =\langle \mathcal {P} r\rangle $
and Tu’s Theorem 3.7, we obtain the following.
Corollary 3.15. Suppose G is a second countable, locally compact, Hausdorff groupoid. Assume that there exists a proper G-
![]() $C^*$
-algebra P such that
$C^*$
-algebra P such that
![]() $P\cong C_0(G^0)$
in
$P\cong C_0(G^0)$
in
![]() $\operatorname {\mathrm {KK}}^G$
. Then G satisfies the strong Baum–Connes conjecture with coefficients.
$\operatorname {\mathrm {KK}}^G$
. Then G satisfies the strong Baum–Connes conjecture with coefficients.
The previous corollary applies in particular to all amenable groupoids and more generally to all a-T-menable groupoids (a-T-menability is also known as the Haagerup property) by [Reference Tu58, Proposition 3.8].
The following lemma shows that we can use Theorem 3.10 to rephrase the definition of
![]() $\mathcal {N}$
as the category of contractible objects with respect to the kernel of the joint restriction functor to all proper open subgroupoids (instead of just the compact actions).
$\mathcal {N}$
as the category of contractible objects with respect to the kernel of the joint restriction functor to all proper open subgroupoids (instead of just the compact actions).
Lemma 3.16. Let
![]() $B\in \operatorname {\mathrm {KK}}^G$
. Then
$B\in \operatorname {\mathrm {KK}}^G$
. Then
![]() $B\in \mathcal {N}$
if and only if
$B\in \mathcal {N}$
if and only if
![]() $\operatorname {\mathrm {Res}}_G^H(\mathrm {id}_B)=0$
for all proper open subgroupoids
$\operatorname {\mathrm {Res}}_G^H(\mathrm {id}_B)=0$
for all proper open subgroupoids
![]() $H\subseteq G$
.
$H\subseteq G$
.
Proof. Suppose that
![]() $B\in \mathcal {N}$
. By Theorem 3.10 and the fact that
$B\in \mathcal {N}$
. By Theorem 3.10 and the fact that
![]() $(\langle \mathcal {C}\mathcal {I}\rangle ,\mathcal {N})$
is a pair of complementary subcategories, we get that
$(\langle \mathcal {C}\mathcal {I}\rangle ,\mathcal {N})$
is a pair of complementary subcategories, we get that
![]() $\operatorname {\mathrm {KK}}^G(A,B)=0$
for all
$\operatorname {\mathrm {KK}}^G(A,B)=0$
for all
![]() $A\in \mathcal {P} r$
. If
$A\in \mathcal {P} r$
. If
![]() $H\subseteq G$
is a proper open subgroupoid, then
$H\subseteq G$
is a proper open subgroupoid, then
![]() $\operatorname {\mathrm {Ind}}_H^G D\in \mathcal {P} r$
for all
$\operatorname {\mathrm {Ind}}_H^G D\in \mathcal {P} r$
for all
![]() $D\in \operatorname {\mathrm {KK}}^H$
. Using the induction-restriction adjunction, we get that
$D\in \operatorname {\mathrm {KK}}^H$
. Using the induction-restriction adjunction, we get that
for all
![]() $D\in \operatorname {\mathrm {KK}}^H$
. If we apply this to
$D\in \operatorname {\mathrm {KK}}^H$
. If we apply this to
![]() $D=\operatorname {\mathrm {Res}}_G^H(B)$
, we get, in particular, that
$D=\operatorname {\mathrm {Res}}_G^H(B)$
, we get, in particular, that
![]() $\operatorname {\mathrm {Res}}_G^H(\mathrm {id}_B)=\mathrm {id}_{\operatorname {\mathrm {Res}}_G^H B}=0$
. The converse follows from the definition of
$\operatorname {\mathrm {Res}}_G^H(\mathrm {id}_B)=\mathrm {id}_{\operatorname {\mathrm {Res}}_G^H B}=0$
. The converse follows from the definition of
![]() $\mathcal {N}$
and the fact that each
$\mathcal {N}$
and the fact that each
![]() $Q\in \mathcal {F}$
is a proper open subgroupoid of G.
$Q\in \mathcal {F}$
is a proper open subgroupoid of G.
4 Applications
4.1 The UCT
The article [Reference Bönicke and Dell’Aiera12] established a connection between the Baum–Connes conjecture for groupoids and the Künneth formula for groupoid crossed products. Now, the UCT introduced in [Reference Rosenberg and Schochet55] is formally stronger than the Künneth formula, so philosophically speaking it may not come as a surprise that a similar relation exists between the strong Baum–Connes conjecture and the UCT.
Proposition 4.1. Let
![]() $(A,G,\alpha )$
be a groupoid dynamical system with A type I. Then
$(A,G,\alpha )$
be a groupoid dynamical system with A type I. Then
![]() $P(A)\rtimes _r G$
satisfies the UCT. If furthermore G satisfies the strong Baum–Connes conjecture, then
$P(A)\rtimes _r G$
satisfies the UCT. If furthermore G satisfies the strong Baum–Connes conjecture, then
![]() $A\rtimes _r G$
satisfies the UCT.
$A\rtimes _r G$
satisfies the UCT.
Proof. If A is a type I
![]() $\mathrm {C}^*$
-algebra and H is a proper groupoid, the crossed product
$\mathrm {C}^*$
-algebra and H is a proper groupoid, the crossed product
![]() $A\rtimes H$
is type I by [Reference Tu58, Proposition 10.3]. Given A as in the claim, and
$A\rtimes H$
is type I by [Reference Tu58, Proposition 10.3]. Given A as in the claim, and
![]() $H\subseteq G$
a proper open subgroupoid acting on A, then
$H\subseteq G$
a proper open subgroupoid acting on A, then
![]() $C_0(G_{H^0})\otimes A$
is type I,
$C_0(G_{H^0})\otimes A$
is type I,
![]() $C_0(G_{H^0})\otimes _{H^0} A$
is type I (because it is a quotient) and
$C_0(G_{H^0})\otimes _{H^0} A$
is type I (because it is a quotient) and
![]() $L_H(A):= \operatorname {\mathrm {Ind}}_H^G\operatorname {\mathrm {Res}}_G^H(A)$
is type I as well. Hence,
$L_H(A):= \operatorname {\mathrm {Ind}}_H^G\operatorname {\mathrm {Res}}_G^H(A)$
is type I as well. Hence,
![]() $L_H(A)$
belongs to the bootstrap class. Since
$L_H(A)$
belongs to the bootstrap class. Since
![]() $L_H(A)\rtimes _r G$
is Morita equivalent to
$L_H(A)\rtimes _r G$
is Morita equivalent to
![]() $A\rtimes _r H$
and
$A\rtimes _r H$
and
![]() $P(A)\rtimes _r G$
belongs to the localising subcategory of
$P(A)\rtimes _r G$
belongs to the localising subcategory of
![]() $\operatorname {\mathrm {KK}}$
generated by
$\operatorname {\mathrm {KK}}$
generated by
it follows that
![]() $P(A)\rtimes _r G$
belongs to the bootstrap class as well.
$P(A)\rtimes _r G$
belongs to the bootstrap class as well.
Since the bootstrap class is closed under
![]() $\operatorname {\mathrm {KK}}$
-equivalence, the strong Baum–Connes conjecture yields the result.
$\operatorname {\mathrm {KK}}$
-equivalence, the strong Baum–Connes conjecture yields the result.
We do in particular obtain the following corollary, generalising [Reference Barlak and Li3, Reference Kwaśniewski, Li and Skalski28]. To state it, recall that a twist over G is a central extension
and that one can associate the twisted groupoid
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C_r^*(G,\Sigma )$
to these data (see [Reference Renault54] for the details of this construction).
$C_r^*(G,\Sigma )$
to these data (see [Reference Renault54] for the details of this construction).
Corollary 4.2. Let
![]() $\Sigma $
be a twist over an étale groupoid G. If G satisfies the strong Baum–Connes conjecture, then
$\Sigma $
be a twist over an étale groupoid G. If G satisfies the strong Baum–Connes conjecture, then
![]() $C_r^*(G,\Sigma )$
satisfies the UCT.
$C_r^*(G,\Sigma )$
satisfies the UCT.
Proof. Apply the stabilisation trick [Reference van Erp and Williams61, Proposition 5.1] to replace
![]() $C_r^*(G,\Sigma )$
up to Morita-equivalence by
$C_r^*(G,\Sigma )$
up to Morita-equivalence by
![]() $K(H)\rtimes _r G$
, where
$K(H)\rtimes _r G$
, where
![]() $K(H)$
denotes the algebra of compact operators on a suitable Hilbert
$K(H)$
denotes the algebra of compact operators on a suitable Hilbert
![]() $C_0(G^0)$
-module. As
$C_0(G^0)$
-module. As
![]() $K(H)$
is type I, the previous proposition applies.
$K(H)$
is type I, the previous proposition applies.
4.2 The going-down principle
We generalize some results obtained by the first author for ample groupoids [Reference Bönicke10] to the general étale case.
Theorem 4.3. Suppose there is an element
![]() $f\in \operatorname {\mathrm {KK}}^G(A,B)$
such that
$f\in \operatorname {\mathrm {KK}}^G(A,B)$
such that
is an isomorphism for all
![]() $H\in \mathcal {F}$
and separable H-
$H\in \mathcal {F}$
and separable H-
![]() $C^*$
-algebras D. Then f is a weak equivalence, and in particular the Kasparov product induces an isomorphism
$C^*$
-algebras D. Then f is a weak equivalence, and in particular the Kasparov product induces an isomorphism
Proof. Using the induction-restriction adjunction the hypothesis is equivalent to the following map being an isomorphism for any
![]() $\tilde {D}\in \mathcal {C}\mathcal {I}$
,
$\tilde {D}\in \mathcal {C}\mathcal {I}$
,
Applying the functor
![]() $\operatorname {\mathrm {KK}}^G(\tilde {D}, -)$
to a mapping cone triangle for f and using the five lemma we deduce that
$\operatorname {\mathrm {KK}}^G(\tilde {D}, -)$
to a mapping cone triangle for f and using the five lemma we deduce that
![]() $\operatorname {\mathrm {KK}}^G(\tilde {D}, \operatorname {\mathrm {Cone}}(f))\cong 0$
for all
$\operatorname {\mathrm {KK}}^G(\tilde {D}, \operatorname {\mathrm {Cone}}(f))\cong 0$
for all
![]() $\tilde {D}$
in
$\tilde {D}$
in
![]() $\langle \mathcal {C}\mathcal {I}\rangle $
. Now, by Theorem 1.12 we get
$\langle \mathcal {C}\mathcal {I}\rangle $
. Now, by Theorem 1.12 we get
![]() $\operatorname {\mathrm {Cone}}(f)\in N_{\mathcal {I}}$
. The rest follows from Theorems 3.12 and 3.14.
$\operatorname {\mathrm {Cone}}(f)\in N_{\mathcal {I}}$
. The rest follows from Theorems 3.12 and 3.14.
If we are only interested in studying the assembly map, then we might want to prove Equation (12) without necessarily proving that A and B have isomorphic cellular approximations. The following result is a version of the previous one ‘after
![]() $K_*(-\rtimes G)$
’, and it can be proved with slightly weaker assumptions.
$K_*(-\rtimes G)$
’, and it can be proved with slightly weaker assumptions.
Theorem 4.4 (cf. [Reference Bönicke10, Theorem 7.10]).
Let
![]() $f\in \mathrm {KK}^G(A_1,A_2)$
be an element such that the induced map
$f\in \mathrm {KK}^G(A_1,A_2)$
be an element such that the induced map
is an isomorphism for all proper open subgroupoids
![]() $H\subseteq Q$
for all
$H\subseteq Q$
for all
![]() $Q\in \mathcal {F}$
. Then
$Q\in \mathcal {F}$
. Then
is an isomorphism.
The proof requires some preparation. For a subgroupoid
![]() $H\subseteq G$
let
$H\subseteq G$
let
![]() $L_H:= \mathrm {Ind}_H^G\circ \mathrm {Res}_G^H$
. Consider the class
$L_H:= \mathrm {Ind}_H^G\circ \mathrm {Res}_G^H$
. Consider the class
![]() $\mathcal {P}_0$
of G-algebras of the form
$\mathcal {P}_0$
of G-algebras of the form
![]() $(L_{H_n}\circ \cdots \circ L_{H_1})(C_0(G^0))$
for
$(L_{H_n}\circ \cdots \circ L_{H_1})(C_0(G^0))$
for
![]() $n\in \mathbb N$
and
$n\in \mathbb N$
and
![]() $H_i\in \mathcal {F}$
.
$H_i\in \mathcal {F}$
.
Lemma 4.5.
![]() $P(C_0(G^0))\in \langle \mathcal {P}_0\rangle $
.
$P(C_0(G^0))\in \langle \mathcal {P}_0\rangle $
.
Proof. By [Reference Meyer39, Proposition 3.18], the
![]() $\mathcal {CI}$
-cellular approximation
$\mathcal {CI}$
-cellular approximation
![]() $P(C_0(G^0))$
can be computed as the homotopy limit of a phantom castle over
$P(C_0(G^0))$
can be computed as the homotopy limit of a phantom castle over
![]() $C_0(G^0)$
. Hence, it is enough to show that such a phantom castle can be found inside
$C_0(G^0)$
. Hence, it is enough to show that such a phantom castle can be found inside
![]() $\langle \mathcal {P}_0\rangle $
. Using the fact that
$\langle \mathcal {P}_0\rangle $
. Using the fact that
![]() $\langle \mathcal {P}_0\rangle $
is localising, an inspection of the construction of such a phantom castle in [Reference Meyer39] shows that it suffices to show that
$\langle \mathcal {P}_0\rangle $
is localising, an inspection of the construction of such a phantom castle in [Reference Meyer39] shows that it suffices to show that
![]() $C_0(G^0)$
admits a projective resolution by objects in
$C_0(G^0)$
admits a projective resolution by objects in
![]() $\langle \mathcal {P}_0\rangle $
. The standard way to construct such a projective resolution is by considering the algebras
$\langle \mathcal {P}_0\rangle $
. The standard way to construct such a projective resolution is by considering the algebras
![]() $(F^\dagger \circ F)^n(C_0(G^0))$
for
$(F^\dagger \circ F)^n(C_0(G^0))$
for
![]() $n\geq 1$
.
$n\geq 1$
.
We will prove that this resolution is contained in
![]() $\langle \mathcal {P}_0\rangle $
by induction. First, we have
$\langle \mathcal {P}_0\rangle $
by induction. First, we have
![]() $(F^\dagger \circ F)(C_0(G^0))=\bigoplus _{H\in \mathcal {F}} \mathrm {Ind}_H^G \mathrm {Res}_G^H C_0(G^0)\in \langle \mathcal {P}_0\rangle $
. Assuming now that the claim holds for
$(F^\dagger \circ F)(C_0(G^0))=\bigoplus _{H\in \mathcal {F}} \mathrm {Ind}_H^G \mathrm {Res}_G^H C_0(G^0)\in \langle \mathcal {P}_0\rangle $
. Assuming now that the claim holds for
![]() $n-1$
, we compute
$n-1$
, we compute
and the latter is contained in
![]() $\langle \mathcal {P}_0\rangle $
since
$\langle \mathcal {P}_0\rangle $
since
![]() $L_H(\langle \mathcal {P}_0\rangle )\subseteq \langle \mathcal {P}_0\rangle $
(we have
$L_H(\langle \mathcal {P}_0\rangle )\subseteq \langle \mathcal {P}_0\rangle $
(we have
![]() $L_H(\mathcal {P}_0)\subseteq \mathcal {P}_0$
by definition of
$L_H(\mathcal {P}_0)\subseteq \mathcal {P}_0$
by definition of
![]() $\mathcal {P}_0$
and hence the general statement follows from the fact that
$\mathcal {P}_0$
and hence the general statement follows from the fact that
![]() $L_H$
is triangulated and compatible with direct sums).
$L_H$
is triangulated and compatible with direct sums).
Proof of Theorem 4.4.
We will show that
is an isomorphism for all
![]() $B\in \mathcal {P}_0$
. Once this is proven, we can complete the proof as follows: since K-theory is a homological functor (compatible with direct sums), these isomorphisms imply that Equation (13) is also an isomorphism for
$B\in \mathcal {P}_0$
. Once this is proven, we can complete the proof as follows: since K-theory is a homological functor (compatible with direct sums), these isomorphisms imply that Equation (13) is also an isomorphism for
![]() $B\in \langle \mathcal {P}_0\rangle $
by a routine argument involving the five lemma.
$B\in \langle \mathcal {P}_0\rangle $
by a routine argument involving the five lemma.
In particular, we can take
![]() $B=P(C_0(G^0))$
by the previous lemma. Noting further that
$B=P(C_0(G^0))$
by the previous lemma. Noting further that
![]() $P(A)\rtimes G\cong P(A)\rtimes _r G$
in
$P(A)\rtimes G\cong P(A)\rtimes _r G$
in
![]() $\mathrm {KK}$
, the proof will be complete. Thus, in what follows we show that Equation (13) is an isomorphism for all
$\mathrm {KK}$
, the proof will be complete. Thus, in what follows we show that Equation (13) is an isomorphism for all
![]() $B\in \mathcal {P}_0$
.
$B\in \mathcal {P}_0$
.
Step 1: We will first prove that Equation (13) is an isomorphism for
![]() $B=L_H(C_0(G^0))=C_0(G/H)$
whenever
$B=L_H(C_0(G^0))=C_0(G/H)$
whenever
![]() $H\subseteq Q$
for some
$H\subseteq Q$
for some
![]() $Q\in \mathcal {F}$
.. In this case, we have natural G-equivariant isomorphisms
$Q\in \mathcal {F}$
.. In this case, we have natural G-equivariant isomorphisms
and hence
![]() $(B\otimes _{G^0} A_i)\rtimes G$
is Morita equivalent to
$(B\otimes _{G^0} A_i)\rtimes G$
is Morita equivalent to
![]() $\mathrm {Res}_G^H(A_i)\rtimes H$
. Thus, this case follows directly from the assumption.
$\mathrm {Res}_G^H(A_i)\rtimes H$
. Thus, this case follows directly from the assumption.
Step 2: Suppose
![]() $B=L_K(C_0(X))=\mathrm {Ind}_K^G C_0(X|_{K^0})$
, where X is any second countable proper étale G-space with anchor map
$B=L_K(C_0(X))=\mathrm {Ind}_K^G C_0(X|_{K^0})$
, where X is any second countable proper étale G-space with anchor map
![]() $p:X\rightarrow G^0$
, and
$p:X\rightarrow G^0$
, and
![]() $K\in \mathcal {F}$
. We claim that Equation (13) is an isomorphism for this choice of B. Let
$K\in \mathcal {F}$
. We claim that Equation (13) is an isomorphism for this choice of B. Let
![]() $\mathcal {B}$
be a countable basis for the topology of
$\mathcal {B}$
be a countable basis for the topology of
![]() $X|_{K^0}$
consisting of open subsets of
$X|_{K^0}$
consisting of open subsets of
![]() $X|_{K^0}$
on which p restricts to a homeomorphism. Then we can write
$X|_{K^0}$
on which p restricts to a homeomorphism. Then we can write
Since
![]() $\mathcal {B}$
is countable, we may enumerate its elements writing
$\mathcal {B}$
is countable, we may enumerate its elements writing
![]() $\mathcal {B}=\{S_n\mid n\in \mathbb N\}$
. Let
$\mathcal {B}=\{S_n\mid n\in \mathbb N\}$
. Let
![]() $X_n:=\bigcup _{i=1}^n KS_n$
. Then
$X_n:=\bigcup _{i=1}^n KS_n$
. Then
![]() $X_n$
is an open K-invariant subset of X. Moreover,
$X_n$
is an open K-invariant subset of X. Moreover,
![]() $C_0(X|_{K^0})=\varinjlim _n C_0(X_n)$
where the connecting maps are just given by the canonical inclusions. Since the induction functor, tensor products and the maximal crossed product as well as K-theory are all compatible with inductive limits, it suffices to show that Equation (13) is an isomorphism for
$C_0(X|_{K^0})=\varinjlim _n C_0(X_n)$
where the connecting maps are just given by the canonical inclusions. Since the induction functor, tensor products and the maximal crossed product as well as K-theory are all compatible with inductive limits, it suffices to show that Equation (13) is an isomorphism for
![]() $B=\mathrm {Ind}_K^G C_0(X_n)$
. We will do this by induction on n.
$B=\mathrm {Ind}_K^G C_0(X_n)$
. We will do this by induction on n.
For
![]() $n=1$
, observe that for every
$n=1$
, observe that for every
![]() $S\in \mathcal {B}$
there are identifications
$S\in \mathcal {B}$
there are identifications
![]() $KS\cong K\times _{\mathrm {Stab}(S)} S$
, where
$KS\cong K\times _{\mathrm {Stab}(S)} S$
, where
![]() $\mathrm {Stab}(S)$
is the proper open subgroupoid of K defined as
$\mathrm {Stab}(S)$
is the proper open subgroupoid of K defined as
![]() $\mathrm {Stab}(S)=\{g\in K\mid gS\subseteq S\}$
. Note that the restriction of the anchor map induces a homeomorphism
$\mathrm {Stab}(S)=\{g\in K\mid gS\subseteq S\}$
. Note that the restriction of the anchor map induces a homeomorphism
![]() $S\cong \mathrm {Stab}(S)^0$
. It follows that
$S\cong \mathrm {Stab}(S)^0$
. It follows that
and using induction in stages we conclude that
Since
![]() $\mathrm {Stab}(S)$
is a proper open subgroupoid of
$\mathrm {Stab}(S)$
is a proper open subgroupoid of
![]() $K\in \mathcal {F}$
, it follows that Equation (13) is an isomorphism for
$K\in \mathcal {F}$
, it follows that Equation (13) is an isomorphism for
![]() $B=\mathrm {Ind}_K^G C_0(KS)$
by Step 1 above.
$B=\mathrm {Ind}_K^G C_0(KS)$
by Step 1 above.
Next, consider a union
![]() $KS\cup KT$
for
$KS\cup KT$
for
![]() $S,T\in \mathcal {B}$
. Then we have two short exact sequences of K-algebras
$S,T\in \mathcal {B}$
. Then we have two short exact sequences of K-algebras
and
Using that the functors
![]() $\mathrm {Ind}_K^G -$
,
$\mathrm {Ind}_K^G -$
,
![]() $(-\, \otimes _{G^0} A_i)$
, and
$(-\, \otimes _{G^0} A_i)$
, and
![]() $(-\,\rtimes G)$
are all exact, we can apply them (in this order) to the above sequences and the result remains exact. Hence, we obtain induced six-term exact sequences in K-theory, which can be compared using the maps induced by f. Thus, using the case
$(-\,\rtimes G)$
are all exact, we can apply them (in this order) to the above sequences and the result remains exact. Hence, we obtain induced six-term exact sequences in K-theory, which can be compared using the maps induced by f. Thus, using the case
![]() $n=1$
above, to prove the claim for the union
$n=1$
above, to prove the claim for the union
![]() $KS\cup KT$
for
$KS\cup KT$
for
![]() $S,T\in \mathcal {B}$
, it suffices to prove it for
$S,T\in \mathcal {B}$
, it suffices to prove it for
![]() $KS\cap KT$
. To this end, note that
$KS\cap KT$
. To this end, note that
Considering the subgroupoid
![]() $\mathrm {Stab}(S\cap KT)$
of K defined as above, we can employ the same arguments as in the case
$\mathrm {Stab}(S\cap KT)$
of K defined as above, we can employ the same arguments as in the case
![]() $n=1$
to conclude that
$n=1$
to conclude that
![]() $C_0(KS\cap KT))\cong \mathrm {Ind}_{\mathrm {Stab}(S\cap KT)}^K(C_0(\mathrm {Stab}(S\cap KT)^0))$
, and hence using induction in stages again, we conclude that Equation (13) is an isomorphism for
$C_0(KS\cap KT))\cong \mathrm {Ind}_{\mathrm {Stab}(S\cap KT)}^K(C_0(\mathrm {Stab}(S\cap KT)^0))$
, and hence using induction in stages again, we conclude that Equation (13) is an isomorphism for
Inductively, we can continue in this way to prove the isomorphism in line (13) for all
![]() $B=\mathrm {Ind}_K^G C_0(X_n)$
and hence complete step 2 by passing to the inductive limit.
$B=\mathrm {Ind}_K^G C_0(X_n)$
and hence complete step 2 by passing to the inductive limit.
Step 3: We can now prove that Equation (13) is an isomorphism for all
![]() $B\in \mathcal {P}_0$
by induction. The base case is contained in Step 1 above. For the induction step, note that
$B\in \mathcal {P}_0$
by induction. The base case is contained in Step 1 above. For the induction step, note that
![]() $L_{H_n}\cdots L_{H_1}(C_0(G^0))\cong C_0(G/H_n\times _{G^0}\ldots \times _{G^0}G/H_1)$
and observe that the space
$L_{H_n}\cdots L_{H_1}(C_0(G^0))\cong C_0(G/H_n\times _{G^0}\ldots \times _{G^0}G/H_1)$
and observe that the space
![]() $X:=G/H_n\times _{G^0}\ldots \times _{G^0}G/H_1$
is an étale proper G-space. Thus, we can just apply Step 2 to complete the proof.
$X:=G/H_n\times _{G^0}\ldots \times _{G^0}G/H_1$
is an étale proper G-space. Thus, we can just apply Step 2 to complete the proof.
This result directly allows to generalize several results obtained by the first author for ample groupoids to the general étale case.
4.2.1 Homotopies of twists
Let G be an étale groupoid. A homotopy of twists is a twist over
![]() $G\times [0,1]$
, that is, a central extension of the form
$G\times [0,1]$
, that is, a central extension of the form
Theorem 4.6. Let G be a second countable étale groupoid satisfying the Baum–Connes conjecture with coefficients. If
![]() $\Sigma $
is a homotopy of twists over G, then for each
$\Sigma $
is a homotopy of twists over G, then for each
![]() $t\in [0,1]$
the canonical map
$t\in [0,1]$
the canonical map
![]() $q_t:C_r^*(G\times [0,1],\Sigma )\rightarrow C_r^*(G,\Sigma _t)$
induces an isomorphism in K-theory.
$q_t:C_r^*(G\times [0,1],\Sigma )\rightarrow C_r^*(G,\Sigma _t)$
induces an isomorphism in K-theory.
Proof . The idea of the proof is the same as for the main result in [Reference Bönicke11]: Using a groupoid version of the Packer–Raeburn stabilisation trick and the going-down principle (Theorem 4.4), one only has to prove the result for all proper open subgroupoids of all elements
![]() $H\in \mathcal {F}$
in place of G. Recall that all the groupoids
$H\in \mathcal {F}$
in place of G. Recall that all the groupoids
![]() $H\in \mathcal {F}$
are (isomorphic to) transformation groupoids of finite groups. Hence, if the original homotopy of twists over G is topologically trivial in the sense that the map j has a continuous section (this means that the twist is equivalent to a continuous
$H\in \mathcal {F}$
are (isomorphic to) transformation groupoids of finite groups. Hence, if the original homotopy of twists over G is topologically trivial in the sense that the map j has a continuous section (this means that the twist is equivalent to a continuous
![]() $2$
-cocycle), one can apply an earlier result of Gillaspy [Reference Gillaspy22] to finish the proof. In the setting of ample groupoids treated in [Reference Bönicke11], the requirement that the twist is topologically trivial is not actually a restriction by [Reference Bönicke11, Proposition 4.2].
$2$
-cocycle), one can apply an earlier result of Gillaspy [Reference Gillaspy22] to finish the proof. In the setting of ample groupoids treated in [Reference Bönicke11], the requirement that the twist is topologically trivial is not actually a restriction by [Reference Bönicke11, Proposition 4.2].
In the étale setting twists are no longer automatically topologically trivial, so instead we use a refinement of the going-down principle. Observe that the constructions and results from the previous section allow some flexibility in choosing the family
![]() $\mathcal {F}$
of subgroupoids of G. Indeed, if
$\mathcal {F}$
of subgroupoids of G. Indeed, if
![]() $\mathcal {F}'$
is another family of subgroupoids of G with the property that every proper action of G is locally induced by members of
$\mathcal {F}'$
is another family of subgroupoids of G with the property that every proper action of G is locally induced by members of
![]() $\mathcal {F}'$
, we can replace
$\mathcal {F}'$
, we can replace
![]() $\mathcal {F}$
by
$\mathcal {F}$
by
![]() $\mathcal {F}'$
in all the results of Section 3 and hence also in Theorem 4.3.
$\mathcal {F}'$
in all the results of Section 3 and hence also in Theorem 4.3.
Now, given a homotopy of twists with quotient map
![]() $j: \Sigma \rightarrow G\times [0,1]$
we claim that there exists a family
$j: \Sigma \rightarrow G\times [0,1]$
we claim that there exists a family
![]() $\mathcal {F}'$
of compact actions for G as above with the additional property that the restricted twist
$\mathcal {F}'$
of compact actions for G as above with the additional property that the restricted twist
![]() $j^{-1}(H\times [0,1])\rightarrow H\times [0,1]$
(this is now a homotopy of twists over H) admits a continuous cross section.
$j^{-1}(H\times [0,1])\rightarrow H\times [0,1]$
(this is now a homotopy of twists over H) admits a continuous cross section.
Let us explain how this works: By the proof of [Reference Bönicke11, Proposition 4.2] every
![]() $g\in G$
admits an open neighbourhood V such that there exists a local section
$g\in G$
admits an open neighbourhood V such that there exists a local section
![]() $V\times [0,1]\rightarrow \Sigma $
of j. Now, given a proper action of G we will proceed as in the proof of Proposition 3.2, but (in the notation of that proof) we additionally choose the bisections
$V\times [0,1]\rightarrow \Sigma $
of j. Now, given a proper action of G we will proceed as in the proof of Proposition 3.2, but (in the notation of that proof) we additionally choose the bisections
![]() $W_g$
to be the domains of local sections of j as above. Since the
$W_g$
to be the domains of local sections of j as above. Since the
![]() $W_g$
can be assumed to be pairwise disjoint and the remaining construction in the proof of Proposition 3.2 just shrinks them further, we can patch the resulting finitely many local sections
$W_g$
can be assumed to be pairwise disjoint and the remaining construction in the proof of Proposition 3.2 just shrinks them further, we can patch the resulting finitely many local sections
![]() $W_g\times [0,1]\rightarrow \Sigma $
together to obtain the desired continuous section
$W_g\times [0,1]\rightarrow \Sigma $
together to obtain the desired continuous section
![]() $H\times [0,1]\rightarrow \Sigma $
. Since H is of the form
$H\times [0,1]\rightarrow \Sigma $
. Since H is of the form
![]() $\Gamma \ltimes U$
for a finite group
$\Gamma \ltimes U$
for a finite group
![]() $\Gamma $
and an open subset
$\Gamma $
and an open subset
![]() $U\subseteq G^0$
we are again the position to apply Gillaspy’s result to conclude that
$U\subseteq G^0$
we are again the position to apply Gillaspy’s result to conclude that
![]() $q_t$
induces an isomorphism for all
$q_t$
induces an isomorphism for all
![]() $H\in \mathcal {F}'$
. To lift the result from this to all of G, one can follow the arguments in [Reference Bönicke11] again.
$H\in \mathcal {F}'$
. To lift the result from this to all of G, one can follow the arguments in [Reference Bönicke11] again.
4.3 Amenability at infinity
Recall that a locally compact Hausdorff groupoid G is called amenable at infinity, if there exists a G-space Y with proper momentum map
![]() $p:Y\rightarrow G^{0}$
and such that
$p:Y\rightarrow G^{0}$
and such that
![]() $G\ltimes Y$
is (topologically) amenable.
$G\ltimes Y$
is (topologically) amenable.
It is called strongly amenable at infinity if, in addition, the momentum map p admits a continuous cross section. Since p is a proper map, it induces an equivariant
![]() $\ast $
-homomorphism
$\ast $
-homomorphism
![]() $C_0(G^0)\rightarrow C_0(Y)$
and can hence be viewed as a morphism
$C_0(G^0)\rightarrow C_0(Y)$
and can hence be viewed as a morphism
It was shown in [Reference Anantharaman-Delaroche2, Lemma 4.9] that if G is strongly amenable at infinity, then the space Y witnessing this can be chosen second countable. Replacing this space further by the space of probability measures on Y supported in fibres we may also assume that each fibre (with respect to p) is a convex space and that G acts by affine transformations. The following result is [Reference Bönicke10, Proposition 8.2]:
Proposition 4.7. Let G be a second countable étale groupoid, and let Y be a fibrewise convex space on which G acts by affine transformations. Suppose further that the anchor map
![]() $p:Y\rightarrow G^{0}$
admits a continuous cross section. If
$p:Y\rightarrow G^{0}$
admits a continuous cross section. If
![]() $H\subseteq G$
is a proper open subgroupoid, then the restriction of p to
$H\subseteq G$
is a proper open subgroupoid, then the restriction of p to
![]() $p^{-1}(H^{0})$
is an H-equivariant homotopy equivalence. In particular,
$p^{-1}(H^{0})$
is an H-equivariant homotopy equivalence. In particular,
![]() $\operatorname {\mathrm {Res}}_G^H(\mathbf {p})\in \operatorname {\mathrm {KK}}^H(C_0(H^{0}),C_0(p^{-1}(H^{0}))$
is invertible.
$\operatorname {\mathrm {Res}}_G^H(\mathbf {p})\in \operatorname {\mathrm {KK}}^H(C_0(H^{0}),C_0(p^{-1}(H^{0}))$
is invertible.
We obtain the following consequence:
Theorem 4.8. Let G be a second countable étale groupoid which is strongly amenable at infinity. Then there exists an element
![]() $\eta \in \operatorname {\mathrm {KK}}^G(C_0(G^0),P(C_0(G^0)))$
such that
$\eta \in \operatorname {\mathrm {KK}}^G(C_0(G^0),P(C_0(G^0)))$
such that
![]() $\eta \circ D=\mathrm {id}_{P(C_0(G^0))}$
, where D denotes the Dirac morphism for G. In particular, the Baum–Connes assembly map
$\eta \circ D=\mathrm {id}_{P(C_0(G^0))}$
, where D denotes the Dirac morphism for G. In particular, the Baum–Connes assembly map
![]() $\mu _A$
for G is split injective for all
$\mu _A$
for G is split injective for all
![]() $A\in \operatorname {\mathrm {KK}}^G$
.
$A\in \operatorname {\mathrm {KK}}^G$
.
Proof. It follows immediately from Theorem 4.3 and Proposition 4.7 that
![]() $p\in \operatorname {\mathrm {KK}}^G(C_0(G^{0}),C_0(Y))$
is a weak equivalence. Hence,
$p\in \operatorname {\mathrm {KK}}^G(C_0(G^{0}),C_0(Y))$
is a weak equivalence. Hence,
![]() $P(p)$
is an isomorphism in
$P(p)$
is an isomorphism in
![]() $\operatorname {\mathrm {KK}}^G$
. Moreover, since G acts amenably on Y, the natural morphism
$\operatorname {\mathrm {KK}}^G$
. Moreover, since G acts amenably on Y, the natural morphism
![]() $D_{C_0(Y)}:P(C_0(Y))\rightarrow C_0(Y)$
is an isomorphism in
$D_{C_0(Y)}:P(C_0(Y))\rightarrow C_0(Y)$
is an isomorphism in
![]() $\operatorname {\mathrm {KK}}^{G\ltimes Y}$
. Consider the canonical forgetful functor
$\operatorname {\mathrm {KK}}^{G\ltimes Y}$
. Consider the canonical forgetful functor
![]() $p_*:\operatorname {\mathrm {KK}}^{G\ltimes Y}\rightarrow \operatorname {\mathrm {KK}}^G$
induced by the anchor map
$p_*:\operatorname {\mathrm {KK}}^{G\ltimes Y}\rightarrow \operatorname {\mathrm {KK}}^G$
induced by the anchor map
![]() $p:Y\to G^0$
. It is not hard to see that
$p:Y\to G^0$
. It is not hard to see that
![]() $p_*$
is a triangulated functor. Moreover, it maps proper objects to proper objects (if Z is a proper
$p_*$
is a triangulated functor. Moreover, it maps proper objects to proper objects (if Z is a proper
![]() $G\ltimes Y$
space, then Z is also a proper G-space). Hence, by Theorem 3.4 it maps the localizing subcategory generated by the projective objects in
$G\ltimes Y$
space, then Z is also a proper G-space). Hence, by Theorem 3.4 it maps the localizing subcategory generated by the projective objects in
![]() $\operatorname {\mathrm {KK}}^{G\ltimes Y}$
to the corresponding localizing subcategory generated by projective objects in
$\operatorname {\mathrm {KK}}^{G\ltimes Y}$
to the corresponding localizing subcategory generated by projective objects in
![]() $\operatorname {\mathrm {KK}}^G$
.
$\operatorname {\mathrm {KK}}^G$
.
Then, since the Dirac morphism is determined uniquely up to isomorphism of the associated exact triangles, we may assume that the natural morphism
![]() $D_{C_0(Y)}\in \operatorname {\mathrm {KK}}^{G}(P(C_0(Y)),C_0(Y))$
is an isomorphism as well. Let
$D_{C_0(Y)}\in \operatorname {\mathrm {KK}}^{G}(P(C_0(Y)),C_0(Y))$
is an isomorphism as well. Let
![]() $\beta $
denote its inverse. Then the composition
$\beta $
denote its inverse. Then the composition
![]() $\eta :=P(p)^{-1}\circ \beta \circ p\in \operatorname {\mathrm {KK}}^G(C_0(G^{0}),P(C_0(G^{0})))$
is the desired morphism. The final assertion then follows from the commutative diagram (11).
$\eta :=P(p)^{-1}\circ \beta \circ p\in \operatorname {\mathrm {KK}}^G(C_0(G^{0}),P(C_0(G^{0})))$
is the desired morphism. The final assertion then follows from the commutative diagram (11).
An element
![]() $\eta $
as in the theorem above is often called a dual Dirac morphism for G (see [Reference Meyer and Nest41, Definition 8.1]) and is unique (if it exists).
$\eta $
as in the theorem above is often called a dual Dirac morphism for G (see [Reference Meyer and Nest41, Definition 8.1]) and is unique (if it exists).
4.4 Permanence properties
In this section, we will often need to compare the subcategories
![]() $\langle \mathcal {C}\mathcal {I}\rangle $
and
$\langle \mathcal {C}\mathcal {I}\rangle $
and
![]() $\mathcal {N}$
for different groupoids. To highlight this, we will slightly adjust our notation and write
$\mathcal {N}$
for different groupoids. To highlight this, we will slightly adjust our notation and write
![]() $\mathcal {N}_G$
for the weakly contractible objects in
$\mathcal {N}_G$
for the weakly contractible objects in
![]() $\operatorname {\mathrm {KK}}^G$
and
$\operatorname {\mathrm {KK}}^G$
and
![]() $\mathcal {CI}_G$
for the compactly induced objects.
$\mathcal {CI}_G$
for the compactly induced objects.
Sometimes we write ‘BC’ as a shorthand for ‘Baum–Connes conjecture’.
4.4.1 Subgroupoids
Given a second countable étale groupoid G and a subgroupoid
![]() $H\subseteq G$
, we may ask how the (strong) Baum–Connes conjectures for G and H are related. We need
$H\subseteq G$
, we may ask how the (strong) Baum–Connes conjectures for G and H are related. We need
Lemma 4.9. Suppose
![]() $H\subseteq G$
is a subgroupoid. Then the following hold:
$H\subseteq G$
is a subgroupoid. Then the following hold:
-
1. If
 $H\subseteq G$
is open, then
$H\subseteq G$
is open, then
 $\operatorname {\mathrm {Res}}^H_G(\mathcal {N}_G)\subseteq \mathcal {N}_H$
.
$\operatorname {\mathrm {Res}}^H_G(\mathcal {N}_G)\subseteq \mathcal {N}_H$
. -
2. If H is closed in
 $G|_{H^0}$
, then
$G|_{H^0}$
, then
 $\operatorname {\mathrm {Res}}^H_G(\langle \mathcal {CI}_G\rangle )\subseteq \langle \mathcal {CI}_H\rangle $
.
$\operatorname {\mathrm {Res}}^H_G(\langle \mathcal {CI}_G\rangle )\subseteq \langle \mathcal {CI}_H\rangle $
. -
3. If H is open in G and closed in
 $G|_{H^0}$
, then
$G|_{H^0}$
, then
 $\operatorname {\mathrm {Res}}_G^H$
maps a Dirac triangle for G to a Dirac triangle for H.
$\operatorname {\mathrm {Res}}_G^H$
maps a Dirac triangle for G to a Dirac triangle for H.
Proof. To show the first item suppose H is an open subgroupoid of G and let
![]() $N\in \mathcal {N}_G\subseteq \operatorname {\mathrm {KK}}^G$
. Suppose that Q is a proper open subgroupoid of H. Then Q is also a proper open subgroupoid of G and hence
$N\in \mathcal {N}_G\subseteq \operatorname {\mathrm {KK}}^G$
. Suppose that Q is a proper open subgroupoid of H. Then Q is also a proper open subgroupoid of G and hence
![]() $\operatorname {\mathrm {Res}}_H^Q(\operatorname {\mathrm {Res}}_G^H(\mathrm {id}_N))=\operatorname {\mathrm {Res}}_G^Q(\mathrm {id}_N)\stackrel {3.16}{=}0$
. Another application of Lemma 3.16 yields the result.
$\operatorname {\mathrm {Res}}_H^Q(\operatorname {\mathrm {Res}}_G^H(\mathrm {id}_N))=\operatorname {\mathrm {Res}}_G^Q(\mathrm {id}_N)\stackrel {3.16}{=}0$
. Another application of Lemma 3.16 yields the result.
Next, suppose H is closed in
![]() $G|_{H^0}$
. Whenever G acts properly on a space Z with anchor map
$G|_{H^0}$
. Whenever G acts properly on a space Z with anchor map
![]() $p:Z\rightarrow G^0$
, then the action restricts to a proper action of H on
$p:Z\rightarrow G^0$
, then the action restricts to a proper action of H on
![]() $p^{-1}(H^0)$
. In particular, it follows that
$p^{-1}(H^0)$
. In particular, it follows that
![]() $\operatorname {\mathrm {Res}}^H_G(\mathcal {C}\mathcal {I}_G)\subseteq \Pr _H$
and hence
$\operatorname {\mathrm {Res}}^H_G(\mathcal {C}\mathcal {I}_G)\subseteq \Pr _H$
and hence
![]() $\operatorname {\mathrm {Res}}_G^H(\langle \mathcal {C}\mathcal {I}_G\rangle )\subseteq \langle \mathcal {C}\mathcal {I}_H\rangle $
by Theorem 3.10.
$\operatorname {\mathrm {Res}}_G^H(\langle \mathcal {C}\mathcal {I}_G\rangle )\subseteq \langle \mathcal {C}\mathcal {I}_H\rangle $
by Theorem 3.10.
The final assertion is a direct consequence of the first two statements.
Lemma 4.10. Suppose
![]() $H\subseteq G$
is a subgroupoid such that H is closed in
$H\subseteq G$
is a subgroupoid such that H is closed in
![]() $G|_{H^0}$
. Then the following hold:
$G|_{H^0}$
. Then the following hold:
is triangulated,
![]() $\operatorname {\mathrm {Ind}}_H^G(\mathcal {N}_H)\subseteq \mathcal {N}_G$
, and
$\operatorname {\mathrm {Ind}}_H^G(\mathcal {N}_H)\subseteq \mathcal {N}_G$
, and
![]() $\operatorname {\mathrm {Ind}}_H^G\langle \mathcal {C}\mathcal {I}_H\rangle \subseteq \langle \mathcal {C}\mathcal {I}_G\rangle $
. In particular, it maps Dirac triangles to Dirac triangles.
$\operatorname {\mathrm {Ind}}_H^G\langle \mathcal {C}\mathcal {I}_H\rangle \subseteq \langle \mathcal {C}\mathcal {I}_G\rangle $
. In particular, it maps Dirac triangles to Dirac triangles.
Proof. Induction in stages gives that a compactly induced object in
![]() $\operatorname {\mathrm {KK}}^H$
is mapped to a proper object in
$\operatorname {\mathrm {KK}}^H$
is mapped to a proper object in
![]() $\operatorname {\mathrm {KK}}^G$
. Indeed, if
$\operatorname {\mathrm {KK}}^G$
. Indeed, if
![]() $Q\subseteq H$
is a compact action, then
$Q\subseteq H$
is a compact action, then
![]() $\operatorname {\mathrm {Ind}}_H^G(\operatorname {\mathrm {Ind}}_Q^H A)=\operatorname {\mathrm {Ind}}_Q^G A$
. It follows from our assumption that Q is closed in
$\operatorname {\mathrm {Ind}}_H^G(\operatorname {\mathrm {Ind}}_Q^H A)=\operatorname {\mathrm {Ind}}_Q^G A$
. It follows from our assumption that Q is closed in
![]() $G|_{Q^0}$
, and hence the action of G on
$G|_{Q^0}$
, and hence the action of G on
![]() $G_{Q^0}/Q$
is proper. It follows immediately that
$G_{Q^0}/Q$
is proper. It follows immediately that
![]() $\operatorname {\mathrm {Ind}}_Q^G A$
is a proper G-algebra (see also the induction picture in [Reference Bönicke10]). Whence,
$\operatorname {\mathrm {Ind}}_Q^G A$
is a proper G-algebra (see also the induction picture in [Reference Bönicke10]). Whence,
![]() $\operatorname {\mathrm {Ind}}_H^G\langle \mathcal {C}\mathcal {I}_H\rangle \subseteq \langle \mathcal {C}\mathcal {I}_G\rangle $
by Theorem 3.10.
$\operatorname {\mathrm {Ind}}_H^G\langle \mathcal {C}\mathcal {I}_H\rangle \subseteq \langle \mathcal {C}\mathcal {I}_G\rangle $
by Theorem 3.10.
Finally, let
![]() $A\in \mathcal {N}_H\subseteq \operatorname {\mathrm {KK}}^H$
. Then by Lemma 4.9.(2) we have
$A\in \mathcal {N}_H\subseteq \operatorname {\mathrm {KK}}^H$
. Then by Lemma 4.9.(2) we have
Using Lemma 2.6, we conclude that
as well.
The following result was already observed by Tu [Reference Tu57] for the classical Baum–Connes conjecture. Unfortunately, his proof relies on [Reference Tu57, Lemma 3.9], which seems to be erroneous. A counterexample where G is the compact space
![]() $[0,1]$
(viewed as a trivial groupoid just consisting of units) is exhibited in [Reference Dadarlat and Meyer17, Example 5.6] and [Reference Bauval4, p.36].
$[0,1]$
(viewed as a trivial groupoid just consisting of units) is exhibited in [Reference Dadarlat and Meyer17, Example 5.6] and [Reference Bauval4, p.36].
Theorem 4.11. Let G be a second countable groupoid,
![]() $H\subseteq G$
be an étale subgroupoid that is closed in
$H\subseteq G$
be an étale subgroupoid that is closed in
![]() $G|_{H^0}$
, and
$G|_{H^0}$
, and
![]() $A\in \operatorname {\mathrm {KK}}^H$
. Then there is a natural
$A\in \operatorname {\mathrm {KK}}^H$
. Then there is a natural
![]() $\operatorname {\mathrm {KK}}$
-equivalence between
$\operatorname {\mathrm {KK}}$
-equivalence between
![]() $P_G(\operatorname {\mathrm {Ind}}_H^G A)\rtimes _r G$
and
$P_G(\operatorname {\mathrm {Ind}}_H^G A)\rtimes _r G$
and
![]() $P_H(A)\rtimes _r H$
. Hence, the (strong) Baum–Connes conjecture with coefficients passes to closed subgroupoids and restrictions to open subsets.
$P_H(A)\rtimes _r H$
. Hence, the (strong) Baum–Connes conjecture with coefficients passes to closed subgroupoids and restrictions to open subsets.
Proof. From the previous lemma, we conclude that
![]() $P_G(\operatorname {\mathrm {Ind}}_H^G A)\rtimes _r G\cong \operatorname {\mathrm {Ind}}_H^G (P_H(A))\rtimes _r G$
. The latter, however, is canonically Morita-equivalent (and hence in particular
$P_G(\operatorname {\mathrm {Ind}}_H^G A)\rtimes _r G\cong \operatorname {\mathrm {Ind}}_H^G (P_H(A))\rtimes _r G$
. The latter, however, is canonically Morita-equivalent (and hence in particular
![]() $\operatorname {\mathrm {KK}}$
-equivalent) to
$\operatorname {\mathrm {KK}}$
-equivalent) to
![]() $P_H(A)\rtimes _r H$
. The result about the (strong) Baum–Connes conjecture follows readily.
$P_H(A)\rtimes _r H$
. The result about the (strong) Baum–Connes conjecture follows readily.
4.4.2 Continuity in the coefficient algebra
Let
![]() $(A_n)_n$
be an inductive system of G-
$(A_n)_n$
be an inductive system of G-
![]() $C^*$
algebras, and let
$C^*$
algebras, and let
![]() $A=\varinjlim A_n$
be the inductive limit. In [Reference Bönicke and Dell’Aiera12, Section 3], it was shown that A carries a canonical G-action making all the structure maps equivariant, that is, the inductive limit exists in the category of G-
$A=\varinjlim A_n$
be the inductive limit. In [Reference Bönicke and Dell’Aiera12, Section 3], it was shown that A carries a canonical G-action making all the structure maps equivariant, that is, the inductive limit exists in the category of G-
![]() $C^*$
-algebras.
$C^*$
-algebras.
Proposition 4.12. Let
![]() $(A_n)_n$
be an admissible inductive system of G-
$(A_n)_n$
be an admissible inductive system of G-
![]() $C^*$
algebras, and let
$C^*$
algebras, and let
![]() $A=\varinjlim A_n$
. Then
$A=\varinjlim A_n$
. Then
![]() $P(A)\rtimes _r G$
is naturally
$P(A)\rtimes _r G$
is naturally
![]() $\operatorname {\mathrm {KK}}$
-equivalent to
$\operatorname {\mathrm {KK}}$
-equivalent to
![]() $\text {ho-lim}\, (P(A_n)\rtimes _r G)$
, and
$\text {ho-lim}\, (P(A_n)\rtimes _r G)$
, and
![]() $N(A)\rtimes _r G$
is naturally
$N(A)\rtimes _r G$
is naturally
![]() $\operatorname {\mathrm {KK}}$
-equivalent to
$\operatorname {\mathrm {KK}}$
-equivalent to
![]() $\text {ho-lim}\, (N(A_n)\rtimes _r G)$
.
$\text {ho-lim}\, (N(A_n)\rtimes _r G)$
.
If furthermore G satisfies the (strong) Baum–Connes conjecture with coefficients in
![]() $A_n$
for all
$A_n$
for all
![]() $n\in \mathbb {N}$
, then G satisfies the (strong) Baum–Connes conjecture with coefficients in A.
$n\in \mathbb {N}$
, then G satisfies the (strong) Baum–Connes conjecture with coefficients in A.
Proof. Let us consider the following diagram:

The horizontal maps in the left-hand square are the natural isomorphisms obtained from the facts that the categories
![]() $\langle \mathcal {C}\mathcal {I}\rangle $
and
$\langle \mathcal {C}\mathcal {I}\rangle $
and
![]() $\mathcal {N}$
are closed under direct sums and the Dirac triangle is unique. The square on the right commutes by naturality of the Dirac morphism. By [Reference Beilinson, Bernstein and Deligne5, Proposition 1.1.11], the outer square forms the center of a larger diagram, in which each row and column is an exact triangle, and each square commutes (up to a sign), as shown below.
$\mathcal {N}$
are closed under direct sums and the Dirac triangle is unique. The square on the right commutes by naturality of the Dirac morphism. By [Reference Beilinson, Bernstein and Deligne5, Proposition 1.1.11], the outer square forms the center of a larger diagram, in which each row and column is an exact triangle, and each square commutes (up to a sign), as shown below.

Since the horizontal maps in the middle square are the morphisms defining the homotopy limit uniquely up to isomorphisms, it is clear which objects appear in the first and last row. In the diagram above, we have already made use of the fact that the sequence
![]() $(A_n)_n$
is admissible by replacing
$(A_n)_n$
is admissible by replacing
![]() $\text {ho-lim}\, A_n$
by the inductive limit
$\text {ho-lim}\, A_n$
by the inductive limit
![]() $A=\lim A_n$
. Consider now the bottom row of the diagram. Since
$A=\lim A_n$
. Consider now the bottom row of the diagram. Since
![]() $\langle \mathcal {C}\mathcal {I}\rangle $
and
$\langle \mathcal {C}\mathcal {I}\rangle $
and
![]() $\mathcal {N}$
are localizing subcategories, they are closed under homotopy direct limits. Hence, by uniqueness, the bottom row is naturally isomorphic to the exact triangle
$\mathcal {N}$
are localizing subcategories, they are closed under homotopy direct limits. Hence, by uniqueness, the bottom row is naturally isomorphic to the exact triangle
Taking reduced crossed products is a triangulated functor on
![]() $\operatorname {\mathrm {KK}}^G$
, so we can take crossed products throughout the diagram, completing the proof of the first assertion.
$\operatorname {\mathrm {KK}}^G$
, so we can take crossed products throughout the diagram, completing the proof of the first assertion.
Now, if G satisfies the strong Baum–Connes conjecture with coefficients in
![]() $A_n$
for each n, then the horizontal arrows in the central square are
$A_n$
for each n, then the horizontal arrows in the central square are
![]() $\operatorname {\mathrm {KK}}$
-equivalences (after taking reduced crossed products). It then follows immediately that
$\operatorname {\mathrm {KK}}$
-equivalences (after taking reduced crossed products). It then follows immediately that
![]() $\jmath ^G_r(D_A)$
is also a
$\jmath ^G_r(D_A)$
is also a
![]() $\operatorname {\mathrm {KK}}$
-equivalence. For the classical version of the Baum–Connes conjecture, first apply the reduced crossed product functor to the diagram above and then note that the two middle columns in the resulting diagram induce a homomorphism of long exact sequences in K-theory. An application of the five lemma yields the result.
$\operatorname {\mathrm {KK}}$
-equivalence. For the classical version of the Baum–Connes conjecture, first apply the reduced crossed product functor to the diagram above and then note that the two middle columns in the resulting diagram induce a homomorphism of long exact sequences in K-theory. An application of the five lemma yields the result.
4.4.3 Products and unions of subgroupoids
Let
![]() $G=\bigcup G_n$
be a union of a sequence of clopen subgroupoids. We shall need the
$G=\bigcup G_n$
be a union of a sequence of clopen subgroupoids. We shall need the
![]() $G_n$
to be open so that, if
$G_n$
to be open so that, if
![]() $A\in \operatorname {\mathrm {KK}}^G$
, we can write the crossed product as an inductive limit
$A\in \operatorname {\mathrm {KK}}^G$
, we can write the crossed product as an inductive limit
![]() $A\rtimes _r G=\lim A\rtimes _r G_n$
as well. Since the
$A\rtimes _r G=\lim A\rtimes _r G_n$
as well. Since the
![]() $G_n$
are also closed, we obtain canonical restriction maps
$G_n$
are also closed, we obtain canonical restriction maps
![]() $\Gamma _c(G,\mathcal {A})\rightarrow \Gamma _c(G_n,\mathcal {A})$
, which induce completely positive contractions
$\Gamma _c(G,\mathcal {A})\rightarrow \Gamma _c(G_n,\mathcal {A})$
, which induce completely positive contractions
![]() $A\rtimes _r G\rightarrow A\rtimes _r G_n$
. It follows that the inductive system
$A\rtimes _r G\rightarrow A\rtimes _r G_n$
. It follows that the inductive system
![]() $(A\rtimes _r G_n)_n$
is admissible and hence in the category
$(A\rtimes _r G_n)_n$
is admissible and hence in the category
![]() $\operatorname {\mathrm {KK}}$
we can identify the direct limit
$\operatorname {\mathrm {KK}}$
we can identify the direct limit
![]() $A\rtimes _r G$
with the homotopy direct limit
$A\rtimes _r G$
with the homotopy direct limit
![]() $\text {ho-lim}\,A \rtimes _r G_n$
.
$\text {ho-lim}\,A \rtimes _r G_n$
.
Proposition 4.13. Let
![]() $(G_n)_n$
be a sequence of clopen subgroupoids of G such that
$(G_n)_n$
be a sequence of clopen subgroupoids of G such that
![]() $G=\bigcup _n G_n$
. Suppose
$G=\bigcup _n G_n$
. Suppose
![]() $A\in \operatorname {\mathrm {KK}}^G$
such that
$A\in \operatorname {\mathrm {KK}}^G$
such that
![]() $G_n$
satisfies (strong) BC with coefficients in
$G_n$
satisfies (strong) BC with coefficients in
![]() $\operatorname {\mathrm {Res}}_G^{G_n}(A)$
for all
$\operatorname {\mathrm {Res}}_G^{G_n}(A)$
for all
![]() $n\in \mathbb {N}$
. Then G satisfies (strong) BC with coefficients in A.
$n\in \mathbb {N}$
. Then G satisfies (strong) BC with coefficients in A.
Proof. We know from Lemma 4.9 that
![]() $\operatorname {\mathrm {Res}}_G^{G_n}$
preserves Dirac triangles. It follows that in
$\operatorname {\mathrm {Res}}_G^{G_n}$
preserves Dirac triangles. It follows that in
![]() $\operatorname {\mathrm {KK}}$
we have identifications
$\operatorname {\mathrm {KK}}$
we have identifications
and similarly
By taking limits, we get
and similarly
Recall that G satisfies the (strong) Baum–Connes conjecture with coefficients in A if and only if
![]() $N(A)\rtimes _r G$
is K-contractible (or
$N(A)\rtimes _r G$
is K-contractible (or
![]() $\operatorname {\mathrm {KK}}$
-contractible for the strong version). Since the categories of K-contractible (resp.
$\operatorname {\mathrm {KK}}$
-contractible for the strong version). Since the categories of K-contractible (resp.
![]() $\operatorname {\mathrm {KK}}$
-contractible) objects are localising, they are closed under homotopy direct limits. The result follows.
$\operatorname {\mathrm {KK}}$
-contractible) objects are localising, they are closed under homotopy direct limits. The result follows.
Let us now turn our attention to direct products. Suppose
![]() $G=G_1\times G_2$
is the product of two étale groupoids
$G=G_1\times G_2$
is the product of two étale groupoids
![]() $G_1,G_2$
. Suppose further that
$G_1,G_2$
. Suppose further that
![]() $A_i\in \operatorname {\mathrm {KK}}^{G_i}$
for
$A_i\in \operatorname {\mathrm {KK}}^{G_i}$
for
![]() $i=1,2$
. If either
$i=1,2$
. If either
![]() $A_1$
or
$A_1$
or
![]() $A_2$
is exact, the minimal tensor product
$A_2$
is exact, the minimal tensor product
![]() $A:=A_1\otimes A_2$
comes equipped with a diagonal action and hence can be viewed as an object in
$A:=A_1\otimes A_2$
comes equipped with a diagonal action and hence can be viewed as an object in
![]() $\operatorname {\mathrm {KK}}^G$
.
$\operatorname {\mathrm {KK}}^G$
.
Proposition 4.14. If
![]() $G_i$
satisfies strong BC with coefficients in
$G_i$
satisfies strong BC with coefficients in
![]() $A_i$
for
$A_i$
for
![]() $i=1,2$
, then
$i=1,2$
, then
![]() $G_1\times G_2$
satisfies strong BC with coefficients in
$G_1\times G_2$
satisfies strong BC with coefficients in
![]() $A_1\otimes A_2$
.
$A_1\otimes A_2$
.
Proof. We claim that
![]() $\mathcal {C}\mathcal {I}_{G_1}\otimes \mathcal {C}\mathcal {I}_{G_2}\subseteq \mathcal {C}\mathcal {I}_{G_1\times G_2}$
and
$\mathcal {C}\mathcal {I}_{G_1}\otimes \mathcal {C}\mathcal {I}_{G_2}\subseteq \mathcal {C}\mathcal {I}_{G_1\times G_2}$
and
![]() $\mathcal {N}_{G_1}\otimes \mathcal {N}_{G_2}\subseteq \mathcal {N}_{G_1\times G_2}$
. It follows in particular, that, if
$\mathcal {N}_{G_1}\otimes \mathcal {N}_{G_2}\subseteq \mathcal {N}_{G_1\times G_2}$
. It follows in particular, that, if
![]() $P_i\rightarrow C_0(G_i^0)\rightarrow N_i$
is a Dirac triangle for
$P_i\rightarrow C_0(G_i^0)\rightarrow N_i$
is a Dirac triangle for
![]() $G_i$
,
$G_i$
,
![]() $i=1,2$
, then
$i=1,2$
, then
is a Dirac triangle for
![]() $G=G_1\times G_2$
. Since the minimal tensor product behaves well with respect to reduced crossed products, we have canonical isomorphisms
$G=G_1\times G_2$
. Since the minimal tensor product behaves well with respect to reduced crossed products, we have canonical isomorphisms
 $$ \begin{gather*} A\rtimes_r G \cong (A_1\rtimes_r G_1)\otimes(A_2\rtimes_r G_2)\\ P_G(A)\rtimes_r G \cong (P_{G_1}(A_1)\otimes P_{G_2}(A_2))\rtimes_r G \cong (P_{G_1}(A_1)\rtimes_r G_1)\otimes (P_{G_2}(A_2)\rtimes_r G_2), \end{gather*} $$
$$ \begin{gather*} A\rtimes_r G \cong (A_1\rtimes_r G_1)\otimes(A_2\rtimes_r G_2)\\ P_G(A)\rtimes_r G \cong (P_{G_1}(A_1)\otimes P_{G_2}(A_2))\rtimes_r G \cong (P_{G_1}(A_1)\rtimes_r G_1)\otimes (P_{G_2}(A_2)\rtimes_r G_2), \end{gather*} $$
where the first
![]() $\operatorname {\mathrm {KK}}$
-equivalence follows from the above observation about Dirac triangles. Under these identifications, the Baum–Connes assembly map
$\operatorname {\mathrm {KK}}$
-equivalence follows from the above observation about Dirac triangles. Under these identifications, the Baum–Connes assembly map
![]() $P_G(A)\rtimes _r G\rightarrow A\rtimes _r G$
decomposes as the exterior tensor product of the Baum–Connes assembly maps
$P_G(A)\rtimes _r G\rightarrow A\rtimes _r G$
decomposes as the exterior tensor product of the Baum–Connes assembly maps
![]() $P_{G_i}(A_i)\rtimes _r G_i\rightarrow A_i\rtimes _r G_i$
. Since the exterior tensor product of
$P_{G_i}(A_i)\rtimes _r G_i\rightarrow A_i\rtimes _r G_i$
. Since the exterior tensor product of
![]() $\operatorname {\mathrm {KK}}$
-equivalences is a
$\operatorname {\mathrm {KK}}$
-equivalences is a
![]() $\operatorname {\mathrm {KK}}$
-equivalence itself, the result follows.
$\operatorname {\mathrm {KK}}$
-equivalence itself, the result follows.
As a an immediate consequence, we have the following:
Corollary 4.15. Let
![]() $A_1,A_2\in \operatorname {\mathrm {KK}}^G$
such that at least one of the two is exact. Then
$A_1,A_2\in \operatorname {\mathrm {KK}}^G$
such that at least one of the two is exact. Then
![]() $A_1\otimes _{G^0}A_2\in \operatorname {\mathrm {KK}}^G$
, where
$A_1\otimes _{G^0}A_2\in \operatorname {\mathrm {KK}}^G$
, where
![]() $\otimes _{G^0}$
denotes the balanced minimal tensor product. If we further assume that G satisfies strong BC with coefficients in
$\otimes _{G^0}$
denotes the balanced minimal tensor product. If we further assume that G satisfies strong BC with coefficients in
![]() $A_1$
and
$A_1$
and
![]() $A_2$
, then G satisfies strong BC with coefficients in
$A_2$
, then G satisfies strong BC with coefficients in
![]() $A_1\otimes _{G^0}A_2$
.
$A_1\otimes _{G^0}A_2$
.
Proof. Proposition 4.14 implies that
![]() $G\times G$
satisfies the strong Baum–Connes conjecture with coefficients in
$G\times G$
satisfies the strong Baum–Connes conjecture with coefficients in
![]() $A_1\otimes A_2$
. View G as a closed subgroupoid of
$A_1\otimes A_2$
. View G as a closed subgroupoid of
![]() $G\times G$
via the diagonal inclusion. Since
$G\times G$
via the diagonal inclusion. Since
![]() $\operatorname {\mathrm {Res}}_{G\times G}^G(A_1\otimes A_2)\cong A_1\otimes _{G^0} A_2$
, the result follows from Theorem 4.11.
$\operatorname {\mathrm {Res}}_{G\times G}^G(A_1\otimes A_2)\cong A_1\otimes _{G^0} A_2$
, the result follows from Theorem 4.11.
The corresponding results for the classical Baum–Connes conjecture require further assumptions since the Künneth formula for the computation of the K-theory of a tensor product does not always hold. A detailed study in this direction has been carried out by Dell’Aiera and the first named author in [Reference Bönicke and Dell’Aiera12].
Using the methods developed in the present article the results on the classical Baum–Connes conjecture with coefficients in a minimal balanced tensor product presented in [Reference Bönicke and Dell’Aiera12] can be extended to all étale groupoids.
4.5 Group bundles
We can now strengthen the results on group bundles obtained in [Reference Bönicke10].
Theorem 4.16. Let G be a second countable étale group bundle which is strongly amenable at infinity. We suppose further that
![]() $G^0$
is locally finite-dimensional. Let A be a separable G-algebra which is continuous as a field of
$G^0$
is locally finite-dimensional. Let A be a separable G-algebra which is continuous as a field of
![]() $C^*$
-algebras over
$C^*$
-algebras over
![]() $G^0$
. If the discrete group
$G^0$
. If the discrete group
![]() $G_u^u$
satisfies BC with coefficients in
$G_u^u$
satisfies BC with coefficients in
![]() $A_u$
for every
$A_u$
for every
![]() $u\in G^0$
, then G satisfies BC with coefficients in A.
$u\in G^0$
, then G satisfies BC with coefficients in A.
Proof. We will first prove this in the case that
![]() $G^{0}$
is compact and finite-dimensional. Since we are working with second countable compact Hausdorff spaces the covering dimension of X coincides with the small inductive dimension of X, which we are going to employ. The proof will proceed by induction on the dimension of X. The zero-dimensional case has already been considered in [Reference Bönicke10, Theorem 8.11]. Assume that
$G^{0}$
is compact and finite-dimensional. Since we are working with second countable compact Hausdorff spaces the covering dimension of X coincides with the small inductive dimension of X, which we are going to employ. The proof will proceed by induction on the dimension of X. The zero-dimensional case has already been considered in [Reference Bönicke10, Theorem 8.11]. Assume that
![]() $dim(X)=n$
and the result has been shown for all spaces of dimension strictly smaller than n. It is enough to show
$dim(X)=n$
and the result has been shown for all spaces of dimension strictly smaller than n. It is enough to show
![]() $(1-\gamma _A)K_*(A\rtimes _r G)=\{0\}$
. So let
$(1-\gamma _A)K_*(A\rtimes _r G)=\{0\}$
. So let
![]() $x\in (1-\gamma _A)K_i(A\rtimes _rG)$
. By our assumption that
$x\in (1-\gamma _A)K_i(A\rtimes _rG)$
. By our assumption that
![]() $G_u^u$
satisfies BC with coefficients in
$G_u^u$
satisfies BC with coefficients in
![]() $A_u$
and [Reference Bönicke10, Lemma 8.10], we have
$A_u$
and [Reference Bönicke10, Lemma 8.10], we have
![]() $q_{u,*}(x)=0$
for all
$q_{u,*}(x)=0$
for all
![]() $u\in G^{0}$
. Using [Reference Chabert, Echterhoff and Nest15, Lemma 3.4], we can find an open neighbourhood
$u\in G^{0}$
. Using [Reference Chabert, Echterhoff and Nest15, Lemma 3.4], we can find an open neighbourhood
![]() $U_u$
of u in
$U_u$
of u in
![]() $G^{0}$
such that
$G^{0}$
such that
![]() $q_{\overline {U_u},*}(x)=0$
. Next, apply the fact that
$q_{\overline {U_u},*}(x)=0$
. Next, apply the fact that
![]() $G^{0}$
has inductive dimension at most n to replace each of the sets
$G^{0}$
has inductive dimension at most n to replace each of the sets
![]() $U_u$
by a smaller neighbourhood of u to assume additionally, that
$U_u$
by a smaller neighbourhood of u to assume additionally, that
![]() $\dim (\overline {U_u}\setminus U_u)\leq n-1$
. Using compactness of
$\dim (\overline {U_u}\setminus U_u)\leq n-1$
. Using compactness of
![]() $G^{0}$
, we may find a finite subcover say
$G^{0}$
, we may find a finite subcover say
![]() $U_1,\ldots , U_l$
such that
$U_1,\ldots , U_l$
such that
![]() $\dim (\overline {U_i}\setminus U_i)\leq n-1$
and
$\dim (\overline {U_i}\setminus U_i)\leq n-1$
and
![]() $q_{\overline {U_i},*}(x)=0$
for all
$q_{\overline {U_i},*}(x)=0$
for all
![]() $1\leq i\leq l$
. Consider the open set
$1\leq i\leq l$
. Consider the open set
![]() $O:=G^{0}\setminus \bigcup _{i=1}^l \partial U_i$
and the associated ideal
$O:=G^{0}\setminus \bigcup _{i=1}^l \partial U_i$
and the associated ideal
![]() $A_O:=C_0(O)A$
. Then
$A_O:=C_0(O)A$
. Then
![]() $C_0(O)(A\rtimes _r G)= A_O\rtimes _r G_O$
. Since G is exact, we have a short exact sequence of
$C_0(O)(A\rtimes _r G)= A_O\rtimes _r G_O$
. Since G is exact, we have a short exact sequence of
![]() $C^*$
-algebras
$C^*$
-algebras
We want to consider the induced six-term exact sequence in K-theory. Since the boundaries
![]() $\partial U_i$
are closed and at most
$\partial U_i$
are closed and at most
![]() $(n-1)$
-dimensional so is their union
$(n-1)$
-dimensional so is their union
![]() $Y:=\bigcup _{i=1}^l \partial U_i$
. Applying the induction hypothesis yields that
$Y:=\bigcup _{i=1}^l \partial U_i$
. Applying the induction hypothesis yields that
![]() $(1-\gamma _{A_{Y}})K_*(A_{Y}\rtimes _r G_{Y})=0$
. Hence, the six-term exact sequence in K-theory shows that the canonical inclusion map induces an isomorphism
$(1-\gamma _{A_{Y}})K_*(A_{Y}\rtimes _r G_{Y})=0$
. Hence, the six-term exact sequence in K-theory shows that the canonical inclusion map induces an isomorphism
It follows that there exists a unique element
![]() $x'\in (1-\gamma _{A_O})K_i(A_O\rtimes _r G_O)$
whose image under the inclusion map is x. Furthermore, O can be decomposed as a finite disjoint union of open sets
$x'\in (1-\gamma _{A_O})K_i(A_O\rtimes _r G_O)$
whose image under the inclusion map is x. Furthermore, O can be decomposed as a finite disjoint union of open sets
![]() $O=\bigsqcup _{j=1}^m W_j$
such that each
$O=\bigsqcup _{j=1}^m W_j$
such that each
![]() $W_j$
is contained in at least one of the sets
$W_j$
is contained in at least one of the sets
![]() $U_i$
by a standard inclusion/exclusion argument. Corresponding to this decomposition is a decomposition of the crossed product
$U_i$
by a standard inclusion/exclusion argument. Corresponding to this decomposition is a decomposition of the crossed product
![]() $A_O\rtimes _r G_O$
as
$A_O\rtimes _r G_O$
as
 $$ \begin{align*}A_O\rtimes G_O= \bigoplus_{j=1}^m A_{W_j}\rtimes_r G_{W_j}.\end{align*} $$
$$ \begin{align*}A_O\rtimes G_O= \bigoplus_{j=1}^m A_{W_j}\rtimes_r G_{W_j}.\end{align*} $$
It follows that
![]() $x'=\sum _{j=1}^l x_j'$
where
$x'=\sum _{j=1}^l x_j'$
where
![]() $x_j'$
is in the image of the inclusion map
$x_j'$
is in the image of the inclusion map
![]() $(1-\gamma _{A_{W_j}}) K_i(A_{W_j}\rtimes G_{W_j})\rightarrow (1-\gamma _{A_O})K_i(A_O\rtimes _r G_O)$
. Thus, it is enough to show that
$(1-\gamma _{A_{W_j}}) K_i(A_{W_j}\rtimes G_{W_j})\rightarrow (1-\gamma _{A_O})K_i(A_O\rtimes _r G_O)$
. Thus, it is enough to show that
![]() $x_j'=0$
for all
$x_j'=0$
for all
![]() $j=1,\ldots , l$
. To this end, consider the short exact sequence
$j=1,\ldots , l$
. To this end, consider the short exact sequence
Since
![]() $\partial W_j\subseteq \partial U_i$
is a closed subset for some
$\partial W_j\subseteq \partial U_i$
is a closed subset for some
![]() $U_i$
, the boundary of
$U_i$
, the boundary of
![]() $W_j$
has dimension at most
$W_j$
has dimension at most
![]() $n-1$
. Hence, we can apply the induction hypothesis again to see that
$n-1$
. Hence, we can apply the induction hypothesis again to see that
![]() $(1-\gamma _{A_{\partial W_j}}) K_*(A_{\partial W_j}\rtimes _r G_{\partial W_j})=0$
. The six-term exact sequence in K-theory induced by (14) shows that the inclusion map induces an isomorphism
$(1-\gamma _{A_{\partial W_j}}) K_*(A_{\partial W_j}\rtimes _r G_{\partial W_j})=0$
. The six-term exact sequence in K-theory induced by (14) shows that the inclusion map induces an isomorphism
![]() $(1-\gamma _{A_{W_j}})K_i(A_{W_j}\rtimes G_{W_j})\rightarrow (1-\gamma _{A_{\overline {W_j}}}) K_i(A_{\overline {W_j}}\rtimes _r G_{\overline {W_j}}).$
The image of
$(1-\gamma _{A_{W_j}})K_i(A_{W_j}\rtimes G_{W_j})\rightarrow (1-\gamma _{A_{\overline {W_j}}}) K_i(A_{\overline {W_j}}\rtimes _r G_{\overline {W_j}}).$
The image of
![]() $x_j'$
under this map coincides with the image of x under the restriction map
$x_j'$
under this map coincides with the image of x under the restriction map
![]() $q_{\overline {W_j},*}$
. Since
$q_{\overline {W_j},*}$
. Since
![]() $W_j\subseteq U_i$
for some
$W_j\subseteq U_i$
for some
![]() $1\leq i\leq n$
, we get that
$1\leq i\leq n$
, we get that
![]() $q_{\overline {W_j},*}(x)=q_{\overline {W_j},*}(q_{\overline {U_i},*}(x))=0$
, and this completes the proof for compact and finite-dimensional unit spaces.
$q_{\overline {W_j},*}(x)=q_{\overline {W_j},*}(q_{\overline {U_i},*}(x))=0$
, and this completes the proof for compact and finite-dimensional unit spaces.
Finally, if
![]() $G^0$
is a locally finite-dimensional and locally compact space, write
$G^0$
is a locally finite-dimensional and locally compact space, write
![]() $G^0$
as an increasing union
$G^0$
as an increasing union
![]() $\bigcup K_n$
of compact subsets of
$\bigcup K_n$
of compact subsets of
![]() $G^0$
such that
$G^0$
such that
![]() $K_n\subseteq \mathrm {int}(K_{n+1})$
. Using that
$K_n\subseteq \mathrm {int}(K_{n+1})$
. Using that
![]() $G^0$
is locally finite-dimensional, we may assume that each
$G^0$
is locally finite-dimensional, we may assume that each
![]() $K_n$
has finite dimension. The first part of this proof implies that
$K_n$
has finite dimension. The first part of this proof implies that
![]() $G|_{K_n}$
satisfies BC with coefficients in
$G|_{K_n}$
satisfies BC with coefficients in
![]() $A|_{K_n}$
and
$A|_{K_n}$
and
![]() $G|_{\partial K_n}$
satisfies BC with coefficients in
$G|_{\partial K_n}$
satisfies BC with coefficients in
![]() $A|_{\partial K_n}$
. A six-term exact sequence argument (using exactness of G!) then shows that
$A|_{\partial K_n}$
. A six-term exact sequence argument (using exactness of G!) then shows that
![]() $G|_{\mathrm {int}(K_n)}$
satisfies BC with coefficients in
$G|_{\mathrm {int}(K_n)}$
satisfies BC with coefficients in
![]() $A|_{\mathrm {int}(K_n)}$
for all
$A|_{\mathrm {int}(K_n)}$
for all
![]() $n\in \mathbb {N}$
. Now, we can write
$n\in \mathbb {N}$
. Now, we can write
![]() $A=\lim A|_{\mathrm {int}(K_n)}$
. Picking an approximate unit
$A=\lim A|_{\mathrm {int}(K_n)}$
. Picking an approximate unit
![]() $(\rho _n)_n$
with
$(\rho _n)_n$
with
![]() $\rho _n\in C_c(\mathrm {int}(K_n))$
, we can define completely positive contractions
$\rho _n\in C_c(\mathrm {int}(K_n))$
, we can define completely positive contractions
![]() $A\rightarrow A|_{\mathrm {int}(K_n)}$
by
$A\rightarrow A|_{\mathrm {int}(K_n)}$
by
![]() $a\mapsto \rho _n a$
which converge pointwise to the identity. Hence, the sequence
$a\mapsto \rho _n a$
which converge pointwise to the identity. Hence, the sequence
![]() $A|_{\mathrm {int}(K_n)}$
is admissible and the result follows from Proposition 4.12.
$A|_{\mathrm {int}(K_n)}$
is admissible and the result follows from Proposition 4.12.
The class of infinite-dimensional spaces to which the previous result applies includes all locally compact CW complexes. An example of a compact space that is not covered by the result is the Hilbert cube.
Acknowledgements.
We would like to thank R. Meyer, R. Nest and M. Yamashita for many helpful suggestions. We are also grateful to A. Miller and S. Nishikawa for pointing out errors in a previous version of this manuscript.
The first author was supported by the Alexander von Humboldt Foundation.
The second author was supported by: Science and Technology Commission of Shanghai Municipality (grant No. 18dz2271000), Foreign Young Talents’ grant (National Natural Science Foundation of China), CREST Grant Number JPMJCR19T2 (Japan), Marie Skłodowska-Curie Individual Fellowship (project number 101063362).
Competing interests
The authors have no competing interest to declare.