Hostname: page-component-7dd5485656-dk7s8 Total loading time: 0 Render date: 2025-10-31T14:53:11.465Z Has data issue: false hasContentIssue false
  • English
  • Français

Singular SPDEs on homogeneous lie groups

Part of: Close-to-elliptic equations and systems Parabolic equations and systems

Published online by Cambridge University Press:  18 February 2025

Avi Mayorcas Open the ORCID record for Avi Mayorcas [Opens in a new window]  and
Harprit Singh Open the ORCID record for Harprit Singh [Opens in a new window]
Avi Mayorcas*
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath, United Kingdom (avimayorcas@gmail.com) (corresponding author)
Harprit Singh
Affiliation:
School of Mathematics, University of Edinburgh, Edinburgh, United Kingdom (harprit.singh@ed.ac.uk)
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

The aim of this article is to extend the scope of the theory of regularity structures in order to deal with a large class of singular stochastic partial differential equations of the form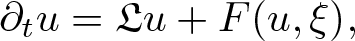

\begin{equation*}\partial_t u = \mathfrak{L} u+ F(u, \xi),\end{equation*}

where the differential operator 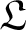$\mathfrak{L}$ fails to be elliptic. This is achieved by interpreting the base space 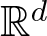$\mathbb{R}^{d}$ as a non-trivial homogeneous Lie group 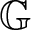$\mathbb{G}$ such that the differential operator 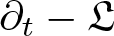$\partial_t -\mathfrak{L}$ becomes a translation invariant hypoelliptic operator on 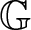$\mathbb{G}$. Prime examples are the kinetic Fokker-Planck operator 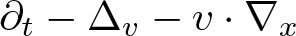$\partial_t -\Delta_v - v\cdot \nabla_x$ and heat-type operators associated with sub-Laplacians. As an application of the developed framework, we solve a class of parabolic Anderson type equations

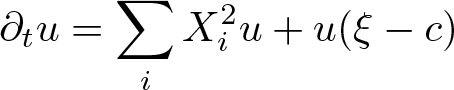\begin{equation*}\partial_t u = \sum_{i} X^2_i u + u (\xi-c)\end{equation*}

on the compact quotient of an arbitrary Carnot group.

Keywords

homogeneous lie groupshypoelliptic operatorsregularity structuresstochastic partial differential equations

MSC classification

Secondary: 35H10: Hypoelliptic equations 35K70: Ultraparabolic equations, pseudoparabolic equations, etc.

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 72
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Agrachev, A., Barilari, D. and Boscain, U.. A comprehensive introduction to sub-Riemannian geometry. Cambridge Studies in Advanced Mathematics, Vol.181 (Cambridge University Press, Cambridge, 2020).Google Scholar
Allez, R. and Chouk, K.. The continuous Anderson hamiltonian in dimension two. ArXiv preprint. (2015), arXiv:1511.02718.Google Scholar
Antoine, M.. Weyl law for the Anderson Hamiltonian on a two-dimensional manifold. Ann. Inst. Henri Poincaré Probab. Stat. 58 (2022), 1385–1425.Google Scholar
Bailleul, I. and , A. Mouzard Paracontrolled calculus for quasilinear singular PDEs. Stoch. Partial Differ. Equ. Anal. Comput. 11 (2023), 599–650.Google Scholar
Bailleul, I. and Bernicot, F.. Heat semigroup and singular PDEs. J. Funct. Anal. 270 (2016), 3344–3452.CrossRefGoogle Scholar
Bailleul, I. and Bernicot, F.. High order paracontrolled calculus. Forum Math. Sigma. 7 (2019), .CrossRefGoogle Scholar
Bailleul, I. and Bruned, Y.. Locality for singular stochastic PDEs. arXiv preprint. (2021), arXiv:2109.00399.Google Scholar
Bailleul, I., Dang, N. V. and Mouzard, A.. Analysis of the Anderson operator. arXiv preprint. (2022), arXiv:2201.04705.Google Scholar
Bailleul, I., Hoshino, M. and Kusuoka, S.. Regularity structures for quasilinear singular SPDEs. Archive for Rational Mechanics and Analysis. 248 (2024), .CrossRefGoogle Scholar
Baudoin, F., Ouyang, C., Tindel, S. and Wang, J.. Parabolic Anderson model on Heisenberg groups: the Itô setting. J. Funct. Anal. 285 (2023), .CrossRefGoogle Scholar
Bell, D. R.. Degenerate stochastic differential equations and hypoellipticity. Pitman Monographs and Surveys in Pure and Applied Mathematics, Vol.79 (Longman, Harlow, 1995).Google Scholar
Bramanti, M.. An Invitation to Hypoelliptic Operators and Hörmander’s Vector fields (Springer Briefs in Mathematics, Springer, Cham, 2014).CrossRefGoogle Scholar
Bruned, Y., Chandra, A., Chevyrev, I. and Hairer, M.. Renormalising SPDEs in regularity structures. J. Eur. Math. Soc. (JEMS). 23 (2021), 869–947.CrossRefGoogle Scholar
Bruned, Y., Hairer, M. and Zambotti, L.. Algebraic renormalisation of regularity structures. Inventiones mathematicae. 215 (2019), 1039–1156.CrossRefGoogle Scholar
Caravenna, F. and Zambotti, L.. Hairer’s reconstruction theorem without regularity structures. EMS Surv. Math. Sci. 7 (2020), 207–251.CrossRefGoogle Scholar
Carmona, R. A. and Molchanov, S. A.. Parabolic Anderson problem and intermittency. Mem. Amer. Math. Soc. 108 (1994), .Google Scholar
Chandra, A. and Hairer, M.. An analytic BPHZ theorem for regularity structures. arXiv preprint, arXiv:1612.08138. (2016).Google Scholar
Chandra, A. and Shen, H.. Moment bounds for SPDEs with non-Gaussian fields and application to the Wong-Zakai problem. Electron. J. Probab. 22 (2017), 1–32.CrossRefGoogle Scholar
Chen, X.. Precise intermittency for the parabolic Anderson equation with an $(1+1)$-dimensional time-space white noise. Ann. Inst. Henri Poincaré Probab. Stat. 51 (2015), 1486–1499.CrossRefGoogle Scholar
Chen, Y. and Xu, W.. Periodic homogenisation for $P(\unicode{x03D5})_2$. (2023), arXiv preprint, arXiv:2311.16398.Google Scholar
Chouk, K. and van Zuijlen, W.. Asymptotics of the eigenvalues of the Anderson Hamiltonian with white noise potential in two dimensions. The Annals of Probability. 49 (2021), 1917–1964.CrossRefGoogle Scholar
Da Prato, G. and Zabczyk, J.. Stochastic equations in infinite dimensions. Encyclopedia of Mathematics and its Applications, 2nd edn. (Cambridge: Cambridge University Press, 2014).Google Scholar
Dahlqvist, A., Diehl, J. and Driver, B. K.. The parabolic Anderson model on Riemann surfaces. Probab. Theory Related Fields. 174 (2019), 369–444.CrossRefGoogle Scholar
Dalang, R. C.. Extending the martingale measure stochastic integral with applications to spatially homogeneous S.P.D.E.’s. Electron. J. Probab. 4 (1999), 1–29.CrossRefGoogle Scholar
Dalang, R. C.. Corrections to: “Extending the martingale measure stochastic integral with applications to spatially homogeneous S.P.D.E.’s” [Electron J. Probab. 4 (1999), 1-29; MR1684157 (2000b:60132)]. Electron. J. Probab. 6 (2001), .Google Scholar
Dalang, R., Khoshnevisan, D., Mueller, C., Nualart, D. and Xiao, Y.. A minicourse on stochastic partial differential equations. Lecture Notes in Mathematics, Vol.1962 (Springer-Verlag, Berlin, 2009).Google Scholar
Fedrizzi, E., Flandoli, F., Priola, E. and Vovelle, J.. Regularity of stochastic kinetic equations. Electronic Journal of Probability. 22, (2017).CrossRefGoogle Scholar
Fischer, V. and Ruzhanksy, M.. Quantization on nilpotent Lie groups. Progress in Mathematics, Vol. 314 Progress in Mathematics (Birkhäuser/Springer, Basel 2016).Google Scholar
Folland, G. B.. Subelliptic estimates and function spaces on nilpotent Lie groups. Ark. Mat. 13 (1975), 161–207.CrossRefGoogle Scholar
Folland, G. B. and Stein, E. M.. Estimates for the ${\bar\partial}_{b}$ complex and analysis on the Heisenberg group. Comm. Pure Appl. Math. 27 (1974), 429–522.CrossRefGoogle Scholar
Folland, G. B. and Stein, E. M.. Parametrices and estimates for the ${\bar\partial}_{b}$ complex on strongly pseudoconvex boundaries. Bull. Amer. Math. Soc. 80 (1974), 253–258.CrossRefGoogle Scholar
Folland, G. B. and Stein, E. M.. Hardy spaces on homogeneous groups. Mathematical Notes, Vol. 28 (University of Tokyo Press, Tokyo, 1982).Google Scholar
Friz, P. and Hairer, M.. A Course on Rough paths: With an Introduction to Regularity structures (Universitext, (Springer International Publishing, 2020). ).CrossRefGoogle Scholar
Frobenius, G.. Über das Pfaffsche Problem. J. Reine Angew. Math. 82 (1877), 230–315.Google Scholar
Gerencsér, M. and Hairer, M.. Singular SPDEs in domains with boundaries. Probab. Theory Related Fields. 173 (2019), 697–758.CrossRefGoogle Scholar
Gerencsér, M. and Hairer, M.. A solution theory for quasilinear singular SPDEs. Comm. Pure Appl. Math. 72 (2019), 1983–2005.CrossRefGoogle Scholar
Gerencsér, M. and Hairer, M.. Boundary renormalisation of SPDEs. Comm. Partial Differential Equations. 47 (2022), 2070–2123.CrossRefGoogle Scholar
Gubinelli, M., Imkeller, P. and Perkowski, N.. Paracontrolled distributions and singular PDEs. Forum Math. Pi. 3 (2015), .CrossRefGoogle Scholar
Gubinelli, M., Ugurcan, B. and Zachhuber, I.. Semilinear evolution equations for the Anderson Hamiltonian in two and three dimensions. Stochastics and Partial Differential Equations: Analysis and Computations. 8 (2019), 82–149.CrossRefGoogle Scholar
Hörmander, L.. Hypoelliptic second order differential equations. Acta Mathematica. 119 (1967), 147–171.CrossRefGoogle Scholar
Hairer, M.. A theory of regularity structures. Inventiones Mathematicae. 198 (2014), 269–504.CrossRefGoogle Scholar
Hairer, M., Advanced stochastic analysis, Tech. Rep. (University of Warwick, 2016). Available at http://hairer.org/notes/Malliavin.pdf.Google Scholar
Hairer, M. and Labbé, C.. A simple construction of the continuum parabolic Anderson model on $\mathbb{R}^2$. Electron. Commun. Probab. 20 (2015), .CrossRefGoogle Scholar
Hairer, M. and Labbé, C.. Multiplicative stochastic heat equations on the whole space. J. Eur. Math. Soc. 20 (2018), 1005–1054.CrossRefGoogle Scholar
Hairer, M. and Pardoux, E.. A Wong–Zakai theorem for stochastic PDEs. J. Math. Soc. Japan. 67 (2015), 1551–1604.CrossRefGoogle Scholar
Hairer, M. and Singh, H.. Regularity structures on manifolds and vector bundles. (2023), arXiv preprint, arXiv:2308.05049.Google Scholar
Hairer, M. and Singh, H.. Periodic space-time homogenisation of the $\unicode{x03D5}^4_2$ equation. J. Funct. Anal. 288, (2025).CrossRefGoogle Scholar
Hairer, M. and Steele, R.. The BPHZ theorem for regularity structures via the spectral gap inequality. Paper No. 248 (2024), .Google Scholar
Hao, Z., Zhang, X., Zhu, R. and Zhu, X.. Singular kinetic equations and applications. Ann. Probab. 52 (2024), 576–657.CrossRefGoogle Scholar
Il’in, A. M. and Khas’minskii, R. Z.. On equations of brownian motion. Theory of Probability & Its Applications. 9 (1964), 421–444.CrossRefGoogle Scholar
König, W.. The parabolic Anderson model: random walk in random potential. Pathways in Mathematics (Basel: Springer International Publishing, 2016).Google Scholar
Labbé, C.. The continuous Anderson Hamiltonian in $d\leqslant 3$. J. Funct. Anal. 277 (2019), 3187–3235.CrossRefGoogle Scholar
Lee, J. M.. Introduction to smooth manifolds. Graduate Texts in Mathematics, 2nd edn., Vol. 218 (Springer, New York, 2013).Google Scholar
Linares, P. and Otto, F.. A tree-free approach to regularity structures: the regular case for quasi-linear equations. (2022), arXiv preprint, arXiv:2207.10627.Google Scholar
Linares, P., Otto, F. and Tempelmayr, M.. The structure group for quasi-linear equations via universal enveloping algebras. Commun. Am. Math. Soc. 3 (2023), 1–64.CrossRefGoogle Scholar
Lototsky, S. V. and Rozovsky, B. L.. Stochastic Partial Differential Equations (Springer, 2017).CrossRefGoogle Scholar
Manfredini, M.. The Dirichlet problem for a class of ultraparabolic equations. Adv. Differential Equations. 2 (1997), 831–866.CrossRefGoogle Scholar
Otto, F., Sauer, J., Smith, S. and Weber, H.. A priori bounds for quasi-linear SPDEs in the full sub-critical regime. (2021), arXiv preprint, arXiv:2103.11039.Google Scholar
Otto, F. and Weber, H.. Quasilinear SPDEs via rough paths. Archive for Rational Mechanics and Analysis. 232 (2019), 873–950.CrossRefGoogle Scholar
Peszat, S. and Tindel, S.. Stochastic heat and wave equations on a Lie group. Stoch. Anal. Appl. 28 (2010), 662–695.CrossRefGoogle Scholar
Prévôt, C. and Röckner, M.. A Concise Course on Stochastic Partial Differential Equations (Springer, 2007).Google Scholar
Raghunathan, M. S.. Discrete subgroups of Lie groups. Math. Student. (2007), 59–70.Google Scholar
Rothschild, L. P. and Stein, E. M.. Hypoelliptic differential operators and nilpotent groups. Acta Mathematica. 137 (1976), 247–320.CrossRefGoogle Scholar
Singh, H.. Canonical solutions to non-translation invariant singular SPDEs. (2023), arXiv preprint, arXiv:2310.01085.Google Scholar
Tindel, S. and Viens, F.. On space-time regularity for the stochastic heat equation on Lie groups. J. Funct. Anal. 169 (1999), 559–603.CrossRefGoogle Scholar
Tindel, S. and Viens, F.. Regularity conditions for parabolic SPDEs on Lie groups. in Seminar on Stochastic Analysis, Random Fields and Applications, III (Ascona, 1999), Progr. Probab., Vol.52, (Birkhäuser, Basel, 2002).Google Scholar
Walsh, J. B.. An introduction to stochastic partial differential equations, in École d’été de probabilités de Saint-Flour, XIV—1984. Lecture Notes in Math., Vol.1180, (Springer, Berlin, 1986).Google Scholar