Hostname: page-component-7f64f4797f-kjzhn Total loading time: 0 Render date: 2025-11-04T08:55:41.265Z Has data issue: false hasContentIssue false
  • English
  • Français

On a class of special Euler–Lagrange equations

Part of: Equations and systems of special type Representations of solutions Optimality conditions

Published online by Cambridge University Press:  21 September 2023

Baisheng Yan Open the ORCID record for Baisheng Yan [Opens in a new window]
Baisheng Yan*
Affiliation:
Department of Mathematics, Michigan State University, East Lansing, MI 48824, USA (yanb@msu.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

We make some remarks on the Euler–Lagrange equation of energy functional $I(u)=\int _\Omega f(\det Du)\,{\rm d}x,$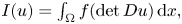 where $f\in C^1(\mathbb {R}).$ 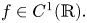For certain weak solutions $u$ 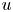we show that the function $f'(\det Du)$ 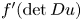must be a constant over the domain $\Omega$ 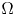and thus, when $f$ 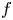is convex, all such solutions are an energy minimizer of $I(u).$ 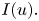However, other weak solutions exist such that $f'(\det Du)$ 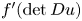is not constant on $\Omega.$ 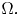We also prove some results concerning the homeomorphism solutions, non-quasimonotonicity and radial solutions, and finally we prove some stability results and discuss some related questions concerning certain approximate solutions in the 2-Dimensional cases.

Keywords

Special Euler–Lagrange equationshomeomorphism solutionsradial solutions

MSC classification

Primary: 35D30: Weak solutions
Secondary: 35M30: Systems of mixed type 49K20: Problems involving partial differential equations

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 155 , Issue 2 , April 2025 , pp. 429 - 452
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ball, J. M.. Global invertibility of Sobolev functions and the interpenetration of matter. Proc. R. Soc. Edinburgh. 88A (1981), 315–328.CrossRefGoogle Scholar
Chabrowski, J. and Zhang, K.. Quasi-monotonicity and perturbated systems with critical growth. Indiana Univ. Math. J. 41 (1992), 483–504.CrossRefGoogle Scholar
Dacorogna, B.. A relaxation theorem and its application to the equilibrium of gases. Arch. Rational Mech. Anal. 77 (1981), 359–386.CrossRefGoogle Scholar
Dacorogna, B.. Direct methods in the calculus of variations, 2nd Ed. (Springer-Verlag, Berlin, Heidelberg, New York, 2008).Google Scholar
Evans, L. C., Savin, O. and Gangbo, W.. Diffeomorphisms and nonlinear heat flows. SIAM J. Math. Anal. 37 (2005), 737–751.CrossRefGoogle Scholar
Fuchs, M.. Regularity theorems for nonlinear systems of partial differential equations under natural ellipticity conditions. Analysis 7 (1987), 83–93.CrossRefGoogle Scholar
Hamburger, C.. Quasimonotonicity, regularity and duality for nonlinear systems of partial differential equations. Annali di Matematica pura ed applicata (IV). 169 (1995), 321–354.Vol. CLXIXCrossRefGoogle Scholar
Kirchheim, B., Müller, S. and Šverák, V., Studying nonlinear pde by geometry in matrix space, in Geometric analysis and nonlinear partial differential equations (Springer, Berlin, 2003), pp. 347–395.CrossRefGoogle Scholar
Krömer, S.. Global invertibility for orientation-preserving Sobolev maps via invertibility on or near the boundary. Arch. Ration. Mech. Anal. 238 (2020), 1113–1155.CrossRefGoogle Scholar
Kristensen, J. and Mingione, G.. The singular set of minima of integral functionals. Arch. Ration. Mech. Anal. 180 (2006), 331–398.CrossRefGoogle Scholar
Landes, R.. Quasimonotone versus pseudomonotone. Proc. Royal Soc. Edinburgh. 126A (1996), 705–717.CrossRefGoogle Scholar
Lehto, O. and Virtanen, K.. Quasiconformal mappings in the plane (Springer-Verlag, New York, 1973).CrossRefGoogle Scholar
Müller, S. and Šverák, V.. Convex integration for Lipschitz mappings and counterexamples to regularity. Ann. Math (2). 157 (2003), 715–742.CrossRefGoogle Scholar
Marcus, M. and Mizel, V. J.. Transformations by functions in Sobolev spaces and lower semicontinuity for parametric variational problems. Bull. Amer. Math. Soc. 79 (1973), 790–795.CrossRefGoogle Scholar
Reshetnyak, Yu. G., Space Mappings with Bounded Distortion, Transl. Math. Monograph, 73, Amer. Math. Soc., 1989.Google Scholar
Székelyhidi, L. Jr. The regularity of critical points of polyconvex functionals. Arch. Ration. Mech. Anal. 172 (2004), 133–152.CrossRefGoogle Scholar
Taheri, A.. On critical points of functionals with polyconvex integrands. J. Convex Anal. 9 (2002), 55–72.Google Scholar
Tartar, L., Some remarks on separately convex functions, in Microstructure and Phase Transitions, IMA Vol. Math. Appl. 54 (D. Kinderlehrer, R. D. James, M. Luskin and J. L. Ericksen, eds.) (Springer-Verlag, New York, 1993), pp. 191–204.CrossRefGoogle Scholar
Tione, R., Critical points of degenerate polyconvex energies. arXiv:2203.12284v1[math.AP] 23 Mar 2022.Google Scholar
Yan, B.. Convex integration for diffusion equations and Lipschitz solutions of polyconvex gradient flows. Calc. Var. Partial Differ. Equ. 59 (2020), 123.CrossRefGoogle Scholar
Zhang, K., On the Dirichlet problem for a class of quasilinear elliptic systems of partial differential equations in divergence form, in ‘Proceedings of Tianjin Conference on Partial Differential Equations in 1986’, (S. S. Chern ed.) Vol. 1306, Lecture Notes in Mathematics, (Springer, Berlin, Heidelberg, New York, 1988), pp. 262–277.Google Scholar