Hostname: page-component-7dd5485656-bt4hw Total loading time: 0 Render date: 2025-10-30T20:51:34.694Z Has data issue: false hasContentIssue false
  • English
  • Français

BP-cohomology of projective Stiefel manifolds

Part of: Homology and homotopy of topological groups and related structures Homology and cohomology theories Spectral sequences Homotopy theory

Published online by Cambridge University Press:  21 March 2022

Samik Basu  and
Debanil Dasgupta
Samik Basu
Affiliation:
Stat-Math Unit, Indian Statistical Institute, B. T. Road, Kolkata 700108, India (samik.basu2@gmail.com; samikbasu@isical.ac.in; debanil12@gmail.com)
Debanil Dasgupta
Affiliation:
Stat-Math Unit, Indian Statistical Institute, B. T. Road, Kolkata 700108, India (samik.basu2@gmail.com; samikbasu@isical.ac.in; debanil12@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we compute the $BP$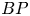-cohomology of complex projective Stiefel manifolds. The method involves the homotopy fixed point spectral sequence, and works for complex oriented cohomology theories. We also use these calculations and $BP$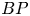-operations to prove new results about equivariant maps between Stiefel manifolds.

Keywords

Stiefel manifoldsBP-cohomologyprojective Stiefel manifoldshomotopy fixed point spectral sequence

MSC classification

Primary: 55N20: Generalized (extraordinary) homology and cohomology theories 57T15: Homology and cohomology of homogeneous spaces of Lie groups
Secondary: 55T25: Generalized cohomology 55P91: Equivariant homotopy theory

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 2 , April 2023 , pp. 679 - 701
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adams, J. F.. Stable homotopy and generalised homology, Chicago Lectures in Mathematics (University of Chicago Press, Chicago, IL, 1995). Reprint of the 1974 original.Google Scholar
Araki, S.. Multiplicative operations in $BP$ cohomology. Osaka Math. J. 12 (1975), 343–356.Google Scholar
Astey, L., Gitler, S., Micha, E. and Pastor, G.. Cohomology of complex projective Stiefel manifolds. Canad. J. Math. 51 (1999), 897–914.CrossRefGoogle Scholar
Basu, S. and Kundu, B.. The index of certain stiefel manifolds. available at https://arxiv.org/abs/2103.02500.Google Scholar
Basu, S. and Subhash, B.. Topology of certain quotient spaces of Stiefel manifolds. Canad. Math. Bull. 60 (2017), 235–245.CrossRefGoogle Scholar
Boardman, J. M.. Conditionally convergent spectral sequences, in Homotopy invariant algebraic structures (Baltimore, MD, 1998), vol. 239 of Contemp. Math., Amer. Math. Soc., Providence, RI, 1999, pp. 49–84.CrossRefGoogle Scholar
Borel, A.. Sur la cohomologie des espaces fibrés principaux et des espaces homogènes de groupes de Lie compacts. Ann. Math. (2) 57 (1953), 115–207.CrossRefGoogle Scholar
Bruner, R. R. and Rognes, J.. Differentials in the homological homotopy fixed point spectral sequence. Algebr. Geom. Topol. 5 (2005), 653–690.CrossRefGoogle Scholar
Conner, P. E. and Floyd, E. E.. The relation of cobordism to K-theories, Lecture Notes in Mathematics, Vol. 28 (Springer-Verlag, Berlin-New York, 1966).CrossRefGoogle Scholar
Dugger, D.. Multiplicative structures on homotopy spectral sequences II. 2003.Google Scholar
Gitler, S. and Handel, D.. The projective Stiefel manifolds. I Topology 7 (1968), 39–46.CrossRefGoogle Scholar
Greenlees, J. P. C. and May, J. P.. Generalized Tate cohomology. Mem. Amer. Math. Soc. 113 (1995), viii+178.Google Scholar
Gondhali, S.. The complex $K^{*}$ ring of the complex projective Stiefel manifold. J. Algebraic Combin. 51 (2020), 455–468.CrossRefGoogle Scholar
May, J. P.. Equivariant homotopy and cohomology theory, vol. 91 of CBMS Regional Conference Series in Mathematics, Published for the Conference Board of the Mathematical Sciences, Washington, DC; by the American Mathematical Society, Providence, RI, 1996. With contributions by M. Cole, G. Comezaña, S. Costenoble, A. D. Elmendorf, J. P. C. Greenlees, L. G. Lewis, Jr., R. J. Piacenza, G. Triantafillou, and S. Waner.Google Scholar
Mimura, M. and Toda, H.. Topology of Lie groups. I, II, Vol. 91 of Translations of Mathematical Monographs American Mathematical Society, Providence, RI, 1991. Translated from the 1978 Japanese edition by the authors.Google Scholar
Mosher, R. E. and Tangora, M. C.. Cohomology operations and applications in homotopy theory (Harper & Row, Publishers, New York-London, 1968).Google Scholar
Petrović, Z. Z. and Prvulović, B. I.. Equivariant maps between complex Stiefel manifolds. Osaka J. Math. 50 (2013), 187–196.Google Scholar
Ravenel, D. C.. Complex cobordism and stable homotopy groups of spheres, vol. 121 of Pure and Applied Mathematics, Academic Press, Inc., Orlando, FL, 1986.Google Scholar
Smith, L.. Some remarks on projective Stiefel manifolds, immersions of projective spaces and spheres. Proc. Amer. Math. Soc. 80 (1980), 663–669.CrossRefGoogle Scholar
Whitehead, G. W.. Elements of homotopy theory, Vol. 61 of Graduate Texts in Mathematics (Springer-Verlag, New York-Berlin, 1978).Google Scholar