Hostname: page-component-7dd5485656-wxk4p Total loading time: 0 Render date: 2025-10-31T06:30:28.792Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetrized and non-symmetrized asymptotic mean value Laplacian in metric measure spaces

Part of: Partial differential equations Analysis on metric spaces Elliptic equations and systems

Published online by Cambridge University Press:  28 November 2023

Andreas Minne Open the ORCID record for Andreas Minne [Opens in a new window]  and
David Tewodrose Open the ORCID record for David Tewodrose [Opens in a new window]
Andreas Minne
Affiliation:
KTH Royal Institute of Technology, 100 44 Stockholm, Sweden (minne@kth.se)
David Tewodrose
Affiliation:
Laboratoire de Mathématiques Jean Leray, Nantes Université, UMR CNRS 6629, 2 rue de la Houssiniére BP 92208, F-44322 Nantes Cedex 3, France (david.tewodrose@vub.be)
Get access Rights & Permissions [Opens in a new window]

Abstract

The asymptotic mean value Laplacian—AMV Laplacian—extends the Laplace operator from $\mathbb {R}^n$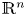 to metric measure spaces through limits of averaging integrals. The AMV Laplacian is however not a symmetric operator in general. Therefore, we consider a symmetric version of the AMV Laplacian, and focus lies on when the symmetric and non-symmetric AMV Laplacians coincide. Besides Riemannian and 3D contact sub-Riemannian manifolds, we show that they are identical on a large class of metric measure spaces, including locally Ahlfors regular spaces with suitably vanishing distortion. In addition, we study the context of weighted domains of $\mathbb {R}^n$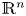—where the two operators typically differ—and provide explicit formulae for these operators, including points where the weight vanishes.

Keywords

Laplace operatormetric measure spacemean value propertyaverage integral

MSC classification

Primary: 35J05: Laplacian operator, reduced wave equation (Helmholtz equation), Poisson equation
Secondary: 35B05: Oscillation, zeros of solutions, mean value theorems, etc. 30L99: None of the above, but in this section

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 155 , Issue 3 , June 2025 , pp. 916 - 953
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adamowicz, T., Kijowski, A. and Soultanis, E.. Asymptotically mean value harmonic functions in doubling metric measure spaces. Anal. Geom. Metric Spaces 10 (2022), 344–372.CrossRefGoogle Scholar
Adamowicz, T., Kijowski, A. and Soultanis, E.. Asymptotically mean value harmonic functions in subriemannian and RCD settings. J. Geom. Anal. 33 (2023), 80.CrossRefGoogle Scholar
Agrachev, A., Barilari, D. and Boscain, U.. A comprehensive introduction to sub-Riemannian geometry, Vol. 181 (Cambridge University Press, Cambridge, 2019).CrossRefGoogle Scholar
Aldaz, J. M.. Local comparability of measures, averaging and maximal averaging operators. Potential Anal. 49 (2018), 309–330.CrossRefGoogle Scholar
Aldaz, J. M.. Boundedness of averaging operators on geometrically doubling metric spaces. Annes Acad. Scienti. Fennicae Math. 44 (2019), 497–503.CrossRefGoogle Scholar
Ambrosio, L., Calculus, heat flow and curvature-dimension bounds in metric measure spaces. In Proceedings of the International Congress of Mathematicians: Rio de Janeiro 2018 (World Scientific, 2018), pp. 301–340. .CrossRefGoogle Scholar
Barilari, D., Beschastnyi, I. and Lerario, A.. Volume of small balls and sub-Riemannian curvature in 3D contact manifolds. J. Symplectic Geom. 18 (2020), 355–384.CrossRefGoogle Scholar
Barlow, M. T., Diffusions on fractals. In Lectures on probability theory and statistics. (Springer, 1998), pp. 1–121.CrossRefGoogle Scholar
Bourdon, M. and Pajot, H.. Poincaré inequalities and quasiconformal structure on the boundary of some hyperbolic buildings. Proc. Am. Math. Soc. 127 (1999), 2315–2324.CrossRefGoogle Scholar
Bruè, E., Mondino, A. and Semola, D.. The metric measure boundary of spaces with Ricci curvature bounded below. Geom. Funct. Anal. 33 (2023), 593–636.CrossRefGoogle Scholar
Colbois, B., El Soufi, A. and Savo, A.. Eigenvalues of the laplacian on a compact manifold with density. Communi. Anal. Geom. 23 (2015), 639–670.CrossRefGoogle Scholar
De Philippis, G. and Gigli, N.. Non-collapsed spaces with Ricci curvature bounded from below. J. de l’École Polytechnique—Mathématiques 5 (2018), 613–650.CrossRefGoogle Scholar
Gallot, S., Hulin, D. and Lafontaine, J.. Riemannian geometry, Vol. 2 (Springer-Verlag, Berlin, 1990).CrossRefGoogle Scholar
Gigli, N.. Nonsmooth differential geometry—an approach tailored for spaces with Ricci curvature bounded from below. Mem. Amer. Math. Soc. 251 (2018), 161.Google Scholar
Heinonen, J., Koskela, P., Shanmugalingam, N. and Tyson, J. T.. Sobolev spaces on metric measure spaces, Vol. 27 (Cambridge University Press, Cambridge, 2015).CrossRefGoogle Scholar
Kapovitch, V., Lytchak, A. and Petrunin, A.. Metric-measure boundary and geodesic flow on Alexandrov spaces. J. Euro. Math. Soc. 23 (2020), 29–62.CrossRefGoogle Scholar
Kijowski, A.. Characterization of mean value harmonic functions on norm induced metric measure spaces with weighted Lebesgue measure. Electron. J. Diff. Equ. 2020 (2020), 1–26.Google Scholar
Kleiner, B. and Schioppa, A.. PI spaces with analytic dimension 1 and arbitrary topological dimension. Indiana Univ. Math. J. 66 (2017), 495–546.CrossRefGoogle Scholar
Korevaar, N. J. and Schoen, R. M.. Sobolev spaces and harmonic maps for metric space targets. Comm. Anal. Geom. 1 (1993), 561–659.CrossRefGoogle Scholar
Laakso, T. J.. Ahlfors $Q$-regular spaces with arbitrary $Q>1$ admitting weak Poincaré inequality. Geom. Funct. Anal. 10 (2000), 111–123.CrossRefGoogle Scholar
Minne, A. and Tewodrose, D.. Asymptotic mean value Laplacian in metric measure spaces. J. Math. Anal. Appl. 491 (2020), 124330.CrossRefGoogle Scholar
Munteanu, O. and Wang, J.. Smooth metric measure spaces with non-negative curvature. Communi. Anal. Geom. 19 (2011), 451–486.CrossRefGoogle Scholar
Naor, A. and Tao, T.. Random martingales and localization of maximal inequalities. J. Funct. Anal. 259 (2010), 731–779.CrossRefGoogle Scholar