Hostname: page-component-7dd5485656-hw7sx Total loading time: 0 Render date: 2025-10-31T06:55:52.675Z Has data issue: false hasContentIssue false
  • English
  • Français

Principal bundle structure of the space of metric measure spaces

Part of: Global differential geometry Differential topology

Published online by Cambridge University Press:  18 November 2024

Daisuke Kazukawa ,
Hiroki Nakajima  and
Takashi Shioya
Daisuke Kazukawa
Affiliation:
Faculty of Mathematics, Kyushu University, Fukuoka-shi, Fukuoka-ken 819-0395, Japan (kazukawa@math.kyushu-u.ac.jp) (corresponding author)
Hiroki Nakajima
Affiliation:
Mathematical Sciences Course, Ehime University, Matsuyama-shi, Ehime-ken 790-8577, Japan (nakajima.hiroki.nz@ehime-u.ac.jp)
Takashi Shioya
Affiliation:
Mathematical Institute, Tohoku University, Sendai-shi, Miyagi-ken 980-8578, Japan (shioya@math.tohoku.ac.jp)
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the topological structure of the space 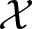$\mathcal{X}$ of isomorphism classes of metric measure spaces equipped with the box or concentration topologies. We consider the scale-change action of the multiplicative group 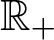${\mathbb{R}}_+$ of positive real numbers on 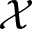$\mathcal{X}$, which has a one-point metric measure space, say $*$, as only one fixed-point. We prove that the 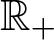${\mathbb{R}}_+$-action on 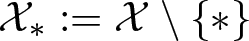$\mathcal{X}_* := \mathcal{X} \setminus \{*\}$ admits the structure of non-trivial and locally trivial principal 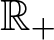${\mathbb{R}}_+$-bundle over the quotient space. Our bundle 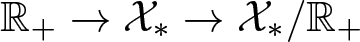${\mathbb{R}}_+ \to \mathcal{X}_* \to \mathcal{X}_*/{\mathbb{R}}_+$ is a curious example of a non-trivial principal fibre bundle with contractible fibre. A similar statement is obtained for the pyramidal compactification of 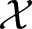$\mathcal{X}$, where we completely determine the structure of the fixed-point set of the 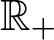${\mathbb{R}}_+$-action on the compactification.

Keywords

Box distanceconcentration topologymetric measure spaceprincipal bundlepyramid

MSC classification

Primary: 53C23: Global geometric and topological methods (à la Gromov); differential geometric analysis on metric spaces
Secondary: 57R22: Topology of vector bundles and fiber bundles

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 31
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Banakh, T., Cauty, R. and Zarichnyi, M.. Open problems in infinite-dimensional topology. Open Problems in Topology, II, (ed. Pearl, E.), (Elsevier, 2007), .Google Scholar
Choksi, J. R.. Inverse limits of measure spaces. Proc. London Math. Soc. (3). 8 (1958), 321–342.CrossRefGoogle Scholar
Dold, A.. Partitions of unity in the theory of fibrations. Ann. Math. (2). 78 (1963), 223–255.CrossRefGoogle Scholar
Esaki, S., Kazukawa, D. and Mitsuishi, A.. Invariants for Gromov’s pyramids and their applications. Adv. Math. 442 (2024), .CrossRefGoogle Scholar
Greven, A., Pfaffelhuber, P. and Winter, A.. Convergence in distribution of random metric measure spaces (Λ-coalescent measure trees). Probab. Theory Related Fields. 145 (2009), 285–322.CrossRefGoogle Scholar
Gromov, M.. Metric Structures for Riemannian and non-Riemannian spaces Modern BirkhÄuser Classics. , (Birkhäuser Boston, Inc., Boston, MA, 2007) ISBN 978-0-8176-4582-3, ISBN 0-8176-4582-9.Google Scholar
Husemoller, D.. Fibre bundles Graduate Texts in Mathematics. 3rd edn, Vol. 20, , (Springer-Verlag, New York, 1994) ISBN 0-387-94087-1.CrossRefGoogle Scholar
Ivanov, A. O. and Tuzhilin, A. A.. Isometry group of Gromov–Hausdorff space. Mat. Vesnik. 71 (2019), 123–154.Google Scholar
Kazukawa, D.. Concentration of product spaces. Anal. Geom. Metr. Spaces. 9 (2021), 186–218.CrossRefGoogle Scholar
Kazukawa, D.. Convergence of metric transformed spaces. Israel J. Math. 252 (2022), 243–290.CrossRefGoogle Scholar
Kazukawa, D., Nakajima, H. and Shioya, T.. Topological aspects of the space of metric measure spaces. Geom. Dedicata. 218 (2024), .CrossRefGoogle Scholar
Löhr, W.. Equivalence of Gromov-Prohorov- and Gromov’s $\underline{\square}_\lambda$-metric on the space of metric measure spaces. Electron. Commun. Probab. 18 (2013), .Google Scholar
Lévy, P.. Problèmes Concrets d’Analyse fonctionnelle. Avec un compléMent sur les Fonctionnelles Analytiques par F. Pellegrino. 2nd edn, , (Gauthier-Villars, Paris, 1951) French.Google Scholar
Ledoux, M.. The Concentration of Measure phenomenon, Mathematical Surveys and Monographs. Vol. 89, , (American Mathematical Society, Providence, RI, 2001) ISBN 0-8218-2864-9.Google Scholar
Milman, V. D.. The heritage of P. Lévy in geometrical functional analysis, Colloque Paul Lévy sur les Processus Stochastiques (Palaiseau, 1987). AstéRisque 157–158 (1988), 273–301.Google Scholar
Ozawa, R. and Shioya, T.. Limit formulas for metric measure invariants and phase transition property. Math. Z. 280 (2015), 759–782.CrossRefGoogle Scholar
Ozawa, R. and Yokota, T.. Stability of RCD condition under concentration topology. Calc. Var. Part. Differ. Equ. 58 (2019), .CrossRefGoogle Scholar
Shioya, T.. Gromov’s theory of convergence and concentration of metrics and measures, Metric Measure geometry, IRMA Lectures in Mathematics and Theoretical Physics. Vol. 25, , (EMS Publishing House, Zürich, 2016) ISBN 978-3-03719-158-3.CrossRefGoogle Scholar
Sturm, K. -T.. The space of spaces: curvature bounds and gradient flows on the space of metric measure spaces. Mem. Amer. Math. Soc. 290 (2023), .Google Scholar