Hostname: page-component-7dd5485656-j7khd Total loading time: 0 Render date: 2025-10-30T12:37:37.242Z Has data issue: false hasContentIssue false
  • English
  • Français

General study on limit cycle bifurcation near a double eight figure loop

Part of: Local and nonlocal bifurcation theory Qualitative theory

Published online by Cambridge University Press:  18 November 2024

Hongwei Shi
Hongwei Shi*
Affiliation:
School of Mathematical Sciences, Qufu Normal University, Qufu, Shandong 273165, P.R. China (shihw7@qfnu.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we explore the bifurcation problem of limit cycles near the double eight figure loop (compound cycle with a 2-polycycle connecting two homoclinic loops). A general theory is established to find the lower bound of the maximal number of limit cycles (isolated periodic orbits) near the double eight figure loop. The Liénard system, a well-known nonlinear dynamical model, appears in a natural way in physics, chemistry, engineering, and so on, where periodic phenomena play a relevant role. As an application, we investigate an 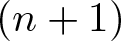$(n+1)$th-order generalized Liénard system and prove the system has at least 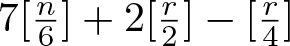$7[\frac{n}{6}]+2[\frac{r}{2}]-[\frac{r}{4}]$ limit cycles near the double eight figure loop for any 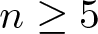$n\geq5$ and 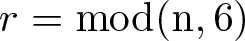$r=\rm mod(n,6)$, and their distribution is also gained.

Keywords

heteroclinic loophomoclinic loopLiénard systemlimit cycleMelnikov function

MSC classification

Primary: 34C07: Theory of limit cycles of polynomial and analytic vector fields (existence, uniqueness, bounds, Hilbert's 16th problem and ramifications)
Secondary: 37G15: Bifurcations of limit cycles and periodic orbits

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 17
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Arnold, V. I.. Loss of stability of self-oscillations close to resonance and versal deformations of equivariant vector fields. Funct. Anal. Appl. 11 (1977), 85–92.CrossRefGoogle Scholar
Asheghi, R. and Zangeneh, H. R. Z.. Bifurcations of limit cycles from quintic Hamiltonian systems with an eye-figure loop. Nonlinear Anal. 68 (2008), 2957–2976.CrossRefGoogle Scholar
Asheghi, R. and Zangeneh, H. R. Z.. Bifurcations of limit cycles from quintic Hamiltonian systems with an eye-figure loop. II. Nonlinear Anal. 69 (2008), 4143–4162.CrossRefGoogle Scholar
Cen, X., Liu, C., Sun, Y. and Wang, J.. Cyclicity of period annulus for a class of quadratic reversible systems with a nonrational first integral. Proc. Roy. Soc. Edinburgh Sect. A 153 (2023), 1706–1728.CrossRefGoogle Scholar
Chen, H., Chen, X., Jia, M. and Tang, Y.. A quintic $\Bbb Z_2$-equivariant Liénard system arising from the complex Ginzburg-Landau equation. SIAM J. Math. Anal. 55 (2023), 5993–6038.CrossRefGoogle Scholar
Chen, H., Feng, Z., Li, Z. and Wang, Z.. Dynamical behaviors of van der Pol-Duffing systems with indefinite degree. Discrete Contin. Dyn. Syst. 44 (2024), 281–317.CrossRefGoogle Scholar
Dulac, H.. Sur les cycles limites. Bull. Soc. Math. France 51 (1923), 45–188.CrossRefGoogle Scholar
Dumortier, F. and Li, C.. Perturbation from an elliptic Hamiltonian of degree four. IV. Figure eight-loop. J. Differ. Equ. 188 (2003), 512–554.CrossRefGoogle Scholar
Euzébio, R. D., Llibre, J. and Tonon, D. J.. Lower bounds for the number of limit cycles in a generalised Rayleigh-Liénard oscillator. Nonlinearity 35 (2022), 3883–3906.CrossRefGoogle Scholar
García-Saldaña, J. D., Gasull, A. and Giacomini, H.. A new approach for the study of limit cycles. J. Differ. Equ. 269 (2020), 6269–6292.CrossRefGoogle Scholar
Gavrilov, L. and Iliev, I. D.. Perturbations of quadratic Hamiltonian two-saddle cycles. Ann. Inst. H. Poincaré C Anal. Non Linéaire. 32 (2015), 307–324.CrossRefGoogle Scholar
Gavrilov, L. and Iliev, I. D.. The limit cycles in a generalized Rayleigh-Liénard oscillator. Discrete Contin. Dyn. Syst. 43 (2023), 2381–2400.CrossRefGoogle Scholar
Geng, W. and Tian, Y.. Bifurcation of limit cycles near heteroclinic loops in near-Hamiltonian systems. Commun. Nonlinear Sci. Numer. Simul. 95 (2021), .CrossRefGoogle Scholar
Han, M.. On Hopf cyclicity of planar systems. J. Math. Anal. Appl. 245 (2000), 404–422.CrossRefGoogle Scholar
Han, M.. Asymptotic expansions of Melnikov functions and limit cycle bifurcations. Internat. J. Bifur. Chaos Appl. Sci. Engrg. 22 (2012), .CrossRefGoogle Scholar
Han, M.. Bifurcation Theory of Limit Cycles (Alpha Science International Ltd.), Beijing, Beijing; Oxford, 2017.Google Scholar
Han, M., Yang, J. and Li, J.. General study on limit cycle bifurcation near a double homoclinic loop. J. Differ. Equ. 347 (2023), 1–23.CrossRefGoogle Scholar
Han, M., Yang, J., Tarţa, A. A. and Gao, Y.. Limit cycles near homoclinic and heteroclinic loops. J. Dynam. Differ. Equ. 20 (2008), 923–944.CrossRefGoogle Scholar
Han, M., and Ye, Y.. On the coefficients appearing in the expansion of Melnikov functions in homoclinic bifurcations. Ann. Differ. Equ. 14 (1998), 156–162.Google Scholar
Han, M., Zang, H. and Yang, J.. Limit cycle bifurcations by perturbing a cuspidal loop in a Hamiltonian system. J. Differ. Equ. 246 (2009), 129–163.CrossRefGoogle Scholar
Jiang, Q. and Han, M.. Melnikov functions and perturbation of a planar Hamiltonian system. Chinese Ann. Math. Ser. B 20 (1999), 233–246.CrossRefGoogle Scholar
Leimkuhler, B. and Reich, S.. Simulating Hamiltonian dynamics. Cambridge Monographs on Applied and Computational Mathematics, Vol. 14 (Cambridge University Press, Cambridge, 2004).Google Scholar
Li, L. and Yang, J.. On the number of limit cycles for a quintic Liénard system under polynomial perturbations. J. Appl. Anal. Comput. 9 (2019), 2464–2481.Google Scholar
Li, W., Llibre, J. and Zhang, X.. Melnikov functions for period annulus, nondegenerate centers, heteroclinic and homoclinic cycles. Pacific J. Math. 213 (2004), 49–77.CrossRefGoogle Scholar
Liu, C.. Estimate of the number of zeros of Abelian integrals for an elliptic Hamiltonian with figure-of-eight loop. Nonlinearity 16 (2003), 1151–1163.CrossRefGoogle Scholar
Petrov, G. S.. Complex zeroes of an elliptic integral. Funktsional. Anal. i Prilozhen. 23 (1989), 88–89.Google Scholar
Qi, M. and Zhao, L.. Bifurcations of limit cycles from a quintic Hamiltonian system with a figure double-fish. Internat. J. Bifur. Chaos Appl. Sci. Engrg. 23 (2013), .CrossRefGoogle Scholar
Roussarie, R.. On the number of limit cycles which appear by perturbation of separatrix loop of planar vector fields. Bol. Soc. Brasil. Mat. 17 (1986), 67–101.CrossRefGoogle Scholar
Tian, Y. and Han, M.. Hopf and homoclinic bifurcations for near-Hamiltonian systems. J. Differ. Equ. 262 (2017), 3214–3234.CrossRefGoogle Scholar
Tuckerman, M. E.. Statistical Mechanics: Theory and Molecular Simulation (Oxford Graduate Texts, Oxford University Press, Oxford, 2010).Google Scholar
Wei, L., Zhang, Q. and Zhang, X.. On limit cycles near two centres and a double homoclinic loop in Liénard differential system. J. Differ. Equ. 300 (2021), 226–251.CrossRefGoogle Scholar
Wei, L., Zhang, X., and Zhu, J.. Limit cycles near a centre and a heteroclinic loop in a near-Hamiltonian differential system. J. Dynam. Differ. Equ. 36 (2024), 405–420.CrossRefGoogle Scholar
Wu, Y., Han, M. and Chen, X.. On the study of limit cycles of the generalized Rayleigh-Lienard oscillator. Internat. J. Bifur. Chaos Appl. Sci. Engrg. 14 (2004), 2905–2914.CrossRefGoogle Scholar
Xiong, Y. and Zhong, H.. The number of limit cycles in a Z 2-equivariant Liénard system. Internat. J. Bifur. Chaos Appl. Sci. Engrg. 23 (2013), .CrossRefGoogle Scholar
Xu, W. and Li, C.. Number of limit cycles of some polynomial Liénard systems. Internat. J. Bifur. Chaos Appl. Sci. Engrg. 23 (2013), .CrossRefGoogle Scholar
Yang, J. and Han, M.. Limit cycles near a compound cycle in a near-Hamiltonian system with smooth perturbations. Chaos, Solitons and Fractals 184 (2024), .CrossRefGoogle Scholar
Yang, J. and Zhao, L.. The perturbation of a class of hyper-elliptic Hamilton system with a double eight figure loop. Qual. Theory Dyn. Syst. 16 (2017), 317–360.CrossRefGoogle Scholar
Zang, H., Zhang, T. and Chen, W.. Bifurcations of limit cycles from quintic Hamiltonian systems with a double figure eight loop. J. Complexity 20 (2004), 544–560.Google Scholar
Zang, H., Zhang, T. and Han, M.. Bifurcations of limit cycles from quintic Hamiltonian systems with a double figure eight loop. Bull. Sci. Math. 130 (2006), 71–86.CrossRefGoogle Scholar
Zhang, T., Tadé, M. O. and Tian, Y.. On the zeros of the Abelian integrals for a class of Liénard systems. Phys. Lett. A 358 (2006), 262–274.CrossRefGoogle Scholar
Zhang, T., Zang, H. and Tade, M. O.. Bifurcations of limit cycles for a perturbed cubic system with double figure eight loop. Internat. J. Bifur. Chaos Appl. Sci. Engrg. 23 (2013), .CrossRefGoogle Scholar
Zhao, L. and Li, D.. Bifurcations of limit cycles from a quintic Hamiltonian system with a heteroclinic cycle. Acta Math. Sin. (Engl. Ser.) 30 (2014), 411–422.CrossRefGoogle Scholar
Zhao, L., Qi, M. and Liu, C.. The cyclicity of period annuli of a class of quintic Hamiltonian systems. J. Math. Anal. Appl. 403 (2013), 391–407.CrossRefGoogle Scholar
Zhao, Y. and Zhang, Z.. Linear estimate of the number of zeros of Abelian integrals for a kind of quartic Hamiltonians. J. Differ. Equ. 155 (1999), 73–88.CrossRefGoogle Scholar