1 Introduction
On a normal variety X over a field of positive characteristic, a
![]() $1$
-foliation is a saturated sub-sheaf of
$1$
-foliation is a saturated sub-sheaf of
![]() $T_X$
that is closed under Lie brackets and pth powers. A fruitful construction, when having a
$T_X$
that is closed under Lie brackets and pth powers. A fruitful construction, when having a
![]() $1$
-foliation at our disposal, is the associated infinitesimal quotient of the underlying variety. It has been used multiple times to construct surprising or pathological examples in positive characteristic: see, for example, [Reference Hirokado20–Reference Hirokado22], [Reference Kurke34], [Reference Liedtke35], [Reference Miyanishi and Russell45], [Reference Rössler and Schröer52]. The goal of this paper is to study the singularities of such quotients.
$1$
-foliation at our disposal, is the associated infinitesimal quotient of the underlying variety. It has been used multiple times to construct surprising or pathological examples in positive characteristic: see, for example, [Reference Hirokado20–Reference Hirokado22], [Reference Kurke34], [Reference Liedtke35], [Reference Miyanishi and Russell45], [Reference Rössler and Schröer52]. The goal of this paper is to study the singularities of such quotients.
Since any finite purely inseparable morphism between normal varieties can be decomposed into a sequence of infinitesimal quotients, some restrictions on the
![]() $1$
-foliations are necessary if we want qualitative results about the singularities. It is well-known that, at least on regular varieties, quotients by so-called multiplicative derivations are particularly simple [Reference Hirokado21] (see Proposition 4.1). We give a mild generalization, in case the variety supporting the derivation is not necessarily regular. This applies in particular to quotient by
$1$
-foliations are necessary if we want qualitative results about the singularities. It is well-known that, at least on regular varieties, quotients by so-called multiplicative derivations are particularly simple [Reference Hirokado21] (see Proposition 4.1). We give a mild generalization, in case the variety supporting the derivation is not necessarily regular. This applies in particular to quotient by
![]() $1$
-foliations of rank
$1$
-foliations of rank
![]() $>1$
which are formally generated, up to saturation, by a finite set of commuting multiplicative derivations (
$>1$
which are formally generated, up to saturation, by a finite set of commuting multiplicative derivations (
![]() $1$
-foliations with at worst multiplicative singularities in our terminology: see Definition 2.20).
$1$
-foliations with at worst multiplicative singularities in our terminology: see Definition 2.20).
Theorem 1.1 (Iterated applications of Theorem 4.3)
Let X be a normal variety over a perfect field of characteristic
![]() $p>0$
, and let
$p>0$
, and let
![]() $\mathcal {F}$
be a
$\mathcal {F}$
be a
![]() $1$
-foliation on X with at worst multiplicative singularities. Then:
$1$
-foliation on X with at worst multiplicative singularities. Then:
-
1. If X is Cohen–Macaulay, so is
 $X/\mathcal {F}$
.
$X/\mathcal {F}$
. -
2. If X is F-pure (resp. F-rational, F-injective or F-regular), so is
 $X/\mathcal {F}$
.
$X/\mathcal {F}$
.
The idea is that any multiplicative derivation induces, after passing to an appropriate étale neighborhood, an action of the infinitesimal group scheme
![]() $\mu _p$
. Quotients by
$\mu _p$
. Quotients by
![]() $\mu _p$
-actions have the remarkable property that the inclusion of the sub-ring of invariants is split (see, e.g., [Reference Jantzen26, I.2.11]), and many cohomological properties are stable by taking a split sub-ring of equal dimension.
$\mu _p$
-actions have the remarkable property that the inclusion of the sub-ring of invariants is split (see, e.g., [Reference Jantzen26, I.2.11]), and many cohomological properties are stable by taking a split sub-ring of equal dimension.
It is interesting to note that not every usual cohomological property descends to quotients by multiplicative derivations: for example, the Gorenstein property usually does not (see Remark 4.2), while the more geometric-flavored
![]() $\mathbb {Q}$
-Gorenstein property does (Lemma 4.9). A detailed discussion of descent of properties such as Gorenstein and Buchsbaum (for the quotient by a single, non-necessarily p-closed derivation that is still “multiplicative” in an appropriate sense) is given in [Reference Aramova and Avramov3] and [Reference Aramova2].
$\mathbb {Q}$
-Gorenstein property does (Lemma 4.9). A detailed discussion of descent of properties such as Gorenstein and Buchsbaum (for the quotient by a single, non-necessarily p-closed derivation that is still “multiplicative” in an appropriate sense) is given in [Reference Aramova and Avramov3] and [Reference Aramova2].
Another perspective on singularities is given by the Minimal Model Program. One can define birational singularities of
![]() $\mathbb {Q}$
-Gorenstein
$\mathbb {Q}$
-Gorenstein
![]() $1$
-foliations just as birational singularities of varieties and pairs, as first noticed by McQuillan [Reference McQuillan42]. A remarkable feature is that quotients by (log) canonical
$1$
-foliations just as birational singularities of varieties and pairs, as first noticed by McQuillan [Reference McQuillan42]. A remarkable feature is that quotients by (log) canonical
![]() $1$
-foliations can only improve the birational singularities of the underlying variety.
$1$
-foliations can only improve the birational singularities of the underlying variety.
Theorem 1.2 (The punchline of Theorem 4.10)
Let X be a normal variety over a perfect field of characteristic
![]() $p>0$
, and
$p>0$
, and
![]() $\mathcal {F}$
be a
$\mathcal {F}$
be a
![]() $1$
-foliation on X.
$1$
-foliation on X.
-
1. If
 $\mathcal {F}$
is canonical, then
$\mathcal {F}$
is canonical, then
 $X/\mathcal {F}$
is terminal (resp. canonical, klt, log canonical) as soon as X is.
$X/\mathcal {F}$
is terminal (resp. canonical, klt, log canonical) as soon as X is. -
2. If
 $\mathcal {F}$
is log canonical, then
$\mathcal {F}$
is log canonical, then
 $X/\mathcal {F}$
is klt (resp. log canonical) as soon as X is.
$X/\mathcal {F}$
is klt (resp. log canonical) as soon as X is.
The proof is a direct comparison of pull-back formulas, leading to the simple equalities (4.4). These equalities also show that any other implication (e.g., X is midly singular if both
![]() $X/\mathcal {F}$
and
$X/\mathcal {F}$
and
![]() $\mathcal {F}$
are) is not possible to obtain in general: see Remark 4.11 on that matter. We apply Theorem 1.2 to normalized p-cyclic covering to obtain Reid-type covering results (i.e., description of the MMP singularities of cyclic covers), see Corollary 4.15.
$\mathcal {F}$
are) is not possible to obtain in general: see Remark 4.11 on that matter. We apply Theorem 1.2 to normalized p-cyclic covering to obtain Reid-type covering results (i.e., description of the MMP singularities of cyclic covers), see Corollary 4.15.
One drawback of Theorem 1.2 is that it is difficult in general to decide whether a given
![]() $1$
-foliation
$1$
-foliation
![]() $\mathcal {F}$
is log canonical, etc., along its singular locus. Proposition 3.10 provides examples of log canonical
$\mathcal {F}$
is log canonical, etc., along its singular locus. Proposition 3.10 provides examples of log canonical
![]() $1$
-foliations of corank
$1$
-foliations of corank
![]() $1$
on singular varieties. For
$1$
on singular varieties. For
![]() $1$
-foliations of rank
$1$
-foliations of rank
![]() $1$
on regular varieties there is a useful characterization of log canonicity due to McQuillan (Proposition 3.6), which turns out to be equivalent to having at worst multiplicative singularities (Corollary 3.7). Using a local computation from [Reference Hara and Sawada17], this leads to a complete characterization of log canonical
$1$
on regular varieties there is a useful characterization of log canonicity due to McQuillan (Proposition 3.6), which turns out to be equivalent to having at worst multiplicative singularities (Corollary 3.7). Using a local computation from [Reference Hara and Sawada17], this leads to a complete characterization of log canonical
![]() $1$
-foliations on regular surfaces.
$1$
-foliations on regular surfaces.
Theorem 1.3 (Lemma 2.37, Proposition 4.12, and Theorem 4.19)
Let S be a regular surface over a perfect field of characteristic
![]() $p>0$
, and
$p>0$
, and
![]() $\mathcal {F}$
be a
$\mathcal {F}$
be a
![]() $1$
-foliation of rank
$1$
-foliation of rank
![]() $1$
on S. Then:
$1$
on S. Then:
-
1.
 $\mathcal {F}$
is canonical if and only if
$\mathcal {F}$
is canonical if and only if
 $\mathcal {F}$
is regular, if and only if
$\mathcal {F}$
is regular, if and only if
 $S/\mathcal {F}$
is regular.
$S/\mathcal {F}$
is regular. -
2.
 $\mathcal {F}$
is log canonical if and only if
$\mathcal {F}$
is log canonical if and only if
 $S/\mathcal {F}$
is F-regular, if and only if
$S/\mathcal {F}$
is F-regular, if and only if
 $S/\mathcal {F}$
is F-pure.
$S/\mathcal {F}$
is F-pure.
(The conditions on
![]() $S/\mathcal {F}$
can be equivalently be formulated for the normalization of S in the field
$S/\mathcal {F}$
can be equivalently be formulated for the normalization of S in the field
![]() $K(S/\mathcal {F})^{1/p}$
.)
$K(S/\mathcal {F})^{1/p}$
.)
This shows that the log canonical condition on
![]() $1$
-foliations is quite restrictive, at least in dimension two. In higher dimensions, little more is known apart from the following corollary.
$1$
-foliations is quite restrictive, at least in dimension two. In higher dimensions, little more is known apart from the following corollary.
Corollary 1.4 (Proposition 4.12 and Corollary 3.7)
Let X be a regular variety over a perfect field of positive characteristic, and let
![]() $\mathcal {F}$
be a non-trivial
$\mathcal {F}$
be a non-trivial
![]() $1$
-foliation.
$1$
-foliation.
-
1.
 $\mathcal {F}$
cannot be terminal, and if it is canonical then it is regular outside a closed subset of codimension
$\mathcal {F}$
cannot be terminal, and if it is canonical then it is regular outside a closed subset of codimension
 $\geq 3$
.
$\geq 3$
. -
2. If
 $\mathcal {F}$
has rank
$\mathcal {F}$
has rank
 $1$
, then it is canonical if and only if it is regular.
$1$
, then it is canonical if and only if it is regular. -
3. If
 $\mathcal {F}$
has rank
$\mathcal {F}$
has rank
 $1$
, then it is log canonical if and only if it has at worst multiplicative singularities.
$1$
, then it is log canonical if and only if it has at worst multiplicative singularities.
Finally, we explore a notion of family of
![]() $1$
-foliations. For technical reasons, we mostly restrict ourselves to the case of smooth fibrations
$1$
-foliations. For technical reasons, we mostly restrict ourselves to the case of smooth fibrations
![]() $\mathcal {X}\to S$
(see Definition 5.1 and Remark 5.2). In this setting, a family of
$\mathcal {X}\to S$
(see Definition 5.1 and Remark 5.2). In this setting, a family of
![]() $1$
-foliations is a coherent sub-module
$1$
-foliations is a coherent sub-module
![]() $\mathcal {F}\hookrightarrow T_{\mathcal {X}/S}$
with S-flat cokernel, whose restriction to every fiber is a
$\mathcal {F}\hookrightarrow T_{\mathcal {X}/S}$
with S-flat cokernel, whose restriction to every fiber is a
![]() $1$
-foliation in the usual sense. The theory of the Quot scheme implies that, when we consider trivial underlying fibration
$1$
-foliation in the usual sense. The theory of the Quot scheme implies that, when we consider trivial underlying fibration
![]() $\mathcal {X}\to S$
, universal families of
$\mathcal {X}\to S$
, universal families of
![]() $1$
-foliations exist (Proposition 5.5). Then we consider whether the operation of taking fibers commute with the operation of taking quotients by the
$1$
-foliations exist (Proposition 5.5). Then we consider whether the operation of taking fibers commute with the operation of taking quotients by the
![]() $1$
-foliation. In general they do not, but we prove the following criterion.
$1$
-foliation. In general they do not, but we prove the following criterion.
Theorem 1.5 (Proposition 5.9)
Let
![]() $(\mathcal {X}\to S,\ \mathcal {F}\hookrightarrow T_{\mathcal {X}/S})$
be a family of
$(\mathcal {X}\to S,\ \mathcal {F}\hookrightarrow T_{\mathcal {X}/S})$
be a family of
![]() $1$
-foliations. Assume that
$1$
-foliations. Assume that
![]() $\mathcal {X}\to S$
is smooth and S is regular. Let
$\mathcal {X}\to S$
is smooth and S is regular. Let
![]() $\mathcal {Q}=T_{\mathcal {X}/S}/\mathcal {F}$
. Then if
$\mathcal {Q}=T_{\mathcal {X}/S}/\mathcal {F}$
. Then if
![]() $\mathcal {Q}_s$
is locally free for some
$\mathcal {Q}_s$
is locally free for some
![]() $s\in S$
, it holds that
$s\in S$
, it holds that
![]() $\mathcal {X}_s/\mathcal {F}_s=(\mathcal {X}/\mathcal {F})_s$
.
$\mathcal {X}_s/\mathcal {F}_s=(\mathcal {X}/\mathcal {F})_s$
.
If
![]() $\mathcal {Q}_s$
is just slightly less regular (for example not Cohen–Macaulay but
$\mathcal {Q}_s$
is just slightly less regular (for example not Cohen–Macaulay but
![]() $S_{\dim \mathcal {X}_s-1}$
), then commutativity may or may not occur, see Examples 5.15 and 5.16. So a more refined criterion seems difficult to formulate in this generality. Nevertheless, a consequence of our definition of families of
$S_{\dim \mathcal {X}_s-1}$
), then commutativity may or may not occur, see Examples 5.15 and 5.16. So a more refined criterion seems difficult to formulate in this generality. Nevertheless, a consequence of our definition of families of
![]() $1$
-foliations is that the natural morphism
$1$
-foliations is that the natural morphism
![]() $\varphi _s\colon \mathcal {X}_s/\mathcal {F}_s\to (\mathcal {X}/\mathcal {F})_s$
is always an isomorphism in codimension one (Corollary 5.10), and this method easily produces
$\varphi _s\colon \mathcal {X}_s/\mathcal {F}_s\to (\mathcal {X}/\mathcal {F})_s$
is always an isomorphism in codimension one (Corollary 5.10), and this method easily produces
![]() $\mathbb {Q}$
-Gorenstein degenerations of regular schemes into non-
$\mathbb {Q}$
-Gorenstein degenerations of regular schemes into non-
![]() $S_2$
-ones.
$S_2$
-ones.
The paper is organized as follows. In Section 2, we gather some basic material on derivations, foliations, and infinitesimal quotients. Most of it is well-known and we claim no originality. However, the available material on
![]() $1$
-foliations in positive characteristic is scattered through the literature (see in particular [Reference Miyaoka and Peternell46], [Reference Patakfalvi and Waldron49], [Reference Rudakov and Safarevic53], [Reference Liedtke35], [Reference McQuillan42], [Reference Tziolas61] and [Reference Bernasconi8]), so we have chosen to reproduce it here for ease of reference. Large parts of the content of our Sections 2 and 4.1 are discussed extensively, with many examples and applications, in a book in preparation by Patakfalvi and Waldron [Reference Patakfalvi and Waldron48]. For the surface theory and extended examples, see also [Reference Tziolas62].
$1$
-foliations in positive characteristic is scattered through the literature (see in particular [Reference Miyaoka and Peternell46], [Reference Patakfalvi and Waldron49], [Reference Rudakov and Safarevic53], [Reference Liedtke35], [Reference McQuillan42], [Reference Tziolas61] and [Reference Bernasconi8]), so we have chosen to reproduce it here for ease of reference. Large parts of the content of our Sections 2 and 4.1 are discussed extensively, with many examples and applications, in a book in preparation by Patakfalvi and Waldron [Reference Patakfalvi and Waldron48]. For the surface theory and extended examples, see also [Reference Tziolas62].
In Section 3, we recall the definition of birational singularities for
![]() $1$
-foliations, and establish a characterization of rank
$1$
-foliations, and establish a characterization of rank
![]() $1$
lc
$1$
lc
![]() $1$
-foliations. In Section 4, we investigate the singularities of some quotients, with the aim of proving Theorems 1.1, 1.2, and 1.3. We discuss families of
$1$
-foliations. In Section 4, we investigate the singularities of some quotients, with the aim of proving Theorems 1.1, 1.2, and 1.3. We discuss families of
![]() $1$
-foliations in Section 5.
$1$
-foliations in Section 5.
Remark 1.6. We do not discuss properties of non-p-closed vector fields in this paper. Interesting features of those are given in [Reference Mendson and Pereira44], [Reference Pereira50].
2 Preliminaries
2.1 Notations
Unless stated otherwise, we work over a perfect field k of positive characteristic
![]() $p>0$
.
$p>0$
.
-
1. A variety (over k) is an integral quasi-projective k-scheme of finite type. A curve (resp. surface, threefold) is k-variety of dimension one (resp. two, three).
-
2. Normalizations of integral Noetherian schemes and algebras are denoted by
 $(\bullet )^\nu $
.
$(\bullet )^\nu $
. -
3. Let
 $f\colon X\to S$
be a morphism of k-schemes. We let
$f\colon X\to S$
be a morphism of k-schemes. We let
 $F_\bullet $
denote the absolute Frobenius. Then we can form the relative Frobenius
$F_\bullet $
denote the absolute Frobenius. Then we can form the relative Frobenius
 $F_{X/S}=(F_X,f)\colon X\to X^{(1)}=X\otimes _{S,F_S}S$
: it is an S-linear morphism. If
$F_{X/S}=(F_X,f)\colon X\to X^{(1)}=X\otimes _{S,F_S}S$
: it is an S-linear morphism. If
 $F_S$
is invertible, for example in the case
$F_S$
is invertible, for example in the case
 $S=\operatorname {\mathrm {Spec}}(k)$
, we can construct the sequence of S-linear morphisms (all denoted by
$S=\operatorname {\mathrm {Spec}}(k)$
, we can construct the sequence of S-linear morphisms (all denoted by
 $F_{X/S}$
), Notice that in this case, the schemes
$F_{X/S}$
), Notice that in this case, the schemes $$ \begin{align*}\dots\to X^{(-1)}\to X\to X^{(1)}\to \cdots\end{align*} $$
$$ \begin{align*}\dots\to X^{(-1)}\to X\to X^{(1)}\to \cdots\end{align*} $$
 $X^{(n)}$
(
$X^{(n)}$
(
 $n\in \mathbb {Z}$
) are abstractly (but usually not S-linearly) isomorphic.
$n\in \mathbb {Z}$
) are abstractly (but usually not S-linearly) isomorphic.
-
4. The conditions
 $S_i$
are the Serre’s conditions, see [1, 0341].
$S_i$
are the Serre’s conditions, see [1, 0341]. -
5. We use at several places standard MMP terminology for singularities, as defined in [Reference Kollár and Mori32, §2.3].
2.2 p-basis
Let A be a k-algebra.
Definition 2.1. Let
![]() $B\subset A$
be a purely inseparable extension of k-algebras, and assume that A has height one over B (that is:
$B\subset A$
be a purely inseparable extension of k-algebras, and assume that A has height one over B (that is:
![]() $A^p\subset B$
). Then a p-basis of A over B is a finite set of elements
$A^p\subset B$
). Then a p-basis of A over B is a finite set of elements
![]() $\{a_1,\dots ,a_n\}\subset A$
with the property that
$\{a_1,\dots ,a_n\}\subset A$
with the property that
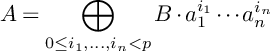 $$ \begin{align*}A=\bigoplus_{0\leq i_1,\dots,i_n<p}B\cdot a_1^{i_1}\cdots a_n^{i_n}\end{align*} $$
$$ \begin{align*}A=\bigoplus_{0\leq i_1,\dots,i_n<p}B\cdot a_1^{i_1}\cdots a_n^{i_n}\end{align*} $$
as
![]() $A^p$
-modules.
$A^p$
-modules.
If A is Noetherian, this notion is equivalent to that of differential basis [Reference Tyc60]: a subset
![]() $\{a_1,\dots ,a_n\}$
is a p-basis of A over B if and only if
$\{a_1,\dots ,a_n\}$
is a p-basis of A over B if and only if
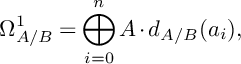 $$ \begin{align*}\Omega^1_{A/B}=\bigoplus_{i=0}^n A\cdot d_{A/B}(a_i),\end{align*} $$
$$ \begin{align*}\Omega^1_{A/B}=\bigoplus_{i=0}^n A\cdot d_{A/B}(a_i),\end{align*} $$
where
![]() $d_{A/B}\colon A\to \Omega ^1_{A/B}$
is the universal derivation relative to
$d_{A/B}\colon A\to \Omega ^1_{A/B}$
is the universal derivation relative to
![]() $B\to A$
. By Kunz theorem [1, 0EC0], if A has a p-basis over
$B\to A$
. By Kunz theorem [1, 0EC0], if A has a p-basis over
![]() $A^p$
then A is regular and F-finite, and the converse also holds as
$A^p$
then A is regular and F-finite, and the converse also holds as
![]() $\Omega ^1_{A/A^p}=\Omega ^1_{A/k}$
will be a finite free A-module.
$\Omega ^1_{A/A^p}=\Omega ^1_{A/k}$
will be a finite free A-module.
Lemma 2.2. Let
![]() $(A,\mathfrak {m})$
be a regular complete local k-algebra, such that
$(A,\mathfrak {m})$
be a regular complete local k-algebra, such that
![]() $k\subset A/\mathfrak {m}$
is a finite extension. Let
$k\subset A/\mathfrak {m}$
is a finite extension. Let
![]() $\{a_1,\dots ,a_n\}$
be a p-basis of A over
$\{a_1,\dots ,a_n\}$
be a p-basis of A over
![]() $A^p$
. Then:
$A^p$
. Then:
-
1. for every i we can write
 $a_i=\lambda _i+x_i$
, where
$a_i=\lambda _i+x_i$
, where
 $\lambda _i\in A^\times $
and
$\lambda _i\in A^\times $
and
 $x_i\in \mathfrak {m}\setminus \mathfrak {m}^2$
;
$x_i\in \mathfrak {m}\setminus \mathfrak {m}^2$
; -
2.
 $\{x_1,\dots ,x_n\}$
is a regular system of parameters of A.
$\{x_1,\dots ,x_n\}$
is a regular system of parameters of A.
Proof. As k is perfect, we obtain that
![]() $A/\mathfrak {m}$
is also perfect. Moreover, by Cohen’s structure theorem [1, 032A], A contains a field of representatives
$A/\mathfrak {m}$
is also perfect. Moreover, by Cohen’s structure theorem [1, 032A], A contains a field of representatives
![]() $k_0$
. So we can write
$k_0$
. So we can write
![]() $A=k_0\oplus \mathfrak {m}$
and
$A=k_0\oplus \mathfrak {m}$
and
![]() $a_i=\lambda _i+x_i$
with
$a_i=\lambda _i+x_i$
with
![]() $\lambda _i\in k_0$
and
$\lambda _i\in k_0$
and
![]() $x_i\in \mathfrak {m}$
. By assumption the
$x_i\in \mathfrak {m}$
. By assumption the
![]() $d_{A/A^p}(a_i)$
’s form a basis for
$d_{A/A^p}(a_i)$
’s form a basis for
![]() $\Omega _{A/A^p}^1$
over A. Since
$\Omega _{A/A^p}^1$
over A. Since
![]() $k_0=k_0^p$
and since
$k_0=k_0^p$
and since
![]() $\Omega ^1_{A/A^p}=\Omega ^1_{A/k}$
, we obtain that the
$\Omega ^1_{A/A^p}=\Omega ^1_{A/k}$
, we obtain that the
![]() $d_{A/k}(x_i)$
’s form an A-basis of
$d_{A/k}(x_i)$
’s form an A-basis of
![]() $\Omega ^1_{A/k}$
. In particular
$\Omega ^1_{A/k}$
. In particular
![]() $n=\dim A$
. Applying Nakayama’s lemma to the isomorphism
$n=\dim A$
. Applying Nakayama’s lemma to the isomorphism
![]() $\mathfrak {m}/\mathfrak {m}^2\cong \Omega ^1_{A/k}\otimes A/\mathfrak {m}$
, we obtain that
$\mathfrak {m}/\mathfrak {m}^2\cong \Omega ^1_{A/k}\otimes A/\mathfrak {m}$
, we obtain that
![]() $\mathfrak {m}=(x_1,\dots ,x_n)$
.
$\mathfrak {m}=(x_1,\dots ,x_n)$
.
2.3 Derivations
Let R be a ring and A be an R-algebra. A derivation of A over R is a R-linear map
![]() $D\colon A\to A$
satisfying the Leibniz rule
$D\colon A\to A$
satisfying the Leibniz rule
The set of those, denoted
![]() $\operatorname {\mathrm {Der}}_R(A)$
, is naturally an A-module. This module is endowed with a Lie bracket
$\operatorname {\mathrm {Der}}_R(A)$
, is naturally an A-module. This module is endowed with a Lie bracket
While the composition of two derivations might not be a derivation, in case R is an
![]() $\mathbb {F}_p$
-algebra the p-fold composition affords an R-linear map
$\mathbb {F}_p$
-algebra the p-fold composition affords an R-linear map
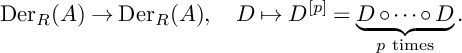 $$ \begin{align*}\operatorname{\mathrm{Der}}_R(A)\to\operatorname{\mathrm{Der}}_R(A),\quad D\mapsto D^{[p]}=\underbrace{D\circ\dots\circ D}_{p\text{ times}}.\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Der}}_R(A)\to\operatorname{\mathrm{Der}}_R(A),\quad D\mapsto D^{[p]}=\underbrace{D\circ\dots\circ D}_{p\text{ times}}.\end{align*} $$
Recall Hochschild’s formula [Reference Matsumura41, Theorem 25.5]: for
![]() $a\in A$
and
$a\in A$
and
![]() $D\in \operatorname {\mathrm {Der}}_R(A)$
we have
$D\in \operatorname {\mathrm {Der}}_R(A)$
we have
The pth power of a sum of derivations is more complicated to describe: a formula of Jacobson [Reference Jacobson24, p. 209] shows that
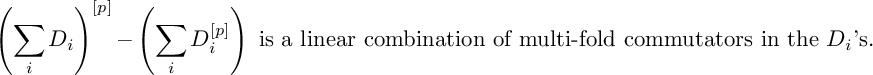 $$ \begin{align*}\left(\sum_i D_i\right)^{[p]}-\left(\sum_i D_i^{[p]}\right) \ \text{is a linear combination of multi-fold commutators in the } D_i\text{'s}.\end{align*} $$
$$ \begin{align*}\left(\sum_i D_i\right)^{[p]}-\left(\sum_i D_i^{[p]}\right) \ \text{is a linear combination of multi-fold commutators in the } D_i\text{'s}.\end{align*} $$
In particular, the naive expression
![]() $(D_1+D_2)^{[p]}=D_1^{[p]}+D_2^{[p]}$
holds if
$(D_1+D_2)^{[p]}=D_1^{[p]}+D_2^{[p]}$
holds if
![]() $[D_1,D_2]=0$
.
$[D_1,D_2]=0$
.
An alternative description of the module of derivation is given by the A-linear canonical isomorphism
![]() $\operatorname {\mathrm {Hom}}_A(\Omega _{A/R}^1,A)\cong \operatorname {\mathrm {Der}}_R(A)$
, obtained by pre-composing any
$\operatorname {\mathrm {Hom}}_A(\Omega _{A/R}^1,A)\cong \operatorname {\mathrm {Der}}_R(A)$
, obtained by pre-composing any
![]() $\varphi \colon \Omega _{A/R}^1\to A$
by the universal R-linear derivation
$\varphi \colon \Omega _{A/R}^1\to A$
by the universal R-linear derivation
![]() $d_{A/R}\colon A\to \Omega _{A/R}^1$
.
$d_{A/R}\colon A\to \Omega _{A/R}^1$
.
Given a multiplicatively closed subset
![]() $S\subset A$
, there is a canonical map
$S\subset A$
, there is a canonical map
![]() $\operatorname {\mathrm {Der}}_R(A)\to \operatorname {\mathrm {Der}}_R(S^{-1}A)$
given by the usual derivation rule for fractions. This is compatible with the localization isomorphism
$\operatorname {\mathrm {Der}}_R(A)\to \operatorname {\mathrm {Der}}_R(S^{-1}A)$
given by the usual derivation rule for fractions. This is compatible with the localization isomorphism
![]() $\operatorname {\mathrm {Hom}}_A(\Omega ^1_{A/R},A)\otimes S^{-1}A\cong \operatorname {\mathrm {Hom}}_{S^{-1}A}(\Omega ^1_{S^{-1}A/R},S^{-1}A)$
. In particular the module of derivations sheafifies, and for any R-scheme X we obtain a sheaf of
$\operatorname {\mathrm {Hom}}_A(\Omega ^1_{A/R},A)\otimes S^{-1}A\cong \operatorname {\mathrm {Hom}}_{S^{-1}A}(\Omega ^1_{S^{-1}A/R},S^{-1}A)$
. In particular the module of derivations sheafifies, and for any R-scheme X we obtain a sheaf of
![]() $\mathcal {O}_X$
-module
$\mathcal {O}_X$
-module
![]() $\operatorname {\mathrm {Der}}_R(\mathcal {O}_X)$
which is the
$\operatorname {\mathrm {Der}}_R(\mathcal {O}_X)$
which is the
![]() $\mathcal {O}_X$
-dual of
$\mathcal {O}_X$
-dual of
![]() $\Omega _{X/R}^1$
. It is customary to write
$\Omega _{X/R}^1$
. It is customary to write
![]() $\operatorname {\mathrm {Der}}_R(\mathcal {O}_X)=T_{X/R}$
(Footnote
1
). The Lie bracket and p-fold composition also sheafify into R-linear operations on
$\operatorname {\mathrm {Der}}_R(\mathcal {O}_X)=T_{X/R}$
(Footnote
1
). The Lie bracket and p-fold composition also sheafify into R-linear operations on
![]() $\operatorname {\mathrm {Der}}_R(\mathcal {O}_X)$
.
$\operatorname {\mathrm {Der}}_R(\mathcal {O}_X)$
.
While the module of derivations commutes with localization, in general it does not commute with completion. Indeed, the module of Kähler differentials
![]() $\Omega _{\widehat {A}/R}$
of a complete local R-algebra
$\Omega _{\widehat {A}/R}$
of a complete local R-algebra
![]() $\widehat {A}$
is usually not of finite type over
$\widehat {A}$
is usually not of finite type over
![]() $\widehat {A}$
. Still, we have the following result (which is known, but I could not locate a suitable compact reference).
$\widehat {A}$
. Still, we have the following result (which is known, but I could not locate a suitable compact reference).
Lemma 2.3. Let
![]() $(A,\mathfrak {m})$
be a local ring essentially of finite type over a Noetherian ring R. Then there is a natural inclusion map
$(A,\mathfrak {m})$
be a local ring essentially of finite type over a Noetherian ring R. Then there is a natural inclusion map
whose image is the sub-
![]() $\widehat {A}$
-module
$\widehat {A}$
-module
![]() $\operatorname {\mathrm {Der}}^{\text {cont}}_R(\widehat {A})$
of continuous R-derivations of the
$\operatorname {\mathrm {Der}}^{\text {cont}}_R(\widehat {A})$
of continuous R-derivations of the
![]() $\mathfrak {m}$
-adic completion
$\mathfrak {m}$
-adic completion
![]() $\widehat {A}$
.
$\widehat {A}$
.
Proof. Since
![]() $\widehat {A}$
is a flat A-module and
$\widehat {A}$
is a flat A-module and
![]() $\Omega _{A/R}^1$
is a finitely presented A-module, the canonical morphism
$\Omega _{A/R}^1$
is a finitely presented A-module, the canonical morphism
is an isomorphism [Reference Bourbaki9, Chapter I, §2, n.10, Proposition 11]. In the rest of the proof, we describe the target of this isomorphism. By the universal property of the inverse limit, it can be written as
Let us describe the Hom-module into
![]() $A/\mathfrak {m}^n$
. On the one hand, an
$A/\mathfrak {m}^n$
. On the one hand, an
![]() $\widehat {A}$
-linear morphism
$\widehat {A}$
-linear morphism
![]() $\Omega _{A/R}^1\otimes \widehat {A}\to A/\mathfrak {m}^n$
is always continuous for the natural topologies, since it is uniquely specified by an A-linear map
$\Omega _{A/R}^1\otimes \widehat {A}\to A/\mathfrak {m}^n$
is always continuous for the natural topologies, since it is uniquely specified by an A-linear map
![]() $\Omega ^1_{A/R}\to A/\mathfrak {m}^n$
. On the other hand by [Reference Liu38, 6.Exercise 1.3], we have a canonical isomorphism
$\Omega ^1_{A/R}\to A/\mathfrak {m}^n$
. On the other hand by [Reference Liu38, 6.Exercise 1.3], we have a canonical isomorphism
Combining these two facts with [Reference Grothendieck14, 20.7.14.4], which we can apply as
![]() $A/\mathfrak {m}^n$
is discrete and is annihilated by
$A/\mathfrak {m}^n$
is discrete and is annihilated by
![]() $\mathfrak {m}^n$
, we obtain a canonical identification
$\mathfrak {m}^n$
, we obtain a canonical identification
Let us apply the inverse limit along n: by the token already used above, it amounts to the same to apply the inverse limit on the second arguments of the Hom modules, and so we get an isomorphism
The right-hand side is a sub-module of
![]() $\operatorname {\mathrm {Hom}}_{\widehat {A}}(\Omega _{\widehat {A}/R}^1,\widehat {A})=\operatorname {\mathrm {Der}}_R(\widehat {A})$
which, by [Reference Grothendieck14, 20.4.8.2], corresponds to the set of continuous R-derivations of
$\operatorname {\mathrm {Hom}}_{\widehat {A}}(\Omega _{\widehat {A}/R}^1,\widehat {A})=\operatorname {\mathrm {Der}}_R(\widehat {A})$
which, by [Reference Grothendieck14, 20.4.8.2], corresponds to the set of continuous R-derivations of
![]() $\widehat {A}$
into itself. This completes the proof.
$\widehat {A}$
into itself. This completes the proof.
In any case, we will use the following convention: Assume that A is a local ring. If
![]() $M\subset \operatorname {\mathrm {Der}}_R(A)$
is a sub-module, then we will say that M satisfies some property formally, if the sub-
$M\subset \operatorname {\mathrm {Der}}_R(A)$
is a sub-module, then we will say that M satisfies some property formally, if the sub-
![]() $\widehat {A}$
-submodule
$\widehat {A}$
-submodule
![]() $M\otimes \widehat {A}\subset \operatorname {\mathrm {Der}}_R(A)\otimes \widehat {A}$
satisfies the said property.
$M\otimes \widehat {A}\subset \operatorname {\mathrm {Der}}_R(A)\otimes \widehat {A}$
satisfies the said property.
Remark 2.4. Let
![]() $(A,\mathfrak {m})$
be a regular local ring essentially of finite type over a perfect field
$(A,\mathfrak {m})$
be a regular local ring essentially of finite type over a perfect field
![]() $k_0$
. Assume that
$k_0$
. Assume that
![]() $A/\mathfrak {m}=k_0$
. If
$A/\mathfrak {m}=k_0$
. If
![]() $x_1,\dots ,x_n$
is a regular system of parameters, then:
$x_1,\dots ,x_n$
is a regular system of parameters, then:
-
1.
 $\operatorname {\mathrm {Der}}_{k_0}(A)$
is freely generated by some derivations
$\operatorname {\mathrm {Der}}_{k_0}(A)$
is freely generated by some derivations
 $D_1,\dots ,D_n$
such that
$D_1,\dots ,D_n$
such that
 $D_i(x_j)=\delta _{ij}$
(the Kronecker delta). This follows from that the
$D_i(x_j)=\delta _{ij}$
(the Kronecker delta). This follows from that the
 $dx_i$
give a basis of
$dx_i$
give a basis of
 $\Omega _{A/{k_0}}^1$
(see, e.g., [Reference Hartshorne18, II, Proposition 8.7 and Theorem 8.8]).
$\Omega _{A/{k_0}}^1$
(see, e.g., [Reference Hartshorne18, II, Proposition 8.7 and Theorem 8.8]). -
2. Under the isomorphism
 , the
, the
 $\widehat {A}$
-module
$\widehat {A}$
-module
 $\operatorname {\mathrm {Der}}^{\text {cont}}_{k_0}(\widehat {A})\cong \operatorname {\mathrm {Der}}_{k_0}(A)\otimes \widehat {A}$
is freely generated by the continuous
$\operatorname {\mathrm {Der}}^{\text {cont}}_{k_0}(\widehat {A})\cong \operatorname {\mathrm {Der}}_{k_0}(A)\otimes \widehat {A}$
is freely generated by the continuous
 $k_0$
-derivations
$k_0$
-derivations
 $\frac {\partial }{\partial x_i}=D_i\otimes 1$
$\frac {\partial }{\partial x_i}=D_i\otimes 1$
 $(i=1,\dots ,n)$
. This follows from the previous item and from Lemma 2.3.
$(i=1,\dots ,n)$
. This follows from the previous item and from Lemma 2.3.
2.3.1 p-closed, additive and multiplicative derivations
Let R be an
![]() $\mathbb {F}_p$
-algebra and A be an R-algebra. We say that
$\mathbb {F}_p$
-algebra and A be an R-algebra. We say that
![]() $D\in \operatorname {\mathrm {Der}}_R(A)$
is p-closed if there is
$D\in \operatorname {\mathrm {Der}}_R(A)$
is p-closed if there is
![]() $a\in A$
such that
$a\in A$
such that
![]() $D^{[p]}=aD$
. Hochschild’s formula (2.1) shows that any scaling of a p-closed derivation is still p-closed. Amongst p-closed derivations, we distinguish two special types as follows.
$D^{[p]}=aD$
. Hochschild’s formula (2.1) shows that any scaling of a p-closed derivation is still p-closed. Amongst p-closed derivations, we distinguish two special types as follows.
Definition 2.5. We say that D is additive if
![]() $D^{[p]}=0$
. We say that D is multiplicative if
$D^{[p]}=0$
. We say that D is multiplicative if
![]() $D^{[p]}=uD$
for some unit
$D^{[p]}=uD$
for some unit
![]() $u\in A^\times $
.
$u\in A^\times $
.
Example 2.6. (Recall that k stands for a perfect field of characteristic
![]() $p>0$
.)
$p>0$
.)
-
1. The derivation
 $x^i\frac {\partial }{\partial x}$
on
$x^i\frac {\partial }{\partial x}$
on
 $k[x,y_1,\dots ,y_{n}]$
is additive for
$k[x,y_1,\dots ,y_{n}]$
is additive for
 $i\neq 1$
, and multiplicative for
$i\neq 1$
, and multiplicative for
 $i=1$
.
$i=1$
. -
2. Consider the derivation
 $\partial _{a,b}=ax\frac {\partial }{\partial x}+by\frac {\partial }{\partial y}$
on
$\partial _{a,b}=ax\frac {\partial }{\partial x}+by\frac {\partial }{\partial y}$
on
 $k[x,y]$
, where
$k[x,y]$
, where
 $a,b\in \mathbb {F}_p$
. We have The element
$a,b\in \mathbb {F}_p$
. We have The element $$ \begin{align*}\left(\partial_{a,b}\right)^{[p]}(x^iy^j)=(ai+bj)^px^iy^j.\end{align*} $$
$$ \begin{align*}\left(\partial_{a,b}\right)^{[p]}(x^iy^j)=(ai+bj)^px^iy^j.\end{align*} $$
 $ai+bj$
is to be understood as an element of
$ai+bj$
is to be understood as an element of
 $\mathbb {F}_p$
, on which the Frobenius is trivial. Thus we see that
$\mathbb {F}_p$
, on which the Frobenius is trivial. Thus we see that
 $(\partial _{a,b})^{[p]}=\partial _{a,b}$
. So
$(\partial _{a,b})^{[p]}=\partial _{a,b}$
. So
 $\partial _{a,b}$
is p-closed and multiplicative.
$\partial _{a,b}$
is p-closed and multiplicative.
-
3. Consider the derivation
 $D=x\frac {\partial }{\partial y}+y\frac {\partial }{\partial x}$
on
$D=x\frac {\partial }{\partial y}+y\frac {\partial }{\partial x}$
on
 $k[x,y]$
. For
$k[x,y]$
. For
 $p=2$
we have
$p=2$
we have
 $D^{[2]}=x\frac {\partial }{\partial x}+y\frac {\partial }{\partial y}$
which is not a scaling of D, so D is not p-closed. For
$D^{[2]}=x\frac {\partial }{\partial x}+y\frac {\partial }{\partial y}$
which is not a scaling of D, so D is not p-closed. For
 $p\neq 2$
, the coordinate change
$p\neq 2$
, the coordinate change
 $x=u+v, y=u-v$
gives
$x=u+v, y=u-v$
gives
 $D=u\frac {\partial }{\partial u}+v\frac {\partial }{\partial v}$
which is p-closed and multiplicative.
$D=u\frac {\partial }{\partial u}+v\frac {\partial }{\partial v}$
which is p-closed and multiplicative.
Warning: The additive and multiplicative properties are usually not stable by scaling. This can be seen from Hochschild’s formula (2.1). Actually a scaling of an additive derivation can be multiplicative, and vice-versa, for instance
![]() $\frac {\partial }{\partial x}$
and
$\frac {\partial }{\partial x}$
and
![]() $x\frac {\partial }{\partial x}$
on
$x\frac {\partial }{\partial x}$
on
![]() $k[x, x^{-1}]$
.
$k[x, x^{-1}]$
.
There is a well-known correspondence between additive and multiplicative derivations, and actions of the infinitesimal group schemes
![]() $\alpha _p$
and
$\alpha _p$
and
![]() $\mu _p$
.
$\mu _p$
.
Proposition 2.7. Let X be a k-scheme and
![]() $D\in \operatorname {\mathrm {Der}}_k(\mathcal {O}_X)(X)$
be a derivation.
$D\in \operatorname {\mathrm {Der}}_k(\mathcal {O}_X)(X)$
be a derivation.
-
1.
 $D^{[p]}=0$
if and only if there is an
$D^{[p]}=0$
if and only if there is an
 $\alpha _p$
-action on X given by
$\alpha _p$
-action on X given by  $$ \begin{align*}\mathcal{O}_X\to\mathcal{O}_X\otimes_k k[t]/(t^p),\quad s\mapsto \sum_{i=0}^{p-1}\frac{D^{\circ i}(s)}{i!}t^i.\end{align*} $$
$$ \begin{align*}\mathcal{O}_X\to\mathcal{O}_X\otimes_k k[t]/(t^p),\quad s\mapsto \sum_{i=0}^{p-1}\frac{D^{\circ i}(s)}{i!}t^i.\end{align*} $$
-
2.
 $D^{[p]}=D$
if and only if there is an
$D^{[p]}=D$
if and only if there is an
 $\mu _p$
-action on X given by
$\mu _p$
-action on X given by  $$ \begin{align*}\mathcal{O}_X\to\mathcal{O}_X\otimes_k k[t]/(t^p-1),\quad s\mapsto \sum_{i=0}^{p-1}\frac{D^{\circ i}(s)}{i!}t^i.\end{align*} $$
$$ \begin{align*}\mathcal{O}_X\to\mathcal{O}_X\otimes_k k[t]/(t^p-1),\quad s\mapsto \sum_{i=0}^{p-1}\frac{D^{\circ i}(s)}{i!}t^i.\end{align*} $$
Proof. See, for example, [Reference Tziolas61, Proposition 3.1].
Remark 2.8. The case
![]() $D^{[p]}=uD$
with
$D^{[p]}=uD$
with
![]() $1\neq u\in A^\times $
does not correspond to a group action on X. However, as we will see in Section 4.1, we recover a group action after a finite étale cover.
$1\neq u\in A^\times $
does not correspond to a group action on X. However, as we will see in Section 4.1, we recover a group action after a finite étale cover.
Example 2.9. Let E be an elliptic curve over k, and let
![]() $\eta \in H^0(E,T_{E/k})$
be a global generator. Then
$\eta \in H^0(E,T_{E/k})$
be a global generator. Then
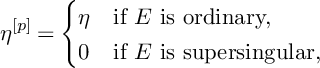 $$ \begin{align*}\eta^{[p]}= \begin{cases} \eta & \text{if }E\text{ is ordinary,}\\ 0 & \text{if }E\text{ is supersingular,} \end{cases}\end{align*} $$
$$ \begin{align*}\eta^{[p]}= \begin{cases} \eta & \text{if }E\text{ is ordinary,}\\ 0 & \text{if }E\text{ is supersingular,} \end{cases}\end{align*} $$
see, for example, [Reference Katz and Mazur27, 12.4.1.3]. So E is ordinary (resp. supersingular) if and only if
![]() $\mu _p$
(resp.
$\mu _p$
(resp.
![]() $\alpha _p$
) acts non-trivially on E.
$\alpha _p$
) acts non-trivially on E.
Lemma 2.10. Let
![]() $\alpha _p$
(respectively
$\alpha _p$
(respectively
![]() $\mu _p$
) acts on a k-scheme X by means of a derivation D. Then the ideal of the fixed locus of the action is the ideal generated by
$\mu _p$
) acts on a k-scheme X by means of a derivation D. Then the ideal of the fixed locus of the action is the ideal generated by
![]() $D(\mathcal {O}_X)$
, and the action is free outside the fixed locus.
$D(\mathcal {O}_X)$
, and the action is free outside the fixed locus.
Proof. We may assume that
![]() $X=\operatorname {\mathrm {Spec}}(A)$
is affine. As
$X=\operatorname {\mathrm {Spec}}(A)$
is affine. As
![]() $\alpha _p$
and
$\alpha _p$
and
![]() $\mu _p$
have no non-trivial subgroup schemes, the action is free outside the fixed locus. The action of
$\mu _p$
have no non-trivial subgroup schemes, the action is free outside the fixed locus. The action of
![]() $\alpha _p$
can be described as follows: given morphisms of affine schemes
$\alpha _p$
can be described as follows: given morphisms of affine schemes
![]() $f\colon (S'\to S\to X)$
, corresponding to ring maps
$f\colon (S'\to S\to X)$
, corresponding to ring maps
and given
![]() $\lambda \in \alpha _p(S)=\{u\in \Gamma (S,\mathcal {O}_S)\mid u^p=0\}$
, the morphism
$\lambda \in \alpha _p(S)=\{u\in \Gamma (S,\mathcal {O}_S)\mid u^p=0\}$
, the morphism
![]() $\lambda \cdot f\colon S'\to X$
corresponds to the ring map
$\lambda \cdot f\colon S'\to X$
corresponds to the ring map
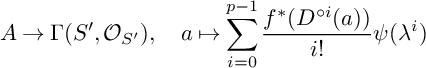 $$ \begin{align*}A\to \Gamma(S',\mathcal{O}_{S'}),\quad a\mapsto \sum_{i=0}^{p-1}\frac{f^{*}(D^{\circ i}(a))}{i!}\psi(\lambda^i)\end{align*} $$
$$ \begin{align*}A\to \Gamma(S',\mathcal{O}_{S'}),\quad a\mapsto \sum_{i=0}^{p-1}\frac{f^{*}(D^{\circ i}(a))}{i!}\psi(\lambda^i)\end{align*} $$
(with the convention that
![]() $0^0=1=0!$
and
$0^0=1=0!$
and
![]() $D^0=\operatorname {\mathrm {id}}$
). Similarly, if we have instead an
$D^0=\operatorname {\mathrm {id}}$
). Similarly, if we have instead an
![]() $\mu _p$
-action, then given f as above and
$\mu _p$
-action, then given f as above and
![]() $\nu \in \mu _p(S)=\{u\in \Gamma (S,\mathcal {O}_S)\mid u^p=1\}$
, the morphism
$\nu \in \mu _p(S)=\{u\in \Gamma (S,\mathcal {O}_S)\mid u^p=1\}$
, the morphism
![]() $\nu \cdot f$
is given by the ring map
$\nu \cdot f$
is given by the ring map
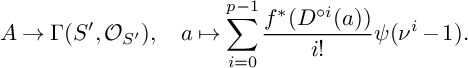 $$ \begin{align*}A\to \Gamma(S',\mathcal{O}_{S'}),\quad a\mapsto \sum_{i=0}^{p-1}\frac{f^{*}(D^{\circ i}(a))}{i!}\psi(\nu^i-1).\end{align*} $$
$$ \begin{align*}A\to \Gamma(S',\mathcal{O}_{S'}),\quad a\mapsto \sum_{i=0}^{p-1}\frac{f^{*}(D^{\circ i}(a))}{i!}\psi(\nu^i-1).\end{align*} $$
The fixed locus of the
![]() $\alpha _p$
-action (resp. of the
$\alpha _p$
-action (resp. of the
![]() $\mu _p$
-action) is the subscheme
$\mu _p$
-action) is the subscheme
![]() $Z\subset X$
with the following property (see, e.g., [Reference Brion10, Definition 2.2.5]):
$Z\subset X$
with the following property (see, e.g., [Reference Brion10, Definition 2.2.5]):
![]() $S\to X$
factors through Z if and only if
$S\to X$
factors through Z if and only if
![]() $\lambda \cdot f=f$
for every f and
$\lambda \cdot f=f$
for every f and
![]() $\lambda $
(resp. by
$\lambda $
(resp. by
![]() $\nu \cdot f=f$
for every f and
$\nu \cdot f=f$
for every f and
![]() $\nu $
). From the description above it is then clear that Z is the closed subscheme of X whose ideal is generated by the set
$\nu $
). From the description above it is then clear that Z is the closed subscheme of X whose ideal is generated by the set
![]() $\{D(a)\mid a\in A\}$
.
$\{D(a)\mid a\in A\}$
.
Remark 2.11. Proposition 2.7 can be generalized as follows.
-
1. Given integers
 $n,m\geq 0$
, actions of
$n,m\geq 0$
, actions of
 $\mu _p^{\times n}\times \alpha _p^{\times m}$
on X corresponds bijectively to sets of
$\mu _p^{\times n}\times \alpha _p^{\times m}$
on X corresponds bijectively to sets of
 $n+m$
derivations
$n+m$
derivations
 $\{D_1,\dots ,D_{n+m}\}\subset \operatorname {\mathrm {Der}}_k(\mathcal {O}_X)(X)$
such that
$\{D_1,\dots ,D_{n+m}\}\subset \operatorname {\mathrm {Der}}_k(\mathcal {O}_X)(X)$
such that-
•
 $D_i^{[p]}=D_i$
for
$D_i^{[p]}=D_i$
for
 $1\leq i\leq n$
,
$1\leq i\leq n$
, -
•
 $D_j^{[p]}=0$
for
$D_j^{[p]}=0$
for
 $n+1\leq j\leq n+m$
, and
$n+1\leq j\leq n+m$
, and -
•
 $D_a\circ D_{b}=D_b\circ D_a$
for any
$D_a\circ D_{b}=D_b\circ D_a$
for any
 $1\leq a,b\leq n+m$
.
$1\leq a,b\leq n+m$
.
-
-
2. Let G be either
 $\alpha _{p^n}$
or
$\alpha _{p^n}$
or
 $\mu _{p^n}$
. Disregarding the Hopf algebra structure of
$\mu _{p^n}$
. Disregarding the Hopf algebra structure of
 $\mathcal {O}(G)$
, we have
$\mathcal {O}(G)$
, we have
 $\mathcal {O}(G)\cong k[t]/(t^{p^n})$
. Thus a scheme morphism
$\mathcal {O}(G)\cong k[t]/(t^{p^n})$
. Thus a scheme morphism
 $a\colon G\times X\to X$
such that corresponds to a k-linear ring map
$a\colon G\times X\to X$
such that corresponds to a k-linear ring map $$ \begin{align*}\left(X\cong \{e_G\}\times X\hookrightarrow G\times X\overset{a}{\longrightarrow} X\right)=\operatorname{\mathrm{id}}_X\end{align*} $$
$$ \begin{align*}\left(X\cong \{e_G\}\times X\hookrightarrow G\times X\overset{a}{\longrightarrow} X\right)=\operatorname{\mathrm{id}}_X\end{align*} $$
 which reduces to
which reduces to
 $\operatorname {\mathrm {id}}_{\mathcal {O}_X}$
modulo t. By [Reference Matsumura41, §Reference Katz and Mazur27] such morphisms correspond bijectively to Hasse–Schmidt derivations
$\operatorname {\mathrm {id}}_{\mathcal {O}_X}$
modulo t. By [Reference Matsumura41, §Reference Katz and Mazur27] such morphisms correspond bijectively to Hasse–Schmidt derivations
 $\mathbf {D}$
of length
$\mathbf {D}$
of length
 $p^n$
. Unravelling the compatibility conditions that are necessary for a to be an action, we obtain necessary and sufficient conditions for
$p^n$
. Unravelling the compatibility conditions that are necessary for a to be an action, we obtain necessary and sufficient conditions for
 $\mathbf {D}$
to define a G-action. For example, if
$\mathbf {D}$
to define a G-action. For example, if
 $G=\alpha _{p^n}$
then we obtain that
$G=\alpha _{p^n}$
then we obtain that
 $\mathbf {D}$
is iterative. Actions of finite products of
$\mathbf {D}$
is iterative. Actions of finite products of
 $\alpha _{p^n}$
and
$\alpha _{p^n}$
and
 $\mu _{p^m}$
are then described in the same way as above.
$\mu _{p^m}$
are then described in the same way as above.
In general, a given p-closed derivation
![]() $D\in \operatorname {\mathrm {Der}}_{\mathbb {F}_p}(A)$
is neither additive not multiplicative. So one can ask whether there is
$D\in \operatorname {\mathrm {Der}}_{\mathbb {F}_p}(A)$
is neither additive not multiplicative. So one can ask whether there is
![]() $0\neq a\in A$
such that
$0\neq a\in A$
such that
![]() $aD$
becomes additive or multiplicative.
$aD$
becomes additive or multiplicative.
It is always possible to scale A so that it becomes additive: the following argument was kindly communicated to me by Yuya Matsumoto.
Lemma 2.12. Let A be an integral
![]() $\mathbb {F}_p$
-algebra, and
$\mathbb {F}_p$
-algebra, and
![]() $0\neq D\in \operatorname {\mathrm {Der}}_{\mathbb {F}_p}(A)$
be a p-closed derivation. Then there exists
$0\neq D\in \operatorname {\mathrm {Der}}_{\mathbb {F}_p}(A)$
be a p-closed derivation. Then there exists
![]() $a\in A$
such that
$a\in A$
such that
![]() $aD$
is non-zero and additive.
$aD$
is non-zero and additive.
Proof. Choose
![]() $x\in A$
such that
$x\in A$
such that
![]() $D(x)\neq 0$
and write
$D(x)\neq 0$
and write
![]() $a=D(x)^{p-1}$
. I claim that
$a=D(x)^{p-1}$
. I claim that
![]() $aD$
is additive. By Hochschild’s formula (2.1) the derivation
$aD$
is additive. By Hochschild’s formula (2.1) the derivation
![]() $aD$
is p-closed, say
$aD$
is p-closed, say
![]() $(aD)^{[p]}=h\cdot aD$
. Then
$(aD)^{[p]}=h\cdot aD$
. Then
Since A is a domain and
![]() $(aD)(x)=D(x)^p\neq 0$
, we deduce that
$(aD)(x)=D(x)^p\neq 0$
, we deduce that
![]() $h=0$
.
$h=0$
.
On the other hand, we observe the following remark.
Remark 2.13. It is not always possible to scale D so it becomes multiplicative: indeed, assuming A is integral, if we could find such a scaling then
![]() $A^D$
would be a multiplicative quotient and thus, assuming that A is Cohen–Macaulay, we would obtain that
$A^D$
would be a multiplicative quotient and thus, assuming that A is Cohen–Macaulay, we would obtain that
![]() $A^D$
is also Cohen–Macaulay by Theorem 4.3. This is usually not the case: for example, using Lemma 2.31 one sees that for
$A^D$
is also Cohen–Macaulay by Theorem 4.3. This is usually not the case: for example, using Lemma 2.31 one sees that for
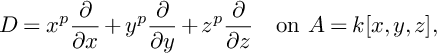 $$ \begin{align*}D=x^p\frac{\partial}{\partial x}+y^p\frac{\partial}{\partial y}+z^p\frac{\partial}{\partial z}\quad \text{on }A=k[x,y,z],\end{align*} $$
$$ \begin{align*}D=x^p\frac{\partial}{\partial x}+y^p\frac{\partial}{\partial y}+z^p\frac{\partial}{\partial z}\quad \text{on }A=k[x,y,z],\end{align*} $$
the invariant subring
![]() $A^D$
is three-dimensional but only
$A^D$
is three-dimensional but only
![]() $S_2$
. So no non-zero scaling of D can be multiplicative.
$S_2$
. So no non-zero scaling of D can be multiplicative.
2.4 Foliations
Let X be a normal connected k-scheme of finite type.
Definition 2.14. A foliation is a coherent subsheaf
![]() $\mathcal {F}\subset T_{X/k}$
which is saturated in
$\mathcal {F}\subset T_{X/k}$
which is saturated in
![]() $T_{X/k}$
(i.e., the quotient
$T_{X/k}$
(i.e., the quotient
![]() $T_{X/k}/\mathcal {F}$
is a torsion-free
$T_{X/k}/\mathcal {F}$
is a torsion-free
![]() $\mathcal {O}_X$
-module) and closed under Lie brackets. A foliation is called a
$\mathcal {O}_X$
-module) and closed under Lie brackets. A foliation is called a
![]() $\mathbf {1}$
-foliation if it is also closed under pth powers (Footnote
2
).
$\mathbf {1}$
-foliation if it is also closed under pth powers (Footnote
2
).
The geometric significance and relevance of
![]() $1$
-foliations is made clear by Jacobson’s correspondence, which we will state in the next subsection (Theorem 2.39). Of course,
$1$
-foliations is made clear by Jacobson’s correspondence, which we will state in the next subsection (Theorem 2.39). Of course,
![]() $T_{X/k}$
and the zero sub-sheaf are
$T_{X/k}$
and the zero sub-sheaf are
![]() $1$
-foliations, which we refer to as the trivial ones.
$1$
-foliations, which we refer to as the trivial ones.
Remark 2.15. Taking the stalk at the generic point establishes a bijective correspondence between saturated coherent subsheaves of
![]() $T_{X/k}$
and sub-
$T_{X/k}$
and sub-
![]() $k(X)$
-vector spaces of
$k(X)$
-vector spaces of
![]() $T_{k(X)/k}$
. Closure under Lie brackets or pth powers are also properties determined at the generic point. In particular, given a coherent subsheaf of
$T_{k(X)/k}$
. Closure under Lie brackets or pth powers are also properties determined at the generic point. In particular, given a coherent subsheaf of
![]() $T_{X/k}$
which is generically closed under Lie brackets (resp. under Lie brackets and pth powers), its saturation in
$T_{X/k}$
which is generically closed under Lie brackets (resp. under Lie brackets and pth powers), its saturation in
![]() $T_{X/k}$
yields a foliation (resp. a
$T_{X/k}$
yields a foliation (resp. a
![]() $1$
-foliation).
$1$
-foliation).
Definition 2.16. Let
![]() $\mathcal {F}$
be a foliation on X and let
$\mathcal {F}$
be a foliation on X and let
![]() $\eta \in X$
be the unique generic point. The rank of
$\eta \in X$
be the unique generic point. The rank of
![]() $\mathcal {F}$
is
$\mathcal {F}$
is
![]() $\dim _{k(\eta )}\mathcal {F}_\eta $
, and the corank of
$\dim _{k(\eta )}\mathcal {F}_\eta $
, and the corank of
![]() $\mathcal {F}$
is
$\mathcal {F}$
is
![]() $\dim _{k(\eta )}(T_{X/k}/\mathcal {F})_\eta $
. We have the relation
$\dim _{k(\eta )}(T_{X/k}/\mathcal {F})_\eta $
. We have the relation
![]() $\operatorname {\mathrm {rk}}(\mathcal {F})+\operatorname {\mathrm {corank}}(\mathcal {F})=\dim X$
.
$\operatorname {\mathrm {rk}}(\mathcal {F})+\operatorname {\mathrm {corank}}(\mathcal {F})=\dim X$
.
Definition 2.17. Let
![]() $\mathcal {F}$
be a foliation on X, and let
$\mathcal {F}$
be a foliation on X, and let
![]() $x\in X$
be a point. We say that
$x\in X$
be a point. We say that
![]() $\mathcal {F}$
is regular at x if
$\mathcal {F}$
is regular at x if
![]() $\mathcal {O}_{X,x}$
is regular and the
$\mathcal {O}_{X,x}$
is regular and the
![]() $\mathcal {O}_X$
-module
$\mathcal {O}_X$
-module
![]() $T_{X/k}/\mathcal {F}$
is locally free at x. Otherwise,
$T_{X/k}/\mathcal {F}$
is locally free at x. Otherwise,
![]() $\mathcal {F}$
is singular at x.
$\mathcal {F}$
is singular at x.
We note that the singular set of a foliation is closed, of codimension
![]() $\geq 2$
, and contains the singular locus of the underlying variety. Notice also that
$\geq 2$
, and contains the singular locus of the underlying variety. Notice also that
![]() $\mathcal {F}$
, as
$\mathcal {F}$
, as
![]() $\mathcal {O}_X$
-module, is reflexive (equivalently it satisfies Serre’s condition
$\mathcal {O}_X$
-module, is reflexive (equivalently it satisfies Serre’s condition
![]() $S_2$
) by [1, 0EBG].
$S_2$
) by [1, 0EBG].
Regular
![]() $1$
-foliations have a simple local description on regular varieties.
$1$
-foliations have a simple local description on regular varieties.
Lemma 2.18 (Seshadri, Yuan)
Let
![]() $(A,\mathfrak {m})$
be a regular local algebra that is essentially of finite type over k and such that
$(A,\mathfrak {m})$
be a regular local algebra that is essentially of finite type over k and such that
![]() $A/\mathfrak {m}=k$
, and
$A/\mathfrak {m}=k$
, and
![]() $\mathcal {F}\subset \operatorname {\mathrm {Der}}_k(A)$
be a regular
$\mathcal {F}\subset \operatorname {\mathrm {Der}}_k(A)$
be a regular
![]() $1$
-foliation on A. Then we can find local coordinates
$1$
-foliation on A. Then we can find local coordinates
![]() $x_1,\dots ,x_n$
of A such that
$x_1,\dots ,x_n$
of A such that
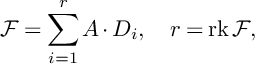 $$ \begin{align*}\mathcal{F}=\sum_{i=1}^rA\cdot D_i, \quad r=\operatorname{\mathrm{rk}} \mathcal{F},\end{align*} $$
$$ \begin{align*}\mathcal{F}=\sum_{i=1}^rA\cdot D_i, \quad r=\operatorname{\mathrm{rk}} \mathcal{F},\end{align*} $$
where the
![]() $D_i$
are as in Lemma 2.4. In particular, A has a p-basis over
$D_i$
are as in Lemma 2.4. In particular, A has a p-basis over
![]() $A^{\mathcal {F}}$
.
$A^{\mathcal {F}}$
.
Proof. See [Reference Seshadri56, Proposition 6] or [Reference Yuan64, Proof of Theorem 12].
More generally, regular (non-necessarily p-closed) derivations of regular complete local ring also admit a normal form, see [Reference McQuillan42, Divertimento II.1.6], but we will not need such a description.
For invertible foliations on regular schemes, there is a simple characterisation of freeness.
Lemma 2.19. Let
![]() $x\in X$
be a regular point and assume that the foliation
$x\in X$
be a regular point and assume that the foliation
![]() $\mathcal {F}\otimes \mathcal {O}_{X,x}$
is invertible as
$\mathcal {F}\otimes \mathcal {O}_{X,x}$
is invertible as
![]() $\mathcal {O}_{X,x}$
-module. Then
$\mathcal {O}_{X,x}$
-module. Then
![]() $\mathcal {F}$
is regular at x if and only if
$\mathcal {F}$
is regular at x if and only if
![]() $\mathcal {F}\not \subset \mathfrak {m}_{X,x}T_{X/k}$
.
$\mathcal {F}\not \subset \mathfrak {m}_{X,x}T_{X/k}$
.
Proof. We apply [Reference Hartshorne18, II, Lemma 8.9] to the cokernel
![]() $\mathcal {N}$
of
$\mathcal {N}$
of
![]() $\mathcal {F}\hookrightarrow T_{X/k}$
: it is free at x if and only if
$\mathcal {F}\hookrightarrow T_{X/k}$
: it is free at x if and only if
![]() $\operatorname {\mathrm {rk}}(\mathcal {N}\otimes k(x))=\dim \mathcal {O}_{X,x}-1$
. This is equivalent to left-exactness of the right-exact sequence
$\operatorname {\mathrm {rk}}(\mathcal {N}\otimes k(x))=\dim \mathcal {O}_{X,x}-1$
. This is equivalent to left-exactness of the right-exact sequence
If
![]() $\mathcal {F}$
is generated by
$\mathcal {F}$
is generated by
![]() $\partial $
at x, then left-exactness holds if and only if
$\partial $
at x, then left-exactness holds if and only if
![]() $\partial \notin \mathfrak {m}_{X,x}T_{X/k}$
.
$\partial \notin \mathfrak {m}_{X,x}T_{X/k}$
.
Next we generalize the regularity condition in the following way.
Definition 2.20. Notations as above. We say that
![]() $\mathcal {F}$
has at worst multiplicative singularities if at every point it is generated formally and up to saturation by multiplicative continuous derivations that commute with each other.
$\mathcal {F}$
has at worst multiplicative singularities if at every point it is generated formally and up to saturation by multiplicative continuous derivations that commute with each other.
Example 2.21.
-
1. Regular
 $1$
-foliations have at worst multiplicative singularities. Indeed, by working formally we reduce through Example 2.18 to
$1$
-foliations have at worst multiplicative singularities. Indeed, by working formally we reduce through Example 2.18 to
 $X=\mathbb {A}^n_{\mathbf {x}}$
and
$X=\mathbb {A}^n_{\mathbf {x}}$
and
 $\mathcal {F}=\sum _{i=1}^r \mathcal {O}_X\cdot \frac {\partial }{\partial x_i}$
. Then while the
$\mathcal {F}=\sum _{i=1}^r \mathcal {O}_X\cdot \frac {\partial }{\partial x_i}$
. Then while the
 $\frac {\partial }{\partial x_i}$
are additive,
$\frac {\partial }{\partial x_i}$
are additive,
 $\mathcal {F}$
is the saturation of
$\mathcal {F}$
is the saturation of
 $\sum _{i=1}^r \mathcal {O}_X\cdot x_i\frac {\partial }{\partial x_i}$
, which is generated by multiplicative derivations commuting with each other.
$\sum _{i=1}^r \mathcal {O}_X\cdot x_i\frac {\partial }{\partial x_i}$
, which is generated by multiplicative derivations commuting with each other. -
2. Let
 $X=\mathbb {A}^3_{\mathbf {x}}$
and
$X=\mathbb {A}^3_{\mathbf {x}}$
and
 $\mathcal {G}=\mathcal {O}_X\cdot \left (x_1\frac {\partial }{\partial x_1}+x_2\frac {\partial }{\partial x_2}\right )+\mathcal {O}_X\cdot \frac {\partial }{\partial x_3}$
. Then
$\mathcal {G}=\mathcal {O}_X\cdot \left (x_1\frac {\partial }{\partial x_1}+x_2\frac {\partial }{\partial x_2}\right )+\mathcal {O}_X\cdot \frac {\partial }{\partial x_3}$
. Then
 $\mathcal {G}$
is the saturation of the sub-module generated by the multiplicative derivations
$\mathcal {G}$
is the saturation of the sub-module generated by the multiplicative derivations
 $x_1\frac {\partial }{\partial x_1}+x_2\frac {\partial }{\partial x_2}$
and
$x_1\frac {\partial }{\partial x_1}+x_2\frac {\partial }{\partial x_2}$
and
 $x_3\frac {\partial }{\partial x_3}$
, and these two derivations commute with each other. So
$x_3\frac {\partial }{\partial x_3}$
, and these two derivations commute with each other. So
 $\mathcal {G}$
has at worst multiplicative singularities.
$\mathcal {G}$
has at worst multiplicative singularities.
Remark 2.22. Much like regular
![]() $1$
-foliations,
$1$
-foliations,
![]() $1$
-foliations with at worst multiplicative singularities have simple formal local descriptions on regular varieties. It will follow from Proposition 4.1 that if A is a regular local k-algebra and
$1$
-foliations with at worst multiplicative singularities have simple formal local descriptions on regular varieties. It will follow from Proposition 4.1 that if A is a regular local k-algebra and
![]() $\mathcal {F}\subset \operatorname {\mathrm {Der}}_k(A)$
is a
$\mathcal {F}\subset \operatorname {\mathrm {Der}}_k(A)$
is a
![]() $1$
-foliation with at worst multiplicative singularities, then we can find formal local coordinates
$1$
-foliation with at worst multiplicative singularities, then we can find formal local coordinates
![]() $x_1,\dots ,x_n$
of
$x_1,\dots ,x_n$
of
![]() $\widehat {A}$
such that
$\widehat {A}$
such that
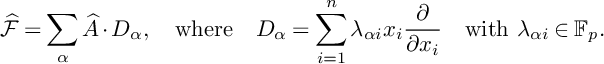 $$ \begin{align*}\widehat{\mathcal{F}}=\sum_\alpha \widehat{A}\cdot D_\alpha,\quad\text{where}\quad D_\alpha= \sum_{i=1}^n\lambda_{\alpha i}x_i\frac{\partial}{\partial x_i}\quad \text{with }\lambda_{\alpha i}\in\mathbb{F}_p.\end{align*} $$
$$ \begin{align*}\widehat{\mathcal{F}}=\sum_\alpha \widehat{A}\cdot D_\alpha,\quad\text{where}\quad D_\alpha= \sum_{i=1}^n\lambda_{\alpha i}x_i\frac{\partial}{\partial x_i}\quad \text{with }\lambda_{\alpha i}\in\mathbb{F}_p.\end{align*} $$
The assumption that
![]() $\mathcal {F}$
is generated formally by commuting derivations is needed in order to find formal coordinates adapted to every
$\mathcal {F}$
is generated formally by commuting derivations is needed in order to find formal coordinates adapted to every
![]() $D_\alpha $
.
$D_\alpha $
.
Example 2.23. Consider the derivation
![]() $\partial _{a,b}$
on
$\partial _{a,b}$
on
![]() $\mathbb {A}^2$
introduced in Example 2.6, and let
$\mathbb {A}^2$
introduced in Example 2.6, and let
![]() $\mathcal {F}_{a,b}$
be the saturation of
$\mathcal {F}_{a,b}$
be the saturation of
![]() $\mathcal {O}\cdot \partial _{a,b}$
. The sheaf
$\mathcal {O}\cdot \partial _{a,b}$
. The sheaf
![]() $\mathcal {F}_{a,b}$
is closed under Lie brackets, essentially because it is generated up to saturation by a single derivation. We have also seen in Example 2.6 that
$\mathcal {F}_{a,b}$
is closed under Lie brackets, essentially because it is generated up to saturation by a single derivation. We have also seen in Example 2.6 that
![]() $\partial _{a,b}$
is p-closed, so
$\partial _{a,b}$
is p-closed, so
![]() $\mathcal {F}_{a,b}$
is a
$\mathcal {F}_{a,b}$
is a
![]() $1$
-foliation. Notice that
$1$
-foliation. Notice that
![]() $\mathcal {F}_{a,b}=\mathcal {F}_{\lambda a,\lambda b}$
for any
$\mathcal {F}_{a,b}=\mathcal {F}_{\lambda a,\lambda b}$
for any
![]() $\lambda \in \mathbb {F}_p^\times $
. Let us look at its singularities.
$\lambda \in \mathbb {F}_p^\times $
. Let us look at its singularities.
-
1. If
 $ab=0$
then
$ab=0$
then
 $\mathcal {F}_{a,b}$
is generated by either
$\mathcal {F}_{a,b}$
is generated by either
 $\frac {\partial }{\partial x}$
or
$\frac {\partial }{\partial x}$
or
 $\frac {\partial }{\partial x}$
, and hence it is regular everywhere.
$\frac {\partial }{\partial x}$
, and hence it is regular everywhere. -
2. If
 $ab\neq 0$
then
$ab\neq 0$
then
 $\mathcal {F}_{a,b}$
is generated by
$\mathcal {F}_{a,b}$
is generated by
 $\partial _{a,b}$
and has a unique singularity at the origin.
$\partial _{a,b}$
and has a unique singularity at the origin.
Hence the
![]() $1$
-foliation
$1$
-foliation
![]() $\mathcal {F}_{a,b}$
has at worst multiplicative singularities.
$\mathcal {F}_{a,b}$
has at worst multiplicative singularities.
Construction 2.24 (Birational pullback)
Let
![]() $\pi \colon Y\to X$
be a birational morphism of normal connected k-schemes. The generic stalk
$\pi \colon Y\to X$
be a birational morphism of normal connected k-schemes. The generic stalk
![]() $\mathcal {F}_{k(X)}$
determines a foliation on Y, which we will usually denote by
$\mathcal {F}_{k(X)}$
determines a foliation on Y, which we will usually denote by
![]() $\pi ^{*}\mathcal {F}$
. If
$\pi ^{*}\mathcal {F}$
. If
![]() $\mathcal {F}$
is a
$\mathcal {F}$
is a
![]() $1$
-foliation, then so is
$1$
-foliation, then so is
![]() $f^{*}\mathcal {F}$
by Remark 2.15.
$f^{*}\mathcal {F}$
by Remark 2.15.
Example 2.25. The reader will check that if
![]() $\pi \colon \mathbb {A}^n_{\mathbf {y}}\to \mathbb {A}^n_{\mathbf {x}}$
is the
$\pi \colon \mathbb {A}^n_{\mathbf {y}}\to \mathbb {A}^n_{\mathbf {x}}$
is the
![]() $y_1$
-chart of the blow-up of
$y_1$
-chart of the blow-up of
![]() $(x_1,\dots ,x_r)$
for
$(x_1,\dots ,x_r)$
for
![]() $r\leq n$
, which means that we have
$r\leq n$
, which means that we have
then the transformation rules are
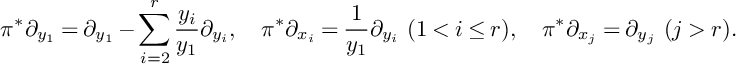 $$ \begin{align*}\pi^{*}\partial_{y_1}=\partial_{y_1}-\sum_{i=2}^r\frac{y_i}{y_1}\partial_{y_i}, \quad \pi^{*}\partial_{x_i}=\frac{1}{y_1}\partial_{y_i} \ (1<i\leq r), \quad \pi^{*}\partial_{x_j}=\partial_{y_j} \ (j>r).\end{align*} $$
$$ \begin{align*}\pi^{*}\partial_{y_1}=\partial_{y_1}-\sum_{i=2}^r\frac{y_i}{y_1}\partial_{y_i}, \quad \pi^{*}\partial_{x_i}=\frac{1}{y_1}\partial_{y_i} \ (1<i\leq r), \quad \pi^{*}\partial_{x_j}=\partial_{y_j} \ (j>r).\end{align*} $$
Definition 2.26. Let
![]() $\mathcal {F}$
be a foliation on X. A prime divisor
$\mathcal {F}$
be a foliation on X. A prime divisor
![]() $E\subset X$
is called invariant for
$E\subset X$
is called invariant for
![]() $\mathcal {F}$
if genericallyFootnote
3
the restricted map
$\mathcal {F}$
if genericallyFootnote
3
the restricted map
![]() $\mathcal {F}|_E\to T^1_{X/k}|_E$
factors through
$\mathcal {F}|_E\to T^1_{X/k}|_E$
factors through
![]() $T^1_{E/k}$
, or equivalently if
$T^1_{E/k}$
, or equivalently if
![]() $\mathcal {F}(I_E)\subset I_E$
at the generic point of E.
$\mathcal {F}(I_E)\subset I_E$
at the generic point of E.
It is convenient to introduce the function
![]() $\epsilon _{\mathcal {F}}$
on the set of prime divisors on X, defined as follows:
$\epsilon _{\mathcal {F}}$
on the set of prime divisors on X, defined as follows:
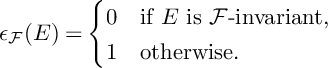 $$ \begin{align} \epsilon_{\mathcal{F}}(E)=\begin{cases} 0 & \text{if }E\text{ is }\mathcal{F}\text{-invariant,}\\ 1 & \text{otherwise.} \end{cases} \end{align} $$
$$ \begin{align} \epsilon_{\mathcal{F}}(E)=\begin{cases} 0 & \text{if }E\text{ is }\mathcal{F}\text{-invariant,}\\ 1 & \text{otherwise.} \end{cases} \end{align} $$
If
![]() $\pi \colon Y\to X$
is birational with Y normal and E is a prime divisor on Y, then we set
$\pi \colon Y\to X$
is birational with Y normal and E is a prime divisor on Y, then we set
![]() $\epsilon _{\mathcal {F}}(E)=\epsilon _{\pi ^{*}\mathcal {F}}(E)$
. This depends only on the divisorial valuation defined by E on
$\epsilon _{\mathcal {F}}(E)=\epsilon _{\pi ^{*}\mathcal {F}}(E)$
. This depends only on the divisorial valuation defined by E on
![]() $K(X)$
, not on
$K(X)$
, not on
![]() $\pi $
. We drop the subscript and write
$\pi $
. We drop the subscript and write
![]() $\epsilon (\bullet )$
is no confusion is likely to arise.
$\epsilon (\bullet )$
is no confusion is likely to arise.
Remark 2.27. Suppose that
![]() $Z\subset X$
is a closed subset, and that X is regular at the generic point of Z. If
$Z\subset X$
is a closed subset, and that X is regular at the generic point of Z. If
![]() $\pi \colon \operatorname {\mathrm {Bl}}_ZX\to X$
is the blow-up, then the (non-)invariance of the (unique)
$\pi \colon \operatorname {\mathrm {Bl}}_ZX\to X$
is the blow-up, then the (non-)invariance of the (unique)
![]() $\pi $
-exceptional divisor E can be a subtle question, already on surfaces.
$\pi $
-exceptional divisor E can be a subtle question, already on surfaces.
-
1. If
 $\mathcal {F}\subsetneq T_{\mathbb {A}^2/k}$
is regular at the origin, then the blow-up of the origin will produce an invariant divisor;
$\mathcal {F}\subsetneq T_{\mathbb {A}^2/k}$
is regular at the origin, then the blow-up of the origin will produce an invariant divisor; -
2. If
 $\mathcal {F}\subsetneq T_{\mathbb {A}^2/k}$
is not regular at the origin, then the blow-up of the origin may or may not produce an invariant divisor: see Example 3.5.
$\mathcal {F}\subsetneq T_{\mathbb {A}^2/k}$
is not regular at the origin, then the blow-up of the origin may or may not produce an invariant divisor: see Example 3.5.
In particular,
![]() $\mathcal {F}(I_Z)\subset I_Z$
does not guarantee that E is
$\mathcal {F}(I_Z)\subset I_Z$
does not guarantee that E is
![]() $\pi ^{*}\mathcal {F}$
-invariant (because of the saturation involved in defining
$\pi ^{*}\mathcal {F}$
-invariant (because of the saturation involved in defining
![]() $\pi ^{*}\mathcal {F}$
).
$\pi ^{*}\mathcal {F}$
).
2.5 Infinitesimal quotients
For simplicity of exposition, let us discuss quotients by derivations before quotients by foliations.
2.5.1 Quotients by derivations
Let A be a k-algebra and
![]() $D\in \operatorname {\mathrm {Der}}_k(A)$
.
$D\in \operatorname {\mathrm {Der}}_k(A)$
.
Definition 2.28. The subring of constants (or: the invariant subring) of D is the subset
![]() $A^D=\{a\in A\mid D(a)=0\}$
.
$A^D=\{a\in A\mid D(a)=0\}$
.
It is easily seen that
![]() $A^D$
is indeed a subring of A, and that it contains
$A^D$
is indeed a subring of A, and that it contains
![]() $k[A^p]$
.
$k[A^p]$
.
Lemma 2.29. Let A and D be as above, and assume that A is integral. Then:
-
1.
 $\operatorname {\mathrm {Frac}}(A)^D=\operatorname {\mathrm {Frac}}(A^D).$
$\operatorname {\mathrm {Frac}}(A)^D=\operatorname {\mathrm {Frac}}(A^D).$
-
2. If A is F-finite or normal, so is
 $A^D$
.
$A^D$
. -
3. If
 $x,y\in A^D$
is a regular sequence in A, then
$x,y\in A^D$
is a regular sequence in A, then
 $x,y$
is also a regular sequence in
$x,y$
is also a regular sequence in
 $A^D$
.
$A^D$
.
Proof. The derivation D extends to
![]() $\operatorname {\mathrm {Frac}}(A)$
following the usual rule for differentiating quotients. Clearly
$\operatorname {\mathrm {Frac}}(A)$
following the usual rule for differentiating quotients. Clearly
![]() $\operatorname {\mathrm {Frac}}(A^D)\subseteq \operatorname {\mathrm {Frac}}(A)^D$
. Conversely, assume that
$\operatorname {\mathrm {Frac}}(A^D)\subseteq \operatorname {\mathrm {Frac}}(A)^D$
. Conversely, assume that
![]() $\frac {a}{b}\in \operatorname {\mathrm {Frac}}(A)^D$
. As
$\frac {a}{b}\in \operatorname {\mathrm {Frac}}(A)^D$
. As
![]() $\frac {a}{b}=\frac {ab^{p-1}}{b^p}$
we have
$\frac {a}{b}=\frac {ab^{p-1}}{b^p}$
we have
 $$ \begin{align*}0=D\left(\frac{a}{b}\right)=\frac{D(ab^{p-1})}{b^p}\end{align*} $$
$$ \begin{align*}0=D\left(\frac{a}{b}\right)=\frac{D(ab^{p-1})}{b^p}\end{align*} $$
and so
![]() $D(ab^{p-1})=0$
. Therefore
$D(ab^{p-1})=0$
. Therefore
![]() $\frac {ab^{p-1}}{b^p}\in \operatorname {\mathrm {Frac}}(A^D)$
, showing the first point.
$\frac {ab^{p-1}}{b^p}\in \operatorname {\mathrm {Frac}}(A^D)$
, showing the first point.
Assume that A is F-finite. Then A is a finite module over
![]() $A^p$
, a fortiori over
$A^p$
, a fortiori over
![]() $A^D$
: by Artin–Tate lemma [1, 00IS] it follows that
$A^D$
: by Artin–Tate lemma [1, 00IS] it follows that
![]() $A^D$
is finite over
$A^D$
is finite over
![]() $A^p$
. Since
$A^p$
. Since
![]() $A^p$
is finite over
$A^p$
is finite over
![]() $(A^D)^p$
, we obtain that
$(A^D)^p$
, we obtain that
![]() $A^D$
is F-finite.
$A^D$
is F-finite.
Assume that A is normal, and suppose that
![]() $x\in \operatorname {\mathrm {Frac}}(A^D)$
satisfies a monic polynomial equation with coefficients in
$x\in \operatorname {\mathrm {Frac}}(A^D)$
satisfies a monic polynomial equation with coefficients in
![]() $A^D$
. Then
$A^D$
. Then
![]() $x\in A$
by normality of A, and
$x\in A$
by normality of A, and
![]() $D(x)=0$
by assumption. So
$D(x)=0$
by assumption. So
![]() $x\in A^D$
, showing that
$x\in A^D$
, showing that
![]() $A^D$
is normal.
$A^D$
is normal.
Finally, assume that
![]() $x,y\in A$
is a regular sequence. Clearly x is not a zero-divisor in the subring
$x,y\in A$
is a regular sequence. Clearly x is not a zero-divisor in the subring
![]() $A^D$
. Now assume that multiplication by y is not injective on
$A^D$
. Now assume that multiplication by y is not injective on
![]() $A^D/xA^D$
. Then we have an equality
$A^D/xA^D$
. Then we have an equality
![]() $zy=wx$
with
$zy=wx$
with
![]() $z,w\in A^D$
and
$z,w\in A^D$
and
![]() $z\notin xA^D$
. Considering this equality in A, we must have
$z\notin xA^D$
. Considering this equality in A, we must have
![]() $z=ax$
for some
$z=ax$
for some
![]() $a\in A$
. But
$a\in A$
. But
![]() $0=D(z)=xD(a)$
hence
$0=D(z)=xD(a)$
hence
![]() $a\in A^D$
and so in fact
$a\in A^D$
and so in fact
![]() $z\in xA^D$
: contradiction. Hence
$z\in xA^D$
: contradiction. Hence
![]() $x,y$
is a regular sequence on
$x,y$
is a regular sequence on
![]() $A^D$
.
$A^D$
.
The singularities of
![]() $A^D$
are difficult to describe beyond this lemma, even if A is regular. We refer to [Reference Aramova2], [Reference Aramova and Avramov3] for a general discussion, and to [Reference Miyanishi and Russell45] for several two-dimensional examples. We will only be interested in the cases where D is p-closed, but this does not simplify the matter by much. If D is additive, all hell may break loose: the following proposition shows that every singularity universally homeomorphic to a regular point is a composition of
$A^D$
are difficult to describe beyond this lemma, even if A is regular. We refer to [Reference Aramova2], [Reference Aramova and Avramov3] for a general discussion, and to [Reference Miyanishi and Russell45] for several two-dimensional examples. We will only be interested in the cases where D is p-closed, but this does not simplify the matter by much. If D is additive, all hell may break loose: the following proposition shows that every singularity universally homeomorphic to a regular point is a composition of
![]() $\alpha _p$
-quotients.
$\alpha _p$
-quotients.
Proposition 2.30. Let
![]() $f\colon X\to Y$
be a finite purely inseparable morphism of normal
$f\colon X\to Y$
be a finite purely inseparable morphism of normal
![]() $\mathbb {F}_p$
-schemes of degree p. Then f is locally an
$\mathbb {F}_p$
-schemes of degree p. Then f is locally an
![]() $\alpha _p$
-quotient.
$\alpha _p$
-quotient.
Proof. Indeed, f is locally the quotient by a p-closed derivation [Reference Matsumoto40, Proposition 2.4]. Now apply Lemma 2.12.
The following lemma illustrates the typical singularities that may arise.
Lemma 2.31. Assume that A is a local normal k-algebra of dimension
![]() $d\geq 3$
and that
$d\geq 3$
and that
![]() $D\in \operatorname {\mathrm {Der}}_k(A)$
is an additive derivation. Suppose that
$D\in \operatorname {\mathrm {Der}}_k(A)$
is an additive derivation. Suppose that
![]() $D(A)$
generates an
$D(A)$
generates an
![]() $\mathfrak {m}_A$
-primary ideal. Then
$\mathfrak {m}_A$
-primary ideal. Then
![]() $A^D$
is not
$A^D$
is not
![]() $S_3$
and not F-injective.
$S_3$
and not F-injective.
Proof. The following argument is essentially contained in [Reference Liedtke, Martin and Matsumoto37, §Reference Artin and Tate5]. Let
![]() $Y=\operatorname {\mathrm {Spec}}(A)$
. By Proposition 2.7 and Lemma 2.10, the derivation D defines an action of
$Y=\operatorname {\mathrm {Spec}}(A)$
. By Proposition 2.7 and Lemma 2.10, the derivation D defines an action of
![]() $\alpha _p$
on Y which is free on
$\alpha _p$
on Y which is free on
![]() $Y^{*}=Y\setminus \{\mathfrak {m}_A\}$
and whose fixed locus is
$Y^{*}=Y\setminus \{\mathfrak {m}_A\}$
and whose fixed locus is
![]() $\mathfrak {m}_A$
. (Indeed, notice that the residual derivation
$\mathfrak {m}_A$
. (Indeed, notice that the residual derivation
![]() $\bar {D}\in \operatorname {\mathrm {Der}}_k(A/\mathfrak {m}_A)$
is zero.) Let
$\bar {D}\in \operatorname {\mathrm {Der}}_k(A/\mathfrak {m}_A)$
is zero.) Let
![]() $X=\operatorname {\mathrm {Spec}}(A^D)=Y/\alpha _p$
be the geometric quotient: it is also a local normal affine scheme of dimension d. Let
$X=\operatorname {\mathrm {Spec}}(A^D)=Y/\alpha _p$
be the geometric quotient: it is also a local normal affine scheme of dimension d. Let
![]() $q\colon Y\to X$
be the quotient map, let
$q\colon Y\to X$
be the quotient map, let
![]() $\mathfrak {n}=q(\mathfrak {m}_A)$
and write
$\mathfrak {n}=q(\mathfrak {m}_A)$
and write
![]() $X^{*}=X\setminus \{\mathfrak {n}\}$
.
$X^{*}=X\setminus \{\mathfrak {n}\}$
.
Recall that
![]() $\alpha _p$
-torsors are classified by the flat cohomology groups
$\alpha _p$
-torsors are classified by the flat cohomology groups
![]() $H^1_{\text {fl}}(\bullet , \alpha _p)$
. The restriction
$H^1_{\text {fl}}(\bullet , \alpha _p)$
. The restriction
![]() $q^{*}\colon Y^{*}\to X^{*}$
is an
$q^{*}\colon Y^{*}\to X^{*}$
is an
![]() $\alpha _p$
-torsor, and thus defines an element
$\alpha _p$
-torsor, and thus defines an element
![]() $[q^{*}]\in H^1_{\text {fl}}(X^{*},\alpha _p)$
. We claim
$[q^{*}]\in H^1_{\text {fl}}(X^{*},\alpha _p)$
. We claim
![]() $[q^{*}]$
does not belong to the natural restriction map
$[q^{*}]$
does not belong to the natural restriction map
![]() $r\colon H^1_{\text {fl}}(X,\alpha _p)\to H^1_{\text {fl}}(X^{*},\alpha _p)$
. Indeed, suppose that there was an
$r\colon H^1_{\text {fl}}(X,\alpha _p)\to H^1_{\text {fl}}(X^{*},\alpha _p)$
. Indeed, suppose that there was an
![]() $\alpha _p$
-torsor
$\alpha _p$
-torsor
![]() $\mathfrak {q}\colon Y'\to X$
such that
$\mathfrak {q}\colon Y'\to X$
such that
![]() $\mathfrak {q}\times _YY^{*}=q^{*}$
. Then
$\mathfrak {q}\times _YY^{*}=q^{*}$
. Then
![]() $Y'$
is affine and
$Y'$
is affine and
![]() $S_2$
. Since
$S_2$
. Since
![]() $\mathfrak {q}$
is finite we see that
$\mathfrak {q}$
is finite we see that
![]() $\mathfrak {q}^{-1}(\mathfrak {n})$
has codimension d and so
$\mathfrak {q}^{-1}(\mathfrak {n})$
has codimension d and so
where, for the last equality, we used that Y is
![]() $S_2$
as well. Therefore
$S_2$
as well. Therefore
![]() $q=\mathfrak {q}$
: but this is impossible since q is not an
$q=\mathfrak {q}$
: but this is impossible since q is not an
![]() $\alpha _p$
-torsor.
$\alpha _p$
-torsor.
Now we relate the non-surjectivity of
![]() $H^1_{\text {fl}}(X,\alpha _p)\to H^1_{\text {fl}}(X^{*},\alpha _p)$
to local cohomology. Evaluate the exact sequence of flat group schemes
$H^1_{\text {fl}}(X,\alpha _p)\to H^1_{\text {fl}}(X^{*},\alpha _p)$
to local cohomology. Evaluate the exact sequence of flat group schemes
on
![]() $X^{*}$
and X. Taking in account that
$X^{*}$
and X. Taking in account that
![]() $H^i_{\text {fl}}(\bullet ,\mathbb {G}_a)=H^i(\bullet ,\mathcal {O}_{\bullet })$
, the beginning of the long exact sequence of cohomology gives the commutative diagram
$H^i_{\text {fl}}(\bullet ,\mathbb {G}_a)=H^i(\bullet ,\mathcal {O}_{\bullet })$
, the beginning of the long exact sequence of cohomology gives the commutative diagram
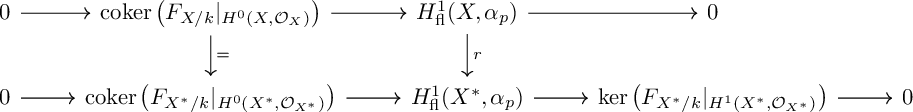
with exact rows. Here we used that
![]() $H^1(X,\mathcal {O}_X)=0$
since X is affine, and the left-most vertical arrow is an equality because X is normal and
$H^1(X,\mathcal {O}_X)=0$
since X is affine, and the left-most vertical arrow is an equality because X is normal and
![]() $X^{*}\subset X$
is big. So the non-surjectivity of r implies that the Frobenius action on
$X^{*}\subset X$
is big. So the non-surjectivity of r implies that the Frobenius action on
![]() $H^1(X^{*},\mathcal {O}_{X^{*}})$
has a non-trivial kernel. Looking at the usual long exact sequence
$H^1(X^{*},\mathcal {O}_{X^{*}})$
has a non-trivial kernel. Looking at the usual long exact sequence
on which the Frobenius acts compatibly, we deduce that the action of the Frobenius on
![]() $H^2_{\mathfrak {n}}(X,\mathcal {O}_X)\cong H^1(X^{*},\mathcal {O}_{X^{*}})$
has a non-trivial kernel. This means that X is not
$H^2_{\mathfrak {n}}(X,\mathcal {O}_X)\cong H^1(X^{*},\mathcal {O}_{X^{*}})$
has a non-trivial kernel. This means that X is not
![]() $S_3$
neither F-injective.
$S_3$
neither F-injective.
The quotients by multiplicative derivations are, in comparison, way nicer: we discuss these in Section 4.1.
Let us compute two examples of subring of constants.
Example 2.32. Consider the derivation
![]() $\partial _{a,b}$
on
$\partial _{a,b}$
on
![]() $k[x,y]$
from Example 2.6. Then we have
$k[x,y]$
from Example 2.6. Then we have
![]() $k[x,y]^{\partial _{a,b}}=k[x^iy^j\mid ai+bj=0 \ (p)]$
.
$k[x,y]^{\partial _{a,b}}=k[x^iy^j\mid ai+bj=0 \ (p)]$
.
Example 2.33. Consider
![]() $D=x^p\frac {\partial }{\partial x}+y^p\frac {\partial }{\partial y}$
on
$D=x^p\frac {\partial }{\partial x}+y^p\frac {\partial }{\partial y}$
on
![]() $k[x,y]$
. Then
$k[x,y]$
. Then
![]() $D^{[p]}=0$
. Clearly
$D^{[p]}=0$
. Clearly
![]() $x^p,y^p$
and
$x^p,y^p$
and
![]() $x^py-xy^p$
belong to the ring of constants, and I claim that they generate it. It suffices to show that
$x^py-xy^p$
belong to the ring of constants, and I claim that they generate it. It suffices to show that
is a normal ring, which is easily seen using the Jacobian criterion.
If
![]() $p=2$
, then in Artin’s terminology [Reference Artin6] this is a
$p=2$
, then in Artin’s terminology [Reference Artin6] this is a
![]() $D^0_{4}$
rational double point (hence a canonical singularity). Using Fedder’s criterion, one checks that it is not F-pure.
$D^0_{4}$
rational double point (hence a canonical singularity). Using Fedder’s criterion, one checks that it is not F-pure.
2.5.2 Quotients by foliations
Let X be a normal Noetherian connected k-scheme and let
![]() $\mathcal {F}\subset \operatorname {\mathrm {Der}}_k(\mathcal {O}_X)$
be a foliation on X. We define the presheaf
$\mathcal {F}\subset \operatorname {\mathrm {Der}}_k(\mathcal {O}_X)$
be a foliation on X. We define the presheaf
![]() $\mathcal {O}_X^{\mathcal {F}}$
on the topological space
$\mathcal {O}_X^{\mathcal {F}}$
on the topological space
![]() $|X|$
by
$|X|$
by
This is a sheaf of algebras on
![]() $|X|$
. It is easy to see that the locally ringed space
$|X|$
. It is easy to see that the locally ringed space
![]() $(|X|,\mathcal {O}_X^{\mathcal {F}})$
is a k-scheme: for if
$(|X|,\mathcal {O}_X^{\mathcal {F}})$
is a k-scheme: for if
![]() $\operatorname {\mathrm {Spec}}(A)$
is an affine chart affine, then
$\operatorname {\mathrm {Spec}}(A)$
is an affine chart affine, then
so
![]() $\operatorname {\mathrm {Spec}}(A^{\mathcal {F}})$
has the same underlying topological space as
$\operatorname {\mathrm {Spec}}(A^{\mathcal {F}})$
has the same underlying topological space as
![]() $\operatorname {\mathrm {Spec}}(A)$
.
$\operatorname {\mathrm {Spec}}(A)$
.
Definition 2.34. The quotient of X by
![]() $\mathcal {F}$
is the k-scheme
$\mathcal {F}$
is the k-scheme
![]() $X/\mathcal {F}=(|X|,\mathcal {O}_X^{\mathcal {F}})$
.
$X/\mathcal {F}=(|X|,\mathcal {O}_X^{\mathcal {F}})$
.
In particular
![]() $X/\mathcal {F}$
comes with a purely inseparable morphism
$X/\mathcal {F}$
comes with a purely inseparable morphism
![]() $q\colon X\to X/\mathcal {F}$
which is a universal homeomorphism and factors the k-linear Frobenius of X (Footnote
4
). If X is F-finite then q is a finite morphism. In this article, we will only consider the case where
$q\colon X\to X/\mathcal {F}$
which is a universal homeomorphism and factors the k-linear Frobenius of X (Footnote
4
). If X is F-finite then q is a finite morphism. In this article, we will only consider the case where
![]() $\mathcal {F}$
is a
$\mathcal {F}$
is a
![]() $1$
-foliation.
$1$
-foliation.
The following well-known lemma will be used implicitly many times.
Lemma 2.35 (cf [Reference Tziolas61, §4.1])
Let A be a normal Noetherian F-finite k-algebra and
![]() $\mathcal {F}$
a foliation on
$\mathcal {F}$
a foliation on
![]() $\operatorname {\mathrm {Spec}}(A)$
. If
$\operatorname {\mathrm {Spec}}(A)$
. If
![]() $\mathfrak {p}$
is a prime ideal of A with contraction
$\mathfrak {p}$
is a prime ideal of A with contraction
![]() $\mathfrak {q}\subset A^{\mathcal {F}}$
, then:
$\mathfrak {q}\subset A^{\mathcal {F}}$
, then:
-
1.
 $A^{\mathcal {F}}$
is Noetherian,
$A^{\mathcal {F}}$
is Noetherian, -
2.
 $(A^{\mathcal {F}})_{\mathfrak {q}}=(A_{\mathfrak {p}})^{\mathcal {F}_{\mathfrak {p}}}$
, and
$(A^{\mathcal {F}})_{\mathfrak {q}}=(A_{\mathfrak {p}})^{\mathcal {F}_{\mathfrak {p}}}$
, and -
3. if
 $\widehat {A}=\widehat {A_{\mathfrak {p}}}$
and
$\widehat {A}=\widehat {A_{\mathfrak {p}}}$
and
 $\widehat {\mathcal {F}}=\mathcal {F}_{\mathfrak {p}}\otimes \widehat {A}$
, then
$\widehat {\mathcal {F}}=\mathcal {F}_{\mathfrak {p}}\otimes \widehat {A}$
, then
 $\widehat {A}^{\widehat {\mathcal {F}}}$
is a local ring and it is equal to the completion of
$\widehat {A}^{\widehat {\mathcal {F}}}$
is a local ring and it is equal to the completion of
 $(A^{\mathcal {F}})_{\mathfrak {q}}$
.
$(A^{\mathcal {F}})_{\mathfrak {q}}$
.
Proof. First we show that
![]() $A^p$
is Noetherian: we have to show that any ideal
$A^p$
is Noetherian: we have to show that any ideal
![]() $I\subset A^p$
is finitely generated. Let
$I\subset A^p$
is finitely generated. Let
![]() $\mathcal {I}=\{f\in A\mid f^p\in I\}$
. Then clearly
$\mathcal {I}=\{f\in A\mid f^p\in I\}$
. Then clearly
![]() $\mathcal {I}$
is an ideal of A, and so it is finitely generated, say
$\mathcal {I}$
is an ideal of A, and so it is finitely generated, say
![]() $\mathcal {I}=(f_1,\dots ,f_r)$
. Then it is easily seen that
$\mathcal {I}=(f_1,\dots ,f_r)$
. Then it is easily seen that
![]() $I=(f_1^p,\dots ,f_r^p)$
. So
$I=(f_1^p,\dots ,f_r^p)$
. So
![]() $A^p$
is Noetherian.
$A^p$
is Noetherian.
As
![]() $A^p$
is Noetherian and A is F-finite, we get that A is a Noetherian
$A^p$
is Noetherian and A is F-finite, we get that A is a Noetherian
![]() $A^p$
-module. As
$A^p$
-module. As
![]() $A^{\mathcal {F}}$
is a sub-
$A^{\mathcal {F}}$
is a sub-
![]() $A^p$
-module, it must be a finite
$A^p$
-module, it must be a finite
![]() $A^p$
-module. The Noetherian ring property of
$A^p$
-module. The Noetherian ring property of
![]() $A^p$
now ascends to
$A^p$
now ascends to
![]() $A^{\mathcal {F}}$
by the Artin–Tate lemma [Reference Artin and Tate5].
$A^{\mathcal {F}}$
by the Artin–Tate lemma [Reference Artin and Tate5].
The localization property is [Reference Tziolas61, Proposition 4.2]. For the completion property, we may assume that A is local with maximal ideal
![]() $\mathfrak {p}$
, so
$\mathfrak {p}$
, so
![]() $B=A^{\mathcal {F}}$
is also local with maximal ideal
$B=A^{\mathcal {F}}$
is also local with maximal ideal
![]() $\mathfrak {q}$
. Since A is F-finite, it is a finite B-module. As
$\mathfrak {q}$
. Since A is F-finite, it is a finite B-module. As
![]() $\mathcal {F}$
is a finite A-module, it is also a finite B-module. So
$\mathcal {F}$
is a finite A-module, it is also a finite B-module. So
![]() $\widehat {A}=A\otimes _B\widehat {B}$
and
$\widehat {A}=A\otimes _B\widehat {B}$
and
![]() $\widehat {\mathcal {F}}=\mathcal {F}\otimes _B\widehat {B}$
. If
$\widehat {\mathcal {F}}=\mathcal {F}\otimes _B\widehat {B}$
. If
![]() $D_1,\dots ,D_n$
generate
$D_1,\dots ,D_n$
generate
![]() $\mathcal {F}$
, then we have an exact sequence
$\mathcal {F}$
, then we have an exact sequence
which remains exact after tensoring by
![]() $\widehat {B}$
, by flatness of completion. As
$\widehat {B}$
, by flatness of completion. As
![]() $\sum _i D_i\otimes _B\widehat {B}=\widehat {\mathcal {F}}$
, we obtain
$\sum _i D_i\otimes _B\widehat {B}=\widehat {\mathcal {F}}$
, we obtain
![]() $\widehat {B}=\widehat {A}^{\widehat {\mathcal {F}}}$
.
$\widehat {B}=\widehat {A}^{\widehat {\mathcal {F}}}$
.
Lemma 2.36. Notations as above.
-
1.
 $K(X)^{\mathcal {F}}=K(X/\mathcal {F}).$
$K(X)^{\mathcal {F}}=K(X/\mathcal {F}).$
-
2. If X is F-finite and normal, so is
 $X/\mathcal {F}$
.
$X/\mathcal {F}$
. -
3. If
 $s,t\in \mathcal {O}_{X/\mathcal {F},q(x)}$
form a regular sequence in
$s,t\in \mathcal {O}_{X/\mathcal {F},q(x)}$
form a regular sequence in
 $\mathcal {O}_{X,x}$
, then
$\mathcal {O}_{X,x}$
, then
 $s,t$
is also a regular sequence in
$s,t$
is also a regular sequence in
 $\mathcal {O}_{X/\mathcal {F},q(x)}$
.
$\mathcal {O}_{X/\mathcal {F},q(x)}$
.
Proof. The question is Zariski-local, so we may assume that
![]() $X=\operatorname {\mathrm {Spec}}(A)$
. Say that
$X=\operatorname {\mathrm {Spec}}(A)$
. Say that
![]() $\mathcal {F}$
is generated by
$\mathcal {F}$
is generated by
![]() $D_1,\dots ,D_n\in \operatorname {\mathrm {Der}}_k(A)$
. Then
$D_1,\dots ,D_n\in \operatorname {\mathrm {Der}}_k(A)$
. Then
![]() $X/\mathcal {F}=\operatorname {\mathrm {Spec}}\left (\bigcap _iA^{D_i}\right )$
. So the assertions follow from Lemma 2.29 applied inductively on
$X/\mathcal {F}=\operatorname {\mathrm {Spec}}\left (\bigcap _iA^{D_i}\right )$
. So the assertions follow from Lemma 2.29 applied inductively on
![]() $A_0=A, A_1=A_0^{D_1}, A_2=A_1^{D_2}$
, etc., once we have observed that in the proof of Lemma 2.29 there is no harm in assuming that the codomain of D was the fraction field.
$A_0=A, A_1=A_0^{D_1}, A_2=A_1^{D_2}$
, etc., once we have observed that in the proof of Lemma 2.29 there is no harm in assuming that the codomain of D was the fraction field.
Lemma 2.37 [Reference Miyaoka and Peternell46, Part I, III.1.9]
Let X be a smooth k-scheme,
![]() $\mathcal {F}$
a
$\mathcal {F}$
a
![]() $1$
-foliation on X. Then
$1$
-foliation on X. Then
![]() $X/\mathcal {F}$
is regular if and only if
$X/\mathcal {F}$
is regular if and only if
![]() $\mathcal {F}$
is regular.
$\mathcal {F}$
is regular.
Proof. We may base-change to the algebraic closure of k and localize at a closed point, so that
![]() $X=\operatorname {\mathrm {Spec}}(A)$
is the spectrum of a regular local k-algebra with algebraically closed residue field k. If
$X=\operatorname {\mathrm {Spec}}(A)$
is the spectrum of a regular local k-algebra with algebraically closed residue field k. If
![]() $\mathcal {F}$
is regular, then by Example 2.18 we can find coordinates
$\mathcal {F}$
is regular, then by Example 2.18 we can find coordinates
![]() $x_1,\dots ,x_n$
of A such that
$x_1,\dots ,x_n$
of A such that
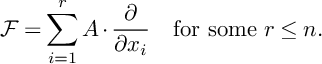 $$ \begin{align*}\mathcal{F}=\sum_{i=1}^rA\cdot \frac{\partial}{\partial x_i} \quad \text{for some }r\leq n.\end{align*} $$
$$ \begin{align*}\mathcal{F}=\sum_{i=1}^rA\cdot \frac{\partial}{\partial x_i} \quad \text{for some }r\leq n.\end{align*} $$
Then clearly ![]() , so
, so
![]() $A^{\mathcal {F}}$
is regular.
$A^{\mathcal {F}}$
is regular.
Conversely, assume that
![]() $A^{\mathcal {F}}$
is regular. We have to check that
$A^{\mathcal {F}}$
is regular. We have to check that
![]() $T_{A/k}/\mathcal {F}$
is free. In fact, by Kunz’s conjecture, a theorem since 1981, see [Reference Kimura and Niitsuma29],
$T_{A/k}/\mathcal {F}$
is free. In fact, by Kunz’s conjecture, a theorem since 1981, see [Reference Kimura and Niitsuma29],
![]() $A^{\mathcal {F}}$
has a p-basis
$A^{\mathcal {F}}$
has a p-basis
![]() $x_{r+1},\dots ,x_n$
over
$x_{r+1},\dots ,x_n$
over
![]() $A^p$
. Then
$A^p$
. Then
![]() $x_{r+1}^p,\dots ,x_n^p$
extend to a set of local coordinates
$x_{r+1}^p,\dots ,x_n^p$
extend to a set of local coordinates
![]() $x_1^p,\dots ,x_n^p$
of
$x_1^p,\dots ,x_n^p$
of
![]() $A^p$
. From this and the Jacobson correspondence it follows immediately that
$A^p$
. From this and the Jacobson correspondence it follows immediately that
![]() $\mathcal {F}=\bigoplus _{i=1}^rA\frac {\partial }{\partial x_i}$
and thus the quotient
$\mathcal {F}=\bigoplus _{i=1}^rA\frac {\partial }{\partial x_i}$
and thus the quotient
![]() $T_X/\mathcal {F}=\bigoplus _{i=r+1}^nA\frac {\partial }{\partial x_i}$
is free.
$T_X/\mathcal {F}=\bigoplus _{i=r+1}^nA\frac {\partial }{\partial x_i}$
is free.
Remark 2.38. The above lemma, together with its proof, should be compared to the following result of Zariski [Reference Zariski65, Lemma 4] (see also the more general Nagata–Zariski–Lipman theorem [Reference Matsumura41, Theorem 30.1]): if
![]() $(A,\mathfrak {m})$
is a complete local ring of characteristic
$(A,\mathfrak {m})$
is a complete local ring of characteristic
![]() $0$
, and
$0$
, and
![]() $D\in \operatorname {\mathrm {Der}}(A)$
such that
$D\in \operatorname {\mathrm {Der}}(A)$
such that
![]() $D(x)\notin \mathfrak {m}$
for some
$D(x)\notin \mathfrak {m}$
for some
![]() $x\in A$
, then there exists a subring
$x\in A$
, then there exists a subring
![]() $A'\subset A$
over which x is analytically independent, such that
$A'\subset A$
over which x is analytically independent, such that ![]() and
and
![]() $D|_{A_1}\equiv 0$
. Notice also that in this case the assumption that A is complete is necessary, whereas in the proof of Lemma 2.37 completion is not needed to find a system of parameters adapted to
$D|_{A_1}\equiv 0$
. Notice also that in this case the assumption that A is complete is necessary, whereas in the proof of Lemma 2.37 completion is not needed to find a system of parameters adapted to
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
For the formation of quotients, the facts that
![]() $\mathcal {F}$
is saturated, closed under Lie brackets and pth powers are irrelevant. However, if we restrict to quotients by
$\mathcal {F}$
is saturated, closed under Lie brackets and pth powers are irrelevant. However, if we restrict to quotients by
![]() $1$
-foliations, we obtain the following geometric meaningful correspondence.
$1$
-foliations, we obtain the following geometric meaningful correspondence.
Theorem 2.39 (Jacobson correspondence: [Reference Jacobson25], [Reference Patakfalvi and Waldron49])
Let X be a normal k-variety. Then there is a bijection between
-
1.
 $1$
-foliations of rank r on X, and
$1$
-foliations of rank r on X, and -
2. factorizations of the k-linear Frobenius
 $F_{X/k}\colon X\overset {f}{\longrightarrow } Y\to X^{(-1)}$
where Y is normal and
$F_{X/k}\colon X\overset {f}{\longrightarrow } Y\to X^{(-1)}$
where Y is normal and
 $\deg (f)=p^r$
.
$\deg (f)=p^r$
.
The bijection is explicitly given by
![]() $\mathcal {F}\mapsto (X\to X/\mathcal {F})$
and
$\mathcal {F}\mapsto (X\to X/\mathcal {F})$
and
![]() $(X\to Y)\mapsto \operatorname {\mathrm {Der}}_{\mathcal {O}_Y}(\mathcal {O}_X)$
.
$(X\to Y)\mapsto \operatorname {\mathrm {Der}}_{\mathcal {O}_Y}(\mathcal {O}_X)$
.
Let us also mention the well-known adjunction formula for quotients.
Definition 2.40. Let
![]() $\mathcal {F}$
be a foliation on X. Any Weil divisor representing the divisorial sheaf
$\mathcal {F}$
be a foliation on X. Any Weil divisor representing the divisorial sheaf
![]() $\det (\mathcal {F})^{-1}$
is called a canonical divisor of
$\det (\mathcal {F})^{-1}$
is called a canonical divisor of
![]() $\mathcal {F}$
, and will be denoted by
$\mathcal {F}$
, and will be denoted by
![]() $K_{\mathcal {F}}$
.
$K_{\mathcal {F}}$
.
Proposition 2.41 (Adjunction formula: [Reference Patakfalvi and Waldron49, Proposition 2.10])
Let
![]() $q\colon X\to X/\mathcal {F}$
be the quotient of a normal k-variety by a
$q\colon X\to X/\mathcal {F}$
be the quotient of a normal k-variety by a
![]() $1$
-foliation. Then we have an exact sequence
$1$
-foliation. Then we have an exact sequence
and consequently an equality of Weil divisors
3 Birational singularities of
 $1$
-foliations
$1$
-foliations
Given a foliation
![]() $\mathcal {F}$
on a normal k-variety X, we define the birational singularities of
$\mathcal {F}$
on a normal k-variety X, we define the birational singularities of
![]() $\mathcal {F}$
in the spirit of the MMP (see [Reference Kollár and Mori32]). We formulate the definition for any foliation, but we will only use it for
$\mathcal {F}$
in the spirit of the MMP (see [Reference Kollár and Mori32]). We formulate the definition for any foliation, but we will only use it for
![]() $1$
-foliations. It is convenient to do so in presence of a
$1$
-foliations. It is convenient to do so in presence of a
![]() $\mathbb {Q}$
-Weil divisor
$\mathbb {Q}$
-Weil divisor
![]() $\Delta $
.
$\Delta $
.
Definition 3.1. We say that
![]() $(\mathcal {F},\Delta )$
is a (
$(\mathcal {F},\Delta )$
is a (
![]() $\mathbb {Q}$
-)Gorenstein foliated pair if
$\mathbb {Q}$
-)Gorenstein foliated pair if
![]() $K_{\mathcal {F}}+\Delta $
is (
$K_{\mathcal {F}}+\Delta $
is (
![]() $\mathbb {Q}$
-)Cartier.
$\mathbb {Q}$
-)Cartier.
Assume that
![]() $(\mathcal {F},\Delta )$
is
$(\mathcal {F},\Delta )$
is
![]() $\mathbb {Q}$
-Gorenstein. Then if
$\mathbb {Q}$
-Gorenstein. Then if
![]() $\pi \colon Y\to X$
is a birational proper k-morphism of normal varieties, we can write
$\pi \colon Y\to X$
is a birational proper k-morphism of normal varieties, we can write
where E runs through the
![]() $\pi $
-exceptional prime divisors. Recalling the function
$\pi $
-exceptional prime divisors. Recalling the function
![]() $\epsilon $
from (2.2), we can make the following definition.
$\epsilon $
from (2.2), we can make the following definition.
Definition 3.2 [Reference McQuillan42, Reference Spicer57]
Suppose that
![]() $(\mathcal {F},\Delta )$
is
$(\mathcal {F},\Delta )$
is
![]() $\mathbb {Q}$
-Gorenstein. Then
$\mathbb {Q}$
-Gorenstein. Then
![]() $(\mathcal {F},\Delta )$
is:
$(\mathcal {F},\Delta )$
is:
-
1. terminal (resp. canonical) if
 $a(E;\mathcal {F},\Delta )>0$
(resp.
$a(E;\mathcal {F},\Delta )>0$
(resp.
 $a(E;\mathcal {F},\Delta )\geq 0$
) for all exceptional prime divisors E over X;
$a(E;\mathcal {F},\Delta )\geq 0$
) for all exceptional prime divisors E over X; -
2. klt if
 $\lfloor \Delta \rfloor =0$
and
$\lfloor \Delta \rfloor =0$
and
 $a(E;\mathcal {F},\Delta )> -\epsilon _{\mathcal {F}}(E)$
for all exceptional E over X;
$a(E;\mathcal {F},\Delta )> -\epsilon _{\mathcal {F}}(E)$
for all exceptional E over X; -
3. log canonical (lc) if
 $a(E;\mathcal {F},\Delta )\geq -\epsilon _{\mathcal {F}}(E)$
for all exceptional E over X.
$a(E;\mathcal {F},\Delta )\geq -\epsilon _{\mathcal {F}}(E)$
for all exceptional E over X.
Some remarks are in order. It follows from the definitions that the following implications hold:
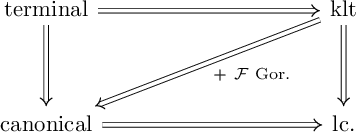
However, if
![]() $\mathcal {F}$
is canonical then it is not necessarily klt.
$\mathcal {F}$
is canonical then it is not necessarily klt.
The terminal and klt conditions seem rather restrictive for foliations. It will follow from Proposition 4.12 that if a
![]() $1$
-foliation
$1$
-foliation
![]() $\mathcal {F}$
is terminal at a point
$\mathcal {F}$
is terminal at a point
![]() $x\in X$
then
$x\in X$
then
![]() $\mathcal {O}_{X,x}$
must be singular. In particular the terminal locus of
$\mathcal {O}_{X,x}$
must be singular. In particular the terminal locus of
![]() $1$
-foliations is never open.
$1$
-foliations is never open.
Moreover, in positive characteristic the birational singularities of X and
![]() $\mathcal {F}$
may have little in common (Footnote
5
): see [Reference Bernasconi8, Example 2.14].
$\mathcal {F}$
may have little in common (Footnote
5
): see [Reference Bernasconi8, Example 2.14].
As an example, we describe the birational singularities of regular
![]() $1$
-foliations on regular varieties.
$1$
-foliations on regular varieties.
Lemma 3.3. Regular
![]() $1$
-foliations on regular varieties are canonical.
$1$
-foliations on regular varieties are canonical.
Proof. We use an observation of Bernasconi [Reference Bernasconi8, Remark 2.12 and Example 2.13]. The statement is étale-local, so it suffices to consider the case
![]() $X=\mathbb {A}^n_{\mathbf {x}}$
and
$X=\mathbb {A}^n_{\mathbf {x}}$
and
![]() $\mathcal {F}=\bigoplus _{i=1}^r\mathcal {O}_X\cdot \frac {\partial }{\partial x_i}$
. Then
$\mathcal {F}=\bigoplus _{i=1}^r\mathcal {O}_X\cdot \frac {\partial }{\partial x_i}$
. Then
![]() $K_{\mathcal {F}}$
is the line bundle generated inside
$K_{\mathcal {F}}$
is the line bundle generated inside
![]() $\bigwedge ^rT_X^1$
by the r-vector field
$\bigwedge ^rT_X^1$
by the r-vector field
![]() $\theta $
dual to the r-form
$\theta $
dual to the r-form
![]() $dx_1\wedge \dots \wedge dx_r\in \Omega _X^r$
. If
$dx_1\wedge \dots \wedge dx_r\in \Omega _X^r$
. If
![]() $f\colon Y\to X$
is birational and
$f\colon Y\to X$
is birational and
![]() $\tilde {\theta }$
is the pullback of
$\tilde {\theta }$
is the pullback of
![]() $\theta $
, then
$\theta $
, then
![]() $f^{*}(dx_1\wedge \dots \wedge dx_r)(\tilde {\theta })=1$
. As
$f^{*}(dx_1\wedge \dots \wedge dx_r)(\tilde {\theta })=1$
. As
![]() $f^{*}(dx_1\wedge \dots \wedge dx_r)$
is a regular r-form, we see that
$f^{*}(dx_1\wedge \dots \wedge dx_r)$
is a regular r-form, we see that
![]() $\tilde {\theta }$
does not have any zero along exceptional divisors. This implies that
$\tilde {\theta }$
does not have any zero along exceptional divisors. This implies that
![]() $K_{f^{*}\mathcal {F}}-K_{\mathcal {F}}\geq 0$
, and so
$K_{f^{*}\mathcal {F}}-K_{\mathcal {F}}\geq 0$
, and so
![]() $\mathcal {F}$
is canonical.
$\mathcal {F}$
is canonical.
Lemma 3.4. Non-trivial regular
![]() $1$
-foliations on regular varieties are not terminal.
$1$
-foliations on regular varieties are not terminal.
Proof. We follow the method of [Reference Bernasconi8, Example 2.13]. Let X be a regular variety and
![]() $\mathcal {F}$
be a non-trivial regular
$\mathcal {F}$
be a non-trivial regular
![]() $1$
-foliation. If
$1$
-foliation. If
![]() $\mathcal {N}_{\mathcal {F}}$
is the cokernel of
$\mathcal {N}_{\mathcal {F}}$
is the cokernel of
![]() $\mathcal {F}\hookrightarrow T_{X/k}$
, then
$\mathcal {F}\hookrightarrow T_{X/k}$
, then
![]() $K_{\mathcal {F}}=K_X\otimes \det (\mathcal {N}_{\mathcal {F}}^\vee )^{-1}$
. If
$K_{\mathcal {F}}=K_X\otimes \det (\mathcal {N}_{\mathcal {F}}^\vee )^{-1}$
. If
![]() $\pi \colon X'\to X$
is birational, then a convenient way to compute
$\pi \colon X'\to X$
is birational, then a convenient way to compute
![]() $K_{\mathcal {F}'}$
(where
$K_{\mathcal {F}'}$
(where
![]() $\mathcal {F}'=\pi ^{*}\mathcal {F}$
) is the following. Write
$\mathcal {F}'=\pi ^{*}\mathcal {F}$
) is the following. Write
where the right-hand side is uniquely determined by the property that E is an exceptional
![]() $\pi $
-divisor and
$\pi $
-divisor and
![]() $\mathcal {M}$
is locally generated by a
$\mathcal {M}$
is locally generated by a
![]() $(\operatorname {\mathrm {corank}}\mathcal {F})$
-form without pole nor zero along
$(\operatorname {\mathrm {corank}}\mathcal {F})$
-form without pole nor zero along
![]() $\operatorname {\mathrm {Exc}}(\pi )$
(in our case
$\operatorname {\mathrm {Exc}}(\pi )$
(in our case
![]() $E\leq 0$
by Lemma 3.3). Then we have
$E\leq 0$
by Lemma 3.3). Then we have
![]() $K_{\mathcal {F}'}=K_{X'}\otimes \mathcal {M}^{-1}$
.
$K_{\mathcal {F}'}=K_{X'}\otimes \mathcal {M}^{-1}$
.
The result we want to establish is local, so we may work at the stalk
![]() $\mathcal {O}_{X,s}$
of the variety at a closed point. We will construct a weighted blow-up of
$\mathcal {O}_{X,s}$
of the variety at a closed point. We will construct a weighted blow-up of
![]() $\mathcal {O}_{X,s}$
whose coarse moduli witnesses the non-terminality of
$\mathcal {O}_{X,s}$
whose coarse moduli witnesses the non-terminality of
![]() $\widehat {\mathcal {F}}$
. By Example 2.18, we may find local coordinates
$\widehat {\mathcal {F}}$
. By Example 2.18, we may find local coordinates
![]() $x_1,\dots ,x_n\in \mathcal {O}_{X,s}$
such that
$x_1,\dots ,x_n\in \mathcal {O}_{X,s}$
such that
![]() $\mathcal {F}$
is generated by
$\mathcal {F}$
is generated by
![]() $\partial /\partial x_i$
for
$\partial /\partial x_i$
for
![]() $i=1,\dots ,r$
(where
$i=1,\dots ,r$
(where
![]() $1\leq r<n$
). Now blow-up the ideal
$1\leq r<n$
). Now blow-up the ideal
![]() $(x_1,x_n^p)$
: we obtain a morphism
$(x_1,x_n^p)$
: we obtain a morphism
![]() $\pi \colon X'\to \operatorname {\mathrm {Spec}}(\mathcal {O}_{X,s})$
. Its base-change along the completion can be written as
$\pi \colon X'\to \operatorname {\mathrm {Spec}}(\mathcal {O}_{X,s})$
. Its base-change along the completion can be written as
where the grading is given by
![]() $\deg X_1=1$
and
$\deg X_1=1$
and
![]() $\deg X_n=p$
. A simple computation on the affine chart
$\deg X_n=p$
. A simple computation on the affine chart
![]() $D_+(X_1)$
, using the method of the first paragraph, shows that
$D_+(X_1)$
, using the method of the first paragraph, shows that
![]() $K_{\widehat {\pi }^{*}\mathcal {F}'}=\widehat {\pi }^{*}K_{\mathcal {F}}$
. So
$K_{\widehat {\pi }^{*}\mathcal {F}'}=\widehat {\pi }^{*}K_{\mathcal {F}}$
. So
![]() $\mathcal {F}$
is indeed not terminal.
$\mathcal {F}$
is indeed not terminal.
Example 3.5. Consider the
![]() $1$
-foliation
$1$
-foliation
![]() $\mathcal {F}_{a,b}$
on
$\mathcal {F}_{a,b}$
on
![]() $\mathbb {A}^2$
introduced in Example 2.23, and assume that
$\mathbb {A}^2$
introduced in Example 2.23, and assume that
![]() $ab\neq 0$
. I claim that it is log canonical, but not canonical nor klt. Let us show that these are not canonical nor klt; the log canonical property can be obtained by similar considerations, using that any divisorial valuation on
$ab\neq 0$
. I claim that it is log canonical, but not canonical nor klt. Let us show that these are not canonical nor klt; the log canonical property can be obtained by similar considerations, using that any divisorial valuation on
![]() $\mathbb {A}^2$
can be reached by a sequence of blow-ups of points [Reference Kollár and Mori32, Lemma 2.45], or alternatively by using Proposition 3.6.
$\mathbb {A}^2$
can be reached by a sequence of blow-ups of points [Reference Kollár and Mori32, Lemma 2.45], or alternatively by using Proposition 3.6.
We may assume that
![]() $a\neq 0$
. Let us blow-up the origin and consider the chart given by
$a\neq 0$
. Let us blow-up the origin and consider the chart given by
Explicit computations show that
![]() $\partial _{a,b}$
lifts to
$\partial _{a,b}$
lifts to
![]() $\partial _{a,b-a}$
on
$\partial _{a,b-a}$
on
![]() $\mathbb {A}^2_{u,v}$
.
$\mathbb {A}^2_{u,v}$
.
-
1. Assume that
 $a=b$
, so we may assume that both are equal to
$a=b$
, so we may assume that both are equal to
 $1$
. Then the induced (saturated)
$1$
. Then the induced (saturated)
 $1$
-foliation
$1$
-foliation
 $\pi ^{*}\mathcal {F}_{1,1}$
is
$\pi ^{*}\mathcal {F}_{1,1}$
is
 $\mathcal {F}_{1,0}$
, generated by
$\mathcal {F}_{1,0}$
, generated by
 $\frac {\partial }{\partial u}$
, and we have
$\frac {\partial }{\partial u}$
, and we have
 $\pi ^{*}K_{\mathcal {F}_{1,1}}=K_{\mathcal {F}_{1,0}}+E$
where
$\pi ^{*}K_{\mathcal {F}_{1,1}}=K_{\mathcal {F}_{1,0}}+E$
where
 $E=(u=0)$
is the exceptional divisor. Since E is not invariant, this shows that
$E=(u=0)$
is the exceptional divisor. Since E is not invariant, this shows that
 $\mathcal {F}_{1,1}$
is not canonical and also not klt, and that E is a log canonical place for the foliated pair
$\mathcal {F}_{1,1}$
is not canonical and also not klt, and that E is a log canonical place for the foliated pair
 $(\mathbb {A}^2,\mathcal {F}_{1,1})$
.
$(\mathbb {A}^2,\mathcal {F}_{1,1})$
. -
2. Next assume that
 $a\neq b$
. Then no saturation is needed to obtain the induced
$a\neq b$
. Then no saturation is needed to obtain the induced
 $1$
-foliation
$1$
-foliation
 $\pi ^{*}\mathcal {F}_{a,b}=\mathcal {F}_{a,b-a}$
. In particular
$\pi ^{*}\mathcal {F}_{a,b}=\mathcal {F}_{a,b-a}$
. In particular
 $\pi ^{*}K_{\mathcal {F}_{a,b}}=K_{\mathcal {F}_{a,b-a}}$
. The exceptional divisor is invariant for
$\pi ^{*}K_{\mathcal {F}_{a,b}}=K_{\mathcal {F}_{a,b-a}}$
. The exceptional divisor is invariant for
 $\mathcal {F}_{a,b-a}$
, which shows that
$\mathcal {F}_{a,b-a}$
, which shows that
 $\mathcal {F}_{a,b}$
is not klt.
$\mathcal {F}_{a,b}$
is not klt.Let
 $n>0$
be minimal such that
$n>0$
be minimal such that
 $b-na=0$
in
$b-na=0$
in
 $\mathbb {F}_p$
. If we iterate this blow-up procedure n times, we find a birational morphism
$\mathbb {F}_p$
. If we iterate this blow-up procedure n times, we find a birational morphism
 $\varphi \colon \mathbb {A}^2\to \mathbb {A}^2$
such that
$\varphi \colon \mathbb {A}^2\to \mathbb {A}^2$
such that
 $\varphi ^{*}K_{\mathcal {F}_{a,b}}=K_{\mathcal {F}_{1,0}}+E$
where E is a prime
$\varphi ^{*}K_{\mathcal {F}_{a,b}}=K_{\mathcal {F}_{1,0}}+E$
where E is a prime
 $\varphi $
-exceptional divisor which is invariant for
$\varphi $
-exceptional divisor which is invariant for
 $\mathcal {F}_{1,0}$
. So
$\mathcal {F}_{1,0}$
. So
 $\mathcal {F}_{a,b}$
is not canonical.
$\mathcal {F}_{a,b}$
is not canonical.
In case X is regular and
![]() $\mathcal {F}$
is a line bundle, there is a simple local characterization of log canonical foliations due to McQuillan.
$\mathcal {F}$
is a line bundle, there is a simple local characterization of log canonical foliations due to McQuillan.
Proposition 3.6. Suppose
![]() $(x\in X)$
is the spectrum of a regular local ring with maximal ideal
$(x\in X)$
is the spectrum of a regular local ring with maximal ideal
![]() $\mathfrak {m}$
and residue field
$\mathfrak {m}$
and residue field
![]() $k(x)$
, and
$k(x)$
, and
![]() $\mathcal {F}$
is an invertible
$\mathcal {F}$
is an invertible
![]() $1$
-foliation generated by
$1$
-foliation generated by
![]() $\partial $
. Then:
$\partial $
. Then:
-
1. if
 $\partial \notin \mathfrak {m}\operatorname {\mathrm {Der}}_k(\mathcal {O}_{X,x})$
then
$\partial \notin \mathfrak {m}\operatorname {\mathrm {Der}}_k(\mathcal {O}_{X,x})$
then
 $\mathcal {F}$
is canonical at x;
$\mathcal {F}$
is canonical at x; -
2. if
 $\partial \in \mathfrak {m}\operatorname {\mathrm {Der}}_k(\mathcal {O}_{X,x})$
, then
$\partial \in \mathfrak {m}\operatorname {\mathrm {Der}}_k(\mathcal {O}_{X,x})$
, then
 $\mathcal {F}$
is log canonical at x if and only if the
$\mathcal {F}$
is log canonical at x if and only if the
 $k(x)$
-linear endomorphism
$k(x)$
-linear endomorphism
 $\partial _0\in \operatorname {\mathrm {End}}_{k(x)}(\mathfrak {m}/\mathfrak {m}^2)$
is not nilpotent.
$\partial _0\in \operatorname {\mathrm {End}}_{k(x)}(\mathfrak {m}/\mathfrak {m}^2)$
is not nilpotent.
This is stated in [Reference McQuillan42], but as locating the precise argument is a non-trivial task we sketch the proof for the convenience of the reader.
Proof. The first part follows immediately from Lemmas 2.19 and 3.3. Thus we may assume that
![]() $\partial \in \mathfrak {m}\operatorname {\mathrm {Der}}_k(\mathcal {O}_{X,x})$
.
$\partial \in \mathfrak {m}\operatorname {\mathrm {Der}}_k(\mathcal {O}_{X,x})$
.
First, observe that
![]() $\mathcal {O}_X\cdot \partial =K_{\mathcal {F}}^{-1}$
. So if E is any exceptional prime divisor appearing on
$\mathcal {O}_X\cdot \partial =K_{\mathcal {F}}^{-1}$
. So if E is any exceptional prime divisor appearing on
![]() $\pi \colon Y\to X$
, then at the generic point of E we can write
$\pi \colon Y\to X$
, then at the generic point of E we can write
![]() $\pi ^{*}\partial = t_E^{-a(E;\mathcal {F})}\partial '$
, where
$\pi ^{*}\partial = t_E^{-a(E;\mathcal {F})}\partial '$
, where
![]() $t_E$
is a uniformizer of
$t_E$
is a uniformizer of
![]() $\mathcal {O}_{Y,E}$
and
$\mathcal {O}_{Y,E}$
and
![]() $\partial '$
belongs to
$\partial '$
belongs to
![]() $T_{Y/k}$
but not to
$T_{Y/k}$
but not to
![]() $\mathfrak {m}_E T_{Y/k}$
. The number
$\mathfrak {m}_E T_{Y/k}$
. The number
![]() $a(E,\mathcal {F})$
is necessarily an integer.
$a(E,\mathcal {F})$
is necessarily an integer.
Non-log canonicity implies nilpotence. Let E be as above, centered at x, and assume that
![]() $a(E,\mathcal {F})<-\epsilon _{\mathcal {F}}(E)$
. Write
$a(E,\mathcal {F})<-\epsilon _{\mathcal {F}}(E)$
. Write
![]() $e=-a(E;\mathcal {F})$
. We distinguish two cases:
$e=-a(E;\mathcal {F})$
. We distinguish two cases:
-
1. Assume that
 $e\geq 2$
. Then
$e\geq 2$
. Then
 $\pi ^{*}\partial (\mathfrak {m}_E^n)\subset \mathfrak {m}_E^{n+e-1}$
. Letting
$\pi ^{*}\partial (\mathfrak {m}_E^n)\subset \mathfrak {m}_E^{n+e-1}$
. Letting
 $\mathfrak {p}_n=\mathfrak {m}_E^n\cap \mathcal {O}_{X,x}$
, we obtain
$\mathfrak {p}_n=\mathfrak {m}_E^n\cap \mathcal {O}_{X,x}$
, we obtain
 $\partial (\mathfrak {p}_n)\subset \mathfrak {p}_{n+e-1}$
. As the
$\partial (\mathfrak {p}_n)\subset \mathfrak {p}_{n+e-1}$
. As the
 $\mathfrak {p}_n$
’s generate the
$\mathfrak {p}_n$
’s generate the
 $\mathfrak {m}_{X,x}$
-adic topology, we deduce that the continuous extension of
$\mathfrak {m}_{X,x}$
-adic topology, we deduce that the continuous extension of
 $\partial $
to
$\partial $
to
 $\widehat {\mathcal {O}}_{X,x}$
is topologically nilpotent. In particular,
$\widehat {\mathcal {O}}_{X,x}$
is topologically nilpotent. In particular,
 $\partial ^{[N]}(\mathfrak {m}_{X,x})\subset \mathfrak {m}_{X,x}^2$
for some
$\partial ^{[N]}(\mathfrak {m}_{X,x})\subset \mathfrak {m}_{X,x}^2$
for some
 $N\gg 0$
. This implies that
$N\gg 0$
. This implies that
 $\partial _0^{[N]}=0$
.
$\partial _0^{[N]}=0$
. -
2. The remaining case is
 $e=1$
. Then E must be invariant for
$e=1$
. Then E must be invariant for
 $\pi ^{*}\mathcal {F}$
, which means that
$\pi ^{*}\mathcal {F}$
, which means that
 $\partial '(\mathfrak {m}_E)\subset \mathfrak {m}_E$
. Then
$\partial '(\mathfrak {m}_E)\subset \mathfrak {m}_E$
. Then
 $\partial (\mathfrak {p}_n)\subset \mathfrak {p}_{n+1}$
and the same argument gives that
$\partial (\mathfrak {p}_n)\subset \mathfrak {p}_{n+1}$
and the same argument gives that
 $\partial _0$
is nilpotent.
$\partial _0$
is nilpotent.
Nilpotence implies non-log canonicity. We also distinguish two cases, in which we explicitly produce a divisor with discrepancy
![]() $\leq -2$
. The main tool is the formulas of Example 2.25.
$\leq -2$
. The main tool is the formulas of Example 2.25.
-
1.
 $\partial _0=0$
. Then
$\partial _0=0$
. Then
 $\partial \in \mathfrak {m}^2T_X$
, where
$\partial \in \mathfrak {m}^2T_X$
, where
 $\mathfrak {m}$
is the maximal ideal of the closed point x. The blow-up of the closed point produces an exceptional divisor E whose discrepancy is
$\mathfrak {m}$
is the maximal ideal of the closed point x. The blow-up of the closed point produces an exceptional divisor E whose discrepancy is
 $< -\epsilon (E)$
. To see this, we may work étale-locally and reduce to the case where we blow-up
$< -\epsilon (E)$
. To see this, we may work étale-locally and reduce to the case where we blow-up
 $\mathbb {A}^n_{x_1,\dots ,x_n}$
along the ideal
$\mathbb {A}^n_{x_1,\dots ,x_n}$
along the ideal
 $I=(x_1,\dots ,x_l)$
(with
$I=(x_1,\dots ,x_l)$
(with
 $l\leq n$
), and
$l\leq n$
), and
 $\partial =\sum _{i=1}^nf_i\partial _{x_i}$
satisfies
$\partial =\sum _{i=1}^nf_i\partial _{x_i}$
satisfies
 $\min _i \operatorname {\mathrm {ord}}_If_i=d\geq 2$
. If
$\min _i \operatorname {\mathrm {ord}}_If_i=d\geq 2$
. If
 $\pi \colon \mathbb {A}^n_{\mathbf {y}}\to \mathbb {A}^n_{\mathbf {x}}$
is the
$\pi \colon \mathbb {A}^n_{\mathbf {y}}\to \mathbb {A}^n_{\mathbf {x}}$
is the
 $y_1$
-patch of the blow-up, then we have where the
$y_1$
-patch of the blow-up, then we have where the $$ \begin{align*}\pi^{*}\partial = y_1^{d-1}\left[\tilde{f}_1(\mathbf{y})\partial_{y_1} + \sum_{i=2}^l \frac{1}{y_1}\left(\tilde{f}_i(\mathbf{y})- y_i\tilde{f}_1(\mathbf{y})\right) \partial_{y_i} +\sum_{j=l+1}^n \tilde{f}_j(\mathbf{y})\partial_{y_j}\right], \end{align*} $$
$$ \begin{align*}\pi^{*}\partial = y_1^{d-1}\left[\tilde{f}_1(\mathbf{y})\partial_{y_1} + \sum_{i=2}^l \frac{1}{y_1}\left(\tilde{f}_i(\mathbf{y})- y_i\tilde{f}_1(\mathbf{y})\right) \partial_{y_i} +\sum_{j=l+1}^n \tilde{f}_j(\mathbf{y})\partial_{y_j}\right], \end{align*} $$
 $\tilde {f}_\bullet (\mathbf {y})=y_1^{-d+1}(f_\bullet (\mathbf {x})\circ \pi )$
are regular functions that are still divisible by
$\tilde {f}_\bullet (\mathbf {y})=y_1^{-d+1}(f_\bullet (\mathbf {x})\circ \pi )$
are regular functions that are still divisible by
 $y_1$
. If the exceptional divisor
$y_1$
. If the exceptional divisor
 $E=(y_1=0)$
is invariant, then
$E=(y_1=0)$
is invariant, then
 $a(E;\mathcal {F})\leq -d+1<0=-\epsilon (E)$
. Assume that E is not invariant: as
$a(E;\mathcal {F})\leq -d+1<0=-\epsilon (E)$
. Assume that E is not invariant: as
 $\tilde {f}_1(\mathbf {y})|_{(y_1=0)}=0$
, this implies that the derivation in brackets is still divisible by
$\tilde {f}_1(\mathbf {y})|_{(y_1=0)}=0$
, this implies that the derivation in brackets is still divisible by
 $y_1$
, and therefore
$y_1$
, and therefore
 $a(E;\mathcal {F})\leq -d<-\epsilon (E)$
.
$a(E;\mathcal {F})\leq -d<-\epsilon (E)$
.
-
2. If
 $\partial _0\neq 0$
is nilpotent, we will show that after a few well-chosen blow-ups we reduce to the previous case. The Jordan normal form of
$\partial _0\neq 0$
is nilpotent, we will show that after a few well-chosen blow-ups we reduce to the previous case. The Jordan normal form of
 $\partial _0$
is defined over
$\partial _0$
is defined over
 $k(x)$
, since its only eigenvalue is
$k(x)$
, since its only eigenvalue is
 $0$
. So we may choose local coordinates with respect to which the matrix of
$0$
. So we may choose local coordinates with respect to which the matrix of
 $\partial _0$
is already in Jordan normal form. The centers of the blow-ups will depend only on these coordinates. Thus we may again work étale-locally on
$\partial _0$
is already in Jordan normal form. The centers of the blow-ups will depend only on these coordinates. Thus we may again work étale-locally on
 $\mathbb {A}^n_{x_1,\dots ,x_n}$
, say that the point x corresponds to the ideal
$\mathbb {A}^n_{x_1,\dots ,x_n}$
, say that the point x corresponds to the ideal
 $I=(x_1,\dots ,x_l)$
(with
$I=(x_1,\dots ,x_l)$
(with
 $l\leq n$
), and assume that a nilpotent non-zero Jordan block is spanned by
$l\leq n$
), and assume that a nilpotent non-zero Jordan block is spanned by
 $x_1,\dots ,x_r$
(with
$x_1,\dots ,x_r$
(with
 $r\leq l$
). We are going to blow-up
$r\leq l$
). We are going to blow-up
 $(x_1,\dots ,x_r)$
: since this does not affect the other Jordan blocks, we may as well assume that
$(x_1,\dots ,x_r)$
: since this does not affect the other Jordan blocks, we may as well assume that
 $r=l$
. So write
$r=l$
. So write  $$ \begin{align*}\partial=\sum_{i=1}^{r-1}x_i\partial_{x_{i+1}} +\delta, \quad \delta\in I^2T_{\mathbb{A}^2/k}.\end{align*} $$
$$ \begin{align*}\partial=\sum_{i=1}^{r-1}x_i\partial_{x_{i+1}} +\delta, \quad \delta\in I^2T_{\mathbb{A}^2/k}.\end{align*} $$
If
 $\pi \colon \mathbb {A}^n_{\mathbf {y}}\to \mathbb {A}^n_{\mathbf {x}}$
is the
$\pi \colon \mathbb {A}^n_{\mathbf {y}}\to \mathbb {A}^n_{\mathbf {x}}$
is the
 $y_r$
-patch of the I-blow-up, then one finds that
$y_r$
-patch of the I-blow-up, then one finds that  $$ \begin{align*}\pi^{*}\partial= \sum_{i=1}^{r-2}y_i\partial_{y_{i+1}} + \left[ y_{r-1}y_r\partial_{y_r} -\sum_{i=1}^{r-1}y_{r-1}y_i\partial_{y_i}+\pi^{*}\delta \right].\end{align*} $$
$$ \begin{align*}\pi^{*}\partial= \sum_{i=1}^{r-2}y_i\partial_{y_{i+1}} + \left[ y_{r-1}y_r\partial_{y_r} -\sum_{i=1}^{r-1}y_{r-1}y_i\partial_{y_i}+\pi^{*}\delta \right].\end{align*} $$
The derivation in parenthesis belongs to
 $(y_1,\dots ,y_r)^2T_{\mathbb {A}^n/k}$
, and the dimension of the
$(y_1,\dots ,y_r)^2T_{\mathbb {A}^n/k}$
, and the dimension of the
 $0$
-eigenspace at the origin has increased. Notice also that
$0$
-eigenspace at the origin has increased. Notice also that
 $\pi ^{*}\partial $
is not divisible by
$\pi ^{*}\partial $
is not divisible by
 $y_r$
, so the discrepancy of the (invariant)
$y_r$
, so the discrepancy of the (invariant)
 $\pi $
-exceptional divisor is
$\pi $
-exceptional divisor is
 $0$
. By induction, we therefore reduce to the case where
$0$
. By induction, we therefore reduce to the case where
 $\partial _0=0$
.
$\partial _0=0$
.
The proof is complete.
Corollary 3.7. Let X be a regular variety over k, and
![]() $\mathcal {F}$
be a
$\mathcal {F}$
be a
![]() $1$
-foliation of rank
$1$
-foliation of rank
![]() $1$
on X. Then:
$1$
on X. Then:
-
1.
 $\mathcal {F}$
is canonical if and only if
$\mathcal {F}$
is canonical if and only if
 $\mathcal {F}$
is regular.
$\mathcal {F}$
is regular. -
2.
 $\mathcal {F}$
is lc if and only if
$\mathcal {F}$
is lc if and only if
 $\mathcal {F}$
has at worst multiplicative singularities.
$\mathcal {F}$
has at worst multiplicative singularities.
Proof. By Proposition 3.6 and Definition 2.20 this is a formal-local question, so we may assume that
![]() $X=\operatorname {\mathrm {Spec}}(\mathcal {O})$
is the spectrum of a complete regular local ring, with maximal ideal
$X=\operatorname {\mathrm {Spec}}(\mathcal {O})$
is the spectrum of a complete regular local ring, with maximal ideal
![]() $\mathfrak {m}$
, and
$\mathfrak {m}$
, and
![]() $\mathcal {F}$
is generated by
$\mathcal {F}$
is generated by
![]() $\partial \in \operatorname {\mathrm {Der}}_k^{\text {cont}}(\mathcal {O})$
(for
$\partial \in \operatorname {\mathrm {Der}}_k^{\text {cont}}(\mathcal {O})$
(for
![]() $\mathcal {F}$
is a divisorial sheaf on a regular variety, hence an invertible sheaf). We may assume that
$\mathcal {F}$
is a divisorial sheaf on a regular variety, hence an invertible sheaf). We may assume that
![]() $\partial (\mathfrak {m})\subset \mathfrak {m}$
, so we get an induced endomorphism
$\partial (\mathfrak {m})\subset \mathfrak {m}$
, so we get an induced endomorphism
![]() $\partial _0\in \operatorname {\mathrm {End}}_{\mathcal {O}/\mathfrak {m}}(\mathfrak {m}/\mathfrak {m}^2)$
.
$\partial _0\in \operatorname {\mathrm {End}}_{\mathcal {O}/\mathfrak {m}}(\mathfrak {m}/\mathfrak {m}^2)$
.
First assume that
![]() $\mathcal {F}$
is lc. By Proposition 3.6,
$\mathcal {F}$
is lc. By Proposition 3.6,
![]() $\partial _0$
is not nilpotent. But we have
$\partial _0$
is not nilpotent. But we have
![]() $\partial ^{[p]}=u\partial $
for some
$\partial ^{[p]}=u\partial $
for some
![]() $u\in \mathcal {O}$
, since
$u\in \mathcal {O}$
, since
![]() $\mathcal {F}$
is closed under pth powers. In particular
$\mathcal {F}$
is closed under pth powers. In particular
![]() $\partial _0^{\circ p}=\bar {u}\partial _0$
, where
$\partial _0^{\circ p}=\bar {u}\partial _0$
, where
![]() $\bar {u}$
is the image of u in the residue field. Thus
$\bar {u}$
is the image of u in the residue field. Thus
![]() $u\notin \mathfrak {m}$
. This implies that
$u\notin \mathfrak {m}$
. This implies that
![]() $\partial $
is multiplicative.
$\partial $
is multiplicative.
Conversely, if
![]() $\mathcal {F}$
has at worst singularities, we may assume that
$\mathcal {F}$
has at worst singularities, we may assume that
![]() $\partial $
is multiplicative. Then the function
$\partial $
is multiplicative. Then the function
![]() $n\mapsto \partial _0^{\circ n}$
is p-periodic. Moreover
$n\mapsto \partial _0^{\circ n}$
is p-periodic. Moreover
![]() $\partial _0\neq 0$
by Remark 2.22, thus
$\partial _0\neq 0$
by Remark 2.22, thus
![]() $\partial _0$
is not nilpotent and so
$\partial _0$
is not nilpotent and so
![]() $\mathcal {F}$
is lc.
$\mathcal {F}$
is lc.
If
![]() $\mathcal {F}$
is regular, we already know it is canonical (Lemma 3.3). Conversely, if
$\mathcal {F}$
is regular, we already know it is canonical (Lemma 3.3). Conversely, if
![]() $\mathcal {F}$
is canonical then it is lc and thus has at worst multiplicative singularities. So we may assume that
$\mathcal {F}$
is canonical then it is lc and thus has at worst multiplicative singularities. So we may assume that
![]() $\mathcal {F}$
is generated up to saturation by
$\mathcal {F}$
is generated up to saturation by
![]() $\sum _i \lambda _i x_i\partial _{x_i}$
, where
$\sum _i \lambda _i x_i\partial _{x_i}$
, where
![]() $x_1,\dots ,x_n\in \mathcal {O}$
are formal coordinates and
$x_1,\dots ,x_n\in \mathcal {O}$
are formal coordinates and
![]() $\lambda _i\in \mathbb {F}_p$
. If more than one
$\lambda _i\in \mathbb {F}_p$
. If more than one
![]() $\lambda _i$
is non-zero, then a series of blow-ups as in Example 3.5 show that
$\lambda _i$
is non-zero, then a series of blow-ups as in Example 3.5 show that
![]() $\mathcal {F}$
is not canonical. Thus a single
$\mathcal {F}$
is not canonical. Thus a single
![]() $\lambda _i$
is non-zero, and it follows that
$\lambda _i$
is non-zero, and it follows that
![]() $\mathcal {F}$
is regular.
$\mathcal {F}$
is regular.
3.1 Foliations on group quotient singularities
Let us give a series of examples of lc
![]() $1$
-foliations on singular varieties. First, consider
$1$
-foliations on singular varieties. First, consider
![]() $f\colon X\to Y$
a finite surjective Galois morphism of normal connected k-schemes of finite type. If G is the Galois group of the function field extension
$f\colon X\to Y$
a finite surjective Galois morphism of normal connected k-schemes of finite type. If G is the Galois group of the function field extension
![]() $K(Y)\subset K(X)$
, then G acts on the
$K(Y)\subset K(X)$
, then G acts on the
![]() $K(X)$
-vector space
$K(X)$
-vector space
![]() $\operatorname {\mathrm {Der}}_k(K(X))$
by
$\operatorname {\mathrm {Der}}_k(K(X))$
by
and the
![]() $K(Y)$
-vector field of invariants is
$K(Y)$
-vector field of invariants is
![]() $\operatorname {\mathrm {Der}}_k(K(Y))$
. By Galois descent, the
$\operatorname {\mathrm {Der}}_k(K(Y))$
. By Galois descent, the
![]() $K(Y)$
-subspaces of
$K(Y)$
-subspaces of
![]() $\operatorname {\mathrm {Der}}_k(K(Y))$
correspond to the
$\operatorname {\mathrm {Der}}_k(K(Y))$
correspond to the
![]() $K(X)$
-subspaces of
$K(X)$
-subspaces of
![]() $\operatorname {\mathrm {Der}}_k(K(X))$
which are stable under the action of G.
$\operatorname {\mathrm {Der}}_k(K(X))$
which are stable under the action of G.
Lemma 3.8. In the above situation, pullback along f at the generic point gives a rank-preserving bijective correspondence between
-
1.
 $1$
-foliations on X whose generic stalk is preserved by the G-action, and
$1$
-foliations on X whose generic stalk is preserved by the G-action, and -
2.
 $1$
-foliations on Y.
$1$
-foliations on Y.
Proof. This is a direct application of Remark 2.15 and Galois descent, except for the fact that if
![]() $\mathcal {F}\subset T_{X/k}$
is a
$\mathcal {F}\subset T_{X/k}$
is a
![]() $1$
-foliation on Y then
$1$
-foliation on Y then
![]() $\mathcal {F}_{K(Y)}\otimes K(X)$
is closed under Lie brackets and pth powers. This is an immediate calculation (using Hochschild’s formula (2.1) for pth powers).
$\mathcal {F}_{K(Y)}\otimes K(X)$
is closed under Lie brackets and pth powers. This is an immediate calculation (using Hochschild’s formula (2.1) for pth powers).
Definition 3.9. In the above situation:
-
1. if
 $\mathcal {F}\subset T_{Y/k}$
is a
$\mathcal {F}\subset T_{Y/k}$
is a
 $1$
-foliation, we let
$1$
-foliation, we let
 $f^{*}\mathcal {F}\subset T_{X/k}$
be the unique
$f^{*}\mathcal {F}\subset T_{X/k}$
be the unique
 $1$
-foliation which generic stalk
$1$
-foliation which generic stalk
 $\mathcal {F}_{K(Y)}\otimes K(X)$
;
$\mathcal {F}_{K(Y)}\otimes K(X)$
; -
2. if the generic stalk of
 $\mathcal {H}\subset T_{X/k}$
is G-stable, we let
$\mathcal {H}\subset T_{X/k}$
is G-stable, we let
 $\mathcal {H}/G\subset T_{Y/k}$
be the unique
$\mathcal {H}/G\subset T_{Y/k}$
be the unique
 $1$
-foliation whose generic stalk is
$1$
-foliation whose generic stalk is
 $(\mathcal {H}_{K(X)})^G$
.
$(\mathcal {H}_{K(X)})^G$
.
We can now state and prove the following proposition.
Proposition 3.10. Let
![]() $\mathcal {H}$
be a log canonical
$\mathcal {H}$
be a log canonical
![]() $1$
-foliation of corank
$1$
-foliation of corank
![]() $1$
on a normal connected
$1$
on a normal connected
![]() $\mathbb {Q}$
-factorial k-scheme X of finite type. Let G be a finite group of order invertible in k, acting on
$\mathbb {Q}$
-factorial k-scheme X of finite type. Let G be a finite group of order invertible in k, acting on
![]() $(X,\mathcal {G})$
. If
$(X,\mathcal {G})$
. If
![]() $(Y=X/G,\mathcal {F}=\mathcal {H}/G)$
is the quotient, then
$(Y=X/G,\mathcal {F}=\mathcal {H}/G)$
is the quotient, then
![]() $\mathcal {F}$
is log canonical.
$\mathcal {F}$
is log canonical.
Proof. The quotient Y is
![]() $\mathbb {Q}$
-factorial, so
$\mathbb {Q}$
-factorial, so
![]() $\mathcal {F}$
is automatically
$\mathcal {F}$
is automatically
![]() $\mathbb {Q}$
-Gorenstein. So consider a birational proper morphism
$\mathbb {Q}$
-Gorenstein. So consider a birational proper morphism
![]() $f\colon Y'\to Y$
, and let
$f\colon Y'\to Y$
, and let
![]() $X'$
be the integral closure of
$X'$
be the integral closure of
![]() $Y'$
in
$Y'$
in
![]() $K(X)$
. Then G acts on
$K(X)$
. Then G acts on
![]() $X'$
with quotient
$X'$
with quotient
![]() $Y'$
, and we have a commutative diagram
$Y'$
, and we have a commutative diagram
where
![]() $q,q'$
are the quotient morphisms. If
$q,q'$
are the quotient morphisms. If
![]() $\mathcal {F}'$
and
$\mathcal {F}'$
and
![]() $\mathcal {H}'$
denote the birational pullback of
$\mathcal {H}'$
denote the birational pullback of
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {H}$
then by Lemma 3.8 we have
$\mathcal {H}$
then by Lemma 3.8 we have
![]() $q^{*}\mathcal {F}=\mathcal {H}$
and
$q^{*}\mathcal {F}=\mathcal {H}$
and
![]() $(q')^{*}\mathcal {F}'=\mathcal {H}'$
. By the foliated version of Riemann–Hurwitz [Reference Spicer57, Proposition 3.7] (Footnote
6
) it holds that
$(q')^{*}\mathcal {F}'=\mathcal {H}'$
. By the foliated version of Riemann–Hurwitz [Reference Spicer57, Proposition 3.7] (Footnote
6
) it holds that
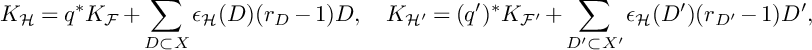 $$ \begin{align*}K_{\mathcal{H}}=q^{*}K_{\mathcal{F}}+\sum_{D\subset X}\epsilon_{\mathcal{H}}(D)(r_D-1)D, \quad K_{\mathcal{H}'}=(q')^{*}K_{\mathcal{F}'}+\sum_{D'\subset X'}\epsilon_{\mathcal{H}}(D')(r_{D'}-1)D',\end{align*} $$
$$ \begin{align*}K_{\mathcal{H}}=q^{*}K_{\mathcal{F}}+\sum_{D\subset X}\epsilon_{\mathcal{H}}(D)(r_D-1)D, \quad K_{\mathcal{H}'}=(q')^{*}K_{\mathcal{F}'}+\sum_{D'\subset X'}\epsilon_{\mathcal{H}}(D')(r_{D'}-1)D',\end{align*} $$
where
![]() $r_{\bullet }$
denotes the ramification index of divisors with respect to the action of G.
$r_{\bullet }$
denotes the ramification index of divisors with respect to the action of G.
Let E be a prime f-exceptional divisor. We want to estimate
![]() $a(E;\mathcal {F})$
. If
$a(E;\mathcal {F})$
. If
![]() $q'$
is étale over the generic point of E then
$q'$
is étale over the generic point of E then
![]() $a(E;\mathcal {F})=a(E';\mathcal {H})\geq 0$
where
$a(E;\mathcal {F})=a(E';\mathcal {H})\geq 0$
where
![]() $E'\subset X'$
is any divisor lying over E. So we may assume that
$E'\subset X'$
is any divisor lying over E. So we may assume that
![]() $r_{E'}>1$
. Notice that
$r_{E'}>1$
. Notice that
![]() $(q')^{*}E=\sum _{E'}r_{E'}E'$
.
$(q')^{*}E=\sum _{E'}r_{E'}E'$
.
We compute
![]() $(q\circ f')^{*}K_{\mathcal {F}}=(f\circ q')^{*}K_{\mathcal {F}}$
at the generic points of
$(q\circ f')^{*}K_{\mathcal {F}}=(f\circ q')^{*}K_{\mathcal {F}}$
at the generic points of
![]() $(q')^{-1}(E)$
. On the one hand
$(q')^{-1}(E)$
. On the one hand
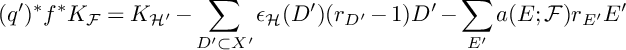 $$ \begin{align*}(q')^{*}f^{*}K_{\mathcal{F}}=K_{\mathcal{H}'} -\sum_{D'\subset X'}\epsilon_{\mathcal{H}}(D')(r_{D'}-1)D' -\sum_{E'}a(E;\mathcal{F})r_{E'}E'\end{align*} $$
$$ \begin{align*}(q')^{*}f^{*}K_{\mathcal{F}}=K_{\mathcal{H}'} -\sum_{D'\subset X'}\epsilon_{\mathcal{H}}(D')(r_{D'}-1)D' -\sum_{E'}a(E;\mathcal{F})r_{E'}E'\end{align*} $$
and on the other
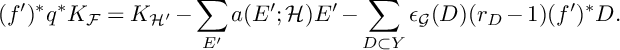 $$ \begin{align*}(f')^{*}q^{*}K_{\mathcal{F}}=K_{\mathcal{H}'} -\sum_{E'} a(E';\mathcal{H})E' -\sum_{D\subset Y}\epsilon_{\mathcal{G}}(D)(r_D-1)(f')^{*}D.\end{align*} $$
$$ \begin{align*}(f')^{*}q^{*}K_{\mathcal{F}}=K_{\mathcal{H}'} -\sum_{E'} a(E';\mathcal{H})E' -\sum_{D\subset Y}\epsilon_{\mathcal{G}}(D)(r_D-1)(f')^{*}D.\end{align*} $$
Equating the two, we find that
where
![]() $\delta \geq 0$
. As
$\delta \geq 0$
. As
![]() $\epsilon _{\mathcal {H}}(E')=\epsilon _{\mathcal {F}}(E)$
and
$\epsilon _{\mathcal {H}}(E')=\epsilon _{\mathcal {F}}(E)$
and
![]() $a(E';\mathcal {H})\geq -\epsilon _{\mathcal {H}}(E')$
, we find that
$a(E';\mathcal {H})\geq -\epsilon _{\mathcal {H}}(E')$
, we find that
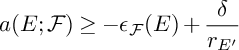 $$ \begin{align*}a(E;\mathcal{F})\geq -\epsilon_{\mathcal{F}}(E)+\frac{\delta}{r_{E'}}\end{align*} $$
$$ \begin{align*}a(E;\mathcal{F})\geq -\epsilon_{\mathcal{F}}(E)+\frac{\delta}{r_{E'}}\end{align*} $$
which shows that
![]() $\mathcal {F}$
is lc.
$\mathcal {F}$
is lc.
Example 3.11. Let k be an algebraically closed field of characteristic
![]() $p>2$
, and let
$p>2$
, and let
![]() $G=\mathbb {Z}/2\mathbb {Z}$
act k-linearly on
$G=\mathbb {Z}/2\mathbb {Z}$
act k-linearly on
![]() $\mathbb {A}^2_{x,y}$
by
$\mathbb {A}^2_{x,y}$
by
![]() $(x,y)\mapsto (-x,-y)$
. Let
$(x,y)\mapsto (-x,-y)$
. Let
![]() $Y=\operatorname {\mathrm {Spec}} k[x^2,y^2,xy]$
be the quotient: it is an
$Y=\operatorname {\mathrm {Spec}} k[x^2,y^2,xy]$
be the quotient: it is an
![]() $A_1$
-singularity. If
$A_1$
-singularity. If
![]() $\mathcal {H}$
is the
$\mathcal {H}$
is the
![]() $1$
-foliation on
$1$
-foliation on
![]() $\mathbb {A}^2$
generated by
$\mathbb {A}^2$
generated by
![]() $\partial _x$
, then
$\partial _x$
, then
![]() $\mathcal {H}/G$
is generated by
$\mathcal {H}/G$
is generated by
![]() $x\partial _x$
and
$x\partial _x$
and
![]() $y\partial _x$
. Consider the isomorphism
$y\partial _x$
. Consider the isomorphism
Then
![]() $x\partial _x$
corresponds to
$x\partial _x$
corresponds to
![]() $\psi =2u\partial _u+s\partial _s$
, and
$\psi =2u\partial _u+s\partial _s$
, and
![]() $y\partial _x$
corresponds to
$y\partial _x$
corresponds to
![]() $2s\partial _u+v\partial _s$
. They generate an lc
$2s\partial _u+v\partial _s$
. They generate an lc
![]() $1$
-foliation
$1$
-foliation
![]() $\mathcal {F}=\mathcal {H}/G$
on Y.
$\mathcal {F}=\mathcal {H}/G$
on Y.
By Theorem 4.10 to be proved below,
![]() $Y/\mathcal {F}$
is a klt affine singularity. Its coordinate ring is generated over k by the sections v and
$Y/\mathcal {F}$
is a klt affine singularity. Its coordinate ring is generated over k by the sections v and
![]() $u^ns^m$
where
$u^ns^m$
where
![]() $n,m\geq 0$
are such that
$n,m\geq 0$
are such that
![]() $2n+m=p$
.
$2n+m=p$
.
4 Singularities of quotients
4.1 Quotients by multiplicative derivations
In this subsection, we indicate a soft approach to singularities of quotients by multiplicative derivations. So let A be any k-algebra, and let
![]() $D\in \operatorname {\mathrm {Der}}_k(A)$
be such that
$D\in \operatorname {\mathrm {Der}}_k(A)$
be such that
![]() $D^{[p]}=uD$
where
$D^{[p]}=uD$
where
![]() $u\in A^\times $
. By [Reference Matsumoto40, Lemma 2.3] we have
$u\in A^\times $
. By [Reference Matsumoto40, Lemma 2.3] we have
![]() $u\in A^D$
. Notice that
$u\in A^D$
. Notice that
![]() $u^{-1}\in A^D$
as well. We consider the finite extension of rings
$u^{-1}\in A^D$
as well. We consider the finite extension of rings
Since u is invertible and
![]() $p-1$
is coprime with p, we see that
$p-1$
is coprime with p, we see that
![]() $\varphi $
is finite étale. In particular D lifts uniquely to a k-derivation of
$\varphi $
is finite étale. In particular D lifts uniquely to a k-derivation of
![]() $A'$
, which we denote again by D. We have
$A'$
, which we denote again by D. We have
and so
![]() $D(\lambda )=0$
. Moreover, by Hochschild’s formula (2.1) we have
$D(\lambda )=0$
. Moreover, by Hochschild’s formula (2.1) we have
So by Proposition 2.7 the derivation
![]() $D'=\lambda D$
on
$D'=\lambda D$
on
![]() $A'$
gives rise to a
$A'$
gives rise to a
![]() $\mu _p$
-group action on
$\mu _p$
-group action on
![]() $A'$
, which is equivalent to a
$A'$
, which is equivalent to a
![]() $\mathbb {Z}/p$
-grading
$\mathbb {Z}/p$
-grading
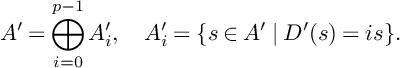 $$ \begin{align*}A'=\bigoplus_{i=0}^{p-1}A^{\prime}_i, \quad A_i'=\{s\in A'\mid D'(s)=is\}.\end{align*} $$
$$ \begin{align*}A'=\bigoplus_{i=0}^{p-1}A^{\prime}_i, \quad A_i'=\{s\in A'\mid D'(s)=is\}.\end{align*} $$
Since
![]() $D'(\lambda )=0$
we have
$D'(\lambda )=0$
we have
![]() $A^{\prime }_0=A^D[\lambda ]$
, and thus a commutative diagram
$A^{\prime }_0=A^D[\lambda ]$
, and thus a commutative diagram
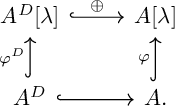
Both vertical arrows
![]() $\varphi ,\varphi ^D$
are split, as they are
$\varphi ,\varphi ^D$
are split, as they are
![]() $\mu _{p-1}$
-cyclic covers. Thus we obtain that the injection
$\mu _{p-1}$
-cyclic covers. Thus we obtain that the injection
![]() $A^D\hookrightarrow A$
splits as map of
$A^D\hookrightarrow A$
splits as map of
![]() $A^D$
-modules (Footnote
7
).
$A^D$
-modules (Footnote
7
).
We now derive some consequences of the above discussion. First we exploit the fact that, up to an étale cover, a multiplicative derivation is given by a
![]() $\mu _p$
-action. In particular, combining this observation with basic computations involving Jordan decomposition, we recover a well-known result about multiplicative quotients of regular local rings (see, e.g., [Reference Rudakov and Safarevic53, Theorem 2]).
$\mu _p$
-action. In particular, combining this observation with basic computations involving Jordan decomposition, we recover a well-known result about multiplicative quotients of regular local rings (see, e.g., [Reference Rudakov and Safarevic53, Theorem 2]).
Proposition 4.1. Suppose that A a regular local k-algebra. If
![]() $D\in \operatorname {\mathrm {Der}}_k(A)$
is multiplicative then there exist formal coordinates
$D\in \operatorname {\mathrm {Der}}_k(A)$
is multiplicative then there exist formal coordinates
![]() $x_1,\dots ,x_d\in \widehat {A}$
and
$x_1,\dots ,x_d\in \widehat {A}$
and
![]() $\lambda _1,\dots ,\lambda _d\in \mathbb {F}_p$
such that
$\lambda _1,\dots ,\lambda _d\in \mathbb {F}_p$
such that
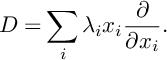 $$ \begin{align*}D=\sum_i\lambda_ix_i\frac{\partial}{\partial x_i}.\end{align*} $$
$$ \begin{align*}D=\sum_i\lambda_ix_i\frac{\partial}{\partial x_i}.\end{align*} $$
In particular, the completion of
![]() $A^D$
is normal toric.
$A^D$
is normal toric.
Proof. Since the vertical arrows in (4.1) are étale and induce isomorphisms on residue fields, they induce isomorphisms of completions. So we may assume that A is complete and that D is given by a continuous
![]() $\mu _p$
-action. The action of
$\mu _p$
-action. The action of
![]() $\mu _p$
on
$\mu _p$
on ![]() can be linearized, see the proof of [Reference Satriano54, Corollary 1.8]. Then it is given by the action of a single matrix
can be linearized, see the proof of [Reference Satriano54, Corollary 1.8]. Then it is given by the action of a single matrix
![]() $M\in \operatorname {\mathrm {GL}}_n(k(A))$
. We have
$M\in \operatorname {\mathrm {GL}}_n(k(A))$
. We have
![]() $M^p=M$
and thus the minimal polynomial of M divides
$M^p=M$
and thus the minimal polynomial of M divides
![]() $T^p-T$
. So it cannot have multiple roots, and we deduce that M is semi-simple. As
$T^p-T$
. So it cannot have multiple roots, and we deduce that M is semi-simple. As
![]() $M^p=M$
we see that its eigenvalues are elements of
$M^p=M$
we see that its eigenvalues are elements of
![]() $\mathbb {F}_p$
. So after a
$\mathbb {F}_p$
. So after a
![]() $k(A)$
-linear change of coordinates we may assume that M is diagonal. Therefore the derivation D can be given a normal form
$k(A)$
-linear change of coordinates we may assume that M is diagonal. Therefore the derivation D can be given a normal form
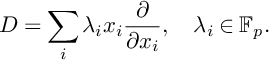 $$ \begin{align*} D=\sum_i\lambda_ix_i\frac{\partial}{\partial x_i},\quad \lambda_i\in\mathbb{F}_p. \end{align*} $$
$$ \begin{align*} D=\sum_i\lambda_ix_i\frac{\partial}{\partial x_i},\quad \lambda_i\in\mathbb{F}_p. \end{align*} $$
From this it is easily seen that
![]() $A^D$
is generated by monomials, and thus it is toric.
$A^D$
is generated by monomials, and thus it is toric.
Remark 4.2. Quotients of regular local rings by multiplicative derivations are formally toric, hence klt. In general, they are not canonical: if we consider the action of
![]() $\partial _{a,b}$
on
$\partial _{a,b}$
on
![]() $\mathbb {A}^2$
(see Example 2.23), then the quotient singularity is canonical if and only if it is Gorenstein, which happens if and only if
$\mathbb {A}^2$
(see Example 2.23), then the quotient singularity is canonical if and only if it is Gorenstein, which happens if and only if
![]() $(a,b)=(1,-1)$
or
$(a,b)=(1,-1)$
or
![]() $(a,b)=(1,0)$
[Reference Hirokado21, Remark 2.4.1].
$(a,b)=(1,0)$
[Reference Hirokado21, Remark 2.4.1].
Next we use the splitting of the bottom arrows in (4.1) to descend some cohomological properties from A to
![]() $A^D$
. For the definitions of F-singularities appearing in the next theorem, see, for example, [Reference Ma and Polstra39].
$A^D$
. For the definitions of F-singularities appearing in the next theorem, see, for example, [Reference Ma and Polstra39].
Theorem 4.3. Suppose that A is Noetherian and F-finite, and that
![]() $D\in \operatorname {\mathrm {Der}}_k(A)$
is multiplicative. Then:
$D\in \operatorname {\mathrm {Der}}_k(A)$
is multiplicative. Then:
-
1. If A satisfies Serre’s property
 $S_r$
then so does
$S_r$
then so does
 $A^D$
.
$A^D$
. -
2. If A is F-pure (resp. F-rational, F-injective, F-regular), so is
 $A^D$
.
$A^D$
.
Proof. All these properties can be checked on localizations, and passing to the ring of constants commutes with localization at prime ideals. So we may assume that A is local with maximal ideal
![]() $\mathfrak {m}$
. Then
$\mathfrak {m}$
. Then
![]() $A^D$
is also local with maximal ideal
$A^D$
is also local with maximal ideal
![]() $\mathfrak {n}=\mathfrak {m}^D$
. By F-finiteness the map
$\mathfrak {n}=\mathfrak {m}^D$
. By F-finiteness the map
![]() $A^D\hookrightarrow A$
is finite, so
$A^D\hookrightarrow A$
is finite, so
![]() $\dim A=\dim A^D$
.
$\dim A=\dim A^D$
.
Our main observation is the following one: since
![]() $\sqrt {\mathfrak {n} A}=\mathfrak {m}$
, we have
$\sqrt {\mathfrak {n} A}=\mathfrak {m}$
, we have
where on the right-hand side we consider A as an
![]() $A^D$
-module [Reference Iyengar, Leuschke, Leykin, Miller, Miller, Singh and Walther23, Propositions 7.3 and 7.15(2)]. As mentioned above, by (4.1) we can write
$A^D$
-module [Reference Iyengar, Leuschke, Leykin, Miller, Miller, Singh and Walther23, Propositions 7.3 and 7.15(2)]. As mentioned above, by (4.1) we can write
![]() $A=A^D\oplus B$
for some finite
$A=A^D\oplus B$
for some finite
![]() $A^D$
-module B, and so the local cohomology splits accordingly, that is
$A^D$
-module B, and so the local cohomology splits accordingly, that is
Let us show the first statement. Serre’s property
![]() $S_r$
states that, after localizing at any prime, the depth along the maximal ideal is at least
$S_r$
states that, after localizing at any prime, the depth along the maximal ideal is at least
![]() $\min \{\dim , r\}$
. Since
$\min \{\dim , r\}$
. Since
![]() $\dim A=\dim A^D$
, it suffices to show that the depth does not decrease upon passing to the sub-ring of constants. By [Reference Iyengar, Leuschke, Leykin, Miller, Miller, Singh and Walther23, Theorem 9.1], we have
$\dim A=\dim A^D$
, it suffices to show that the depth does not decrease upon passing to the sub-ring of constants. By [Reference Iyengar, Leuschke, Leykin, Miller, Miller, Singh and Walther23, Theorem 9.1], we have
So it follows from (4.2) that
![]() $\operatorname {\mathrm {depth}}_{\mathfrak {n}} A^D\geq \operatorname {\mathrm {depth}}_{\mathfrak {m}} A$
as desired.
$\operatorname {\mathrm {depth}}_{\mathfrak {n}} A^D\geq \operatorname {\mathrm {depth}}_{\mathfrak {m}} A$
as desired.
Next we discuss descent of F-singularities. F-purity and F-regularity descend to split subrings [Reference Ma and Polstra39, Theorem 3.9 and Exercise 9, p. 13]. F-injectivity and F-rationality do not in general (see [Reference Ma and Polstra39, Section 8] and [Reference Watanabe63]). Hopefully, the key fact is our situation is that
![]() $\dim A=\dim A^D$
. We prove that F-rationality descends, the F-injective case is similar.
$\dim A=\dim A^D$
. We prove that F-rationality descends, the F-injective case is similar.
Suppose that A is F-rational: this means that A is Cohen–Macaulay and that given any
![]() $c\in A$
not contained in any minimal prime, there exists an
$c\in A$
not contained in any minimal prime, there exists an
![]() $e>0$
such that the composition
$e>0$
such that the composition
is injective, where
![]() $d=\dim A$
and
$d=\dim A$
and
![]() $f_A^e=H^d_{\mathfrak {m}}(A\to F_*^eA)$
. As seen above,
$f_A^e=H^d_{\mathfrak {m}}(A\to F_*^eA)$
. As seen above,
![]() $A^D$
is also Cohen–Macaulay. If we assume that
$A^D$
is also Cohen–Macaulay. If we assume that
![]() $c\in A^D$
is not contained in any minimal prime, then by going-up c is not contained in any minimal prime of A either, and the above sequence is thus injective. Each local cohomology module in the sequence splits accordingly to (4.2). Since
$c\in A^D$
is not contained in any minimal prime, then by going-up c is not contained in any minimal prime of A either, and the above sequence is thus injective. Each local cohomology module in the sequence splits accordingly to (4.2). Since
![]() $c\in A^D$
, the action of
$c\in A^D$
, the action of
![]() $F_e^{*}c$
preserves each one of the summands. In other words, (4.3) splits as
$F_e^{*}c$
preserves each one of the summands. In other words, (4.3) splits as
Since it is injective, the sequence given by the first summands is also injective. Thus
![]() $A^D$
is F-rational, as claimed.
$A^D$
is F-rational, as claimed.
This has the following consequence for surface singularities. We say that a two-dimensional germ of surface over k is a linearly reductive quotient singularity if
![]() $\widehat {\mathcal {O}}$
is isomorphic to
$\widehat {\mathcal {O}}$
is isomorphic to ![]() where G is a linearly reductive group scheme acting freely away from the origin [Reference Liedtke, Martin and Matsumoto36, §6].
where G is a linearly reductive group scheme acting freely away from the origin [Reference Liedtke, Martin and Matsumoto36, §6].
Corollary 4.4. Suppose that k is algebraically closed. Let
![]() $(\mathcal {O},\mathfrak {m})$
be a two-dimensional linearly reductive quotient singularity over k, and
$(\mathcal {O},\mathfrak {m})$
be a two-dimensional linearly reductive quotient singularity over k, and
![]() $D\in \operatorname {\mathrm {Der}}_k(\mathcal {O})$
be a multiplicative derivation. Then
$D\in \operatorname {\mathrm {Der}}_k(\mathcal {O})$
be a multiplicative derivation. Then
![]() $\mathcal {O}^D$
is a linearly reductive quotient singularity.
$\mathcal {O}^D$
is a linearly reductive quotient singularity.
Proof. Recall that two-dimensional linearly reductive quotient singularities are the same as F-regular ones [Reference Liedtke, Martin and Matsumoto36, Theorem 5.11]. So
![]() $\mathcal {O}$
is F-regular, and then
$\mathcal {O}$
is F-regular, and then
![]() $\mathcal {O}^D$
is F-regular by Theorem 4.3.
$\mathcal {O}^D$
is F-regular by Theorem 4.3.
Remark 4.5. In the notations of the corollary, say that ![]() . Then it is not known whether
. Then it is not known whether
![]() $\widehat {\mathcal {O}}^D$
is the quotient of
$\widehat {\mathcal {O}}^D$
is the quotient of ![]() by an extension of G and
by an extension of G and
![]() $\mu _p$
.
$\mu _p$
.
This is the case when G is discrete (with order invertible in k). Indeed, as
![]() $\widehat {\mathbb {A}}^2_{x,y}\to \operatorname {\mathrm {Spec}}(\widehat {\mathcal {O}})$
is étale above the complement of the closed point, D can be lifted to a G-invariant element of
$\widehat {\mathbb {A}}^2_{x,y}\to \operatorname {\mathrm {Spec}}(\widehat {\mathcal {O}})$
is étale above the complement of the closed point, D can be lifted to a G-invariant element of ![]() . By reflexivity, D extends to a regular element of
. By reflexivity, D extends to a regular element of ![]() . It defines a continuous
. It defines a continuous
![]() $\mu _p$
-action on
$\mu _p$
-action on
![]() $\widehat {\mathbb {A}}^2$
which commutes with the action of G. Then
$\widehat {\mathbb {A}}^2$
which commutes with the action of G. Then
![]() $\widehat {\mathcal {O}}^D$
is the quotient of
$\widehat {\mathcal {O}}^D$
is the quotient of ![]() by
by
![]() $G\times \mu _p$
.
$G\times \mu _p$
.
However, if G is not discrete then the question is much more complicated. See [Reference Liedtke, Martin and Matsumoto37, §8.2, especially Lemma 8.14] and the references therein for further discussion.
4.2 Birational singularities of quotients
In this section, we study singularities of infinitesimal quotients in arbitrary dimensions from the point of view of birational geometry. It is convenient to do so for pairs and not only varieties, so we make the following definition.
Definition 4.6. Let X be a normal k-scheme of finite type,
![]() $\Delta $
a
$\Delta $
a
![]() $\mathbb {Q}$
-Weil divisor on X and
$\mathbb {Q}$
-Weil divisor on X and
![]() $\mathcal {F}$
a
$\mathcal {F}$
a
![]() $1$
-foliation on X. Let
$1$
-foliation on X. Let
![]() $q\colon X\to X/\mathcal {F}=Y$
be the quotient. We define on Y the
$q\colon X\to X/\mathcal {F}=Y$
be the quotient. We define on Y the
![]() $\mathbb {Q}$
-Weil divisor
$\mathbb {Q}$
-Weil divisor
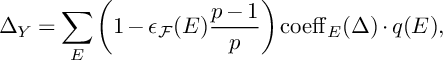 $$ \begin{align*}\Delta_Y=\sum_{E}\left(1-\epsilon_{\mathcal{F}}(E)\frac{p-1}{p} \right)\operatorname{\mathrm{coeff}}_{E}(\Delta)\cdot q(E),\end{align*} $$
$$ \begin{align*}\Delta_Y=\sum_{E}\left(1-\epsilon_{\mathcal{F}}(E)\frac{p-1}{p} \right)\operatorname{\mathrm{coeff}}_{E}(\Delta)\cdot q(E),\end{align*} $$
where E runs through the prime divisors of
![]() $\operatorname {\mathrm {Supp}}(\Delta )$
.
$\operatorname {\mathrm {Supp}}(\Delta )$
.
The extra factors are thrown in to accommodate the adjunction formula along q (that is, Proposition 2.41) in presence of an extra divisor. Indeed, we have the following lemma.
Lemma 4.7 (cf [Reference Rudakov and Safarevic53, Proposition 1])
Let X be a normal k-scheme of finite type and
![]() $\mathcal {F}$
be a
$\mathcal {F}$
be a
![]() $1$
-foliation on X. Let
$1$
-foliation on X. Let
![]() $q\colon X\to Y$
be the quotient. For a prime divisor
$q\colon X\to Y$
be the quotient. For a prime divisor
![]() $E\subset X$
with image
$E\subset X$
with image
![]() $q(E)=E^Y\subset Y$
:
$q(E)=E^Y\subset Y$
:
-
1. if E is
 $\mathcal {F}$
-invariant then
$\mathcal {F}$
-invariant then
 $q^{*}E^Y=E$
;
$q^{*}E^Y=E$
; -
2. if E is not
 $\mathcal {F}$
-invariant then
$\mathcal {F}$
-invariant then
 $q^{*}E^Y=pE$
.
$q^{*}E^Y=pE$
.
Proof. We can work on an étale neighborhood of the generic point of E, where X and E are regular and
![]() $\mathcal {F}$
a sub-bundle of the tangent sheaf. Then by Example 2.18 we may assume that
$\mathcal {F}$
a sub-bundle of the tangent sheaf. Then by Example 2.18 we may assume that
![]() $X=\mathbb {A}^n_{x_1,\dots ,x_n}$
, that
$X=\mathbb {A}^n_{x_1,\dots ,x_n}$
, that
![]() $\mathcal {F}$
is generated by
$\mathcal {F}$
is generated by
![]() $\frac {\partial }{\partial x_1},\dots , \frac {\partial }{\partial x_r}$
with
$\frac {\partial }{\partial x_1},\dots , \frac {\partial }{\partial x_r}$
with
![]() $r<n$
, and that E is cut out by a linear polynomial. The invariant subring, whose spectrum gives Y, is given by
$r<n$
, and that E is cut out by a linear polynomial. The invariant subring, whose spectrum gives Y, is given by
![]() $k[x_1^p,\dots ,x_r^p,x_{r+1},\dots ,x_r]$
.
$k[x_1^p,\dots ,x_r^p,x_{r+1},\dots ,x_r]$
.
-
• If the polynomial is not a linear combination of
 $x_1,\dots ,x_r$
, we make a change of coordinate and assume that E is given by
$x_1,\dots ,x_r$
, we make a change of coordinate and assume that E is given by
 $(x_{r+1}=0)$
. Then E is
$(x_{r+1}=0)$
. Then E is
 $\mathcal {F}$
-invariant and
$\mathcal {F}$
-invariant and
 $E_Y=(x_{r+1}=0)$
so
$E_Y=(x_{r+1}=0)$
so
 $q^{*}E^Y=E$
.
$q^{*}E^Y=E$
. -
• If the polynomial is cut out by the
 $x_1,\dots ,x_r$
, we may similarly assume that
$x_1,\dots ,x_r$
, we may similarly assume that
 $E=(x_r=0)$
. Then E is not
$E=(x_r=0)$
. Then E is not
 $\mathcal {F}$
-invariant, as
$\mathcal {F}$
-invariant, as
 $\frac {\partial }{\partial x_r}|_E\notin T_E$
, and
$\frac {\partial }{\partial x_r}|_E\notin T_E$
, and
 $E^Y=(x_r^p=0)$
so
$E^Y=(x_r^p=0)$
so
 $q^{*}E^Y=pE$
.
$q^{*}E^Y=pE$
.
This completes the proof.
Proposition 4.8 (Log adjunction formula)
Notations as in Definition 4.6. Then we have an equality of
![]() $\mathbb {Q}$
-Weil divisors
$\mathbb {Q}$
-Weil divisors
Proof. Let E be a prime divisor on
![]() $\operatorname {\mathrm {Supp}}(\Delta )$
. Then by Lemma 4.7, we have in any case
$\operatorname {\mathrm {Supp}}(\Delta )$
. Then by Lemma 4.7, we have in any case
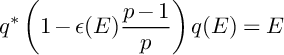 $$ \begin{align*}q^{*}\left(1-\epsilon(E)\frac{p-1}{p}\right)q(E)=E\end{align*} $$
$$ \begin{align*}q^{*}\left(1-\epsilon(E)\frac{p-1}{p}\right)q(E)=E\end{align*} $$
and so
![]() $q^{*}\Delta _Y=\Delta $
. Combining this equality with the adjunction formula Proposition 2.41 yields the result.
$q^{*}\Delta _Y=\Delta $
. Combining this equality with the adjunction formula Proposition 2.41 yields the result.
We also note that taking quotients preserves
![]() $\mathbb {Q}$
-Gorenstein properties.
$\mathbb {Q}$
-Gorenstein properties.
Lemma 4.9. Let X be a normal k-scheme of finite type,
![]() $\mathcal {F}$
be a
$\mathcal {F}$
be a
![]() $1$
-foliation on X with quotient
$1$
-foliation on X with quotient
![]() $q\colon X\to Y$
. Let
$q\colon X\to Y$
. Let
![]() $\Delta $
be a
$\Delta $
be a
![]() $\mathbb {Q}$
-Weil divisor on X. If
$\mathbb {Q}$
-Weil divisor on X. If
![]() $K_X+\Delta $
and
$K_X+\Delta $
and
![]() $K_{\mathcal {F}}$
are
$K_{\mathcal {F}}$
are
![]() $\mathbb {Q}$
-Cartier, then
$\mathbb {Q}$
-Cartier, then
![]() $K_Y+\Delta _Y$
is also
$K_Y+\Delta _Y$
is also
![]() $\mathbb {Q}$
-Cartier.
$\mathbb {Q}$
-Cartier.
Proof. Since Y is normal, it has a well-defined canonical divisor
![]() $K_Y$
which is invertible on a big open subset U. Over that locus, the log adjunction reads
$K_Y$
which is invertible on a big open subset U. Over that locus, the log adjunction reads
![]() $q^{*}(K_Y+\Delta _Y)|_U=(K_X+\Delta +(p-1)K_{\mathcal {F}})|_{q^{-1}U}$
. Now
$q^{*}(K_Y+\Delta _Y)|_U=(K_X+\Delta +(p-1)K_{\mathcal {F}})|_{q^{-1}U}$
. Now
![]() $K_X+\Delta $
and
$K_X+\Delta $
and
![]() $K_{\mathcal {F}}$
are by assumption
$K_{\mathcal {F}}$
are by assumption
![]() $\mathbb {Q}$
-Cartier, so for
$\mathbb {Q}$
-Cartier, so for
![]() $n>0$
big enough the Weil divisor
$n>0$
big enough the Weil divisor
![]() $n(K_X+\Delta +(p-1)K_{\mathcal {F}})$
is Cartier. Thus its pullback on
$n(K_X+\Delta +(p-1)K_{\mathcal {F}})$
is Cartier. Thus its pullback on
![]() $Y^{(-1)}$
is Cartier as well. Since it is represented on the big open subset
$Y^{(-1)}$
is Cartier as well. Since it is represented on the big open subset
![]() $U^{(-1)}$
by the divisor
$U^{(-1)}$
by the divisor
![]() $np(K_{Y^{(-1)}}+\Delta _{Y^{(-1)}})$
, it follows that
$np(K_{Y^{(-1)}}+\Delta _{Y^{(-1)}})$
, it follows that
![]() $K_{Y^{(-1)}}+\Delta _{Y^{(-1)}}$
is
$K_{Y^{(-1)}}+\Delta _{Y^{(-1)}}$
is
![]() $\mathbb {Q}$
-Cartier, and therefore
$\mathbb {Q}$
-Cartier, and therefore
![]() $K_Y+\Delta _Y$
is
$K_Y+\Delta _Y$
is
![]() $\mathbb {Q}$
-Cartier as claimed.
$\mathbb {Q}$
-Cartier as claimed.
The main theorem of this section reads as follows.
Theorem 4.10. Let
![]() $(X,\Delta )$
be a normal pair and
$(X,\Delta )$
be a normal pair and
![]() $\mathcal {F}$
be a
$\mathcal {F}$
be a
![]() $\mathbb {Q}$
-Gorenstein
$\mathbb {Q}$
-Gorenstein
![]() $1$
-foliation on X. Let
$1$
-foliation on X. Let
![]() $q\colon X\to X/\mathcal {F}=Y$
be the quotient morphism and
$q\colon X\to X/\mathcal {F}=Y$
be the quotient morphism and
![]() $\Delta _Y$
be the divisor on Y induced by
$\Delta _Y$
be the divisor on Y induced by
![]() $\Delta $
as in Definition 4.6 above.
$\Delta $
as in Definition 4.6 above.
-
1. Assume that
 $\mathcal {F}$
is canonical. Then if
$\mathcal {F}$
is canonical. Then if
 $(X,\Delta )$
is terminal (resp. canonical, klt, lc), so is
$(X,\Delta )$
is terminal (resp. canonical, klt, lc), so is
 $(Y,\Delta _Y)$
.
$(Y,\Delta _Y)$
. -
2. Assume that
 $\mathcal {F}$
is klt. If
$\mathcal {F}$
is klt. If
 $(X,\Delta )$
has at worst lc singularities, then
$(X,\Delta )$
has at worst lc singularities, then
 $(Y,\Delta _Y)$
is klt.
$(Y,\Delta _Y)$
is klt. -
3. Assume that
 $\mathcal {F}$
is lc. Then:
$\mathcal {F}$
is lc. Then:-
(a) If
 $(X,\Delta )$
has at worst klt singularities, so does
$(X,\Delta )$
has at worst klt singularities, so does
 $(Y,\Delta _Y)$
;
$(Y,\Delta _Y)$
; -
(b) If
 $(X,\Delta )$
is lc, so is
$(X,\Delta )$
is lc, so is
 $(Y,\Delta _Y)$
.
$(Y,\Delta _Y)$
.
-
Remark 4.11.
-
1. As the proof will show, in concrete cases a finer analysis might be possible (see Proposition 4.13 for some examples).
-
2. Assume that
 $\mathcal {F}$
is strictly log canonical. Then even if X is smooth, the singularities of Y need not be milder than klt, as we saw in Remark 4.2.
$\mathcal {F}$
is strictly log canonical. Then even if X is smooth, the singularities of Y need not be milder than klt, as we saw in Remark 4.2. -
3. If both X and Y are regular, then
 $\mathcal {F}$
is regular according to Lemma 2.37. But in general the singularities of
$\mathcal {F}$
is regular according to Lemma 2.37. But in general the singularities of
 $\mathcal {F}$
cannot be quantified from the singularities of X and Y: in Example 2.33 we have seen the canonical singularity
$\mathcal {F}$
cannot be quantified from the singularities of X and Y: in Example 2.33 we have seen the canonical singularity
 $D^0_{4}$
$D^0_{4}$
 $(p=2)$
arising as the quotient of
$(p=2)$
arising as the quotient of  by the non-lc derivation
by the non-lc derivation
 $x^2\partial _x+y^2\partial _y$
. See [Reference Liedtke35, Proposition 2.3] for more examples with
$x^2\partial _x+y^2\partial _y$
. See [Reference Liedtke35, Proposition 2.3] for more examples with
 $p=2$
. The surface case is nonetheless special, and we will see in Theorem 4.19 below that what is at play here is that the
$p=2$
. The surface case is nonetheless special, and we will see in Theorem 4.19 below that what is at play here is that the
 $D^0_4$
singularity is not F-pure.
$D^0_4$
singularity is not F-pure. -
4. Even if
 $\mathcal {F}$
and
$\mathcal {F}$
and
 $X/\mathcal {F}$
are midly singular, X need not be so. Indeed, consider the affine scheme
$X/\mathcal {F}$
are midly singular, X need not be so. Indeed, consider the affine scheme
 $X=\operatorname {\mathrm {Spec}}(k[\mathbf {x},z]/(z^p-s(\mathbf {x}))$
and the
$X=\operatorname {\mathrm {Spec}}(k[\mathbf {x},z]/(z^p-s(\mathbf {x}))$
and the
 $1$
-foliation
$1$
-foliation
 $\mathcal {F}$
generated by
$\mathcal {F}$
generated by
 $\partial /\partial z$
. As observed in [Reference Bernasconi8, Example 2.14],
$\partial /\partial z$
. As observed in [Reference Bernasconi8, Example 2.14],
 $\mathcal {F}$
is canonical. The quotient
$\mathcal {F}$
is canonical. The quotient
 $X/\mathcal {F}$
is the affine variety with coordinate ring
$X/\mathcal {F}$
is the affine variety with coordinate ring
 $k[\mathbf {x},z^p]/(z^p-s(\mathbf {x}))\cong k[\mathbf {x}]$
, hence it is regular. But we can choose
$k[\mathbf {x},z^p]/(z^p-s(\mathbf {x}))\cong k[\mathbf {x}]$
, hence it is regular. But we can choose
 $s(\mathbf {x})$
such that X is normal but not lc: for example
$s(\mathbf {x})$
such that X is normal but not lc: for example
 $s(\mathbf {x})=x_1^n+x_2^m$
with
$s(\mathbf {x})=x_1^n+x_2^m$
with
 $n,m\gg 1$
not divisible by p.
$n,m\gg 1$
not divisible by p.
Proof. By Lemma 4.9 the
![]() $\mathbb {Q}$
-Weil log canonical divisor
$\mathbb {Q}$
-Weil log canonical divisor
![]() $K_Y+\Delta _Y$
is
$K_Y+\Delta _Y$
is
![]() $\mathbb {Q}$
-Cartier, and thus we may investigate its birational singularities. Consider a proper birational morphism
$\mathbb {Q}$
-Cartier, and thus we may investigate its birational singularities. Consider a proper birational morphism
![]() $\mu \colon Y'\to Y$
, and write
$\mu \colon Y'\to Y$
, and write
![]() $K_{Y'}+\mu _*^{-1}\Delta _{Y}=\mu ^{*}(K_Y+\Delta _Y)+\sum a_{E}E$
where E runs through the exceptional prime divisors of
$K_{Y'}+\mu _*^{-1}\Delta _{Y}=\mu ^{*}(K_Y+\Delta _Y)+\sum a_{E}E$
where E runs through the exceptional prime divisors of
![]() $\mu $
. We are interested in the numbers
$\mu $
. We are interested in the numbers
![]() $a_E$
. To compute them we look at the following commutative diagram
$a_E$
. To compute them we look at the following commutative diagram
where
![]() $X'$
is the normalization of
$X'$
is the normalization of
![]() $Y'$
in
$Y'$
in
![]() $K(X)$
. The morphism
$K(X)$
. The morphism
![]() $\nu \colon X'\to X$
indeed exists and is uniquely determined by Zariski’s Main theorem. Notice that
$\nu \colon X'\to X$
indeed exists and is uniquely determined by Zariski’s Main theorem. Notice that
![]() $q'$
is an homeomorphism; in particular
$q'$
is an homeomorphism; in particular
![]() $q'$
induces a bijection between the
$q'$
induces a bijection between the
![]() $\mu $
-exceptional prime divisors and the
$\mu $
-exceptional prime divisors and the
![]() $\nu $
-exceptional ones. So if E is
$\nu $
-exceptional ones. So if E is
![]() $\mu $
-exceptional, let us write
$\mu $
-exceptional, let us write
![]() $E'$
the corresponding
$E'$
the corresponding
![]() $\nu $
-exceptional divisor. Let also
$\nu $
-exceptional divisor. Let also
![]() $\mathcal {F}'=\nu ^{*}\mathcal {F}$
be the foliation induced by
$\mathcal {F}'=\nu ^{*}\mathcal {F}$
be the foliation induced by
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $X'$
, so that
$X'$
, so that
![]() $q'$
is the quotient morphism.
$q'$
is the quotient morphism.
We now write down the pullback formulas for every canonical divisor in sight:
 $$ \begin{align*} K_{Y'}+\mu_*^{-1}\Delta_Y &= \mu^{*}(K_Y+\Delta_Y)+\sum a_EE, \\K_X+\Delta &= q^{*}(K_Y+\Delta_Y)+(1-p)K_{\mathcal{F}}, \\K_{X'}+\nu^{-1}_*\Delta &=(q')^{*}(K_{Y'}+\mu_*^{-1}\Delta_Y)+(1-p)K_{\mathcal{F}'},\\K_{\mathcal{F}'}&=\nu^{*}K_{\mathcal{F}}+\sum b_{E'}E', \\K_{X'}+\nu_*^{-1}\Delta &= \nu^{*}(K_X+\Delta)+\sum c_{E'}E'. \end{align*} $$
$$ \begin{align*} K_{Y'}+\mu_*^{-1}\Delta_Y &= \mu^{*}(K_Y+\Delta_Y)+\sum a_EE, \\K_X+\Delta &= q^{*}(K_Y+\Delta_Y)+(1-p)K_{\mathcal{F}}, \\K_{X'}+\nu^{-1}_*\Delta &=(q')^{*}(K_{Y'}+\mu_*^{-1}\Delta_Y)+(1-p)K_{\mathcal{F}'},\\K_{\mathcal{F}'}&=\nu^{*}K_{\mathcal{F}}+\sum b_{E'}E', \\K_{X'}+\nu_*^{-1}\Delta &= \nu^{*}(K_X+\Delta)+\sum c_{E'}E'. \end{align*} $$
Here we use the notations of Definition 4.6, and the third equality follows from Proposition 4.8 and the observation that
![]() $(\nu ^{-1}_*\Delta )_{Y'}=\mu ^{-1}_*\Delta _Y$
(which can be verified over the generic points of
$(\nu ^{-1}_*\Delta )_{Y'}=\mu ^{-1}_*\Delta _Y$
(which can be verified over the generic points of
![]() $\mu ^{-1}\Delta _Y$
, where
$\mu ^{-1}\Delta _Y$
, where
![]() $\mu $
is an isomorphism). To simplify the notations, we may localize at the generic point of some E, and assume that there is a unique exceptional divisor. If we apply
$\mu $
is an isomorphism). To simplify the notations, we may localize at the generic point of some E, and assume that there is a unique exceptional divisor. If we apply
![]() $(q')^{*}$
to the very first equation in the above list, we find
$(q')^{*}$
to the very first equation in the above list, we find
where
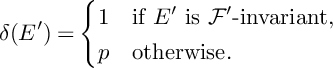 $$ \begin{align*}\delta(E')=\begin{cases} 1 & \text{if }E'\text{ is }\mathcal{F}'\text{-invariant}, \\ p & \text{otherwise}. \end{cases}\end{align*} $$
$$ \begin{align*}\delta(E')=\begin{cases} 1 & \text{if }E'\text{ is }\mathcal{F}'\text{-invariant}, \\ p & \text{otherwise}. \end{cases}\end{align*} $$
Using the canonical isomorphism
![]() $(q')^{*}\mu ^{*}\cong \nu ^{*}q^{*}$
and substituting in the other formulae on the right-hand side, we find the equation
$(q')^{*}\mu ^{*}\cong \nu ^{*}q^{*}$
and substituting in the other formulae on the right-hand side, we find the equation
In other words,
 $$ \begin{align} \begin{cases} \text{if }E'\text{ is }\mathcal{F}'\text{-invariant}:& a_E=c_{E'}+(p-1)b_{E'}\\ \text{if }E'\text{ is not }\mathcal{F}'\text{-invariant}:& a_E=\frac{1}{p}\left(c_{E'}+(p-1)b_{E'}\right). \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \text{if }E'\text{ is }\mathcal{F}'\text{-invariant}:& a_E=c_{E'}+(p-1)b_{E'}\\ \text{if }E'\text{ is not }\mathcal{F}'\text{-invariant}:& a_E=\frac{1}{p}\left(c_{E'}+(p-1)b_{E'}\right). \end{cases} \end{align} $$
The number
![]() $c_{E'}$
has a lower bound according to the birational singularities of
$c_{E'}$
has a lower bound according to the birational singularities of
![]() $(X,\Delta )$
. The number
$(X,\Delta )$
. The number
![]() $b_{E'}$
has a lower bound according to the birational singularities of the foliation
$b_{E'}$
has a lower bound according to the birational singularities of the foliation
![]() $\mathcal {F}$
(and in the log canonical and klt cases, it might depend on the
$\mathcal {F}$
(and in the log canonical and klt cases, it might depend on the
![]() $\mathcal {F}'$
-invariance of
$\mathcal {F}'$
-invariance of
![]() $E'$
; in particular, if
$E'$
; in particular, if
![]() $b_{E'}$
is negative then
$b_{E'}$
is negative then
![]() $E'$
is not
$E'$
is not
![]() $\mathcal {F}'$
-invariant). A simple case-by-case analysis based on (4.4) concludes the proof.
$\mathcal {F}'$
-invariant). A simple case-by-case analysis based on (4.4) concludes the proof.
We indicate several corollaries of Theorem 4.10.
Corollary 4.12. Let X be a regular variety and
![]() $\mathcal {F}$
a
$\mathcal {F}$
a
![]() $1$
-foliation on X. Then:
$1$
-foliation on X. Then:
-
1. if
 $\mathcal {F}$
is canonical then it is regular outside a closed subset of codimension
$\mathcal {F}$
is canonical then it is regular outside a closed subset of codimension
 $\geq 3$
.
$\geq 3$
. -
2. if
 $\mathcal {F}\subsetneq T_{X/k}$
then
$\mathcal {F}\subsetneq T_{X/k}$
then
 $\mathcal {F}$
cannot be terminal.
$\mathcal {F}$
cannot be terminal.
Proof. By [Reference Kollár30, Corollary 2.30] a terminal variety is regular in codimension
![]() $2$
. So if
$2$
. So if
![]() $\mathcal {F}$
is canonical, then by Theorem 4.10 the quotient
$\mathcal {F}$
is canonical, then by Theorem 4.10 the quotient
![]() $X/\mathcal {F}$
is terminal, hence regular in codimension
$X/\mathcal {F}$
is terminal, hence regular in codimension
![]() $2$
. Thus
$2$
. Thus
![]() $\mathcal {F}$
is regular in codimension
$\mathcal {F}$
is regular in codimension
![]() $2$
by Lemma 2.37.
$2$
by Lemma 2.37.
Now if
![]() $\mathcal {F}\subsetneq T_{X/k}$
was terminal then it would be generically regular by the previous paragraph, but by Example 3.4 regular foliations on regular varieties are not terminal: contradiction.
$\mathcal {F}\subsetneq T_{X/k}$
was terminal then it would be generically regular by the previous paragraph, but by Example 3.4 regular foliations on regular varieties are not terminal: contradiction.
As a consequence, we see that on regular surfaces in positive characteristic, there is no terminal
![]() $1$
-foliations and that the only canonical ones are the regular ones. This is in sharp contrast with the characteristic zero
$1$
-foliations and that the only canonical ones are the regular ones. This is in sharp contrast with the characteristic zero
![]() $0$
case, where there is a larger supply of canonical foliations [Reference McQuillan and Panazzolo43, III.i.3].
$0$
case, where there is a larger supply of canonical foliations [Reference McQuillan and Panazzolo43, III.i.3].
If we consider singular underlying surfaces, then the discrepancies of
![]() $\mathcal {F}$
along the minimal resolution are usually non-negative.
$\mathcal {F}$
along the minimal resolution are usually non-negative.
Proposition 4.13. Let S be a normal surface and
![]() $\mathcal {F}$
be a
$\mathcal {F}$
be a
![]() $\mathbb {Q}$
-Gorenstein
$\mathbb {Q}$
-Gorenstein
![]() $1$
-foliation on S. Assume that
$1$
-foliation on S. Assume that
![]() $S/\mathcal {F}$
has canonical singularities (resp. is regular). Then
$S/\mathcal {F}$
has canonical singularities (resp. is regular). Then
![]() $a(E;\mathcal {F})\geq 0$
(resp.
$a(E;\mathcal {F})\geq 0$
(resp.
![]() $a(E;\mathcal {F})>0$
) for every exceptional divisor E on the minimal resolution of S.
$a(E;\mathcal {F})>0$
) for every exceptional divisor E on the minimal resolution of S.
Proof. Let
![]() $T=S/\mathcal {F}$
, let
$T=S/\mathcal {F}$
, let
![]() $\pi \colon S'\to S$
be the minimal resolution of S, and let
$\pi \colon S'\to S$
be the minimal resolution of S, and let
![]() $T'$
be quotient of
$T'$
be quotient of
![]() $S'$
by
$S'$
by
![]() $\pi ^{*}\mathcal {F}$
. Then we have a commutative diagram
$\pi ^{*}\mathcal {F}$
. Then we have a commutative diagram
Let
![]() $E\subset S'$
be a prime
$E\subset S'$
be a prime
![]() $\pi $
-exceptional divisor, with image
$\pi $
-exceptional divisor, with image
![]() $E'=q(E)\subset T'$
. Then as in the proof of Theorem 4.10, we find
$E'=q(E)\subset T'$
. Then as in the proof of Theorem 4.10, we find
First assume that T is canonical. As
![]() $\delta (E)\in \{1,p\}$
, the left-hand side of the equality is non-negative. Since
$\delta (E)\in \{1,p\}$
, the left-hand side of the equality is non-negative. Since
![]() $S'$
is the minimal resolution of S, we have
$S'$
is the minimal resolution of S, we have
![]() $a(E;S')\leq 0$
. Thus we must have
$a(E;S')\leq 0$
. Thus we must have
![]() $a(E;\mathcal {F})\geq 0$
. If T is regular, then the left-hand side is positive and so
$a(E;\mathcal {F})\geq 0$
. If T is regular, then the left-hand side is positive and so
![]() $a(E;\mathcal {F})>0$
.
$a(E;\mathcal {F})>0$
.
Example 4.14. Let
![]() $T=(\mathbf {0}\in \mathbb {A}^2_{x,y})$
and
$T=(\mathbf {0}\in \mathbb {A}^2_{x,y})$
and
![]() $\mathcal {G}$
be the
$\mathcal {G}$
be the
![]() $1$
-foliation generated by
$1$
-foliation generated by
![]() $\partial _{a,-b}$
(Example 2.6). Then
$\partial _{a,-b}$
(Example 2.6). Then
![]() $S=T/\mathcal {G}$
is klt (even canonical if
$S=T/\mathcal {G}$
is klt (even canonical if
![]() $a=-b$
). Let
$a=-b$
). Let
![]() $\mathcal {F}$
be the unique
$\mathcal {F}$
be the unique
![]() $1$
-foliation such that
$1$
-foliation such that
![]() $T^{(-1)}=S/\mathcal {F}$
. Then
$T^{(-1)}=S/\mathcal {F}$
. Then
![]() $\mathcal {F}$
is
$\mathcal {F}$
is
![]() $\mathbb {Q}$
-Gorenstein since S is
$\mathbb {Q}$
-Gorenstein since S is
![]() $\mathbb {Q}$
-factorial [Reference Tanaka59, Corollary 4.11]. By the above proposition, if
$\mathbb {Q}$
-factorial [Reference Tanaka59, Corollary 4.11]. By the above proposition, if
![]() $\pi \colon S'\to S$
is the minimal resolution then
$\pi \colon S'\to S$
is the minimal resolution then
![]() $K_{\pi ^{*}\mathcal {F}}=K_{\mathcal {F}}+E$
where
$K_{\pi ^{*}\mathcal {F}}=K_{\mathcal {F}}+E$
where
![]() $E\geq 0$
and
$E\geq 0$
and
![]() $\operatorname {\mathrm {Supp}}(E)=\operatorname {\mathrm {Exc}}(\pi )$
.
$\operatorname {\mathrm {Supp}}(E)=\operatorname {\mathrm {Exc}}(\pi )$
.
Corollary 4.15. Let X be an lc (resp. klt) k-scheme of finite type and
![]() $s\in H^0(X,\mathcal {O}_X)$
. If the
$s\in H^0(X,\mathcal {O}_X)$
. If the
![]() $1$
-foliation
$1$
-foliation
![]() $\operatorname {\mathrm {Ann}}(s)$
defined by
$\operatorname {\mathrm {Ann}}(s)$
defined by
is lc and properly contained in
![]() $T_{X/k}$
, then the normalized p-cyclic cover
$T_{X/k}$
, then the normalized p-cyclic cover
![]() $\left ( X[\sqrt [p]{s}]\right )^\nu $
is lc (resp. klt).
$\left ( X[\sqrt [p]{s}]\right )^\nu $
is lc (resp. klt).
Proof. It is easy to check that
![]() $\operatorname {\mathrm {Ann}}(s)$
is indeed a
$\operatorname {\mathrm {Ann}}(s)$
is indeed a
![]() $1$
-foliation, and that
$1$
-foliation, and that
![]() $\operatorname {\mathrm {Ann}}(s)\neq T_{X/k}$
if and only if s is not a pth power. If Y is the normalization of
$\operatorname {\mathrm {Ann}}(s)\neq T_{X/k}$
if and only if s is not a pth power. If Y is the normalization of
![]() $X[\sqrt [p]{s}]$
then
$X[\sqrt [p]{s}]$
then
![]() $X/\operatorname {\mathrm {Ann}}(s)=Y^{(-1)}$
. As Y and
$X/\operatorname {\mathrm {Ann}}(s)=Y^{(-1)}$
. As Y and
![]() $Y^{(-1)}$
are abstractly isomorphic, the result follows from Theorem 4.10.
$Y^{(-1)}$
are abstractly isomorphic, the result follows from Theorem 4.10.
Remark 4.16.
-
1. Corollary 4.15 can be generalized to more general p-cyclic coverings as follows. Let
 $\mathcal {L}$
be a line bundle on X, and
$\mathcal {L}$
be a line bundle on X, and
 $s\in H^0(X,\mathcal {L}^{-p})$
be a section that does not have a pth root in
$s\in H^0(X,\mathcal {L}^{-p})$
be a section that does not have a pth root in
 $H^0(X,\mathcal {L}^{-1})$
. Then we use
$H^0(X,\mathcal {L}^{-1})$
. Then we use
 $s\colon \mathcal {L}^p\to \mathcal {O}_X$
to give an
$s\colon \mathcal {L}^p\to \mathcal {O}_X$
to give an
 $\mathcal {O}_X$
-algebra structure to the direct sum
$\mathcal {O}_X$
-algebra structure to the direct sum
 $\bigoplus _{i=0}^{p-1}\mathcal {L}^i$
. Taking its normalized relative spectrum over X yields a finite purely inseparable
$\bigoplus _{i=0}^{p-1}\mathcal {L}^i$
. Taking its normalized relative spectrum over X yields a finite purely inseparable
 $Y\to X$
. Let
$Y\to X$
. Let
 $\{U_\alpha \}$
be a affine cover that trivializes
$\{U_\alpha \}$
be a affine cover that trivializes
 $\mathcal {L}$
. For each
$\mathcal {L}$
. For each
 $U_\alpha $
, choose a generator
$U_\alpha $
, choose a generator
 $\sigma _\alpha \in \mathcal {L}(U_\alpha )$
: we can write
$\sigma _\alpha \in \mathcal {L}(U_\alpha )$
: we can write
 $s|_{U_\alpha }=u_\alpha \sigma _{\alpha }^{-p}$
in
$s|_{U_\alpha }=u_\alpha \sigma _{\alpha }^{-p}$
in
 $\mathcal {L}^{-p}(U_\alpha )$
for some
$\mathcal {L}^{-p}(U_\alpha )$
for some
 $u_\alpha \in \mathcal {O}_X(U_\alpha )$
. This element
$u_\alpha \in \mathcal {O}_X(U_\alpha )$
. This element
 $u_\alpha $
does not depend on
$u_\alpha $
does not depend on
 $\sigma _\alpha $
, up to scaling by an element of
$\sigma _\alpha $
, up to scaling by an element of
 $\mathcal {O}_X(U_\alpha )^p$
. Thus the assignments define a
$\mathcal {O}_X(U_\alpha )^p$
. Thus the assignments define a $$ \begin{align*}U_\alpha\mapsto \{D\in T_{X/k}(U_\alpha)\mid D(u_\alpha)=0\}\end{align*} $$
$$ \begin{align*}U_\alpha\mapsto \{D\in T_{X/k}(U_\alpha)\mid D(u_\alpha)=0\}\end{align*} $$
 $1$
-foliation
$1$
-foliation
 $\operatorname {\mathrm {Ann}}(s)$
on X. Since we may apply Corollary 4.15 to obtain some singularity restrictions on Y as soon as
$\operatorname {\mathrm {Ann}}(s)$
on X. Since we may apply Corollary 4.15 to obtain some singularity restrictions on Y as soon as $$ \begin{align*}Y_{U_\alpha}\cong \operatorname{\mathrm{Spec}} \left(\mathcal{O}_X(U_\alpha)[T]/(T^p-u_\alpha)\right)^\nu\end{align*} $$
$$ \begin{align*}Y_{U_\alpha}\cong \operatorname{\mathrm{Spec}} \left(\mathcal{O}_X(U_\alpha)[T]/(T^p-u_\alpha)\right)^\nu\end{align*} $$
 $\operatorname {\mathrm {Ann}}(s)$
is lc.
$\operatorname {\mathrm {Ann}}(s)$
is lc.
-
2. If X is a regular variety, it is easy to find local generators of
 $\operatorname {\mathrm {Ann}}(s)$
, at least up to saturation. Let
$\operatorname {\mathrm {Ann}}(s)$
, at least up to saturation. Let
 $x_1,\dots ,x_n$
be a regular system of parameters of
$x_1,\dots ,x_n$
be a regular system of parameters of
 $\mathcal {O}_{X,z}$
. By Lemma 2.4, there exist
$\mathcal {O}_{X,z}$
. By Lemma 2.4, there exist
 $D_i\in \operatorname {\mathrm {Der}}_k(\mathcal {O}_{X,z})$
such that
$D_i\in \operatorname {\mathrm {Der}}_k(\mathcal {O}_{X,z})$
such that
 $D_i(x_j)=\delta _{ij}$
. Write
$D_i(x_j)=\delta _{ij}$
. Write
 $s_i=D_i(s)$
: since s is not a pth power, we may assume that
$s_i=D_i(s)$
: since s is not a pth power, we may assume that
 $s_1\neq 0$
. Then it is immediate that Now
$s_1\neq 0$
. Then it is immediate that Now $$ \begin{align*}s_{i}D_1-s_{1}D_i\in\operatorname{\mathrm{Ann}}(s) \quad \forall i=2,\dots,n.\end{align*} $$
$$ \begin{align*}s_{i}D_1-s_{1}D_i\in\operatorname{\mathrm{Ann}}(s) \quad \forall i=2,\dots,n.\end{align*} $$
 $\operatorname {\mathrm {Ann}}(s)$
has corank
$\operatorname {\mathrm {Ann}}(s)$
has corank
 $1$
, so these
$1$
, so these
 $n-1$
derivations generate
$n-1$
derivations generate
 $\operatorname {\mathrm {Ann}}(s)$
up to saturation as they are generically linearly independent.
$\operatorname {\mathrm {Ann}}(s)$
up to saturation as they are generically linearly independent.
-
3. For example, let
 $(s\in S)$
be a germ of regular surface and take
$(s\in S)$
be a germ of regular surface and take
 $\varphi \in H^0(S,\mathcal {O}_S)$
. Choose a regular system of parameters
$\varphi \in H^0(S,\mathcal {O}_S)$
. Choose a regular system of parameters
 $x,y\in \mathcal {O}_{S,s}$
and let
$x,y\in \mathcal {O}_{S,s}$
and let
 $D_x,D_y\in \operatorname {\mathrm {Der}}_k(\mathcal {O}_{S,s})$
be the derivations afforded by Lemma 2.4. Then
$D_x,D_y\in \operatorname {\mathrm {Der}}_k(\mathcal {O}_{S,s})$
be the derivations afforded by Lemma 2.4. Then
 $\operatorname {\mathrm {Ann}}(\varphi )$
is generated up to saturation by
$\operatorname {\mathrm {Ann}}(\varphi )$
is generated up to saturation by
 $D_y(\varphi )D_x-D_x(\varphi )D_y$
. Expanding
$D_y(\varphi )D_x-D_x(\varphi )D_y$
. Expanding
 $\varphi =\sum _{i,j}\varphi _{ij}x^iy^j$
in
$\varphi =\sum _{i,j}\varphi _{ij}x^iy^j$
in
 $\widehat {\mathcal {O}}_{S,s}$
, we have where the equalities are taken module
$\widehat {\mathcal {O}}_{S,s}$
, we have where the equalities are taken module $$ \begin{align*}D_y(\varphi)\equiv\varphi_{01}+\varphi_{11}x+2\varphi_{02}y \quad\text{and}\quad D_x(\varphi)\equiv \varphi_{10}+2\varphi_{20}x+\varphi_{11}y,\end{align*} $$
$$ \begin{align*}D_y(\varphi)\equiv\varphi_{01}+\varphi_{11}x+2\varphi_{02}y \quad\text{and}\quad D_x(\varphi)\equiv \varphi_{10}+2\varphi_{20}x+\varphi_{11}y,\end{align*} $$
 $\mathfrak {m}^2$
. Assuming that
$\mathfrak {m}^2$
. Assuming that
 $D_y(\varphi )$
and
$D_y(\varphi )$
and
 $D_x(\varphi )$
have trivial greatest common divisor, we see:
$D_x(\varphi )$
have trivial greatest common divisor, we see:
-
(a)
 $\operatorname {\mathrm {Ann}}(\varphi )$
is regular at s if and only if
$\operatorname {\mathrm {Ann}}(\varphi )$
is regular at s if and only if
 $d\varphi =D_x(\varphi )dx+D_y(\varphi )dy\notin \mathfrak {m}\Omega ^1_{S/k}$
;
$d\varphi =D_x(\varphi )dx+D_y(\varphi )dy\notin \mathfrak {m}\Omega ^1_{S/k}$
; -
(b)
 $\operatorname {\mathrm {Ann}}(\varphi )$
is strictly lc at s if and only if:
$\operatorname {\mathrm {Ann}}(\varphi )$
is strictly lc at s if and only if:
 $\varphi _{01}=0=\varphi _{10}$
and the matrix is non-nilpotent (that is, its determinant and its trace are not both zero).
$\varphi _{01}=0=\varphi _{10}$
and the matrix is non-nilpotent (that is, its determinant and its trace are not both zero). $$ \begin{align*}\begin{pmatrix} \varphi_{11} & -2\varphi_{20} \\ 2\varphi_{02} & -\varphi_{11} \end{pmatrix}\end{align*} $$
$$ \begin{align*}\begin{pmatrix} \varphi_{11} & -2\varphi_{20} \\ 2\varphi_{02} & -\varphi_{11} \end{pmatrix}\end{align*} $$
-
-
4. On surfaces, singularities of normalized p-cyclic covers can be handled with other methods: for example, see [Reference Arima4], [Reference Kawamata28] for the case of canonical index-one cover of klt surfaces.
4.3 Singularities of surface quotients
In this section, we consider more specifically the singularities of quotients of regular surfaces. From Theorem 4.10 we get the following corollary.
Corollary 4.17. Let
![]() $(s\in S)$
be a normal surface germ and
$(s\in S)$
be a normal surface germ and
![]() $\mathcal {F}$
a log canonical
$\mathcal {F}$
a log canonical
![]() $1$
-foliation on S. Assume either that
$1$
-foliation on S. Assume either that
-
1. S is klt, or
-
2. there exists a non-zero
 $\mathbb {Q}$
-Weil divisor
$\mathbb {Q}$
-Weil divisor
 $\Delta $
such that
$\Delta $
such that
 $(S,\Delta )$
is lc.
$(S,\Delta )$
is lc.
Then the germ
![]() $(s\in S/\mathcal {F})$
has rational singularities.
$(s\in S/\mathcal {F})$
has rational singularities.
Proof. Let
![]() $T=S/\mathcal {F}$
be the quotient. In the first case, T is also klt by the theorem and klt surfaces are rational [Reference Tanaka58, Fact 3.4]. In the second case, if
$T=S/\mathcal {F}$
be the quotient. In the first case, T is also klt by the theorem and klt surfaces are rational [Reference Tanaka58, Fact 3.4]. In the second case, if
![]() $\Delta _T$
is defined as in Definition 4.6 then
$\Delta _T$
is defined as in Definition 4.6 then
![]() $(T,\Delta _T)$
is lc by the theorem. As
$(T,\Delta _T)$
is lc by the theorem. As
![]() $\Delta _T\neq 0$
we deduce from [Reference Kollár30, Proposition 2.28] that T has rational singularities.
$\Delta _T\neq 0$
we deduce from [Reference Kollár30, Proposition 2.28] that T has rational singularities.
Remark 4.18. Corollary 4.17 may fail if
![]() $\mathcal {F}$
is not log canonical: see [Reference Liedtke35, Proposition 2.3] for an example where the quotient has an elliptic singularity. It would be interesting to determine what may happen when S is an elliptic singularity, and
$\mathcal {F}$
is not log canonical: see [Reference Liedtke35, Proposition 2.3] for an example where the quotient has an elliptic singularity. It would be interesting to determine what may happen when S is an elliptic singularity, and
![]() $\mathcal {F}$
a log canonical
$\mathcal {F}$
a log canonical
![]() $1$
-foliation.
$1$
-foliation.
In the surface case, a partial converse of Theorem 4.10 holds.
Theorem 4.19. Let S be a regular surface over k, and
![]() $\mathcal {F}$
be a
$\mathcal {F}$
be a
![]() $1$
-foliation of rank
$1$
-foliation of rank
![]() $1$
on S. Then the following are equivalent:
$1$
on S. Then the following are equivalent:
-
1.
 $S/\mathcal {F}$
is F-regular (equivalently klt if
$S/\mathcal {F}$
is F-regular (equivalently klt if
 $p>5$
),
$p>5$
), -
2.
 $S/\mathcal {F}$
is F-pure,
$S/\mathcal {F}$
is F-pure, -
3.
 $\mathcal {F}$
is lc.
$\mathcal {F}$
is lc.
Proof. We may assume that k is algebraically closed and that
![]() $S=\operatorname {\mathrm {Spec}}(\mathcal {O})$
is the spectrum of a complete regular local two-dimensional ring with residue field k, and that
$S=\operatorname {\mathrm {Spec}}(\mathcal {O})$
is the spectrum of a complete regular local two-dimensional ring with residue field k, and that
![]() $\mathcal {F}$
is not regular.
$\mathcal {F}$
is not regular.
Suppose that
![]() $\mathcal {F}$
is lc. By Corollary 3.7 the
$\mathcal {F}$
is lc. By Corollary 3.7 the
![]() $1$
-foliation
$1$
-foliation
![]() $\mathcal {F}$
has multiplicative singularities. Then by
$\mathcal {F}$
has multiplicative singularities. Then by
![]() $S/\mathcal {F}$
is F-regular by Theorem 4.3.
$S/\mathcal {F}$
is F-regular by Theorem 4.3.
Since F-regularity implies F-purity, we only need to show that if
![]() $A=\mathcal {O}^{\mathcal {F}}$
is F-pure then
$A=\mathcal {O}^{\mathcal {F}}$
is F-pure then
![]() $\mathcal {F}$
is lc. We follow the argument of [Reference Hara and Sawada17, Proposition 2.4]. The sheaf
$\mathcal {F}$
is lc. We follow the argument of [Reference Hara and Sawada17, Proposition 2.4]. The sheaf
![]() $\mathcal {F}$
is free of rank
$\mathcal {F}$
is free of rank
![]() $1$
, so pick a generator
$1$
, so pick a generator
![]() $\partial $
. We have
$\partial $
. We have
![]() $\partial ^{[p]}=\alpha \partial $
for some
$\partial ^{[p]}=\alpha \partial $
for some
![]() $\alpha \in \mathcal {O}$
. We will show that
$\alpha \in \mathcal {O}$
. We will show that
![]() $\partial $
is multiplicative, which will conclude by Corollary 3.7.
$\partial $
is multiplicative, which will conclude by Corollary 3.7.
The inclusion
![]() $A\hookrightarrow A^{1/p}$
splits as map of A-modules. Since it factors through
$A\hookrightarrow A^{1/p}$
splits as map of A-modules. Since it factors through
![]() $\mathcal {O}$
, by restriction we get an A-module map
$\mathcal {O}$
, by restriction we get an A-module map
![]() $\varphi \colon \mathcal {O}\to A$
splitting the natural inclusion. Over the regular locus of
$\varphi \colon \mathcal {O}\to A$
splitting the natural inclusion. Over the regular locus of
![]() $S/\mathcal {F}$
the sheaf
$S/\mathcal {F}$
the sheaf
![]() ${\mathcal {H}\operatorname {om}}_{\mathcal {O}_{S/\mathcal {F}}}(\mathcal {O}_S,\mathcal {O}_S)$
is generated by
${\mathcal {H}\operatorname {om}}_{\mathcal {O}_{S/\mathcal {F}}}(\mathcal {O}_S,\mathcal {O}_S)$
is generated by
![]() $\partial $
over
$\partial $
over
![]() $\mathcal {O}_S$
[Reference Yuan64]. This regular locus is big and the Hom sheaf is reflexive, thus
$\mathcal {O}_S$
[Reference Yuan64]. This regular locus is big and the Hom sheaf is reflexive, thus
![]() $\partial $
generates over
$\partial $
generates over
![]() $\mathcal {O}$
the endomorphism ring
$\mathcal {O}$
the endomorphism ring
![]() $\operatorname {\mathrm {Hom}}_A(\mathcal {O},\mathcal {O})$
. So we can write
$\operatorname {\mathrm {Hom}}_A(\mathcal {O},\mathcal {O})$
. So we can write
![]() $\varphi =\sum _{i=0}^{p-1}a_i\partial ^{[i]}$
for some
$\varphi =\sum _{i=0}^{p-1}a_i\partial ^{[i]}$
for some
![]() $a_i\in \mathcal {O}$
. Since
$a_i\in \mathcal {O}$
. Since
![]() $\varphi $
splits
$\varphi $
splits
![]() $A=\mathcal {O}^\partial \hookrightarrow \mathcal {O}$
, we see that
$A=\mathcal {O}^\partial \hookrightarrow \mathcal {O}$
, we see that
![]() $a_0=1$
and
$a_0=1$
and
![]() $\partial \circ \varphi =0$
. As the
$\partial \circ \varphi =0$
. As the
![]() $\partial ^{[i]}$
are
$\partial ^{[i]}$
are
![]() $\mathcal {O}$
-linearly independent [Reference Matsumura41, Theorem 25.4], by considering the
$\mathcal {O}$
-linearly independent [Reference Matsumura41, Theorem 25.4], by considering the
![]() $i=1$
term of
$i=1$
term of
![]() $\partial \circ \varphi $
we find
$\partial \circ \varphi $
we find
Now
![]() $\partial (a_1)$
belongs to the maximal ideal of
$\partial (a_1)$
belongs to the maximal ideal of
![]() $\mathcal {O}$
(because
$\mathcal {O}$
(because
![]() $\mathcal {F}$
is assumed to be singular, cf Lemma 2.19). Therefore
$\mathcal {F}$
is assumed to be singular, cf Lemma 2.19). Therefore
![]() $\alpha $
must be invertible, and so
$\alpha $
must be invertible, and so
![]() $\partial $
is multiplicative.
$\partial $
is multiplicative.
5 Families of foliations
We introduce a notion of parametrized families of foliations. We fix once and for all a perfect field k of characteristic
![]() $p>0$
.
$p>0$
.
5.1 Definitions and universal families
Definition 5.1. Let S be a locally Noetherian F-finite k-scheme. A family of foliations of rank r over S is the data of
-
• a flat finite type k-morphism
 $f\colon \mathcal {X}\to S$
,
$f\colon \mathcal {X}\to S$
, -
• two coherent
 $\mathcal {O}_{\mathcal {X}}$
-modules
$\mathcal {O}_{\mathcal {X}}$
-modules
 $\mathcal {F}\hookrightarrow \mathfrak {T}_{\mathcal {X}/S}$
,
$\mathcal {F}\hookrightarrow \mathfrak {T}_{\mathcal {X}/S}$
,
subject to the following properties:
-
1. the fibers of
 $\mathcal {X}\to S$
are geometrically normal and
$\mathcal {X}\to S$
are geometrically normal and
 $f_*\mathcal {O}_{\mathcal {X}}=\mathcal {O}_S$
holds,
$f_*\mathcal {O}_{\mathcal {X}}=\mathcal {O}_S$
holds, -
2.
 $\mathfrak {T}_{\mathcal {X}/S}$
is flat over S, and its restriction to
$\mathfrak {T}_{\mathcal {X}/S}$
is flat over S, and its restriction to
 $\mathcal {X}_s$
can naturally be identified with the tangent sheaf
$\mathcal {X}_s$
can naturally be identified with the tangent sheaf
 $T_{\mathcal {X}_s/k(s)}$
for every
$T_{\mathcal {X}_s/k(s)}$
for every
 $s\in S$
,
$s\in S$
, -
3. the quotient sheaf
 $\mathcal {Q}=\mathfrak {T}_{\mathcal {X}/S}/\mathcal {F}$
is flat over S, and
$\mathcal {Q}=\mathfrak {T}_{\mathcal {X}/S}/\mathcal {F}$
is flat over S, and -
4. for any
 $s\in S$
, the fiber
$s\in S$
, the fiber
 $\mathcal {F}_s\hookrightarrow T_{\mathcal {X}_s/k(s)}$
is a foliation of rank r.
$\mathcal {F}_s\hookrightarrow T_{\mathcal {X}_s/k(s)}$
is a foliation of rank r.
We define analogously families of
![]() $1$
-foliations of rank r on
$1$
-foliations of rank r on
![]() $\mathcal {X}$
over S.
$\mathcal {X}$
over S.
What is implicit in the definition is that, since both
![]() $\mathfrak {T}_{\mathcal {X}/S}$
and
$\mathfrak {T}_{\mathcal {X}/S}$
and
![]() $\mathcal {Q}$
are flat over S, the sheaf
$\mathcal {Q}$
are flat over S, the sheaf
![]() $\mathcal {F}$
is also flat over S and so for every
$\mathcal {F}$
is also flat over S and so for every
![]() $s\in S$
we have an exact sequence
$s\in S$
we have an exact sequence
where we write
![]() $\mathcal {F}_s=\mathcal {F}\otimes k(s)$
and
$\mathcal {F}_s=\mathcal {F}\otimes k(s)$
and
![]() $\mathcal {Q}_s=\mathcal {Q}\otimes k(s)$
.
$\mathcal {Q}_s=\mathcal {Q}\otimes k(s)$
.
Remark 5.2. In practice, a family of foliations
![]() $\mathcal {F}\subset \mathfrak {T}_{\mathcal {X}/S}$
is interesting if we can interpret
$\mathcal {F}\subset \mathfrak {T}_{\mathcal {X}/S}$
is interesting if we can interpret
![]() $\mathcal {F}$
itself as a collection of vector fields over S. So typically we want
$\mathcal {F}$
itself as a collection of vector fields over S. So typically we want
![]() $\mathfrak {T}_{\mathcal {X}/S}=T_{\mathcal {X}/S}$
, and this is the only case we will consider. Given an arbitrary
$\mathfrak {T}_{\mathcal {X}/S}=T_{\mathcal {X}/S}$
, and this is the only case we will consider. Given an arbitrary
![]() $\mathcal {X}\to S$
, for every
$\mathcal {X}\to S$
, for every
![]() $s\in S$
there is a natural morphism
$s\in S$
there is a natural morphism
![]() $T_{\mathcal {X}/S}\otimes k(s)\to T_{\mathcal {X}_s/k(s)}$
but in general it is not an isomorphism. In a few special cases it is, however:
$T_{\mathcal {X}/S}\otimes k(s)\to T_{\mathcal {X}_s/k(s)}$
but in general it is not an isomorphism. In a few special cases it is, however:
-
1. When the morphism
 $\mathcal {X}\to S$
is smooth, because then
$\mathcal {X}\to S$
is smooth, because then
 $\Omega ^1_{\mathcal {X}/S}$
is locally free.
$\Omega ^1_{\mathcal {X}/S}$
is locally free. -
2. When S is regular, and
 $T_{\mathcal {X}/S}$
is
$T_{\mathcal {X}/S}$
is
 $S_{2+\dim S}$
and flat over S. (Footnote
8
)
$S_{2+\dim S}$
and flat over S. (Footnote
8
) -
3. When
 $T_{\mathcal {X}/S}$
is its own universal hull, in the sense of [Reference Kollár31, §9.4].
$T_{\mathcal {X}/S}$
is its own universal hull, in the sense of [Reference Kollár31, §9.4].
Lemma 5.3. Let
![]() $ \mathcal {F}\hookrightarrow T_{\mathcal {X}/S}$
be a family of foliations (resp. of
$ \mathcal {F}\hookrightarrow T_{\mathcal {X}/S}$
be a family of foliations (resp. of
![]() $1$
-foliations) of rank r. Assume that S is
$1$
-foliations) of rank r. Assume that S is
![]() $S_2$
. Then
$S_2$
. Then
![]() $\mathcal {F}$
is a foliation (resp. a
$\mathcal {F}$
is a foliation (resp. a
![]() $1$
-foliation) of rank r.
$1$
-foliation) of rank r.
Proof. We need to prove that
![]() $\mathcal {F}$
is saturated in
$\mathcal {F}$
is saturated in
![]() $T_{\mathcal {X}/S}$
, since its generic fiber is already closed under Lie brackets (resp. under pth powers), see Remark 2.15. Now
$T_{\mathcal {X}/S}$
, since its generic fiber is already closed under Lie brackets (resp. under pth powers), see Remark 2.15. Now
![]() $\mathcal {F}$
is flat over S and its restriction to any fiber is
$\mathcal {F}$
is flat over S and its restriction to any fiber is
![]() $S_2$
. As S is
$S_2$
. As S is
![]() $S_2$
, if follows from [Reference Grothendieck15, 6.4.1(ii)] that
$S_2$
, if follows from [Reference Grothendieck15, 6.4.1(ii)] that
![]() $\mathcal {F}$
is an
$\mathcal {F}$
is an
![]() $S_2$
$S_2$
![]() $\mathcal {O}_{\mathcal {X}}$
-module. It follows that the quotient sheaf
$\mathcal {O}_{\mathcal {X}}$
-module. It follows that the quotient sheaf
![]() $\mathcal {Q}$
is
$\mathcal {Q}$
is
![]() $S_1$
(see [Reference Kollár30, Lemma 2.60]). Since
$S_1$
(see [Reference Kollár30, Lemma 2.60]). Since
![]() $\mathcal {Q}$
has full support, it is torsion-free [1, 0AUV]. Hence
$\mathcal {Q}$
has full support, it is torsion-free [1, 0AUV]. Hence
![]() $\mathcal {F}$
is saturated in
$\mathcal {F}$
is saturated in
![]() $T_{\mathcal {X}/S}$
.
$T_{\mathcal {X}/S}$
.
Non-trivial families of foliations (resp. of
![]() $1$
-foliations) on constant smooth families exist. In fact, assuming the fiber to be is projective, there are even universal such families. This is a straightforward Quot scheme argument, which we spell out for completeness. We refer to [Reference Fantechi, Göttsche, Illusie, Kleiman, Nitsure and Vistoli13] for the definition and the construction of the Quot scheme.
$1$
-foliations) on constant smooth families exist. In fact, assuming the fiber to be is projective, there are even universal such families. This is a straightforward Quot scheme argument, which we spell out for completeness. We refer to [Reference Fantechi, Göttsche, Illusie, Kleiman, Nitsure and Vistoli13] for the definition and the construction of the Quot scheme.
Lemma 5.4. Let
![]() $T\to S$
be a proper morphism of Noetherian schemes and
$T\to S$
be a proper morphism of Noetherian schemes and
![]() $u\colon \mathcal {M}\to \mathcal {N}$
a surjective morphism of coherent
$u\colon \mathcal {M}\to \mathcal {N}$
a surjective morphism of coherent
![]() $\mathcal {O}_T$
-modules. Assume that
$\mathcal {O}_T$
-modules. Assume that
![]() $\mathcal {M}$
is flat over S. Then there is a closed subscheme
$\mathcal {M}$
is flat over S. Then there is a closed subscheme
![]() $S'$
of S such that: a morphism
$S'$
of S such that: a morphism
![]() $V\to S$
factorizes through
$V\to S$
factorizes through
![]() $S'$
if and only if
$S'$
if and only if
![]() $u_V$
is an isomorphism.
$u_V$
is an isomorphism.
Proof. This is [Reference Raynaud51, Chapter 2, §4, Proposition].
Proposition 5.5. Let X be a regular projective connected k-scheme X and
![]() $\dim X>r\geq 1$
be an integer. Then there is a locally closed subscheme
$\dim X>r\geq 1$
be an integer. Then there is a locally closed subscheme
![]() $Q_0(r)$
(resp. a locally closed subscheme
$Q_0(r)$
(resp. a locally closed subscheme
![]() $Q_1(r)$
) of
$Q_1(r)$
) of
![]() $\operatorname {\mathrm {Quot}}_{T_{X/k}/X/k}$
that parametrizes families of foliations (resp. of
$\operatorname {\mathrm {Quot}}_{T_{X/k}/X/k}$
that parametrizes families of foliations (resp. of
![]() $1$
-foliations) of rank r on X over Noetherian bases.
$1$
-foliations) of rank r on X over Noetherian bases.
Proof. Write
![]() $T=T_{X/k}$
. Notice that since X is regular, for every k-scheme S the sheaf
$T=T_{X/k}$
. Notice that since X is regular, for every k-scheme S the sheaf
![]() $T_{X_S/S}$
is the pullback of T through the projection
$T_{X_S/S}$
is the pullback of T through the projection
![]() $X_S=X\times _kS\to X$
. Fix an ample line bundle L on X. The Quot scheme
$X_S=X\times _kS\to X$
. Fix an ample line bundle L on X. The Quot scheme
![]() $\operatorname {\mathrm {Quot}}_{T/X/k}$
is the disjoint union of the projective schemes
$\operatorname {\mathrm {Quot}}_{T/X/k}$
is the disjoint union of the projective schemes
![]() $Q(\varphi )=\operatorname {\mathrm {Quot}}_{T/X/k}^{L,\varphi }$
, where
$Q(\varphi )=\operatorname {\mathrm {Quot}}_{T/X/k}^{L,\varphi }$
, where
![]() $\varphi \in \mathbb {Q}[t]$
. Each product
$\varphi \in \mathbb {Q}[t]$
. Each product
![]() $X_{Q(\varphi )}$
supports a universal quotient
$X_{Q(\varphi )}$
supports a universal quotient
![]() $T_{X_{Q(\varphi )}/Q(\varphi )}\twoheadrightarrow \mathcal {Q}^{\varphi ,\text {univ}}$
. Let
$T_{X_{Q(\varphi )}/Q(\varphi )}\twoheadrightarrow \mathcal {Q}^{\varphi ,\text {univ}}$
. Let
![]() $\mathcal {F}^{\varphi ,\text {univ}}$
be its kernel. Note that the relative rank of
$\mathcal {F}^{\varphi ,\text {univ}}$
be its kernel. Note that the relative rank of
![]() $\mathcal {F}^{\varphi ,\text {univ}}$
over
$\mathcal {F}^{\varphi ,\text {univ}}$
over
![]() $Q(\varphi )$
is uniquely determined by the Hilbert polynomial
$Q(\varphi )$
is uniquely determined by the Hilbert polynomial
![]() $\varphi $
.
$\varphi $
.
We have to show that there exist a locally closed subscheme
![]() $Q_0(r,\varphi )$
(resp.
$Q_0(r,\varphi )$
(resp.
![]() $Q_1(r,\varphi )$
) of
$Q_1(r,\varphi )$
) of
![]() $Q(\varphi )$
such that
$Q(\varphi )$
such that
![]() $S\to Q(\varphi )$
factors through
$S\to Q(\varphi )$
factors through
![]() $Q_0(r,\varphi )$
(resp. through
$Q_0(r,\varphi )$
(resp. through
![]() $Q_1(r,\varphi )$
) if and only if the pullback of the universal quotient through
$Q_1(r,\varphi )$
) if and only if the pullback of the universal quotient through
![]() $X_S\to X_Q$
is a family of foliations (resp. of
$X_S\to X_Q$
is a family of foliations (resp. of
![]() $1$
-foliations) on X. Then we will have
$1$
-foliations) on X. Then we will have
![]() $Q_i(r)=\bigsqcup _\varphi Q_i(r,\varphi )$
.
$Q_i(r)=\bigsqcup _\varphi Q_i(r,\varphi )$
.
For simplicity, from now on we drop the
![]() $\varphi $
from the notation. For every point
$\varphi $
from the notation. For every point
![]() $q\in Q$
, by flatness of
$q\in Q$
, by flatness of
![]() $\mathcal {Q}^{\text {univ}}$
we have an exact sequence of
$\mathcal {Q}^{\text {univ}}$
we have an exact sequence of
![]() $\mathcal {O}_{X_{k(q)}}$
-coherent modules:
$\mathcal {O}_{X_{k(q)}}$
-coherent modules:
We define a few subschemes of Q as follows.
-
1. There is an open subset
 $\mathcal {U}$
parametrizing saturated and reflexive
$\mathcal {U}$
parametrizing saturated and reflexive
 $\mathcal {F}^{\text {univ}}_q$
. The fibers
$\mathcal {F}^{\text {univ}}_q$
. The fibers
 $\mathcal {Q}^{\text {univ}}_q$
have all full support, so they are torsion-free if and only if if they are
$\mathcal {Q}^{\text {univ}}_q$
have all full support, so they are torsion-free if and only if if they are
 $S_1$
[1, 0AUV]. Moreover by [1, 0EB8] and the above exact sequence, if
$S_1$
[1, 0AUV]. Moreover by [1, 0EB8] and the above exact sequence, if
 $\mathcal {Q}^{\text {univ}}_q$
is torsion-free then
$\mathcal {Q}^{\text {univ}}_q$
is torsion-free then
 $\mathcal {F}^{\text {univ}}_q$
is reflexive. Since
$\mathcal {F}^{\text {univ}}_q$
is reflexive. Since
 $\mathcal {Q}^{\text {univ}}$
is proper and flat over Q, the set of
$\mathcal {Q}^{\text {univ}}$
is proper and flat over Q, the set of
 $q\in Q$
over which
$q\in Q$
over which
 $\mathcal {Q}^{\text {univ}}_q$
is
$\mathcal {Q}^{\text {univ}}_q$
is
 $S_1$
is open in Q [Reference Grothendieck16, 12.2.1], call it
$S_1$
is open in Q [Reference Grothendieck16, 12.2.1], call it
 $\mathcal {U}$
.
$\mathcal {U}$
. -
2. There is a closed subscheme
 $\mathcal {L}$
parametrizing those
$\mathcal {L}$
parametrizing those
 $\mathcal {F}^{\text {univ}}_q$
which are closed under Lie brackets. Consider the composite morphism sending
$\mathcal {F}^{\text {univ}}_q$
which are closed under Lie brackets. Consider the composite morphism sending $$ \begin{align*}L_{\mathcal{F}^{\text{univ}}}\colon \bigwedge^2\mathcal{F}^{\text{univ}}\to T_{X_Q/Q}\to \mathcal{Q}^{\text{univ}}\end{align*} $$
$$ \begin{align*}L_{\mathcal{F}^{\text{univ}}}\colon \bigwedge^2\mathcal{F}^{\text{univ}}\to T_{X_Q/Q}\to \mathcal{Q}^{\text{univ}}\end{align*} $$
 $v\wedge w$
to the class of
$v\wedge w$
to the class of
 $[v,w]$
in
$[v,w]$
in
 $\mathcal {Q}^{\text {univ}}$
. Its image
$\mathcal {Q}^{\text {univ}}$
. Its image
 $\operatorname {\mathrm {im}}(L_{\mathcal {F}^{\text {univ}}})$
is a coherent subsheaf of
$\operatorname {\mathrm {im}}(L_{\mathcal {F}^{\text {univ}}})$
is a coherent subsheaf of
 $\mathcal {Q}^{\text {univ}}$
. For a morphism
$\mathcal {Q}^{\text {univ}}$
. For a morphism
 $S\to Q$
, the pullback morphism
$S\to Q$
, the pullback morphism
 $(L_{\mathcal {F}^{\text {univ}}})_S$
is zero if and only if the surjection
$(L_{\mathcal {F}^{\text {univ}}})_S$
is zero if and only if the surjection
 $\operatorname {\mathrm {im}}(L_{\mathcal {F}^{\text {univ}}})\to 0$
becomes an isomorphism. By Lemma 5.4 this defines a closed subscheme
$\operatorname {\mathrm {im}}(L_{\mathcal {F}^{\text {univ}}})\to 0$
becomes an isomorphism. By Lemma 5.4 this defines a closed subscheme
 $\mathcal {L}$
of Q.
$\mathcal {L}$
of Q.
-
3. There is a closed subscheme
 $\mathcal {P}$
of
$\mathcal {P}$
of
 $\mathcal {L}$
parametrizing those
$\mathcal {L}$
parametrizing those
 $\mathcal {F}^{\text {univ}}_q$
which are closed under Lie brackets and under pth powers. This is similar to the previous point, with the additional subtlety that the pth power is not linear. However, Hochschild’s formula (2.1) shows that
$\mathcal {F}^{\text {univ}}_q$
which are closed under Lie brackets and under pth powers. This is similar to the previous point, with the additional subtlety that the pth power is not linear. However, Hochschild’s formula (2.1) shows that
 $(aD)^{[p]}$
is the sum of
$(aD)^{[p]}$
is the sum of
 $a^pD^{[p]}$
and a scaling of D; and a formula due to Jacobson [Reference Jacobson24, (15) on p. 209] says that
$a^pD^{[p]}$
and a scaling of D; and a formula due to Jacobson [Reference Jacobson24, (15) on p. 209] says that
 $(D_1+D_2)^{[p]}-D_1^{[p]}-D_2^{[p]}$
is a sum of commutators involving only
$(D_1+D_2)^{[p]}-D_1^{[p]}-D_2^{[p]}$
is a sum of commutators involving only
 $D_1$
and
$D_1$
and
 $D_2$
. Thus, restricting over
$D_2$
. Thus, restricting over
 $\mathcal {L}$
, we get a linear map sending v to the class of
$\mathcal {L}$
, we get a linear map sending v to the class of $$ \begin{align*}P_{\mathcal{F}^{\text{univ}}}\colon F_{X_{\mathcal{L}}/\mathcal{L}}^{*}\left(\mathcal{F}^{\text{univ}}_{\mathcal{L}}\right)\longrightarrow \mathcal{Q}^{\text{univ}}_{\mathcal{L}}\end{align*} $$
$$ \begin{align*}P_{\mathcal{F}^{\text{univ}}}\colon F_{X_{\mathcal{L}}/\mathcal{L}}^{*}\left(\mathcal{F}^{\text{univ}}_{\mathcal{L}}\right)\longrightarrow \mathcal{Q}^{\text{univ}}_{\mathcal{L}}\end{align*} $$
 $v^{[p]}$
in
$v^{[p]}$
in
 $\mathcal {Q}^{\text {univ}}_{\mathcal {L}}$
, where
$\mathcal {Q}^{\text {univ}}_{\mathcal {L}}$
, where
 $F_{X_{\mathcal {L}}/\mathcal {L}}\colon X_{\mathcal {L}}\to X_{\mathcal {L}}^{(1)}$
is the
$F_{X_{\mathcal {L}}/\mathcal {L}}\colon X_{\mathcal {L}}\to X_{\mathcal {L}}^{(1)}$
is the
 $\mathcal {L}$
-linear Frobenius. As above, the function
$\mathcal {L}$
-linear Frobenius. As above, the function
 $P_{\mathcal {F}^{\text {univ}}}$
vanishes functorially over a closed subset
$P_{\mathcal {F}^{\text {univ}}}$
vanishes functorially over a closed subset
 $\mathcal {P}\subset \mathcal {L}$
.
$\mathcal {P}\subset \mathcal {L}$
.
Now we set
![]() $Q_0(r)=\mathcal {U}\cap \mathcal {L}$
and
$Q_0(r)=\mathcal {U}\cap \mathcal {L}$
and
![]() $Q_1(r)=\mathcal {U}\cap \mathcal {P}$
. By construction they have the desired properties (Footnote
9
), and the proof is complete.
$Q_1(r)=\mathcal {U}\cap \mathcal {P}$
. By construction they have the desired properties (Footnote
9
), and the proof is complete.
5.2 Quotients and fibers
We turn to the following interrogation.
Question 5.6. Let
![]() $(f\colon \mathcal {X}\to S,\mathcal {F}\hookrightarrow T_{\mathcal {X}/S})$
be a family of
$(f\colon \mathcal {X}\to S,\mathcal {F}\hookrightarrow T_{\mathcal {X}/S})$
be a family of
![]() $1$
-foliations; we continue to assume, just as in Remark 5.2, that
$1$
-foliations; we continue to assume, just as in Remark 5.2, that
![]() $T_{\mathcal {X}/S}$
commutes with restriction to fibers. Let
$T_{\mathcal {X}/S}$
commutes with restriction to fibers. Let
![]() $Z=\mathcal {X}/\mathcal {F}$
be the quotient. Since the derivations in
$Z=\mathcal {X}/\mathcal {F}$
be the quotient. Since the derivations in
![]() $\mathcal {F}$
are
$\mathcal {F}$
are
![]() $\mathcal {O}_S$
-linear, the morphism f factors as
$\mathcal {O}_S$
-linear, the morphism f factors as
With these notations, we ask:
-
1. Is
 $g\colon Z\to S$
a flat morphism?
$g\colon Z\to S$
a flat morphism? -
2. For
 $s\in S$
, how do
$s\in S$
, how do
 $Z_s$
and
$Z_s$
and
 $\mathcal {X}_s/\mathcal {F}_s$
relate?
$\mathcal {X}_s/\mathcal {F}_s$
relate?
For the first question, we have the following result.
Proposition 5.7. Notations as above. If S is regular of dimension
![]() $\leq 2$
, then
$\leq 2$
, then
![]() $g\colon Z\to S$
is flat.
$g\colon Z\to S$
is flat.
Proof. We may assume that
![]() $S=\operatorname {\mathrm {Spec}}(R)$
is regular local of dimension two with maximal ideal
$S=\operatorname {\mathrm {Spec}}(R)$
is regular local of dimension two with maximal ideal
![]() $(x,y)$
(the dimension one case will be similar), and that
$(x,y)$
(the dimension one case will be similar), and that
![]() $\mathcal {X}=\operatorname {\mathrm {Spec}}(A)$
. Since A is flat over R, the elements
$\mathcal {X}=\operatorname {\mathrm {Spec}}(A)$
. Since A is flat over R, the elements
![]() $x,y\in A^{\mathcal {F}}$
form a regular sequence in A. By Lemma 2.36 the sequence
$x,y\in A^{\mathcal {F}}$
form a regular sequence in A. By Lemma 2.36 the sequence
![]() $x,y$
is also regular in
$x,y$
is also regular in
![]() $A^{\mathcal {F}}$
. By [1, 07DY] it follows that
$A^{\mathcal {F}}$
. By [1, 07DY] it follows that
![]() $A^{\mathcal {F}}$
is flat over R.
$A^{\mathcal {F}}$
is flat over R.
Remark 5.8.
-
1. The statement of Proposition 5.7 still holds if we only assume that
 $\mathcal {F}$
is a
$\mathcal {F}$
is a
 $1$
-foliation contained in
$1$
-foliation contained in
 $T_{\mathcal {X}/S}$
, instead of being a family of
$T_{\mathcal {X}/S}$
, instead of being a family of
 $1$
-foliations. Thus we generalize the flatness result of [Reference Schröer55, Corollary 2.8].
$1$
-foliations. Thus we generalize the flatness result of [Reference Schröer55, Corollary 2.8]. -
2. Proposition 5.7 does not hold in general if
 $\dim S\geq 3$
. For example, consider and let
$\dim S\geq 3$
. For example, consider and let $$ \begin{align*}\mathcal{X}=\mathbb{A}^3_{\mathbf{x}}\times \mathbb{A}^3_{\mathbf{s}}, \quad g=\operatorname{\mathrm{pr}}_2\colon \mathcal{X}\to \mathbb{A}^3_{\mathbf{s}}=S,\end{align*} $$
$$ \begin{align*}\mathcal{X}=\mathbb{A}^3_{\mathbf{x}}\times \mathbb{A}^3_{\mathbf{s}}, \quad g=\operatorname{\mathrm{pr}}_2\colon \mathcal{X}\to \mathbb{A}^3_{\mathbf{s}}=S,\end{align*} $$
 $\mathcal {F}$
be the family of
$\mathcal {F}$
be the family of
 $1$
-foliations generated by
$1$
-foliations generated by
 $\partial =\sum _{i=1}^3s_i\partial _{x_i}$
. This derivation defines an
$\partial =\sum _{i=1}^3s_i\partial _{x_i}$
. This derivation defines an
 $\alpha _p$
-action, whose fixed locus is
$\alpha _p$
-action, whose fixed locus is
 $V(s_1,s_2,s_3)\subset \mathcal {X}$
. Let
$V(s_1,s_2,s_3)\subset \mathcal {X}$
. Let
 $\xi $
be the generic point of this fixed locus. Then
$\xi $
be the generic point of this fixed locus. Then
 $\mathcal {O}_{\mathcal {X},\xi }^\partial =\mathcal {O}_{Z,q(\xi )}$
has depth
$\mathcal {O}_{\mathcal {X},\xi }^\partial =\mathcal {O}_{Z,q(\xi )}$
has depth
 $2$
by Lemma 2.31. Since
$2$
by Lemma 2.31. Since
 $f(\xi )$
is the origin on
$f(\xi )$
is the origin on
 $\mathbb {A}^3_{\mathbf {s}}$
, we see that
$\mathbb {A}^3_{\mathbf {s}}$
, we see that
 $\mathcal {O}_{S,f(\xi )}\to \mathcal {O}_{Z,q(\xi )}$
is not flat, for otherwise
$\mathcal {O}_{S,f(\xi )}\to \mathcal {O}_{Z,q(\xi )}$
is not flat, for otherwise
 $\mathcal {O}_{Z,q(\xi )}$
would have depth
$\mathcal {O}_{Z,q(\xi )}$
would have depth
 $3$
. Hence
$3$
. Hence
 $Z\to S$
is not flat.
$Z\to S$
is not flat.
Next let us compare
![]() $Z_s$
with the quotient
$Z_s$
with the quotient
![]() $\mathcal {X}_s/\mathcal {F}_s$
. To begin with, for every
$\mathcal {X}_s/\mathcal {F}_s$
. To begin with, for every
![]() $s\in S$
we construct a comparison morphism
$s\in S$
we construct a comparison morphism
![]() $\varphi _s\colon \mathcal {X}_s/\mathcal {F}_s\to Z_s$
as follows. Locally, pick a section
$\varphi _s\colon \mathcal {X}_s/\mathcal {F}_s\to Z_s$
as follows. Locally, pick a section
![]() $\partial \in \mathcal {F}$
: it is a local derivation on
$\partial \in \mathcal {F}$
: it is a local derivation on
![]() $\mathcal {X}$
which, as it belongs to
$\mathcal {X}$
which, as it belongs to
![]() $T_{\mathcal {X}/S}$
, is
$T_{\mathcal {X}/S}$
, is
![]() $\mathcal {O}_S$
-linear. By the exact sequence (5.1), the restriction
$\mathcal {O}_S$
-linear. By the exact sequence (5.1), the restriction
![]() $\partial _s\in \mathcal {F}_s$
is a local derivation of
$\partial _s\in \mathcal {F}_s$
is a local derivation of
![]() $\mathcal {X}_s$
that can be defined by the commutativity of the diagram
$\mathcal {X}_s$
that can be defined by the commutativity of the diagram
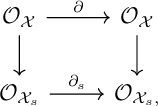
So if
![]() $a\in \mathcal {O}_{\mathcal {X}}$
is annihilated by
$a\in \mathcal {O}_{\mathcal {X}}$
is annihilated by
![]() $\partial $
, its image
$\partial $
, its image
![]() $\bar {a}\in \mathcal {O}_{\mathcal {X}_s}$
is annihilated by
$\bar {a}\in \mathcal {O}_{\mathcal {X}_s}$
is annihilated by
![]() $\partial _s$
. Letting
$\partial _s$
. Letting
![]() $\partial $
range through the elements of
$\partial $
range through the elements of
![]() $\mathcal {F}$
, we obtain a factorization of the
$\mathcal {F}$
, we obtain a factorization of the
![]() $k(s)$
-linear Frobenius of
$k(s)$
-linear Frobenius of
![]() $\mathcal {X}_s$
as follows:
$\mathcal {X}_s$
as follows:
This induces a universal homeomorphism
![]() $\varphi _s\colon \mathcal {X}_s/\mathcal {F}_s\to Z_s$
which factors the
$\varphi _s\colon \mathcal {X}_s/\mathcal {F}_s\to Z_s$
which factors the
![]() $k(s)$
-linear Frobenius of
$k(s)$
-linear Frobenius of
![]() $\mathcal {X}_s$
. Notice that the arrow
$\mathcal {X}_s$
. Notice that the arrow
![]() $c_s\colon \mathcal {O}_Z\otimes k(s)\to \mathcal {O}_{\mathcal {X}_s/\mathcal {F}_s}$
in (5.3) is a priori not injective. In fact, its kernel is p-nilpotent because
$c_s\colon \mathcal {O}_Z\otimes k(s)\to \mathcal {O}_{\mathcal {X}_s/\mathcal {F}_s}$
in (5.3) is a priori not injective. In fact, its kernel is p-nilpotent because
![]() $\mathcal {O}_Z^p\subseteq \mathcal {O}_{\mathcal {X}^{(1)}}$
, and as
$\mathcal {O}_Z^p\subseteq \mathcal {O}_{\mathcal {X}^{(1)}}$
, and as
![]() $\mathcal {O}_{\mathcal {X}_s}$
is reduced we get in fact that
$\mathcal {O}_{\mathcal {X}_s}$
is reduced we get in fact that
![]() $c_s$
is an injective map if and only if
$c_s$
is an injective map if and only if
![]() $Z_s$
is reduced.
$Z_s$
is reduced.
If the morphism
![]() $\varphi _s$
is an isomorphism, we say that taking fiber and quotient commutes over s.
$\varphi _s$
is an isomorphism, we say that taking fiber and quotient commutes over s.
While
![]() $\varphi _s$
is defined quite generally, we will concentrate on the case where
$\varphi _s$
is defined quite generally, we will concentrate on the case where
![]() $\mathcal {X}\to S$
is smooth and S is regular.
$\mathcal {X}\to S$
is smooth and S is regular.
Proposition 5.9. Notations as in (5.2). Assume that the exact sequence
![]() $\mathcal {F}\hookrightarrow T_{\mathcal {X}/S}\twoheadrightarrow \mathcal {Q}$
is split at
$\mathcal {F}\hookrightarrow T_{\mathcal {X}/S}\twoheadrightarrow \mathcal {Q}$
is split at
![]() $z\in \mathcal {X}$
, that f is smooth at z and that S is regular at
$z\in \mathcal {X}$
, that f is smooth at z and that S is regular at
![]() $s=f(z)$
. Then
$s=f(z)$
. Then
![]() $\varphi _{s}\colon \mathcal {X}_s/\mathcal {F}_s\to Z_s$
is an isomorphism at z.
$\varphi _{s}\colon \mathcal {X}_s/\mathcal {F}_s\to Z_s$
is an isomorphism at z.
Proof. The question is local, so we may assume that
![]() $S=\operatorname {\mathrm {Spec}}(A)$
and
$S=\operatorname {\mathrm {Spec}}(A)$
and
![]() $\mathcal {X}=\operatorname {\mathrm {Spec}}(B)$
are affine with
$\mathcal {X}=\operatorname {\mathrm {Spec}}(B)$
are affine with
![]() $(A,\mathfrak {m}_A)$
regular local and B a smooth A-algebra. We may also shrink B so that
$(A,\mathfrak {m}_A)$
regular local and B a smooth A-algebra. We may also shrink B so that
![]() $\mathcal {F}$
becomes a direct summand of
$\mathcal {F}$
becomes a direct summand of
![]() $T_{B/A}$
, and
$T_{B/A}$
, and
![]() $T_{B/A}$
a direct summand of
$T_{B/A}$
a direct summand of
![]() $T_{B/k}$
. So
$T_{B/k}$
. So
![]() $\mathcal {F}$
is a direct summand of
$\mathcal {F}$
is a direct summand of
![]() $T_{B/k}$
. Then by Example 2.18, there is a partial system of local coordinates
$T_{B/k}$
. Then by Example 2.18, there is a partial system of local coordinates
![]() $v_1,\dots ,v_r\in B$
such that we can write
$v_1,\dots ,v_r\in B$
such that we can write
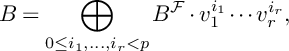 $$ \begin{align*}B=\bigoplus_{0\leq i_1,\dots,i_r< p}B^{\mathcal{F}}\cdot v_1^{i_1}\cdots v_r^{i_r},\end{align*} $$
$$ \begin{align*}B=\bigoplus_{0\leq i_1,\dots,i_r< p}B^{\mathcal{F}}\cdot v_1^{i_1}\cdots v_r^{i_r},\end{align*} $$
and moreover
![]() $\mathcal {F}$
is generated by
$\mathcal {F}$
is generated by
![]() $\partial _1,\dots ,\partial _r$
with the property that
$\partial _1,\dots ,\partial _r$
with the property that
![]() $\partial _i(v_j)=\delta _{ij}$
(the Kronecker delta). By A-linearity, the image of the structural map
$\partial _i(v_j)=\delta _{ij}$
(the Kronecker delta). By A-linearity, the image of the structural map
![]() $A\to B$
is contained in
$A\to B$
is contained in
![]() $B^{\mathcal {F}}$
. Thus the fiber over the closed point of S is given by
$B^{\mathcal {F}}$
. Thus the fiber over the closed point of S is given by
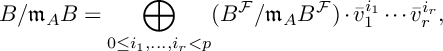 $$ \begin{align*}B/\mathfrak{m}_A B=\bigoplus_{0\leq i_1,\dots,i_r< p}(B^{\mathcal{F}}/\mathfrak{m}_A B^{\mathcal{F}})\cdot \bar{v}_1^{i_1}\cdots \bar{v}_r^{i_r},\end{align*} $$
$$ \begin{align*}B/\mathfrak{m}_A B=\bigoplus_{0\leq i_1,\dots,i_r< p}(B^{\mathcal{F}}/\mathfrak{m}_A B^{\mathcal{F}})\cdot \bar{v}_1^{i_1}\cdots \bar{v}_r^{i_r},\end{align*} $$
where
![]() $\bar {v}_i$
is the image of
$\bar {v}_i$
is the image of
![]() $v_i$
through the quotient
$v_i$
through the quotient
![]() $B\to B/\mathfrak {m}_A B$
. Moreover
$B\to B/\mathfrak {m}_A B$
. Moreover
![]() $\mathcal {F}_s$
is generated by the restrictions
$\mathcal {F}_s$
is generated by the restrictions
![]() $\bar {\partial }_i$
of the
$\bar {\partial }_i$
of the
![]() $\partial _i$
’s, and we still have the property
$\partial _i$
’s, and we still have the property
![]() $\bar {\partial }_i(\bar {v}_j)=\delta _{ij}$
. Thus if
$\bar {\partial }_i(\bar {v}_j)=\delta _{ij}$
. Thus if
![]() $\bar {w}\in B/\mathfrak {m}_AB$
is annihilated by every element of
$\bar {w}\in B/\mathfrak {m}_AB$
is annihilated by every element of
![]() $\mathcal {F}_s$
, it belongs to the summand
$\mathcal {F}_s$
, it belongs to the summand
![]() $i_1=\dots =i_r=0$
, and we can find a preimage of
$i_1=\dots =i_r=0$
, and we can find a preimage of
![]() $\bar {w}$
in the corresponding summand of B. That preimage will be annihilated by every element of
$\bar {w}$
in the corresponding summand of B. That preimage will be annihilated by every element of
![]() $\mathcal {F}$
. This shows that the map
$\mathcal {F}$
. This shows that the map
![]() $c_s$
in (5.3) is an equality at
$c_s$
in (5.3) is an equality at
![]() $z\in \mathcal {X}_s$
.
$z\in \mathcal {X}_s$
.
Our main application of the proposition above is the following one (compare with [Reference Bergqvist7, Theorem 4.1.7]).
Corollary 5.10. Notations as in (5.2). Assume that S is regular. Then for every
![]() $s\in S$
, the morphism
$s\in S$
, the morphism
![]() $\varphi _s$
is finite and an isomorphism in codimension one. Moreover it is an isomorphism at
$\varphi _s$
is finite and an isomorphism in codimension one. Moreover it is an isomorphism at
![]() $z\in \mathcal {X}_s$
if and only if
$z\in \mathcal {X}_s$
if and only if
![]() $Z_s$
is
$Z_s$
is
![]() $S_2$
at z.
$S_2$
at z.
Proof. By assumption every fiber
![]() $\mathcal {X}_s$
is F-finite, so it is easily seen from the above construction that every
$\mathcal {X}_s$
is F-finite, so it is easily seen from the above construction that every
![]() $\varphi _s$
is finite. Take
$\varphi _s$
is finite. Take
![]() $z\in \mathcal {X}_s$
such that
$z\in \mathcal {X}_s$
such that
![]() $\operatorname {\mathrm {codim}}_{\mathcal {X}_s}(z)\leq 1$
: we check that the hypothesis of Proposition 5.9 hold. Since
$\operatorname {\mathrm {codim}}_{\mathcal {X}_s}(z)\leq 1$
: we check that the hypothesis of Proposition 5.9 hold. Since
![]() $\mathcal {X}_s$
is normal, the local ring
$\mathcal {X}_s$
is normal, the local ring
![]() $\mathcal {O}_{\mathcal {X}_s,z}$
is regular. As f is flat and S is regular, we deduce that
$\mathcal {O}_{\mathcal {X}_s,z}$
is regular. As f is flat and S is regular, we deduce that
![]() $\mathcal {O}_{\mathcal {X},z}$
is regular. Therefore f is smooth at
$\mathcal {O}_{\mathcal {X},z}$
is regular. Therefore f is smooth at
![]() $z\in \mathcal {X}$
. Moreover
$z\in \mathcal {X}$
. Moreover
![]() $\mathcal {Q}_s$
is free at
$\mathcal {Q}_s$
is free at
![]() $z\in \mathcal {X}_s$
(use the exact sequence (5.1) and the assumption that
$z\in \mathcal {X}_s$
(use the exact sequence (5.1) and the assumption that
![]() $\mathcal {F}_s$
is saturated), and since
$\mathcal {F}_s$
is saturated), and since
![]() $\mathcal {Q}$
is flat over S it follows that
$\mathcal {Q}$
is flat over S it follows that
![]() $\mathcal {Q}$
is free at z [1, 00MH]. Thus
$\mathcal {Q}$
is free at z [1, 00MH]. Thus
![]() $T_{\mathcal {X}/S}\to \mathcal {Q}$
splits at z. So Proposition 5.9 indeed applies, and
$T_{\mathcal {X}/S}\to \mathcal {Q}$
splits at z. So Proposition 5.9 indeed applies, and
![]() $\varphi _s$
is an isomorphism at z.
$\varphi _s$
is an isomorphism at z.
As
![]() $\mathcal {X}_s/\mathcal {F}_s$
is
$\mathcal {X}_s/\mathcal {F}_s$
is
![]() $S_2$
, the previous paragraph implies that
$S_2$
, the previous paragraph implies that
![]() $\varphi _s$
is the
$\varphi _s$
is the
![]() $S_2$
-fication of
$S_2$
-fication of
![]() $\operatorname {\mathrm {red}}(Z_s)$
. Since
$\operatorname {\mathrm {red}}(Z_s)$
. Since
![]() $Z_s$
is generically reduced by the above paragraph, if it is
$Z_s$
is generically reduced by the above paragraph, if it is
![]() $S_2$
then it is reduced everywhere and so
$S_2$
then it is reduced everywhere and so
![]() $\varphi _s$
is an isomorphism.
$\varphi _s$
is an isomorphism.
Another sufficient condition for commutativity is the following one (compare with [Reference Bergqvist7, Theorem 4.1.5]).
Proposition 5.11. Notations as in (5.2). Assume that S is regular, and that at a closed point
![]() $z\in \mathcal {X}$
the
$z\in \mathcal {X}$
the
![]() $1$
-foliation
$1$
-foliation
![]() $\mathcal {F}$
has at worst multiplicative singularities. If
$\mathcal {F}$
has at worst multiplicative singularities. If
![]() $s=f(z)$
, then
$s=f(z)$
, then
![]() $g\colon Z\to S$
is flat at
$g\colon Z\to S$
is flat at
![]() $q(z)$
and
$q(z)$
and
![]() $\varphi _s$
is an isomorphism at
$\varphi _s$
is an isomorphism at
![]() $z\in \mathcal {X}_s/\mathcal {F}_s$
.
$z\in \mathcal {X}_s/\mathcal {F}_s$
.
Proof. This can be checked at the completion of
![]() $\mathcal {X}$
at z. So we may assume that
$\mathcal {X}$
at z. So we may assume that
![]() $\mathcal {X}=\operatorname {\mathrm {Spec}}(A)$
is local complete and that
$\mathcal {X}=\operatorname {\mathrm {Spec}}(A)$
is local complete and that
![]() $\mathcal {F}$
is generated up to saturation by commuting multiplicative derivations. If
$\mathcal {F}$
is generated up to saturation by commuting multiplicative derivations. If
![]() $D_1,D_2\in \operatorname {\mathrm {Der}}(A)$
commute, then
$D_1,D_2\in \operatorname {\mathrm {Der}}(A)$
commute, then
![]() $D_2$
descends to
$D_2$
descends to
![]() $\operatorname {\mathrm {Der}}(A^{D_1})$
; hence we may assume that
$\operatorname {\mathrm {Der}}(A^{D_1})$
; hence we may assume that
![]() $\mathcal {F}$
is generated up to saturation by a single multiplicative derivation
$\mathcal {F}$
is generated up to saturation by a single multiplicative derivation
![]() $\partial \in \operatorname {\mathrm {Der}}(A)$
defining a
$\partial \in \operatorname {\mathrm {Der}}(A)$
defining a
![]() $\mu _p$
-action on A. Write
$\mu _p$
-action on A. Write
![]() $A=\bigoplus _{i=0}^{p-1} A_i$
where
$A=\bigoplus _{i=0}^{p-1} A_i$
where
![]() $A_i=\{a\in A\mid \partial (a)=ia\}$
; each
$A_i=\{a\in A\mid \partial (a)=ia\}$
; each
![]() $A_i$
is an
$A_i$
is an
![]() $A_0$
-module, and hence an
$A_0$
-module, and hence an
![]() $\mathcal {O}_{S,s}$
-module. Then
$\mathcal {O}_{S,s}$
-module. Then
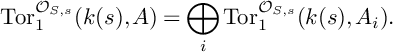 $$ \begin{align*}\operatorname{\mathrm{Tor}}^{\mathcal{O}_{S,s}}_1(k(s),A)=\bigoplus_i \operatorname{\mathrm{Tor}}^{\mathcal{O}_{S,s}}_1(k(s),A_i).\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Tor}}^{\mathcal{O}_{S,s}}_1(k(s),A)=\bigoplus_i \operatorname{\mathrm{Tor}}^{\mathcal{O}_{S,s}}_1(k(s),A_i).\end{align*} $$
By the local criterion for flatness [1, 00MK], we obtain that the flatness of A over
![]() $\mathcal {O}_{S,s}$
implies the flatness of
$\mathcal {O}_{S,s}$
implies the flatness of
![]() $A_0=A^\partial $
over
$A_0=A^\partial $
over
![]() $\mathcal {O}_{S,s}$
.
$\mathcal {O}_{S,s}$
.
To prove that
![]() $\varphi _s$
is an isomorphism at z, by Corollary 5.10 we may assume that
$\varphi _s$
is an isomorphism at z, by Corollary 5.10 we may assume that
![]() $\operatorname {\mathrm {codim}}_{\mathcal {X}_s}(z)\geq 2$
and show that
$\operatorname {\mathrm {codim}}_{\mathcal {X}_s}(z)\geq 2$
and show that
![]() $\operatorname {\mathrm {depth}}_{q(z)}(A_0\otimes k(s))\geq 2$
. (Alternatively, one can use that
$\operatorname {\mathrm {depth}}_{q(z)}(A_0\otimes k(s))\geq 2$
. (Alternatively, one can use that
![]() $A_0$
is a universal geometric quotient, see the proof of [Reference Mumford, Fogarty and Kirwan47, Chapter 1, §2, Theorem 1.1].) Since
$A_0$
is a universal geometric quotient, see the proof of [Reference Mumford, Fogarty and Kirwan47, Chapter 1, §2, Theorem 1.1].) Since
![]() $\mathcal {O}_{S,s}$
is regular and
$\mathcal {O}_{S,s}$
is regular and
![]() $A_0$
is flat over it, it is equivalent to show that
$A_0$
is flat over it, it is equivalent to show that
![]() $\operatorname {\mathrm {depth}}_{q(z)}(A_0)\geq 2+\dim f$
. But
$\operatorname {\mathrm {depth}}_{q(z)}(A_0)\geq 2+\dim f$
. But
![]() $A\otimes k(s)$
is normal, so
$A\otimes k(s)$
is normal, so
![]() $\operatorname {\mathrm {depth}}_z(A)\geq 2+\dim f$
by flatness. By (the proof of) Theorem 4.3 it follows that
$\operatorname {\mathrm {depth}}_z(A)\geq 2+\dim f$
by flatness. By (the proof of) Theorem 4.3 it follows that
![]() $A_0$
has the desired property.
$A_0$
has the desired property.
To conclude, we give some examples of (non-)commutativity.
Example 5.12. Assume that S is a regular curve with generic point
![]() $\eta $
, that
$\eta $
, that
![]() $\mathcal {X}\to S$
is smooth, and let
$\mathcal {X}\to S$
is smooth, and let
![]() $\mathcal {F}\subsetneq T_{\mathcal {X}/S}$
be a family of
$\mathcal {F}\subsetneq T_{\mathcal {X}/S}$
be a family of
![]() $1$
-foliations of corank
$1$
-foliations of corank
![]() $1$
. If
$1$
. If
![]() $\mathcal {Q}_\eta $
is
$\mathcal {Q}_\eta $
is
![]() $S_2$
(equivalently a line bundle by [Reference Hartshorne19, Proposition 1.9]), then
$S_2$
(equivalently a line bundle by [Reference Hartshorne19, Proposition 1.9]), then
![]() $\varphi _s$
is an isomorphism for every
$\varphi _s$
is an isomorphism for every
![]() $s\in S$
.
$s\in S$
.
Indeed, if s is a closed point then as
![]() $\mathcal {Q}_s$
is
$\mathcal {Q}_s$
is
![]() $S_1$
we see that
$S_1$
we see that
![]() $\mathcal {Q}$
is
$\mathcal {Q}$
is
![]() $S_2$
along
$S_2$
along
![]() $\mathcal {X}_s$
. Therefore
$\mathcal {X}_s$
. Therefore
![]() $\mathcal {Q}$
is an
$\mathcal {Q}$
is an
![]() $S_2$
rank
$S_2$
rank
![]() $1$
sheaf on
$1$
sheaf on
![]() $\mathcal {X}$
. As
$\mathcal {X}$
. As
![]() $\mathcal {X}$
is regular we deduce that
$\mathcal {X}$
is regular we deduce that
![]() $\mathcal {Q}$
is in fact a line bundle and we apply Proposition 5.9.
$\mathcal {Q}$
is in fact a line bundle and we apply Proposition 5.9.
Example 5.13 (Quotients of
 $\mathbb {P}^2$
)
$\mathbb {P}^2$
)
Fix an excellent DVR R over k, with fraction field K. Let
![]() $\mathcal {F}\subset T_{\mathbb {P}^2_R/R}$
be the
$\mathcal {F}\subset T_{\mathbb {P}^2_R/R}$
be the
![]() $1$
-foliation generated by
$1$
-foliation generated by
![]() $\partial =fx\partial _x+gy\partial _y\in T_{\mathbb {A}^2_{x,y}/k}$
where
$\partial =fx\partial _x+gy\partial _y\in T_{\mathbb {A}^2_{x,y}/k}$
where
![]() $f,g\in R^\times $
have distinct images in the residue field of R. Then
$f,g\in R^\times $
have distinct images in the residue field of R. Then
![]() $\partial $
is multiplicative. I claim that
$\partial $
is multiplicative. I claim that
![]() $\mathcal {F}$
is lc everywhere. Indeed, cover
$\mathcal {F}$
is lc everywhere. Indeed, cover
![]() $\mathbb {P}^2_R$
with the three open sets
$\mathbb {P}^2_R$
with the three open sets
One has
Using these transformation rules and Proposition 3.6, one sees that
![]() $\mathcal {F}$
is lc everywhere. Combining Theorem 4.10 and Proposition 5.11, we get that
$\mathcal {F}$
is lc everywhere. Combining Theorem 4.10 and Proposition 5.11, we get that
![]() $\mathbb {P}^2_R/\mathcal {F}\to \operatorname {\mathrm {Spec}}(R)$
is a locally stable family (in the sense of [Reference Kollár31, §2.1]) with normal special fiber.
$\mathbb {P}^2_R/\mathcal {F}\to \operatorname {\mathrm {Spec}}(R)$
is a locally stable family (in the sense of [Reference Kollár31, §2.1]) with normal special fiber.
Example 5.14 (Quotients of
 $\mathbb {P}^2$
, continued)
$\mathbb {P}^2$
, continued)
In the notations of the previous example, consider on
![]() $\mathbb {A}^2_{x,y}$
the p-closed derivation
$\mathbb {A}^2_{x,y}$
the p-closed derivation
which on
![]() $\mathbb {A}^2_{u,v}$
becomes
$\mathbb {A}^2_{u,v}$
becomes
Hence this is a multiplicative derivation, which generates an lc
![]() $1$
-foliation
$1$
-foliation
![]() $\mathcal {F}\subset T_{\mathbb {P}^2_R/R}$
. Thus, as above,
$\mathcal {F}\subset T_{\mathbb {P}^2_R/R}$
. Thus, as above,
![]() $\mathcal {S}=\mathbb {P}^2/\mathcal {F}\to \operatorname {\mathrm {Spec}}(R)$
is a locally stable family with normal central fiber.
$\mathcal {S}=\mathbb {P}^2/\mathcal {F}\to \operatorname {\mathrm {Spec}}(R)$
is a locally stable family with normal central fiber.
Both fibers of
![]() $\mathcal {S}\to \operatorname {\mathrm {Spec}}(R)$
are klt surfaces of Picard rank
$\mathcal {S}\to \operatorname {\mathrm {Spec}}(R)$
are klt surfaces of Picard rank
![]() $1$
. As
$1$
. As
![]() $K_{\mathcal {F}}\cong \mathcal {O}(np-1)$
, by Proposition 2.41 we see that
$K_{\mathcal {F}}\cong \mathcal {O}(np-1)$
, by Proposition 2.41 we see that
![]() $\mathcal {S}$
is canonically polarized when
$\mathcal {S}$
is canonically polarized when
![]() $p\geq 3$
(if
$p\geq 3$
(if
![]() $p=2$
we can also get a del Pezzo or a Calabi–Yau surface). Notice that by [Reference Hirokado21, Example 3.6], if
$p=2$
we can also get a del Pezzo or a Calabi–Yau surface). Notice that by [Reference Hirokado21, Example 3.6], if
![]() $p\geq 3$
then for most choices of
$p\geq 3$
then for most choices of
![]() $\lambda $
and n, the minimal resolution of either fibers of
$\lambda $
and n, the minimal resolution of either fibers of
![]() $\mathcal {S}$
has a non-zero non-closed global
$\mathcal {S}$
has a non-zero non-closed global
![]() $1$
-form.
$1$
-form.
Example 5.15. Assume that
![]() $\varphi _s$
is an isomorphism: then
$\varphi _s$
is an isomorphism: then
![]() $\mathcal {Q}_s$
need not be free or even Cohen–Macaulay (which amounts to the same if
$\mathcal {Q}_s$
need not be free or even Cohen–Macaulay (which amounts to the same if
![]() $\mathcal {X}_s$
is regular). Indeed, consider the constant family
$\mathcal {X}_s$
is regular). Indeed, consider the constant family
![]() $\mathbb {A}^3_{x,y,t}\to \mathbb {A}^1_t$
over a field of characteristic
$\mathbb {A}^3_{x,y,t}\to \mathbb {A}^1_t$
over a field of characteristic
![]() $2$
, and the derivation
$2$
, and the derivation
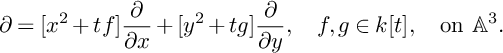 $$ \begin{align*}\partial=[x^2+tf]\frac{\partial}{\partial x}+[y^2+tg] \frac{\partial}{\partial y},\quad f,g\in k[t],\quad \text{on }\mathbb{A}^3.\end{align*} $$
$$ \begin{align*}\partial=[x^2+tf]\frac{\partial}{\partial x}+[y^2+tg] \frac{\partial}{\partial y},\quad f,g\in k[t],\quad \text{on }\mathbb{A}^3.\end{align*} $$
Then
![]() $\partial \in T_{\mathbb {A}^3/\mathbb {A}^1}$
generates a family of
$\partial \in T_{\mathbb {A}^3/\mathbb {A}^1}$
generates a family of
![]() $1$
-foliations, say
$1$
-foliations, say
![]() $\mathcal {F}$
. Let
$\mathcal {F}$
. Let
![]() $\partial _0$
be the restriction of the derivation
$\partial _0$
be the restriction of the derivation
![]() $\partial $
to the fiber
$\partial $
to the fiber
![]() $t=0$
.
$t=0$
.
-
• The quotient
 $T_{\mathbb {A}^2_{x,y}}/\mathcal {F}_0$
is given by which is torsion-free but not free (and hence not Cohen–Macaulay) at the origin.
$T_{\mathbb {A}^2_{x,y}}/\mathcal {F}_0$
is given by which is torsion-free but not free (and hence not Cohen–Macaulay) at the origin. $$ \begin{align*}\frac{k[x,y]\frac{\partial}{\partial x}\oplus k[x,y]\frac{\partial}{\partial y}}{x^2\frac{\partial}{\partial x}+y^2\frac{\partial}{\partial y}},\end{align*} $$
$$ \begin{align*}\frac{k[x,y]\frac{\partial}{\partial x}\oplus k[x,y]\frac{\partial}{\partial y}}{x^2\frac{\partial}{\partial x}+y^2\frac{\partial}{\partial y}},\end{align*} $$
-
• However, I claim that the fiber of
 $k[x,y,z]^\partial $
over
$k[x,y,z]^\partial $
over
 $t=0$
is equal to
$t=0$
is equal to
 $k[x,y]^{\partial _0}$
. We have computed in Example 2.33 the subring of constants of the derivation
$k[x,y]^{\partial _0}$
. We have computed in Example 2.33 the subring of constants of the derivation
 $\partial _0$
: it is given by
$\partial _0$
: it is given by
 $k[x^2,y^2,xy^2-x^2y]$
. Thus it suffices to find
$k[x^2,y^2,xy^2-x^2y]$
. Thus it suffices to find
 $h\in k[x,y,t]$
such that
$h\in k[x,y,t]$
such that
 $xy^2-x^2y+th\in k[x,y,t]^\partial $
. One checks that
$xy^2-x^2y+th\in k[x,y,t]^\partial $
. One checks that
 $h=gx+fy$
does the job.
$h=gx+fy$
does the job.
Example 5.16. Consider the family of
![]() $1$
-foliations
$1$
-foliations
![]() $\mathcal {F}$
on
$\mathcal {F}$
on
![]() $\mathcal {X}=\mathbb {A}^4_{x,y,z,t}\to \mathbb {A}^1_t$
generated by the additive derivation
$\mathcal {X}=\mathbb {A}^4_{x,y,z,t}\to \mathbb {A}^1_t$
generated by the additive derivation
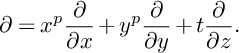 $$ \begin{align*}\partial= x^p\frac{\partial}{\partial x}+y^p\frac{\partial}{\partial y}+t\frac{\partial}{\partial z}.\end{align*} $$
$$ \begin{align*}\partial= x^p\frac{\partial}{\partial x}+y^p\frac{\partial}{\partial y}+t\frac{\partial}{\partial z}.\end{align*} $$
Then
![]() $z\in k[x,y,z]$
is a constant for
$z\in k[x,y,z]$
is a constant for
![]() $\partial _0$
, so it belongs to
$\partial _0$
, so it belongs to
![]() $\mathcal {O}_{\mathcal {X}_0/\mathcal {F}_0}$
. Say that
$\mathcal {O}_{\mathcal {X}_0/\mathcal {F}_0}$
. Say that
![]() $f\in k[x,y,z,t]$
satisfies
$f\in k[x,y,z,t]$
satisfies
![]() $\partial (z+tf)=0$
. Then it follows that
$\partial (z+tf)=0$
. Then it follows that
where
![]() $f_x,f_y,f_z$
are the partial derivatives of f. But this cannot hold in a neighborhood of sub-scheme defined by the ideal
$f_x,f_y,f_z$
are the partial derivatives of f. But this cannot hold in a neighborhood of sub-scheme defined by the ideal
![]() $(x,y,t)$
. Thus
$(x,y,t)$
. Thus
![]() $\varphi _0\colon \mathcal {X}_0/\mathcal {F}_0\to (\mathcal {X}/\mathcal {F})_0$
is not an isomorphism along the image of the line
$\varphi _0\colon \mathcal {X}_0/\mathcal {F}_0\to (\mathcal {X}/\mathcal {F})_0$
is not an isomorphism along the image of the line
![]() $(x=y=0)$
. Observe however that it is an isomorphism everywhere else.
$(x=y=0)$
. Observe however that it is an isomorphism everywhere else.
While
![]() $\mathcal {X}/\mathcal {F}=Y\to \mathbb {A}^1$
is smooth over the complement of the origin, the singularities along the central fiber are quite complicated. In fact, I claim that
$\mathcal {X}/\mathcal {F}=Y\to \mathbb {A}^1$
is smooth over the complement of the origin, the singularities along the central fiber are quite complicated. In fact, I claim that
![]() $Y\to S$
is not a locally stable family over
$Y\to S$
is not a locally stable family over
![]() $0\in \mathbb {A}^1$
—by which I mean that
$0\in \mathbb {A}^1$
—by which I mean that
![]() $(Y,Y_0)$
is not lc—if
$(Y,Y_0)$
is not lc—if
![]() $p>2$
. Assume it is. Then for
$p>2$
. Assume it is. Then for
![]() $n>1$
not divisible by p, the base-change of
$n>1$
not divisible by p, the base-change of
![]() $Y\to \mathbb {A}^1_t$
along
$Y\to \mathbb {A}^1_t$
along
![]() $\mathbb {A}^1_u\to \mathbb {A}^1_t, t=u^n$
, is again locally stable over
$\mathbb {A}^1_u\to \mathbb {A}^1_t, t=u^n$
, is again locally stable over
![]() $0\in \mathbb {A}^1_u$
[Reference Kollár31, 2.16.5]. Let us call it
$0\in \mathbb {A}^1_u$
[Reference Kollár31, 2.16.5]. Let us call it
![]() $Y'\to \mathbb {A}^1_u$
. Since
$Y'\to \mathbb {A}^1_u$
. Since
![]() $\mathbb {A}^1_u\to \mathbb {A}^1_t$
is flat, we can compute
$\mathbb {A}^1_u\to \mathbb {A}^1_t$
is flat, we can compute
![]() $Y'$
as the quotient of
$Y'$
as the quotient of
![]() $\mathcal {X}'=\mathbb {A}^4_{x,y,z,u}$
by the
$\mathcal {X}'=\mathbb {A}^4_{x,y,z,u}$
by the
![]() $1$
-foliation
$1$
-foliation
![]() $\mathcal {F}'$
generated by
$\mathcal {F}'$
generated by
 $$ \begin{align*}\partial'= x^p\frac{\partial}{\partial x}+y^p\frac{\partial}{\partial y}+u^n\frac{\partial}{\partial z}\end{align*} $$
$$ \begin{align*}\partial'= x^p\frac{\partial}{\partial x}+y^p\frac{\partial}{\partial y}+u^n\frac{\partial}{\partial z}\end{align*} $$
(cf the proof of Lemma 2.35). Now let
![]() $\mu \colon W\to \mathcal {X}'$
be the blow-up of the ideal
$\mu \colon W\to \mathcal {X}'$
be the blow-up of the ideal
![]() $(x,y,z,u)$
, and consider the induced commutative diagram
$(x,y,z,u)$
, and consider the induced commutative diagram
Then a local computation shows that the
![]() $\mu $
-exceptional divisor E is
$\mu $
-exceptional divisor E is
![]() $\mathcal {F}'$
-invariant, and that
$\mathcal {F}'$
-invariant, and that
If
![]() $F=q(E)$
, then (4.4) shows that
$F=q(E)$
, then (4.4) shows that
This is smaller than
![]() $-1$
as soon as
$-1$
as soon as
![]() $p,n>2$
, but contradicts the log canonicity of
$p,n>2$
, but contradicts the log canonicity of
![]() $(Y',Y^{\prime }_0)$
.
$(Y',Y^{\prime }_0)$
.
Acknowledgements
I am grateful to Fabio Bernasconi, to Yuya Matsumoto and to the referee for many helpful comments. I would also like to thank Zsolt Patakfalvi, who introduced me to the topic of foliations in positive characteristic. The author is supported by the grant Postdoc Mobility
![]() $\sharp $
P500PT/210980 of the Swiss National Science Foundation, and is thankful to Stefan Schröer’s group at the Heinrich-Heine-Universität of Düsseldorf for hosting him.
$\sharp $
P500PT/210980 of the Swiss National Science Foundation, and is thankful to Stefan Schröer’s group at the Heinrich-Heine-Universität of Düsseldorf for hosting him.