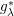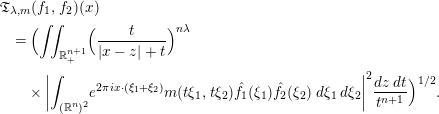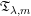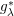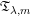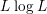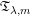1 Introduction
1.1 Background
It is well known that the 
$N$-linear 
$(N\geqslant 1)$ Fourier multiplier operator 
$T_{m}$ is defined as follows:
$$\begin{eqnarray}T_{m}(f_{1},\ldots ,f_{N})(x)=\frac{1}{(2\unicode[STIX]{x1D70B})^{nN}}\int _{(\mathbb{R}^{n})^{N}}e^{ix\cdot (\unicode[STIX]{x1D709}_{1}+\cdots +\unicode[STIX]{x1D709}_{N})}m(\unicode[STIX]{x1D709})\widehat{f_{1}}(\unicode[STIX]{x1D709}_{1})\cdots \widehat{f_{N}}(\unicode[STIX]{x1D709}_{N})\,d\unicode[STIX]{x1D709},\end{eqnarray}$$ for 
$m\in L^{\infty }(\mathbb{R}^{N})$ and 
$f_{1},\ldots ,f_{N}\in {\mathcal{S}}$, where 
$x\in \mathbb{R}^{n},\unicode[STIX]{x1D709}=(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{m})\in (\mathbb{R}^{n})^{N}.$ By using paraproducts, Coifman and Meyer [Reference Coifman and Meyer8] proved that if 
$m$ is a bounded function on 
$\mathbb{R}^{nN}\backslash \{0\}$ and it satisfies that
$$\begin{eqnarray}|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}_{1}}^{\unicode[STIX]{x1D6FC}_{1}}\cdots \unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}_{N}}^{\unicode[STIX]{x1D6FC}_{N}}m(\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{N})|\leqslant C_{\unicode[STIX]{x1D6FC}}(|\unicode[STIX]{x1D709}_{1}|+\cdots +|\unicode[STIX]{x1D709}_{m}|)^{-(|\unicode[STIX]{x1D6FC}_{1}|+\cdots +|\unicode[STIX]{x1D6FC}_{N}|)},\end{eqnarray}$$ away from the origin for 
$|\unicode[STIX]{x1D6FC}_{1}|+\cdots +|\unicode[STIX]{x1D6FC}_{N}|\leqslant L$ with 
$L$ sufficiently large, then 
$T_{m}$ is bounded from 
$L^{p_{1}}(\mathbb{R}^{n})\times \cdots \times L^{p_{N}}(\mathbb{R}^{n})$ to 
$L^{p}(\mathbb{R}^{n})$. By decreasing the smoothness condition of 
$T_{m}$ in [Reference Coifman and Meyer8], Tomita [Reference Tomita25] gave a Hörmander type theorem for 
$T_{m}$. Later on, Fujita and Tomita [Reference Fujita and Tomita14] demonstrated a weighted version of the results in [Reference Tomita25] for 
$T_{m}$ under the Hörmander condition with classical 
$A_{p}$ weights. In 2013, Bui and Duong [Reference Bui and Duong2] established the norm inequality for a class of Calderón–Zygmund singular integral operators with kernels satisfying some mild regularity condition. As an application, they [Reference Bui and Duong2] obtained the multiple weighted norm inequality of multilinear Fourier multipliers. For more works about multilinear Fourier multipliers, we refer the reader to [Reference Grafakos and Si15, Reference Li and Sun20, Reference Li, Xue and Yabuta21]. Recently, Si, Xue and Yabuta [Reference Zengyan, Xue and Yabuta28] considered the bilinear square-function Fourier multiplier operator defined as follows,
$$\begin{eqnarray}\displaystyle \mathfrak{T}_{m}(f_{1},f_{2})(x)=\Big(\int _{0}^{\infty }|T_{m}^{t}(f_{1},f_{2})(x)|^{2}\frac{dt}{t}\Big)^{1/2}, & & \displaystyle \nonumber\end{eqnarray}$$where
$$\begin{eqnarray}T_{m}^{t}(f_{1},f_{2})(x)=\int _{(\mathbb{R}^{n})^{2}}e^{2\unicode[STIX]{x1D70B}ix\cdot (\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2})}m(t\unicode[STIX]{x1D709}_{1},t\unicode[STIX]{x1D709}_{2})\hat{f}_{1}(\unicode[STIX]{x1D709}_{1})\hat{f}_{2}(\unicode[STIX]{x1D709}_{2})\,d\unicode[STIX]{x1D709}_{1}\,d\unicode[STIX]{x1D709}_{2}.\end{eqnarray}$$ By studying a class of multilinear square functions, the authors in [Reference Zengyan, Xue and Yabuta28] demonstrated the multiple weighted norm inequality for 
$\mathfrak{T}_{m}$ and obtained some weighted estimates for the commutators of 
$\mathfrak{T}_{m}$ with 
$BMO$ functions.
Remark 1.1. Note that if 
$t=1$, then 
$T_{m}^{1}$ coincides with the well-known bilinear Fourier multiplier operator defined and studied in [Reference Coifman and Meyer8]. The operator studied in [Reference Zengyan, Xue and Yabuta28] can be looked as a vector valued or square version of bilinear Fourier multiplier operator 
$T_{m}^{1}$.
In this paper, we investigate the boundedness of the following bilinear square-function Fourier multiplier operator 
$\mathfrak{T}_{\unicode[STIX]{x1D706},m}$, which is associated with the multilinear 
$g_{\unicode[STIX]{x1D706}}^{\ast }$-function defined in [Reference Shi, Xue and Yabuta23].
$$\begin{eqnarray}\mathfrak{T}_{\unicode[STIX]{x1D706},m}(f_{1},f_{2})(x)=\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{t}{|x-z|+t}\Big)^{n\unicode[STIX]{x1D706}}\Big|T_{m}^{t}(f_{1},f_{2})(x)|^{2}\frac{dt}{t}\Big|^{2}\frac{dz\,dt}{t^{n+1}}\Big)^{1/2}.\end{eqnarray}$$ Let 
$\vec{f}=(f_{1},f_{2})$ and 
$K_{t}(x,y_{1},y_{2})=\frac{1}{t^{2n}}\check{m}\big(\frac{x-y_{1}}{t},\frac{x-y_{2}}{t}\big)$. Then, 
$\mathfrak{T}_{\unicode[STIX]{x1D706},m}$ can be written as
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathfrak{T}_{\unicode[STIX]{x1D706},m}(\vec{f})(x)=\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{t}{|x-z|+t}\Big)^{n\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\Big|\int _{(\mathbb{R}^{n})^{2}}K_{t}(x,y_{1},y_{2})f_{1}(y_{1})f_{2}(y_{2})\,dy_{1}\,dy_{2}\Big|^{2}\frac{dz\,dt}{t^{n+1}}\Big)^{1/2}.\nonumber\end{eqnarray}$$ The commutator of 
$\mathfrak{T}_{\unicode[STIX]{x1D706},m}$ is defined by
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathfrak{T}_{\unicode[STIX]{x1D706},m}^{\vec{b}}(\vec{f})(x)=\mathop{\sum }_{i=1}^{2}\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{t}{|x-z|+t}\Big)^{n\unicode[STIX]{x1D706}}\Big|\int _{(\mathbb{R}^{n})^{2}}(b_{i}(x)-b_{i}(y))\nonumber\\ \displaystyle & & \displaystyle \quad \times \,K_{t}(x,y_{1},y_{2})f_{1}(y_{1})f_{2}(y_{2})\,dy_{1}\,dy_{2}\Big|^{2}\frac{dz\,dt}{t^{n+1}}\Big)^{1/2},\quad \vec{b}=(b_{1},b_{2}).\nonumber\end{eqnarray}$$Remark 1.2. In [Reference Shi, Xue and Yabuta23], the authors studied a class of multilinear 
$g_{\unicode[STIX]{x1D706}}^{\ast }$ function associated with convolution type kernels. The endpoint 
$L^{1}\times \cdots \times L^{1}\rightarrow L^{1/m,\infty }$ boundedness, and multiple weighted boundedness for the multilinear 
$g_{\unicode[STIX]{x1D706}}^{\ast }$ function were established. Later, in [Reference Xue and Yan27] the same results were extended to kernels of nonconvolution type. For more previous nice works of the classical 
$g_{\unicode[STIX]{x1D706}}^{\ast }$ function, one may see the famous works of Stein [Reference Stein24], Fefferman [Reference Fefferman13], Muckenhoupt and Wheeden [Reference Muckenhoupt and Wheeden22].
Our object of investigation in this paper is the multilinear square-function Fourier multiplier operator associated with the multilinear 
$g_{\unicode[STIX]{x1D706}}^{\ast }$ function. Before stating our main results, we need to introduce some more notations and definitions. For 
$m$ exponents 
$p_{1},\ldots ,p_{m}$, denote by 
$p$ the number given by 
$1/p=1/p_{1}+\cdots +1/p_{m}$, and 
$\vec{P}$ for the vector 
$\vec{P}=(p_{1},\ldots ,p_{m})$. For any real number 
$r>1$, the vector 
$\vec{P}/r$ is given by 
$\vec{P}/r=(p_{1}/r,\ldots ,p_{m}/r).$ The following multiple weights classes 
$A_{\vec{P}}$ were introduced and studied by Lerner et al. [Reference Lerner, Ombrosi, Pérez, Torres and Trujillo-González19].
Definition 1.3. (Multiple weights [Reference Lerner, Ombrosi, Pérez, Torres and Trujillo-González19].) Let 
$1\leqslant p_{1},\ldots ,p_{m}<\infty ,1/p=1/p_{1}+\cdots +1/p_{m}.$ Given 
$\vec{\unicode[STIX]{x1D714}}=(\unicode[STIX]{x1D714}_{1},\ldots ,\unicode[STIX]{x1D714}_{m})$, set 
$\unicode[STIX]{x1D708}_{\vec{\unicode[STIX]{x1D714}}}=\prod _{i=1}^{m}\unicode[STIX]{x1D714}_{i}^{p/p_{i}}.$ We say that 
$\vec{\unicode[STIX]{x1D714}}$ satisfies the 
$A_{\vec{P}}$ condition if
$$\begin{eqnarray}\sup _{Q}\Big(\frac{1}{|Q|}\int _{Q}\mathop{\prod }_{i=1}^{m}\unicode[STIX]{x1D714}_{i}^{p/p_{i}}\Big)^{1/p}\mathop{\prod }_{i=1}^{m}\Big(\frac{1}{|Q|}\int _{Q}\unicode[STIX]{x1D714}_{i}^{1-p_{i}^{\prime }}\Big)^{1/p_{i}^{\prime }}<\infty ,\end{eqnarray}$$ when 
$p_{i}=1,((1/|Q|)\int _{Q}\unicode[STIX]{x1D714}_{i}^{1-p_{i}^{\prime }})^{1/p_{i}^{\prime }}$ is understood as 
$(\inf _{Q}\unicode[STIX]{x1D714}_{i})^{-1}.$
Throughout this paper, we always assume that 
$m\in L^{\infty }((\mathbb{R}^{n})^{2})$ and satisfies the conditions
$$\begin{eqnarray}|\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FC}}m(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})|\lesssim \frac{(|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|)^{-|\unicode[STIX]{x1D6FC}|+\unicode[STIX]{x1D700}_{1}}}{(1+|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|)^{\unicode[STIX]{x1D700}_{1}+\unicode[STIX]{x1D700}_{2}}}\end{eqnarray}$$and
$$\begin{eqnarray}|m(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})|\lesssim \frac{(|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|)^{-s+\unicode[STIX]{x1D700}_{1}}}{(1+|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|)^{\unicode[STIX]{x1D700}_{1}+\unicode[STIX]{x1D700}_{2}}}\end{eqnarray}$$ for some 
$\unicode[STIX]{x1D700}_{1},\unicode[STIX]{x1D700}_{2}>0$, 
$|\unicode[STIX]{x1D6FC}|\leqslant s$ and 
$n+1\leqslant s\leqslant 2n$ for some integer 
$s.$
Remark 1.4. Note that, for the same 
$\unicode[STIX]{x1D700}_{1},\unicode[STIX]{x1D700}_{2}$, 
$\unicode[STIX]{x1D6FC}$ and 
$s$, conditions (1.1) and (1.2) are more weaker than the following condition:
$$\begin{eqnarray}|\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FC}}m(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})|\lesssim \left\{\begin{array}{@{}l@{}}\displaystyle (|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|)^{-s-|\unicode[STIX]{x1D6FC}|-\unicode[STIX]{x1D700}_{2}},\quad ~|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|>1;\\ \displaystyle (|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|)^{-|\unicode[STIX]{x1D6FC}|+\unicode[STIX]{x1D700}_{1}},\quad ~0<|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|\leqslant 1.\end{array}\right.\end{eqnarray}$$ Moreover, for 
$|\unicode[STIX]{x1D6FC}|\leqslant s$, condition (1.3) is equivalent with
$$\begin{eqnarray}|\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FC}}m(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})|\lesssim \left\{\begin{array}{@{}l@{}}\displaystyle \frac{(|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|)^{-|\unicode[STIX]{x1D6FC}|+\unicode[STIX]{x1D700}_{1}}}{(1+|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|)^{s+\unicode[STIX]{x1D700}_{1}+\unicode[STIX]{x1D700}_{2}}},\quad ~|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|>1;\\[2.0pt] \displaystyle \frac{(|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|)^{-|\unicode[STIX]{x1D6FC}|+\unicode[STIX]{x1D700}_{1}}}{(1+|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|)^{s+\unicode[STIX]{x1D700}_{1}+\unicode[STIX]{x1D700}_{2}}},\quad ~0<|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|\leqslant 1.\end{array}\right.\end{eqnarray}$$These facts show that conditions (1.1) and (1.2) are still more weaker than (1.4), which, in turn, also indicates that our conditions (1.1) and (1.2) are reasonable.
The main results of this paper are:
Theorem 1.1. Let 
$s$ be an integer with 
$s\in [n+1,2n]$ and 
$\unicode[STIX]{x1D706}>2s/n+1$, 
$p_{0}$ be a number satisfying 
$2n/s\leqslant p_{0}\leqslant 2$. Let 
$p_{0}\leqslant p_{1},p_{2}<\infty$, 
$1/p=1/p_{1}+1/p_{2}$, and 
$\vec{\unicode[STIX]{x1D714}}\in A_{\vec{P}/p_{0}}$. Suppose that 
$m\in L^{\infty }((\mathbb{R}^{n})^{2})$ satisfies (1.1) and (1.2) and that the bilinear square Fourier multiplier operator 
$\mathfrak{T}_{\unicode[STIX]{x1D706},m}$ is bounded from 
$L^{q_{1}}\times L^{q_{2}}$ into 
$L^{q,\infty }$, for any 
$p_{0}<q_{1},q_{2}$ and 
$1/q=1/q_{1}+1/q_{2}$. Then the following weighted estimates hold.
(i) If
$p_{1},p_{2}>p_{0}$, then $||\mathfrak{T}_{\unicode[STIX]{x1D706},m}(\vec{f})||_{L^{p}(\unicode[STIX]{x1D708}_{\vec{\unicode[STIX]{x1D714}}})}\leqslant C||f_{1}||_{L^{p_{1}}(\unicode[STIX]{x1D714}_{1})}||f_{2}||_{L^{p_{2}}(\unicode[STIX]{x1D714}_{2})}$.(ii) If
$p_{0}>2n/s$ and $p_{1}=p_{0}$ or $p_{2}=p_{0}$, then $$\begin{eqnarray}||\mathfrak{T}_{\unicode[STIX]{x1D706},m}(\vec{f})||_{L^{p,\infty }(\unicode[STIX]{x1D708}_{\vec{\unicode[STIX]{x1D714}}})}\leqslant C||f_{1}||_{L^{p_{1}}(\unicode[STIX]{x1D714}_{1})}||f_{2}||_{L^{p_{2}}(\unicode[STIX]{x1D714}_{2})}.\end{eqnarray}$$
Theorem 1.2. Let 
$s$, 
$\unicode[STIX]{x1D706}$, 
$p_{0},p_{1},p_{2},p$, 
$\vec{\unicode[STIX]{x1D714}}$, 
$m$ and 
$\mathfrak{T}_{\unicode[STIX]{x1D706},m}$ be the same as in Theorem 1.1. Then the following weighted estimates hold for the commutators of 
$\mathfrak{T}_{\unicode[STIX]{x1D706},m}(\vec{f})$.
(i) If
$p_{1},p_{2}>p_{0}$, then for any $\vec{b}\in BMO^{2}$, it holds that where$$\begin{eqnarray}||\mathfrak{T}_{\unicode[STIX]{x1D706},m}^{\vec{b}}(\vec{f})||_{L^{p}(\unicode[STIX]{x1D708}_{\vec{\unicode[STIX]{x1D714}}})}\leqslant C||\vec{b}||_{BMO}||f_{1}||_{L^{p_{1}}(\unicode[STIX]{x1D714}_{1})}||f_{2}||_{L^{p_{2}}(\unicode[STIX]{x1D714}_{2})},\end{eqnarray}$$$||\vec{b}||_{BMO}=\max _{j}||b_{j}||_{BMO}$.(ii) Let
$\vec{\unicode[STIX]{x1D714}}\in A_{(1,1)}$ and $\vec{b}\in BMO^{2}.$ Then, there exists a constant $C$ (depending on $\vec{b}$) such that where$$\begin{eqnarray}\unicode[STIX]{x1D708}_{\vec{\unicode[STIX]{x1D714}}}\big(\big\{x\in \mathbb{R}^{n}:|\mathfrak{T}_{\unicode[STIX]{x1D706},m}^{\vec{b}}(\vec{f})(x)|>t^{2}\big\}\big)\leqslant C\mathop{\prod }_{j=1}^{2}\Big(\int _{\mathbb{R}^{n}}\unicode[STIX]{x1D6F7}\Big(\frac{|f_{j}(x)|}{t}\Big)\unicode[STIX]{x1D714}_{j}(x)\Big)^{1/2},\end{eqnarray}$$$\unicode[STIX]{x1D6F7}(t)=t^{p_{0}}(1+\log ^{+}t)^{p_{0}}$, and the function $\log ^{+}t$ is defined by $\log ^{+}t=\log t$, if $t>1$, otherwise $\log ^{+}t=0$.
The article is organized as follows. Proof of Theorems 1.1 and 1.2 will be shown in Section 2. In Section 3, we give an example to show that the assumption that 
$\mathfrak{T}_{\unicode[STIX]{x1D706},m}$ is bounded from 
$L^{q_{1}}\times L^{q_{2}}$ into 
$L^{q,\infty }$ in Theorems 1.1 and 1.2 is reasonable.
2 Proofs of Theorems 1.1 and 1.2
This section will be devoted to prove Theorems 1.1 and 1.2. The following two propositions provide a foundation for our proofs.
2.1 Two key propositions
Proposition 2.1. Let 
$s\in \mathbb{N}$ satisfy 
$n+1\leqslant s\leqslant 2n$. Suppose 
$m\in L^{\infty }((\mathbb{R}^{n})^{2})$ satisfies (1.1) and (1.2). Then, for any 
$2n/s<p\leqslant 2$, 
$\unicode[STIX]{x1D706}>2s/n+1$, there exist 
$C>0$ and 
$\unicode[STIX]{x1D6FF}>n/p$, such that
$$\begin{eqnarray}\displaystyle & & \displaystyle \Big(\int _{S_{j}(Q)}\int _{S_{k}(Q)}\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{t}{|z|+t}\Big)^{n\unicode[STIX]{x1D706}}\Big|\check{m}\Big(\frac{x-z-y_{1}}{t},\frac{x-z-y_{2}}{t}\Big)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\check{m}\Big(\frac{\bar{x}-y_{1}}{t},\frac{\bar{x}-y_{2}}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C\frac{|x-\bar{x}|^{2(\unicode[STIX]{x1D6FF}-n/p)}}{|Q|^{2\unicode[STIX]{x1D6FF}/n}}2^{-2\unicode[STIX]{x1D6FF}\max (j,k)}\end{eqnarray}$$ for all balls 
$Q$, all 
$x,\bar{x}\in (1/2)Q$ and 
$(j,k)\neq (0,0)$.
Proof. For convenience, we denote the left-hand side of (2.1) by 
$A_{j,k}(m,Q)(x,\bar{x})$. Let 
$u=ax$
$(a>0)$, 
$Q=B(x_{0},R)$, 
$v=az$ and 
$\unicode[STIX]{x1D70F}=at$, we may get
$$\begin{eqnarray}\displaystyle A_{j,k}(m,Q)(x,\bar{x}) & = & \displaystyle a^{1/2-2n/p^{\prime }}\Big(\int _{S_{j}(Q^{a})}\int _{S_{k}(Q^{a})}\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{at}{|v|+at}\Big)^{n\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & & \displaystyle \times \,\Big|\check{m}\Big(\frac{x^{a}-v-u_{1}}{at},~~~\frac{x^{a}-v-u_{2}}{at}\Big)\nonumber\\ \displaystyle & & \displaystyle -\,\check{m}\Big(\frac{\bar{x}^{a}-u_{1}}{at},\frac{\bar{x}^{a}-u_{2}}{at}\Big)\Big|^{2}\frac{dvdt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,du_{1}\,du_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & = & \displaystyle a^{2n/p}\Big(\int _{S_{j}(Q^{a})}\int _{S_{k}(Q^{a})}\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{\unicode[STIX]{x1D70F}}{|v|+\unicode[STIX]{x1D70F}}\Big)^{n\unicode[STIX]{x1D706}}\Big|\nonumber\\ \displaystyle & & \displaystyle \times \,\check{m}\Big(\frac{x^{a}-v-u_{1}}{\unicode[STIX]{x1D70F}},\frac{x^{a}-v-u_{2}}{\unicode[STIX]{x1D70F}}\Big)\nonumber\\ \displaystyle & & \displaystyle -\,\check{m}\Big(\frac{\bar{x}^{a}-u_{1}}{\unicode[STIX]{x1D70F}},\frac{\bar{x}^{a}-u_{2}}{\unicode[STIX]{x1D70F}}\Big)\Big|^{2}\frac{dvd\unicode[STIX]{x1D70F}}{\unicode[STIX]{x1D70F}^{4n+1}}\Big)^{p^{\prime }/2}\,du_{1}\,du_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & = & \displaystyle a^{2n/p}A_{j,k}(m,Q^{a})(x^{a},\bar{x}^{a}),\nonumber\end{eqnarray}$$ where 
$Q^{a}=B(ax_{0},aR)$, 
$x^{a}=ax$ and 
$\bar{x}^{a}=a\bar{x}$. Thus, if we take 
$a=1/(2^{\max (j,k)}R)$, it is easy to see that the following estimate implies the desired one.
$$\begin{eqnarray}\displaystyle A_{j,k}(m,Q^{a})(x^{a},\bar{x}^{a}) & {\lesssim} & \displaystyle \frac{|x^{a}-\bar{x}^{a}|^{2(\unicode[STIX]{x1D6FF}-n/p)}}{|Q^{a}|^{2\unicode[STIX]{x1D6FF}/n}}2^{-2\unicode[STIX]{x1D6FF}\max (j,k)}\nonumber\\ \displaystyle & = & \displaystyle |x^{a}-\bar{x}^{a}|^{2(\unicode[STIX]{x1D6FF}-n/p)}.\end{eqnarray}$$ Since 
$x^{a},\bar{x}^{a}\in (1/2)Q^{a}$, 
$aR=1/2^{\max (j,k)}$. Therefore, in order to prove (2.2), we only need to show (2.1) is true for all balls 
$Q$ with radius 
$R=1/2^{\max (j,k)}$. Without loss of generality, we may assume 
$|h|=|x-\bar{x}|<1/2$ and 
$k\geqslant j$ (hence 
$k\geqslant 1$). Thus, the proof of Proposition 2.1 is reduced to show that
$$\begin{eqnarray}A_{j,k}(m,Q)(x,\bar{x})\lesssim |x-\bar{x}|^{2(\unicode[STIX]{x1D6FF}-n/p)},\end{eqnarray}$$ where 
$Q=B(x_{0},2^{-k})$ and 
$\unicode[STIX]{x1D6FF}>n/p$.
Let 
$\unicode[STIX]{x1D6F9}\in {\mathcal{S}}(\mathbb{R}^{2n})$ satisfying 
$\operatorname{supp}\unicode[STIX]{x1D6F9}\in \{(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}):1/2\leqslant |\unicode[STIX]{x1D709}|+|\unicode[STIX]{x1D702}|\leqslant 2\}$ and
$$\begin{eqnarray}\mathop{\sum }_{j\in \mathbb{Z}}\unicode[STIX]{x1D6F9}(2^{-j}\unicode[STIX]{x1D709},2^{-j}\unicode[STIX]{x1D702})=1,\quad forall(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\in (\mathbb{R}^{2n})\setminus \{0\}.\end{eqnarray}$$Thus, we can write
$$\begin{eqnarray}\displaystyle m(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})=\mathop{\sum }_{j\in \mathbb{Z}}m_{j}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}):=\mathop{\sum }_{j\in \mathbb{Z}}\unicode[STIX]{x1D6F9}(2^{-j}\unicode[STIX]{x1D709},2^{-j}\unicode[STIX]{x1D702})m(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}) & & \displaystyle \nonumber\end{eqnarray}$$ and hence 
$\operatorname{supp}m_{j}\subseteq \{(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702}):2^{j-1}\leqslant |\unicode[STIX]{x1D709}|+|\unicode[STIX]{x1D702}|\leqslant 2^{j+1}\}$.
Using the change of variables, (2.3) is equivalent to that
$$\begin{eqnarray}\displaystyle & & \displaystyle \Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{t}{|z|+t}\Big)^{n\unicode[STIX]{x1D706}}\Big|\check{m}\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\check{m}\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\leqslant C|h|^{2(\unicode[STIX]{x1D6FF}-n/p)},\nonumber\end{eqnarray}$$ for 
$Q=B(x_{0},2^{-k})$, 
$h=x-\bar{x}$ and 
$Q_{\bar{x}}=Q-\bar{x}$. We prove this in the following three cases.
(a) The case
$2n/p<s<2n/p+1$. Since (1.1) and (1.2) remain valid for any smaller positive number than 
$\unicode[STIX]{x1D700}_{1}$, we may take 
$\unicode[STIX]{x1D700}_{1}$ sufficiently close to 
$s-2n/p$ so that 
$0<\unicode[STIX]{x1D700}_{1}<s-2n/p$.
First we introduce 
$A_{\ell }$ and 
$A_{\ell }(I)$ as follows,
$$\begin{eqnarray}\displaystyle A_{\ell } & := & \displaystyle \Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{t}{|z|+t}\Big)^{n\unicode[STIX]{x1D706}}\Big|\check{m}\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)\nonumber\\ \displaystyle & & \displaystyle -\,\check{m}\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }};\nonumber\\ \displaystyle A_{\ell }(I) & := & \displaystyle \Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\!\int _{\mathbb{R}^{n}}\int _{I}\Big(\frac{t}{|z|+t}\Big)^{n\unicode[STIX]{x1D706}}\Big|\check{m}\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)\nonumber\\ \displaystyle & & \displaystyle -\,\check{m}\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }},\nonumber\end{eqnarray}$$ where 
$I$ is any interval in 
$\mathbb{R}_{+}$, in particular, 
$I$ could be right half-infinite.
In addition, we denote
$$\begin{eqnarray}\displaystyle & & \displaystyle E_{1}=\{z\in \mathbb{R}^{n}:|z|<t,|z|<1/8\},\qquad E_{2}=\{z\in \mathbb{R}^{n}:|z|<t,1/8\leqslant |z|<3\},\nonumber\\ \displaystyle & & \displaystyle E_{3}=\{z\in \mathbb{R}^{n}:|z|<t,|z|\geqslant 3\},\qquad E_{4}=\{z\in \mathbb{R}^{n}:|z|\geqslant t,|z|<1/8\},\nonumber\\ \displaystyle & & \displaystyle E_{5}=\{z\in \mathbb{R}^{n}:|z|\geqslant t,1/8\leqslant |z|<3\},\qquad E_{6}=\{z\in \mathbb{R}^{n}:|z|\geqslant t,|z|\geqslant 3\},\nonumber\end{eqnarray}$$ then we have 
$A_{\ell }(I)\leqslant \sum _{i=1}^{6}A_{\ell }^{i}(I)$, where
$$\begin{eqnarray}\displaystyle A_{\ell }^{i}(I) & := & \displaystyle \Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\int _{E_{i}}\int _{I}\Big(\frac{t}{|z|+t}\Big)^{n\unicode[STIX]{x1D706}}\Big|\check{m}\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)\nonumber\\ \displaystyle & & \displaystyle -\,\check{m}\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}.\nonumber\end{eqnarray}$$ Now, we begin with the estimate of 
$A_{\ell }^{1}(I)$.
Estimate for
$A_{\ell }^{1}(I)$. Since 
$Q_{\bar{x}}=B(x_{0}-\bar{x},1/2^{k})$, then 
$2^{-2}\leqslant |y_{1}+h|\leqslant 2$ and 
$|y_{2}+h|\leqslant 2^{j-k+1}$ for all 
$y_{1}\in S_{k}(Q_{\bar{x}})$ and 
$y_{2}\in S_{j}(Q_{\bar{x}})$. Note that 
$|z|<1/8$, we have 
$1/8<|y_{1}+h-z|\leqslant 17/8$. This implies that
$$\begin{eqnarray}\displaystyle & & \displaystyle A_{\ell }^{1}(I)\leqslant \Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\int _{|z|\leqslant \min \{1/8,t\}}\int _{I}\Big|\check{m}\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad -\,\check{m}\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim \Big(\int _{|y_{2}|\leqslant 2^{j-k+2}}\int _{1/8<|y_{1}|\leqslant 17/8}\Big(\int _{|z|\leqslant \min \{1/8,t\}}\int _{I}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\Big|\check{m}\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \Big(\int _{|y_{2}|\leqslant 2^{j-k+2}}\int _{1/8<|y_{1}|\leqslant 17/8}\Big(\int _{I}\Big|\check{m}\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{2}\frac{dt}{t^{4n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}.\nonumber\end{eqnarray}$$ Note that 
$|y_{1}|\sim 1$ in the last integration above, by the Minkowski inequality and the Hausdorff–Young inequality, for 
$|\unicode[STIX]{x1D6FC}|=s$, we have
$$\begin{eqnarray}\displaystyle A_{\ell }^{1}(I) & {\lesssim} & \displaystyle \Big(\int _{|y_{2}|\leqslant 2^{j-k+2}}\int _{1/8<|y_{1}|\leqslant 17/8}\nonumber\\ \displaystyle & & \displaystyle \times \,\Big(\int _{I}|y_{1}^{\unicode[STIX]{x1D6FC}}|^{2}\Big|\check{m}_{\ell }\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{2}\frac{dt}{t^{4n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \Big(\int _{I}\Big(\int _{|y_{2}|\leqslant 2^{j-k+2}}\int _{1/8<|y_{1}|\leqslant 17/8}\nonumber\\ \displaystyle & & \displaystyle \times \,\Big|y_{1}^{\unicode[STIX]{x1D6FC}}\check{m}_{\ell }\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{p^{\prime }}\,dy_{1}\,dy_{2}\Big)^{2/p^{\prime }}\frac{dt}{t^{4n+1}}\Big)^{1/2}\nonumber\\ \displaystyle & = & \displaystyle \Big(\int _{I}\Big(\int _{|ty_{2}|\leqslant 2^{j-k+2}}\int _{1/8<|ty_{1}|\leqslant 17/8}\nonumber\\ \displaystyle & & \displaystyle \times \,|y_{1}^{\unicode[STIX]{x1D6FC}}\check{m}_{\ell }(y_{1},y_{2})|^{p^{\prime }}\,dy_{1}\,dy_{2}\Big)^{2/p^{\prime }}t^{2|\unicode[STIX]{x1D6FC}|+4n/p^{\prime }}\frac{dt}{t^{4n+1}}\Big)^{1/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \Big(\int _{I}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D6FC}}m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{2/p}t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \Big(\int _{I}t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D6FC}}m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{1/p}.\end{eqnarray}$$Hence, we obtain
$$\begin{eqnarray}A_{\ell }^{1}(I)\lesssim \frac{(2^{\ell })^{\unicode[STIX]{x1D700}_{1}-|\unicode[STIX]{x1D6FC}|+2n/p}}{(1+2^{\ell })^{\unicode[STIX]{x1D700}_{1}+\unicode[STIX]{x1D700}_{2}}}\Big(\int _{I}t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}.\end{eqnarray}$$ Now, setting 
$\unicode[STIX]{x1D711}_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})=m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})(e^{2\unicode[STIX]{x1D70B}it^{-1}h\cdot (\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702})}-1)$, we have
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \check{m}_{\ell }\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)-\check{m}_{\ell }\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big)\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\check{\unicode[STIX]{x1D711}}_{\ell }\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big).\nonumber\end{eqnarray}$$Proceeding the same argument as before, we have
$$\begin{eqnarray}\displaystyle A_{\ell }^{1}(I) & {\lesssim} & \displaystyle \Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\int _{|z|\leqslant \min \{1/8,t\}}\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{I}\Big|(y_{1}-z)^{\unicode[STIX]{x1D6FC}}\Big(\check{m}_{\ell }\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)\nonumber\\ \displaystyle & & \displaystyle -\,\check{m}_{\ell }\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big)\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \Big(\int _{I}\Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big|y_{1}^{\unicode[STIX]{x1D6FC}}\check{\unicode[STIX]{x1D711}}_{\ell }\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{p^{\prime }}\,dy_{1}\,dy_{2}\Big)^{2/p^{\prime }}\frac{dt}{t^{4n+1}}\Big)^{1/2}\nonumber\\ \displaystyle & = & \displaystyle \Big(\int _{I}\Big(\int _{S_{j}(t^{-1}Q_{\bar{x}})}\int _{S_{k}(t^{-1}Q_{\bar{x}})}|y_{1}^{\unicode[STIX]{x1D6FC}}\check{\unicode[STIX]{x1D711}}_{\ell }(y_{1},y_{2})|^{p^{\prime }}\,dy_{1}\,dy_{2}\Big)^{2/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \times \,t^{2|\unicode[STIX]{x1D6FC}|+4n/p^{\prime }}\frac{dt}{t^{4n+1}}\Big)^{1/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \Big(\int _{I}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D711}_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{2/p}t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}\nonumber\\ \displaystyle & = & \displaystyle \Big(\int _{I}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D6FC}}[m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})(e^{-2\unicode[STIX]{x1D70B}it^{-1}h\cdot (\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702})}-1)]|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{2/p}\nonumber\\ \displaystyle & & \displaystyle \times \,t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}.\end{eqnarray}$$Estimate for
$A_{\ell }^{2}(I)$.
$$\begin{eqnarray}\displaystyle A_{\ell }^{2}(I) & {\leqslant} & \displaystyle \Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\int _{1/8\leqslant |z|\leqslant \min \{3,t\}}\int _{I}\frac{1}{t^{5n+1}}\nonumber\\ \displaystyle & & \displaystyle \times \,\Big|\check{m}\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)\nonumber\\ \displaystyle & & \displaystyle -\,\check{m}\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big)\Big|^{2}dzdt\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\int _{1/8\leqslant |z|\leqslant \min \{3,t\}}\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{I}\Big|\check{m}\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle +\,\Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\int _{1/8\leqslant |z|\leqslant \min \{3,t\}}\int _{I}\Big|\check{m}\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big)\Big|^{2}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & =: & \displaystyle A_{\ell }^{2,1}(I)+A_{\ell }^{2,2}(I).\nonumber\end{eqnarray}$$ We observe that if 
$z\in E_{2}$, then 
$t\geqslant 1/8$. The Minkowski inequality and the Hausdorff–Young inequality yield that
$$\begin{eqnarray}\displaystyle A_{\ell }^{2,1}(I) & {\lesssim} & \displaystyle \Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\int _{|z|\leqslant t}\int _{\{t\in I:t\geqslant 1/8\}}\nonumber\\ \displaystyle & & \displaystyle \times \,\Big|\check{m}_{\ell }\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \Big(\int _{\{t\in I:t\geqslant 1/8\}}\int _{|z|\leqslant t}\Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\nonumber\\ \displaystyle & & \displaystyle \times \,\Big|\check{m}_{\ell }\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)\Big|^{p^{\prime }}dy_{1}\,dy_{2}\Big)^{2/p^{\prime }}\frac{dt}{t^{5n+1}}\Big)^{1/2}\nonumber\\ \displaystyle & = & \displaystyle \Big(\int _{\{t\in I:t\geqslant 1/8\}}\int _{|z|\leqslant t}\Big(\int _{S_{j}(t^{-1}Q_{\bar{x}})}\int _{S_{k}(t^{-1}Q_{\bar{x}})}\nonumber\\ \displaystyle & & \displaystyle \times \,\Big|\check{m}_{\ell }\Big(\frac{u_{1}}{t},\frac{u_{2}}{t}\Big)\Big|^{p^{\prime }}\,du_{1}\,du_{2}\Big)^{2/p^{\prime }}\frac{dt}{t^{5n+1-4n/p^{\prime }}}\Big)^{1/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{1/p}\Big(\int _{\{t\in I:t\geqslant 1/8\}}t^{2s-4n/p-1}\,dt\Big)^{1/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{(2^{\ell })^{\unicode[STIX]{x1D700}_{1}-s+2n/p}}{(1+2^{\ell })^{\unicode[STIX]{x1D700}_{1}+\unicode[STIX]{x1D700}_{2}}}\Big(\int _{I}t^{2s-4n/p-1}\,dt\Big)^{1/2}.\nonumber\end{eqnarray}$$Repeating the same estimates above, we may obtain
$$\begin{eqnarray}\displaystyle A_{\ell }^{2,2}(I)\lesssim \frac{(2^{\ell })^{\unicode[STIX]{x1D700}_{1}-s+2n/p}}{(1+2^{\ell })^{\unicode[STIX]{x1D700}_{1}+\unicode[STIX]{x1D700}_{2}}}\Big(\int _{I}t^{2s-4n/p-1}\,dt\Big)^{1/2}. & & \displaystyle \nonumber\end{eqnarray}$$On the other hand, similar to inequality (2.6), we have
$$\begin{eqnarray}\displaystyle A_{\ell }^{2}(I) & {\lesssim} & \displaystyle \Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\int _{|z|\leqslant t}\int _{\{t\in I:t\geqslant 1/8\}}\frac{1}{t^{5n+1}}\nonumber\\ \displaystyle & & \displaystyle \times \,\Big|\Big(\check{m}_{\ell }\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)\nonumber\\ \displaystyle & & \displaystyle -\,\check{m}_{\ell }\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big)\Big)\Big|^{2}dzdt\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \Big(\int _{|z|\leqslant t}\int _{\{t\in I:t\geqslant 1/8\}}\Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\nonumber\\ \displaystyle & & \displaystyle \times \,\Big|\check{\unicode[STIX]{x1D711}}_{\ell }\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{p^{\prime }}\,dy_{1}\,dy_{2}\Big)^{2/p^{\prime }}\frac{dz\,dt}{t^{2s+5n+1}}\Big)^{1/2}\nonumber\\ \displaystyle & = & \displaystyle \Big(\int _{I}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})(e^{-2\unicode[STIX]{x1D70B}it^{-1}h\cdot (\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702})}-1)|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{2/p}\nonumber\\ \displaystyle & & \displaystyle \times \,t^{2s-4n/p-1}\,dt\Big)^{1/2}.\nonumber\end{eqnarray}$$Estimate for
$A_{\ell }^{3}(I)$.
$$\begin{eqnarray}\displaystyle A_{\ell }^{3}(I) & {\leqslant} & \displaystyle \Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\int _{3<|z|\leqslant t}\int _{I}\Big|\check{m}\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)\nonumber\\ \displaystyle & & \displaystyle -\,\check{m}\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\int _{|z|\leqslant t}\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{I}\Big|\check{m}\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle +\,\Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\int _{|z|\leqslant t}\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{I}\Big|\check{m}\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & =: & \displaystyle A_{\ell }^{3,1}(I)+A_{\ell }^{3,2}(I).\nonumber\end{eqnarray}$$ Note that 
$z>3$ and 
$1/2^{2}\leqslant |y_{1}+h|\leqslant 2$, then 
$|y_{1}+h-z|>|z|-|y_{1}+h|>1$ and 
$|y_{1}-z|>|z|-|y_{1}|>2$. Similar to the estimate for 
$A_{\ell }^{1}(I)$, we get
$$\begin{eqnarray}\displaystyle A_{\ell }^{3}(I)\lesssim \Big(\int _{I}t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D6FC}}m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{1/p} & & \displaystyle \nonumber\end{eqnarray}$$and
$$\begin{eqnarray}\displaystyle A_{\ell }^{3}(I) & {\lesssim} & \displaystyle \Big(\int _{I}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D6FC}}\big[m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})\nonumber\\ \displaystyle & & \displaystyle \times \,(e^{-2\unicode[STIX]{x1D70B}it^{-1}h\cdot (\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702})}-1)\big]|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{2/p}t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}.\nonumber\end{eqnarray}$$Estimate for
$A_{\ell }^{4}(I)$. Note that 
$|y_{1}+h-z|\sim 1$, 
$|y_{1}-z|\sim 1$ and 
$\unicode[STIX]{x1D706}>2s/p+1$, employ the Minkowski inequality and the Hausdorff–Young inequality, we may obtain
$$\begin{eqnarray}\displaystyle A_{\ell }^{4}(I) & {\leqslant} & \displaystyle \mathop{\sum }_{i=1}^{\infty }\Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\int _{2^{i-1}t\leqslant |z|\leqslant \min \{2^{i}t,1/8\}}\int _{I}\Big(\frac{t}{|z|+t}\Big)^{n\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & & \displaystyle \times \,\Big|\check{m}\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)\nonumber\\ \displaystyle & & \displaystyle -\,\check{m}\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{i=1}^{\infty }2^{-(i-1)n\unicode[STIX]{x1D706}/2}\Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\int _{2^{i-1}t\leqslant |z|\leqslant \min \{2^{i}t,1/8\}}\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{I}\Big|\check{m}\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)\nonumber\\ \displaystyle & & \displaystyle -\,\check{m}\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \mathop{\sum }_{i=1}^{\infty }2^{-(i-1)n\unicode[STIX]{x1D706}/2}\Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\int _{2^{i-1}t\leqslant |z|\leqslant \min \{2^{i}t,1/8\}}\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{I}\Big|\check{m}\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \mathop{\sum }_{i=1}^{\infty }2^{-(i-1)n\unicode[STIX]{x1D706}/2}\Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\int _{2^{i-1}t\leqslant |z|\leqslant \min \{2^{i}t,1/8\}}\nonumber\\ \displaystyle & & \displaystyle \times \,\int _{I}\Big|(y_{1})^{\unicode[STIX]{x1D6FC}}\check{m}\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{i=1}^{\infty }2^{-(i-1)n\unicode[STIX]{x1D706}/2}\Big(\int _{I}\int _{2^{i-1}t\leqslant |z|\leqslant \min \{2^{i}t,1/8\}}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}\nonumber\\ \displaystyle & & \displaystyle \times \,|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D6FC}}m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{2/p}t^{-5n-1+2|\unicode[STIX]{x1D6FC}|+4n/p^{\prime }}\,dzdt\Big)^{1/2}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{i=1}^{\infty }2^{-(i-1)n\unicode[STIX]{x1D706}/2-in/2}\Big(\int _{I}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}\nonumber\\ \displaystyle & & \displaystyle \times \,|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D6FC}}m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{2/p}t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \Big(\int _{I}t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D6FC}}m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{1/p}.\nonumber\end{eqnarray}$$Recall that
$$\begin{eqnarray}\check{m}_{\ell }\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)-\check{m}_{\ell }\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big)=\check{\unicode[STIX]{x1D711}}_{\ell }\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big).\end{eqnarray}$$Similarly,
$$\begin{eqnarray}\displaystyle & & \displaystyle A_{\ell }^{4}(I)\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim \mathop{\sum }_{i=1}^{\infty }\Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\int _{2^{i-1}t\leqslant |z|\leqslant \min \{2^{i}t,1/8\}}\int _{I}\Big(\frac{t}{|z|+t}\Big)^{n\unicode[STIX]{x1D706}}\Big|(y_{1}-z)^{\unicode[STIX]{x1D6FC}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\check{\unicode[STIX]{x1D711}}_{\ell }\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{i=1}^{\infty }2^{-(i-1)n\unicode[STIX]{x1D706}/2-in/2}\Big(\int _{I}\Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\Big|y_{1}^{\unicode[STIX]{x1D6FC}}\check{\unicode[STIX]{x1D711}}_{\ell }\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{p^{\prime }}\,dy_{1}\,dy_{2}\Big)^{2/p^{\prime }}\frac{dt}{t^{4n+1}}\Big)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \Big(\int _{I}\Big(\int _{S_{j}(t^{-1}Q_{\bar{x}})}\int _{S_{k}(t^{-1}Q_{\bar{x}})}|y_{1}^{\unicode[STIX]{x1D6FC}}\check{\unicode[STIX]{x1D711}}_{\ell }(y_{1},y_{2})|^{p^{\prime }}\,dy_{1}\,dy_{2}\Big)^{2/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,t^{2|\unicode[STIX]{x1D6FC}|+4n/p^{\prime }}\frac{dt}{t^{4n+1}}\Big)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \Big(\int _{I}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D711}_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{2/p}t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad =\Big(\int _{I}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D6FC}}[m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})(e^{-2\unicode[STIX]{x1D70B}it^{-1}h\cdot (\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702})}-1)]|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{2/p}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}.\nonumber\end{eqnarray}$$Estimate for
$A_{\ell }^{5}(I)$. Denote 
$F=\{2^{i-1}t,1/8\}\leqslant |z|\leqslant \min \{2^{i}t,3\}$, we get
$$\begin{eqnarray}\displaystyle A_{\ell }^{5}(I) & {\leqslant} & \displaystyle \mathop{\sum }_{i=1}^{\infty }\Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\int _{F}\int _{I}\Big(\frac{t}{|z|+t}\Big)^{n\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & & \displaystyle \times \,\Big|\check{m}\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)\nonumber\\ \displaystyle & & \displaystyle -\,\check{m}\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{i=1}^{\infty }2^{-(i-1)n\unicode[STIX]{x1D706}/2}\Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\int _{F}\int _{I}\nonumber\\ \displaystyle & & \displaystyle \times \,\Big|\check{m}\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)\Big|^{2}\nonumber\\ \displaystyle & & \displaystyle \times \,\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}+\mathop{\sum }_{i=1}^{\infty }2^{-(i-1)n\unicode[STIX]{x1D706}/2}\Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\nonumber\\ \displaystyle & & \displaystyle \times \,\Big(\int _{F}\int _{I}\Big|\check{m}\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & =: & \displaystyle A_{\ell }^{5,1}(I)+A_{\ell }^{5,2}(I).\nonumber\end{eqnarray}$$ We observe that if 
$\{2^{i-1}t,1/8\}\leqslant |z|\leqslant \min \{2^{i}t,3\}$, then 
$t\sim 2^{-i}$. By the Minkowski inequality and the Hausdorff–Young inequality, we have
$$\begin{eqnarray}\displaystyle & & \displaystyle A_{\ell }^{5,1}(I)\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{i=1}^{\infty }2^{-(i-1)n\unicode[STIX]{x1D706}/2}\Big(\int _{F}\int _{I}\Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\Big|\check{m}_{\ell }\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)\Big|^{p^{\prime }}\,dy_{1}\,dy_{2}\Big)^{2/p^{\prime }}\frac{dt}{t^{5n+1}}\Big)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{i=1}^{\infty }2^{-(i-1)n\unicode[STIX]{x1D706}/2}\Big(\int _{F}\int _{I}\Big(\int _{S_{j}(t^{-1}Q_{\bar{x}})}\int _{S_{k}(t^{-1}Q_{\bar{x}})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\Big|\check{m}_{\ell }\Big(u_{1},u_{2}\Big)\Big|^{p^{\prime }}\,du_{1}\,du_{2}\Big)^{2/p^{\prime }}\frac{dz\,dt}{t^{5n+1-4n/p^{\prime }}}\Big)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{i=1}^{\infty }2^{-(i-1)n\unicode[STIX]{x1D706}/2+in/2+2s}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{1/p}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\Big(\int _{I}t^{2s-4n/p-1}\,dt\Big)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \frac{(2^{\ell })^{\unicode[STIX]{x1D700}_{1}-s+2n/p}}{(1+2^{\ell })^{\unicode[STIX]{x1D700}_{1}+\unicode[STIX]{x1D700}_{2}}}\Big(\int _{I}t^{2s-4n/p-1}\,dt\Big)^{1/2}.\nonumber\end{eqnarray}$$Repeating the same estimates above, we may obtain
$$\begin{eqnarray}\displaystyle A_{\ell }^{5,2}(I)\lesssim \frac{(2^{\ell })^{\unicode[STIX]{x1D700}_{1}-s+2n/p}}{(1+2^{\ell })^{\unicode[STIX]{x1D700}_{1}+\unicode[STIX]{x1D700}_{2}}}\Big(\int _{I}t^{2s-4n/p-1}\,dt\Big)^{1/2}. & & \displaystyle \nonumber\end{eqnarray}$$On the other hand, similar to inequality (2.6), we have
$$\begin{eqnarray}\displaystyle & & \displaystyle A_{\ell }^{5}(I)\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim \mathop{\sum }_{i=1}^{\infty }2^{-(i-1)n\unicode[STIX]{x1D706}/2}\Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\!\Big(\!\int _{F}\int _{I}\Big|\Big(\check{m}_{\ell }\Big(\frac{y_{1}+h-z}{t},\frac{y_{2}+h-z}{t}\Big)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\check{m}_{\ell }\Big(\frac{y_{1}-z}{t},\frac{y_{2}-z}{t}\Big)\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{i=1}^{\infty }2^{-(i-1)n\unicode[STIX]{x1D706}/2}\Big(\int _{F}\int _{I}\Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\Big|\check{\unicode[STIX]{x1D711}}_{\ell }\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{p^{\prime }}\,dy_{1}\,dy_{2}\Big)^{2/p^{\prime }}\frac{dz\,dt}{t^{2s+5n+1}}\Big)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{i=1}^{\infty }2^{-(i-1)n\unicode[STIX]{x1D706}/2+in/2+2s}\Big(\int _{I}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,|m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})(e^{-2\unicode[STIX]{x1D70B}it^{-1}h\cdot (\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702})}-1)|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{2/p}t^{2s-4n/p-1}\,dt\Big)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \Big(\int _{I}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})(e^{-2\unicode[STIX]{x1D70B}it^{-1}h\cdot (\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702})}-1)|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{2/p}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,t^{2s-4n/p-1}\,dt\Big)^{1/2}.\nonumber\end{eqnarray}$$ Finally, we consider for 
$A_{\ell }^{6}(I)$.
Estimate for
$A_{\ell }^{6}(I)$. Since 
$|z|>3$, then 
$|y_{1}+h-z|>1$, 
$|y_{1}-z|>2$. Repeating the similar estimate for 
$A_{\ell }^{4}(I)$, the Minkowski inequality and the Hausdorff–Young inequality yield
$$\begin{eqnarray}\displaystyle A_{\ell }^{6}(I)\lesssim \Big(\int _{I}t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D6FC}}m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{1/p} & & \displaystyle \nonumber\end{eqnarray}$$and
$$\begin{eqnarray}\displaystyle A_{\ell }^{6}(I) & {\lesssim} & \displaystyle \Big(\int _{I}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D6FC}}[m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})(e^{-2\unicode[STIX]{x1D70B}it^{-1}h\cdot (\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702})}-1)]|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{2/p}\nonumber\\ \displaystyle & & \displaystyle \times \,t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}.\nonumber\end{eqnarray}$$Combining all estimates of these six terms, it yields that
$$\begin{eqnarray}\displaystyle A_{\ell }(I) & {\lesssim} & \displaystyle \Big(\int _{I}t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D6FC}}m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{1/p}\nonumber\\ \displaystyle & & \displaystyle +\,\Big(\int _{I}t^{2s-4n/p-1}\,dt\Big)^{1/2}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{1/p}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{(2^{\ell })^{\unicode[STIX]{x1D700}_{1}-s+2n/p}}{(1+2^{\ell })^{\unicode[STIX]{x1D700}_{1}+\unicode[STIX]{x1D700}_{2}}}\Big(\int _{I}t^{2s-4n/p-1}\,dt\Big)^{1/2}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{(2^{\ell })^{\unicode[STIX]{x1D700}_{1}-|\unicode[STIX]{x1D6FC}|+2n/p}}{(1+2^{\ell })^{\unicode[STIX]{x1D700}_{1}+\unicode[STIX]{x1D700}_{2}}}\Big(\int _{I}t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}\nonumber\end{eqnarray}$$and
$$\begin{eqnarray}\displaystyle A_{\ell }(I) & {\lesssim} & \displaystyle \Big(\int _{I}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D6FC}}[m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})(e^{-2\unicode[STIX]{x1D70B}it^{-1}h\cdot (\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702})}-1)]|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{2/p}\nonumber\\ \displaystyle & & \displaystyle \times \,t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}\nonumber\\ \displaystyle & & \displaystyle +\,\Big(\int _{I}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})(e^{-2\unicode[STIX]{x1D70B}it^{-1}h\cdot (\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702})}-1)|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{2/p}\nonumber\\ \displaystyle & & \displaystyle \times \,t^{2s-4n/p-1}\,dt\Big)^{1/2}.\nonumber\end{eqnarray}$$By the following fact
$$\begin{eqnarray}\displaystyle & & \displaystyle |\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D6FC}}[m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})(e^{-2\unicode[STIX]{x1D70B}it^{-1}h\cdot (\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702})}-1)]|\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim \frac{2^{\ell }|h|}{t}\frac{(2^{\ell })^{\unicode[STIX]{x1D700}_{1}-|\unicode[STIX]{x1D6FC}|}}{(1+2^{\ell })^{\unicode[STIX]{x1D700}_{1}+\unicode[STIX]{x1D700}_{2}}}+\mathop{\sum }_{\unicode[STIX]{x1D6FD}=1}^{|\unicode[STIX]{x1D6FC}|}\Big(\frac{|h|}{t}\Big)^{\unicode[STIX]{x1D6FD}}\frac{(2^{\ell })^{\unicode[STIX]{x1D700}_{1}-|\unicode[STIX]{x1D6FC}|+\unicode[STIX]{x1D6FD}}}{(1+2^{\ell })^{\unicode[STIX]{x1D700}_{1}+\unicode[STIX]{x1D700}_{2}}}\nonumber\end{eqnarray}$$and
$$\begin{eqnarray}|m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})(e^{-2\unicode[STIX]{x1D70B}it^{-1}h\cdot (\unicode[STIX]{x1D709}+\unicode[STIX]{x1D702})}-1)|\lesssim \frac{2^{\ell }|h|}{t}\frac{(2^{\ell })^{\unicode[STIX]{x1D700}_{1}-s}}{(1+2^{\ell })^{\unicode[STIX]{x1D700}_{1}+\unicode[STIX]{x1D700}_{2}}},\end{eqnarray}$$it follows that
$$\begin{eqnarray}\displaystyle A_{\ell }(I) & {\lesssim} & \displaystyle \Big(\int _{I}\Big(\frac{2^{\ell }|h|}{t}\frac{(2^{\ell })^{\unicode[STIX]{x1D700}_{1}-|\unicode[STIX]{x1D6FC}|}}{(1+2^{\ell })^{\unicode[STIX]{x1D700}_{1}+\unicode[STIX]{x1D700}_{2}}}+\mathop{\sum }_{\unicode[STIX]{x1D6FD}=1}^{|\unicode[STIX]{x1D6FC}|}\Big(\frac{|h|}{t}\Big)^{\unicode[STIX]{x1D6FD}}\frac{(2^{\ell })^{\unicode[STIX]{x1D700}_{1}-|\unicode[STIX]{x1D6FC}|+\unicode[STIX]{x1D6FD}}}{(1+2^{\ell })^{\unicode[STIX]{x1D700}_{1}+\unicode[STIX]{x1D700}_{2}}}\Big)^{2}\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \times \,2^{4n\ell /p}t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \mathop{\sum }_{\unicode[STIX]{x1D6FD}=0}^{|\unicode[STIX]{x1D6FC}|}|h|^{\max (\unicode[STIX]{x1D6FD},1)}\frac{2^{\ell (-|\unicode[STIX]{x1D6FC}|+2n/p+\max (\unicode[STIX]{x1D6FD},1)+\unicode[STIX]{x1D700}_{1})}}{(1+2^{\ell })^{\unicode[STIX]{x1D700}_{1}+\unicode[STIX]{x1D700}_{2}}}\nonumber\\ \displaystyle & & \displaystyle \times \,\Big(\int _{I}t^{2(|\unicode[STIX]{x1D6FC}|-2n/p-\max (\unicode[STIX]{x1D6FD},1))-1}\,dt\Big)^{1/2}.\end{eqnarray}$$ Now, we fix sufficiently small 
$\unicode[STIX]{x1D700}>0$ so that 
$\unicode[STIX]{x1D700}(s-2n/p)<\min \{\unicode[STIX]{x1D700}_{1},\unicode[STIX]{x1D700}_{2}\}$. Then, if 
$2^{\ell }|h|\geqslant 1$, noting 
$2n/p<s<2n/p+1$ and using (2.5) for 
$I=(0,(2^{\ell }|h|)^{1+\unicode[STIX]{x1D700}}]$, we have
$$\begin{eqnarray}\displaystyle & & \displaystyle A_{\ell }((0,(2^{\ell }|h|)^{1+\unicode[STIX]{x1D700}}])\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim 2^{-\ell (s+\unicode[STIX]{x1D700}_{2}-2n/p)}(2^{\ell }|h|)^{(1+\unicode[STIX]{x1D700})(s-2n/p)}=|h|^{(1+\unicode[STIX]{x1D700})(s-2n/p)}2^{\ell (\unicode[STIX]{x1D700}(s-2n/p)-\unicode[STIX]{x1D700}_{2})}.\nonumber\end{eqnarray}$$ By (2.8) for 
$I=[(2^{\ell }|h|)^{1+\unicode[STIX]{x1D700}},\infty )$, we have
$$\begin{eqnarray}\displaystyle & & \displaystyle A_{\ell }([(2^{\ell }|h|)^{1+\unicode[STIX]{x1D700}},\infty ))\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim \mathop{\sum }_{\unicode[STIX]{x1D6FD}=0}^{|\unicode[STIX]{x1D6FC}|}|h|^{\max (\unicode[STIX]{x1D6FD},1)}2^{\ell (-|\unicode[STIX]{x1D6FC}|+2n/p+\max (\unicode[STIX]{x1D6FD},1))}(2^{\ell }|h|)^{(1+\unicode[STIX]{x1D700})(s-2n/p-\max (\unicode[STIX]{x1D6FD},1))}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\unicode[STIX]{x1D6FD}=0}^{|\unicode[STIX]{x1D6FC}|}|h|^{-\unicode[STIX]{x1D700}\max (\unicode[STIX]{x1D6FD},1)+(1+\unicode[STIX]{x1D700})(s-2n/p)}2^{\ell \unicode[STIX]{x1D700}((s-2n/p)-\max (\unicode[STIX]{x1D6FD},1))}.\nonumber\end{eqnarray}$$ Thus, noting 
$\unicode[STIX]{x1D700}(s-2n/p)-\unicode[STIX]{x1D700}_{2}<0$ and 
$|h|<1$, we obtain
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{2^{\ell }|h|\geqslant 1}A_{\ell } & {\lesssim} & \displaystyle \mathop{\sum }_{2^{\ell }|h|\geqslant 1}|h|^{(1+\unicode[STIX]{x1D700})(s-2n/p)}2^{\ell (\unicode[STIX]{x1D700}(s-2n/p)-\unicode[STIX]{x1D700}_{2})}\nonumber\\ \displaystyle & & \displaystyle +\mathop{\sum }_{2^{\ell }|h|\geqslant 1}\mathop{\sum }_{\unicode[STIX]{x1D6FD}=0}^{|\unicode[STIX]{x1D6FC}|}|h|^{-\unicode[STIX]{x1D700}\max (\unicode[STIX]{x1D6FD},1)+(1+\unicode[STIX]{x1D700})(s-2n/p)}2^{\ell \unicode[STIX]{x1D700}((s-2n/p)-\max (\unicode[STIX]{x1D6FD},1))}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle |h|^{s-2n/p+\unicode[STIX]{x1D700}_{2}}+\mathop{\sum }_{\unicode[STIX]{x1D6FD}=0}^{|\unicode[STIX]{x1D6FC}|}|h|^{s-2n/p}\lesssim |h|^{s-2n/p}.\end{eqnarray}$$ In the case 
$2^{\ell }|h|<1$, using (2.5) for 
$I=(0,(2^{\ell }|h|)^{1-\unicode[STIX]{x1D700}}]$, we have
$$\begin{eqnarray}\displaystyle A_{\ell }((0,(2^{\ell }|h|)^{1-\unicode[STIX]{x1D700}}]) & {\lesssim} & \displaystyle 2^{\ell (-s+2n/p+\unicode[STIX]{x1D700}_{1})}(2^{\ell }|h|)^{(1-\unicode[STIX]{x1D700})(s-2n/p)}\nonumber\\ \displaystyle & = & \displaystyle |h|^{(1-\unicode[STIX]{x1D700})(s-2n/p)}2^{\ell (-\unicode[STIX]{x1D700}(s-2n/p)+\unicode[STIX]{x1D700}_{1})}.\nonumber\end{eqnarray}$$ Furthermore, by using (2.8) for 
$I=[(2^{\ell }|h|)^{1-\unicode[STIX]{x1D700}},\infty )$, we have
$$\begin{eqnarray}\displaystyle & & \displaystyle A_{\ell }([(2^{\ell }|h|)^{1-\unicode[STIX]{x1D700}},\infty ))\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim \mathop{\sum }_{\unicode[STIX]{x1D6FD}=0}^{|\unicode[STIX]{x1D6FC}|}|h|^{\max (\unicode[STIX]{x1D6FD},1)}2^{\ell (-s+2n/p+\max (\unicode[STIX]{x1D6FD},1))}(2^{\ell }|h|)^{(1-\unicode[STIX]{x1D700})(s-2n/p-\max (\unicode[STIX]{x1D6FD},1))}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{\unicode[STIX]{x1D6FD}=0}^{|\unicode[STIX]{x1D6FC}|}|h|^{\unicode[STIX]{x1D700}\max (\unicode[STIX]{x1D6FD},1)+(1-\unicode[STIX]{x1D700})(s-2n/p)}2^{-\unicode[STIX]{x1D700}\ell (s-2n/p-\max (\unicode[STIX]{x1D6FD},1))}.\nonumber\end{eqnarray}$$ By the fact that 
$\unicode[STIX]{x1D700}(s-2n/p)-\unicode[STIX]{x1D700}_{1}<0$ and 
$|h|<1$, we obtain
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{2^{\ell }|h|<1}A_{\ell } & {\lesssim} & \displaystyle \mathop{\sum }_{2^{\ell }|h|<1}|h|^{(1-\unicode[STIX]{x1D700})(s-2n/p)}2^{\ell (-\unicode[STIX]{x1D700}(s-2n/p)+\unicode[STIX]{x1D700}_{1})}\nonumber\\ \displaystyle & & \displaystyle +\mathop{\sum }_{2^{\ell }|h|<1}\mathop{\sum }_{\unicode[STIX]{x1D6FD}=0}^{|\unicode[STIX]{x1D6FC}|}|h|^{\unicode[STIX]{x1D700}\max (\unicode[STIX]{x1D6FD},1)+(1-\unicode[STIX]{x1D700})(s-2n/p)}2^{-\unicode[STIX]{x1D700}\ell (s-2n/p-\max (\unicode[STIX]{x1D6FD},1))}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle |h|^{s-2n/p-\unicode[STIX]{x1D700}_{1}}+\mathop{\sum }_{\unicode[STIX]{x1D6FD}=0}^{|\unicode[STIX]{x1D6FC}|}|h|^{s-2n/p}\lesssim |h|^{s-2n/p-\unicode[STIX]{x1D700}_{1}}+|h|^{s-2n/p}.\end{eqnarray}$$ Noting that 
$0<\unicode[STIX]{x1D700}_{1}<s-2n/p$ and taking 
$\unicode[STIX]{x1D6FF}=(s-\unicode[STIX]{x1D700}_{1})/2$, by (2.9) and (2.10), it holds that
$$\begin{eqnarray}\displaystyle & & \displaystyle \Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{t}{|z|+t}\Big)^{n\unicode[STIX]{x1D706}}\Big|\check{m}\Big(\frac{y_{1}+h}{t},\frac{y_{2}+h}{t}\Big)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\check{m}\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy\,dz\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{\ell \in \mathbb{Z}}A_{\ell }\lesssim |h|^{2(\unicode[STIX]{x1D6FF}-n/p)}.\nonumber\end{eqnarray}$$ This leads to the conclusion of Proposition 2.1 in the case 
$2n/p<s<2n/p+1$.
(b) The case
$2n/p<s=2n/p+1$. First, we choose 
$1<p_{0}<p$ such that 
$2n/p_{0}<s$. Then 
$p_{0}$ satisfies 
$2n/p_{0}<s=2n/p+1<2n/p_{0}+1$. Hence, for all balls 
$Q$, all 
$x,\bar{x}\in \frac{1}{2}Q$ and 
$(j,k)\neq (0,0)$, by step (a), we have
$$\begin{eqnarray}\displaystyle & & \displaystyle \Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\!\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{t}{|z|+t}\Big)^{n\unicode[STIX]{x1D706}}\Big|\check{m}\Big(\frac{y_{1}+h}{t},\frac{y_{2}+h}{t}\Big)-\check{m}\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\frac{dz\,dt}{t^{5n+1}}\Big)^{p_{0}^{\prime }/2}\,dy\,dz\Big)^{1/p_{0}^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C\frac{|h|^{2\unicode[STIX]{x1D6FF}-2n/p_{0}}}{|Q|^{2\unicode[STIX]{x1D6FF}/n}}2^{-2\unicode[STIX]{x1D6FF}\max (j,k)}.\nonumber\end{eqnarray}$$By the Hölder inequality, it yields that
$$\begin{eqnarray}\displaystyle & & \displaystyle \Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\!\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{t}{|z|+t}\Big)^{n\unicode[STIX]{x1D706}}\Big|\check{m}\Big(\frac{y_{1}+h}{t},\frac{y_{2}+h}{t}\Big)-\check{m}\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy\,dz\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant (2^{n(j+k)}|Q|^{2})^{(1/p_{0})-(1/p)}\Big(\int _{S_{j}(Q_{\bar{x}})}\int _{S_{k}(Q_{\bar{x}})}\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{t}{|z|+t}\Big)^{n\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\Big|\check{m}\Big(\frac{y_{1}+h}{t},\frac{y_{2}+h}{t}\Big)-\check{m}\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy\,dz\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim (2^{2n\max (j,k)}|Q|^{2})^{(1/p_{0})-(1/p)}\frac{|h|^{2\unicode[STIX]{x1D6FF}-2n/p_{0}}}{|Q|^{2\unicode[STIX]{x1D6FF}/n}}\frac{1}{2^{2\unicode[STIX]{x1D6FF}\max (j,k)}}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{|h|^{(2\unicode[STIX]{x1D6FF}-2n/p_{0}+2n/p)-2n/p}}{|Q|^{(2\unicode[STIX]{x1D6FF}-2n/p_{0}+2n/p)/n}}2^{-(2\unicode[STIX]{x1D6FF}-2n/p_{0}+2n/p)\max (j,k)}.\nonumber\end{eqnarray}$$ Therefore, taking 
$\unicode[STIX]{x1D6FF}-n/p_{0}+n/p>n/p$ as 
$\unicode[STIX]{x1D6FF}$ newly, we obtain the desired estimate.
(c) The case
$2n/p+1<s\leqslant 2n$. In this case there is an integer 
$l$ such that 
$2n/p+l<s\leqslant 2n/p+1+l$. Then it follows that 
$2n/p<s-l\leqslant 2n/p+1$. Thus, regarding 
$s-l$ as 
$s$, we may deduce this case to the previous case (a) or case (b). This completes the proof of Proposition 2.1.
Proposition 2.2. Let 
$s\in \mathbb{N}$ with 
$n+1\leqslant s\leqslant 2n$. Let 
$m\in L^{\infty }((\mathbb{R}^{n})^{2})$ and satisfy (1.1) and (1.2). Then, for 
$2n/s<p\leqslant 2$, 
$\unicode[STIX]{x1D706}>2s/n+1$, there exists a constant 
$C>0$, such that the following inequality holds for all balls 
$Q$ with center at 
$x$ and 
$(j,k)\neq (0,0)$.
$$\begin{eqnarray}\displaystyle & & \displaystyle \Big(\int _{S_{j}(Q)}\int _{S_{k}(Q)}\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{t}{|x-z|+t}\Big)^{n\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\Big|\check{m}\Big(\frac{x-y_{1}}{t},\frac{x-y_{2}}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C\frac{1}{|Q|^{2/p}}2^{-2n\max (j,k)/p}.\end{eqnarray}$$Proof. Let 
$Q=B(x,R)$, 
$u=ax$
$(a>0)$ and 
$s=at$, we have
$$\begin{eqnarray}\displaystyle & & \displaystyle B_{j,k}(m,Q)(x):\nonumber\\ \displaystyle & & \displaystyle \quad =\Big(\int _{S_{j}(Q)}\int _{S_{k}(Q)}\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{t}{|x-z|+t}\Big)^{n\unicode[STIX]{x1D706}}\Big|\check{m}\Big(\frac{x-y_{1}}{t},\frac{x-y_{2}}{t}\Big)\Big|^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\frac{dz\,dt}{t^{4n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad =a^{2n/p}\Big(\int _{S_{j}(Q^{a})}\int _{S_{k}(Q^{a})}\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{s}{|x^{a}-v|+s}\Big)^{n\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\Big|\check{m}\Big(\frac{x^{a}-u_{1}}{t},\frac{x^{a}-u_{2}}{s}\Big)\Big|^{2}\frac{dvds}{s^{5n+1}}\Big)^{p^{\prime }/2}\,du_{1}\,du_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad =a^{2n/p}B_{j,k}(m,Q^{a})(x^{a}),\nonumber\end{eqnarray}$$ where 
$Q^{a}=B(ax,aR)$, 
$x^{a}=ax$. So, taking 
$a=1/(2^{\max (j,k)}R)$, the estimate 
$B_{j,k}(m,Q^{a})(x^{a})\lesssim 1$ implies the desired estimate. Thus, we only need to show (2.11) in the case 
$R=1/2^{\max (j,k)}$. We may also assume 
$k\geqslant j$ and hence 
$k\geqslant 1$. Then, for 
$Q=B(x,2^{-k})$, it is sufficient to show that
$$\begin{eqnarray}B_{j,k}(m,Q)(x)\lesssim 1.\end{eqnarray}$$By changing variables, it is enough to show that
$$\begin{eqnarray}\displaystyle & & \displaystyle \Big(\int _{S_{j}(Q_{x})}\int _{S_{k}(Q_{x})}\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{t}{|x-z|+t}\Big)^{n\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\Big|\check{m}\Big(\frac{y}{t},\frac{z}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C\frac{1}{|Q|^{2/p}}2^{-2n\max (j,k)/p},\end{eqnarray}$$ where 
$Q_{x}=Q-x$.
For every interval 
$I$ in 
$\mathbb{R}_{+}$, let
$$\begin{eqnarray}\displaystyle & & \displaystyle B_{j,k}(m_{\ell },Q,I)(x)\nonumber\\ \displaystyle & & \displaystyle \quad =B_{j,k}^{1}(m_{\ell },Q,I)(x)+B_{j,k}^{2}(m_{\ell },Q,I)(x)\nonumber\\ \displaystyle & & \displaystyle \quad :=\Big(\int _{S_{j}(Q_{x})}\int _{S_{k}(Q_{x})}\Big(\int _{\mathbb{R}^{n}}\int _{I}\Big(\frac{t}{|x-z|+t}\Big)^{n\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\Big|\check{m}_{\ell }\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad =\Big(\int _{S_{j}(Q_{x})}\int _{S_{k}(Q_{x})}\Big(\int _{|x-z|<t}\int _{I}\Big|\check{m}_{\ell }\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \qquad +\mathop{\sum }_{i=1}^{\infty }2^{-(i-1)n\unicode[STIX]{x1D706}}\Big(\int _{S_{j}(Q_{x})}\int _{S_{k}(Q_{x})}\Big(\int _{2^{i-1}t\leqslant |x-z|<2^{i}t}\int _{I}\Big|\check{m}_{\ell }\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}.\nonumber\end{eqnarray}$$ Note that 
$y_{1}\sim 1$. The Minkowski inequality, together with the Hausdorff–Young inequality implies that
$$\begin{eqnarray}\displaystyle & & \displaystyle B_{j,k}^{1}(m_{\ell },Q,I)(x)\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim (2^{k}R)^{-|\unicode[STIX]{x1D6FC}|}\Big(\int _{S_{j}(Q_{x})}\int _{S_{k}(Q_{x})}\Big(\int _{|x-z|<t}\int _{I}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\Big|y_{1}^{\unicode[STIX]{x1D6FC}}\check{m}_{\ell }\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{2}\frac{dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim (2^{k}R)^{-|\unicode[STIX]{x1D6FC}|}\Big(\int _{I}\Big(\int _{S_{j}(Q_{x})}\int _{S_{k}(Q_{x})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\Big|y_{1}^{\unicode[STIX]{x1D6FC}}\check{m}_{\ell }\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{p^{\prime }}\,dy_{1}\,dy_{2}\Big)^{2/p^{\prime }}\frac{dt}{t^{4n+1}}\Big)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad =C(2^{k}R)^{-|\unicode[STIX]{x1D6FC}|}\Big(\int _{I}\Big(\int _{S_{j}(t^{-1}Q_{x})}\int _{S_{k}(t^{-1}Q_{x})}|y_{1}^{\unicode[STIX]{x1D6FC}}\check{m}_{\ell }(y_{1},y_{2})|^{p^{\prime }}\,dy_{1}\,dy_{2}\Big)^{2/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,t^{2|\unicode[STIX]{x1D6FC}|+4n/p^{\prime }}\frac{dt}{t^{4n+1}}\Big)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim (2^{k}R)^{-|\unicode[STIX]{x1D6FC}|}\Big(\int _{I}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D6FC}}m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{2/p}t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim (2^{k}R)^{-|\unicode[STIX]{x1D6FC}|}\Big(\int _{I}t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D6FC}}m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{1/p}.\nonumber\end{eqnarray}$$Similarly,
$$\begin{eqnarray}\displaystyle & & \displaystyle B_{j,k}^{2}(m_{\ell },Q,I)(x)\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim (2^{k}R)^{-|\unicode[STIX]{x1D6FC}|}\mathop{\sum }_{i=1}^{\infty }2^{-(i-1)n\unicode[STIX]{x1D706}/2}\Big(\int _{S_{j}(Q_{x})}\int _{S_{k}(Q_{x})}\Big(\int _{2^{i-1}t\leqslant |x-z|<2^{i}t}\int _{I}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\Big|y_{1}^{\unicode[STIX]{x1D6FC}}\check{m}_{\ell }\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{2}\frac{dz\,dt}{t^{5n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim (2^{k}R)^{-|\unicode[STIX]{x1D6FC}|}\mathop{\sum }_{i=1}^{\infty }2^{-(i-1)n\unicode[STIX]{x1D706}/2+in/2}\Big(\int _{S_{j}(Q_{x})}\int _{S_{k}(Q_{x})}\Big(\int _{I}\Big|y_{1}^{\unicode[STIX]{x1D6FC}}\check{m}_{\ell }\Big(\frac{y_{1}}{t},\frac{y_{2}}{t}\Big)\Big|^{2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\frac{dt}{t^{4n+1}}\Big)^{p^{\prime }/2}\,dy_{1}\,dy_{2}\Big)^{1/p^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim (2^{k}R)^{-|\unicode[STIX]{x1D6FC}|}\Big(\int _{I}t^{2|\unicode[STIX]{x1D6FC}|-4n/p-1}\,dt\Big)^{1/2}\Big(\int _{\mathbb{R}^{n}}\int _{\mathbb{R}^{n}}|\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}^{\unicode[STIX]{x1D6FC}}m_{\ell }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})|^{p}\,d\unicode[STIX]{x1D709}\,d\unicode[STIX]{x1D702}\Big)^{1/p}.\nonumber\end{eqnarray}$$ Next, we consider two cases according to the value of 
$\ell .$
Case (a). 
$\ell <0$. In this case, taking 
$|\unicode[STIX]{x1D6FC}|=0$ and 
$I=[2^{\ell (1+\unicode[STIX]{x1D700})},\infty )$, the estimate in (1.2) implies that
$$\begin{eqnarray}B_{j,k}(m_{\ell },Q,[2^{\ell (1+\unicode[STIX]{x1D700})},\infty ))\lesssim 2^{\ell (1+\unicode[STIX]{x1D700})(-2n/p)}2^{\ell \unicode[STIX]{x1D700}_{1}}2^{\ell (2n/p)}=2^{\ell (\unicode[STIX]{x1D700}_{1}-2\unicode[STIX]{x1D700}n/p)}.\end{eqnarray}$$ In virtue of 
$2^{k}R=1$, taking 
$|\unicode[STIX]{x1D6FC}|=s$ and 
$I=[0,2^{\ell (1+\unicode[STIX]{x1D700})}]$, the estimate in (1.1) implies that
$$\begin{eqnarray}B_{j,k}(m_{\ell },Q,[0,2^{\ell (1+\unicode[STIX]{x1D700})}])\lesssim 2^{\ell (1+\unicode[STIX]{x1D700})(s-2n/p)}2^{-\ell (s-2n/p)}=2^{\ell \unicode[STIX]{x1D700}(s-2n/p)}.\end{eqnarray}$$Hence,
$$\begin{eqnarray}B_{j,k}(m_{\ell },Q,[0,\infty ))\lesssim 2^{\ell (\unicode[STIX]{x1D700}_{1}-2\unicode[STIX]{x1D700}n/p)}+2^{\ell \unicode[STIX]{x1D700}(s-2n/p)}.\end{eqnarray}$$ Case (b). 
$\ell \geqslant 0$. By repeating the same arguments as in case (a), we get
$$\begin{eqnarray}B_{j,k}(m_{\ell },Q,[2^{\ell (1-\unicode[STIX]{x1D700})},\infty ))\lesssim 2^{\ell (1-\unicode[STIX]{x1D700})(-2n/p)}2^{-\ell \unicode[STIX]{x1D700}_{2}}2^{\ell (2n/p)}=2^{\ell (2\unicode[STIX]{x1D700}n/p-\unicode[STIX]{x1D700}_{2})}\end{eqnarray}$$and
$$\begin{eqnarray}B_{j,k}(m_{\ell },Q,[0,2^{\ell (1-\unicode[STIX]{x1D700})}])\lesssim 2^{\ell (1-\unicode[STIX]{x1D700})(s-2n/p)}2^{-\ell (s-2n/p)}=2^{-\ell \unicode[STIX]{x1D700}(s-2n/p)}.\end{eqnarray}$$Therefore,
$$\begin{eqnarray}B_{j,k}(m_{\ell },Q,[0,\infty ))\lesssim 2^{\ell (2\unicode[STIX]{x1D700}n/p-\unicode[STIX]{x1D700}_{2})}+2^{-\ell \unicode[STIX]{x1D700}(s-2n/p)}.\end{eqnarray}$$ Choosing 
$\unicode[STIX]{x1D700}>0$ so that 
$2n\unicode[STIX]{x1D700}/p<\min (\unicode[STIX]{x1D700}_{1},\unicode[STIX]{x1D700}_{2})$, we obtain from case (a) and case (b)
$$\begin{eqnarray}\displaystyle B_{j,k}(m,Q)(x) & {\leqslant} & \displaystyle \mathop{\sum }_{\ell <0}B_{j,k}(m_{\ell },Q,[0,\infty ))+\mathop{\sum }_{\ell \geqslant 0}B_{j,k}(m_{\ell },Q,[0,\infty ))\nonumber\\ \displaystyle & {\lesssim} & \displaystyle \mathop{\sum }_{\ell <0}[2^{\ell (\unicode[STIX]{x1D700}_{1}-2\unicode[STIX]{x1D700}n/p)}+2^{\ell \unicode[STIX]{x1D700}(s-2n/p)}]\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{\ell \geqslant 0}[2^{\ell (2\unicode[STIX]{x1D700}n/p-\unicode[STIX]{x1D700}_{2})}+2^{-\ell \unicode[STIX]{x1D700}(s-2n/p)}]\lesssim 1.\nonumber\end{eqnarray}$$This completes the proof of Proposition 2.2.
2.2 Related multilinear square function
In order to finish our proof, we need to introduce some definitions and necessary Lemmas.
Definition 2.1. (multilinear square function $T_{\unicode[STIX]{x1D706}}$)
Let 
$K$ be a locally integrable function defined away from the diagonal 
$x=y_{1}=\cdots =y_{m}$ in 
$(\mathbb{R}^{n})^{m+1}$ and 
$K_{t}=t^{-mn}K(\cdot /t)$. Then, the multilinear square function 
$T_{\unicode[STIX]{x1D706}}$ is defined as follows
$$\begin{eqnarray}T_{\unicode[STIX]{x1D706}}(\vec{f})(x)=\Big(\iint _{\mathbb{R}_{+}^{n+1}}\!\Big(\!\frac{t}{|x-z|+t}\Big)^{n\unicode[STIX]{x1D706}}\bigg|\int _{\mathbb{R}^{mn}}\!K_{t}(z,\vec{y})\mathop{\prod }_{j=1}^{m}f_{j}(y_{j})\,d\vec{y}\bigg|^{2}\frac{dz\,dt}{t^{n+1}}\Big)^{1/2},\end{eqnarray}$$ where 
$\vec{f}=(f_{1},\ldots ,f_{m})\in {\mathcal{S}}(\mathbb{R}^{n})\times \cdots \times {\mathcal{S}}(\mathbb{R}^{n})$ and all 
$x\notin \bigcap _{j=1}^{m}\text{supp}f_{j}$.
For 
$x\in \mathbb{R}^{n}$, 
$r,a>0$, we set 
$B(x,r)=\{y\in \mathbb{R}^{n}:|y-x|<r\}$ and 
$aB(x,r)=\{y\in \mathbb{R}^{n}:|y-x|<ar\}$. For all balls 
$Q$, let 
$S_{j}(Q)=2^{j}Q\setminus 2^{j-1}Q$ if 
$j\geqslant 1,$ and 
$S_{0}(Q)=Q$.
Definition 2.2. (kernel condition)
Let 
$1\leqslant p_{0}<\infty .$ Then, assume that
(H1) For all
$p_{0}\leqslant q_{1},q_{2},\ldots ,q_{m}<\infty$ and $0<q<\infty$ with $1/q_{1}+\cdots +1/q_{m}=1/q,$$T$ maps $L^{q_{1}}\times \cdots \times L^{q_{m}}$ into $L^{q,\infty }.$(H2) There exists
$\unicode[STIX]{x1D6FF}>n/p_{0}$ so that for the conjugate exponent $p_{0}^{\prime }$ of $p_{0},$ one has for all balls$$\begin{eqnarray}\displaystyle & & \displaystyle \Big(\int _{S_{j_{m}}(Q)}\cdots \int _{S_{j_{1}}(Q)}\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{t}{|z|+t}\Big)^{n\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\big|K_{t}(x-z,\vec{y})-K_{t}(x^{\prime }-z,\vec{y})|^{2}\frac{dz\,dt}{t^{n+1}}\Big)^{p_{0}^{\prime }/2}\,d\vec{y}\Big)^{1/p_{0}^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C\frac{|x-x^{\prime }|^{m(\unicode[STIX]{x1D6FF}-n/p_{0})}}{|Q|^{m\unicode[STIX]{x1D6FF}/n}}2^{-m\unicode[STIX]{x1D6FF}j_{0}}\nonumber\end{eqnarray}$$$Q$, all $x,z\in (1/2)Q$ and $(j_{1},\ldots ,j_{m})\neq (0,\ldots ,0),$ where $j_{0}=\max _{k=1,\ldots ,m}\{j_{k}\}$.(H3) There exists some positive constant
$C>0$ such that for all balls$$\begin{eqnarray}\displaystyle & & \displaystyle \Big(\int _{S_{j_{m}}(Q)}\cdots \int _{S_{j_{1}}(Q)}\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{t}{|x-z|+t}\Big)^{n\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\big|K_{t}(x,\vec{y})|^{2}\frac{dz\,dt}{t^{n+1}}\Big)^{p_{0}^{\prime }/2}\,d\vec{y}\Big)^{1/p_{0}^{\prime }}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant C\frac{2^{-mnj_{0}/p_{0}}}{|Q|^{m/p_{0}}}\nonumber\end{eqnarray}$$$Q$ with center at $x$ and $(j_{1},\ldots ,j_{m})\neq (0,\ldots ,0),$ where $j_{0}=\max _{k=1,\ldots ,m}\{j_{k}\}$.
Definition 2.3. (Commutators of multilinear square operator)
The commutators of multilinear square operator 
$T_{\unicode[STIX]{x1D706}}$ with BMO functions 
$\vec{b}=(b_{1},b_{2},\ldots ,b_{m})$ are defined by
$$\begin{eqnarray}\displaystyle & & \displaystyle T_{\unicode[STIX]{x1D706},\vec{b}}(\vec{f})(x)=\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big(\frac{t}{|x-z|+t}\Big)^{n\unicode[STIX]{x1D706}}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\bigg|\int _{\mathbb{R}^{mn}}(b_{i}(x)-b_{i}(y_{i}))K_{t}(z,\vec{y})\mathop{\prod }_{j=1}^{m}f_{j}(y_{j})\,d\vec{y}\bigg|^{2}\frac{dz\,dt}{t^{n+1}}\Big)^{1/2},\end{eqnarray}$$ for any 
$\vec{f}=(f_{1},\ldots ,f_{m})\in {\mathcal{S}}(\mathbb{R}^{n})\times \cdots \times {\mathcal{S}}(\mathbb{R}^{n})$ and all 
$x\notin \bigcap _{j=1}^{m}\text{supp}f_{j}.$
We may obtain the following weighted estimates.
Lemma 2.3. Let 
$T_{\unicode[STIX]{x1D706}}$ be the multilinear square function with a kernel satisfying conditions (H1), (H2) and (H3) for some 
$1\leqslant p_{0}<\infty .$ Then, for any 
$p_{0}\leqslant p_{1},\ldots ,p_{m}<\infty$, 
$1/p=1/p_{1}+\cdots +1/p_{m}$ and 
$\vec{\unicode[STIX]{x1D714}}\in A_{\vec{P}/p_{0}}$, the following weighted estimates hold.
(i) If there is no
$p_{i}=p_{0}$, then $\Vert T_{\unicode[STIX]{x1D706}}(\vec{f})\Vert _{L^{p}(\unicode[STIX]{x1D708}_{\vec{w}})}\leqslant C\prod _{i=1}^{m}\Vert f_{i}\Vert _{L^{p_{i}}(w_{i})}.$(ii) If there is a
$p_{i}=p_{0}$, then $\Vert T_{\unicode[STIX]{x1D706}}(\vec{f})\Vert _{L^{p,\infty }(\unicode[STIX]{x1D708}_{\vec{w}})}\leqslant C\prod _{i=1}^{m}\Vert f_{i}\Vert _{L^{p_{i}}(w_{i})}.$
As for the commutators of 
$T$, we obtain the following weighted estimates.
Lemma 2.4. Let 
$T_{\unicode[STIX]{x1D706}}$ be the multilinear square function with a kernel satisfying conditions (H1), (H2) and (H3) for some 
$1\leqslant p_{0}<\infty$. Let 
$\vec{b}\in BMO^{m}$. Then, for any 
$p_{0}<p_{1},\ldots ,p_{m}<\infty$, 
$1/p=1/p_{1}+\cdots +1/p_{m}$ and 
$\vec{\unicode[STIX]{x1D714}}\in A_{\vec{P}/p_{0}}$, we have
$$\begin{eqnarray}||T_{\unicode[STIX]{x1D706},\vec{b}}\vec{f}||_{L^{p}(\unicode[STIX]{x1D708}_{\vec{\unicode[STIX]{x1D714}}})}\leqslant C||\vec{b}||_{BMO}\mathop{\prod }_{i=1}^{m}||f_{i}||_{L^{p_{i}}(\unicode[STIX]{x1D714}_{i})},\end{eqnarray}$$ where 
$||\vec{b}||_{BMO}=\max _{j}||b_{j}||_{BMO}.$
Lemma 2.5. Let 
$T_{\unicode[STIX]{x1D706}}$ be the multilinear square function with a kernel satisfying conditions (H1), (H2) and (H3) for some 
$1\leqslant p_{0}<\infty$. Let 
$\vec{b}\in BMO^{m}$. Let 
$\vec{\unicode[STIX]{x1D714}}\in A_{(1,\ldots ,1)}$ and 
$\vec{b}\in BMO^{m}.$ Then, there exists a constant 
$C$ (depending on 
$\vec{b}$) such that
$$\begin{eqnarray}\unicode[STIX]{x1D708}_{\vec{\unicode[STIX]{x1D714}}}(\big\{x\in \mathbb{R}^{n}:|T_{\unicode[STIX]{x1D706},\vec{b}}\vec{f}(x)|>t^{m}\big\})\leqslant C\mathop{\prod }_{j=1}^{m}\Big(\int _{\mathbb{R}^{n}}\unicode[STIX]{x1D6F7}\Big(\frac{|f_{j}(x)|}{t}\Big)\unicode[STIX]{x1D714}_{j}(x)\,dx\Big)^{1/m},\end{eqnarray}$$ where 
$\unicode[STIX]{x1D6F7}(t)=t^{p_{0}}(1+\log ^{+}t)^{p_{0}}$.
Remark 2.4. The proofs of Lemmas 2.3–2.5 are almost the same as the [Reference Zengyan, Xue and Yabuta28, proofs of Theorems 1.3–1.5] with few modifications, so we omit them here.
With Propositions 2.1–2.2 and Lemmas 2.3–2.5 in hand, the proofs of Theorems 1.1 and 1.2 will be quite direct.
2.3 Proofs of Theorems 1.1 and 1.2.
Proof. (a) The case 
$p_{0}>2n/s$. By Proposition 2.1 and Proposition 2.2, it is easy to see that the associated kernel of 
$\mathfrak{T}_{\unicode[STIX]{x1D706},m}$ satisfies the conditions (H2) and (H3). Since we have supposed (H1) from the beginning, applying Lemmas 2.3–2.5, we obtain the desired conclusions in Theorems 1.1 and 1.2.
(b) The case 
$p_{0}=2n/s$. By the property of 
$A_{p}$ weights, there exists a real number 
$\tilde{p}_{0}$ satisfying 
$p_{0}=2n/s<\tilde{p}_{0}<\min (p_{1},p_{2},2)$ and 
$\vec{\unicode[STIX]{x1D714}}\in A_{\vec{p}/\tilde{p}_{0}}$ (see [Reference Bui and Duong1] or [Reference Lerner, Ombrosi, Pérez, Torres and Trujillo-González19]). Therefore, by step (a), we finish the proofs of Theorems 1.1 and 1.2.
3 An example
In this section, an example will be given to show that there are some multilinear Fourier multiplier operators 
$\mathfrak{T}_{\unicode[STIX]{x1D706},m}$ which are bounded from 
$L^{q_{1}}\times L^{q_{2}}$ to 
$L^{q}$. Thus, the assumption that 
$\mathfrak{T}_{\unicode[STIX]{x1D706},m}$ is bounded from 
$L^{q_{1}}\times L^{q_{2}}$ into 
$L^{q,\infty }$ in Theorems 1.1–1.2 is reasonable.
Denote 
$h_{t}(x,u)=(1+|x-u|/t)^{-n\unicode[STIX]{x1D706}}$. The bilinear Fourier multiplier operators 
$\mathfrak{T}_{\unicode[STIX]{x1D706},m}$ can be written as
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathfrak{T}_{\unicode[STIX]{x1D706},m}(f_{1},f_{2})(x)=\Big(\iint _{\mathbb{R}_{+}^{n+1}}\Big|\int _{(\mathbb{R}^{n})^{2}}e^{2\unicode[STIX]{x1D70B}ix\cdot (\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,m(t\unicode[STIX]{x1D709}_{1},t\unicode[STIX]{x1D709}_{2})\hat{f}_{1}(\unicode[STIX]{x1D709}_{1})\hat{f}_{2}(\unicode[STIX]{x1D709}_{2})\,d\unicode[STIX]{x1D709}_{1}\,d\unicode[STIX]{x1D709}_{2}\Big|^{2}h_{t}(x,u)\frac{du\,dt}{t^{n+1}}\Big)^{1/2}.\nonumber\end{eqnarray}$$First, we consider its bilinearization in the following form:
$$\begin{eqnarray}\displaystyle & & \displaystyle \widetilde{{\mathcal{T}}}_{\unicode[STIX]{x1D706},m}(\vec{f})(x)\nonumber\\ \displaystyle & & \displaystyle \quad =\iint _{\mathbb{R}_{+}^{n+1}}\int _{(\mathbb{R}^{n})^{4}}e^{2\unicode[STIX]{x1D70B}ix\cdot (\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D709}_{3}+\unicode[STIX]{x1D709}_{4})}m(t\unicode[STIX]{x1D709}_{1},t\unicode[STIX]{x1D709}_{2})m(t\unicode[STIX]{x1D709}_{3},t\unicode[STIX]{x1D709}_{4})\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\mathop{\prod }_{i=1}^{4}\hat{f}_{i}(\unicode[STIX]{x1D709}_{i})\,d\unicode[STIX]{x1D709}_{i}\,h_{t}(x,u)\frac{du\,dt}{t^{n+1}}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{(\mathbb{R}^{n})^{4}}\iint _{\mathbb{R}_{+}^{n+1}}e^{2\unicode[STIX]{x1D70B}ix\cdot (\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D709}_{3}+\unicode[STIX]{x1D709}_{4})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,m(t\unicode[STIX]{x1D709}_{1},t\unicode[STIX]{x1D709}_{2})m(t\unicode[STIX]{x1D709}_{3},t\unicode[STIX]{x1D709}_{4})\,\Big(1+\frac{|x-u|}{t}\Big)^{-n\unicode[STIX]{x1D706}}\frac{du\,dt}{t^{n+1}}\mathop{\prod }_{i=1}^{4}\hat{f}_{i}(\unicode[STIX]{x1D709}_{i})\,d\unicode[STIX]{x1D709}_{i}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{(\mathbb{R}^{n})^{4}}\Big(\iint _{\mathbb{R}_{+}^{n+1}}e^{-2\unicode[STIX]{x1D70B}itu\cdot (\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D709}_{3}+\unicode[STIX]{x1D709}_{4})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,m(t\unicode[STIX]{x1D709}_{1},t\unicode[STIX]{x1D709}_{2})m(t\unicode[STIX]{x1D709}_{3},t\unicode[STIX]{x1D709}_{4})\,(1+|u|)^{-n\unicode[STIX]{x1D706}}\frac{du\,dt}{t^{n+1}}\Big)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,e^{2\unicode[STIX]{x1D70B}ix\cdot (\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D709}_{3}+\unicode[STIX]{x1D709}_{4})}\mathop{\prod }_{i=1}^{4}\hat{f}_{i}(\unicode[STIX]{x1D709}_{i})\,d\unicode[STIX]{x1D709}_{i}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{(\mathbb{R}^{n})^{4}}e^{2\unicode[STIX]{x1D70B}ix\cdot (\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D709}_{3}+\unicode[STIX]{x1D709}_{4})}\tilde{m}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},\unicode[STIX]{x1D709}_{3},\unicode[STIX]{x1D709}_{4})\mathop{\prod }_{i=1}^{4}\hat{f}_{i}(\unicode[STIX]{x1D709}_{i})\,d\unicode[STIX]{x1D709}_{i}\nonumber\end{eqnarray}$$where
$$\begin{eqnarray}\displaystyle & & \displaystyle \tilde{m}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},\unicode[STIX]{x1D709}_{3},\unicode[STIX]{x1D709}_{4})\nonumber\\ \displaystyle & & \displaystyle \quad =\iint _{\mathbb{R}_{+}^{n+1}}e^{-2\unicode[STIX]{x1D70B}itu\cdot (\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D709}_{3}+\unicode[STIX]{x1D709}_{4})}m(t\unicode[STIX]{x1D709}_{1},t\unicode[STIX]{x1D709}_{2})m(t\unicode[STIX]{x1D709}_{3},t\unicode[STIX]{x1D709}_{4})\,(1+|u|)^{-n\unicode[STIX]{x1D706}}\frac{du\,dt}{t^{n+1}}.\nonumber\end{eqnarray}$$Example 3.1. Suppose that 
$m(0,0)=0$ and there exists some 
$\unicode[STIX]{x1D700}>0$ such that
$$\begin{eqnarray}|\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FC}}m(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})|\leqslant (1+|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|)^{-2n-1-\unicode[STIX]{x1D700}},\quad forall|\unicode[STIX]{x1D6FC}|\leqslant 2n+1.\end{eqnarray}$$ Then, there exists a constant 
$\unicode[STIX]{x1D6FF},$ with 
$0<\unicode[STIX]{x1D6FF}\leqslant 1$, such that
(i)
$\widetilde{{\mathcal{T}}}_{\unicode[STIX]{x1D706},m}$ is bounded from $L^{q_{1}}(\mathbb{R}^{n})\times L^{q_{2}}(\mathbb{R}^{n})\times L^{q_{3}}(\mathbb{R}^{n})\times L^{q_{4}}(\mathbb{R}^{n})$ to $L^{q}(\mathbb{R}^{n})$ for $2-\unicode[STIX]{x1D6FF}<q_{1},q_{2},q_{3},q_{4}<\infty$ with $1/q=1/q_{1}+1/q_{2}+1/q_{3}+1/q_{4}$.(ii)
$\mathfrak{T}_{\unicode[STIX]{x1D706},m}$ is bounded from $L^{q_{1}}(\mathbb{R}^{n})\times L^{q_{2}}(\mathbb{R}^{n})$ to $L^{q}(\mathbb{R}^{n})$ for $2-\unicode[STIX]{x1D6FF}<q_{1},q_{2}<\infty$ with $1/q=1/q_{1}+1/q_{2}$.
Proof. (i) The assumption 
$m(0,0)=0$ and the mean-value theorem gives that 
$|m(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})|\leqslant |\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|$. This together with (3.1) implies that 
$|m(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2})|\leqslant (|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|)^{1/4}/(1+|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|)^{3/4}$ for 
$\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2}\in \mathbb{R}^{n}$. Note that 
$\unicode[STIX]{x1D706}>1$, we have
$$\begin{eqnarray}\displaystyle & & \displaystyle |\tilde{m}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},\unicode[STIX]{x1D709}_{3},\unicode[STIX]{x1D709}_{4})|\nonumber\\ \displaystyle & & \displaystyle \quad =\bigg|\iint _{\mathbb{R}_{+}^{n+1}}e^{-2\unicode[STIX]{x1D70B}itu\cdot (\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D709}_{3}+\unicode[STIX]{x1D709}_{4})}m(t\unicode[STIX]{x1D709}_{1},t\unicode[STIX]{x1D709}_{2})m(t\unicode[STIX]{x1D709}_{3},t\unicode[STIX]{x1D709}_{4})\,(1+|u|)^{-n\unicode[STIX]{x1D706}}\frac{du\,dt}{t^{n+1}}\bigg|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{\mathbb{R}^{n}}(1+|u|)^{-n\unicode[STIX]{x1D706}}\,du\int _{0}^{\infty }\frac{(|t\unicode[STIX]{x1D709}_{1}|+|t\unicode[STIX]{x1D709}_{2}|)^{1/4}}{(1+|t\unicode[STIX]{x1D709}_{1}|+|t\unicode[STIX]{x1D709}_{2}|)^{3/4}}\frac{(|t\unicode[STIX]{x1D709}_{3}|+|t\unicode[STIX]{x1D709}_{4}|)^{1/4}}{(1+|t\unicode[STIX]{x1D709}_{3}|+|t\unicode[STIX]{x1D709}_{4}|)^{3/4}}\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim \int _{0}^{\infty }\frac{(t(|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|))(t(|\unicode[STIX]{x1D709}_{3}|+|\unicode[STIX]{x1D709}_{4}|))^{1/4}}{(1+t(|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|+|\unicode[STIX]{x1D709}_{3}|+|\unicode[STIX]{x1D709}_{4}|))^{3/4}}\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{0}^{\infty }\frac{s^{1/2}}{(1+s)^{3/4}}\frac{ds}{s}<\infty .\nonumber\end{eqnarray}$$ Next we consider the case 
$0<s\leqslant 2n+1$. We get
$$\begin{eqnarray}\displaystyle & & \displaystyle |\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FC}}\tilde{m}(\unicode[STIX]{x1D709}_{1},\unicode[STIX]{x1D709}_{2},\unicode[STIX]{x1D709}_{3},\unicode[STIX]{x1D709}_{4})|\nonumber\\ \displaystyle & & \displaystyle \quad =\Big|\iint _{\mathbb{R}_{+}^{n+1}}\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FC}}\big(e^{-2\unicode[STIX]{x1D70B}itu\cdot (\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D709}_{3}+\unicode[STIX]{x1D709}_{4})}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,m(t\unicode[STIX]{x1D709}_{1},t\unicode[STIX]{x1D709}_{2})m(t\unicode[STIX]{x1D709}_{3},t\unicode[STIX]{x1D709}_{4})\big)\,(1+|u|)^{-n\unicode[STIX]{x1D706}}\frac{du\,dt}{t^{n+1}}\Big|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \mathop{\sum }_{0\leqslant |\unicode[STIX]{x1D6FD}|\leqslant s}\Big|\iint _{\mathbb{R}_{+}^{n+1}}\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD}}\big(m(t\unicode[STIX]{x1D709}_{1},t\unicode[STIX]{x1D709}_{2})m(t\unicode[STIX]{x1D709}_{3},t\unicode[STIX]{x1D709}_{4})\big)\unicode[STIX]{x2202}^{\unicode[STIX]{x1D6FD}}\big(e^{-2\unicode[STIX]{x1D70B}itu\cdot (\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D709}_{3}+\unicode[STIX]{x1D709}_{4})}\big)\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,(1+|u|)^{-n\unicode[STIX]{x1D706}}\frac{du\,dt}{t^{n+1}}\Big|\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim \mathop{\sum }_{0\leqslant |\unicode[STIX]{x1D6FD}|\leqslant s}\int _{\mathbb{R}^{n}}(1+|u|)^{-n\unicode[STIX]{x1D706}}\,du\int _{0}^{\infty }\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\frac{t^{|\unicode[STIX]{x1D6FC}|}}{(1+|t\unicode[STIX]{x1D709}_{1}|+|t\unicode[STIX]{x1D709}_{2}|)^{2n+1+\unicode[STIX]{x1D700}}(1+|t\unicode[STIX]{x1D709}_{3}|+|t\unicode[STIX]{x1D709}_{4}|)^{2n+1+\unicode[STIX]{x1D700}}}\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \quad \lesssim \int _{0}^{\infty }\frac{t^{|\unicode[STIX]{x1D6FC}|}}{(1+t(|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|+|\unicode[STIX]{x1D709}_{3}|+|\unicode[STIX]{x1D709}_{4}|))^{2n+1+\unicode[STIX]{x1D700}}}\frac{dt}{t}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{(|\unicode[STIX]{x1D709}_{1}|+|\unicode[STIX]{x1D709}_{2}|+|\unicode[STIX]{x1D709}_{3}|+|\unicode[STIX]{x1D709}_{4}|)^{|\unicode[STIX]{x1D6FC}|}}\int _{0}^{\infty }\frac{s^{|\unicode[STIX]{x1D6FC}|}}{(1+s)^{2n+1+\unicode[STIX]{x1D700}}}\frac{ds}{s}.\nonumber\end{eqnarray}$$ By Theorem 1 in [Reference Grafakos and Si15], we may obtain that there exists 
$0<\unicode[STIX]{x1D6FF}\leqslant 1$ such that 
$\widetilde{{\mathcal{T}}}_{\unicode[STIX]{x1D706},m}$ is bounded from 
$L^{q_{1}}(\mathbb{R}^{n})\times L^{q_{2}}(\mathbb{R}^{n})\times L^{q_{3}}(\mathbb{R}^{n})\times L^{q_{4}}(\mathbb{R}^{n})$ to 
$L^{q}(\mathbb{R}^{n})$ for 
$2-\unicode[STIX]{x1D6FF}<q_{1},q_{2},q_{3},q_{4}$ with 
$1/q=1/q_{1}+1/q_{2}+1/q_{3}+1/q_{4}$.
(ii) Note that
$$\begin{eqnarray}\displaystyle \mathfrak{T}_{\unicode[STIX]{x1D706},m}(\vec{f})(x)^{2} & = & \displaystyle \iint _{\mathbb{R}_{+}^{n+1}}\int _{(\mathbb{R}^{n})^{4}}e^{2\unicode[STIX]{x1D70B}ix\cdot (\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2}-\unicode[STIX]{x1D709}_{3}-\unicode[STIX]{x1D709}_{4})}\nonumber\\ \displaystyle & & \displaystyle \times \,m(t\unicode[STIX]{x1D709}_{1},t\unicode[STIX]{x1D709}_{2})\overline{m(t\unicode[STIX]{x1D709}_{3},t\unicode[STIX]{x1D709}_{4})}\hat{f}_{1}(\unicode[STIX]{x1D709}_{1})\hat{f}_{2}(\unicode[STIX]{x1D709}_{2})\nonumber\\ \displaystyle & & \displaystyle \times \,\overline{\hat{f}_{1}(\unicode[STIX]{x1D709}_{1})\hat{f}_{2}(\unicode[STIX]{x1D709}_{2})}\,d\unicode[STIX]{x1D709}_{1}\,d\unicode[STIX]{x1D709}_{2}\,d\unicode[STIX]{x1D709}_{3}\,d\unicode[STIX]{x1D709}_{4}\,h_{t}(x,u)\frac{du\,dt}{t^{n+1}}\nonumber\\ \displaystyle & = & \displaystyle \iint _{\mathbb{R}_{+}^{n+1}}\int _{(\mathbb{R}^{n})^{4}}e^{2\unicode[STIX]{x1D70B}ix\cdot (\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2}+\unicode[STIX]{x1D709}_{3}+\unicode[STIX]{x1D709}_{4})}m(t\unicode[STIX]{x1D709}_{1},t\unicode[STIX]{x1D709}_{2})\overline{m(-t\unicode[STIX]{x1D709}_{3},-t\unicode[STIX]{x1D709}_{4})}\nonumber\\ \displaystyle & & \displaystyle \times \,\hat{f}_{1}(\unicode[STIX]{x1D709}_{1})\hat{f}_{2}(\unicode[STIX]{x1D709}_{2})\overline{\hat{f}_{1}(-\unicode[STIX]{x1D709}_{1})\hat{f}_{2}(-\unicode[STIX]{x1D709}_{2})}\,d\unicode[STIX]{x1D709}_{1}\,d\unicode[STIX]{x1D709}_{2}\,d\unicode[STIX]{x1D709}_{3}\,d\unicode[STIX]{x1D709}_{4}\,h_{t}(x,u)\frac{du\,dt}{t^{n+1}}.\nonumber\end{eqnarray}$$ Then, as a consequence of (i), we obtain that 
$\mathfrak{T}_{\unicode[STIX]{x1D706},m}$ is bounded from 
$L^{q_{1}}(\mathbb{R}^{n})\times L^{q_{2}}(\mathbb{R}^{n})$ to 
$L^{q}(\mathbb{R}^{n})$ for 
$2-\unicode[STIX]{x1D6FF}<q_{1},q_{2}<\infty$ with 
$1/q=1/q_{1}+1/q_{2}$.
Acknowledgment
The authors would like to thank the referee for his/her nice comments and suggestions which made this paper more readable.
