Hostname: page-component-7dd5485656-dk7s8 Total loading time: 0 Render date: 2025-10-29T12:06:01.167Z Has data issue: false hasContentIssue false
  • English
  • Français

ON VARIETIES WITH TRIVIAL TANGENT BUNDLE IN CHARACTERISTIC 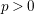$p>0$

Part of: Surfaces and higher-dimensional varieties Special varieties Abelian varieties and schemes Families, fibrations

Published online by Cambridge University Press:  26 June 2019

KIRTI JOSHI Open the ORCID record for KIRTI JOSHI [Opens in a new window]
KIRTI JOSHI*
Affiliation:
Math. Department, University of Arizona, 617 N Santa Rita, Tucson 85721-0089, USA email kirti@math.arizona.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, I give a crystalline characterization of abelian varieties amongst the class of smooth projective varieties with trivial tangent bundles in characteristic 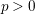$p>0$. Using my characterization, I show that a smooth, projective, ordinary variety with trivial tangent bundle is an abelian variety if and only if its second crystalline cohomology is torsion-free. I also show that a conjecture of KeZheng Li about smooth projective varieties with trivial tangent bundles in characteristic 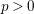$p>0$ is true for smooth projective surfaces. I give a new proof of a result by Li and prove a refinement of it. Based on my characterization of abelian varieties, I propose modifications of Li’s conjecture, which I expect to be true.

MSC classification

Primary: 14K99: None of the above, but in this section 14M99: None of the above, but in this section 14J99: None of the above, but in this section 14D99: None of the above, but in this section

Information

Type
Article
Information
Nagoya Mathematical Journal , Volume 242 , June 2021 , pp. 35 - 51
Check for updates
Copyright
© 2019 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Berthelot, P. and Ogus, A., Notes on crystalline cohomology, Math. Notes 21, Princeton University Press, Princeton, 1978.Google Scholar
Birkenhake, C. and Lange, H., Complex Abelian Varieties, Springer, 2004.Google Scholar
Bombieri, E. and Mumford, D., “Enriques’ classification of surfaces in characteristic p, II”, Complex Analysis and Algebraic Geometry, 23–42. Iwanami Shoten, Tokyo, 1977.Google Scholar
Chai, C.-L., Mumfords example of non-flat $\operatorname{Pic}^{\unicode[STIX]{x1D70F}}$. Unpublished, http://www.math.upenn.edu/∼chai/papers_pdf/mumford_ex.pdf.Google Scholar
Chai, C.-L., Conrad, B. and Oort, F., “Complex multiplication and lifting problems”, in Mathematical Surveys and Monographs 197, American Math. Society, 2014.Google Scholar
Deligne, P. and Illusie, L., Relévements modulo p 2 et decomposition du complexe de de Rham, Invent. Math. 89(2) (1987), 247–270.Google Scholar
Faltings, G. and Chai, C.-L., Degeneration of Abelian Varieties, Ergebnisse de mathematik und ihrer grenzgebiete 22, Springer, 1980.Google Scholar
Fogarty, J. and Mumford, D., Geometric Invariant Theory, Ergebnisse der Mathematik und ihrer Grenzgebiete, Springer.Google Scholar
Hartshorne, R., Algebraic Geometry, Graduate Texts in Mathematics 52, Springer, New York-Heidelberg, 1977.Google Scholar
Igusa, J. i., Some problems in abstract algebraic geometry, Proc. Natl Acad. Sci. USA 41 (1955), 964–967.Google Scholar
Illusie, L., Complexe de de Rham–Witt et cohomologie cristalline, Ann. Sci. Éc. Norm. Supér. 12 (1979), 501–661.Google Scholar
Joshi, K., Exotic torsion, Frobenius splitting and the slope spectral sequence, Canad. Math. Bull. 50(4) (2007), 567–578.Google Scholar
Lang, S., Complex Multiplication, first edition, Grundlehren der mathematischen wissenschaften 255, Springer, New York, 1983.Google Scholar
Lange, H., Hyperelliptic varieties, Tohoku Math. J. 53 (2001), 491–510.Google Scholar
Li, KeZheng, Actions of group schemes, Compos. Math. 80 (1991), 55–74.Google Scholar
Li, KeZheng, Differential operators and automorphism schemes, Sci. China Math. 53(9) (2010), 2363–2380.Google Scholar
Liedtke, C., A note on non-reduced Picard schemes, J. Pure Appl. Algebra 213 (2009), 737–741.Google Scholar
Mehta, V. B. and Srinivas, V., Varieties in positive characteristic with trivial tangent bundle, Compos. Math. 64 (1987), 191–212.Google Scholar
Ogus, A., Supersingular K3-crystals, Asterisque 64 (1979), 3–86.Google Scholar
Yu, C.-F., The isomorphism classes of abelian varieties of CM-type, J. Pure Appl. Algebra 187 (2003), 305–319.Google Scholar