Hostname: page-component-7dd5485656-zlgnt Total loading time: 0 Render date: 2025-10-31T01:23:48.480Z Has data issue: false hasContentIssue false
  • English
  • Français

Improved bounds for skew corner-free sets

Part of: Sequences and sets Extremal combinatorics

Published online by Cambridge University Press:  04 April 2025

ADRIAN BEKER
ADRIAN BEKER*
Affiliation:
Department of Mathematics, Faculty of Science, University of Zagreb, Bijenička cesta 30, 10000 Zagreb, Croatia. e-mail: adrian.beker@math.hr
Get access Rights & Permissions [Opens in a new window]

Abstract

We construct skew corner-free subsets of 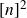$[n]^2$ of size 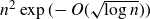$n^2\exp(\!-O(\sqrt{\log n}))$, thereby improving on recent bounds of the form 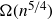$\Omega(n^{5/4})$ obtained by Pohoata and Zakharov. We also prove that any such set has size at most 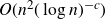$O(n^2(\log n)^{-c})$ for some absolute constant 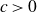$c \gt 0$. This improves on the previously best known upper bound 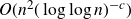$O(n^2(\log\log n)^{-c})$, coming from Shkredov’s work on the corners theorem.

MSC classification

Primary: 11B30: Arithmetic combinatorics; higher degree uniformity
Secondary: 05D99: None of the above, but in this section

Information

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 178 , Issue 2 , March 2025 , pp. 177 - 192
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ajtai, M. and Szemerédi, E.. Sets of lattice points that form no squares. Studia Sci. Math. Hungar. 9 (1974), 9–11.Google Scholar
Behrend, F. A.. On sets of integers which contain no three terms in arithmetical progression. Proc. Nat. Acad. Sci. U.S.A. 32 (1946), 331–332.Google Scholar
Erdös, P. and Turán, P.. On Some Sequences of Integers. J. London Math. Soc. 11 (1936), 261–264.CrossRefGoogle Scholar
Gowers, W. T.. A new proof of Szemerédi’s theorem. Geom. Funct. Anal. 11 (2001), 465–588.CrossRefGoogle Scholar
Gowers, W. T.. A uniform set with fewer than expected arithmetic progressions of length 4. Acta Math. Hungar. 161 (2020), 756–767.CrossRefGoogle Scholar
Green, B.. Progressions of length 3 following Szemerédi, (1999). Manuscript, available at: https://people.maths.ox.ac.uk/greenbj/papers/szemeredi-roth.pdf Google Scholar
Green, B.. An argument of Shkredov in the finite field setting, (2004). Manuscript, available at: https://people.maths.ox.ac.uk/greenbj/papers/corners.pdf.Google Scholar
Green, B.. Finite field models in additive combinatorics. In Surveys in combinatorics. London Math. Soc. Lecture Note Ser. vol. 327 (Cambridge University Press, Cambridge, 2005), pp. 1-27.CrossRefGoogle Scholar
Green, B.. Lower bounds for corner-free sets. New Zealand J. Math. 51 (2021), 1–2.CrossRefGoogle Scholar
Heath-Brown, D. R.. Integer sets containing no arithmetic progressions. J. London Math. Soc. (2) 35 (1987), 385–394.CrossRefGoogle Scholar
Henriot, K.. Bourgain’s bounds for Roth’s theorem, (2013). Manuscript, available at: https://khenriot.wordpress.com/wp-content/uploads/2016/03/bourgainroth.pdf.Google Scholar
Kelley, Z. and Meka, R.. Strong bounds for 3-progressions. In 2023 IEEE 64th Annual Symposium on Foundations of Computer Science, pp. 933–973. IEEE Computer Soc., Los Alamitos, CA.CrossRefGoogle Scholar
Lacey, M. T. and McClain, W.. On an argument of Shkredov on two-dimensional corners. Online J. Anal. Comb. (2007), art. 2, 21.Google Scholar
Meshulam, R.. On subsets of finite abelian groups with no 3-term arithmetic progressions. J. Combin. Theory Ser. A 71 (1995), 168–172.CrossRefGoogle Scholar
Peluse, S.. Finite field models in arithmetic combinatorics – twenty years on. ArXiv:2312.08100.Google Scholar
Peluse, S.. Recent progress on bounds for sets with no three terms in arithmetic progression. Astérisque (2022), no. 1196, 581.Google Scholar
Pohoata, C. and Zakharov, D.. On skew corner-free sets. ArXiv:2401.17507.Google Scholar
Pratt, K.. On generalised corners and matrix multiplication. ArXiv:2309.03878.Google Scholar
Pratt, K.. A variant of the corners problem. MathOverflow (2023), https://mathoverflow.net/questions/451580/a-variant-of-the-corners-problem.Google Scholar
Roth, K. F.. On certain sets of integers. J. London Math. Soc. 28 (1953), 104–109.CrossRefGoogle Scholar
Schmidt, W. M.. Diophantine Approximation, volume 785 of Lecture Notes in Math. vol. 785 (Springer, Berlin, 1980).Google Scholar
Shkredov, I. D.. On a generalisation of Szemerédi’s theorem. Proc. London Math. Soc. (3) 93 (2006), 723–760.CrossRefGoogle Scholar
Solymosi, J.. Note on a generalisation of Roth’s theorem. In Discrete Comput. Geom. Algorithms Combin. vol 25 (Springer, Berlin, 2003), pp. 825–827.CrossRefGoogle Scholar
Szemerédi, E.. Integer sets containing no arithmetic progressions. Acta Math. Hungar. 56 (1990), 155–158.CrossRefGoogle Scholar