Hostname: page-component-7dd5485656-wjfd9 Total loading time: 0 Render date: 2025-10-31T08:47:17.242Z Has data issue: false hasContentIssue false
  • English
  • Français

Generating the liftable mapping class groups of regular cyclic covers

Part of: Low-dimensional topology

Published online by Cambridge University Press:  10 March 2025

SOUMYA DEY ,
NEERAJ K. DHANWANI ,
HARSH PATIL  and
KASHYAP RAJEEVSARATHY
SOUMYA DEY
Affiliation:
Krea University, 5655, Central Expressway, Sri City, Andhra Pradesh 517646, India e-mail: soumya.sxccal@gmail.com URL: https://sites.google.com/site/soumyadeymathematics
NEERAJ K. DHANWANI
Affiliation:
Department of Mathematical Sciences, Indian Institute of Science Education and Research Mohali, Knowledge city, Sector 81, SAS Nagar, Manauli PO 140306, India e-mail: neerajk.dhanwani@gmail.com
HARSH PATIL
Affiliation:
Department of Mathematics, University of Bristol, Beacon House, Queens Road, Bristol, BS8 1QU, UK e-mail: cr22307@bristol.ac.uk
KASHYAP RAJEEVSARATHY
Affiliation:
Department of Mathematics, Indian Institute of Science Education and Research Bhopal, Bhopal Bypass Road, Bhauri, Bhopal 462 066, Madhya Pradesh, India e-mail: kashyap@iiserb.ac.in URL: https://home.iiserb.ac.in/~kashyap/
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 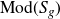$\mathrm{Mod}(S_g)$ be the mapping class group of the closed orientable surface of genus 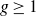$g \geq 1$, and let 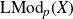$\mathrm{LMod}_{p}(X)$ be the liftable mapping class group associated with a finite-sheeted branched cover 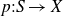$p:S \to X$, where X is a hyperbolic surface. For 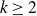$k \geq 2$, let 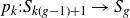$p_k: S_{k(g-1)+1} \to S_g$ be the standard k-sheeted regular cyclic cover. In this paper, we show that 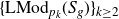$\{\mathrm{LMod}_{p_k}(S_g)\}_{k \geq 2}$ forms an infinite family of self-normalising subgroups in 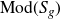$\mathrm{Mod}(S_g)$, which are also maximal when k is prime. Furthermore, we derive explicit finite generating sets for $\mathrm{LMod}_{p_k}(S_g)$ for $g \geq 3$ and $k \geq 2$, and $\mathrm{LMod}_{p_2}(S_2)$. For $g \geq 2$, as an application of our main result, we also derive a generating set for $\mathrm{LMod}_{p_2}(S_g) \cap C_{\mathrm{Mod}(S_g)}(\iota)$, where $C_{\mathrm{Mod}(S_g)}(\iota)$ is the centraliser of the hyperelliptic involution $\iota \in \mathrm{Mod}(S_g)$. Let $\mathcal{L}$ be the infinite ladder surface, and let $q_g : \mathcal{L} \to S_g$ be the standard infinite-sheeted cover induced by $\langle h^{g-1} \rangle$ where h is the standard handle shift on $\mathcal{L}$. As a final application, we derive a finite generating set for $\mathrm{LMod}_{q_g}(S_g)$ for 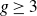$g \geq 3$.

MSC classification

Secondary: 57M60: Group actions in low dimensions

Information

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 178 , Issue 2 , March 2025 , pp. 157 - 176
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

N. Agarwal, S. Dey, Dhanwani, N. K. and Rajeevsarathy, K.. Liftable mapping class groups of regular cyclic covers. Houston J. Math. 47(1) (2021), 223–243.Google Scholar
Aoki, H.. On Siegel paramodular forms of degree 2 with small levels. Internat. J. Math. 27(2) (2016), 1650011, 20.CrossRefGoogle Scholar
J. Aramayona and N. G. Vlamis. Big mapping class groups: an overview. In the Tradition of Thurston: Geometry and Topology, (Springer, 2020), chapter 12, pages 459–496.Google Scholar
Berrick, A. J., Gebhardt, V. and Paris, L.. Finite index subgroups of mapping class groups. Proc. Lond. Math. Soc. (3), 108(3) (2014), 575–599.CrossRefGoogle Scholar
Birman, J. S. and Hilden, H. M.. On the mapping class groups of closed surfaces as covering spaces. In Advances in the Theory of Riemann Surfaces (Proc. Conf., Stony Brook, N.Y., 1969), Ann. of Math. Studies, no. 66 (1971), pages 81–115.CrossRefGoogle Scholar
Birman, J. S. and Hilden, H. M.. Isotopies of homeomorphisms of Riemann surfaces and a theorem about Artin’s braid group. Bull. Amer. Math. Soc. 78 (1972), 1002–1004.CrossRefGoogle Scholar
Birman, J. S. and Hilden, H. M.. On isotopies of homeomorphisms of Riemann surfaces. Ann. of Math. (2), 97 (1973), 424–439.CrossRefGoogle Scholar
Cohen, F. R.. On the mapping class groups for punctured spheres, the hyperelliptic mapping class groups, ${\mathrm{SO}}(3)$ , and ${\mathrm{Spin}}^c(3)$ . Amer. J. Math. 115(2) (1993), 389–434.CrossRefGoogle Scholar
Diamantis, N., Knopp, M., Mason, G., and O’Sullivan, C.. L-functions of second-order cusp forms. Ramanujan J. 12(3) (2006), 327–347.CrossRefGoogle Scholar
Benson, F. and Margalit, D.. A Primer on Mapping Class Groups, Princeton Mathematical Series, vol.49 (Princeton University Press, Princeton, NJ, 2012).Google Scholar
Ghaswala, T.. The liftable mapping class group. PhD. thesis. University of Waterloo (2017).Google Scholar
Ghaswala, T. and McLeay, A.. Mapping class groups of covers with boundary and braid group embeddings. Algebr. Geom. Topol. 20(1) (2020), 239–278.CrossRefGoogle Scholar
Ghaswala, T. and Winarski, R. R.. The liftable mapping class group of balanced superelliptic covers. New York J. Math. 23 (2017), 133–164.Google Scholar
Ghaswala, T. and Winarski, R. R.. Lifting homeomorphisms and cyclic branched covers of spheres. Michigan Math. J. 66(4) (2017), 885–890.CrossRefGoogle Scholar
Ibukiyama, T. and Onodera, F.. On the graded ring of modular forms of the Siegel paramodular group of level 2. Abh. Math. Sem. Univ. Hamburg 67 (1997), 297–305.CrossRefGoogle Scholar
Johnson, D.. The structure of the torelli group I: a finite set of generators for J. Ann. of Math. 118(3) (1983), pages 423–442.CrossRefGoogle Scholar
Kawazumi, N.. Homology of hyperelliptic mapping class groups for surfaces. Topology Appl. 76(3) (1997), 203–216.CrossRefGoogle Scholar
Lickorish, W. B. R.. A finite set of generators for the homeotopy group of a 2-manifold. Proc. Camb. Phil. Soc. 60 (1964), 769–778.Google Scholar
Margalit, D.. Problems, questions, and conjectures about mapping class groups. In Breadth in Contemporary Topology. Proc. Sympos. Pure Math., vol. 102. (Amer. Math. Soc., Providence, RI, 2019), pages 157–186.CrossRefGoogle Scholar
Margalit, D. and Winarski, R. R.. Braids groups and mapping class groups: the Birman–Hilden theory. Bull. London Math. Soc. 53(3) (2021), 643–659.Google Scholar
McCullough, D. and Miller, A.. The genus 2 Torelli group is not finitely generated. Topology Appl., 22(1):43–49, 1986.CrossRefGoogle Scholar
Miyake, T.. Modular Forms. Springer Monogr. Math. (Springer-Verlag, Berlin, english edition, 2006). Translated from the 1976 Japanese original by Yoshitaka Maeda.Google Scholar
Nakamura, G. and Nakanishi, T.. Generation of finite subgroups of the mapping class group of genus 2 surface by Dehn twists. J. Pure Appl. Algebra 222(11) (2018), 3585–3594.CrossRefGoogle Scholar
Rajeevsarathy, K. and Sanghi, A.. Metacyclic actions on surfaces. Journal of Topology and Analysis. https://doi.org/10.1142/S1793525324500420.Google Scholar
Roberts, B. and Schmidt, R.. On modular forms for the paramodular groups. In Automorphic Forms and Zeta Functions. (World Scientific Publishing, Hackensack, NJ, 2006), pages 334–364.CrossRefGoogle Scholar
Stein, W.. Modular Forms, a Computational Approach, Graduate Stud. in Math. vol. 79. (American Mathematical Society, Providence, RI, 2007). With an appendix by Paul E. Gunnells.CrossRefGoogle Scholar