Hostname: page-component-7dd5485656-kp629 Total loading time: 0 Render date: 2025-10-31T00:57:37.291Z Has data issue: false hasContentIssue false
  • English
  • Français

DT INVARIANTS FROM VERTEX ALGEBRAS

Part of: Projective and enumerative geometry Lie algebras and Lie superalgebras Representation theory of rings and algebras

Published online by Cambridge University Press:  20 September 2024

Vladimir Dotsenko Open the ORCID record for Vladimir Dotsenko [Opens in a new window]  and
Sergey Mozgovoy
Vladimir Dotsenko*
Affiliation:
Institut de Recherche Mathématique Avancée, UMR 7501, Université de Strasbourg et CNRS, 7 rue René-Descartes, 67000 Strasbourg, France
Sergey Mozgovoy
Affiliation:
School of Mathematics, Trinity College Dublin, Dublin 2, Ireland and Hamilton Mathematics Institute, Dublin 2, Ireland (mozgovoy@maths.tcd.ie)
*
vdotsenko@unistra.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We obtain a new interpretation of the cohomological Hall algebra 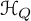$\mathcal {H}_Q$ of a symmetric quiver Q in the context of the theory of vertex algebras. Namely, we show that the graded dual of 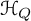$\mathcal {H}_Q$ is naturally identified with the underlying vector space of the principal free vertex algebra associated to the Euler form of Q. Properties of that vertex algebra are shown to account for the key results about 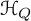$\mathcal {H}_Q$. In particular, it has a natural structure of a vertex bialgebra, leading to a new interpretation of the product of 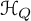$\mathcal {H}_Q$. Moreover, it is isomorphic to the universal enveloping vertex algebra of a certain vertex Lie algebra, which leads to a new interpretation of Donaldson–Thomas invariants of Q (and, in particular, re-proves their positivity). Finally, it is possible to use that vertex algebra to give a new interpretation of CoHA modules made of cohomologies of non-commutative Hilbert schemes.

Keywords

cohomological Hall algebrasvertex Lie algebrasymmetric quivernon-commutative Hilbert scheme

MSC classification

Primary: 17B69: Vertex operators; vertex operator algebras and related structures
Secondary: 14N35: Gromov-Witten invariants, quantum cohomology, Gopakumar-Vafa invariants, Donaldson-Thomas invariants 16G20: Representations of quivers and partially ordered sets

Information

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 24 , Issue 1 , January 2025 , pp. 291 - 339
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Arakawa, T. Representation theory of -algebras. Invent. Math. 169(2) (2007), 219–320.CrossRefGoogle Scholar
Bergman, G. M. The diamond lemma for ring theory. Adv. Math. 29(2) (1978), 178–218.CrossRefGoogle Scholar
Bojko, A. Wall-crossing for zero-dimensional sheaves and Hilbert schemes of points on Calabi–Yau 4-folds. https://arxiv.org/abs/2102.01056 (2021).Google Scholar
Borcherds, R. E. Vertex algebras, Kac-Moody algebras, and the Monster. Proc. Nat. Acad. Sci. USA 83(10) (1986), 3068–3071.CrossRefGoogle ScholarPubMed
Bridgeland, T. and Laredo, V. T. Stability conditions and Stokes factors. Invent. Math. 187(1) (2012), 61–98.CrossRefGoogle Scholar
Carlitz, L. and Riordan, J. Two element lattice permutation numbers and their $q$ -generalization. Duke Math. J. 31 (1964), 371–388.Google Scholar
Chriss, N. and Ginzburg, V. Representation Theory and Complex Geometry. Boston, MA: Birkhäuser, (1997).Google Scholar
Davison, B. The critical CoHA of a quiver with potential. Q. J. Math. 68(2) (2017), 635–703.CrossRefGoogle Scholar
Davison, B. and Meinhardt, S. Cohomological Donaldson-Thomas theory of a quiver with potential and quantum enveloping algebras. Invent. Math. 221(3) (2020), 777–871.CrossRefGoogle Scholar
Dotsenko, V. Parking functions and vertex operators. Selecta Math. (N.S.) 14(2) (2009), 229–245.CrossRefGoogle Scholar
Dotsenko, V., Feigin, E. and Reineke, M. Koszul algebras and Donaldson–Thomas invariants. Lett. Math. Phys. 112(5) (2022), Paper No. 106, 39 pp.CrossRefGoogle Scholar
Dotsenko, V. and Tamaroff, P. Endofunctors and Poincaré–Birkhoff–Witt theorems. Int. Math. Res. Not. IMRN 2021(16) (2021), 12670–12690.CrossRefGoogle Scholar
Edidin, D. and Graham, W. Equivariant intersection theory. Invent. Math. 131(3) (1998), 595–634.CrossRefGoogle Scholar
Efimov, A. I. Cohomological Hall algebra of a symmetric quiver. Compos. Math. 148(4) (2012), 1133–1146.CrossRefGoogle Scholar
Engel, J. and Reineke, M. Smooth models of quiver moduli. Math. Z. 262(4) (2009), 817–848.CrossRefGoogle Scholar
Feĭgin, B. L. and Stoyanovskiĭ, A. V. Functional models of the representations of current algebras, and semi-infinite Schubert cells. Funktsional. Anal. i Prilozhen. 28(1) (1994), 68–90, 96.Google Scholar
Franzen, H. On Chow Rings of Fine Quiver Moduli and Modules over the Cohomological Hall Algebra. PhD dissertation, Wuppertal University, (2014).Google Scholar
Franzen, H. On cohomology rings of non-commutative Hilbert schemes and CoHa-modules. Math. Res. Lett. 23(3) (2016), 805–840.CrossRefGoogle Scholar
Franzen, H. and Mozgovoy, S. Tautological bases of CoHA modules. https://arxiv.org/abs/2111.10114 (2021).Google Scholar
Frenkel, E. and Ben-Zvi, D. Vertex Algebras and Algebraic Curves, vol 88 (2004), second edn. Mathematical Surveys and Monographs. Providence, RI: American Mathematical Society.Google Scholar
Frenkel, I. B. and Kac, V. G. Basic representations of affine Lie algebras and dual resonance models. Invent. Math. 62(1) (1980/81), 23–66.CrossRefGoogle Scholar
Frenkel, I. B., Lepowsky, J. and Meurman, A. A natural representation of the Fischer-Griess Monster with the modular function $J$ as character. Proc. Nat. Acad. Sci. USA 81(10) (1984), 3256–3260.CrossRefGoogle Scholar
Frenkel, I. B., Lepowsky, J., and Meurman, A. Vertex Operator Algebras and the Monster, vol. 134 (1988). Pure and Applied Mathematics. Boston, MA: Academic Press Inc. Google Scholar
Getzler, E. Mixed Hodge structures of configuration spaces. https://arxiv.org/abs/alg-geom/9510018 (1995).Google Scholar
Green, J. A. Hall algebras, hereditary algebras and quantum groups. Invent. Math. 120(2) (1995), 361–377.CrossRefGoogle Scholar
Grojnowski, I. Instantons and affine algebras I: the Hilbert scheme and vertex operators. Math. Res. Lett. 3(2) (1996), 275–291.CrossRefGoogle Scholar
Gross, J. The homology of moduli stacks of complexes. https://arxiv.org/abs/1907.03269 (2019).Google Scholar
Gross, J., Joyce, D. and Tanaka, Y. Universal structures in $\mathbb{C}$ -linear enumerative invariant theories. SIGMA Symmetry Integrability Geom. Methods Appl. 18 (2022), Paper No. 068, 61 pp.Google Scholar
Han, J., Li, H. and Xiao, Y. Cocommutative vertex bialgebras”. J. Algebra 598 (2022), 536–569.CrossRefGoogle Scholar
Harvey, J. A. and Moore, G. On the algebras of BPS states. Comm. Math. Phys. 197(3) (1998), 489–519.CrossRefGoogle Scholar
Heinloth, F. A note on functional equations for zeta functions with values in Chow motives. Ann. Inst. Fourier (Grenoble) 57(6) (2007), 1927–1945.CrossRefGoogle Scholar
Joyce, D. Configurations in abelian categories. II. Ringel-Hall algebras. Adv. Math. 210(2) (2007), 635–706.CrossRefGoogle Scholar
Joyce, D. Ringel-Hall style vertex algebra and Lie algebra structures on the homology of moduli spaces. https://people.maths.ox.ac.uk/joyce/hall.pdf (2018).Google Scholar
Kac, V. Vertex Algebras for Beginners, vol. 10 (1997). University Lecture Series. Providence, RI: American Mathematical Society.Google Scholar
Kontsevich, M. and Soibelman, Y. Stability structures, motivic Donaldson-Thomas invariants and cluster transformations. https://arxiv.org/abs/0811.2435 (2008).Google Scholar
Kontsevich, M. and Soibelman, Y. Cohomological Hall algebra, exponential Hodge structures and motivic Donaldson-Thomas invariants. Commun. Num. Theor. Phys. 5 (2011), 231–352.CrossRefGoogle Scholar
Latyntsev, A. Cohomological Hall algebras and vertex algebras. https://arxiv.org/abs/2110.14356 (2021).Google Scholar
Lehn, M. Chern classes of tautological sheaves on Hilbert schemes of points on surfaces. Invent. Math. 136(1) (1999), 157–207.CrossRefGoogle Scholar
Lehn, M. and Sorger, C. Symmetric groups and the cup product on the cohomology of Hilbert schemes. Duke Math. J. 110(2) (2001), 345–357.CrossRefGoogle Scholar
Lepowsky, J. and Li, H. Introduction to Vertex Operator Algebras and Their Representations, vol. 227. Progress in Mathematics. Boston, MA: Birkhäuser (2004).CrossRefGoogle Scholar
Li, H. Local systems of vertex operators, vertex superalgebras and modules. J. Pure Appl. Algebra 109(2) (1996), 143–195.CrossRefGoogle Scholar
Li, H. A smash product construction of nonlocal vertex algebras. Commun. Contemp. Math. 9(5) (2007), 605–637.CrossRefGoogle Scholar
Li, W., Qin, Z. and Wang, W. Vertex algebras and the cohomology ring structure of Hilbert schemes of points on surfaces. Math. Ann. 324(1) (2002), 105–133.CrossRefGoogle Scholar
Loday, J.-L. Generalized bialgebras and triples of operads. Astérisque 320 (2008), x+116.Google Scholar
Lusztig, G. Quivers, perverse sheaves, and quantized enveloping algebras. J. Amer. Math. Soc. 4(2) (1991), 365–365.CrossRefGoogle Scholar
Macdonald, I. G. Symmetric Functions and Hall Polynomials, second edn. Oxford Classic Texts in the Physical Sciences. New York: The Clarendon Press, Oxford University Press (2015).Google Scholar
Milas, A. and Penn, M. Lattice vertex algebras and combinatorial bases: general case and W-algebras. New York J. Math. 18 (2012), 621–650.Google Scholar
Mozgovoy, S. A computational criterion for the Kac conjecture. J. Algebra 318(2) (2007), 669–679.CrossRefGoogle Scholar
Nakajima, H. Heisenberg algebra and Hilbert schemes of points on projective surfaces. Ann. of Math. (2) 145(2) (1997), 379–388.CrossRefGoogle Scholar
Nakajima, H. Quiver varieties and finite-dimensional representations of quantum affine algebras. J. Amer. Math. Soc. 14(1) (2001), 145–238.CrossRefGoogle Scholar
Primc, M. Vertex algebras generated by Lie algebras. J. Pure Appl. Algebra 135(3) (1999), 253–293.CrossRefGoogle Scholar
Quillen, D. Rational homotopy theory. Ann. of Math. (2) 90 (1969), 205–295.CrossRefGoogle Scholar
Rapčák, M., Soibelman, Y., Yang, Y. and Zhao, G. Cohomological Hall algebras, vertex algebras and instantons. Comm. Math. Phys. 376(3) (2020), 1803–1873.CrossRefGoogle Scholar
Reineke, M. Cohomology of noncommutative Hilbert schemes. Algebr. Represent. Theory 8(4) (2005), 541–561.CrossRefGoogle Scholar
Ringel, C. M. Hall algebras and quantum groups. Invent. Math. 101(3) (1990), 583–591.CrossRefGoogle Scholar
Ringel, C. M. Lie algebras arising in representation theory. In Representations of Algebras and Related Topics (Kyoto, 1990), vol. 168. London Math. Soc. Lecture Note Ser. Cambridge: Cambridge University Press, (1992), 284–291.CrossRefGoogle Scholar
Roitman, M. On free conformal and vertex algebras. J. Algebra 217(2) (1999), 496–527.CrossRefGoogle Scholar
Roitman, M. Combinatorics of free vertex algebras. J. Algebra 255(2) (2002), 297–323.CrossRefGoogle Scholar
Rosellen, M. A course in vertex algebra. https://arxiv.org/abs/math/0607270 (2006).Google Scholar
Schiffmann, O. and Vasserot, E. Cherednik algebras, W-algebras and the equivariant cohomology of the moduli space of instantons on $\mathbf{A}^2$ . Publ. Math. Inst. Hautes Études Sci. 118 (2013), 213–342.CrossRefGoogle Scholar
Schiffmann, O. and Vasserot, E. The elliptic Hall algebra and the K-theory of the Hilbert scheme of $A2$ . Duke Math. J. 162(2) (2013).CrossRefGoogle Scholar
Soibelman, Y. Remarks on cohomological Hall algebras and their representations. In Arbeitstagung Bonn 2013, vol. 319. Progress in Mathematics. Cham: Birkhäuser/Springer, (2016), 355–385.CrossRefGoogle Scholar
Wilson, K. G. Non-Lagrangian models of current algebra. Phys. Rev. (2) 179 (1969), 1499–1512.CrossRefGoogle Scholar
Wilson, K. G. and Zimmermann, W. Operator product expansions and composite field operators in the general framework of quantum field theory. Comm. Math. Phys. 24 (1972), 87–106.CrossRefGoogle Scholar
Xiao, J. Drinfeld double and Ringel-Green theory of Hall algebras. J. Algebra 190(1) (1997), 100–144.CrossRefGoogle Scholar
Yang, Y. and Zhao, G. Cohomological Hall algebras and affine quantum groups. Selecta Math. (N.S.) 24(2) (2018), 1093–1119.CrossRefGoogle Scholar