Let 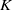 $K$ be a commutative ring with unity,
$K$ be a commutative ring with unity, 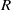 $R$ an associative
$R$ an associative 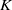 $K$-algebra of characteristic different from
$K$-algebra of characteristic different from 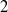 $2$ with unity element and no nonzero nil right ideal, and
$2$ with unity element and no nonzero nil right ideal, and 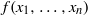 $f({x}_{1} , \ldots , {x}_{n} )$ a multilinear polynomial over
$f({x}_{1} , \ldots , {x}_{n} )$ a multilinear polynomial over 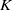 $K$. Assume that, for all
$K$. Assume that, for all 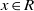 $x\in R$ and for all
$x\in R$ and for all 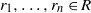 ${r}_{1} , \ldots , {r}_{n} \in R$ there exist integers
${r}_{1} , \ldots , {r}_{n} \in R$ there exist integers 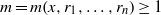 $m= m(x, {r}_{1} , \ldots , {r}_{n} )\geq 1$ and
$m= m(x, {r}_{1} , \ldots , {r}_{n} )\geq 1$ and 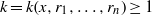 $k= k(x, {r}_{1} , \ldots , {r}_{n} )\geq 1$ such that
$k= k(x, {r}_{1} , \ldots , {r}_{n} )\geq 1$ such that 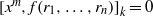 $\mathop{[{x}^{m} , f({r}_{1} , \ldots , {r}_{n} )] }\nolimits_{k} = 0$. We prove that: (1) if
$\mathop{[{x}^{m} , f({r}_{1} , \ldots , {r}_{n} )] }\nolimits_{k} = 0$. We prove that: (1) if 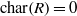 $\text{char} (R)= 0$ then
$\text{char} (R)= 0$ then 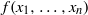 $f({x}_{1} , \ldots , {x}_{n} )$ is central-valued on
$f({x}_{1} , \ldots , {x}_{n} )$ is central-valued on  $R$; and (2) if
$R$; and (2) if 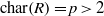 $\text{char} (R)= p\gt 2$ and
$\text{char} (R)= p\gt 2$ and 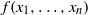 $f({x}_{1} , \ldots , {x}_{n} )$ is not a polynomial identity in
$f({x}_{1} , \ldots , {x}_{n} )$ is not a polynomial identity in  $p\times p$ matrices of characteristic
$p\times p$ matrices of characteristic 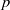 $p$, then
$p$, then 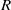 $R$ satisfies
$R$ satisfies 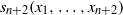 ${s}_{n+ 2} ({x}_{1} , \ldots , {x}_{n+ 2} )$ and for any
${s}_{n+ 2} ({x}_{1} , \ldots , {x}_{n+ 2} )$ and for any 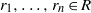 ${r}_{1} , \ldots , {r}_{n} \in R$ there exists
${r}_{1} , \ldots , {r}_{n} \in R$ there exists 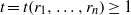 $t= t({r}_{1} , \ldots , {r}_{n} )\geq 1$ such that
$t= t({r}_{1} , \ldots , {r}_{n} )\geq 1$ such that 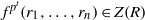 ${f}^{{p}^{t} } ({r}_{1} , \ldots , {r}_{n} )\in Z(R)$, the center of
${f}^{{p}^{t} } ({r}_{1} , \ldots , {r}_{n} )\in Z(R)$, the center of 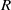 $R$.
$R$.
 $K$-GROUPS
$K$-GROUPS