1. Introduction
A fundamental and important problem in continuum mechanics is the interaction of waves with the inhomogeneity of the medium through which they propagate. The waves could be linear or nonlinear and, in many cases, the inhomogeneity can be modelled as externally imposed through prescribed variable coefficients to a wave-type partial differential equation (PDE) [Reference Chew6]. When the waves and the medium are dynamically coupled, a common occurrence in geophysical fluid dynamics [Reference Bühler3], the problem becomes more challenging to describe analytically. A natural framework to approach this class of problems is to utilize scale separation and derive equations separating the motion of waves and averaged quantities, e.g. the mean fluid density and velocity. While the focus of analytical studies was historically on linear or weakly nonlinear waves interacting with mean flows [Reference Bühler3], a recent body of work has emerged for the case where the waves are strongly nonlinear, i.e. solitons or solitary waves; see, e.g. the review [Reference Ablowitz, Cole, Gennady, Hoefer and Luo1]. A schematic of such wave-mean flow scenarios involving solitary wave interaction with rarefaction and dispersive shock waves is shown in Figure 1.
Figure 1. Scenarios of the solitary wave-mean flow interaction in shallow water waves. (a, c) Solitary wave transmission; (b, d) solitary wave trapping. Reproduced, with permission, from [Reference Ablowitz, Cole, Gennady, Hoefer and Luo1].
For the asymptotic analysis of solitary wave-mean flow interaction, the mean flow is assumed to vary on a much slower spatial scale than the solitary wave width. In this case, the mean flow evolution decouples from solitary wave motion so that the interaction is one-way: only the mean influences the motion of the solitary wave, not vice-versa. This problem was first considered theoretically and experimentally in the unidirectional case where a solitary wave and either a rarefaction wave (RW) mean flow or a dispersive shock wave (DSW) mean flow exhibited an overtaking interaction [Reference Maiden, Anderson, Franco, Gennady and Hoefer40]. Depending on the conditions, the solitary wave was observed to be either transmitted through or trapped by the mean flow as 
$t \to \infty$. The key mathematical insight was the determination of the solitary wave limit of the Whitham modulation equations – a quasi-linear system of first order equations that describe the slow evolution of nonlinear wavetrains [Reference Whitham56] – and its subsequent diagonalization in terms of Riemann invariants. A general approach for obtaining the solitary wave limit in the case of Hamiltonian partial differential equations with a local Hamiltonian can be found in [Reference Benzoni-Gavage, Mietka and Rodrigues52].
While Riemann invariants can in principle be obtained for any system of two quasi-linear, first order PDEs, they are most easily obtained for completely integrable equations such as the Korteweg-de Vries (KdV) equation, either directly [Reference Whitham55] or using the finite gap method [Reference Flaschka, Forest and McLaughlin16, Reference Kamchatnov32]. But Whitham theory can be developed for integrable and non-integrable equations alike [Reference El and Hoefer12]. A recent paper has obtained the diagonalization, i.e. the Riemann invariants, for the non-integrable Benjamin-Bona-Mahony (BBM) equation [Reference Benjamin, Bona and Mahony4] by deriving an exact representation of the solitary wave limit of the BBM-Whitham modulation equations [Reference Gavrilyuk and Shyue20].
One of our main results in this paper is the derivation of the modulation solitary wave limit for the apparently non-integrable Serre-Green-Naghdi (SGN) equations [Reference Green, Laws and Naghdi25, Reference Green and Naghdi26, Reference Serre48, Reference Su and Gardner50] describing long, strongly nonlinear free surface waves on a flat bottom in a fluid of constant density. The Hamiltonian structure of this system is non-local [Reference Gavrilyuk and Teshukov24, Reference Li38], so the generic results of [Reference Benzoni-Gavage, Mietka and Rodrigues52] cannot be used. The SGN system shares many properties with the BBM equation: they have similar dispersion relations and similar nonlocal Hamiltonian structure [Reference Olver46]. Compared to the BBM equation, which is a unidirectional, scalar equation, the SGN system is a Galilean invariant system containing more physics than the BBM equation. The Whitham modulation equations for the SGN equations were obtained in [Reference El, Grimshaw and Smyth10]. Their hyperbolicity was proven in [Reference Tkachenko, Gavrilyuk and Shyue53]. Being second order in time, the SGN equations support bi-directional wave propagation and the resulting solitary wave limit quasi-linear system of the SGN-Whitham equations is third order. In this work, we prove the existence of Riemann invariants if and only if simple waves in the decoupled mean flow equations are considered.
The analysis of unidirectional wave-mean flow interaction has been carried out for solitons and RWs, DSWs for a general class of unidirectional nonlinear dispersive wave equations in [Reference Maiden, Anderson, Franco, Gennady and Hoefer40] by analysing the solitary wave limit of the Whitham modulation equations. In the same paper, the approach was applied to the conduit equation and compared with experiments on viscous fluid conduits. The approach was further refined and applied to the KdV equation [Reference Ablowitz, Cole, Gennady, Hoefer and Luo1] and the modified-KdV equation [Reference van der Sande, El and Hoefer54] where, in addition, the kink (monotone, heteroclinic travelling wave solution) serves as either the wave or the mean flow. The extension to oblique, two-dimensional line solitons interacting with RWs and DSWs was developed for the Kadomtsev-Petviashvili equation in [Reference Ryskamp, Hoefer and Biondini47]. A similar analysis of soliton-mean field interaction was extended to the bi-directional case of the defocusing nonlinear Schrödinger (NLS) equation where, in addition to overtaking interactions, RWs and DSWs experience head-on interactions with solitons [Reference Sprenger, Hoefer and El49].
The soliton-mean flow interaction problem for integrable equations has also been studied using the inverse scattering transform (IST) for the the KdV equation [Reference Ablowitz, Cole, Gennady, Hoefer and Luo1, Reference Ablowitz, Luo and Cole2] and the focusing NLS equation [Reference Biondini, Sitai and Mantzavinos5] where some solitons were shown to leave a trailing “wake” inside the DSW after passing through. Other analytical approaches include perturbation theory [Reference Ablowitz, Cole, Gennady, Hoefer and Luo1], the Darboux transformation [Reference Mucalica and Pelinovsky45], both for KdV soliton-RW interaction, and a Hamiltonian formulation of the problem that borrows ideas from soliton perturbation theory and Whitham theory to obtain an approximate, analytical description of solitary wave-mean flow interaction for a generalized KdV equation [Reference Kamchatnov and Shaykin34] and the NLS equation [Reference Ivanov and Kamchatnov30, Reference Kamchatnov33].
In this paper, we utilise the derived SGN-Whitham equations in the solitary wave limit to analytically describe the head-on and overtaking interaction of a solitary wave and a RW mean flow. The results are then extended to solitary wave-DSW mean flow interaction. One important finding in this paper is that the original approach proposed in [Reference Maiden, Anderson, Franco, Gennady and Hoefer40] and utilised elsewhere [Reference Kamchatnov and Shaykin34] that rely upon the DSW fitting method and its conjugate wavenumber/dispersion relation [Reference El8] to obtain the soliton Riemann invariant is only approximate. By obtaining the exact representation of the solitary wave limit of the SGN-Whitham equations and corresponding Riemann invariants for simple wave mean flows, we are able to prove that the conjugate wavenumber/dispersion yields a second order in amplitude accurate prediction for solitary wave motion through a RW. It also provides a second order accurate prediction for the DSW’s solitary wave edge. Careful numerical simulations of the SGN equations agree with these findings. While this is an improvement to the first order accurate, weakly nonlinear KdV approximation, it identifies a limitation of the DSW fitting approach.
The plan of the paper is as follows. In section 2, we give a detailed presentation of the SGN equations and their periodic travelling wave solutions are presented in section 3. In section 4, the modulation equations are given both in the mass Lagrangian coordinates and in Eulerian coordinates. The reason is that the solitary wave limit is mathematically easier to carry out in Lagrangian coordinates, while the physical interpretation is easier in Eulerian coordinates. In section 5, we study the interaction of solitary waves with RWs and DSWs. In particular, the transmission and trapping effect is studied. The closed-form analytical results are in good agreement with the numerical ones for the SGN equations. Finally, the main technical details (the different forms of the modulation equations, the passage to the solitary limit, numerical method, etc.) are given in four Appendices.
2. Serre–Green–Naghdi equations
The SGN equations over a flat bottom approximating the free-surface Euler equations in the long wave limit are [Reference Green, Laws and Naghdi25, Reference Green and Naghdi26, Reference Serre48, Reference Su and Gardner50]
\begin{align}
&h_t+(h u)_x = 0,
\end{align}
\begin{align}
&u_t+uu_x+ g h_x=\frac{1}{h}\left(\frac{h^3}{3}(u_{xt}+uu_{xx}-
u_x^2)\right)_x,
\end{align}where h is the total depth, u is the depth-averaged horizontal velocity and g is the acceleration due to gravity. In what follows, we scale independent and dependent variables so that g = 1.
The SGN equations (2.1), (2.2) are non-integrable and represent a fully nonlinear generalization of the classical Boussinesq equations. The first equation (2.1) is the exact equation for conservation of mass, and the second equation (2.2) can be manipulated into the equation for conservation of horizontal momentum
\begin{equation}
(h u)_t + \left ( h u^2 + \frac{1}{2} h^2 \right )_x = \left(\frac{h^3}{3} \left ( u_{tx} + u u_{xx} - u_x^2 \right ) \right)_x.
\end{equation}An equivalent form of the momentum equation is
\begin{equation}
(h u)_t + \left( h u^2 + \frac{1}{2} h^2
+\frac{1}{3}h^{2}\frac{d^2h}{dt^2} \right)_x = 0,
\end{equation} where 
$\displaystyle\frac{d}{dt}$ is the material derivative notation,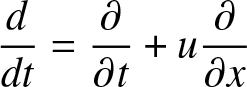 
$\displaystyle \frac{d}{dt}=\frac{\partial }{\partial t}+u\frac{\partial }{\partial x}$ and 
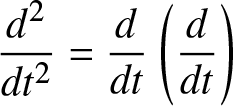$\displaystyle \frac{d^2}{dt^2}=\frac{d}{dt} \left( \frac{d}{dt} \right)$ is the second material derivative. The conservation of energy manifests in the additional conservation law
\begin{equation}
\left(\frac{1}{2} h \left ( h + u^2 + \frac{1}{3} h^2
u_{x}^2 \right ) \right)_t + \left( h u\left ( h +
\frac{1}{2} u^2 + \frac{1}{2} h^2 u_x^2 - \frac{1}{3}
h^2(u_{xt} + u u_{xx} ) \right ) \right)_x =0.
\end{equation} Finally, a fourth conservation law (the so-called Bernoulli conservation law) can be derived. It is usually written for the variable 
$\displaystyle {\cal{K}}=u-\frac{1}{3h}\left(h^3 u_x\right)_x$ representing the tangent component of the fluid velocity at the free surface [Reference Gavrilyuk, Kalisch and Khorsand17]
\begin{equation}
{\cal{K}}_{t}+\left( {\cal{K}} u+h
-\frac{u^{2}}{2}-\frac{1}{2}h_{x}^2 u^2\right)_{x}=0.
\end{equation}A mathematical justification of the SGN model (2.1), (2.2) can be found in [Reference Lannes35, Reference Makarenko42]. Recent years have seen increased activity in both the study of qualitative properties of the solutions to the SGN equations and in the development of numerical discretization techniques [Reference Favrie and Gavrilyuk15, Reference Gavrilyuk and Klein18, Reference Gavrilyuk and Shyue21, Reference Le Métayer, Gavrilyuk and Hank36, Reference Maojun, Guyenne, Fengyan and Liwei43].
The Lagrangian for (2.1), (2.2), where the mass conservation law (2.1) is considered a constraint, is given as [Reference Gavrilyuk and Teshukov24]
\begin{equation}
{\cal L}=\int_{-\infty}^{+\infty}
h\left(\frac{u^{2}}{2}+\frac{1}{6}\left(\frac{dh}{dt}\right)^2
-\frac{h}{2}\right) dx.
\end{equation} In order to obtain analytically tractable expressions, we will make use of mass Lagrangian coordinates introduced as follows. Let 
$h_0(x)$ be the initial position of the free surface and Y be the classical Lagrangian coordinate. The mass Lagrangian coordinate q is defined as 
$\displaystyle q=\int_0^Y h_0(s)ds$. Let 
$x=x(t,q)$ be the trajectories of fluid particles. Since the mass conservation law is in the form 
$\displaystyle h\frac{\partial x}{\partial q}=1$, the Lagrangian (2.7) can be transformed to
\begin{equation}
\tilde {\cal L}=\int_{-\infty}^{+\infty}\left(\frac{u^2}{2}-\tilde
e(\tau, \tau_t)\right)dq,
\end{equation} where 
$\tau=1/h$ and the potential 
$\tilde e (\tau, \tau_t)$ is
\begin{equation}
\tilde e (\tau, \tau_t)=\frac{1}{2\tau}-\frac{1}{6}\left(\frac{\partial}{
\partial t} \left(\frac{1}{\tau}\right)\right)^2 =
\frac{1}{2\tau} -\frac{\tau_t^2}{6\tau^4}.
\end{equation} For a general potential 
$\tilde e(\tau, \tau_t)$, the Euler-Lagrange equations for (2.8) are [Reference Gavrilyuk22]:
\begin{equation}
\tau_{t}- u_{q}=0,\quad u_{t}+p_{q}=0,
\end{equation}where the pressure p is defined by
\begin{equation}
p=-\frac{\delta \tilde e}{\delta \tau} = -\left(\frac{\partial
\tilde e}{\partial \tau}-\frac{\partial }{\partial t}
\left(\frac{\partial \tilde e}{\partial \tau_t}\right)\right).
\end{equation}System (2.10) is reminiscent of the p-system for the barotropic Euler equations. However, in our case, the pressure p defined by (2.11) depends not only on τ, but also on its first and second temporal derivatives. The variable τ is the analogue of the specific volume for the corresponding Euler equations. As a consequence of Noether’s theorem, the variational formulation implies the conservation of energy and Bernoulli equation
\begin{align}
\left( \frac{u^2}{2}+\varepsilon\right)_t+\left( pu\right)_q = 0, \quad
\varepsilon = \tilde e- &\tau_t \tilde e_{\tau_t},
\end{align}
\begin{align}
\left(\tau u-\tau_q\frac{\partial \tilde
e}{\partial\tau_t}\right)_t-\left(\frac{u^2}{2}-\tau p-\tilde
e\right)_q &= 0.
\end{align}that are the analogues of eqs. (2.5) and (2.6). The conservation laws (2.10), (2.12), (2.13) are averaged to obtain the modulation equations in Lagrangian coordinates in Appendix A.
3. Periodic travelling wave solutions
We now present the form of periodic travelling wave solutions in both Eulerian and Lagrangian coordinates. Several parametrisations of the four dimensional family of periodic travelling waves will be presented.
3.1. Eulerian coordinates
The travelling wave solutions 
$h(x,t) = h(\xi) = h(x-ct)$, 
$u(x,t) = u(\xi) = u(x-ct)$ to the SGN equations (2.1), (2.2) are specified by
\begin{align}
&\left(\frac{dh}{d\xi}\right)^2 = \frac{3}{h_1 h_2
h_3}(h-h_1)(h-h_2)(h_3 - h)=\frac{3}{h_1 h_2
h_3}P(h),
\end{align}
\begin{align}
&u=c - \sigma \frac{\sqrt{h_1h_2h_3}}{h},\quad
\sigma = \pm 1,
\end{align} where, similar to the defocusing nonlinear Schrödinger equation, the wave is characterised by four independent parameters h 1, h 2, h 3 (the roots of the third order polynomial P(h)), the travelling wave velocity c, and 
$\sigma=+1$ (
$\sigma=-1$) corresponds to the fast (slow) waves. Here, the depth variations in the wave occur in the interval 
$\left[h_2, h_3\right]$, for 
$ h_1 \lt h_2 \lt h \lt h_3$ with the amplitude 
$a=h_3-h_2$. It is assumed that there are no vacuum points for non-trivial periodic travelling wave solutions: 
$h_1 \gt 0$. The ODE in (3.1) can be integrated to obtain
\begin{equation}
h = h_2 + (h_3- h_2)\mathrm{cn}^2\left
(\frac12\sqrt{\frac{3(h_3 - h_1)}{h_1 h_2 h_3}} \xi
, m\right), \quad m=\frac{h_3 - h_2}{h_3 - h_1},
\end{equation} where 
$\mathrm{cn}$ is the Jacobi cosine elliptic function [Reference McClain44]. We express the physical parameters (amplitude a, wavenumber k, and the period averages of depth 
${\overline{h}}$ and velocity 
${\overline{u}}$) in terms of the basic parameter set 
$(h_1, h_2, h_3, c)$ as
\begin{equation}
\begin{split}
&a = h_3 - h_2, \quad k = \sqrt {\frac{3(h_3 -
h_1)}{h_1 h_2 h_3}} \frac{\pi}{2 \mathrm{K}(m)}, \quad
\overline h = h_1 +
(h_3 - h_1)\frac{\mathrm{E}(m)}{\mathrm{K}(m)} , \\
& \overline{h (u-c)} =
{- \sigma} \sqrt{h_1 h_2 h_3}, \quad
{\overline{u}} = c {- \sigma} \sqrt{h_1 h_2 h_3}\; \frac{\Pi \left (1-\frac{h_2}{h_3} ,m \right)}{h_3 \mathrm{K}(m)},
\end{split}
\end{equation} where 
$\mathrm{K}$, 
$\mathrm{E}$ and Π are the complete elliptic integrals of the first, second and third kinds, respectively [Reference McClain44]. We introduce the phase
\begin{equation}
\theta = k \xi = kx - \omega t,
\end{equation} so that the travelling wave is 2π-periodic in θ: 
$h(\xi) = h(\theta/k) = h((\theta+2\pi)/k)$, 
$u(\xi) = u(\theta/k) = u((\theta + 2\pi)/k)$. The wavelength of the travelling wave L is related to the wavenumber k by 
$L=2\pi/k$.
The solitary wave limit of (3.3) is achieved when 
$h_2 \to h_1$ so that m → 1. Its explicit form is
\begin{equation}
h(x,t)= {\overline{h}} + a \,\mathrm{sech}^2 \left(\frac{1}{2} \frac{\sqrt{3a}}{{\overline{h}}
\sqrt{{\overline{h}} + a}} (x - c t)\right),\quad u(x,t)= {\overline{u}} + \sigma
\sqrt{{\overline{h}} + a} \left ( 1 - \frac{{\overline{h}}}{h(x,t)} \right).
\end{equation} Fast (
$\sigma=+1$) and slow (
$\sigma=-1$) elevation solitary waves propagate on the background 
$h={\overline{h}}, u={\overline{u}}$, and are characterised by the speed-amplitude relation
\begin{equation}
c=c_s(a, \bar h, {\overline{u}}) \equiv {\overline{u}} +\sigma \sqrt{{\overline{h}} +a}.
\end{equation} Fast solitary waves move faster than the dispersionless long-wave velocity 
$V_+ = {\overline{u}} + \sqrt{{\overline{h}}}$, and slow solitary waves move slower than the dispersionless long-wave velocity 
$V_- = {\overline{u}} - \sqrt{{\overline{h}}}$ (see Figure 2).
Figure 2. Relations (3.7) between the velocity of a fast (slow) solitary wave and the corresponding long-wave velocity 
$V_+$ (
$V_-$) are represented schematically on the left (right).
In the opposite, harmonic, limit, 
$h_2 \to h_3$ so that m → 0, yields a small-amplitude linear wave characterised by the dispersion relation 
$\omega_0(k)$ (frequency-wavenumber relation) for linear waves propagating on the background 
$ ({{\overline{h}}},{\overline{u}})$
\begin{equation}
\omega = k c= \omega_0(k,{\overline{h}}, {\overline{u}})\equiv k {\overline{u}} + \sigma
k \sqrt{\frac{{\overline{h}}}{1+ {\overline{h}}^2k^2/3}}.
\end{equation}3.2. Lagrangian coordinates
Consider now SGN’s travelling wave solutions in the co-moving mass Lagrangian coordinate 
$\zeta = q - \tilde{c}t$ instead of the Eulerian coordinate 
$\xi = x - ct$: 
$h=h(\zeta)$, 
$u=u(\zeta)$. Since 
$\displaystyle\frac{d\zeta}{d\xi}=h$, the equation for travelling waves is
\begin{equation}
\left(\frac{dh}{d\zeta}\right)^2 = \frac{3}{h_1 h_2
h_3}\frac{P(h)}{h^2}.
\end{equation}The velocity u is found from the relation
\begin{equation}
\tilde c \,\tau+\; u={\rm cst}, \quad {\rm with}\quad
\tau=\frac{1}{h}.
\end{equation} The wave velocity 
$\tilde c$ is related to the roots of the polynomial P(h) by the formula (see Appendix A)
\begin{equation}
\tilde{c}^2=h_1h_2h_3.
\end{equation}4. Modulation equations and their solitonic reduction
The SGN equations possess all the necessary prerequisites for the application of Whitham averaging. They support a family of 2π–periodic travelling wave solutions 
$h(\theta/k), u(\theta/k)$ specified by (3.3), (3.5) and characterized by the four independent parameters 
$h_1, h_2, h_3, c$ while admitting four independent conservation laws (2.1), (2.2), (2.5) and (2.6).
The modulation equations for the SGN equations in Eulerian coordinates are given in [Reference El, Grimshaw and Smyth10, Reference Tkachenko, Gavrilyuk and Shyue53]. According to the general averaging procedure [Reference Whitham55], the modulation system for the SGN equations can be obtained by period averaging any three conservation laws, such as mass (2.1), momentum (2.3) and energy (2.5), over the periodic family (3.3), and augmenting them by the wave conservation equation 
$k_t +
(kc)_x=0$. Doing so results in
\begin{equation}
\begin{split}
&\overline{h}_t+(\overline{h u})_x = 0, \\
&( \overline{h u} )_t+\left( \ \tfrac 12 \overline{h^2}+\overline{h
u^2}- \tfrac{1}{3} \overline{h^3\left( (u-c)
u_{\xi \xi}
-u_{\xi\xi}^2\right)} \ \right)_x=0, \\
&\left(\frac{1}{2} \overline{h \left ( h + u^2 + \frac{1}{3} h^2
u_{\xi}^2 \right )} \right)_t + \left( \overline{h u\left( h +
\frac{1}{2} u^2 + \frac{1}{2} h^2 u_\xi^2 - \frac{1}{3}
h^2(u-c) u_{\xi\xi} ) \right)} \right)_x =0 ,\\
&k_t + \left ( k c \right )_x=0.
\end{split}
\end{equation}The averages in (4.1) are evaluated using the general definition
\begin{equation}
\overline {f(h)} = \dfrac{\displaystyle\int_{h_2}^{h_3}
\dfrac{f(h)dh}{\sqrt{P(h)}}}{\displaystyle\int_{h_2}^{h_3}\dfrac{dh}{\sqrt{P(h)}}
},
\end{equation}where f(h) is any function of h.
The system (4.1) is consistent with the averaged Bernoulli conservation law (2.6):
\begin{equation}
\left( \ \overline{u}+\tfrac{1}{6} \overline{h^2u_{\xi
\xi}} \ \right)_t +
\left( \ \tfrac12 \overline{u^2}+\overline{h}-\tfrac12
\overline{h^2
\left(\left(\tfrac23 u- c\right) u_{\xi
\xi}-u_\xi^2\right)} \
\right)_x=0,
\end{equation}which can be used instead of any of the averaged conservation laws (4.1), e.g. instead of the wave conservation equation, yielding an equivalent modulation system. This equivalence is proved in the mass Lagrangian coordinates in Appendix A.
As a result, the system (4.1) can be explicitly represented in canonical quasilinear form for the state vector 
$\textbf{b}= (h_1(x,t), h_2(x,t), h_3(x,t), c(x,t))^T$; see Appendix B. However, due to the lack of integrable structure for the SGN equations, the associated modulation system cannot be reduced to a diagonal form. This makes the analysis of its properties – hyperbolicity, genuine nonlinearity, simple waves, etc. – difficult. The weakly nonlinear regime of the modulation equations was studied in [Reference El, Grimshaw and Smyth10]. The hyperbolicity of the modulation equations was proven in [Reference Tkachenko, Gavrilyuk and Shyue53]. However, their full analytical study remains a difficult task. This is why we study here a reduction of the full modulation system in the limit of waves of large wavelength (the solitary wave limit), allowing us to present some analytical results. The difficulty of obtaining the solitary wave limit of the modulation equations is that the phase equation 
$k_t+(ck)_x=0$ is degenerate in this singular limit. One possibility is to pass to the limit in the wave action conservation law, an exact conservation law of the full SGN-Whitham system. Such a method was, in particular, exploited in [Reference Gurevich, Krylov and El27] for the KdV equation, in [Reference Gavrilyuk and Shyue20] for the BBM equation and in [Reference Benzoni-Gavage, Mietka and Rodrigues52] for Hamiltonian systems of Euler-Korteweg or dispersive Eulerian type (so-called second gradient fluids). The wave action integral for the SGN-Whitham equations was already obtained in [Reference Gavrilyuk22] in a general setting that includes the SGN-Whitham equations by using mass Lagrangian coordinates. We use this result to first find the solitary wave limit in mass Lagrangian coordinates and then re-express the limit equations in Eulerian coordinates (see Appendix A). In the mass Lagrangian coordinates, one has only to replace the polynomial P(h) by 
$P(h)/h^2$ when computing averages (see (3.9)):
\begin{equation}
\overline{f(h)} = \dfrac{\displaystyle \int_{h_2}^{h_3}
\dfrac{hf(h)dh} {\sqrt{P(h)}}}
{\displaystyle\int_{h_2}^{h_3}\dfrac{hdh} {\sqrt{P(h)}}}.
\end{equation}To double-check our computation of the solitary wave limit in mass Lagrangian coordinates, we also compute the limit directly in Eulerian coordinates (see Appendix B) using a symbolic package.
A straightforward analysis shows that in the solitary wave limit, one has 
${\overline{h}}=h_1$, 
$\overline{h^2} = h_1^2 = {\overline{h}}^2$, 
$\overline{1/h}=1/h_1=1/{\overline{h}}$, and the average of the mass and momentum equations in mass Lagrangian coordinates (2.10) are thus the classical Saint–Venant equations describing hydrostatic (dispersionless) shallow water equations
\begin{equation}
\left(\frac{1}{{\overline{h}}} \right)_t-{\overline{u}}_q=0, \quad
{\overline{u}}_t-\left(\frac{{\overline{h}}^2}{2}\right)_q=0.
\end{equation}This decoupling of the dispersionless limit equations for the evolution of the mean flow in the solitary wave limit is a general property of dispersive hydrodynamics [Reference El8, Reference El and Hoefer12, Reference Hoefer29]. It is also physically intuitive: the effect of a single soliton on a large-scale mean flow is negligibly small.
A non-trivial amplitude equation comes from the solitary wave limit of the wave action conservation equation. For general periodic travelling waves in mass Lagrangian coordinates, the wave action equation is (see Appendix A)
\begin{equation}
\left(\tilde c \left(\frac{\overline{h_\zeta^2}}{3k}
+\frac{\overline{\tau^2} -\overline{\tau}^2}{k}\right)\right)_t
+\left(\tilde c^2\, \frac{\overline{\tau^2}
-\overline{\tau}^2}{k}\right)_q=0.
\end{equation} The solitary wave limit (
$k\rightarrow 0$) is singular, because 
$\overline{h_\zeta^2}\rightarrow 0$ and 
$\overline{\tau^2}-\overline{\tau}^2\rightarrow 0$. In Appendix A, we show that equation (4.6) limits to
\begin{equation}
F(n,{\overline{h}})_t+G(n,{\overline{h}})_q=0,
\end{equation}with
\begin{align}
&F(n,{\overline{h}}) =\frac{{\overline{h}}^{\frac{3}{2}}}{\sqrt{1-n}}
\left(\frac{(6-2n)\sqrt{n}}{3(1-n)} +{\rm
ln}\left({\frac{1-\sqrt{n}}{1+\sqrt{n}}}\right)\right),
\end{align}
\begin{align}
& G(n, \overline{h})=\sigma \frac{{\overline{h}}^{3}}{1-n}
\left(\frac{\sqrt{n}}{1-n}+\frac{1}{2}{\rm
ln}\left({\frac{1-\sqrt{n}}{1+\sqrt{n}}}\right)\right).
\end{align} The quantity n is related to the solitary wave amplitude 
$a=h_3-h_1$ as
\begin{equation}n=\frac{a}{\overline{h}+a}.\end{equation}The characteristic velocity corresponding to equation (4.7) is
\begin{equation}
\lambda=\frac{G_n}{F_n}=\sigma\frac{{\overline{h}}^{3/2}}{\sqrt{1-n}}=\sigma
{\overline{h}}\sqrt{{\overline{h}}+a} = \tilde{c}_s.
\end{equation} The velocity 
$\tilde{c}_s$ is related to the Eulerian velocity of solitary waves cs by (3.7).
In Eulerian coordinates, the system (4.5), (4.7) becomes
\begin{align}
&{\overline{h}}_t+({\overline{h}} {\overline{u}})_x=0,
\end{align}
\begin{align}
&{\overline{u}}_t+{\overline{u}}\,{\overline{u}}_x+ {\overline{h}}_x=0,
\end{align}
\begin{align}
&z_t+ \left({\overline{u}} + \sigma \sqrt{{\overline{h}}(1+z^2)} \right) z_x + \sigma \frac{3 \left(z^2+1\right)^{3/2}}{2z} \, \frac{
z \sqrt{z^2+1} -\sinh ^{-1}(z)}{2
z \sqrt{z^2+1}- \sinh
^{-1}(z)}\, \frac{{\overline{h}}_x}{\sqrt{{\overline{h}}}}\\
&-\frac{\sqrt{z^2+1}}{2z}\, \frac{3z+2z^3-3\sqrt{z^2+1}\sinh
^{-1}(z)}{2z\sqrt{z^2+1}-\sinh
^{-1}(z)}\, {\overline{u}}_x=0. \nonumber
\end{align} where 
$z^2=a/{\overline{h}}$ and 
$\sinh^{-1}(z)=\ln(z+\sqrt{z^2+1})$. We call the system (4.12)–(4.14) the solitonic modulation system. We stress that the solitonic modulation system is an exact reduction of the full SGN-Whitham modulation system.
The first two equations of the solitonic modulation system are the Saint-Venant (shallow water) equations written in Eulerian coordinates. They are completely decoupled from the third equation for z. Other than classical fast and slow surface waves of the shallow water equations with characteristic velocities 
$V_{\pm}={\overline{u}}\pm \sqrt{{\overline{h}}}$, the characteristic velocity corresponding to the amplitude equation for the dimensionless amplitude z 2 also represents fast and slow solitary waves propagating with the third characteristic velocity 
$c_s={\overline{u}} + \sigma \sqrt{{\overline{h}}(1+z^2)}$, the solitary wave velocity (3.7). By direct verification, we find that the system is strictly hyperbolic 
$V_- \lt V_+ \lt c$, if 
$\sigma=+1$, 
${\overline{h}} \gt 0$, and z > 0 or 
$c \lt V_- \lt V_+$, if 
$\sigma=-1$, 
${\overline{h}} \gt 0$, and z > 0 and the corresponding eigenfields are genuinely nonlinear in the sense of Lax.
The solitonic modulation system (4.12)–(4.14) inherits two Riemann invariants, those of the decoupled shallow water equations (4.12), (4.13). However, the third Riemann invariant does not exist, i.e. the system cannot be fully diagonalized (see Appendix C for the proof). Nevertheless, given the solution of (4.12) and (4.13) (obtained for example by the hodograph transform or a simple wave reduction), eq. (4.14) can then be integrated using the method of characteristics. Moreover, if one of the shallow water Riemann invariants is constant (the simple wave reduction), there are just two equations left, e.g. (4.13) and (4.14), and so the amplitude equation (4.14) can also be diagonalized in that case. The resulting extra Riemann invariant 
$Q(x,t)$ plays the role of an adiabatic invariant for solitary wave-mean flow interaction and determines the transmission (tunnelling) and trapping conditions for the interaction of a solitary wave with a RW or DSW mean flow generated by step initial data (Riemann) problems.
5. Solitary wave transmission and trapping
The expression “solitary wave tunnelling” comes from quantum mechanics and conveys the possibility of a quantum particle passing through a classically impenetrable potential barrier. In the context of the SGN equations, the solitary wave plays the role of the quantum particle. More precisely, for a given solitary wave amplitude, we are able to use the solitary wave limit of the SGN-Whitham equations to analytically determine if the solitary wave passes (transmits or tunnels) through a RW or its counterpart, a DSW. Both a RW and a DSW represent a continuous transition between two constant mean flows and therefore solitary wave-mean flow transmission occurs when a solitary wave, initiated on one side of a RW or DSW, emerges on the other side. Otherwise, we say that the solitary wave has been trapped.
The system (4.12), (4.13) is independent of z and can be diagonalized. The corresponding Riemann invariants are:
\begin{equation}
r_+ = {\overline{u}} + 2\sqrt{{\overline{h}}},\quad r_- = {\overline{u}} - 2\sqrt{{\overline{h}}},
\end{equation}yielding
\begin{align}
&(r_+)_t + V_+ (r_+)_x=0,\quad V_+ = {\overline{u}} + \sqrt{{\overline{h}}} =
\frac{3r_++r_-}{4},
\end{align}
\begin{align}
&(r_-)_t + V_- (r_-)_x=0,\quad V_- = {\overline{u}} - \sqrt{{\overline{h}}} =
\frac{r_++3r_-}{4}.
\end{align}This system has two simple wave solutions:
\begin{equation}
r_{-\mu}={\overline{u}}-2\mu \sqrt{{\overline{h}}} = {\rm cst},
\quad V_{\mu} = x/t,
\end{equation} where 
$\mu=+1$ for the fast wave and 
$\mu=-1$ for the slow wave.
5.1. Exact simple wave Riemann invariants
To study the interaction of the solitary wave with the simple wave (5.4), we hold one of the Riemann invariants r −µ constant, yielding a relation between 
${\overline{h}}$ and 
${\overline{u}}$ (5.4) [Reference Sprenger, Hoefer and El49]. The reduced solitonic modulation system is thus obtained by substituting (5.4) in (4.12), (4.14) (or equivalently (4.13), (4.14)), yielding the system of two equations:
\begin{align}
&{\overline{h}}_t+\left(r_{-\mu}+3\mu\sqrt{{\overline{h}}}\right){\overline{h}}_x=0,
\end{align}
\begin{align}
& z_t+\left(r_{-\mu}+2\mu\sqrt{{\overline{h}}}+ \sigma \sqrt{{\overline{h}}(1+z^2)}
\right) z_x + \sigma g_{\sigma \mu}(z)\frac{{\overline{h}}_x}{\sqrt{{\overline{h}}}}
=0,
\end{align}with
\begin{equation}
g_{\sigma \mu}(z)=\frac{3 \left(z^2+1\right)^{3/2}}{2z} \, \frac{
z \sqrt{z^2+1} -\sinh ^{-1}(z)}{2
z \sqrt{z^2+1}- \sinh^{-1}(z)}-\sigma \mu \frac{1+z^2}{2z} \,
\frac{(3z+2z^3)(1+z^2)^{-1/2}-3\sinh
^{-1}(z)}{2z\sqrt{1+z^2}-\sinh
^{-1}(z)}.
\end{equation} Since now this is a quasi-linear system of just two equations, it is diagonalizable with one Riemann invariant manifestly 
${\overline{h}}$. By making the simple-wave ansatz 
$z=z({\overline{h}})$ in eqs. (5.5) and (5.6), the second Riemann invariant can be obtained as the constant of integration of the ODE
\begin{equation}
\frac{dz}{d{\overline{h}}} + \frac{g_{\sigma \mu}(z)}{{\overline{h}}
\left(\sqrt{1+z^2}-\sigma \mu\right)} =0.
\end{equation}The integral of (5.8) can be written in the form
\begin{equation}
Q_{\sigma \mu}({\overline{h}},z) = {\overline{h}} \exp(f_{\sigma \mu}(z)),\quad
f_{\sigma \mu}(z) = \int^z \frac{\sqrt{1+s^2}-\sigma\mu}{g_{\sigma \mu}(s)}\, ds.
\end{equation} One can see that the Riemann invariant 
$Q_{\sigma \mu}$ (5.9) only depends on the sign σµ, which determines the interaction type. The value 
$\sigma \mu=+1$ corresponds to the overtaking interaction between a fast solitary wave and a fast simple wave (or equivalently slow-slow waves) whereas 
$\sigma \mu=-1$ corresponds to the head-on interaction between a fast solitary wave and a slow simple wave (or equivalently slow-fast waves).
Note that in the small amplitude limit z → 0, we obtain the following expansion for the Riemann invariant in the case of an overtaking interaction (
$\sigma \mu=+1$)
\begin{equation}
Q_+({\overline{h}},z) = {\overline{h}} \left(1+\frac{z^2}{2}-\frac{z^4}{48}
-\frac{61}{1440} z^6+ O(z^8)\right).
\end{equation} As we will now show, this expression is asymptotically equivalent, to order 
$\mathcal{O}(z^4)$, to the Riemann invariant obtained by the DSW fitting method.
5.2. Approximate simple wave Riemann invariants: the DSW fitting method
An efficient approach to obtain the solitary wave limit of the Whitham equations can be deduced from the dispersive shock wave (DSW) fitting method [Reference El8]. This method enables the determination, under certain assumptions, of the harmonic and solitary wave edges of a DSW directly, bypassing the derivation and asymptotic analysis of the full Whitham modulation system. The DSW fitting method has been successfully applied to many dispersive hydrodynamic systems, both integrable and non-integrable, see e.g. [Reference Congy, El, Hoefer and Shearer7, Reference El, Gammal, Khamis, Kraenkel and Kamchatnov9, Reference El, Grimshaw and Smyth10, Reference El, Khodorovskii and Tyurina13, Reference Esler and Pearce14, Reference Hoefer29, Reference Jamshidi and Johnson31, Reference Lowman and Hoefer39]. In cases when the dispersive equation is integrable such as in the KdV, NLS, and Kaup-Boussinesq equations, the method’s results are consistent with the available exact modulation solutions. For non-integrable systems, when the exact theory is not available, the method yields an excellent comparison with direct numerical simulations of the dispersive equation, beyond the classical weakly nonlinear KdV approximation. Here, we shall use the part of the DSW fitting construction pertaining to the determination of the DSW’s solitary wave edge.
A major assumption in the DSW fitting method is that of convexity (strict hyperbolicity and genuine nonlinearity) of the full Whitham modulation system. This assumption is not always easily verifiable for the entire range of parameters involved, so one can say that DSW fitting generally provides a convex approximation of the exact DSW edge dynamics. In particular, it is known that the SGN-Whitham modulation system exhibits non-convexity for sufficiently large amplitudes [Reference El, Grimshaw and Smyth10, Reference Hoefer29] but nevertheless, the DSW fitting results agree with direct SGN numerics remarkably well for a broad range of amplitudes, far beyond the weakly nonlinear KdV regime.
The DSW fitting method relies on the existence of exact reductions of the Whitham modulation system in two distinguished limits: the harmonic limit a → 0 and the solitary wave limit k → 0. The latter one is our interest here and has the general form of an equation for the solitary wave amplitude (or a related amplitude type variable), coupled to the dispersionless limit system for the large-scale background (the mean flow) [Reference El and Hoefer12]. In the present context of the SGN-Whitham equations, the solitary wave reduction is given by the system (4.12)–(4.14), however, the derivation of the exact form of the amplitude equation (4.14) and further, of the Riemann invariant 
$Q_{\sigma \mu}$ in eq. (5.9) – the main technical hurdle in the analysis of the solitary wave limit of the modulation system – is not required for the application of the DSW fitting method. Instead, the determination of the requisite Riemann invariant involves only the linear dispersion relation 
$\omega_0(k, {\overline{h}}, {\overline{u}})$ for waves on the mean background 
$({\overline{h}},{\overline{u}})$ along with the simple-wave relation 
${\overline{u}}({\overline{h}})$ for the dispersionless limit equations. All of this information is readily available with no additional analysis of the SGN-Whitham modulation system required. In the context of soliton-mean flow interaction, the Riemann invariant Q acquires the meaning of an adiabatic invariant [Reference Maiden, Anderson, Franco, Gennady and Hoefer40]. This adiabatic invariant also plays a key role in the solitary wave resolution method [Reference El, Grimshaw and Smyth11, Reference Maiden, Franco, Webb, El and Hoefer41], where it is an analogue of the spectral parameter in the Lax pair associated with integrable equations in the semi-classical limit. See also the recent papers [Reference Kamchatnov33, Reference Kamchatnov and Shaykin34] where soliton-mean field interaction has been interpreted in terms of Hamiltonian mechanics of the motion of a soliton along a large-scale background.
Note that the DSW fitting construction applies directly to the overtaking solitary wave-mean field interaction, not the head-on interaction, due to the unidirectional nature of DSW generation in Riemann problems. The DSW fitting method was applied to undular bore theory for the SGN system in [Reference El, Grimshaw and Smyth10], so we shall take advantage of the results of that work and adapt them to the current setting of the overtaking solitary wave-mean flow interaction. To be definite, we consider the fast-fast interaction, 
$\sigma = \mu =+1$.
For the fast simple-wave mean field we have (cf. (5.5))
\begin{equation}
{\overline{u}}({\overline{h}})=r_-+ 2\sqrt{{\overline{h}}}, \quad {\overline{h}}_t+V_+({\overline{h}}) {\overline{h}}_x=0,\quad V_+ =
r_{-}+3\sqrt{{\overline{h}}},
\end{equation} where 
$r_-= {\overline{u}} - 2 \sqrt{{\overline{h}}} = const$ is the Riemann invariant of the dispersionless shallow-water equations. The fast branch of the dispersion relation (3.8) for linearised waves on the simple-wave background (5.11) is given by
\begin{equation}
\omega_0(k,{\overline{h}}, {\overline{u}}({\overline{h}})) = k\left(r_{-}+2 \sqrt{{\overline{h}}} \right) +
k \sqrt{\frac{{\overline{h}}}{1+ {\overline{h}}^2k^2/3}}.
\end{equation}Solitary wave motion on the simple-wave background is defined by the conjugate dispersion relation (see [Reference El8] for details)
\begin{equation}
{\widetilde{\omega}}({\widetilde{k}},{\overline{h}})=-i\omega_0 \left(i {\widetilde{k}},{\overline{h}}, {\overline{u}}({\overline{h}}) \right) ={\widetilde{k}}
\left(r_{-}+2 \sqrt{{\overline{h}}} \right) +
{\widetilde{k}} \sqrt{\frac{{\overline{h}}}{1- {\overline{h}}^2 {\widetilde{k}}^2/3}},
\end{equation} where the conjugate wavenumber 
${\widetilde{k}}$ (essentially the inverse width of the solitary wave) is related to the solitary wave amplitude a by
\begin{equation}
\frac{{\widetilde{\omega}}}{{\widetilde{k}}} = c_s(a,{\overline{h}},{\overline{u}}({\overline{h}})),
\end{equation} with 
$c_s(a,{\overline{h}},{\overline{u}})={\overline{u}} + \sqrt{{\overline{h}} +a}$ the fast branch of the SGN solitary wave speed-amplitude relation (3.7).
Within the fitting approach to solitary wave-mean flow interaction, the amplitude modulation equation is obtained directly in diagonal form. The corresponding Riemann invariant 
$\tilde Q_+(\tilde k, {\overline{h}})$ satisfying
\begin{equation}
\frac{\partial \tilde Q_+}{\partial t} + C(\tilde Q_+, {\overline{h}}) \frac{\partial \tilde Q_+}{\partial x} =0, \quad C(\tilde Q_+, {\overline{h}}) = c_s(a(\tilde k, {\overline{h}}), {\overline{h}}, {\overline{u}}({\overline{h}})),
\end{equation}is found as an integral of the characteristic ODE
\begin{equation}
\frac{d {\widetilde{k}}}{d {\overline{h}}} = \frac{{\widetilde{\omega}}_{\overline{h}}}{V_+({\overline{h}})-{\widetilde{\omega}}_{\widetilde{k}}} =
\frac{{\widetilde{k}}\left( \left(1+\frac{{\overline{h}}^2 {\widetilde{k}}^2}{3}\right)+2
\left(1-\frac{{\overline{h}}^2 {\widetilde{k}}^2}{3}\right)^{3/2}+1 \right)}{2 {\overline{h}}
\left( \left(1-\frac{{\overline{h}}^2 {\widetilde{k}}^2}{3}\right)^{3/2}-1 \right)}.
\end{equation}Equation (5.16) is a convex approximation counterpart to the ODE (5.8) obtained by the exact evaluation of the solitary wave limit of the SGN-Whitham modulation system.
With the change of variable
\begin{equation}
\alpha = \frac{1}{\sqrt{1-\frac{{\overline{h}}^2 {\widetilde{k}}^2}{3}}} =
\sqrt{1+\frac{a}{{\overline{h}}}} = \sqrt{1+z^2},
\end{equation}eq. (5.16) reduces to the separable ODE
\begin{equation}\frac{d\alpha}{d\overline h}=\frac{\alpha\left(1+\alpha\right)(\alpha-4)}{2\overline h\left(1+\alpha+\alpha^2\right)},\end{equation}which is readily integrated with the constant of integration
\begin{equation}
\tilde Q_+ = \frac{2^{2/5} 3^{21/10}{\overline{h}} \alpha^{1/2}}{(\alpha
+1)^{2/5} (4-\alpha)^{21/10}}.
\end{equation} The normalization coefficient in (5.19) is chosen by the natural requirement that in the zero-amplitude/infinite width limit a → 0 of the solitary wave (3.6), the Riemann invariant 
$\tilde Q_+ \to {\overline{h}}$ so that equation (5.15) degenerates into the simple wave mean flow equation (5.11) for 
${\overline{h}}$. Equation (5.19) is equivalent to eq. (49) in [Reference El, Grimshaw and Smyth10].
One can see that the expression (5.19) does not coincide with the rigorous asymptotic result (5.9) for 
$Q_+$ corresponding to 
$\mu=\sigma=1$. However, it provides a quite accurate approximation in the physically relevant range of amplitude-depth ratios 
$z^2=a/{\overline{h}}$. Indeed, the small amplitude expansion of the fitting approach result (5.19) is
\begin{equation}
\tilde Q_+ = {\overline{h}} \left ( 1+\frac{z^2}{2}-\frac{z^4}{48}
-\frac{37}{864} z^6+ {\cal O}(z^8) \right ).
\end{equation} The first two terms in this expansion correspond to the Riemann invariant of the KdV modulation system in the soliton limit [Reference El and Hoefer12], i.e. is accurate to 
$\mathcal{O}(a)$ (
$\mathcal{O}(z^2)$) as a → 0. But the fitting approach improves upon the classical KdV prediction since (5.20) and the exact result (5.10) asymptotically agree up to 
$\mathcal{O}(a^2)$ (
$\mathcal{O}(z^4)$). Even further, the difference between the two expansions at 
$\mathcal{O}(a^3)$ (
$\mathcal{O}(z^6)$) is just 
$\sim 10^{-3} a^3$, i.e. the exact (5.9) and convex approximation (5.19) curves are in excellent agreement for physically admissible 
$a/{\overline{h}} \lt a_{\rm max}/{\overline{h}} \approx 0.8$ [Reference El, Grimshaw and Smyth10], see Figure 3. At the same time, the existence of such a discrepancy poses the important question: what is the cause of this 
$\mathcal{O}(a^3)$ asymptotic discrepancy and what does it mean for the asymptotic validity of the DSW fitting method, particularly for non-integrable systems?
5.3. Riemann problem and transmission condition
We consider the Riemann problem for the system (4.12), (4.13), (4.14), for which the initial condition is a step function:
\begin{equation}
\left({\overline{h}}(x,0),{\overline{u}}(x,0),z(x,0)\right) = \begin{cases} \left(\displaystyle h_-,u_-,z_-\equiv\sqrt{\frac{a_-}{h_-}}\right), &x \lt 0,
\\
\\
\left(\displaystyle h_+,u_+,z_+\equiv\sqrt{\frac{a_+}{h_+}}\right), &x \gt 0,
\end{cases}
\end{equation} with the constraint 
$u_--2\mu \sqrt{h_-}=u_+-2\mu \sqrt{h_+}$. The solution of interest is the simple wave solution
\begin{align}
&Q_{\sigma\mu}({\overline{h}},z)=Q_{\sigma\mu}(h_-,z_-) = Q_{\sigma\mu}(h_+,z_+),\quad
V_\mu = r_{-\mu}+3\mu\sqrt{{\overline{h}}} = x/t.
\end{align} Equation (5.22) implicitly determines 
${\overline{h}}$ and 
$z^2=a/{\overline{h}}$ as functions of 
$x/t$. It describes the fast RW with 
$h_- \lt h_+$. To simplify the discussion of the solution, we restrict our study to fast solitary waves (
$\sigma = +1$). In this case, the Riemann problem for the modulation system models the interaction of an incident solitary wave with parameter 
$z_-$, initially located far to the left of the initial step x < 0, interacting with a RW or a DSW generated by the initial step.
It is important to note here that, although the solitary wave limit of the SGN-Whitham equations (4.12)–(4.14) do not admit DSW modulation solutions, they can be used to determine the nature of the interaction between a solitary wave and a DSW. The only region of space-time where equations (4.12)–(4.14) break down is within the DSW itself. Outside of the DSW, equations (4.12)–(4.14) are perfectly valid, so that the simple wave solution (5.22) applies outside of the DSW. If all we wish to determine is whether the solitary wave has been transmitted or trapped by the DSW and, if transmitted, the transmitted solitary wave amplitude, we can use the Riemann invariant relation from (5.22) with 
$h_- \gt h_+$ to ascertain this as described below. This concept of hydrodynamic reciprocity was first theoretically predicted and simultaneously experimentally observed in the interfacial fluid dynamics of a viscous fluid conduit [Reference Maiden, Anderson, Franco, Gennady and Hoefer40]. The concept has since been applied to solitary wave-DSW interaction for other equations [Reference Ablowitz, Cole, Gennady, Hoefer and Luo1, Reference Ryskamp, Hoefer and Biondini47, Reference Sprenger, Hoefer and El49, Reference van der Sande, El and Hoefer54]. In order to describe the interaction of the solitary wave within the DSW, one must appeal to multi-phase Whitham modulation theory as has been carried out for the KdV equation [Reference Ablowitz, Cole, Gennady, Hoefer and Luo1].
The first equation in (5.22) yields a relation between the left and right parameters 
$(h_\pm,z_\pm)$ of the initial condition, i.e. a relation between the parameters of the incident and transmitted waves
\begin{equation}
f_{\sigma \mu}(z_+)+ \ln h_+ =f_{\sigma \mu}\left( z_-\right) + \ln
h_-,\quad z_\pm^2 = \frac{a_\pm}{h_\pm}.
\end{equation} If transmitted, the solitary wave amplitude 
$a_+ \gt 0$ is determined by solving for 
$z_+$ in eq. (5.23).
In the interaction with a fast simple wave, where 
$\sigma \mu=+1$, one can choose the constant of integration in (5.9) such that 
$f_+(0)=0$. In that case, 
$f_+(z) \geq 0$ (see Fig. 4(a)) and one can find 
$z_+$ from Eq. (5.23) if
\begin{equation}
f_+\left( z_-\right) + \ln\left( \frac{h_-}{h_+}\right) \gt 0.
\end{equation}
Figure 4. (a) Variation of 
$f_+(z)$. (b) The critical transmission curve 
$z_{\min}^2(h_+/h_-)$ for the overtaking interaction between a fast solitary wave and a fast RW (
$h_- \lt h_+$) given by the exact formula (5.25) (continuous line) and the convex approximation formula (5.26) (dashed line). (c) Relation between 
$z_{+}^2$ and 
$z_{-}^2$ for the interaction with a fast RW, 
$(h_-,h_+)=(1,1.5)$ (solid line) and a fast DSW, 
$(h_-,h_+)=(1.5,1)$ (dashed line).
This condition is called the transmission condition. It is always fulfilled in the interaction with a fast DSW where 
$h_- \gt h_+$. In the interaction with a fast RW, this condition can be written in the form:
\begin{equation}
z_- \gt z_{\rm min}(h_+/h_-) = f_+^{-1} \left( \ln \left(\frac{h_+}{h_-}\right)\right),
\end{equation}plotted in Fig. 4(b) – solid line. If the normalized amplitude of the incident solitary wave is smaller than z min, then the wave becomes trapped inside the RW, similar to [Reference Maiden, Anderson, Franco, Gennady and Hoefer40] in the case of the KdV and conduit equations, see Fig. 1(b).
If the approximate Riemann invariant 
$\tilde Q_+$ (5.19) is used in the transmission relation (5.23) then the fitting counterpart of the exact condition (5.25) assumes the form
\begin{equation}
z_- \gt z_{\min}(h_+/h_-)={\tilde f}_+^{-1}\left(\frac{h_+}{h_-}\right),
\end{equation}where
\begin{equation}
{\tilde f}_+(z)=\frac{2^{2/5} 3^{21/10} \alpha^{1/2}}{(\alpha
+1)^{2/5} (4-\alpha)^{21/10}}, \quad \alpha=\sqrt{1+z^2}.
\end{equation}The curve (5.26) is plotted in Fig. 4(b) in dashed line. There is a very close agreement between the exact and convex approximation curves.
If the fast solitary wave is placed in front of the fast DSW two scenarios are possible depending on the solitary wave amplitude 
$z_+$ relative to the DSW leading edge amplitude 
$z^*_+$ (see Equation (5.28) below). If 
$z_+ \gt z^*_+$ then the solitary wave propagates faster than the DSW and no interaction occurs. If 
$z_+ \lt z^*_+$ then the DSW overtakes the solitary wave and the latter gets trapped inside the DSW, see Fig. 1(d) for the illustration. The analysis of the trapping dynamics characterised by the formation of travelling breathers [Reference Ablowitz, Cole, Gennady, Hoefer and Luo1, Reference Yifeng, Chandramouli, Wenqian and Hoefer57] is beyond the scope of this paper.
In the head on interaction with a slow simple wave, where 
$\sigma \mu=-1$, 
$f_-(z)$ is singular at z = 0 (see Fig. 5(a) where 
$f_-(1)=0$), and the range of 
$f_-(z)$ spans the whole real axis. One can always find 
$z_-$ from Eq. (5.23). The transmission condition is always satisfied in this case, i.e. the incident fast solitary wave is never trapped by the RW or DSW.
Figure 5. (a) Variation of 
$f_-(z)$. (b) Relation between 
$z_+^2$ and 
$z_-^2$ for the head on interaction of a fast solitary wave with a slow DSW, 
$(h_-,h_+)=(1,1.5)$ (solid line) and a slow RW, 
$(h_-,h_+)=(1.5,1)$ (dashed line).
5.4. DSW: solitary wave edge
The transmission condition (5.23) can also be used to approximate the SGN DSW’s solitary wave leading edge amplitude and speed. When 
$h_- \gt h_+$, a DSW is generated by the simple wave Riemann problem (5.21). The DSW’s solitary wave leading edge amplitude 
$a_+ = h_+ (z_+^*)^2$ can be estimated by evaluating the Riemann invariant at the transmission/trapping bifurcation point when 
$z_- = 0$. In other words, a fast solitary wave of infinitesimally small amplitude gets transmitted exactly to the DSW leading edge. As follows from the transmission relation (5.23) this corresponds to
\begin{equation}
z_+^* = f_+^{-1} \left ( \ln\left ( \frac{h_-}{h_+} \right ) \right ).
\end{equation} The DSW solitary wave amplitude is 
$a_+ = h_+ (z_+^*)^2$ and edge speed is therefore 
$c_{\rm s}(a_+,h_+,u_+) = u_+ + \sqrt{h_+ + a_+}$.
The SGN DSW leading solitary wave amplitude prediction from eq. (5.28) is an approximation of the amplitude that results from integrating the appropriate integral curve (in this case, for 
$h_- \gt h_+$, a 3-wave) of the full SGN-Whitham equations. The approximation rests upon the hypothesis of hydrodynamic reciprocity – in which the solitary wave Riemann invariant 
$Q_{+1}({\overline{h}},z)$ (5.9) is the same behind and ahead of a DSW [Reference Maiden, Anderson, Franco, Gennady and Hoefer40] – and a more subtle, convexity condition that the full Whitham modulation system remains strictly hyperbolic along the entire solitary wave trajectory for all so-called admissible states; see, Section 3.2 in [Reference van der Sande, El and Hoefer54] for a discussion. Although these conditions are exactly true, within the context of Whitham modulation theory, for a fast (slow) solitary wave interacting with a fast (slow) rarefaction wave mean-field, they are assumed to be true for the fast (slow) DSW mean-field. Because of this, we refer to eq. (5.28) as the mean-field DSW approximation.
If instead of the exact Riemann invariant (5.9), its convex (DSW fitting) approximation (5.19) is used in the transmission condition (5.22), the DSW leading edge amplitude 
$\tilde{a}_+ = h_+(\tilde{z}_+^*)^2$ is found by solving the equation [Reference El, Grimshaw and Smyth10]
\begin{equation}
\begin{split}
\frac{h_-/h_+}{((\tilde{z}_+^*)^2+1)^{1/4}}-\left(\frac{3}{4-\sqrt{(\tilde{z}_+^*)^2+1}}\right)^{21/10}
\left(\frac{2}{1+\sqrt{(\tilde{z}_+^*)^2+1}}\right)^{2/5}=0.
\end{split}
\end{equation} Equation (5.29) is subject to the admissibility conditions – the convexity restrictions ensuring monotone behaviour of the DSW edge speeds as functions of 
$h_-, h_+$ [Reference Hoefer29]. This yields the admissible range of initial steps 
$1 \lt h_-/h_+ \lesssim 1.43$ for which the SGN DSW fitting results are applicable [Reference El, Grimshaw and Smyth10].
The small-jump expansions of (5.28) and (5.29) give
\begin{align}
\frac{a_+}{h_+} &= 2 \delta + \frac{1}{6}\delta^2 + \frac{127}{180} \delta^3
+ \mathcal{O}(\delta^4),
\end{align}
\begin{align}
\frac{\tilde{a}_+}{h_+} &= 2 \delta + \frac{1}{6}\delta^2 -
\frac{71}{108} \delta^3 +
\mathcal{O}(\delta^4),
\end{align} respectively, where 
$\delta = \frac{h_-}{h_+} - 1 \ll 1$. To leading order, both results agree with the famous result for the KdV equation that the lead solitary wave amplitude is twice the initial DSW jump height [Reference Gurevich and Pitaevskii28]. The mean-field DSW and DSW fitting approximations agree at second order as well, consistent with the agreement between the expansions of the exact (5.10) and convex approximation (5.20) for the solitary wave Riemann invariants. The curves 
$a_+(h_-/h_+)$ given by (5.28), (5.29) along with the values of 
$a_+$ extracted from the numerical simulations are shown in Figure 6. One can see that both the mean-field DSW equation (5.28) and the DSW fitting formula (5.29) provide very good approximations of the SGN DSW solitary wave edge amplitude within the admissible range of initial steps. The numerical results in Fig. 6 suggest that the mean-field DSW prediction somewhat improves upon the DSW fitting result.
5.5. Transmission: comparison between analytical and numerical results
Figure 7 shows the interaction of a fast solitary wave with fast and slow rarefaction waves. The amplitude of the transmitted solitary wave 
$a_+$ obtained by the direct numerical simulation of the SGN equations (2.1), (2.2) compares well with the analytical prediction (5.23). The details of the numerical scheme are given in Appendix D. In the case of a fast solitary wave with a slow rarefaction wave, the amplitude of the transmitted solitary wave is always larger than that of the incident solitary wave. Physically speaking, the slow rarefaction wave is formed by retracting a piston to the right, so it will accelerate the right-going solitary wave (see Figure 7). A new feature also appears in this case: a small amplitude solitary wave forms behind the transmitted large amplitude solitary wave. This is in contrast with the typical radiation emitted when a solitary wave interacts with another wave in non-integrable systems. Despite the generation of additional solitary waves in this Riemann problem due to the non-integrable nature of the SGN equations, the accuracy of the analytical predictions from Whitham theory is remarkable.
Figure 7. Left figure: Comparison between the transmission relation (5.23) and the numerical simulation for the fast solitary wave interaction with a fast RW (dashed red line) and a slow rarefaction wave (solid blue line). Middle figure: an example of the interaction with a fast RW. Right figure: an example of the interaction with a slow RW.
Figure 8 shows the interaction of a solitary wave with fast and slow DSWs. The analytical formulas are in agreement with direct numerical simulations. This time, small amplitude radiation is generated after the solitary wave passes through the slow DSW.
Figure 8. Left figure: comparison between the transmission relation (5.23) and the numerical simulation for the fast solitary wave interaction with a fast DSW (dashed red line) and a slow DSW (solid blue line). Middle figure: an example of the interaction with a fast DSW. Right figure: an example of the interaction with a slow DSW.
6. Conclusion
We have studied the interaction of a solitary wave with a slowly varying mean flow for the Serre-Green-Naghdi (SGN) equations that model fully nonlinear, bidirectional shallow water gravity waves over a flat bottom. This was achieved by the determination and analysis of the exact solitary wave limit of the Whitham modulation equations for the SGN system. The derivation of the Whitham equations was performed via the averaged conservation law approach in both Eulerian and Lagrangian coordinates. The SGN system is not integrable so the SGN-Whitham equations cannot be diagonalized, which makes their analysis a nontrivial problem.
Due to the singular nature of the solitary wave limit, the appropriate choice for the modulation parameters is crucial. We utilize the wave action density, which is shown to be a particularly well-behaved conserved quantity in the solitary wave limit. The resulting solitonic modulation system consists of the shallow water equations for the mean flow coupled to an amplitude equation for the solitary wave. Although the SGN solitonic system is not diagonalizable, its restriction to simple waves for the mean flow equations admits Riemann invariants that we use to analytically describe the head-on and overtaking interactions of a solitary wave with a rarefaction wave and dispersive shock wave (DSW). These scenarios lead to solitary wave trapping or transmission by the mean flow. The analytical results are shown to be in excellent agreement with corresponding numerical solutions of the full SGN equations. This work extends previous results on solitary wave-mean flow interaction in unidirectional, non-integrable systems (BBM and conduit equations) to the bidirectional case.
One important outcome of this paper is the comparison between the exact analytical results from SGN modulation theory for overtaking interactions with the results obtained from a simpler approach that is based on the DSW fitting method. The latter method, involving several major assumptions of the full modulation system (strict hyperbolicity, convexity), has been successfully applied to many dispersive hydrodynamic equations. It yields exact results for integrable equations, relies only upon knowledge of the linear dispersion relation and the dispersionless, mean-flow equations, and provides consistently good comparisons with direct numerical simulations for non-integrable equations. However, analytical estimates of DSW fitting theory accuracy have not been available. In this paper, we show that the DSW fitting results for the SGN equation are not exact but are accurate to the second order in the solitary wave amplitude, beyond the first order accurate Korteweg-de Vries approximation. This comparison between the exact and fitting results for the SGN-Whitham equations provides an important asymptotic benchmark for the DSW fitting method in non-integrable equations.
The analysis of the solitary wave limit of the SGN system presented here can be extended to other non-integrable evolutionary equations that admit a family of explicit periodic traveling wave solutions in terms of known elementary or special functions, e.g. Jacobi elliptic functions. So long as these solutions include limiting solitary waves, the calculation of the Whitham modulation equations and their associated solitary wave limit is possible. We have shown that the wave action conservation law, a general feature of the modulation equations obtained via Whitham’s averaged variational principle (Lagrangian) approach, is an important mathematical tool for the calculation of the solitary wave limit.
This work paves the way for additional studies of solitary wave interactions with mean flows in bidirectional, strongly nonlinear, physically relevant systems. One of the future directions could be the generalization of the developed theory for bidirectional solitary wave-mean flow interactions to soliton gases – large, random ensembles of interacting solitary waves [Reference Suret, Randoux, Gelash, Agafontsev, Doyon and Gennady51].
Data availability statement
This study did not generate any new data.
Acknowledgements
Acknowledgement TC, GE, SG and MH would like to thank the Isaac Newton Institute for Mathematical Sciences, Cambridge, for support and hospitality during the satellite program “Emergent phenomena in nonlinear dispersive waves” at Northumbria University, Newcastle, UK where work on this paper was undertaken. KMS thanks the Institut Mécanique et Ingénierie of Marseille and INRIA-Sophia-Antipolis-Méditerranée for financial support during his stay at IUSTI, Marseille. The authors thank M. Rodrigues for useful discussions.
Author contributions
All authors contributed equally to this work.
Funding statement
This work was supported by EPSRC Grant No. EP/R014604/1 and NSF Grant No. DMS-2306319.
Competing interests
None.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Appendix A. Lagrangian and Eulerian descriptions
If t is time, and q is the mass Lagrangian coordinate, the spatial Eulerian coordinate is defined through the motion of the continuum 
$x=x(t,q)$. The mass conservation equation in the Lagrangian coordinates can be written as 
$\rho(t,q)x_q=\rho_0(q)$, where 
$\rho(t,q)$ and 
$\rho_0(q)$ are the actual and the reference mass densities, so that 
$\rho(t,q)dx=\rho_0 (q)dq$. One can see that if we choose 
$\rho_0 (q) \equiv 1$, the Lagrangian variable q will effectively coincide with the mass (one-dimensional). A general conservation law in Lagrangian coordinates (t, q)
\begin{equation*}
a_t+b_q=0,
\end{equation*}is expressed in Eulerian coordinates (t, x) as
\begin{equation*}
\left({\rho a}\right)_t+\left(\rho ua+b\right)_x=0.
\end{equation*} When looking for travelling wave solutions that depend on 
$\tilde \xi =q-\tilde c t$ in Lagrangian coordinates, or 
$\xi =x-ct$ in Eulerian coordinates, the velocities 
$\tilde c$ and c are related by the mass conservation law
\begin{equation*}
\rho(u-c)=-\tilde c.
\end{equation*}We will first pass to the solitary wave limit in the modulation equations expressed in terms of mass Lagrangian coordinates and then we transform the limit equations to Eulerian form.
The governing Euler-Lagrange equations derived from the Lagrangian (2.8) are
\begin{equation}
\tau_{t}- u_{q}=0,\quad u_{t}+p_{q}=0,
\end{equation} where p is given in (2.11). Here, 
$\tau = 1/h$ is the specific volume, u is the velocity, and 
$\tilde e(\tau, \tau_t)$ is the potential (2.9). The system admits the energy equation (2.12) and Bernoulli equation (2.13). Following Whitham [Reference Whitham56], we are looking for the solution of (A.1) subject to (2.11) in the form
\begin{equation*}
\dbinom{\tau}{u}=\dbinom{\tau(T,X,\theta,\epsilon)}{u(T,X,\theta,
\epsilon)}, \quad T=\epsilon t,\quad X=\epsilon q, \quad
\theta=\frac{\Theta\left(T,X\right)}{\epsilon},
\end{equation*} where 
$0 \lt \epsilon \ll 1$ is a small, positive parameter. The function 
$\Theta(T,X)$ is called the phase. We define the local wave number k and the local frequency ω by the relations:
\begin{equation}
k=\Theta_X, \quad \omega=-\Theta_T.
\end{equation} We will suppose that the solution is 2π-periodic with respect to the rapid variable θ. Below, for any function 
$f(T,X,\theta,\epsilon)$, 
$\bar f$ is the 2π-period-average with respect to θ
\begin{equation}
\bar f
(T,X,\epsilon)=\frac{1}{2\pi}
\int_0^{2\pi}f(T,X,\theta,\epsilon)\,d\theta.
\end{equation}Expanding f in an asymptotic series in ϵ
\begin{equation*}
f=f_0(T,X,\theta)+\epsilon f_1(T,X,\theta)+...,
\end{equation*}and substituting this ansatz into the governing system (A.1), we obtain a system of ordinary differential equations with respect to θ at leading order. One has the following first integrals (the zero subscript is omitted)
\begin{equation}
\tilde{c}\tau +u= \tilde{c}\overline \tau+\overline u, \quad
-\tilde{c}u+p=-\tilde{c}\overline u +\overline p, \quad
\tilde{c}=\frac{\omega}{k}.
\end{equation}The system (A.4) admits the following useful consequences
\begin{align}
&\overline{u^2}-(\overline u)^2=\tilde{c}^2(\overline
{\tau^2}-(\overline \tau)^2),
\end{align}
\begin{align}
&\overline{u\tau}-{\overline u} \; {\overline \tau}
=-\tilde{c}(\overline {\tau^2}-(\overline \tau)^2),
\end{align}
\begin{align}
&\overline{p u}- {\overline p}\; {\overline u}
=\tilde{c}^3(\overline {\tau^2}-(\overline \tau)^2),
\end{align}
\begin{align}
&\overline{p \tau}- {\overline p} \; {\overline \tau}
=-\tilde{c}^2(\overline {\tau^2}-(\overline \tau)^2).
\end{align} To leading order, 
$\mathcal{O}(1)$ as ϵ → 0, one has
\begin{equation}
\tilde e (\tau,\tau_t)\approx \tilde e (\tau, \eta), \quad
\eta=-\omega\tau_\theta, \quad
p=-\left(\tilde e_\tau +\omega\left(\tilde e_{\eta}\right)_\theta \right).
\end{equation}The system (A.4) also admits the first integral in the form:
\begin{equation}
-\tilde{c}\left(\tilde e-\eta \tilde e_\eta
+\frac{u^2}{2}\right)+pu=-\tilde{c}\left(\overline{\tilde e-\eta
\tilde e_\eta +\frac{u^2}{2}}\right) +\overline{p u}.
\end{equation} The integral (A.10) allows us to obtain the nonlinear dispersion relation because the solution is 2π-periodic. At 
$\mathcal{O}(\epsilon)$, after averaging with respect to the rapid variable θ, one obtains the following systems of five compatible conservation laws containing only the leading order terms (the zero subscript is again omitted):
\begin{align*}
&{\overline \tau}_T-{\overline u}_X=0, \\
&{\overline u}_T+{\overline p}_X=0, \\
&\left(\overline{\frac{u^2}{2}+\varepsilon}\right)_T+\left(\overline{pu}\right)_X=0,\quad \varepsilon=\tilde e-\eta \tilde e_\eta, \\
&\left(\overline{\tau u-k\tau_\theta\frac{\partial \tilde
e}{\partial\eta }}\right)_T-\left(\overline{\frac{u^2}{2}-\tau
p-\tilde e}\right)_X =0, \\
&k_T+\omega_X =0.
\end{align*}The last equation is just the compatibility condition coming from the definition of the phase (A.2). It can be also written in the form
\begin{equation*}
k_T+\left(\tilde{c} k\right)_X =0, \quad \tilde{c}=\frac{\omega}{k}.
\end{equation*}Introducing
\begin{equation*}
\Delta =\overline{u\tau}-{\overline u}\; {\overline \tau}, \;
\overline{\varepsilon}=\overline{\tilde e-\eta \tilde e_\eta}, \;
E=\overline{\varepsilon}+\frac{\overline{u^2}-\overline{u}^2}{2}, \;
\Sigma=\overline{\tau_\theta \tilde e_\eta},
\end{equation*}one can obtain a Gibbs-type identity relating the unknowns (see [Reference Gavrilyuk22, Reference Gavrilyuk, Serre, Morioka and Van Wijngaarden23] for proof)
\begin{equation}
dE+\overline{p} \; d\overline{\tau} +\tilde{c}d\Delta=\omega d\Sigma.
\end{equation}It can also be written in the form:
\begin{equation}
d\overline{\varepsilon}+\overline{p} \; d\overline{\tau} -\frac{\tilde{c}^2}{2}d\delta=\omega d\Sigma,\quad \delta=\overline {\tau^2}-(\overline \tau)^2.
\end{equation}The Gibbs identity (A.11) or (A.12) is equivalent to an algebraic nonlinear dispersion relation coming from (A.10) when we are looking for 2π-periodic solutions [Reference Whitham56].
Using the expressions for correlations (A.5)–(A.8), the modulation equations take the conservative form
\begin{equation}
\begin{split}
&{\overline \tau}_T-{\overline u}_X=0, \\
&{\overline u}_T+{\overline p}_X=0, \\
&\left(\overline{\varepsilon}
+\frac{\overline{u}^2}{2}+\frac{\tilde{c}^2}{2}\left(\overline{\tau^2}-
\overline{\tau}^2\right)\right)_T+\left(\overline{p}\; \overline{u}
+\tilde{c}^3
\left(\overline{\tau^2}-\overline{\tau}^2\right)\right)_X=0, \\
&\left(\overline{\tau}\; \overline{u} -\tilde{c}
\left(\overline{\tau^2} -\overline{\tau}^2\right) -k\Sigma\right)_T
-\left(\frac{\overline{u}^2}{2} +\frac{\tilde{c}^2}{2}
\left(\overline{\tau^2} -\overline{\tau}^2\right)-
\overline{\tau}\;\overline{p}+ \tilde{c}^2 \left(\overline{\tau^2}
-\overline{\tau}^2\right) -\overline{\varepsilon}+
\omega\Sigma\right)_X =0, \\
&k_T+(\tilde{c}k)_X =0.
\end{split}
\end{equation} The five conservation laws (A.13) form a system of modulation equations (the SGN-Whitham system) for the four unknowns 
$k,\; \tilde{c},\; \overline{\tau}, \; \overline{u}$. The equations are compatible because the averaged Bernoulli law is a consequence of the mass, momentum, energy and wave conservation laws. This can be proved by direct calculations. Using the Gibbs relation (A.11) or (A.12), one can derive the sixth conservation law for Σ (an averaged entropy conservation law)
\begin{equation}
\left(\Sigma +\frac{\tilde{c}\delta}{k}\right)_T
+\left(\frac{\tilde{c}^2\delta}{k}\right)_X = 0.
\end{equation}For the proof, one can use the energy conservation law in the form
\begin{equation*}
\left(\overline{\varepsilon} + \frac{\overline{u}^2}{2}
+\frac{\tilde{c}^2}{2}\delta\right)_T +\left(\overline{p}\;
\overline{u} +\tilde{c}^3\delta\right)_X=0.
\end{equation*}Expanding it and using Gibbs relation in the form (A.12), one obtains
\begin{equation*}
-\overline{p} \;{\overline{\tau}}_T +\frac{\tilde{c}^2}{2}\delta_T
+\omega\Sigma_T +{\overline{u}}\;{\overline{u}}_T +
\frac{\tilde{c}^2}{2}\delta_T +\tilde{c}\tilde{c}_T
\delta+\overline{p}_X \overline{u}+\overline{p}\; \overline{u}_X
+\tilde{c}(\tilde{c}^2\delta)_X +\tilde{c}^2\tilde{c}_X\delta=0.
\end{equation*}Using the averaged mass and momentum equations, one obtains
\begin{equation*}
\tilde{c}^2\delta_T +\omega\Sigma_T +\tilde{c}\tilde{c}_T\delta
+\tilde{c}(\tilde{c}^2\delta)_X +\tilde{c}^2\delta \tilde{c}_X=0.
\end{equation*} Or, dividing by 
$\tilde{c}$
\begin{equation*}
(\tilde{c}\delta)_T +k\Sigma_T +(\tilde{c}^2\delta)_X
+\tilde{c}\delta \tilde{c}_X=0.
\end{equation*}Dividing by k, one obtains, after some algebra, the conservation law (A.14).
Finally, the full, compatible SGN-Whitham system (A.13)–(A.14) consists of the averaged conservation laws of mass, momentum, energy, wave conservation, the averaged Bernoulli conservation law and that for the averaged entropy Σ. The last conservation law is also called the wave action conservation law [Reference Whitham56].
A.1. Solitary wave limit
The solitary wave limit is 
$k\rightarrow 0$, which implies 
$\omega\rightarrow 0$. In this case, the modulation equations become purely hydrodynamic. For example, the mass and momentum equation become
\begin{equation*}
{\overline \tau}_T-{\overline u}_X=0, \quad
{\overline u}_T+{\overline p}_X=0,
\end{equation*}with
\begin{equation}
\overline p=-\tilde e_\tau (\overline \tau, 0).
\end{equation} The conservation of waves equation identically vanishes because both k and ω are zero in this limit. However, in such a limit, the equation for the wave action is non-trivial. Let us first calculate Σ for the full (non-averaged) SGN equations. With 
$\displaystyle \tau = \frac{1}{h}$, to leading order 
$\mathcal{O}(1)$, one has
\begin{equation}
\tilde e=\frac{h}{2} -\frac{h_t^2}{6} =\frac{1}{2\tau}
-\frac{\tau_t^2}{6\tau^4} \sim
\frac{1}{2\tau}-\frac{\eta^2}{6\tau^4}, \quad \eta =-\omega\tau_\theta.
\end{equation}Then,
\begin{equation}
\tilde e_\eta \sim -\frac{\eta}{3\tau^4},
\end{equation}and
\begin{equation}
\Sigma = -\overline{\frac{\tau_{\theta}
\eta}{3\tau^4}}= \frac{\omega}{3}
\overline{\frac{\tau_{\theta}^2}{\tau^4}}
= \frac{\omega}{3}\;\overline{h_{\theta}^2}.
\end{equation} Setting 
$\zeta=q-\tilde c t$ to be the travelling wave coordinate, then
\begin{equation}
\frac{d }{d\zeta}= k \frac{d }{d\theta}.
\end{equation}Using this, we reduce the problem to the following one. Find the limits
\begin{equation*}
\lim_{k\rightarrow 0}\tilde c \displaystyle
\left(\frac{\overline{\left(\frac{dh}{d\zeta}\right)^2}}{3k}
+\frac{\delta}{k}\right) \quad{\rm and} \quad \lim_{k\rightarrow
0}{\tilde c}^2\frac{\delta}{k}.
\end{equation*} Since the limit of 
$\tilde c$ is 
$\tilde c^2=h_1h_2h_3\rightarrow h_1^2h_3$ as k → 0, we need only to find
\begin{equation*}
\lim_{k\rightarrow 0} \displaystyle
\left(\frac{\overline{\left(\frac{dh}{d\zeta}\right)^2}}{3k}
+\frac{\delta}{k}\right) \quad{\rm and} \quad \lim_{k\rightarrow
0}\frac{\delta}{k}.
\end{equation*}A.2. Computation of average values in mass Lagrangian coordinates
The wavelength in mass Lagrangian coordinates is
\begin{equation}
L=\frac{2\vert\tilde
c\vert}{\sqrt{3}}\int_{h_2}^{h_3}\frac{hdh}{\sqrt{P(h)}}.
\end{equation}Also,
\begin{equation}
\overline{\left(\frac{dh}{d\zeta}\right)^2} =
\frac{2}{L}\sqrt{\frac{3}{\tilde
c^2}}\int_{h_2}^{h_3}\frac{\sqrt{P}dh}{h}.
\end{equation} Then, with 
$k=2\pi/L$, the limit as 
$m\rightarrow 1$ of the ratio
\begin{align*}
\frac{\overline{\left(\frac{dh}{d\zeta}\right)^2}}{3k}
=\frac{1}{2\pi}\frac{2}{3}\sqrt{\frac{3}{\tilde c^2}}
\int_{h_2}^{h_3} \frac{\sqrt{P}dh}{h} &\rightarrow
\frac{1}{2\pi}\frac{4}{\sqrt{3}}
\left(\frac{(3-2n)\sqrt{n}}{3(1-n)}-{\rm ln}
\left(\frac{1+\sqrt{n}}{\sqrt{1-n}}\right)\right) \\
&= \frac{1}{2\pi}\frac{4}{\sqrt{3}}
\left(\frac{(3-2n)\sqrt{n}}{3(1-n)}-\frac{1}{2}{\rm
ln}\left(\frac{1+\sqrt{n}}{1-\sqrt{n}}\right)\right) \\
&= \frac{1}{2\pi}\frac{4}{\sqrt{3}}
\left(\frac{(3-2n)\sqrt{n}}{3(1-n)}+\frac{1}{2}{\rm
ln}\left(\frac{1-\sqrt{n}}{1+\sqrt{n}}\right)\right).
\end{align*}Recall,
\begin{equation}
m=\frac{h_3-h_2}{h_3-h_1}, \quad n=\frac{h_3-h_2}{h_3}, \quad 0 \lt n \lt m \lt 1.
\end{equation} Indeed, making the change of variables 
$h=h_2+t(h_3-h_2)$, 
$t\in [0,1]$ and then 
$t=\cos^2\theta$, 
$\theta\in [0,\pi/2]$, one obtains
\begin{align*}
\int_{h_2}^{h_3} \frac{\sqrt{P}dh}{h}
&=\frac{(h_3-h_2)^2\sqrt{h_3-h_1}}{h_3}\int_0^1
\frac{\sqrt{t(1-t)(1-m(1-t))}}{1-n(1-t)}dt \\
&= \frac{2(h_3-h_2)^2\sqrt{h_3-h_1}}{h_3} \int_{0}^{\pi/2}
\frac{\sin^2\theta \cos^2\theta
\sqrt{1-m\sin^2\theta}}{1-n\sin^2\theta}d\theta \\
&\rightarrow \frac{2(h_3-h_1)^{5/2}}{h_3}
\int_{0}^{\pi/2}\frac{\sin^2\theta \cos^2\theta
\sqrt{1-\sin^2\theta}}{1-n\sin^2\theta}d\theta, \quad \mathrm{as}
~ m \to 1 \\
&= \frac{2(h_3-h_1)^{5/2}}{h_3} \left(\frac{3-2n}{3n^2}
-\frac{1-n}{n^{5/2}}{\rm \ln} \left(\frac{1+\sqrt{n}}{\sqrt{1-n}}
\right)\right).
\end{align*} The next step is the expression for 
$\delta/k$. One has
\begin{equation}
\frac{\delta}{k}= \frac{\overline{\tau^2}
-\left(\overline{\tau}\right)^2}{k}
=\frac{1}{2\pi}\frac{2\vert\tilde c\vert}{\sqrt{3}}
\int_{h_2}^{h_3}\frac{hdh}{\sqrt{P(h)}} \left(
\frac{\int_{h_2}^{h_3}
\frac{dh}{h\sqrt{P}}}{\int_{h_2}^{h_3}\frac{hdh}{\sqrt{P}}}
-\left(\frac{\int_{h_2}^{h_3}
\frac{dh}{\sqrt{P}}}{\int_{h_2}^{h_3}\frac{hdh}{\sqrt{P}}}\right)^2
\right).
\end{equation}The expressions of the integrals
\begin{equation}
\int_{h_2}^{h_3}\frac{dh}{\sqrt{P}}, \quad
\int_{h_2}^{h_3}\frac{dh}{h\sqrt{P}}, \quad\int_{h_2}^{h_3}\frac{hdh}{\sqrt{P}}
\end{equation}are given in [Reference Tkachenko, Gavrilyuk and Shyue53]. They give us
\begin{equation}
\frac{\delta}{k} = \frac{1}{2\pi} \frac{4\vert\tilde
c\vert}{\sqrt{3}} \frac{1}{h_3\sqrt{h_3-h_1}}
\left(\Pi(n,m)-\frac{\mathrm{K}^2(m)}{(1-n/m)\mathrm{K}(m)+(n/m) \mathrm{E}(m)}\right).
\end{equation} As usual, 
$\mathrm{K}(m)$ is the complete elliptic integral of the first kind
\begin{equation}
\mathrm{K}(m)=\int_0^{\pi/2}\frac{d\theta}{\sqrt{1-m\sin^2{\theta}}},
\end{equation} 
$\mathrm{E}(m)$ is the complete elliptic integral of the second kind
\begin{equation}
\mathrm{E}(m)=\int_0^{\pi/2}\sqrt{1-m\sin^2{\theta}}\, d\theta,
\end{equation} and 
$\Pi(n,m)$ is the complete elliptic integral of the third kind
\begin{equation}
\Pi(n,m) = \int_0^{\pi/2}
\frac{d\theta}{(1-n\sin^2\theta)\sqrt{1-m\sin^2{\theta}}}.
\end{equation}The limit
\begin{equation}
\lim_{m\rightarrow
1}\left(\Pi(n,m)-\frac{\mathrm{K}^2(m)}{(1-n/m)\mathrm{K}(m)+(n/m) \mathrm{E}(m)}\right)
\end{equation}is singular. It can be obtained in the form
\begin{equation}
\lim_{m\rightarrow 1} \left(\Pi(n,m) -\frac{\mathrm{K}^2(m)}{(1-n/m)\mathrm{K}(m)+
(n/m) \mathrm{E}(m)}\right) =\frac{n}{(1-n)^2}
+\frac{\sqrt{n}}{2(1-n)}{\ln}
\left(\frac{1-\sqrt{n}}{1+\sqrt{n}}\right).
\end{equation}Hence,
\begin{equation}
\lim_{m\rightarrow 1}\frac{\delta}{k}=\lim_{m\rightarrow 1}
\frac{\overline{\tau^2} -\left(\overline{\tau}\right)^2}{k}
=\frac{1}{2\pi} \frac{4}{\sqrt{3}}\left(\frac{\sqrt{n}}{1-n}
+\frac{1}{2}{\rm ln}
\left(\frac{1-\sqrt{n}}{1+\sqrt{n}}\right)\right).
\end{equation}In particular, this implies
\begin{equation}
\lim_{k\rightarrow 0} \displaystyle\left(
\frac{\overline{\left(\frac{dh}{d\zeta}\right)^2}}{3k}
+\frac{\delta}{k}\right) =\frac{4\sqrt{3}}{2\pi}
\left(\frac{(6-2n)\sqrt{n}}{3(1-n)}+{\rm
ln}\left(\frac{1-\sqrt{n}}{1+\sqrt{n}}\right)\right).
\end{equation} Finally, the limiting SGN-Whitham modulation equation for the solitary wave field in mass Lagrangian coordinates is eq. (4.7) with (4.8) and (4.9). Equation (4.7) is the solitary wave limit of eq. (A.14) and expresses the conservation of wave action. In the limit 
$m\rightarrow 1$, the quantity n becomes eq. (4.10).
Appendix B. Solitary wave limit of the modulation equations in Eulerian coordinates
The solitary wave limit (4.7) can also be obtained from the modulation equations written in Eulerian coordinates (4.1), obtained previously in [Reference El, Grimshaw and Smyth10, Reference Tkachenko, Gavrilyuk and Shyue53]. Here, we use the formulation of [Reference Tkachenko, Gavrilyuk and Shyue53] with the notation c for the phase velocity and g = 1. Note that in [Reference Tkachenko, Gavrilyuk and Shyue53], the phase velocity was denoted by D and the roots of the polynomial were 
$h_0 \lt h_1 \lt h_2$ instead of 
$h_1 \lt h_2 \lt h_3$ used in this work. The SGN-Whitham modulation equations in Eulerian coordinates are
\begin{align}
&\overline{h}_t+(p+\overline{h} c)_x=0,
\end{align}
\begin{align}
&(p+\overline{h} c)_t+\left(\overline{h} c^{2}+\frac{1}{2} I_{2}+2 p c\right)_x=0,
\end{align}
\begin{align}
&\left(\frac{1}{2} \overline{h} c^{2}+\frac{1}{2} I_{1} \overline{h}-\frac{1}{2} I_{2}+ I_{3} \overline{h^{-1}}+p c\right)_t
+\left(\frac{1}{2} \overline{h} c^{3}+\frac{1}{2} I_{1} \overline{h} c+
I_{3} \overline{h^{-1}} c+\frac{3}{2} p c^{2}+\frac{1}{2} p I_{1}\right)_x=0 ,
\end{align}
\begin{align}
&k_t+(k c)_x=0,
\end{align}with
\begin{align}
&I_1=h_1+h_2+h_3, \quad
I_2=h_1 h_2+h_2 h_3+h_1 h_3, \quad
I_3=h_1 h_2 h_3,\quad
p = -\sigma \sqrt{I_3},
\end{align}
\begin{align}
&\overline{h}=h_1+\left(h_3-h_1\right) \frac{\mathrm{E}(m)}{\mathrm{K}(m)}, \quad
\overline{h^{-1}} =\frac{\Pi(n, m)}{h_3 \mathrm{K}(m)}, \quad
\frac{2\pi}{k}= L=4 \sqrt{\frac{h_1 h_2 h_3}{3}}
\frac{\mathrm{K}(m)}{\sqrt{h_3-h_1}}, \quad n=1-\frac{h_2}{h_3}.
\end{align}We first rewrite the quasi-linear system above in the new variables
\begin{equation}
(h_1,h_2,h_3,c) \quad \longrightarrow \quad
\boldsymbol{h} = \left(h_1,h_2,a=h_3-h_2,u_1=c-\sigma\sqrt{h_1+a} \right),
\end{equation} using a symbolic computation package, e.g. Mathematica. Note that h 1, u 1 are the spatial averages 
$\overline{h}$, 
$\overline{u}$ in the solitary wave limit 
$h_2 \to h_1$. The expressions are particularly long and not written here for brevity. We denote the obtained system in the abstract form
\begin{equation}
\boldsymbol{h}_t + M(\boldsymbol{h}) \boldsymbol{h}_x=0,
\end{equation}where 
$M(\boldsymbol{h})$ is a 
$4\times 4$ matrix.
The variables 
$h_1,h_2,a,u_1$ remain finite in the solitary wave limit 
$h_2 \to h_1$ (or m → 1), and the limit of the system (B.8) thus yields non-trivial modulation equations for h 1, u 1 and a. The coefficients of 
$M(\boldsymbol{h})$ are rational functions of h 1, h 2, a, u 1, 
$\mathrm{E}(m)$, 
$\mathrm{K}(m)$ and 
$\Pi(n,m)$. Using the series expansions
\begin{align}
&\mathrm{E}(m) = 1+{\cal O}(1-m),\quad \mathrm{K}(m) = 2\ln(2)-\frac{\ln(1-m)}{2} +
{\cal O}(1-m),
\end{align}
\begin{align}
&\Pi(n,m) = \frac{\sqrt{n}\, \tanh^{-1}(\sqrt{n})-2\ln(2)+\ln(1-m)/2}{n-1}+{\cal O}(1-m),
\end{align}where
\begin{equation}
\tanh^{-1}(\sqrt{n}) = \frac{1}{2}\ln\left(\frac{1+\sqrt
n}{1-\sqrt n} \right)=\sinh^{-1}(z),\quad n = \frac{a}{h_1+a},\quad z=\sqrt{\frac{a}{h_1}},
\end{equation}we obtain the solitary wave limit in Eulerian coordinates
\begin{align}
&h_{1,t}+(u_1h_1)_x=0,
\end{align}
\begin{align}
&u_{1,t}+u_1u_{1,x}+h_{1,x}=0,
\end{align}
\begin{align}
&a_t +c a_x-\sigma \,\frac{(2
n-3) \sqrt{n}+(3-n) (1-n) \tanh
^{-1}\left(\sqrt{n}\right)}{(1-n)^{3/2}\left(2 \sqrt{n}-(1-n) \tanh
^{-1}\left(\sqrt{n}\right)\right)} \, \sqrt{h_1}\, h_{1,x} \nonumber\\
&-\frac{3 \sqrt{n}-(3-n) \tanh
^{-1}\left(\sqrt{n}\right)}{2 \sqrt{n}-(1-n) \tanh
^{-1}\left(\sqrt{n}\right)}\, h_1 \, u_{1,x}=0,
\end{align}
\begin{align}
&c=u_1+\sigma \sqrt{h_1+a}.
\end{align}Equation (B.14) for the wave amplitude a is equivalent to the equation for the wave action (4.7) written in Eulerian coordinates as
\begin{equation}
(h_1 F(n,h_1))_t+\left(h_1 u_1 F(n,h_1) + G(n,h_1)\right)_x=0,
\end{equation}with F and G given by (4.8) and (4.9), respectively. Using the notation 
$h_1=\overline{h}$, 
$u_1=\overline{u}$, and replacing the amplitude a by the dimensionless amplitude 
$\displaystyle z=\sqrt{\frac{a}{\overline{h}}}$, we recover from (B.12)–(B.14) equations (4.12)–(4.14).
Appendix C. Compatibility condition
Theorem 1 Consider an overdetermined system of equations for the unknown 
$w(x_1,x_2,x_3)$
\begin{equation}
w_{x_1}=\alpha(x_1,x_2,x_3) w_{x_2},\quad w_{x_1}=\beta(x_1,x_2,x_3) w_{x_3}.
\end{equation}The system is compatible if and only if
\begin{equation}
\alpha^2{\beta}_{x_2} -\beta^2\alpha_{x_3}+\beta\alpha_{x_1}-\alpha\beta_{x_1}=0.
\end{equation}Proof. The compatibility condition is
\begin{equation}
(\partial_{x_1}-\alpha \partial_{x_2})(\partial_{x_1}-\beta \partial_{x_3})w-(\partial_{x_1}-\beta \partial_{x_3})(\partial_{x_1}-\alpha \partial_{x_2})w=0.
\end{equation}It is equivalent to:
\begin{equation}
\left(\frac{\alpha \beta_{x_2}-\beta_{x_1}}{\beta}-\frac{\beta \alpha_{x_3}-\alpha_{x_1}}{\alpha}\right)u_{x_1}=0.
\end{equation}The last expression is equivalent to (C.2).
In our case the governing equations in the solitary wave limit are
\begin{equation}
\tau_t-u_q=0,\quad u_t-g/\tau^3 \tau_q=0,\quad F(n,\tau)_t+G(n,\tau)_q=0.
\end{equation} Here, we replaced 
$h_1^{-1}$ by τ in the functions 
$F(n,h_1)$ and 
$G(n, h_1)$ and used the same letters F and G for the functions of new arguments. Let us suppose that there exists the Riemann invariant 
$R(n,\tau,u)$ such that
\begin{equation}
R_t+\lambda R_q=0, \quad \lambda=\frac{G_n}{F_n}.
\end{equation}Expanding the equation for R, one obtains
\begin{equation}
R_n (n_t+\lambda n_q)+R_\tau(\tau_t+\lambda \tau_q)+R_u (u_t+\lambda u_q)=0.
\end{equation}Also, replacing the time derivatives nt, ut and τt from (C.5), we obtain two equations corresponding to the vanishing coefficients in front of the derivatives uq and τq. They are of the form
\begin{equation}
R_n=\alpha(n,\tau)R_\tau, \quad R_n=\beta(n,\tau)R_u,
\end{equation} with coefficients α and β that are independent of u. We take thus 
$x_1=n$, 
$x_2=\tau$ and 
$x_3=u$. According to Theorem 1, the compatibility condition is:
\begin{equation}
\beta_\tau=\left(\frac{\beta}{\alpha}\right)_n.
\end{equation}One can check with Mathematica software that this condition is not satisfied. Thus, the Riemann invariant coresponding to the eigenvalue λ doesn’t exist.
Appendix D. Numerical method
Let p be the integrated fluid pressure divided by the constant density ρ and defined by
\begin{equation*}
p= \frac{1}{2} h^{2}+
\frac{h^{2}}{3}\frac{d^{2}h}{dt^{2}}.
\end{equation*}To solve the one-dimensional, homogeneous SGN equations (2.1), (2.2) numerically, as in [Reference Gavrilyuk and Shyue21] for the multidimensional SGN equations over topography, we use the ϖ formulation of the equations:
\begin{align}
& h_{t}+
\left ( hu \right )_{x} = 0,
\end{align}
\begin{align}
& \left( hu \right)_{t} +
\left ( hu^{2}+
\frac{1}{2} h^{2} \right )_x = -\varpi_{x}.
\end{align} Here 
$\displaystyle{\varpi= p-\frac{1}{2} h^{2}}$ denotes the averaged non-hydrostatic part of the pressure that is obtained by solving the linear elliptic problem
\begin{align}
-\frac{h^{3}}{3}
\left ( \frac{\varpi_{x}}{h} \right )_{x}+
\varpi
= \frac{2}{3}
h^{3} u_{x}^{2}+
\frac{h^{3}}{3} h_{xx}.
\end{align}In the algorithm, we employ the hyperbolic-elliptic splitting approach developed previously in [Reference Gavrilyuk, Nkonga, Shyue and Truskinovsky19, Reference Gavrilyuk and Shyue21, Reference Le Métayer, Gavrilyuk and Hank36]. This algorithm consists of two steps. In the first, hyperbolic step, we employ a state-of-the-art method for the numerical solution of the hyperbolic systems of equations (D.1a), (D.1b) over the time step 
$\Delta t$. In the second, elliptic step, using the approximate solution h and u computed during the hyperbolic step, we numerically invert the elliptic operator (D.1c) for ϖ with prescribed boundary conditions.
Note that in the hyperbolic step, rather than writing the equations in the conservation form 
$\boldsymbol{q}_{t} + \boldsymbol{f}(\boldsymbol{q})_{x} = 0$ with 
$\boldsymbol{q} = (h, hu)^{T}$ and 
$\boldsymbol{f} = \left (hu, hu^{2}+ \frac{1}{2} h^{2}+ \varpi
\right)^{T}$, which is essential in the conservative first-order setting [Reference LeVeque37] but is difficult to achieve more than first order accuracy, we write it in the form of a balance law, see [Reference Gavrilyuk, Nkonga, Shyue and Truskinovsky19, Reference Gavrilyuk and Shyue21] for the details of the numerical implementation.
Open access
