Hostname: page-component-7dd5485656-glrdx Total loading time: 0 Render date: 2025-10-31T03:58:51.288Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of columnar convection in a porous medium

Published online by Cambridge University Press:  22 November 2013

Duncan R. Hewitt ,
Jerome A. Neufeld  and
John R. Lister
Duncan R. Hewitt*
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
Jerome A. Neufeld
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK Department of Earth Science, University of Cambridge, Cambridge CB2 3EQ, UK BP Institute, University of Cambridge, Cambridge CB3 0EZ, UK
John R. Lister
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: drh39@cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Convection in a porous medium at high Rayleigh number 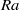$\mathit{Ra}$ exhibits a striking quasisteady columnar structure with a well-defined and 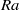$\mathit{Ra}$ -dependent horizontal scale. The mechanism that controls this scale is not currently understood. Motivated by this problem, the stability of a density-driven ‘heat-exchanger’ flow in a porous medium is investigated. The dimensionless flow comprises interleaving columns of horizontal wavenumber 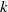$k$ and amplitude 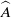$\widehat{A}$ that are driven by a steady balance between vertical advection of a background linear density stratification and horizontal diffusion between the columns. Stability is governed by the parameter 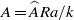$A= \widehat{A}\mathit{Ra}/ k$ . A Floquet analysis of the linear-stability problem in an unbounded two-dimensional domain shows that the flow is always unstable, and that the marginal-stability curve is independent of 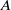$A$ . The growth rate of the most unstable mode scales with 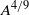${A}^{4/ 9} $ for 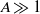$A\gg 1$ , and the corresponding perturbation takes the form of vertically propagating pulses on the background columns. The physical mechanism behind the instability is investigated by an asymptotic analysis of the linear-stability problem. Direct numerical simulations show that nonlinear evolution of the instability ultimately results in a reduction of the horizontal wavenumber of the background flow. The results of the stability analysis are applied to the columnar flow in a porous Rayleigh–Bénard (Rayleigh–Darcy) cell at high 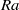$\mathit{Ra}$ , and a balance of the time scales for growth and propagation suggests that the flow is unstable for horizontal wavenumbers 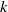$k$ greater than 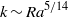$k\sim {\mathit{Ra}}^{5/ 14} $ as 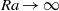$\mathit{Ra}\rightarrow \infty $ . This stability criterion is consistent with hitherto unexplained numerical measurements of 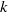$k$ in a Rayleigh–Darcy cell.

JFM classification

Convection: Convection Convection: Convection in porous media Instability: Instability

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 737 , 25 December 2013 , pp. 205 - 231
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
Backhaus, S., Turitsyn, K. & Ecke, R. E. 2011 Convective instability and mass transport of diffusion layers in a hele-shaw geometry. Phys. Rev. Lett. 106, 104501.CrossRefGoogle Scholar
Beaumont, D. N. 1981 The stability of spatially periodic flows. J. Fluid Mech. 108, 461–474.CrossRefGoogle Scholar
Cheng, P. 1978 Heat transfer in geothermal systems. Adv. Heat Transfer 14, 1–105.Google Scholar
Corson, L. T. 2011 Maximising the heat flux in steady unicellular porous media convection. In Proceedings of the 2011 Geophysical Fluid Dynamics Summer Program, pp. 389–412. Woods Hole Oceanographic Institution.Google Scholar
Drazin, P. G. 2002 Introduction to Hydrodynamic Stability. Cambridge University Press.CrossRefGoogle Scholar
Fowler, A. C. 1985 The formation of freckles in binary alloys. IMA J. Appl. Maths 35, 159–174.CrossRefGoogle Scholar
Fu, X., Cueto-Felgueroso, L. & Juanes, R. 2013 Pattern formation and coarsening dynamics in three-dimensional convective mixing in porous media. Phil. Trans. R. Soc. A 371, 20120355.CrossRefGoogle ScholarPubMed
Graham, M. D. & Steen, P. H. 1994 Plume formation and resonant bifurcations in porous-media convection. J. Fluid Mech. 272, 67–89.CrossRefGoogle Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2012 Ultimate regime of high Rayleigh number convection in a porous medium. Phys. Rev. Lett. 108, 224503.CrossRefGoogle Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2013 Convective shutdown in a porous medium at high Rayleigh number. J. Fluid Mech. 719, 551–586.CrossRefGoogle Scholar
Hidalgo, J. J., Fe, J., Cueto-Felgueroso, L. & Juanes, R. 2012 Scaling of convective mixing in porous media. Phys. Rev. Lett. 109, 264503.CrossRefGoogle ScholarPubMed
Holyer, J. Y. 1981 On the collective instability of salt fingers. J. Fluid Mech. 110, 195–207.CrossRefGoogle Scholar
Holyer, J. Y. 1984 The stability of long, steady, two-dimensional salt fingers. J. Fluid Mech. 147, 169–185.CrossRefGoogle Scholar
Huppert, H. E. & Turner, J. S. 1981 Double-diffusive convection. J. Fluid Mech. 106, 299–329.CrossRefGoogle Scholar
Jordan, D. W. & Smith, P. 1999 Nonlinear Ordinary Differential Equations, 3rd edn. Oxford University Press.CrossRefGoogle Scholar
Lapwood, E. R. 1948 Convection of a fluid in a porous medium. Math. Proc. Camb. Phil. Soc. 44, 508–521.CrossRefGoogle Scholar
Metz, B., Davidson, O., de Coninck, H. C., Loos, M. & Meyer, L. 2005 IPCC Special Report on Carbon Dioxide Capture and Storage. Cambridge University Press.Google Scholar
Neufeld, J. A., Hesse, M. A., Riaz, A., Hallworth, M. A., Tchelepi, H. A. & Huppert, H. E. 2010 Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett. 37, 22404.CrossRefGoogle Scholar
Nield, D. A. & Bejan, A. 2006 Convection in Porous media, 3rd edn. Springer.Google Scholar
Orr, F. M Jr. 2009 Onshore geologic storage of ${\mathrm{CO} }_{2} $ . Science 325, 1656–1658.CrossRefGoogle Scholar
Otero, J., Dontcheva, L. A., Johnston, H., Worthing, R. A., Kurganov, A., Petrova, G. & Doering, C. R. 2004 High-Rayleigh-number convection in a fluid-saturated porous layer. J. Fluid Mech. 500, 263–281.CrossRefGoogle Scholar
Pau, G. S. H., Bell, J. B., Pruess, K., Almgren, A. S., Lijewski, M. J. & Zhang, K. 2010 High-resolution simulation and characterization of density-driven flow in ${\mathrm{CO} }_{2} $ storage in saline aquifers. Adv. Water Resour. 33, 443–455.CrossRefGoogle Scholar
Radko, T. & Smith, D. P. 2012 Equilibrium transport in double-diffusive convection. J. Fluid Mech. 692, 5–27.CrossRefGoogle Scholar
Slim, A. C., Bandi, M. M., Miller, J. C. & Mahadevan, L. 2013 Dissolution-driven convection in a Hele–Shaw cell. Phys. Fluids 25, 024101.CrossRefGoogle Scholar
Stern, M. E. 1969 Collective instability of salt fingers. J. Fluid Mech. 35, 209–218.CrossRefGoogle Scholar
Wen, B., Chini, G. P., Dianati, N. & Doering, C. R. 2013 Computational approaches to aspect-ratio-dependent upper bounds and heat flux in porous medium convection. Phys. Lett. A (in press).CrossRefGoogle Scholar
Wen, B., Dianati, N., Lunasin, E., Chini, G. P. & Doering, C. R. 2012 New upper bounds and reduced dynamical modelling for Rayleigh–Bénard convection in a fluid-saturated porous layer. Commun. Nonlinear Sci. Numer. Simul. 17, 2191–2199.CrossRefGoogle Scholar
Wooding, R. A., Tyler, S. W., White, I. & Anderson, P. A. 1997 Convection in groundwater below an evapourating salt lake: 2. Evolution of fingers or plumes. Water Resour. Res. 33, 1219–1228.CrossRefGoogle Scholar