Hostname: page-component-7dd5485656-pnlb5 Total loading time: 0.001 Render date: 2025-10-31T05:16:47.105Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of finite sampling time on estimation of Brownian fluctuation

Published online by Cambridge University Press:  12 February 2015

Shahram Pouya ,
Di Liu  and
Manoochehr M. Koochesfahani
Shahram Pouya*
Affiliation:
Department of Mechanical Engineering, Michigan State University, East Lansing, MI 48824, USA
Di Liu
Affiliation:
Department of Mathematics, Michigan State University, East Lansing, MI 48824, USA
Manoochehr M. Koochesfahani
Affiliation:
Department of Mechanical Engineering, Michigan State University, East Lansing, MI 48824, USA
*
†Email address for correspondence: pouya@egr.msu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a study of the effect of finite detector integration/exposure time 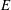$E$ , in relation to interrogation time interval 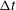${\rm\Delta}t$ , on analysis of Brownian motion of small particles using numerical simulation of the Langevin equation for both free diffusion and hindered diffusion near a solid wall. The simulation result for free diffusion recovers the known scaling law for the dependence of estimated diffusion coefficient on 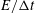$E/{\rm\Delta}t$ , i.e. for 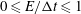$0\leqslant E/{\rm\Delta}t\leqslant 1$ the estimated diffusion coefficient scales linearly as 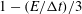$1-(E/{\rm\Delta}t)/3$ . Extending the analysis to the parameter range 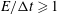$E/{\rm\Delta}t\geqslant 1$ , we find a new nonlinear scaling behaviour given by 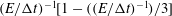$(E/{\rm\Delta}t)^{-1}[1-((E/{\rm\Delta}t)^{-1})/3]$ , for which we also provide an exact analytical solution. The simulation of near-wall diffusion shows that hindered diffusion of particles parallel to a solid wall, when normalized appropriately, follows with a high degree of accuracy the same form of scaling laws given above for free diffusion. Specifically, the scaling laws in this case are well represented by 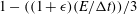$1-((1+{\it\epsilon})(E/{\rm\Delta}t))/3$ , for 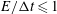$E/{\rm\Delta}t\leqslant 1$ , and 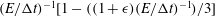$(E/{\rm\Delta}t)^{-1}[1-((1+{\it\epsilon})(E/{\rm\Delta}t)^{-1})/3]$ , for 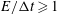$E/{\rm\Delta}t\geqslant 1$ , where the small parameter ${\it\epsilon}$ depends on the size of the near-wall domain used in the estimation of the diffusion coefficient and value of 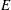$E$ . For the range of parameters reported in the literature, we estimate 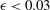${\it\epsilon}<0.03$ . The near-wall simulations also show a bias in the estimated diffusion coefficient parallel to the wall even in the limit 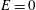$E=0$ , indicating an overestimation which increases with increasing time delay 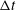${\rm\Delta}t$ . This diffusion-induced overestimation is caused by the same underlying mechanism responsible for the previously reported overestimation of mean velocity in near-wall velocimetry.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics Low-Reynolds-number flows: Stokesian dynamics

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 767 , 25 March 2015 , pp. 65 - 84
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adamczyk, Z., Siwek, B. & Szyk, L. 1995 Flow-induced surface blocking effects in adsorption of colloid particles. J. Colloid Interface Sci. 174 (1), 130–141.Google Scholar
Banerjee, A. & Kihm, K. D. 2005 Experimental verification of near-wall hindered diffusion for the Brownian motion of nanoparticles using evanescent wave microscopy. Phys. Rev. E 72, 042101.Google Scholar
Belongia, B. M. & Baygents, J. C. 1997 Measurements on the diffusion coefficient of colloidal particles by Taylor–Aris dispersion. J. Colloid Interface Sci. 195, 19–31.Google Scholar
Berglund, A. J. 2010 Statistics of camera-based single-particle tracking. Phys. Rev. E 82 (1), 011917.Google Scholar
Bevan, M. A. & Prieve, D. C. 2000 Hindered diffusion of colloidal particles very near to a wall: revisited. J. Chem. Phys. 113 (3), 1228–1236.Google Scholar
Da Prato, G. & Zabczyk, J. 1996 Ergodicity for Infinite Dimensional Systems, vol. 229. Cambridge University Press.CrossRefGoogle Scholar
Destainville, N. & Salomé, L. 2006 Quantification and correction of systematic errors due to detector time-averaging in single-molecule tracking experiments. Biophys. J. 90 (2), L17–L19.Google Scholar
Dunlop, P. J., Harris, K. R. & Young, D. J. 1992 Experimental methods for studying diffusion in gases, liquids and solids. Phys. Meth. Chem. 6, 175–282.Google Scholar
Ermak, D. L. & Mccammon, J. A. 1978 Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 69 (4), 1352–1360.CrossRefGoogle Scholar
Gelles, J., Schnapp, B. J. & Sheetz, M. P. 1988 Tracking kinesin-driven movements with nanometre-scale precision. Nature 331 (6155), 450–453.Google Scholar
Goldman, A. J., Cox, R. G. & Brenner, H. 1967 Slow viscous motion of a sphere parallel to a plane wall—I motion through a quiescent fluid. Chem. Engng Sci. 22 (4), 637–651.Google Scholar
Huang, P. & Breuer, K. S. 2007 Direct measurement of anisotropic near-wall hindered diffusion using total internal reflection velocimetry. Phys. Rev. E 76, 046307.Google Scholar
Huang, P., Guasto, J. S. & Breuer, K. S. 2009 The effects of hindered mobility and depletion of particles in near-wall shear flows and the implications for nanovelocimetry. J. Fluid Mech. 637, 241–265.Google Scholar
Jin, S., Huang, P., Park, J., Yoo, J. Y. & Breuer, K. S. 2004 Near-surface velocimetry using evanescent wave illumination. Exp. Fluids 37 (6), 825–833.Google Scholar
Kazoe, Y. & Yoda, M. 2011 Measurements of the near-wall hindered diffusion of colloidal particles in the presence of an electric field. Appl. Phys. Lett. 99 (12), 124104.Google Scholar
Michalet, X. 2010 Mean square displacement analysis of single-particle trajectories with localization error: Brownian motion in an isotropic medium. Phys. Rev. E 82 (4), 041914.Google Scholar
Michalet, X. & Berglund, A. J. 2012 Optimal diffusion coefficient estimation in single-particle tracking. Phys. Rev. E 85 (6), 061916.Google Scholar
Montiel, D., Cang, H. & Yang, H. 2006 Quantitative characterization of changes in dynamical behavior for single-particle tracking studies. J. Phys. Chem. B 110 (40), 19763–19770.Google Scholar
Oetama, R. J. & Walz, J. Y. 2005 A new approach for analyzing particle motion near an interface using total internal reflection microscopy. J. Colloid Interface Sci. 284, 323–331.Google Scholar
Øksendal, B. 1998 Stochastic Differential Equations, 5th edn. Springer.Google Scholar
Pouya, S., Koochesfahani, M. M., Greytak, A. B., Bawendi, M. G. & Nocera, D. G. 2008 Experimental evidence of diffusion-induced bias in near-wall velocimetry using quantum dot measurements. Exp. Fluids 44 (6), 1035–1038.Google Scholar
Pouya, S., Koochesfahani, M., Snee, P., Bawendi, M. & Nocera, D. 2005 Single quantum dot (QD) imaging of fluid flow near surfaces. Exp. Fluids 39 (4), 784–786.Google Scholar
Qian, H., Sheetz, M. P. & Elson, E. L. 1991 Single particle tracking. Analysis of diffusion and flow in two-dimensional systems. Biophys. J. 60, 910–921.CrossRefGoogle ScholarPubMed
Ritchie, K., Shan, X. Y., Kondo, J., Iwasawa, K., Fujiwara, T. & Kusumi, A. 2005 Detection of non-Brownian diffusion in the cell membrane in single molecule tracking. Biophys. J. 88 (3), 2266–2277.CrossRefGoogle ScholarPubMed
Sadr, R., Hohenegger, C., Li, H., Mucha, P. J. & Yoda, M. 2007 Diffusion-induced bias in near-wall velocimetry. J. Fluid Mech. 577, 443–456.CrossRefGoogle Scholar
Sadr, R., Li, H. & Yoda, M. 2005 Impact of hindered Brownian diffusion on the accuracy of particle-image velocimetry using evanescent-wave illumination. Exp. Fluids 38 (1), 90–98.Google Scholar
Sadr, R., Yoda, M., Zheng, Z. & Conlisk, A. T. 2004 An experimental study of electro-osmotic flow in rectangular microchannels. J. Fluid Mech. 506, 357–367.CrossRefGoogle Scholar
Savin, T. & Doyle, P. S. 2005 Static and dynamic errors in particle tracking microrheology. Biophys. J. 88 (1), 623–638.CrossRefGoogle ScholarPubMed
Sholl, D. S., Fenwick, M. K., Atman, E. & Prieve, D. C. 2000 Brownian dynamics simulation of the motion of a rigid sphere in a viscous fluid very near a wall. J. Chem. Phys. 133 (20), 9268–9278.Google Scholar
Thompson, R. E., Larson, D. R. & Webb, W. W. 2002 Precise nanometer localization analysis for individual fluorescent probes. Biophys. J. 82 (5), 2775–2783.Google Scholar
Unni, H. N. & Yang, C. 2005 Brownian dynamics simulation and experimental study of colloidal particle deposition in a microchannel flow. J. Colloid Interface Sci. 291 (1), 28–36.CrossRefGoogle Scholar
Zettner, C. & Yoda, M. 2003 Particle velocity field measurements in a near-wall flow using evanescent wave illumination. Exp. Fluids 34 (1), 115–121.Google Scholar