Hostname: page-component-7dd5485656-k8lnt Total loading time: 0 Render date: 2025-10-31T07:34:28.963Z Has data issue: false hasContentIssue false
  • English
  • Français

Multi-solitons for nonlinear Klein–Gordon equations

Part of: Equations of mathematical physics and other areas of application

Published online by Cambridge University Press:  09 June 2014

RAPHAËL CÔTE  and
CLAUDIO MUÑOZ
RAPHAËL CÔTE
Affiliation:
CNRS and École polytechnique, Centre de Mathématiques Laurent Schwartz UMR 7640, Route de Palaiseau, 91128 Palaiseau cedex, France; cote@math.polytechnique.fr
CLAUDIO MUÑOZ
Affiliation:
Department of Mathematics, University of Chicago, 5734 South University Avenue, Chicago, IL 60615, U.S.A.; cmunoz@math.uchicago.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we consider the existence of multi-soliton structures for the nonlinear Klein–Gordon (NLKG) equation in 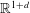$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathbb{R}^{1+d}$ . We prove that, independently of the unstable character of NLKG solitons, it is possible to construct a 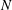$N$ -soliton family of solutions to the NLKG equation, of dimension 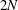$2N$ , globally well defined in the energy space 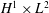$H^1\times L^2$ for all large positive times. The method of proof involves the generalization of previous works on supercritical Nonlinear Schrödinger (NLS) and generalized Korteweg–de Vries (gKdV) equations by Martel, Merle, and the first author [R. Côte, Y. Martel and F. Merle, Rev. Mat. Iberoam. 27 (1) (2011), 273–302] to the wave case, where we replace the unstable mode associated to the linear NLKG operator by two generalized directions that are controlled without appealing to modulation theory. As a byproduct, we generalize the linear theory described in Grillakis, Shatah, and Strauss [J. Funct. Anal. 74 (1) (1987), 160–197] and Duyckaerts and Merle [Int. Math. Res. Pap. IMRP (2008), Art ID rpn002] to the case of boosted solitons, and provide new solutions to be studied using the recent work of Nakanishi and Schlag [Zurich Lectures in Advanced Mathematics, vi+253 pp (European Mathematical Society (EMS), Zürich, 2011)] theory.

MSC classification

Secondary: 35Q51: Soliton-like equations 35Q40: PDEs in connection with quantum mechanics

Information

Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 2 , 01 July 2014 , e15
Creative Commons
Creative Common License - CCCreative Common License - BY
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
Copyright
© The Author(s) 2014

References

Berestycki, H. and Lions, P.-L., ‘Nonlinear scalar field equations I Existence of a ground state’, Arch. Ration. Mech. Anal. 82 (1983), 313–345.CrossRefGoogle Scholar
Bourgain, J., ‘Global solutions of nonlinear Schrödinger equations’, in:AMS Colloquium Publications, 46 (AMS, Providence, RI, 1999).Google Scholar
Côte, R., Martel, Y. and Merle, F., ‘Construction of multi-soliton solutions for the $L^2$ -supercritical gKdV and NLS equations’, Rev. Mat. Iberoam. 27 (1) (2011), 273–302.Google Scholar
Côte, R. and Zaag, H., ‘Construction of a multi-soliton blow-up solution to the semilinear wave equation in one space dimension’, Comm. Pure Appl. Math. 66 (10) (2013), 1541–1581.Google Scholar
Derrick, G. H., ‘Comments on nonlinear wave equations as models for elementary particles’, J. Math. Phys. 5 (1964), 1252.Google Scholar
Duyckaerts, T. and Merle, F., ‘Dynamic of threshold solutions for energy-critical NLS’, GAFA 18 (2008), 1787–1840.Google Scholar
Duyckaerts, T. and Merle, F., ‘Dynamics of threshold solutions for energy-critical wave equation’, Int. Math. Res. Pap. IMRP (2008), Art ID rpn002, 67 pp.Google Scholar
Duyckaerts, T., Kenig, C. E. and Merle, F., ‘Classification of radial solutions of the focusing, energy-critical wave equation’, Cambridge J. of Maths, to appear. Preprint,arXiv:1204.0031.Google Scholar
Gidas, B., Ni, W.-M. and Nirenberg, L., ‘Symmetry and related properties via the maximum principle’, Comm. Math. Phys. 68 (3) (1979), 209–243.CrossRefGoogle Scholar
Grillakis, M., Shatah, J. and Strauss, W., ‘Stability theory of solitary waves in the presence of symmetry I’, J. Funct. Anal. 74 (1) (1987), 160–197.Google Scholar
Grillakis, M., Shatah, J. and Strauss, W., ‘Stability theory of solitary waves in the presence of symmetry II’, J. Funct. Anal. 94 (2) (1990), 308–348.Google Scholar
Ginibre, J. and Velo, G., ‘The global Cauchy problem for the nonlinear Klein–Gordon equation’, Math. Z. 189 (4) (1985), 487–505.CrossRefGoogle Scholar
Krieger, J., Nakanishi, K. and Schlag, W., ‘Global dynamics above the ground state energy for the one-dimensional NLKG equation’, Amer. J. Math. 135 (4) (2013), 935–965.Google Scholar
Kwong, M. K., ‘Uniqueness of positive solutions of $\Delta u-u+u^p=0$ in $\mathbb{R}^n$ ’, Arch. Ration. Mech. Anal. 105 (3) (1989), 243–266.Google Scholar
Maris, M., ‘Existence of nonstationary bubbles in higher dimension’, J. Math. Pures Appl. 81 (2002), 1207–1239.Google Scholar
Martel, Y., ‘Asymptotic $N$ -soliton-like solutions of the subcritical and critical generalized Korteweg-de Vries equations’, Amer. J. Math. 127 (5) (2005), 1103–1140.CrossRefGoogle Scholar
McLeod, K., ‘Uniqueness of positive radial solutions of $\Delta u + f(u) = 0$ in $\mathbb{R}^n$ II’, Trans. Amer. Math. Soc. 339 (1993), 495–505.Google Scholar
Merle, F., ‘Construction of solutions with exactly $k$ blow-up points for the Schrödinger equation with critical nonlinearity’, Comm. Math. Phys. 129 (2) (1990), 223–240.Google Scholar
Martel, Y. and Merle, F., ‘Multi solitary waves for nonlinear Schrödinger equations’, Ann. Inst. H. Poincaré Anal. Non Linéaire 23 (2006), 849–864.CrossRefGoogle Scholar
Martel, Y. and Merle, F., ‘Stability of two soliton collision for nonintegrable gKdV equations’, Comm. Math. Phys. 286 (2009), 39–79.Google Scholar
Martel, Y., Merle, F. and Tsai, T. P., ‘Stability in $H^1$ of the sum of $K$ solitary waves for some nonlinear Schrödinger equations’, Duke Math. J. 133 (3) (2006), 405–466.Google Scholar
Merle, F. and Zaag, H., ‘Existence and classification of characteristic points at blow-up for a semilinear wave equation in one space dimension’, Amer. J. Math. 134 (3) (2012), 581–648.Google Scholar
Nakamura, M. and Ozawa, T., ‘The Cauchy problem for nonlinear Klein–Gordon equations in the Sobolev spaces’, Publ. Res. Inst. Math. Sci. 37 (3) (2001), 255–293.CrossRefGoogle Scholar
Nakanishi, K. and Schlag, W., ‘Invariant manifolds and dispersive Hamiltonian evolution equations’, Zurich Lectures in Advanced Mathematics, vi+253 pp (European Mathematical Society (EMS), Zürich, 2011).Google Scholar
Pego, R. L. and Weinstein, M. I., ‘Eigenvalues, and instabilities of solitary waves’, Philos. Trans. R. Soc. Lond. Ser. A 340 (1656) (1992), 47–94.Google Scholar
Nakanishi, K. and Schlag, W., ‘Global dynamics above the ground state energy for the focusing nonlinear Klein–Gordon equation’, J. Differential Equations 250 (5) (2011), 2299–2333.Google Scholar
Serrin, J. and Tang, M., ‘Uniqueness of ground states for quasilinear elliptic equations’, Indiana Univ. Math. J. 49 (3) (2000), 897–923.Google Scholar
Shatah, J. and Strauss, W., ‘Instability of nonlinear bound states’, Comm. Math. Phys. 100 (2) (1985), 173–190.Google Scholar
Tao, T., ‘Low regularity semi-linear wave equations’, Comm. Partial Differential Equations 24 (1999), 599–630.Google Scholar
Weinstein, M. I., ‘Modulational stability of ground states of nonlinear Schrödinger equations’, SIAM J. Math. Anal. 16 (3) (1985), 472–491.CrossRefGoogle Scholar
Weinstein, M. I., ‘Lyapunov stability of ground states of nonlinear dispersive evolution equations’, Comm. Pure Appl. Math. 39 (1986), 51–68.Google Scholar