Hostname: page-component-7dd5485656-npwhs Total loading time: 0 Render date: 2025-10-31T16:35:59.915Z Has data issue: false hasContentIssue false
  • English
  • Français

FREE GROUPS AND AUTOMORPHISM GROUPS OF INFINITE STRUCTURES

Part of: Structure and classification of infinite or finite groups Special aspects of infinite or finite groups Set theory

Published online by Cambridge University Press:  17 April 2014

PHILIPP LÜCKE  and
SAHARON SHELAH
PHILIPP LÜCKE
Affiliation:
Mathematisches Institut, Rheinische Friedrich-Wilhelms-Universität Bonn, Endenicher Allee 60, 53115 Bonn, Germany pluecke@uni-bonn.de
SAHARON SHELAH
Affiliation:
Einstein Institute of Mathematics, The Hebrew University of Jerusalem, Edmond J. Safra Campus, Givat Ram, Jerusalem 91904, Israel shelah@math.huji.ac.il Department of Mathematics, Hill Center-Busch Campus, Rutgers, The State University of New Jersey, 110 Frelinghuysen Road, Piscataway, NJ 08854-8019, USA

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a cardinal 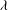$\lambda $ with 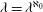$\lambda =\lambda ^{\aleph _0}$ , we show that there is a field of cardinality 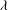$\lambda $ whose automorphism group is a free group of rank 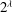$2^\lambda $ . In the proof of this statement, we develop general techniques that enable us to realize certain groups as the automorphism group of structures of a given cardinality. They allow us to show that analogues of this result hold for free objects in various varieties of groups. For example, the free abelian group of rank 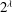$2^\lambda $ is the automorphism group of a field of cardinality 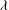$\lambda $ whenever 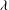$\lambda $ is a cardinal with 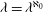$\lambda =\lambda ^{\aleph _0}$ . Moreover, we apply these techniques to show that consistently the assumption that 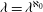$\lambda =\lambda ^{\aleph _0}$ is not necessary for the existence of a field of cardinality 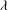$\lambda $ whose automorphism group is a free group of rank 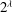$2^\lambda $ . Finally, we use them to prove that the existence of a cardinal 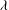$\lambda $ of uncountable cofinality with the property that there is no field of cardinality 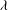$\lambda $ whose automorphism group is a free group of rank greater than 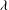$\lambda $ implies the existence of large cardinals in certain inner models of set theory.

MSC classification

Secondary: 03E75: Applications of set theory 20E05: Free nonabelian groups 20F29: Representations of groups as automorphism groups of algebraic systems

Information

Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 2 , 01 July 2014 , e8
Creative Commons
Creative Common License - CCCreative Common License - BY
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
Copyright
© The Author(s) 2014

References

Baumgartner, J. E., ‘Applications of the proper forcing axiom’, inHandbook of set-theoretic topology (North-Holland, Amsterdam, 1984), 913–959.Google Scholar
Baumgartner, J. E., ‘Iterated forcing’, inSurveys in Set Theory, London Math. Soc. Lecture Note Ser., 87 (Cambridge Univ. Press, Cambridge, 1983), 1–59.Google Scholar
de Bruijn, N. G., ‘Embedding theorems for infinite groups’, Nederl. Akad. Wetensch. Proc. Ser. A. 60 = Indag. Math. 19 (1957), 560–569.CrossRefGoogle Scholar
Fried, E. and Kollár, J., ‘Automorphism groups of fields’, inUniversal Algebra (Esztergom, 1977), Colloq. Math. Soc. János Bolyai, 29 (North-Holland, Amsterdam, 1982), 293–303.Google Scholar
Hamkins, J. D., ‘Extensions with the approximation and cover properties have no new large cardinals’, Fund. Math. 180 (3) (2003), 257–277.CrossRefGoogle Scholar
Hodges, W., Model Theory, Encyclopedia of Mathematics and its Applications, 42 (Cambridge University Press, Cambridge, 1993).Google Scholar
Jech, T., ‘More game-theoretic properties of Boolean algebras’, Ann. Pure Appl. Logic. 26 (1) (1984), 11–29.CrossRefGoogle Scholar
Jech, T., Set Theory, Springer Monographs in Mathematics (Springer-Verlag, Berlin, 2003), The third millennium edition, revised and expanded.Google Scholar
Jensen, R. and Steel, J., ‘ ${\rm K}$ without the measurable’, J. Symbolic Logic. 78 (3) (2013), 708–734.CrossRefGoogle Scholar
Just, W., Shelah, S. and Thomas, S., ‘The automorphism tower problem revisited’, Adv. Math. 148 (2) (1999), 243–265.CrossRefGoogle Scholar
Kaplan, I. and Shelah, S., ‘Automorphism towers and automorphism groups of fields without choice’, inGroups and Model Theory, Contemp. Math, 576 (Amer. Math. Soc., Providence, RI, 2012), 187–203.Google Scholar
Mac Lane, S., Categories for the Working Mathematician, 2nd edn, Graduate Texts in Mathematics, 5 (Springer-Verlag, New York, 1998).Google Scholar
Mitchell, W., ‘Aronszajn trees and the independence of the transfer property’, Ann. Math. Logic. 5 (1972/73), 21–46.Google Scholar
Sanerib, R., ‘Automorphism groups of ultrafilters’, Algebra Universalis. 4 (1974), 141–150.CrossRefGoogle Scholar
Schimmerling, E., ‘A core model toolbox and guide’, inHandbook of Set Theory Vols. 1, 2, 3 (Springer, Dordrecht, 2010), 1685–1751.CrossRefGoogle Scholar
Shelah, S., ‘Applications of PCF theory’, J. Symbolic Logic. 65 (4) (2000), 1624–1674.Google Scholar
Shelah, S., ‘A countable structure does not have a free uncountable automorphism group’, Bull. London Math. Soc. 35 (1) (2003), 1–7.Google Scholar
Shelah, S., Cardinal arithmetic, Oxford Logic Guides, 29 (Oxford University Press, New York, 1994), Oxford Science Publications.Google Scholar
Solecki, S., ‘Polish group topologies’, inSets and Proofs Leeds, 1997, London Math. Soc. Lecture Note Ser., 258 (Cambridge University Press, Cambridge, 1999), 339–364.Google Scholar