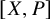1. Introduction
This work is the second in a series of papers enacting a simple but far-reaching recognition, which is the following: many of the classical functors
![]() $F:\mathcal {C}\to \mathcal {D}$
of homological algebra and algebraic topology factor through what we might loosely term a definable version of the category
$F:\mathcal {C}\to \mathcal {D}$
of homological algebra and algebraic topology factor through what we might loosely term a definable version of the category
![]() $\mathcal {D}$
, as in the diagram below:
$\mathcal {D}$
, as in the diagram below:

Two fundamental examples are the functors
![]() $\mathrm {Ext}$
and
$\mathrm {Ext}$
and
![]() $\mathrm {lim}^1$
, each of which maps to the category
$\mathrm {lim}^1$
, each of which maps to the category
![]() $\mathcal {D}=\mathsf {Grp}$
of groups. As this work’s predecessor [Reference Bergfalk and Lupini9] showed, the restrictions of these functors to pairs and towers of countable abelian groups, respectively, each admit a canonical lift to the category
$\mathcal {D}=\mathsf {Grp}$
of groups. As this work’s predecessor [Reference Bergfalk and Lupini9] showed, the restrictions of these functors to pairs and towers of countable abelian groups, respectively, each admit a canonical lift to the category
![]() $\mathsf {GPC}$
of groups with a Polish cover, a category first identified in [Reference Bergfalk and Lupini9] as playing, in these contexts, exactly this role of a definable
$\mathsf {GPC}$
of groups with a Polish cover, a category first identified in [Reference Bergfalk and Lupini9] as playing, in these contexts, exactly this role of a definable
![]() $\mathcal {D}$
. The objects of
$\mathcal {D}$
. The objects of
![]() $\mathsf {GPC}$
are pairs
$\mathsf {GPC}$
are pairs
![]() $(G,N)$
consisting of a Polish group G together with a Polishable normal subgroup
$(G,N)$
consisting of a Polish group G together with a Polishable normal subgroup
![]() $N\leq G$
; its morphisms
$N\leq G$
; its morphisms
![]() $(G,N)\to (H,M)$
are those group homomorphisms
$(G,N)\to (H,M)$
are those group homomorphisms
![]() $G/N\to H/M$
which lift to a Borel function
$G/N\to H/M$
which lift to a Borel function
![]() $G\to H$
. More conceptually, its morphisms are those homomorphisms
$G\to H$
. More conceptually, its morphisms are those homomorphisms
![]() $G/N\to H/M$
which are definable from the Polish topologies on G and H via a computational or expressive power consisting in ‘logic gates’ of countably infinite length. As shown in [Reference Bergfalk and Lupini9],
$G/N\to H/M$
which are definable from the Polish topologies on G and H via a computational or expressive power consisting in ‘logic gates’ of countably infinite length. As shown in [Reference Bergfalk and Lupini9],
![]() $\mathsf {GPC}$
is a significantly finer or more rigid category than
$\mathsf {GPC}$
is a significantly finer or more rigid category than
![]() $\mathsf {Grp}$
; in particular,
$\mathsf {Grp}$
; in particular,
![]() $\mathrm {Hom}_{\mathsf {GPC}}((G,N),(H,M))$
is often a proper – and sometimes quite sparse – subset of
$\mathrm {Hom}_{\mathsf {GPC}}((G,N),(H,M))$
is often a proper – and sometimes quite sparse – subset of
![]() $\mathrm {Hom}_{\mathsf {Grp}}((G/N),(H/M))$
, and from this, it follows that the aforementioned definable lifts of the functors
$\mathrm {Hom}_{\mathsf {Grp}}((G/N),(H/M))$
, and from this, it follows that the aforementioned definable lifts of the functors
![]() $\mathrm {Ext}$
and
$\mathrm {Ext}$
and
![]() $\mathrm {lim}^1$
provide strictly stronger invariants of pairs and towers of countable abelian groups than their classical counterparts.
$\mathrm {lim}^1$
provide strictly stronger invariants of pairs and towers of countable abelian groups than their classical counterparts.
The present work extends this analysis to the Čech cohomology functors from the category
![]() $\mathcal {C}=\mathsf {LC}$
of locally compact Polish spaces to the category
$\mathcal {C}=\mathsf {LC}$
of locally compact Polish spaces to the category
![]() $\mathcal {D}$
of groups. This entails a coordinated study of the Borel content of both the combinatorial and homotopical presentations of these groups. For our work on the latter, and on the homotopy bracket
$\mathcal {D}$
of groups. This entails a coordinated study of the Borel content of both the combinatorial and homotopical presentations of these groups. For our work on the latter, and on the homotopy bracket
![]() $[-,-]$
more generally, we introduce several further definable categories,
$[-,-]$
more generally, we introduce several further definable categories,
![]() $\mathsf {DSet}$
and
$\mathsf {DSet}$
and
![]() $\mathsf {DGrp}$
, each of which extends the subcategory
$\mathsf {DGrp}$
, each of which extends the subcategory
![]() $\mathsf {GPC}$
while retaining many of its regularity properties. By way of this analysis, we show that, like
$\mathsf {GPC}$
while retaining many of its regularity properties. By way of this analysis, we show that, like
![]() $\mathrm {Ext}$
and
$\mathrm {Ext}$
and
![]() $\mathrm {lim}^1$
, the functors
$\mathrm {lim}^1$
, the functors ![]() each factor into a definable cohomology functor to
each factor into a definable cohomology functor to
![]() $\mathsf {GPC}$
followed by a forgetful functor from
$\mathsf {GPC}$
followed by a forgetful functor from
![]() $\mathsf {GPC}$
to
$\mathsf {GPC}$
to
![]() $\mathsf {Grp}$
. In consequence, much as before, definable cohomology is a significantly stronger invariant of topological spaces than its classical counterpart. This we concretely show via a comparison of the classical and definable cohomology groups of mapping telescopes of spheres and tori, objects of central importance to the field of algebraic topology (to the study of localizations, or the construction of Eilenberg-MacLane spaces, for example) [Reference Bott and Tu12, Reference Bousfield and Kan13, Reference May and Ponto59, Reference Milnor63, Reference Sullivan85].
$\mathsf {Grp}$
. In consequence, much as before, definable cohomology is a significantly stronger invariant of topological spaces than its classical counterpart. This we concretely show via a comparison of the classical and definable cohomology groups of mapping telescopes of spheres and tori, objects of central importance to the field of algebraic topology (to the study of localizations, or the construction of Eilenberg-MacLane spaces, for example) [Reference Bott and Tu12, Reference Bousfield and Kan13, Reference May and Ponto59, Reference Milnor63, Reference Sullivan85].
We precede a more detailed discussion of this paper’s contents with a few further words of context. We would stress from the outset, for example, that none of the definable functors under discussion provide particularly esoteric, unmanageable or hard-to-compute invariants for topological spaces or groups; on the contrary, these invariants amount to little more than a retention of the topologies arising naturally in classical computations. As such, they realize a historically persistent impulse within the fields of homological algebra and algebraic topology; to take just one example, Moore’s 1976 work [Reference Moore65] records the following striking premonition of the category
![]() $\mathsf {GPC}$
:
$\mathsf {GPC}$
:
There is one complication in this theory which, as we shall see, simply cannot be avoided and this comes about as follows: We have polonais [i.e., Polish] groups A and B (say abelian) together with a continuous homomorphism from A into B. The quotient group
![]() $B/j(A)$
will be of interest and significance even though in many cases
$B/j(A)$
will be of interest and significance even though in many cases
![]() $j(A)$
is not closed in B. This quotient group would be polonais if
$j(A)$
is not closed in B. This quotient group would be polonais if
![]() $j(A)$
were closed but in general it is some non-Hausdorff topological group, arising in some sense as the ‘quotient’ of two polonais groups. It will be somewhat useful to talk about such objects which with some trepidation one might call pseudo-polonais groups. We would define such objects as triples
$j(A)$
were closed but in general it is some non-Hausdorff topological group, arising in some sense as the ‘quotient’ of two polonais groups. It will be somewhat useful to talk about such objects which with some trepidation one might call pseudo-polonais groups. We would define such objects as triples
![]() $C=(A,B,j)$
where A and B are polonais and j is a continuous homomorphism of A into B, subject to an appropriate equivalence relation which we shall not pursue at this moment.
$C=(A,B,j)$
where A and B are polonais and j is a continuous homomorphism of A into B, subject to an appropriate equivalence relation which we shall not pursue at this moment.
See also Brown’s 1975 remarks on almost polonais groups in [Reference Brown18] and his references therein and in his 1977 article [Reference Brown, Douglas and Fillmore17] to projected (but never subsequently published) works on this theme. It seems likely that what these recognitions’ further development awaited was some framework for the efficient manipulation of Moore’s triples
![]() $(A,B,j)$
(which are evidently equivalent in content to the objects
$(A,B,j)$
(which are evidently equivalent in content to the objects
![]() $(G,N)$
of
$(G,N)$
of
![]() $\mathsf {GPC}$
), and it is in the derivation of just such a framework from the apparatus of invariant descriptive set theory that our work’s main contribution and novelty arguably consist.
$\mathsf {GPC}$
), and it is in the derivation of just such a framework from the apparatus of invariant descriptive set theory that our work’s main contribution and novelty arguably consist.
Along these lines, affinities of the present work with another major contemporary research orientation should be noted. This is the program of ‘doing algebra with topology’ motivating, for example, the condensed mathematics and pyknotic mathematics frameworks of Clausen and Scholze, and Barwick and Haine, respectively ([Reference Barwick and Haine4, Reference Scholze77]; see also [Reference Hoffmann and Spitzweck35]). Though our methods are rather different, much of the underlying impetus is the same: it is the issue of ‘bad quotients’ like those which Moore describes above. More formally, it is the failure of settings like the collection of Polish abelian groups to form an abelian category. In contrast, rather remarkably, as this work’s second author has recently shown, the category
![]() $\mathsf {APC}$
of groups with an abelian Polish cover is an abelian category, one which may moreover be regarded as the canonical abelian extension of the category of Polish abelian groups, in the precise sense that it forms that category’s left heart [Reference Lupini52]. This helps to explain why such large portions of homological algebra and algebraic topology lift to
$\mathsf {APC}$
of groups with an abelian Polish cover is an abelian category, one which may moreover be regarded as the canonical abelian extension of the category of Polish abelian groups, in the precise sense that it forms that category’s left heart [Reference Lupini52]. This helps to explain why such large portions of homological algebra and algebraic topology lift to
![]() $\mathsf {APC}$
and related settings; establishing the main theorems of [Reference Bergfalk and Lupini9] and the present work, for example, entailed the development of definable versions of such a range of core results like the homotopy extension theorem, the simplicial approximation theorem, Milnor exact sequences, Urysohn’s Lemma, the Snake Lemma and so on, that it grows natural to speak of an emergent field of definable homological algebra. And it is in part in these terms also that our project should be understood.
$\mathsf {APC}$
and related settings; establishing the main theorems of [Reference Bergfalk and Lupini9] and the present work, for example, entailed the development of definable versions of such a range of core results like the homotopy extension theorem, the simplicial approximation theorem, Milnor exact sequences, Urysohn’s Lemma, the Snake Lemma and so on, that it grows natural to speak of an emergent field of definable homological algebra. And it is in part in these terms also that our project should be understood.
At the same time, the present work extends the framework of diagram 1 to homotopical and non-abelian settings, through our study of the representation of ![]() as the group
as the group
![]() $[X,K(G,n)]$
of homotopy classes of maps from X to an Eilenberg-MacLane space
$[X,K(G,n)]$
of homotopy classes of maps from X to an Eilenberg-MacLane space
![]() $K(G,n)$
. As noted, and as we will describe in greater detail just below, this analysis necessitated the introduction of a larger category of definable groups
$K(G,n)$
. As noted, and as we will describe in greater detail just below, this analysis necessitated the introduction of a larger category of definable groups
![]() $\mathsf {DGrp}$
, one which features
$\mathsf {DGrp}$
, one which features
![]() $\mathsf {GPC}$
as a full subcategory. This is the natural category for the definable analysis of the homotopy bracket
$\mathsf {GPC}$
as a full subcategory. This is the natural category for the definable analysis of the homotopy bracket
![]() $[-,P]$
of maps to a polyhedron P, and hence (by Brown Representability) of generalized homology and cohomology theories more broadly, as we discuss in our conclusion. The development of definable homotopy groups is a naturally ensuing prospect as well (see Remark 4.7).
$[-,P]$
of maps to a polyhedron P, and hence (by Brown Representability) of generalized homology and cohomology theories more broadly, as we discuss in our conclusion. The development of definable homotopy groups is a naturally ensuing prospect as well (see Remark 4.7).
This brings us to one last preliminary point. It should be clear from our account so far that much of what we herein term definable connotes what might be more precisely rendered Borel definable, but it can also, as in the case of definable sets and groups, mean a little more (see Section 1.2 below). Put differently, our uses of the term herein have been guided by considerations both of concision and of the interrelations between our operative categories, but should be everywhere read to signal a concern for structures and functions embodying only countable amounts of data, in senses such as we noted above.
We turn now to a more detailed description of our results.
1.1. Definable Čech cohomology
As noted, this work builds on its predecessor [Reference Bergfalk and Lupini9], which introduced definable variants of the functors
![]() $\mathrm {Ext}$
,
$\mathrm {Ext}$
,
![]() $\mathrm {Pext}$
and
$\mathrm {Pext}$
and
![]() $\mathrm {lim}^{1}$
, each taking values in the category GPC of groups with a Polish cover. What warrants a view of
$\mathrm {lim}^{1}$
, each taking values in the category GPC of groups with a Polish cover. What warrants a view of
![]() $\mathrm {Ext}(B,F)$
,
$\mathrm {Ext}(B,F)$
,
![]() $\mathrm {Pext}(B,F)$
and
$\mathrm {Pext}(B,F)$
and
![]() $\mathrm {lim}^{1}(\boldsymbol {A})$
as groups with a Polish cover is the observation in [Reference Bergfalk and Lupini9] that each is naturally construed as a cohomology group
$\mathrm {lim}^{1}(\boldsymbol {A})$
as groups with a Polish cover is the observation in [Reference Bergfalk and Lupini9] that each is naturally construed as a cohomology group
![]() $\mathrm {H}^n(C^{\bullet })=\mathrm {ker}(\delta ^{n})/\mathrm {im}(\delta ^{n-1})$
of an appropriate Polish cochain complex
$\mathrm {H}^n(C^{\bullet })=\mathrm {ker}(\delta ^{n})/\mathrm {im}(\delta ^{n-1})$
of an appropriate Polish cochain complex
![]() $C^{\bullet }$
. The latter is simply a cochain complex
$C^{\bullet }$
. The latter is simply a cochain complex
in which each
![]() $\delta ^n\colon C^n\to C^{n-1}$
is a continuous homomorphism between Polish abelian groups; see Section 2.
$\delta ^n\colon C^n\to C^{n-1}$
is a continuous homomorphism between Polish abelian groups; see Section 2.
The present work takes as its focus the definable enrichment of the Čech cohomology groups ![]() of locally compact separable metric spaces X with coefficients in a countable abelian group G. As abstract groups, these Čech cohomology groups admit several formulations. The combinatorial (and classical) approach to Čech cohomology associates to each open cover
of locally compact separable metric spaces X with coefficients in a countable abelian group G. As abstract groups, these Čech cohomology groups admit several formulations. The combinatorial (and classical) approach to Čech cohomology associates to each open cover
![]() $\mathcal {U}\in \mathrm {Cov}(X)$
of X the simplicial cohomology group
$\mathcal {U}\in \mathrm {Cov}(X)$
of X the simplicial cohomology group
![]() $\mathrm {H}^n(\mathrm {Nv}(\mathcal {U});G)$
of its nerve, then defines
$\mathrm {H}^n(\mathrm {Nv}(\mathcal {U});G)$
of its nerve, then defines ![]() as the colimit, over the refinement-ordering of
as the colimit, over the refinement-ordering of
![]() $\mathrm {Cov}(X)$
, of these groups. In its homotopical incarnation, on the other hand,
$\mathrm {Cov}(X)$
, of these groups. In its homotopical incarnation, on the other hand, ![]() is the set
is the set
![]() $[X,K(G,n)]$
of homotopy classes of maps from X to an Eilenberg-MacLane space
$[X,K(G,n)]$
of homotopy classes of maps from X to an Eilenberg-MacLane space
![]() $K(G,n)$
; since
$K(G,n)$
; since
![]() $K(G,n)$
is an abelian H-group – that is, a space equipped with multiplication and inverse operations which satisfy the abelian group axioms up to homotopy –
$K(G,n)$
is an abelian H-group – that is, a space equipped with multiplication and inverse operations which satisfy the abelian group axioms up to homotopy –
![]() $[X,K(G,n)]$
has the structure of an abelian group. Mediating between these two approaches, and between homological and homotopical perspectives more generally, is Huber’s 1961 theorem [Reference Huber40] which states that the groups
$[X,K(G,n)]$
has the structure of an abelian group. Mediating between these two approaches, and between homological and homotopical perspectives more generally, is Huber’s 1961 theorem [Reference Huber40] which states that the groups
![]() $[X,K(G,n)]$
and
$[X,K(G,n)]$
and ![]() are naturally isomorphic.
are naturally isomorphic.
In order to definably enrich these Čech cohomology groups, we isolate and endow the combinatorially defined ![]() and
and
![]() $[X,K(G,n)]$
, each with a natural Borel structure. At a first pass, the associated definable cohomology groups
$[X,K(G,n)]$
, each with a natural Borel structure. At a first pass, the associated definable cohomology groups ![]() and
and
![]() $[X,K(G,n)]_{\mathrm {def}}$
differ in several interesting and complementary ways. For example, much like the aforementioned definable invariants introduced in [Reference Bergfalk and Lupini9],
$[X,K(G,n)]_{\mathrm {def}}$
differ in several interesting and complementary ways. For example, much like the aforementioned definable invariants introduced in [Reference Bergfalk and Lupini9], ![]() admits realization as a group with a Polish cover
admits realization as a group with a Polish cover ![]() , where
, where
![]() $\mathrm {Z}^n(\boldsymbol {\mathcal {U}};G)$
and
$\mathrm {Z}^n(\boldsymbol {\mathcal {U}};G)$
and
![]() $\mathrm {B}^n(\boldsymbol {\mathcal {U}};G)$
are n-dimensional cocycle and coboundary groups deriving from a Polish cochain complex associated to X and G. A drawback of this realization is its reliance on choices of covering systems
$\mathrm {B}^n(\boldsymbol {\mathcal {U}};G)$
are n-dimensional cocycle and coboundary groups deriving from a Polish cochain complex associated to X and G. A drawback of this realization is its reliance on choices of covering systems
![]() $\boldsymbol {\mathcal {U}}$
for each X, rendering the more global coordination or, more precisely, functoriality of the associated assignments
$\boldsymbol {\mathcal {U}}$
for each X, rendering the more global coordination or, more precisely, functoriality of the associated assignments ![]() somewhat obscure. In contrast, the group
somewhat obscure. In contrast, the group
![]() $[X,K(G,n)]_{\mathrm {def}}$
does not, in general, manifest as a group with a Polish cover; some care, in fact, is required in handling its Borel structure. Within the category of definable groups, however – a category which, as noted, shares many regularity properties with the category of groups with a Polish cover – the functoriality of the assignment
$[X,K(G,n)]_{\mathrm {def}}$
does not, in general, manifest as a group with a Polish cover; some care, in fact, is required in handling its Borel structure. Within the category of definable groups, however – a category which, as noted, shares many regularity properties with the category of groups with a Polish cover – the functoriality of the assignment
![]() $X\mapsto [X,K(G,n)]_{\mathrm {def}}$
is clear.
$X\mapsto [X,K(G,n)]_{\mathrm {def}}$
is clear.
The following definable version of Huber’s theorem says that, up to a natural definable isomorphism, these two approaches are equivalent. In particular, the assignment ![]() is functorial and, independent of our choices of covering systems
is functorial and, independent of our choices of covering systems
![]() $\boldsymbol {\mathcal {U}}$
. Furthermore, the definable group
$\boldsymbol {\mathcal {U}}$
. Furthermore, the definable group
![]() $[X,K(G,n)]_{\mathrm {def}}$
is essentially a group with a Polish cover.
$[X,K(G,n)]_{\mathrm {def}}$
is essentially a group with a Polish cover.
Theorem 1.1. The functors determined by the assignments ![]() and
and
![]() $X\mapsto [X,K(G,n)]_{\mathrm {def}}$
are naturally isomorphic in the category of definable groups.
$X\mapsto [X,K(G,n)]_{\mathrm {def}}$
are naturally isomorphic in the category of definable groups.
The proof of Theorem 1.1, which occupies much of Section 5, involves several subsidiary results of independent interest. For example, to show that Huber’s abstract isomorphism ![]() admits a Borel lift, we prove a definable version of the simplicial approximation theorem. The fact that the inverse map
admits a Borel lift, we prove a definable version of the simplicial approximation theorem. The fact that the inverse map ![]() also admits a Borel lift, and hence that it induces an isomorphism between
also admits a Borel lift, and hence that it induces an isomorphism between ![]() and
and
![]() $[X,K(G,n)]_{\mathrm {def}}$
in the category of definable groups, follows from the general theory of definable groups that we develop in Section 3.
$[X,K(G,n)]_{\mathrm {def}}$
in the category of definable groups, follows from the general theory of definable groups that we develop in Section 3.
1.2. Definable groups
At first glance,
![]() $[X,K(G,n)]_{\mathrm {def}}$
is just the quotient
$[X,K(G,n)]_{\mathrm {def}}$
is just the quotient
![]() $\mathrm {Map}(X,K(G,n))/\!\simeq $
of a Polish space by an analytic equivalence relation with the property that the operations of multiplication and inversion on the quotient level lift to Borel maps at the level of
$\mathrm {Map}(X,K(G,n))/\!\simeq $
of a Polish space by an analytic equivalence relation with the property that the operations of multiplication and inversion on the quotient level lift to Borel maps at the level of
![]() $\mathrm {Map}(X,K(G,n))$
. While Borel-definable homomorphisms between such ‘quotient groups’ – which we term semidefinable groups below – determine a category which strictly extends
$\mathrm {Map}(X,K(G,n))$
. While Borel-definable homomorphisms between such ‘quotient groups’ – which we term semidefinable groups below – determine a category which strictly extends
![]() $\mathsf {GPC}$
, the category of semidefinable groups lacks the regularity properties which make
$\mathsf {GPC}$
, the category of semidefinable groups lacks the regularity properties which make
![]() $\mathsf {GPC}$
robust and convenient to work with. For example, a salient feature of the category of groups with a Polish cover, and one instrumental in arguing results like Theorem 1.1, is the fact that an isomorphism on the level of quotient groups admits a Borel lift if and only if its inverse does. Unfortunately, such symmetries do not extend to the generality of the category of semidefinable sets. One may recover them, however, by moving to the intermediate category of definable groups, whose objects, loosely speaking, are Borel and idealistic equivalence relations E on Polish spaces Y whose quotients by E carry natural group structures.
$\mathsf {GPC}$
robust and convenient to work with. For example, a salient feature of the category of groups with a Polish cover, and one instrumental in arguing results like Theorem 1.1, is the fact that an isomorphism on the level of quotient groups admits a Borel lift if and only if its inverse does. Unfortunately, such symmetries do not extend to the generality of the category of semidefinable sets. One may recover them, however, by moving to the intermediate category of definable groups, whose objects, loosely speaking, are Borel and idealistic equivalence relations E on Polish spaces Y whose quotients by E carry natural group structures.

Figure 1 Definable groups: an extension of
![]() $\mathsf {GPC}$
sharing many of its regularity properties.
$\mathsf {GPC}$
sharing many of its regularity properties.
The fact that
![]() $[X,K(G,n)]_{\mathrm {def}}$
is a definable group – a fact which, among others, plays a role in the proof of Theorem 1.1 – is a consequence of the following more general theorem.
$[X,K(G,n)]_{\mathrm {def}}$
is a definable group – a fact which, among others, plays a role in the proof of Theorem 1.1 – is a consequence of the following more general theorem.
Theorem 1.2. Let X be a locally compact separable metric space, and let P be a polyhedral H-group. The relation of being homotopic defines a Borel and idealistic equivalence relation on the Polish space
![]() $\mathrm {Map}(X,P)$
of all continuous functions from X to P.
$\mathrm {Map}(X,P)$
of all continuous functions from X to P.
We note that Theorem 1.2 is very far from being true if we reverse the roles of X and P. Indeed, every analytic equivalence relation is Borel bireducible to the path connectedness relation between points of an appropriately chosen compact metrizable space X; see [Reference Becker5, Theorem 4.1]. Hence, in general, the relation of being homotopic is neither Borel nor idealistic on
![]() $\mathrm {Map}(P,X)$
, even when
$\mathrm {Map}(P,X)$
, even when
![]() $P=\{*\}$
consists of a single point.
$P=\{*\}$
consists of a single point.
As this observation might suggest, Theorem 1.2 is a rather subtle result; the idealistic portion of the theorem (holding in fact for any P which is the geometric realization of a locally finite, countable simplicial complex) forms the main labor of Section 4. The Borel portion of the theorem derives from close analysis of the class of phantom maps – that is, those maps whose restriction to any compact subset of X is nullhomotopic – from X to P.
1.3. Phantom maps and the descriptive set theory of homotopy relations
The analysis of the phantom maps
![]() $(X,A)\to (P,*)$
from a locally compact Polish pair to a pointed polyhedron forms the focus of Section 7 and is of some interest in its own right, for the following reasons:
$(X,A)\to (P,*)$
from a locally compact Polish pair to a pointed polyhedron forms the focus of Section 7 and is of some interest in its own right, for the following reasons:
-
• We provide, for any locally compact Polish pair
 $(X,A)$
and polyhedral H-group
$(X,A)$
and polyhedral H-group
 $(P,*)$
, a definable short exact sequence decomposition of the definable group
$(P,*)$
, a definable short exact sequence decomposition of the definable group
 $[(X,A),(P,\ast )]$
whose kernel is the group of homotopy classes of phantom maps from
$[(X,A),(P,\ast )]$
whose kernel is the group of homotopy classes of phantom maps from
 $(X,A)$
to
$(X,A)$
to
 $(P,*)$
; see Theorem 7.13. This kernel also takes the form of a definable
$(P,*)$
; see Theorem 7.13. This kernel also takes the form of a definable
 $\mathrm {lim}^1$
term within a definable Milnor-type short exact sequence (Proposition 7.14), a connection with the analyses of [Reference Bergfalk and Lupini9] which we exploit in Section 8.
$\mathrm {lim}^1$
term within a definable Milnor-type short exact sequence (Proposition 7.14), a connection with the analyses of [Reference Bergfalk and Lupini9] which we exploit in Section 8. -
• More generally, we provide a topological characterization of the set of phantom maps from
 $(X,A)$
to a pointed polyhedron
$(X,A)$
to a pointed polyhedron
 $(P,\ast )$
: it is the closure in
$(P,\ast )$
: it is the closure in
 $\mathrm {Map}((X,A),(P,\ast ))$
of the set of nullhomotopic maps; see Proposition 7.9, and also Proposition 7.15. This is a representative benefit of approaches which, as we put it above, amount essentially to ‘a retention of the topologies arising naturally in classical computations.’
$\mathrm {Map}((X,A),(P,\ast ))$
of the set of nullhomotopic maps; see Proposition 7.9, and also Proposition 7.15. This is a representative benefit of approaches which, as we put it above, amount essentially to ‘a retention of the topologies arising naturally in classical computations.’ -
• Most broadly, the analyses of Sections 4 through 8 should be understood as foundational work in the descriptive set theoretic study of the homotopy relation on maps from a locally compact Polish space X to a polyhedral P, a framework encompassing a substantial variety of classification problems in mathematics; in addition to Theorem 1.1 and the aforementioned phantom decompositions, Lemma 4.4 (characterizing the homotopy relation when X is compact), Lemma 6.3 (a definable version of Urysohn’s Lemma), Theorem 6.4 (a definable version of Borsuk’s homotopy extension theorem), and Theorem 6.5 (definably mediating between based and unbased homotopy classes of maps) may all be viewed in these terms as well.
This last point brings us to the two main sorts of consequences of our work. The first concerns the study of the Borel complexity of classification problems.
1.4. Classification by (co)homological invariants
One of the most central programs in descriptive set theory measures the intrinsic complexity of various classification problems in mathematics by locating them within the Borel reduction hierarchy. Two of the most prominent benchmarks within this hierarchy are the smooth and the classifiable by countable structures classes of classification problems, largely for the reason that each of these benchmarks captures classification schemes which occur frequently in mathematical practice. The smooth classification problems, for example, are precisely those which may be ‘definably classified’ by real number invariants, such as the problem of classifying all Bernoulli shifts of a given amenable group up to isomorphism; by the celebrated results of Ornstein [Reference Ornstein68] and Ornstein-Weiss [Reference Ornstein and Weiss69], these dynamical systems are completely classified by their entropy. Similarly, the classifiable by countable structures classification problems are precisely those admitting ‘definable classification’ by the isomorphism types of countable structures. A well-known example of dynamical systems which are classified up to isomorphism by such invariants is the class of all ergodic measure-preserving transformations of discrete spectrum; by an equally celebrated but much older result of Halmos and von Neumann, these are completely classified by the isomorphism type of a countable structure coding their spectrum. See [Reference von Neumann88].

Figure 2 Classification by (co)homological invariants within the Borel reduction hierarchy.
An upshot of our analysis here and in [Reference Bergfalk and Lupini9] is that classifiability by (co)homological invariants forms an equally robust complexity class within the Borel reduction hierarchy, one containing a wide array of classification problems from throughout mathematics. This class contains all classification problems which can be ‘definably classified’ using as invariants the elements of a (co)homology group of some Polish (co)chain complex. More formally, let E be an analytic equivalence relation on a Polish space X. We say that
![]() $(X,E)$
is classifiable by (co)homological invariants if there exists a Polish abelian group G, a Polishable subgroup N of G, and a Borel map
$(X,E)$
is classifiable by (co)homological invariants if there exists a Polish abelian group G, a Polishable subgroup N of G, and a Borel map
![]() $f\colon X\to G$
so that for all
$f\colon X\to G$
so that for all
![]() $x,y\in X$
, we have
$x,y\in X$
, we have
![]() $x\,E\,y$
if and only if
$x\,E\,y$
if and only if
![]() $f(x)+N=f(y)+N$
(i.e., if E is Borel reducible to the coset equivalence relation
$f(x)+N=f(y)+N$
(i.e., if E is Borel reducible to the coset equivalence relation
![]() $\mathcal {R}(G/N)$
).
$\mathcal {R}(G/N)$
).
It follows from the recognition that many classical invariants from homological algebra and algebraic topology arise as the (co)homology groups of Polish (co)chain complexes that the aforementioned complexity class is a rich one. By [Reference Bergfalk and Lupini9], for example, it contains the problem of classifying the extensions
![]() $0\to F \to E \to B \to 0$
of any fixed pair
$0\to F \to E \to B \to 0$
of any fixed pair
![]() $(B,F)$
of countable abelian groups. Similarly, it will follow from Section 2 below that any classification problem admitting formulation in terms of the Čech cohomology of a locally compact Polish space falls in this class as well. In particular, by Theorem 1.1, for any countable abelian group G, the problem of classifying maps
$(B,F)$
of countable abelian groups. Similarly, it will follow from Section 2 below that any classification problem admitting formulation in terms of the Čech cohomology of a locally compact Polish space falls in this class as well. In particular, by Theorem 1.1, for any countable abelian group G, the problem of classifying maps
![]() $X\to Y$
from a locally compact Polish space X to a
$X\to Y$
from a locally compact Polish space X to a
![]() $K(G,n)$
space Y up to homotopy falls within this class; such Y include, of course, infinite-dimensional real and complex projective space, any knot complement or, more generally, aspherical space, any finite wedge or product or mapping telescope of circles
$K(G,n)$
space Y up to homotopy falls within this class; such Y include, of course, infinite-dimensional real and complex projective space, any knot complement or, more generally, aspherical space, any finite wedge or product or mapping telescope of circles
![]() $S^1$
, and so on. These examples may easily be multiplied, within areas of study as varied as that of tiling spaces, group cohomology, or gerbes or fiber bundles, for example [Reference Brown16, Reference Brylinski19, Reference Sadun75]; we close this subsection with two representative instances. If B is a locally compact Polish space, a careful inspection of how the assignments
$S^1$
, and so on. These examples may easily be multiplied, within areas of study as varied as that of tiling spaces, group cohomology, or gerbes or fiber bundles, for example [Reference Brown16, Reference Brylinski19, Reference Sadun75]; we close this subsection with two representative instances. If B is a locally compact Polish space, a careful inspection of how the assignments
![]() $p\mapsto c(p)$
and
$p\mapsto c(p)$
and
![]() $\mathcal {A}\mapsto c(\mathcal {A})$
are defined below shows that they are induced by Borel maps at the level of cocycles. As a consequence, the problem of classifying Hermitian line bundles over B up to isomorphism and of classifying continuous-trace separable
$\mathcal {A}\mapsto c(\mathcal {A})$
are defined below shows that they are induced by Borel maps at the level of cocycles. As a consequence, the problem of classifying Hermitian line bundles over B up to isomorphism and of classifying continuous-trace separable
![]() $C^{*}$
-algebras with spectrum B up to Morita equivalence are classifiable by (co)homological invariants in the above formal sense.
$C^{*}$
-algebras with spectrum B up to Morita equivalence are classifiable by (co)homological invariants in the above formal sense.
-
(1) There is an assignment
 $p\mapsto c(p)$
, from Hermitian line bundles
$p\mapsto c(p)$
, from Hermitian line bundles
 $p\colon E\to B$
over B, to
$p\colon E\to B$
over B, to  , so that p and
, so that p and
 $p'$
are isomorphic iff
$p'$
are isomorphic iff
 $c(p)=c(p')$
; see [Reference Raeburn and Williams72, Proposition 4.53].
$c(p)=c(p')$
; see [Reference Raeburn and Williams72, Proposition 4.53]. -
(2) There is an assignment
 $\mathcal {A}\mapsto c(\mathcal {A})$
, from continuous-trace separable
$\mathcal {A}\mapsto c(\mathcal {A})$
, from continuous-trace separable
 $C^{*}$
-algebras
$C^{*}$
-algebras
 $\mathcal {A}$
with spectrum B, to
$\mathcal {A}$
with spectrum B, to  , so that
, so that
 $\mathcal {A}$
and
$\mathcal {A}$
and
 $\mathcal {A}'$
are Morita equivalent iff
$\mathcal {A}'$
are Morita equivalent iff
 $c(\mathcal {A})=c(\mathcal {A}')$
; see [Reference Raeburn and Williams72, Proposition 5.24, Theorem 5.56] or [Reference Blackadar10], and also [Reference Bergfalk, Lupini and Panagiotopoulos8].
$c(\mathcal {A})=c(\mathcal {A}')$
; see [Reference Raeburn and Williams72, Proposition 5.24, Theorem 5.56] or [Reference Blackadar10], and also [Reference Bergfalk, Lupini and Panagiotopoulos8].
1.5. Definable cohomology as a strong invariant
A second consequence of our work is potentially of even wider significance than the first; this is the existence of definable cohomological functors ![]() which strictly refine their classical counterparts. In Section 8, we record three sample applications of this technology. We have mentioned the first of these already; it is the following (see Sections 8.2 and 8.4 for precise definitions):
which strictly refine their classical counterparts. In Section 8, we record three sample applications of this technology. We have mentioned the first of these already; it is the following (see Sections 8.2 and 8.4 for precise definitions):
Theorem 1.3. The definable Čech cohomology groups completely classify homotopy colimits, or, equivalently, mapping telescopes, of nontrivial inductive sequences of d-spheres up to homotopy equivalence, for all
![]() $d\geq 1$
. In contrast, there exist uncountable families of pairwise homotopy inequivalent mapping telescopes of sequences of spheres whose classical Čech cohomology groups, viewed as graded abelian groups, are all isomorphic.
$d\geq 1$
. In contrast, there exist uncountable families of pairwise homotopy inequivalent mapping telescopes of sequences of spheres whose classical Čech cohomology groups, viewed as graded abelian groups, are all isomorphic.
We also prove the variant of this theorem resulting from replacing every instance of spheres therein with tori. Each of these theorems draws on Ulam stability results first established in [Reference Bergfalk and Lupini9], and this, indeed, is much of their interest: each applies fundamentally descriptive set theoretic rigidity results to algebraic and topological settings. We retain hopes for deeper applications along these lines, a point we return to in our conclusion.
Our second application of the functors ![]() is to a generalization of a problem dating to Borsuk and Eilenberg in 1936 [Reference Borsuk and Eilenberg11]. Writing
is to a generalization of a problem dating to Borsuk and Eilenberg in 1936 [Reference Borsuk and Eilenberg11]. Writing
![]() $\Sigma _p$
for the standard unknotted realization of the p-adic solenoid in
$\Sigma _p$
for the standard unknotted realization of the p-adic solenoid in
![]() $S^3$
, this is the problem of classifying the maps
$S^3$
, this is the problem of classifying the maps
![]() $S^3\backslash \Sigma _p\to S^2$
up to homotopy. We review the problem’s pivotal role in the development of algebraic topology in Section 8.6, where we also show the following, together with its higher-dimensional generalizations; the theorem’s statement is an amalgamation of Theorems 8.19 and 8.21.
$S^3\backslash \Sigma _p\to S^2$
up to homotopy. We review the problem’s pivotal role in the development of algebraic topology in Section 8.6, where we also show the following, together with its higher-dimensional generalizations; the theorem’s statement is an amalgamation of Theorems 8.19 and 8.21.
Theorem 1.4. For any prime number p,
![]() $[S^{3}\backslash \Sigma _{p},S^{2}]$
is a definable set, and there is a basepoint-preserving definable bijection between it and the definable group
$[S^{3}\backslash \Sigma _{p},S^{2}]$
is a definable set, and there is a basepoint-preserving definable bijection between it and the definable group
![]() $\mathrm {Ext}(\mathbb {Z}[1/p],\mathbb {Z})$
. In consequence, the Borsuk-Eilenberg problem of classifying maps
$\mathrm {Ext}(\mathbb {Z}[1/p],\mathbb {Z})$
. In consequence, the Borsuk-Eilenberg problem of classifying maps
![]() $S^3\backslash \Sigma _p\to S^2$
up to homotopy is essentially hyperfinite but not smooth.
$S^3\backslash \Sigma _p\to S^2$
up to homotopy is essentially hyperfinite but not smooth.
The result connects to ![]() via Hopf’s Theorem (see Section 7.7) and connects to homotopy colimits via the recognition that
via Hopf’s Theorem (see Section 7.7) and connects to homotopy colimits via the recognition that
![]() $S^{3}\backslash \Sigma _{p}$
is homotopy equivalent to a mapping telescope of
$S^{3}\backslash \Sigma _{p}$
is homotopy equivalent to a mapping telescope of
![]() $1$
-spheres. Note that this is a stronger and subtler result than the recognition that
$1$
-spheres. Note that this is a stronger and subtler result than the recognition that
![]() $[S^{3}\backslash \Sigma _{p},S^{2}]$
is uncountable, in precisely that sense in which Borel cardinality exhibits a richer and subtler degree structure than classical cardinality does; see [Reference Hjorth34] for a brief introduction to these matters. This brings us to the third sample application of our technology, in which we consider equivariant versions of the aforementioned generalized Borsuk-Eilenberg problems. It follows readily from results in both [Reference Bergfalk and Lupini9] and the present work that these classification problems realize both an infinite antichain and an infinite chain of degrees within the Borel reduction heirarchy; a description of these degrees appears as Corollary 8.24.
$[S^{3}\backslash \Sigma _{p},S^{2}]$
is uncountable, in precisely that sense in which Borel cardinality exhibits a richer and subtler degree structure than classical cardinality does; see [Reference Hjorth34] for a brief introduction to these matters. This brings us to the third sample application of our technology, in which we consider equivariant versions of the aforementioned generalized Borsuk-Eilenberg problems. It follows readily from results in both [Reference Bergfalk and Lupini9] and the present work that these classification problems realize both an infinite antichain and an infinite chain of degrees within the Borel reduction heirarchy; a description of these degrees appears as Corollary 8.24.
1.6. Concluding preliminaries
A few final words are in order about the organization of the paper. To begin with, it is, in conception, largely self-contained: although we will repeatedly invoke results from its predecessor [Reference Bergfalk and Lupini9], we do not presume any close familiarity with that work. Not unrelatedly, we have drafted it with readers with a wide variety of backgrounds in mind. Its table of contents, together with our preceding remarks and section introductions below, should convey its overall plan.
A standard setting for much of the topological material we will be considering below is the category HCW of spaces homotopy equivalent to a (countable) CW complex. We should therefore say a bit about our decision to mainly work with two other categories of spaces: that of locally compact separable metric spaces (LC) and that of spaces homotopy equivalent to the geometric realization of a countable, locally finite simplicial complex. As it happens, the latter category is identical to HCW [Reference Milnor64]; a polyhedral emphasis merely facilitates several of our arguments. As for the category
![]() $\mathsf {LC}$
, its virtues for our purposes are multiple:
$\mathsf {LC}$
, its virtues for our purposes are multiple:
-
• for any two objects
 $X,Y$
in
$X,Y$
in
 $\mathsf {LC}$
, the compact-open topology renders the set
$\mathsf {LC}$
, the compact-open topology renders the set
 $\mathrm {Map}(X,Y)$
a Polish space;
$\mathrm {Map}(X,Y)$
a Polish space; -
• Huber’s theorem applies in the generality of
 $\mathsf {LC}$
, and Čech and sheaf cohomology coincide therein as well;
$\mathsf {LC}$
, and Čech and sheaf cohomology coincide therein as well; -
• any space in
 $\mathsf {LC}$
is compactly generated [Reference Steenrod82]; relatedly, the fundamental adjunctions of algebraic topology all hold in
$\mathsf {LC}$
is compactly generated [Reference Steenrod82]; relatedly, the fundamental adjunctions of algebraic topology all hold in
 $\mathsf {LC}$
[Reference Bradley, Bryson and Terilla14, chs. 5–6];
$\mathsf {LC}$
[Reference Bradley, Bryson and Terilla14, chs. 5–6]; -
• any object of
 $\mathsf {LC}$
is a countable increasing union of compact subspaces, or, more briefly, is
$\mathsf {LC}$
is a countable increasing union of compact subspaces, or, more briefly, is
 $\sigma $
-compact.
$\sigma $
-compact.
We have focused exclusively on the group structure of Čech cohomology simply for reasons of space. We count
![]() $0$
among the natural numbers
$0$
among the natural numbers
![]() $\mathbb {N}$
. We turn, after the following acknowledgement, to the main body of our paper.
$\mathbb {N}$
. We turn, after the following acknowledgement, to the main body of our paper.
2. Definable cohomology: the combinatorial approach
A Polish space X is a second countable topological space whose topology is induced by a complete metric. A subset Z of X is analytic if it is the continuous image of a Polish space, and Borel if it belongs to the
![]() $\sigma $
-algebra generated by the open subsets of X. A function
$\sigma $
-algebra generated by the open subsets of X. A function
![]() $f:X\to Y$
between Polish spaces is Borel if its graph is a Borel subset of
$f:X\to Y$
between Polish spaces is Borel if its graph is a Borel subset of
![]() $X\times Y$
or, equivalently, if
$X\times Y$
or, equivalently, if
![]() $f^{-1}(U)$
is Borel for every open
$f^{-1}(U)$
is Borel for every open
![]() $U\subseteq Y$
. A subset Z of X is meager if it is a countable union of nowhere dense subsets of X, and comeager if its complement in X is meager. A Polish group is a topological group whose topology is Polish; a Polishable topological group is one whose Borel structure is generated by a (possibly finer) Polish group topology. Descriptive set theoretic results as well-known as the fact, for example, that a closed subgroup of a Polish group is Polish will typically be invoked below without citation; readers are referred to [Reference Kechris44] or [Reference Gao31] for complete introductions to this material.
$U\subseteq Y$
. A subset Z of X is meager if it is a countable union of nowhere dense subsets of X, and comeager if its complement in X is meager. A Polish group is a topological group whose topology is Polish; a Polishable topological group is one whose Borel structure is generated by a (possibly finer) Polish group topology. Descriptive set theoretic results as well-known as the fact, for example, that a closed subgroup of a Polish group is Polish will typically be invoked below without citation; readers are referred to [Reference Kechris44] or [Reference Gao31] for complete introductions to this material.
A Polish cochain complex
![]() $C^{\bullet }$
is an
$C^{\bullet }$
is an
![]() $\mathbb {Z}$
-indexed sequence of continuous homomorphisms of Polish abelian groups
$\mathbb {Z}$
-indexed sequence of continuous homomorphisms of Polish abelian groups
in which
![]() $\delta ^n\delta ^{n-1}=0$
for all
$\delta ^n\delta ^{n-1}=0$
for all
![]() $n\in \mathbb {Z}$
. Observe that every group
$n\in \mathbb {Z}$
. Observe that every group
![]() $\mathrm {Z}^n:=\mathrm {ker}(\delta ^n)$
of n-cocycles arising in
$\mathrm {Z}^n:=\mathrm {ker}(\delta ^n)$
of n-cocycles arising in
![]() $C^{\bullet }$
is a closed and therefore Polish subgroup of
$C^{\bullet }$
is a closed and therefore Polish subgroup of
![]() $C^n$
, and that the n-coboundary groups
$C^n$
, and that the n-coboundary groups
![]() $\mathrm {B}^n:=\mathrm {im}(\delta ^{n-1})$
arising in
$\mathrm {B}^n:=\mathrm {im}(\delta ^{n-1})$
arising in
![]() $C^{\bullet }$
, being continuous homomorphic images of Polish groups, are all Polishable. We denote by
$C^{\bullet }$
, being continuous homomorphic images of Polish groups, are all Polishable. We denote by
![]() $\mathrm {H}^n:=\mathrm {Z}^n/\mathrm {B}^n$
the (abstract) cohomology group of degree n associated to
$\mathrm {H}^n:=\mathrm {Z}^n/\mathrm {B}^n$
the (abstract) cohomology group of degree n associated to
![]() $C^{\bullet }$
. The definable cohomology group
$C^{\bullet }$
. The definable cohomology group
![]() $\mathrm {H}^n_{\mathrm {def}}$
of degree n associated to
$\mathrm {H}^n_{\mathrm {def}}$
of degree n associated to
![]() $C^{\bullet }$
is
$C^{\bullet }$
is
![]() $\mathrm {Z}^n/\mathrm {B}^n$
endowed with the structure of a group with a Polish cover. As above, recall from [Reference Bergfalk and Lupini9] that groups with a Polish cover
$\mathrm {Z}^n/\mathrm {B}^n$
endowed with the structure of a group with a Polish cover. As above, recall from [Reference Bergfalk and Lupini9] that groups with a Polish cover
![]() $G/N$
form a category
$G/N$
form a category
![]() $\mathsf {GPC}$
whose objects are pairs
$\mathsf {GPC}$
whose objects are pairs
![]() $(G,N)$
in which N is a Polishable normal subgroup of a Polish group G, and whose morphisms, also known as definable homomorphisms, are those group homomorphisms
$(G,N)$
in which N is a Polishable normal subgroup of a Polish group G, and whose morphisms, also known as definable homomorphisms, are those group homomorphisms
![]() $f\colon G/N\to G'/N'$
which lift to a Borel function
$f\colon G/N\to G'/N'$
which lift to a Borel function
![]() $\hat {f}\colon G\to G'$
satisfying
$\hat {f}\colon G\to G'$
satisfying
![]() $f(gN)=\hat {f}(g)N'$
. Within the definable setting of
$f(gN)=\hat {f}(g)N'$
. Within the definable setting of
![]() $\mathsf {GPC}$
, the functor
$\mathsf {GPC}$
, the functor
![]() $\mathrm {H}^n_{\mathrm {def}}$
conserves, in general, considerably more of the data of
$\mathrm {H}^n_{\mathrm {def}}$
conserves, in general, considerably more of the data of
![]() $C^{\bullet }$
than its classical counterpart
$C^{\bullet }$
than its classical counterpart
![]() $\mathrm {H}^n$
; this renders it a significantly stronger invariant than the latter.
$\mathrm {H}^n$
; this renders it a significantly stronger invariant than the latter.
As shown in [Reference Bergfalk and Lupini9], several of the most prominent invariants of homological algebra arise as the cohomology groups of cochain complexes carrying natural Polish topologies, including suitable restrictions of the functors
![]() $\mathrm {Ext}$
and
$\mathrm {Ext}$
and
![]() $\mathrm {lim}^1$
. In this section, we show that the Čech cohomology groups
$\mathrm {lim}^1$
. In this section, we show that the Čech cohomology groups ![]() of a locally compact metrizable space X with coefficients in any countable abelian group G may be similarly construed as groups with a Polish cover, giving rise to the definable cohomology groups
of a locally compact metrizable space X with coefficients in any countable abelian group G may be similarly construed as groups with a Polish cover, giving rise to the definable cohomology groups ![]() of X.
of X.
This work involves technical challenges which were mercifully absent in the cases of
![]() $\mathrm {Ext}$
or
$\mathrm {Ext}$
or
![]() $\mathrm {lim}^1$
. To better describe them, recall that most standard definitions of Čech cohomology group
$\mathrm {lim}^1$
. To better describe them, recall that most standard definitions of Čech cohomology group ![]() are some variation on the following:
are some variation on the following:
where
![]() $\mathcal {U}$
ranges over the collection
$\mathcal {U}$
ranges over the collection
![]() $\mathrm {Cov}(X)$
of all locally finite open covers of X, ordered by refinement, and
$\mathrm {Cov}(X)$
of all locally finite open covers of X, ordered by refinement, and
![]() $\mathrm {H}^n(\mathrm {Nv}(\mathcal {U});G)$
denotes the
$\mathrm {H}^n(\mathrm {Nv}(\mathcal {U});G)$
denotes the
![]() $n^{\mathrm {th}}$
simplicial cohomology group of the nerve of
$n^{\mathrm {th}}$
simplicial cohomology group of the nerve of
![]() $\mathcal {U}$
; see Section 2.1 below. Implicit in this expression is the fact that the refinement relation
$\mathcal {U}$
; see Section 2.1 below. Implicit in this expression is the fact that the refinement relation
![]() $\mathcal {U}\preceq \mathcal {V}$
(i.e.,
$\mathcal {U}\preceq \mathcal {V}$
(i.e.,
![]() $\mathcal {V}$
refines
$\mathcal {V}$
refines
![]() $\mathcal {U}$
) induces a canonical homomorphism
$\mathcal {U}$
) induces a canonical homomorphism
![]() $\mathrm {H}^n(\mathrm {Nv}(\mathcal {U});G)\to \mathrm {H}^n(\mathrm {Nv}(\mathcal {V});G)$
. Two main issues complicate the impulse to regard this object as a group with a Polish cover. The first difficulty is that, as defined above,
$\mathrm {H}^n(\mathrm {Nv}(\mathcal {U});G)\to \mathrm {H}^n(\mathrm {Nv}(\mathcal {V});G)$
. Two main issues complicate the impulse to regard this object as a group with a Polish cover. The first difficulty is that, as defined above, ![]() is not the cohomology group of any single explicit cochain complex. The second issue is that
is not the cohomology group of any single explicit cochain complex. The second issue is that
![]() $\mathrm {Cov}(X)$
does not, in general, contain a countable cofinal subset; in consequence, it is less than immediately clear how to extract the information contained in
$\mathrm {Cov}(X)$
does not, in general, contain a countable cofinal subset; in consequence, it is less than immediately clear how to extract the information contained in ![]() from any separable space of data.
from any separable space of data.
We address these difficulties by introducing the notion of a covering system
![]() $\boldsymbol {\mathcal {U}}$
for X; in Section 2.3, we show that every locally compact metrizable space X admits such a system. Covering systems are families of open covers which are cofinal in
$\boldsymbol {\mathcal {U}}$
for X; in Section 2.3, we show that every locally compact metrizable space X admits such a system. Covering systems are families of open covers which are cofinal in
![]() $\mathrm {Cov}(X)$
and continuously parametrized by
$\mathrm {Cov}(X)$
and continuously parametrized by
![]() $\mathbb {N}^{\mathbb {N}}$
. In Section 2.4, we associate to each covering system
$\mathbb {N}^{\mathbb {N}}$
. In Section 2.4, we associate to each covering system
![]() $\boldsymbol {\mathcal {U}}$
a Polish cochain complex
$\boldsymbol {\mathcal {U}}$
a Polish cochain complex
![]() $C^{\bullet }(\boldsymbol {\mathcal {U}};G)$
, and we introduce the definable cohomology groups of X as the groups with a Polish cover
$C^{\bullet }(\boldsymbol {\mathcal {U}};G)$
, and we introduce the definable cohomology groups of X as the groups with a Polish cover
associated to
![]() $C^{\bullet }(\boldsymbol {\mathcal {U}};G)$
. As abstract groups,
$C^{\bullet }(\boldsymbol {\mathcal {U}};G)$
. As abstract groups, ![]() coincides with the classical Čech cohomology groups. As the notation suggests,
coincides with the classical Čech cohomology groups. As the notation suggests, ![]() does not depend on the choice of
does not depend on the choice of
![]() $\boldsymbol {\mathcal {U}}$
up to definable isomorphism. Moreover, the assignment
$\boldsymbol {\mathcal {U}}$
up to definable isomorphism. Moreover, the assignment ![]() is functorial and invariant under homotopy equivalences. However, we defer the proofs of these claims to Section 5, since they will apply the definable theory of homotopy equivalence which we first develop in Sections 3 and 4. This brings us to a few last points: first, in the following section, we recall only what we need of nerves and simplicial complexes for the combinatorial development of definable cohomology; we extend our treatment of these matters in Sections 4.2 and 4.3. Second, similarly, for simplicity’s sake, we undertake this development primarily in the context of single spaces X, only recording the modifications needed for the cohomology of pairs of spaces
is functorial and invariant under homotopy equivalences. However, we defer the proofs of these claims to Section 5, since they will apply the definable theory of homotopy equivalence which we first develop in Sections 3 and 4. This brings us to a few last points: first, in the following section, we recall only what we need of nerves and simplicial complexes for the combinatorial development of definable cohomology; we extend our treatment of these matters in Sections 4.2 and 4.3. Second, similarly, for simplicity’s sake, we undertake this development primarily in the context of single spaces X, only recording the modifications needed for the cohomology of pairs of spaces
![]() $(X,A)$
at its conclusion, in Section 2.5; there we also show that definable cohomology satisfies the definable version of the Exactness Axiom. Lastly, readers seeking, as background to this section, a more complete classical combinatorial treatment of Čech cohomology are referred to [Reference Eilenberg and Steenrod29, Chapter IX].
$(X,A)$
at its conclusion, in Section 2.5; there we also show that definable cohomology satisfies the definable version of the Exactness Axiom. Lastly, readers seeking, as background to this section, a more complete classical combinatorial treatment of Čech cohomology are referred to [Reference Eilenberg and Steenrod29, Chapter IX].
2.1. Definable cohomology for simplicial complexes
A simplicial complex K is a family of finite sets that is closed downwards (i.e.,
![]() $\sigma \subseteq \tau \in K\implies \sigma \in K$
). A simplex or face of K is any element
$\sigma \subseteq \tau \in K\implies \sigma \in K$
). A simplex or face of K is any element
![]() $\sigma \in K$
. A vertex of K is any element v of
$\sigma \in K$
. A vertex of K is any element v of
![]() $\mathrm {dom}(K):=\bigcup K$
. Let
$\mathrm {dom}(K):=\bigcup K$
. Let
![]() $K,L$
be two simplicial complexes. A simplicial map
$K,L$
be two simplicial complexes. A simplicial map
![]() $f\colon K\rightarrow L$
is then any function
$f\colon K\rightarrow L$
is then any function
![]() $ f\colon \mathrm {dom}(K)\rightarrow \mathrm {dom}(L)$
such that
$ f\colon \mathrm {dom}(K)\rightarrow \mathrm {dom}(L)$
such that
![]() $ \{f(v_{0}),\ldots ,f(v_{n})\}\in L$
for all
$ \{f(v_{0}),\ldots ,f(v_{n})\}\in L$
for all
![]() $\{v_{0},\ldots ,v_{n}\}\in K$
. The dimension
$\{v_{0},\ldots ,v_{n}\}\in K$
. The dimension
![]() $\mathrm {dim}(\sigma )$
of a face
$\mathrm {dim}(\sigma )$
of a face
![]() $\sigma $
of K is simply the number
$\sigma $
of K is simply the number
![]() $|\sigma |-1$
. For example,
$|\sigma |-1$
. For example,
![]() $\mathrm {dim}(\emptyset )=(-1)$
and
$\mathrm {dim}(\emptyset )=(-1)$
and
![]() $\mathrm {dim}(\{v\})=0$
for every
$\mathrm {dim}(\{v\})=0$
for every
![]() $v\in \mathrm {dom}(K)$
. The dimension
$v\in \mathrm {dom}(K)$
. The dimension
![]() $\mathrm {dim}(K)$
of
$\mathrm {dim}(K)$
of
![]() $ K$
is the supremum over
$ K$
is the supremum over
![]() $\{\mathrm {dim}(\sigma )\mid \sigma \in K\}$
. A simplicial complex is finite if it has finitely many vertices, and countable if it has countably many vertices. It is locally finite if each vertex belongs to finitely many faces. For each
$\{\mathrm {dim}(\sigma )\mid \sigma \in K\}$
. A simplicial complex is finite if it has finitely many vertices, and countable if it has countably many vertices. It is locally finite if each vertex belongs to finitely many faces. For each
![]() $n\in \mathbb {N}$
, the singular n-faces
Footnote
1
of K comprise the set
$n\in \mathbb {N}$
, the singular n-faces
Footnote
1
of K comprise the set
We fix an abelian Polish group G and consider, for every
![]() $n\in \mathbb {N}$
, the collection
$n\in \mathbb {N}$
, the collection
of all maps from the countable set
![]() $K^{(n)}$
to G. Endowed with the group operation
$K^{(n)}$
to G. Endowed with the group operation
![]() $(\zeta ,\eta )\mapsto (\zeta +\eta )$
of pointwise addition
$(\zeta ,\eta )\mapsto (\zeta +\eta )$
of pointwise addition
![]() $(\zeta +\eta )(\bar {v})=\zeta (\bar {v})+\eta (\bar {v})$
, and the product topology of countably many copies of G, the collection
$(\zeta +\eta )(\bar {v})=\zeta (\bar {v})+\eta (\bar {v})$
, and the product topology of countably many copies of G, the collection
![]() $C^{n}(K;G)$
forms the abelian Polish group of all G-valued cochains of K. For every
$C^{n}(K;G)$
forms the abelian Polish group of all G-valued cochains of K. For every
![]() $n\geq 0$
, we have the coboundary map
$n\geq 0$
, we have the coboundary map
 $$ \begin{align} \begin{aligned} \delta^{n}:C^{n}(K;G) &\rightarrow C^{n+1}(K;G), \text{ with}\\ \left( \delta^{n}( \zeta) \right) \big((v_{0},\ldots ,v_{n+1})\big) &=\sum_{i=0}^{n}\left( -1\right) ^{i}\zeta (v_{0},\ldots ,\hat{v}_{i},\ldots ,v_{n+1}), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \delta^{n}:C^{n}(K;G) &\rightarrow C^{n+1}(K;G), \text{ with}\\ \left( \delta^{n}( \zeta) \right) \big((v_{0},\ldots ,v_{n+1})\big) &=\sum_{i=0}^{n}\left( -1\right) ^{i}\zeta (v_{0},\ldots ,\hat{v}_{i},\ldots ,v_{n+1}), \end{aligned} \end{align} $$
where
![]() $\hat {v}_{i}$
denotes the omission of
$\hat {v}_{i}$
denotes the omission of
![]() $v_i$
from
$v_i$
from
![]() $\bar {v}$
. Notice that
$\bar {v}$
. Notice that
![]() $\delta ^{n}$
is a continuous homomorphism. This gives rise to the Polish cochain complex
$\delta ^{n}$
is a continuous homomorphism. This gives rise to the Polish cochain complex
![]() $C^{\bullet }(K;G)$
of G-valued cochains of K:
$C^{\bullet }(K;G)$
of G-valued cochains of K:
Definition 2.1. Let K be a countable simplicial complex, and let G be an abelian Polish group. For every
![]() $n\in \mathbb {N}$
, the n-dimensional definable cohomology group
$n\in \mathbb {N}$
, the n-dimensional definable cohomology group
![]() $\mathrm {H}^{n}_{\mathrm {def}}(K;G)$
of K with coefficients in G is the n-dimensional cohomology group
$\mathrm {H}^{n}_{\mathrm {def}}(K;G)$
of K with coefficients in G is the n-dimensional cohomology group
![]() $\mathrm {H}^{n}(K;G)$
of the Polish cochain complex
$\mathrm {H}^{n}(K;G)$
of the Polish cochain complex
![]() $C^{\bullet }(K;G)$
, viewed as the group with a Polish cover
$C^{\bullet }(K;G)$
, viewed as the group with a Polish cover
where
![]() $\mathrm {Z}^{n}(K;G)= \mathrm {ker}(\delta ^{n})$
is the Polish group of n-dimensional G-valued cocycles of K and
$\mathrm {Z}^{n}(K;G)= \mathrm {ker}(\delta ^{n})$
is the Polish group of n-dimensional G-valued cocycles of K and
![]() $\mathrm {B}^{n}(K;G)=\mathrm {im}(\delta ^{n-1})$
is the Polishable group of n-dimensional G-valued coboundaries of K.
$\mathrm {B}^{n}(K;G)=\mathrm {im}(\delta ^{n-1})$
is the Polishable group of n-dimensional G-valued coboundaries of K.
Of course, if we forget about the quotient Borel structure on
![]() $\mathrm {H}^{n}_{\mathrm {def}}(K;G)$
and instead treat it as an abstract group, then we recover the classical n-dimensional simplicial cohomology group of K with coefficients in G.
$\mathrm {H}^{n}_{\mathrm {def}}(K;G)$
and instead treat it as an abstract group, then we recover the classical n-dimensional simplicial cohomology group of K with coefficients in G.
Remark 2.2. Several alternative definitions of the simplicial cohomology groups
![]() $\mathrm {H}^{n}(K;G)$
may be found in the literature. Each involves variants of the cochain complex
$\mathrm {H}^{n}(K;G)$
may be found in the literature. Each involves variants of the cochain complex
![]() $C^{\bullet }(K;G)$
described above. For example, one may work with the chain complex
$C^{\bullet }(K;G)$
described above. For example, one may work with the chain complex
![]() $C^{\bullet }_{\mathrm {alt}}(K;G)$
of alternating cochains instead. An alternating n-cochain is any n-cochain
$C^{\bullet }_{\mathrm {alt}}(K;G)$
of alternating cochains instead. An alternating n-cochain is any n-cochain
![]() $\zeta \in C^{\bullet }(K;G)$
with the property that
$\zeta \in C^{\bullet }(K;G)$
with the property that
for any permutation
![]() $\pi $
of the set
$\pi $
of the set
![]() $\{0,\ldots ,n\}$
. The inclusion
$\{0,\ldots ,n\}$
. The inclusion
![]() $C^{\bullet }_{\mathrm {alt}}(K;G)\hookrightarrow C^{\bullet }(K;G)$
yields an isomorphism between
$C^{\bullet }_{\mathrm {alt}}(K;G)\hookrightarrow C^{\bullet }(K;G)$
yields an isomorphism between
![]() $\mathrm {H}^{n}(K;G)$
and
$\mathrm {H}^{n}(K;G)$
and
![]() $\mathrm {H}^{n}_{\mathrm {alt}}(K;G)$
, as is well known (see, for example, [Reference Serre78]). It is clear that
$\mathrm {H}^{n}_{\mathrm {alt}}(K;G)$
, as is well known (see, for example, [Reference Serre78]). It is clear that
![]() $C^{\bullet }_{\mathrm {alt}}(K;G)$
inherits a Polish structure from
$C^{\bullet }_{\mathrm {alt}}(K;G)$
inherits a Polish structure from
![]() $C^{\bullet }(K;G)$
and that
$C^{\bullet }(K;G)$
and that
![]() $C^{\bullet }_{\mathrm {alt}}(K;G)\hookrightarrow C^{\bullet }(K;G)$
is continuous. Hence,
$C^{\bullet }_{\mathrm {alt}}(K;G)\hookrightarrow C^{\bullet }(K;G)$
is continuous. Hence,
![]() $\mathrm {H}^{n}(K;G)$
and
$\mathrm {H}^{n}(K;G)$
and
![]() $\mathrm {H}^{n}_{\mathrm {alt}}(K;G)$
are definably isomorphic as groups with a Polish cover. As this isomorphism commutes with direct limits, similar remarks will apply to the Čech cohomology groups of locally compact Polish spaces which we define below.
$\mathrm {H}^{n}_{\mathrm {alt}}(K;G)$
are definably isomorphic as groups with a Polish cover. As this isomorphism commutes with direct limits, similar remarks will apply to the Čech cohomology groups of locally compact Polish spaces which we define below.
2.2. An indexing poset
Below, we identify n with the set
![]() $\{0,\ldots ,n-1\}$
. Let
$\{0,\ldots ,n-1\}$
. Let
![]() $\mathbb {N}^n$
be the space of all functions from n to
$\mathbb {N}^n$
be the space of all functions from n to
![]() $\mathbb {N}$
, and set
$\mathbb {N}$
, and set
![]() $\mathbb {N}^{<\mathbb {N}}=\bigcup _{n\in \mathbb {N}}\mathbb {N}^n$
. The Baire space
$\mathbb {N}^{<\mathbb {N}}=\bigcup _{n\in \mathbb {N}}\mathbb {N}^n$
. The Baire space
![]() $\mathcal {N}:=\mathbb {N}^{\mathbb {N}}$
is the space of all functions from
$\mathcal {N}:=\mathbb {N}^{\mathbb {N}}$
is the space of all functions from
![]() $\mathbb {N}$
to
$\mathbb {N}$
to
![]() $\mathbb {N}$
, which we view as a Polish space equipped with the product topology on discrete copies of
$\mathbb {N}$
, which we view as a Polish space equipped with the product topology on discrete copies of
![]() $\mathbb {N}$
. For every
$\mathbb {N}$
. For every
![]() $\alpha \in \mathcal {N}$
and all
$\alpha \in \mathcal {N}$
and all
![]() $n\in \mathbb {N}$
, we let
$n\in \mathbb {N}$
, we let
![]() $\alpha |n\in \mathbb {N}^n$
be the finite sequence
$\alpha |n\in \mathbb {N}^n$
be the finite sequence
![]() $(\alpha (0),\ldots ,\alpha (n-1))$
. For every
$(\alpha (0),\ldots ,\alpha (n-1))$
. For every
![]() $s=(s(0),\ldots ,s(n-1))\in \mathbb {N}^{<\mathbb {N}}$
, we denote by
$s=(s(0),\ldots ,s(n-1))\in \mathbb {N}^{<\mathbb {N}}$
, we denote by
![]() $\mathcal {N}_s$
the clopen subset
$\mathcal {N}_s$
the clopen subset
![]() $\{\alpha \in \mathcal {N}\colon \alpha |n=s \}$
of
$\{\alpha \in \mathcal {N}\colon \alpha |n=s \}$
of
![]() $\mathcal {N}$
. The collection
$\mathcal {N}$
. The collection
![]() $\{\mathcal {N}_s\colon s\in \mathbb {N}^{<\mathbb {N}}\}$
of all such sets forms a basis for the topology on
$\{\mathcal {N}_s\colon s\in \mathbb {N}^{<\mathbb {N}}\}$
of all such sets forms a basis for the topology on
![]() $\mathcal {N}$
. Let
$\mathcal {N}$
. Let
![]() $(X_s\colon s\in \mathbb {N}^{<\mathbb {N}})$
be a family of sets parametrized by
$(X_s\colon s\in \mathbb {N}^{<\mathbb {N}})$
be a family of sets parametrized by
![]() $\mathbb {N}^{<\mathbb {N}}$
. To each such family we may apply Suslin’s
$\mathbb {N}^{<\mathbb {N}}$
. To each such family we may apply Suslin’s
![]() $\mathcal {A}$
-operation, producing the set
$\mathcal {A}$
-operation, producing the set
Notice that while the family
![]() $(X_s)$
is countable, the operation
$(X_s)$
is countable, the operation
![]() $\mathcal {A}$
involves an uncountable union. Historically, this operation was used to explicitly define subsets of the real line which are analytic but not Borel. Indeed, every Borel subset of a Polish space X is the result of the
$\mathcal {A}$
involves an uncountable union. Historically, this operation was used to explicitly define subsets of the real line which are analytic but not Borel. Indeed, every Borel subset of a Polish space X is the result of the
![]() $\mathcal {A}$
-operation applied to some system
$\mathcal {A}$
-operation applied to some system
![]() $(X_s)$
of closed subsets of X – but not all sets derived from the
$(X_s)$
of closed subsets of X – but not all sets derived from the
![]() $\mathcal {A}$
-operation applied to a system of closed subsets is Borel; see [Reference Kechris44, Theorem 25.7].
$\mathcal {A}$
-operation applied to a system of closed subsets is Borel; see [Reference Kechris44, Theorem 25.7].
Here, we will be interested in the closed subset
![]() $\mathcal {N}^{*}$
of
$\mathcal {N}^{*}$
of
![]() $\mathcal {N}$
consisting of all non-decreasing such functions (i.e., all
$\mathcal {N}$
consisting of all non-decreasing such functions (i.e., all
![]() $\alpha =(\alpha (0),\alpha (1),\ldots )\in \mathcal {N}$
such that
$\alpha =(\alpha (0),\alpha (1),\ldots )\in \mathcal {N}$
such that
![]() $\alpha (n)\leq \alpha (n+1)$
for all
$\alpha (n)\leq \alpha (n+1)$
for all
![]() $n\in \mathbb {N}$
). It is easy to see that
$n\in \mathbb {N}$
). It is easy to see that
![]() $\mathcal {N}^{*}$
and
$\mathcal {N}^{*}$
and
![]() $\mathcal {N}$
are homeomorphic. Similarly, we denote by
$\mathcal {N}$
are homeomorphic. Similarly, we denote by
![]() $(\mathbb {N}^n)^{*}$
and
$(\mathbb {N}^n)^{*}$
and
![]() $(\mathbb {N}^{<\mathbb {N}})^{*}$
the sets of all non-decreasing functions in
$(\mathbb {N}^{<\mathbb {N}})^{*}$
the sets of all non-decreasing functions in
![]() $\mathbb {N}^n$
and
$\mathbb {N}^n$
and
![]() $\mathbb {N}^{<\mathbb {N}}$
, respectively. We set
$\mathbb {N}^{<\mathbb {N}}$
, respectively. We set
![]() $\mathcal {N}^{*}_s:=\mathcal {N}_s\cap \mathcal {N}^{*}$
for all
$\mathcal {N}^{*}_s:=\mathcal {N}_s\cap \mathcal {N}^{*}$
for all
![]() $s\in (\mathbb {N}^{<\mathbb {N}})^{*}$
. We endow
$s\in (\mathbb {N}^{<\mathbb {N}})^{*}$
. We endow
![]() $\mathcal {N}^{*}$
with the pointwise partial ordering
$\mathcal {N}^{*}$
with the pointwise partial ordering
![]() $\leq $
and the associated meet operation
$\leq $
and the associated meet operation
![]() $(\alpha ,\beta )\mapsto \alpha \wedge \beta $
and join operation
$(\alpha ,\beta )\mapsto \alpha \wedge \beta $
and join operation
![]() $(\alpha ,\beta )\mapsto \alpha \vee \beta $
, where
$(\alpha ,\beta )\mapsto \alpha \vee \beta $
, where
Occasionally, we will also employ the lexicographic linear ordering
![]() $\leq _{\mathrm {lex}}$
of
$\leq _{\mathrm {lex}}$
of
![]() $\mathcal {N}^{*}$
with
$\mathcal {N}^{*}$
with
Lastly, observe that to every family of sets
![]() $\big {(}X_s\colon s\in (\mathbb {N}^{<\mathbb {N}})^{*}\big {)}$
, parametrized by elements of
$\big {(}X_s\colon s\in (\mathbb {N}^{<\mathbb {N}})^{*}\big {)}$
, parametrized by elements of
![]() $(\mathbb {N}^{<\mathbb {N}})^{*}$
, we may still apply Suslin’s
$(\mathbb {N}^{<\mathbb {N}})^{*}$
, we may still apply Suslin’s
![]() $\mathcal {A}$
-operation by first setting
$\mathcal {A}$
-operation by first setting
![]() $X_s:=\emptyset $
for all
$X_s:=\emptyset $
for all
![]() $s\in \mathbb {N}^{<\mathbb {N}}\setminus (\mathbb {N}^{<\mathbb {N}})^{*}$
.
$s\in \mathbb {N}^{<\mathbb {N}}\setminus (\mathbb {N}^{<\mathbb {N}})^{*}$
.
2.3. Covering systems
Let X be a locally compact Polish space. A cofiltration or exhaustion of X is an increasing sequence
![]() $X_0\subseteq X_1\subseteq \cdots $
of compact subsets of X, with
$X_0\subseteq X_1\subseteq \cdots $
of compact subsets of X, with
![]() $X_0=\emptyset $
and
$X_0=\emptyset $
and
![]() $\bigcup _{n\in \mathbb {N}}X_n=X$
. An open cover of X is any family
$\bigcup _{n\in \mathbb {N}}X_n=X$
. An open cover of X is any family
![]() $\mathcal {U}$
of open sets so that
$\mathcal {U}$
of open sets so that
![]() $\bigcup \mathcal {U}=X$
. An open cover
$\bigcup \mathcal {U}=X$
. An open cover
![]() $\mathcal {U}$
is locally finite if for every
$\mathcal {U}$
is locally finite if for every
![]() $x\in X$
, there is an open neighborhood
$x\in X$
, there is an open neighborhood
![]() $O\subseteq X$
of x which intersects only finitely many elements of
$O\subseteq X$
of x which intersects only finitely many elements of
![]() $\mathcal {U}$
. If
$\mathcal {U}$
. If
![]() $K\subseteq X$
, then we let
$K\subseteq X$
, then we let
![]() $\mathcal {U}\upharpoonright K:=\{U\in \mathcal {U}\colon U\cap K \neq \emptyset \}$
. Notice that if
$\mathcal {U}\upharpoonright K:=\{U\in \mathcal {U}\colon U\cap K \neq \emptyset \}$
. Notice that if
![]() $\mathcal {U}$
is locally finite and K is compact, then
$\mathcal {U}$
is locally finite and K is compact, then
![]() $\mathcal {U}\upharpoonright K$
is finite. Let
$\mathcal {U}\upharpoonright K$
is finite. Let
![]() $\mathcal {U},\mathcal {V}$
be open covers of X. We write
$\mathcal {U},\mathcal {V}$
be open covers of X. We write
![]() $\mathcal {U}\preceq \mathcal {V}$
if
$\mathcal {U}\preceq \mathcal {V}$
if
![]() $\mathcal {V}$
refines
$\mathcal {V}$
refines
![]() $\mathcal {U}$
(i.e., if there exists a function
$\mathcal {U}$
(i.e., if there exists a function
![]() $r\colon \mathcal {V}\to \mathcal {U}$
so that
$r\colon \mathcal {V}\to \mathcal {U}$
so that
![]() $V\subseteq r(V)$
for all
$V\subseteq r(V)$
for all
![]() $V\in \mathcal {V}$
). We term such an r a refinement map.
$V\in \mathcal {V}$
). We term such an r a refinement map.
Definition 2.3. A covering system for X is a triple
![]() $\boldsymbol {\mathcal {U}}=\big {(}(X_n),(\mathcal {U}_{\alpha }),(r^{\beta }_{\alpha })\big {)}$
such that
$\boldsymbol {\mathcal {U}}=\big {(}(X_n),(\mathcal {U}_{\alpha }),(r^{\beta }_{\alpha })\big {)}$
such that
-
•
 $(X_n\colon n\in \mathbb {N})$
is an exhaustion of X,
$(X_n\colon n\in \mathbb {N})$
is an exhaustion of X, -
•
 $(\mathcal {U}_{\alpha }\colon \alpha \in \mathcal {N}^{*})$
is a family of locally finite open covers of X, and
$(\mathcal {U}_{\alpha }\colon \alpha \in \mathcal {N}^{*})$
is a family of locally finite open covers of X, and -
•
 $r^{\beta }_{\alpha }\colon \mathcal {U}_{\beta }\to \mathcal {U}_{\alpha }$
are refinement maps indexed by the pairs
$r^{\beta }_{\alpha }\colon \mathcal {U}_{\beta }\to \mathcal {U}_{\alpha }$
are refinement maps indexed by the pairs
 $\alpha \leq \beta $
in
$\alpha \leq \beta $
in
 $\mathcal {N}^{*}$
and satisfying
$\mathcal {N}^{*}$
and satisfying
 $r^{\alpha }_{\alpha }=\mathrm {id}$
and
$r^{\alpha }_{\alpha }=\mathrm {id}$
and
 $r^{\gamma }_{\alpha }= r^{\beta }_{\alpha } \circ r^{\gamma }_{\beta }$
for all
$r^{\gamma }_{\alpha }= r^{\beta }_{\alpha } \circ r^{\gamma }_{\beta }$
for all
 $\alpha \leq \beta \leq \gamma $
,
$\alpha \leq \beta \leq \gamma $
,
which moreover satisfy the following locality and extensionality axioms for all
![]() $n\in \mathbb {N}$
:
$n\in \mathbb {N}$
:
-
(L1) if
 $\alpha |n=\beta |n$
, then
$\alpha |n=\beta |n$
, then
 $\mathcal {U}_{\alpha }\upharpoonright X_n=\mathcal {U}_{\beta }\upharpoonright X_n$
;
$\mathcal {U}_{\alpha }\upharpoonright X_n=\mathcal {U}_{\beta }\upharpoonright X_n$
; -
(L2) if
 $\alpha \leq \beta $
and
$\alpha \leq \beta $
and
 $\gamma \leq \delta $
, with
$\gamma \leq \delta $
, with
 $\alpha |n=\gamma |n$
and
$\alpha |n=\gamma |n$
and
 $\beta |n=\delta |n$
, then
$\beta |n=\delta |n$
, then
 $r^{\beta }_{\alpha }\upharpoonright (\mathcal {U}_{\beta }\upharpoonright X_n)=r^{\delta }_{\gamma }\upharpoonright (\mathcal {U}_{\delta }\upharpoonright X_n)$
;
$r^{\beta }_{\alpha }\upharpoonright (\mathcal {U}_{\beta }\upharpoonright X_n)=r^{\delta }_{\gamma }\upharpoonright (\mathcal {U}_{\delta }\upharpoonright X_n)$
; -
(L3) if
 $\alpha \leq \beta $
, then
$\alpha \leq \beta $
, then
 $r^{\beta }_{\alpha }\upharpoonright (\mathcal {U}_{\beta }\upharpoonright X_n)$
is surjective on
$r^{\beta }_{\alpha }\upharpoonright (\mathcal {U}_{\beta }\upharpoonright X_n)$
is surjective on
 $\mathcal {U}_{\alpha }\upharpoonright X_n$
;
$\mathcal {U}_{\alpha }\upharpoonright X_n$
; -
(E1) for every open cover
 $\mathcal {U}$
of X and every
$\mathcal {U}$
of X and every
 $m\in \mathbb {N}$
with
$m\in \mathbb {N}$
with
 $n<m$
, if
$n<m$
, if
 $\mathcal {U}\upharpoonright X_n\preceq \mathcal {U}_{\alpha }\upharpoonright X_n$
, then there exists
$\mathcal {U}\upharpoonright X_n\preceq \mathcal {U}_{\alpha }\upharpoonright X_n$
, then there exists
 $\beta \in \mathcal {N}^{*}_{\alpha |n}$
so that
$\beta \in \mathcal {N}^{*}_{\alpha |n}$
so that
 $\mathcal {U}\upharpoonright X_m\preceq \mathcal {U}_{\beta }\upharpoonright X_m$
.
$\mathcal {U}\upharpoonright X_m\preceq \mathcal {U}_{\beta }\upharpoonright X_m$
.
Notice that if
![]() $\boldsymbol {\mathcal {U}}$
is a covering system for X, then for every open cover
$\boldsymbol {\mathcal {U}}$
is a covering system for X, then for every open cover
![]() $\mathcal {U}$
of X and every
$\mathcal {U}$
of X and every
![]() $m\in \mathbb {N}$
, there exists
$m\in \mathbb {N}$
, there exists
![]() $\beta \in \mathcal {N}^{*}$
so that
$\beta \in \mathcal {N}^{*}$
so that
This follows simply from (E1), since
![]() $\{X\}=\mathcal {U}\upharpoonright X_0\preceq \mathcal {U}_{\alpha }\upharpoonright X_0$
for all
$\{X\}=\mathcal {U}\upharpoonright X_0\preceq \mathcal {U}_{\alpha }\upharpoonright X_0$
for all
![]() $\alpha \in \mathcal {N}^{*}$
.
$\alpha \in \mathcal {N}^{*}$
.
While the definition of a covering system
![]() $\boldsymbol {\mathcal {U}}=\big {(}(X_n),(\mathcal {U}_{\alpha }),(r^{\beta }_{\alpha })\big {)}$
for X involves an uncountable family of open covers and an uncountable family of refinement maps,
$\boldsymbol {\mathcal {U}}=\big {(}(X_n),(\mathcal {U}_{\alpha }),(r^{\beta }_{\alpha })\big {)}$
for X involves an uncountable family of open covers and an uncountable family of refinement maps,
![]() $\boldsymbol {\mathcal {U}}$
can still be fully recovered from a certain countable family of ‘finitary approximations’, via a procedure which resembles Suslin’s operation
$\boldsymbol {\mathcal {U}}$
can still be fully recovered from a certain countable family of ‘finitary approximations’, via a procedure which resembles Suslin’s operation
![]() $\mathcal {A}$
. The next definition and the remark following it make this precise. Notice that by (L1) and (L2), the definition of
$\mathcal {A}$
. The next definition and the remark following it make this precise. Notice that by (L1) and (L2), the definition of
![]() $\mathcal {U}_s$
and
$\mathcal {U}_s$
and
![]() $r^{t}_{s}$
below does not depend on the choice of
$r^{t}_{s}$
below does not depend on the choice of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
.
$\beta $
.
Definition 2.4. Let
![]() $\boldsymbol {\mathcal {U}}=\big {(}(X_n),(\mathcal {U}_{\alpha }),(r^{\beta }_{\alpha })\big {)}$
be a covering system for X. For every
$\boldsymbol {\mathcal {U}}=\big {(}(X_n),(\mathcal {U}_{\alpha }),(r^{\beta }_{\alpha })\big {)}$
be a covering system for X. For every
![]() $n\in \mathbb {N}$
and every
$n\in \mathbb {N}$
and every
![]() $s,t\in (\mathcal {N}^n)^{*}$
, with
$s,t\in (\mathcal {N}^n)^{*}$
, with
![]() $s\leq t$
, we choose some
$s\leq t$
, we choose some
![]() $\alpha \in \mathcal {N}^{*}_s$
,
$\alpha \in \mathcal {N}^{*}_s$
,
![]() $\beta \in \mathcal {N}^{*}_t$
, and we define
$\beta \in \mathcal {N}^{*}_t$
, and we define
-
•
 $\mathcal {U}_s:= \mathcal {U}_{\alpha }\upharpoonright X_n$
;
$\mathcal {U}_s:= \mathcal {U}_{\alpha }\upharpoonright X_n$
; -
•
 $r^{t}_{s}:= r^{\beta }_{\alpha } \upharpoonright (\mathcal {U}_{\beta }\upharpoonright X_n)$
.
$r^{t}_{s}:= r^{\beta }_{\alpha } \upharpoonright (\mathcal {U}_{\beta }\upharpoonright X_n)$
.
We collect this data into a pair
![]() $\boldsymbol{\mathcal {U}}_{\mathrm {fin}}=\big {(} (\mathcal {U}_{s}),(r^{t}_{s})\big {)}$
, where
$\boldsymbol{\mathcal {U}}_{\mathrm {fin}}=\big {(} (\mathcal {U}_{s}),(r^{t}_{s})\big {)}$
, where
![]() $s,t$
range over
$s,t$
range over
![]() $(\mathbb {N}^{<\mathbb {N}})^{*}$
with
$(\mathbb {N}^{<\mathbb {N}})^{*}$
with
![]() $|s|=|t|$
and
$|s|=|t|$
and
![]() $s\leq t$
. We say that
$s\leq t$
. We say that
![]() $\boldsymbol {\mathcal {U}}_{\mathrm {fin}}$
is an approximation of
$\boldsymbol {\mathcal {U}}_{\mathrm {fin}}$
is an approximation of
![]() $\boldsymbol {\mathcal {U}}$
, and we write
$\boldsymbol {\mathcal {U}}$
, and we write
![]() $\boldsymbol {\mathcal {U}}=\mathcal {A}(\boldsymbol {\mathcal {U}}_{\mathrm {fin}})$
.
$\boldsymbol {\mathcal {U}}=\mathcal {A}(\boldsymbol {\mathcal {U}}_{\mathrm {fin}})$
.
Remark 2.5. Notice that we can fully recover the covering system
![]() $\boldsymbol {\mathcal {U}}$
from its approximation
$\boldsymbol {\mathcal {U}}$
from its approximation
![]() $\boldsymbol {\mathcal {U}}_{\mathrm {fin}}$
. Indeed, for each
$\boldsymbol {\mathcal {U}}_{\mathrm {fin}}$
. Indeed, for each
![]() $n\in \mathbb {N}$
and any sequence
$n\in \mathbb {N}$
and any sequence
![]() $(s_k)$
in
$(s_k)$
in
![]() $(\mathbb {N}^n)^{*}$
with
$(\mathbb {N}^n)^{*}$
with
![]() $s_0(i)<s_1(i)<\cdots $
for all
$s_0(i)<s_1(i)<\cdots $
for all
![]() $i<n$
, we have that
$i<n$
, we have that
 $$\begin{align*}X_n=\bigcap_{k\in\mathbb{N}} \bigcup_{U\in\, \mathcal{U}_{s_k}}\mathrm{cl}(U).\end{align*}$$
$$\begin{align*}X_n=\bigcap_{k\in\mathbb{N}} \bigcup_{U\in\, \mathcal{U}_{s_k}}\mathrm{cl}(U).\end{align*}$$
The above equality is easily established using (1) and (3) of Lemma 2.6 below. If for
![]() $s\in (\mathbb {N}^n)^{*}$
we momentarily denote by
$s\in (\mathbb {N}^n)^{*}$
we momentarily denote by
![]() $\widehat {\mathcal {U}}_{s}$
the set of all open covers
$\widehat {\mathcal {U}}_{s}$
the set of all open covers
![]() $\mathcal {U}$
of X with
$\mathcal {U}$
of X with
![]() $\mathcal {U}\upharpoonright X_{|s|}= \mathcal {U}_s$
, then
$\mathcal {U}\upharpoonright X_{|s|}= \mathcal {U}_s$
, then
and similarly for the collection
![]() $(r^{\beta }_\alpha )_{\alpha \leq \beta }$
. This motivates the notation
$(r^{\beta }_\alpha )_{\alpha \leq \beta }$
. This motivates the notation
![]() $\boldsymbol {\mathcal {U}}=\mathcal {A}(\boldsymbol {\mathcal {U}}_{\mathrm {fin}})$
in Definition 2.4 for indicating the relationship between a covering system
$\boldsymbol {\mathcal {U}}=\mathcal {A}(\boldsymbol {\mathcal {U}}_{\mathrm {fin}})$
in Definition 2.4 for indicating the relationship between a covering system
![]() $\boldsymbol {\mathcal {U}}$
and its approximation
$\boldsymbol {\mathcal {U}}$
and its approximation
![]() $\boldsymbol {\mathcal {U}}_{\mathrm {fin}}$
.
$\boldsymbol {\mathcal {U}}_{\mathrm {fin}}$
.
Lemma 2.6. Let
![]() $\boldsymbol {\mathcal {U}}=\big {(}(X_n),(\mathcal {U}_{\alpha }),(r^{\beta }_{\alpha })\big {)}$
be a covering system for X. Then
$\boldsymbol {\mathcal {U}}=\big {(}(X_n),(\mathcal {U}_{\alpha }),(r^{\beta }_{\alpha })\big {)}$
be a covering system for X. Then
-
(1) for every compact
 $K\subseteq X$
and every
$K\subseteq X$
and every
 $\alpha \in \mathcal {N}$
,
$\alpha \in \mathcal {N}$
,
 $\mathcal {U}_{\alpha }\upharpoonright K$
is a finite cover of K;
$\mathcal {U}_{\alpha }\upharpoonright K$
is a finite cover of K; -
(2)
 $\bigcup _{\alpha \in \mathcal {N}^{*}} \mathcal {U}_{\alpha }$
is countable;
$\bigcup _{\alpha \in \mathcal {N}^{*}} \mathcal {U}_{\alpha }$
is countable; -
(3) for every open cover
 $\mathcal {U}$
of X, there exists an
$\mathcal {U}$
of X, there exists an
 $\alpha \in \mathcal {N}$
so that
$\alpha \in \mathcal {N}$
so that
 $\mathcal {U}\preceq \mathcal {U}_{\alpha }$
.
$\mathcal {U}\preceq \mathcal {U}_{\alpha }$
. -
(4) there exists an
 $\alpha \in \mathcal {N}$
so that for every
$\alpha \in \mathcal {N}$
so that for every
 $\beta \geq \alpha $
, if
$\beta \geq \alpha $
, if
 $U\in \mathcal {U}_{\beta }$
, then
$U\in \mathcal {U}_{\beta }$
, then
 $\mathrm {cl}(U)$
is compact.
$\mathrm {cl}(U)$
is compact.
Proof. (1) follows from the local finiteness of
![]() $\mathcal {U}_{\alpha }$
, and (4) is a direct consequence of (3), since X is locally compact.
$\mathcal {U}_{\alpha }$
, and (4) is a direct consequence of (3), since X is locally compact.
For (2), we may assume that
![]() $\emptyset \not \in \bigcup _{\alpha \in \mathcal {N}} \mathcal {U}_{\alpha }$
. The rest follows from (1), since by (L1) we have
$\emptyset \not \in \bigcup _{\alpha \in \mathcal {N}} \mathcal {U}_{\alpha }$
. The rest follows from (1), since by (L1) we have
For (3), we will find
![]() $\alpha $
as the limit of a sequence
$\alpha $
as the limit of a sequence
![]() $(\alpha _n)$
in
$(\alpha _n)$
in
![]() $\mathcal {N}$
. We inductively define
$\mathcal {N}$
. We inductively define
![]() $\alpha _n$
as follows: let
$\alpha _n$
as follows: let
![]() $\alpha _0$
be any element of
$\alpha _0$
be any element of
![]() $\mathcal {N}$
; assuming that
$\mathcal {N}$
; assuming that
![]() $\alpha _{n-1}$
has been defined, use (E1) to get
$\alpha _{n-1}$
has been defined, use (E1) to get
![]() $\alpha _{n}\in \mathcal {N}$
with
$\alpha _{n}\in \mathcal {N}$
with
![]() $\alpha _{n}|(n-1)=\alpha _{n-1}|(n-1)$
, so that
$\alpha _{n}|(n-1)=\alpha _{n-1}|(n-1)$
, so that
![]() $\mathcal {U}\upharpoonright X_{n}\preceq \mathcal {U}_{\alpha |n}\upharpoonright X_n$
. Notice that
$\mathcal {U}\upharpoonright X_{n}\preceq \mathcal {U}_{\alpha |n}\upharpoonright X_n$
. Notice that
![]() $(\alpha _n)$
converges to the unique
$(\alpha _n)$
converges to the unique
![]() $\alpha \in \mathcal {N}$
with
$\alpha \in \mathcal {N}$
with
![]() $ \alpha |n=\alpha _n|n$
. By (L1), we have that
$ \alpha |n=\alpha _n|n$
. By (L1), we have that
![]() $\mathcal {U}\upharpoonright X_n\preceq \mathcal {U}_{\alpha }\upharpoonright X_n$
for all
$\mathcal {U}\upharpoonright X_n\preceq \mathcal {U}_{\alpha }\upharpoonright X_n$
for all
![]() $n\in \mathbb {N}$
. Since
$n\in \mathbb {N}$
. Since
![]() $\bigcup _n X_n=X$
, it follows that
$\bigcup _n X_n=X$
, it follows that
![]() $\mathcal {U}\preceq \mathcal {U}_{\alpha }$
.
$\mathcal {U}\preceq \mathcal {U}_{\alpha }$
.
Proposition 2.7. Every locally compact Polish space X admits a covering system
![]() $\boldsymbol {\mathcal {U}}$
.
$\boldsymbol {\mathcal {U}}$
.
Proof. Let d be a metric on X that is compatible with the topology, and let
![]() $(X_n)$
be any exhaustion of X with
$(X_n)$
be any exhaustion of X with
![]() $X_{n}\subseteq \mathrm {int}(X_{n+1})$
. We will attain the desired covering system
$X_{n}\subseteq \mathrm {int}(X_{n+1})$
. We will attain the desired covering system
![]() $\boldsymbol {\mathcal {U}}=\big {(}(X_n),(\mathcal {U}_{\alpha }),(r^{\beta }_{\alpha })\big {)}$
in the form of
$\boldsymbol {\mathcal {U}}=\big {(}(X_n),(\mathcal {U}_{\alpha }),(r^{\beta }_{\alpha })\big {)}$
in the form of
![]() $\mathcal {A}(\boldsymbol {\mathcal {U}}_{\mathrm {fin}})$
where
$\mathcal {A}(\boldsymbol {\mathcal {U}}_{\mathrm {fin}})$
where
![]() $\boldsymbol {\mathcal {U}}_{\mathrm {fin}}=((\mathcal {U}_s),(r^{t}_s))$
will be defined by a double induction.
$\boldsymbol {\mathcal {U}}_{\mathrm {fin}}=((\mathcal {U}_s),(r^{t}_s))$
will be defined by a double induction.
![]() $\underline {\mbox {Induction on the length of } s,t}$
.
$\underline {\mbox {Induction on the length of } s,t}$
.
Set
![]() $U_{\emptyset }=\emptyset $
, and assume that for some
$U_{\emptyset }=\emptyset $
, and assume that for some
![]() $n\in \mathbb {N}$
, we have defined for all
$n\in \mathbb {N}$
, we have defined for all
![]() $s,t,q\in (\mathbb {N}^n)^{*}$
with
$s,t,q\in (\mathbb {N}^n)^{*}$
with
![]() $s\leq t\leq q$
$s\leq t\leq q$
-
(1) a finite family
 $\mathcal {U}_s$
of open subsets of X covering
$\mathcal {U}_s$
of open subsets of X covering
 $X_n$
, so that
$X_n$
, so that
 $\mathcal {U}_s\upharpoonright X_m= \mathcal {U}_{s|m}$
if
$\mathcal {U}_s\upharpoonright X_m= \mathcal {U}_{s|m}$
if
 $m<n$
, and
$m<n$
, and  $$\begin{align*}\mathrm{diam}(U)<\frac{1}{\min\{s(i)\colon i<n\}+1}, \text{ for all } U\in\mathcal{U}_s.\end{align*}$$
$$\begin{align*}\mathrm{diam}(U)<\frac{1}{\min\{s(i)\colon i<n\}+1}, \text{ for all } U\in\mathcal{U}_s.\end{align*}$$
-
(2) a surjective refinement map
 $r^t_s \colon \mathcal {U}_t\to \mathcal {U}_s$
with
$r^t_s \colon \mathcal {U}_t\to \mathcal {U}_s$
with
 $r^{t}_t=\mathrm {id}$
and
$r^{t}_t=\mathrm {id}$
and
 $r^t_s\circ r^q_t=r^q_s$
.
$r^t_s\circ r^q_t=r^q_s$
.
We will extend this system to a system indexed by
![]() $(\mathbb {N}^{n+1})^{*}$
, which satisfies properties (1), (2) above with
$(\mathbb {N}^{n+1})^{*}$
, which satisfies properties (1), (2) above with
![]() $n+1$
in place of n. For that, set
$n+1$
in place of n. For that, set
![]() $\boldsymbol {\bar {\ell }}:=(\ell ,\ldots ,\ell )\in \mathbb {N}^n$
and
$\boldsymbol {\bar {\ell }}:=(\ell ,\ldots ,\ell )\in \mathbb {N}^n$
and
![]() $O_{\ell }:=\bigcup \mathcal {U}_{\boldsymbol {\bar {\ell }}}$
for every
$O_{\ell }:=\bigcup \mathcal {U}_{\boldsymbol {\bar {\ell }}}$
for every
![]() $\ell \in \mathbb {N}$
. Notice that by our inductive assumption, we have a decreasing sequence of open sets
$\ell \in \mathbb {N}$
. Notice that by our inductive assumption, we have a decreasing sequence of open sets
![]() $\underline {\mbox {Induction on } \ell \in \mathbb {N}}$
.
$\underline {\mbox {Induction on } \ell \in \mathbb {N}}$
.
By induction on
![]() $\ell \in \mathbb {N}$
, we choose a sequence
$\ell \in \mathbb {N}$
, we choose a sequence
![]() $\mathcal {V}_{0}, \mathcal {V}_{1},\ldots , \mathcal {V}_{\ell },\ldots $
of finite families of open subsets of X so that
$\mathcal {V}_{0}, \mathcal {V}_{1},\ldots , \mathcal {V}_{\ell },\ldots $
of finite families of open subsets of X so that
![]() $\mathcal {V}_{\ell }$
covers
$\mathcal {V}_{\ell }$
covers
![]() $X_{n+1}\setminus O_{\ell }$
with sets of diameter less than
$X_{n+1}\setminus O_{\ell }$
with sets of diameter less than
![]() $1/(\ell +1)$
, which do not intersect
$1/(\ell +1)$
, which do not intersect
![]() $X_n$
. We can also make sure that
$X_n$
. We can also make sure that
![]() $ \mathcal {V}_{\ell }\cup \mathcal {U_{\boldsymbol {\bar {\ell }}}}\preceq \mathcal {V}_{\ell +1}$
. We may now set
$ \mathcal {V}_{\ell }\cup \mathcal {U_{\boldsymbol {\bar {\ell }}}}\preceq \mathcal {V}_{\ell +1}$
. We may now set
for every
![]() $s^{\frown }\ell \in (\mathbb {N}^{n+1})^{*}$
and observe that the analogue of point (1) above is satisfied by the new system. For example, notice that if
$s^{\frown }\ell \in (\mathbb {N}^{n+1})^{*}$
and observe that the analogue of point (1) above is satisfied by the new system. For example, notice that if
![]() $s^{\frown }\ell \in (\mathbb {N}^{n+1})^{*}$
, then
$s^{\frown }\ell \in (\mathbb {N}^{n+1})^{*}$
, then
![]() $s\leq \boldsymbol {\bar {\ell }}$
, and hence,
$s\leq \boldsymbol {\bar {\ell }}$
, and hence,
![]() $\mathcal {U}_s\preceq \mathcal {U}_{\boldsymbol {\bar {\ell }}}$
. As a consequence,
$\mathcal {U}_s\preceq \mathcal {U}_{\boldsymbol {\bar {\ell }}}$
. As a consequence,
![]() $O_{\ell }\subseteq \bigcup \mathcal {U}_s$
, and therefore,
$O_{\ell }\subseteq \bigcup \mathcal {U}_s$
, and therefore,
![]() $\mathcal {U}_{s^{\frown }\ell }$
covers
$\mathcal {U}_{s^{\frown }\ell }$
covers
![]() $X_{n+1}$
.
$X_{n+1}$
.
We now turn to the definition of the refining maps. Fix
![]() $\ell \in \mathbb {N}$
, and assume inductively that for every pair
$\ell \in \mathbb {N}$
, and assume inductively that for every pair
![]() $s^{\frown }k, t^{\frown } m\in (\mathbb {N}^{n+1})^{*}$
with
$s^{\frown }k, t^{\frown } m\in (\mathbb {N}^{n+1})^{*}$
with
![]() $s^{\frown }k\leq t^{\frown } m$
and
$s^{\frown }k\leq t^{\frown } m$
and
![]() $m\leq \ell $
, we have defined a surjective refinement map
$m\leq \ell $
, we have defined a surjective refinement map
which extends
![]() $r^{ t}_{s}$
, and assume that these maps altogether cohere with respect to composition as in point (2) above. Fix now any refinement map
$r^{ t}_{s}$
, and assume that these maps altogether cohere with respect to composition as in point (2) above. Fix now any refinement map
Notice that in the definition of
![]() $\mathcal {V}_{\ell }$
, we could have arranged, by removing superfluous elements, that
$\mathcal {V}_{\ell }$
, we could have arranged, by removing superfluous elements, that
![]() $\mathcal {V}_{\ell }$
is ‘minimal’ (i.e., if we remove any V from
$\mathcal {V}_{\ell }$
is ‘minimal’ (i.e., if we remove any V from
![]() $\mathcal {V}_{\ell }$
, then the resulting family is not going to be a cover of
$\mathcal {V}_{\ell }$
, then the resulting family is not going to be a cover of
![]() $X_{n+1}\setminus O_{\ell }$
). By imposing this minimality assumption on
$X_{n+1}\setminus O_{\ell }$
). By imposing this minimality assumption on
![]() $\mathcal {V}_{\ell }$
, we have that
$\mathcal {V}_{\ell }$
, we have that
![]() $p^{\ell +1}_{\boldsymbol {\bar {\ell }}^{\frown }\ell }$
is surjective on
$p^{\ell +1}_{\boldsymbol {\bar {\ell }}^{\frown }\ell }$
is surjective on
![]() $\mathcal {V}_{\ell }$
. For every
$\mathcal {V}_{\ell }$
. For every
![]() $s^\frown k \in (\mathbb {N}^{n+1})^{*}$
with
$s^\frown k \in (\mathbb {N}^{n+1})^{*}$
with
![]() $k\leq \ell +1$
, we define a refinement map
$k\leq \ell +1$
, we define a refinement map
by setting
![]() $p^{\ell +1}_{s^{\frown } k }=\mathrm {id}$
, if
$p^{\ell +1}_{s^{\frown } k }=\mathrm {id}$
, if
![]() $k=\ell +1$
; if
$k=\ell +1$
; if
![]() $k<\ell +1$
, then notice that
$k<\ell +1$
, then notice that
![]() $s^{\frown } k\leq \boldsymbol {\bar {\ell }}^{\frown }\ell $
, and we may define
$s^{\frown } k\leq \boldsymbol {\bar {\ell }}^{\frown }\ell $
, and we may define
where the map
![]() $r^{\boldsymbol {\bar {\ell }}^{\frown }\ell }_{s^{\frown } k}$
is given by inductive assumption. Finally, for all
$r^{\boldsymbol {\bar {\ell }}^{\frown }\ell }_{s^{\frown } k}$
is given by inductive assumption. Finally, for all
![]() $s^{\frown } k \leq t^{\frown } (\ell +1)$
, we set
$s^{\frown } k \leq t^{\frown } (\ell +1)$
, we set
The fact that our new system of maps which is indexed by pairs
![]() $s^{\frown }k, t^{\frown } m\in (\mathbb {N}^{n+1})^{*}$
with
$s^{\frown }k, t^{\frown } m\in (\mathbb {N}^{n+1})^{*}$
with
![]() $s^{\frown }k\leq t^{\frown } m$
and
$s^{\frown }k\leq t^{\frown } m$
and
![]() $m\leq \ell +1$
coheres in the sense of point (2) above, follows from our inductive assumptions and the fact that all new maps which are not equal to
$m\leq \ell +1$
coheres in the sense of point (2) above, follows from our inductive assumptions and the fact that all new maps which are not equal to
![]() $\mathrm {id}$
on
$\mathrm {id}$
on
![]() $\mathcal {V}_{\ell +1}$
factor through
$\mathcal {V}_{\ell +1}$
factor through
![]() $\mathcal {U}_{\boldsymbol {\bar {\ell }}^{\frown }\ell }$
.
$\mathcal {U}_{\boldsymbol {\bar {\ell }}^{\frown }\ell }$
.
This ends the induction on
![]() $\ell $
and consequently the induction on the length of
$\ell $
and consequently the induction on the length of
![]() $s,t$
. Let now
$s,t$
. Let now
where
![]() $\boldsymbol {\mathcal {U}}_{\mathrm {fin}}=((\mathcal {U}_s),(r^{t}_s))$
. Using points (1) and (2) above, it is easy to see that
$\boldsymbol {\mathcal {U}}_{\mathrm {fin}}=((\mathcal {U}_s),(r^{t}_s))$
. Using points (1) and (2) above, it is easy to see that
![]() $\boldsymbol {\mathcal {U}}$
is a covering system for X. For example, (E1) follows from the shrinking diameters in point (1) above and Lebesgue’s covering lemma; the fact that each
$\boldsymbol {\mathcal {U}}$
is a covering system for X. For example, (E1) follows from the shrinking diameters in point (1) above and Lebesgue’s covering lemma; the fact that each
![]() $\mathcal {U}_{\alpha }$
is locally finite follows from the assumption
$\mathcal {U}_{\alpha }$
is locally finite follows from the assumption
![]() $X_n\subseteq \mathrm {int}(X_{n+1})$
and the fact that each
$X_n\subseteq \mathrm {int}(X_{n+1})$
and the fact that each
![]() $\mathcal {U}_s$
is finite.
$\mathcal {U}_s$
is finite.
2.4. Definable cohomology with discrete coefficients
Let G be a countable discrete abelian group, and let X be a locally compact Polish space. We will fix a covering system
![]() $\boldsymbol {\mathcal {U}}=\big {(}(X_n),(\mathcal {U}_{\alpha }),(r^{\beta }_{\alpha })\big {)}$
for X and use it to define a Polish cochain complex
$\boldsymbol {\mathcal {U}}=\big {(}(X_n),(\mathcal {U}_{\alpha }),(r^{\beta }_{\alpha })\big {)}$
for X and use it to define a Polish cochain complex
![]() $C^{\bullet }(\boldsymbol {\mathcal {U}};G)$
. The associated cohomology groups
$C^{\bullet }(\boldsymbol {\mathcal {U}};G)$
. The associated cohomology groups ![]() , viewed as groups with Polish cover, form the definable cohomology of X with coefficients in G. If we forget the definable content from
, viewed as groups with Polish cover, form the definable cohomology of X with coefficients in G. If we forget the definable content from ![]() , we recover the classical Čech cohomology groups for X. In Section 5, we will show that, up to definable isomorphism,
, we recover the classical Čech cohomology groups for X. In Section 5, we will show that, up to definable isomorphism, ![]() does not depend on the choice of
does not depend on the choice of
![]() $\boldsymbol {\mathcal {U}}$
. One may extend these ideas to develop definable cohomology groups with coefficients in an arbitrary Polish abelian group G. That project, however, falls beyond the scope of this paper; see Remark 2.13.
$\boldsymbol {\mathcal {U}}$
. One may extend these ideas to develop definable cohomology groups with coefficients in an arbitrary Polish abelian group G. That project, however, falls beyond the scope of this paper; see Remark 2.13.
For every open cover
![]() $\mathcal {U}$
of X, the nerve of
$\mathcal {U}$
of X, the nerve of
![]() $\mathcal {U}$
is the simplicial complex
$\mathcal {U}$
is the simplicial complex
![]() $\mathrm {Nv}(\mathcal {U})$
with
$\mathrm {Nv}(\mathcal {U})$
with
![]() $\sigma \in \mathrm {Nv}(\mathcal {U})$
if and only if
$\sigma \in \mathrm {Nv}(\mathcal {U})$
if and only if
![]() $\sigma $
is a finite subset of
$\sigma $
is a finite subset of
![]() $\mathcal {U}$
with
$\mathcal {U}$
with
![]() $\cap _{U\in \sigma }U\neq \emptyset .$
Notice that
$\cap _{U\in \sigma }U\neq \emptyset .$
Notice that
![]() $\mathrm {dom}(\mathrm {Nv}(\mathcal {U}))=\mathcal {U}\setminus \{\emptyset \}$
. Set
$\mathrm {dom}(\mathrm {Nv}(\mathcal {U}))=\mathcal {U}\setminus \{\emptyset \}$
. Set
for every
![]() $\alpha \in \mathcal {N}^{*}$
, and notice that every refinement map
$\alpha \in \mathcal {N}^{*}$
, and notice that every refinement map
![]() $r^{\beta }_{\alpha }$
induces a simplicial map
$r^{\beta }_{\alpha }$
induces a simplicial map
In this way,
![]() $\boldsymbol {\mathcal {U}}$
determines an inverse system
$\boldsymbol {\mathcal {U}}$
determines an inverse system
![]() $((N_{\alpha }),(r^{\beta }_{\alpha }))$
of simplicial maps. We similarly define the finite complexes
$((N_{\alpha }),(r^{\beta }_{\alpha }))$
of simplicial maps. We similarly define the finite complexes
![]() $N_s:= \mathrm {Nv}(\mathcal {U}_{s})$
and consider the simplicial maps
$N_s:= \mathrm {Nv}(\mathcal {U}_{s})$
and consider the simplicial maps
![]() $r^{t}_s\colon N_{t}\to N_s$
, for every
$r^{t}_s\colon N_{t}\to N_s$
, for every
![]() $s\leq t$
in
$s\leq t$
in
![]() $(\mathbb {N}^{<\mathbb {N}})^{*}$
.
$(\mathbb {N}^{<\mathbb {N}})^{*}$
.
For every
![]() $n\in \mathbb {N}$
, we will define the Polish group
$n\in \mathbb {N}$
, we will define the Polish group
![]() $C^{n}(\boldsymbol {\mathcal {U}};G)$
of n-dimensional cocycles of
$C^{n}(\boldsymbol {\mathcal {U}};G)$
of n-dimensional cocycles of
![]() $\boldsymbol {\mathcal {U}}$
as the quotient of a Polish semigroup
$\boldsymbol {\mathcal {U}}$
as the quotient of a Polish semigroup
![]() $C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
by a certain closed semigroup congruence. Let
$C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
by a certain closed semigroup congruence. Let
be the collection of all functions from the set of singular n-faces of some
![]() $N_{\alpha }$
to G. We endow
$N_{\alpha }$
to G. We endow
![]() $C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
with a semigroup structure by setting for all
$C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
with a semigroup structure by setting for all
![]() $\zeta \colon N^{(n)}_{\alpha }\to G$
and
$\zeta \colon N^{(n)}_{\alpha }\to G$
and
![]() $\eta \colon N^{(n)}_{\beta }\to G$
$\eta \colon N^{(n)}_{\beta }\to G$
We also endow
![]() $C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
with the topology generated by basic open sets of the form
$C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
with the topology generated by basic open sets of the form
![]() $V_{s,p}$
, with
$V_{s,p}$
, with
![]() $s\in \mathbb {N}^{<\mathbb {N}}$
and
$s\in \mathbb {N}^{<\mathbb {N}}$
and
![]() $p\colon N^{(n)}_s\to G$
, which is given by all
$p\colon N^{(n)}_s\to G$
, which is given by all
![]() $\zeta \colon N^{(n)}_{\alpha }\to G$
with
$\zeta \colon N^{(n)}_{\alpha }\to G$
with
![]() $\alpha \in \mathcal {N}_s$
and
$\alpha \in \mathcal {N}_s$
and
![]() $\zeta \upharpoonright N^{(n)}_s= p$
.
$\zeta \upharpoonright N^{(n)}_s= p$
.
Proposition 2.8.
![]() $C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
is an abelian Polish semigroup.
$C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
is an abelian Polish semigroup.
Proof. Since
![]() $\alpha \vee \beta =\beta \vee \alpha $
and G is abelian, so is
$\alpha \vee \beta =\beta \vee \alpha $
and G is abelian, so is
![]() $C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
. It is also a topological semigroup since by (L2), the operation
$C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
. It is also a topological semigroup since by (L2), the operation
![]() $(\zeta ,\eta )\mapsto (\zeta +\eta )$
is continuous. The topology is clearly second countable since it has, by definition, a basis consisting of countably many open sets. Finally, it is easy to check that
$(\zeta ,\eta )\mapsto (\zeta +\eta )$
is continuous. The topology is clearly second countable since it has, by definition, a basis consisting of countably many open sets. Finally, it is easy to check that
![]() $\rho _{\mathrm {sem}}$
below is a complete metric on
$\rho _{\mathrm {sem}}$
below is a complete metric on
![]() $C_{\mathrm {sem}}^{(n)}(\boldsymbol {\mathcal {U}};G)$
that is compatible with the topology: for every
$C_{\mathrm {sem}}^{(n)}(\boldsymbol {\mathcal {U}};G)$
that is compatible with the topology: for every
![]() $\zeta \in C^{n}(N_{\alpha };G)$
and
$\zeta \in C^{n}(N_{\alpha };G)$
and
![]() $\eta \in C^{n}(N_{\beta };G)$
, set
$\eta \in C^{n}(N_{\beta };G)$
, set
![]() $\delta _k:=0$
if
$\delta _k:=0$
if
![]() $\zeta \upharpoonright N^{(n)}_{\alpha |k}=\eta \upharpoonright N^{(n)}_{\beta |k}$
, and set
$\zeta \upharpoonright N^{(n)}_{\alpha |k}=\eta \upharpoonright N^{(n)}_{\beta |k}$
, and set
![]() $\delta _k:=1$
otherwise. Let
$\delta _k:=1$
otherwise. Let
 $$ \begin{align} \rho_{\mathrm{sem}}(\zeta,\eta):= \sum_{k\in\mathbb{N}}\frac{\delta_k}{2^{k}}.\\[-34pt]\notag \end{align} $$
$$ \begin{align} \rho_{\mathrm{sem}}(\zeta,\eta):= \sum_{k\in\mathbb{N}}\frac{\delta_k}{2^{k}}.\\[-34pt]\notag \end{align} $$
We define a congruence
![]() $\sim $
on
$\sim $
on
![]() $C_{\mathrm {sem}}^{(n)}(\boldsymbol {\mathcal {U}};G)$
by setting for all
$C_{\mathrm {sem}}^{(n)}(\boldsymbol {\mathcal {U}};G)$
by setting for all
![]() $\zeta \colon N^{(n)}_{\alpha }\to G$
and
$\zeta \colon N^{(n)}_{\alpha }\to G$
and
![]() $\eta \colon N^{(n)}_{\beta }\to G$
$\eta \colon N^{(n)}_{\beta }\to G$
Lemma 2.9. The relation
![]() $\sim $
is a closed semigroup congruence on
$\sim $
is a closed semigroup congruence on
![]() $C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
$C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
Proof. First, we prove that
![]() $\sim $
is an equivalence relation on
$\sim $
is an equivalence relation on
![]() $C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
. Symmetry follows from
$C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
. Symmetry follows from
![]() $\alpha \vee \beta =\beta \vee \alpha $
and reflexivity from
$\alpha \vee \beta =\beta \vee \alpha $
and reflexivity from
![]() $\alpha \vee \alpha =\alpha $
. For transitivity, let
$\alpha \vee \alpha =\alpha $
. For transitivity, let
![]() $\zeta \colon N^{(n)}_{\alpha }\to G$
,
$\zeta \colon N^{(n)}_{\alpha }\to G$
,
![]() $\eta \colon N^{(n)}_{\beta }\to G$
, and
$\eta \colon N^{(n)}_{\beta }\to G$
, and
![]() $\theta \colon N^{(n)}_{\gamma }\to G$
, with
$\theta \colon N^{(n)}_{\gamma }\to G$
, with
![]() $\zeta \sim \eta $
and
$\zeta \sim \eta $
and
![]() $\eta \sim \gamma $
. In particular, we have that
$\eta \sim \gamma $
. In particular, we have that
But since
![]() $\eta \circ r^{\alpha \vee \beta }_{\beta }\circ r^{\alpha \vee \beta \vee \gamma }_{\alpha \vee \beta }=\eta \circ r^{\alpha \vee \beta \vee \gamma }_{\beta }=\eta \circ r^{\beta \vee \gamma }_{\beta }\circ r^{\alpha \vee \beta \vee \gamma }_{\beta \vee \gamma }$
, we have that
$\eta \circ r^{\alpha \vee \beta }_{\beta }\circ r^{\alpha \vee \beta \vee \gamma }_{\alpha \vee \beta }=\eta \circ r^{\alpha \vee \beta \vee \gamma }_{\beta }=\eta \circ r^{\beta \vee \gamma }_{\beta }\circ r^{\alpha \vee \beta \vee \gamma }_{\beta \vee \gamma }$
, we have that
![]() $\zeta \circ r_{\alpha }^{\alpha \vee \beta \vee \gamma }=\theta \circ r_{\gamma }^{\alpha \vee \beta \vee \gamma }$
, and therefore that
$\zeta \circ r_{\alpha }^{\alpha \vee \beta \vee \gamma }=\theta \circ r_{\gamma }^{\alpha \vee \beta \vee \gamma }$
, and therefore that
![]() $\zeta \circ r_{\alpha }^{\alpha \vee \gamma }\circ r_{\alpha \vee \gamma }^{\alpha \vee \beta \vee \gamma }=\theta \circ r_{\gamma }^{\alpha \vee \gamma }\circ r_{\alpha \vee \gamma }^{\alpha \vee \beta \vee \gamma }$
. Since
$\zeta \circ r_{\alpha }^{\alpha \vee \gamma }\circ r_{\alpha \vee \gamma }^{\alpha \vee \beta \vee \gamma }=\theta \circ r_{\gamma }^{\alpha \vee \gamma }\circ r_{\alpha \vee \gamma }^{\alpha \vee \beta \vee \gamma }$
. Since
![]() $r_{\alpha \vee \gamma }^{\alpha \vee \beta \vee \gamma }$
is surjective, we have that
$r_{\alpha \vee \gamma }^{\alpha \vee \beta \vee \gamma }$
is surjective, we have that
![]() $\zeta \circ r_{\alpha }^{\alpha \vee \gamma }=\theta \circ r_{\gamma }^{\alpha \vee \gamma }$
; hence,
$\zeta \circ r_{\alpha }^{\alpha \vee \gamma }=\theta \circ r_{\gamma }^{\alpha \vee \gamma }$
; hence,
![]() $\zeta \sim \theta $
.
$\zeta \sim \theta $
.
The relation
![]() $\sim $
is closed as a subset of
$\sim $
is closed as a subset of
![]() $C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)\times C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
: indeed, if
$C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)\times C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
: indeed, if
![]() $\zeta \circ r^{\alpha \vee \beta }_{\alpha }=\eta \circ r^{\alpha \vee \beta }_{\beta }$
fails, then there is an
$\zeta \circ r^{\alpha \vee \beta }_{\alpha }=\eta \circ r^{\alpha \vee \beta }_{\beta }$
fails, then there is an
![]() $s=(\alpha \vee \beta )|k$
, for some
$s=(\alpha \vee \beta )|k$
, for some
![]() $k\in \mathbb {N}$
, so that the values of some
$k\in \mathbb {N}$
, so that the values of some
![]() $\overline {U}\in N^{(n)}_{s}$
under
$\overline {U}\in N^{(n)}_{s}$
under
![]() $\zeta \circ r^{\alpha \vee \beta }_{\alpha }$
and
$\zeta \circ r^{\alpha \vee \beta }_{\alpha }$
and
![]() $\eta \circ r^{\alpha \vee \beta }_{\beta }$
differ. This failure is witnessed by some open condition.
$\eta \circ r^{\alpha \vee \beta }_{\beta }$
differ. This failure is witnessed by some open condition.
Finally, to see that
![]() $\sim $
is a semigroup congruence, let
$\sim $
is a semigroup congruence, let
![]() $\zeta \colon N^{(n)}_{\alpha }\to G$
and
$\zeta \colon N^{(n)}_{\alpha }\to G$
and
![]() $\eta \colon N^{(n)}_{\beta }\to G$
and
$\eta \colon N^{(n)}_{\beta }\to G$
and
![]() $\zeta '\colon N^{(n)}_{\alpha '}\to G$
and
$\zeta '\colon N^{(n)}_{\alpha '}\to G$
and
![]() $\eta '\colon N_{\beta '}\to G$
, with
$\eta '\colon N_{\beta '}\to G$
, with
![]() $\zeta \sim \eta $
and
$\zeta \sim \eta $
and
![]() $\zeta '\sim \eta '$
. We will show that
$\zeta '\sim \eta '$
. We will show that
![]() $\zeta +\zeta '\sim \eta +\eta '$
. Indeed, since
$\zeta +\zeta '\sim \eta +\eta '$
. Indeed, since
![]() $\zeta \circ r^{\alpha \vee \beta }_{\alpha }=\eta \circ r^{\alpha \vee \beta }_{\beta }$
and
$\zeta \circ r^{\alpha \vee \beta }_{\alpha }=\eta \circ r^{\alpha \vee \beta }_{\beta }$
and
![]() $\zeta '\circ r^{\alpha '\vee \beta '}_{\alpha '}=\eta '\circ r^{\alpha '\vee \beta '}_{\beta '}$
, we have
$\zeta '\circ r^{\alpha '\vee \beta '}_{\alpha '}=\eta '\circ r^{\alpha '\vee \beta '}_{\beta '}$
, we have
 $$ \begin{align*} \zeta\circ r^{\alpha\vee \beta}_{\alpha} \circ r_{\alpha\vee \beta}^{\alpha\vee \alpha'\vee\beta\vee\beta'} + \zeta'\circ r^{\alpha'\vee \beta'}_{\alpha'}\circ r_{\alpha'\vee \beta'}^{\alpha\vee \alpha'\vee\beta\vee\beta'} &=\eta\circ r^{\alpha\vee \beta}_{\beta} \circ r_{\alpha\vee \beta}^{\alpha\vee \alpha'\vee\beta\vee\beta'} +\eta'\circ r^{\alpha'\vee \beta'}_{\beta'}\circ r_{\alpha'\vee \beta'}^{\alpha\vee \alpha'\vee\beta\vee\beta'}\\ \zeta\circ r_{\alpha}^{\alpha\vee \alpha'\vee\beta\vee\beta'} + \zeta'\circ r_{\alpha'}^{\alpha\vee \alpha'\vee\beta\vee\beta'} &=\eta\circ r_{\beta}^{\alpha\vee \alpha'\vee\beta\vee\beta'} +\eta'\circ r_{\beta'}^{\alpha\vee \alpha'\vee\beta\vee\beta'} \\ (\zeta+\zeta')\circ r_{\alpha\vee\alpha'}^{\alpha\vee \alpha'\vee\beta\vee\beta'} &= (\eta+ \eta' )\circ r_{\beta\vee\beta'}^{\alpha\vee \alpha'\vee\beta\vee\beta'} \\ (\zeta+\zeta') &\sim (\eta+\eta').\\[-36pt] \end{align*} $$
$$ \begin{align*} \zeta\circ r^{\alpha\vee \beta}_{\alpha} \circ r_{\alpha\vee \beta}^{\alpha\vee \alpha'\vee\beta\vee\beta'} + \zeta'\circ r^{\alpha'\vee \beta'}_{\alpha'}\circ r_{\alpha'\vee \beta'}^{\alpha\vee \alpha'\vee\beta\vee\beta'} &=\eta\circ r^{\alpha\vee \beta}_{\beta} \circ r_{\alpha\vee \beta}^{\alpha\vee \alpha'\vee\beta\vee\beta'} +\eta'\circ r^{\alpha'\vee \beta'}_{\beta'}\circ r_{\alpha'\vee \beta'}^{\alpha\vee \alpha'\vee\beta\vee\beta'}\\ \zeta\circ r_{\alpha}^{\alpha\vee \alpha'\vee\beta\vee\beta'} + \zeta'\circ r_{\alpha'}^{\alpha\vee \alpha'\vee\beta\vee\beta'} &=\eta\circ r_{\beta}^{\alpha\vee \alpha'\vee\beta\vee\beta'} +\eta'\circ r_{\beta'}^{\alpha\vee \alpha'\vee\beta\vee\beta'} \\ (\zeta+\zeta')\circ r_{\alpha\vee\alpha'}^{\alpha\vee \alpha'\vee\beta\vee\beta'} &= (\eta+ \eta' )\circ r_{\beta\vee\beta'}^{\alpha\vee \alpha'\vee\beta\vee\beta'} \\ (\zeta+\zeta') &\sim (\eta+\eta').\\[-36pt] \end{align*} $$
We now define
![]() $C^{n}(\boldsymbol {\mathcal {U}};G):=C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)/\sim $
to be the collection of all congruence classes
$C^{n}(\boldsymbol {\mathcal {U}};G):=C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)/\sim $
to be the collection of all congruence classes
![]() $[\zeta ]$
of elements
$[\zeta ]$
of elements
![]() $\zeta $
of
$\zeta $
of
![]() $C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
. A priori,
$C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
. A priori,
![]() $C^{n}(\boldsymbol {\mathcal {U}};G)$
is merely an abelian semigroup which is additionally endowed with the quotient topology:
$C^{n}(\boldsymbol {\mathcal {U}};G)$
is merely an abelian semigroup which is additionally endowed with the quotient topology:
![]() $V\subseteq C^{n}(\boldsymbol {\mathcal {U}};G)$
is open in
$V\subseteq C^{n}(\boldsymbol {\mathcal {U}};G)$
is open in
![]() $C^{n}(\boldsymbol {\mathcal {U}};G)$
if and only if its union
$C^{n}(\boldsymbol {\mathcal {U}};G)$
if and only if its union
![]() $\bigcup V=\{\zeta \colon [\zeta ]\in V\}$
is open in
$\bigcup V=\{\zeta \colon [\zeta ]\in V\}$
is open in
![]() $C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
. It turns out that
$C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
. It turns out that
![]() $C^{n}(\boldsymbol {\mathcal {U}};G)$
is a much richer structure.
$C^{n}(\boldsymbol {\mathcal {U}};G)$
is a much richer structure.
Proposition 2.10.
![]() $C^{n}(\boldsymbol {\mathcal {U}};G)$
is a non-archimedean abelian Polish group.
$C^{n}(\boldsymbol {\mathcal {U}};G)$
is a non-archimedean abelian Polish group.
Proof. First, notice that any two maps
![]() $0_{\alpha }\colon N^{(n)}_{\alpha }\to G$
and
$0_{\alpha }\colon N^{(n)}_{\alpha }\to G$
and
![]() $0_{\beta }\colon N^{(n)}_{\beta }\to G$
which are constantly equal to
$0_{\beta }\colon N^{(n)}_{\beta }\to G$
which are constantly equal to
![]() $0_{G}$
are congruent to each other. Moreover, it is clear that the associated congruence class
$0_{G}$
are congruent to each other. Moreover, it is clear that the associated congruence class
![]() $0_{\boldsymbol {\mathcal {U}}}:=[0_{\alpha }]=[0_{\beta }]$
is the identity element of
$0_{\boldsymbol {\mathcal {U}}}:=[0_{\alpha }]=[0_{\beta }]$
is the identity element of
![]() $C^{n}(\boldsymbol {\mathcal {U}};G)$
and that for every
$C^{n}(\boldsymbol {\mathcal {U}};G)$
and that for every
![]() $\zeta \colon N^{(n)}_{\alpha }\to G$
, we have that
$\zeta \colon N^{(n)}_{\alpha }\to G$
, we have that
![]() $[\zeta ]+[-\zeta ]=[0_{\alpha }]$
. It follows that
$[\zeta ]+[-\zeta ]=[0_{\alpha }]$
. It follows that
![]() $C^{n}(\boldsymbol {\mathcal {U}};G)$
is an abelian group. Moreover, notice that if
$C^{n}(\boldsymbol {\mathcal {U}};G)$
is an abelian group. Moreover, notice that if
![]() $\zeta '\sim \zeta $
for some
$\zeta '\sim \zeta $
for some
![]() $\zeta \colon N^{(n)}_{\alpha }\to G$
and
$\zeta \colon N^{(n)}_{\alpha }\to G$
and
![]() $\zeta '\colon N^{(n)}_{\beta }\to G$
with
$\zeta '\colon N^{(n)}_{\beta }\to G$
with
![]() $\zeta \upharpoonright N^{(n)}_{\alpha |k}=0_{\alpha }\upharpoonright N^{(n)}_{\alpha |k}$
, then
$\zeta \upharpoonright N^{(n)}_{\alpha |k}=0_{\alpha }\upharpoonright N^{(n)}_{\alpha |k}$
, then
![]() $\eta \upharpoonright N^{(n)}_{\beta |k}=0_{\beta }\upharpoonright N^{(n)}_{\beta |k}$
. Hence, the identity
$\eta \upharpoonright N^{(n)}_{\beta |k}=0_{\beta }\upharpoonright N^{(n)}_{\beta |k}$
. Hence, the identity
![]() $0_{\boldsymbol {\mathcal {U}}}$
admits a neighborhood basis in
$0_{\boldsymbol {\mathcal {U}}}$
admits a neighborhood basis in
![]() $C^{n}(\boldsymbol {\mathcal {U}};G)$
consisting of the following open subgroups:
$C^{n}(\boldsymbol {\mathcal {U}};G)$
consisting of the following open subgroups:
The topology of a quotient of a separable space is separable. We now define a complete metric on
![]() $C^{n}(\boldsymbol {\mathcal {U}};G)$
that is compatible with its topology. Let
$C^{n}(\boldsymbol {\mathcal {U}};G)$
that is compatible with its topology. Let
![]() $\rho _{\mathrm {sem}}$
be the complete metric on
$\rho _{\mathrm {sem}}$
be the complete metric on
![]() $C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
given by (5) above. For every
$C_{\mathrm {sem}}^{n}(\boldsymbol {\mathcal {U}};G)$
given by (5) above. For every
![]() $[\zeta ],[\eta ]\in C^{n}(\boldsymbol {\mathcal {U}};G)$
, we let
$[\zeta ],[\eta ]\in C^{n}(\boldsymbol {\mathcal {U}};G)$
, we let
It is easy to see that one can directly compute the value of
![]() $\rho ([\zeta ],[\eta ])$
by picking any representatives
$\rho ([\zeta ],[\eta ])$
by picking any representatives
![]() $\zeta '\colon N^{(n)}_{\alpha }\to G$
and
$\zeta '\colon N^{(n)}_{\alpha }\to G$
and
![]() $\eta '\colon N^{(n)}_{\beta }\to G$
of
$\eta '\colon N^{(n)}_{\beta }\to G$
of
![]() $[\zeta ]$
and
$[\zeta ]$
and
![]() $[\eta ]$
and alternatively setting
$[\eta ]$
and alternatively setting
The fact that the latter quantity does not depend on the choice of
![]() $\eta '$
and
$\eta '$
and
![]() $\zeta '$
follows by the same argument we used to prove transitivity of
$\zeta '$
follows by the same argument we used to prove transitivity of
![]() $\sim $
, using local surjectivity (L3) in place of surjectivity. By (6), it is clear that
$\sim $
, using local surjectivity (L3) in place of surjectivity. By (6), it is clear that
![]() $\rho $
is a metric, given that by (7), we have
$\rho $
is a metric, given that by (7), we have
![]() $\rho ([\zeta ],[\eta ])>0$
if
$\rho ([\zeta ],[\eta ])>0$
if
![]() $[\zeta ]\neq [\eta ]$
. To see that
$[\zeta ]\neq [\eta ]$
. To see that
![]() $\rho $
is compatible with the topology of
$\rho $
is compatible with the topology of
![]() $C^{n}(\boldsymbol {\mathcal {U}};G)$
, notice that since the topology is first countable, it suffices to show that a subset F of
$C^{n}(\boldsymbol {\mathcal {U}};G)$
, notice that since the topology is first countable, it suffices to show that a subset F of
![]() $C^{n}(\boldsymbol {\mathcal {U}};G)$
is closed if and only if for every sequence
$C^{n}(\boldsymbol {\mathcal {U}};G)$
is closed if and only if for every sequence
![]() $([\zeta _n])_{n}$
in F with
$([\zeta _n])_{n}$
in F with
![]() $[\zeta _n]\to _{\rho } [\zeta ]$
, we have that
$[\zeta _n]\to _{\rho } [\zeta ]$
, we have that
![]() $[\zeta ]\in F$
.
$[\zeta ]\in F$
.
If
![]() $[\zeta _n]\to _{\rho } [\zeta ]$
and F is closed, then using (7), we may choose the representatives
$[\zeta _n]\to _{\rho } [\zeta ]$
and F is closed, then using (7), we may choose the representatives
![]() $\zeta _n$
and
$\zeta _n$
and
![]() $\zeta $
so that
$\zeta $
so that
![]() $\zeta _n\to \zeta $
in
$\zeta _n\to \zeta $
in
![]() $C^{n}_{\mathrm {sem}}(\boldsymbol {\mathcal {U}};G)$
. Since the quotient map
$C^{n}_{\mathrm {sem}}(\boldsymbol {\mathcal {U}};G)$
. Since the quotient map
![]() $\pi \colon C^{n}_{\mathrm {sem}}(\boldsymbol {\mathcal {U}};G)\to C^{n}(\boldsymbol {\mathcal {U}};G)$
is continuous, we have that
$\pi \colon C^{n}_{\mathrm {sem}}(\boldsymbol {\mathcal {U}};G)\to C^{n}(\boldsymbol {\mathcal {U}};G)$
is continuous, we have that
![]() $\pi ^{-1}(F)$
is closed. Hence,
$\pi ^{-1}(F)$
is closed. Hence,
![]() $\zeta \in \pi ^{-1}(F)$
(i.e.,
$\zeta \in \pi ^{-1}(F)$
(i.e.,
![]() $[\zeta ]\in F$
). Conversely, assume that whenever
$[\zeta ]\in F$
). Conversely, assume that whenever
![]() $[\zeta _n]\to _{\rho } [\zeta ]$
, we have
$[\zeta _n]\to _{\rho } [\zeta ]$
, we have
![]() $[\zeta ]\in F$
. We will show that
$[\zeta ]\in F$
. We will show that
![]() $\pi ^{-1}(F)$
is closed. Let
$\pi ^{-1}(F)$
is closed. Let
![]() $(\zeta _n),\zeta $
be elements of
$(\zeta _n),\zeta $
be elements of
![]() $C^{n}_{\mathrm {sem}}(\boldsymbol {\mathcal {U}};G)$
such that
$C^{n}_{\mathrm {sem}}(\boldsymbol {\mathcal {U}};G)$
such that
![]() $\zeta _n\to \zeta $
. Then by (7), we have that
$\zeta _n\to \zeta $
. Then by (7), we have that
![]() $[\zeta _n]\to _{\rho } [\zeta ]$
. Hence,
$[\zeta _n]\to _{\rho } [\zeta ]$
. Hence,
![]() $[\zeta ]\in F$
, and therefore,
$[\zeta ]\in F$
, and therefore,
![]() $\zeta \in \pi ^{-1}(F)$
. Finally, the fact that
$\zeta \in \pi ^{-1}(F)$
. Finally, the fact that
![]() $\rho $
is complete follows from completeness of
$\rho $
is complete follows from completeness of
![]() $\rho _{\mathrm {sem}}$
and (7).
$\rho _{\mathrm {sem}}$
and (7).
Finally, notice that for every
![]() $\zeta \colon N^{(n)}_{\alpha }\to G$
and
$\zeta \colon N^{(n)}_{\alpha }\to G$
and
![]() $\zeta '\colon N^{(n)}_{\alpha '}\to G$
with
$\zeta '\colon N^{(n)}_{\alpha '}\to G$
with
![]() $\zeta \sim \zeta '$
, we have
$\zeta \sim \zeta '$
, we have
![]() $\eta \sim \eta '$
, where
$\eta \sim \eta '$
, where
 $$\begin{align*}\eta \big(v_{0},\ldots ,v_{n}\big)=\sum_{i=0}^{n}\left( -1\right) ^{i}\zeta (v_{0},\ldots ,\hat{v}_{i},\ldots ,v_{n}) \text{ and } \eta' \big(v_{0},\ldots ,v_{n}\big)=\sum_{i=0}^{n}\left( -1\right) ^{i}\zeta' (v_{0},\ldots ,\hat{v}_{i},\ldots ,v_{n}).\end{align*}$$
$$\begin{align*}\eta \big(v_{0},\ldots ,v_{n}\big)=\sum_{i=0}^{n}\left( -1\right) ^{i}\zeta (v_{0},\ldots ,\hat{v}_{i},\ldots ,v_{n}) \text{ and } \eta' \big(v_{0},\ldots ,v_{n}\big)=\sum_{i=0}^{n}\left( -1\right) ^{i}\zeta' (v_{0},\ldots ,\hat{v}_{i},\ldots ,v_{n}).\end{align*}$$
As a consequence, for every
![]() $n>0$
, we have a continuous coboundary map
$n>0$
, we have a continuous coboundary map
 $$ \begin{align} \begin{aligned} \delta^{n}:C^{n-1}(\boldsymbol{\mathcal{U}};G)&\rightarrow C^{n}(\boldsymbol{\mathcal{U}};G), \text{ where } \\ \delta^{n}\left( [\zeta] \right)= [\eta], \text{ with } \eta (v_{0},\ldots ,v_{n})&=\sum_{i=0}^{n}\left( -1\right) ^{i}\zeta (v_{0},\ldots ,\hat{v}_{i},\ldots ,v_{n}). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \delta^{n}:C^{n-1}(\boldsymbol{\mathcal{U}};G)&\rightarrow C^{n}(\boldsymbol{\mathcal{U}};G), \text{ where } \\ \delta^{n}\left( [\zeta] \right)= [\eta], \text{ with } \eta (v_{0},\ldots ,v_{n})&=\sum_{i=0}^{n}\left( -1\right) ^{i}\zeta (v_{0},\ldots ,\hat{v}_{i},\ldots ,v_{n}). \end{aligned} \end{align} $$
This defines the Polish cochain complex
![]() $C^{\bullet }(\boldsymbol {\mathcal {U}};G)$
of G-valued cochains of
$C^{\bullet }(\boldsymbol {\mathcal {U}};G)$
of G-valued cochains of
![]() $\boldsymbol {\mathcal {U}}$
.
$\boldsymbol {\mathcal {U}}$
.
Definition 2.11. Let X be a locally compact Polish space, and let G be a countable abelian Polish group. Fix a covering system
![]() $\boldsymbol {\mathcal {U}}$
for X, and for every
$\boldsymbol {\mathcal {U}}$
for X, and for every
![]() $n\in \mathbb {N}$
, define the n-dimensional definable cohomology group
$n\in \mathbb {N}$
, define the n-dimensional definable cohomology group ![]() of X with coefficients in G to be the n-dimensional cohomology group of the Polish cochain complex
of X with coefficients in G to be the n-dimensional cohomology group of the Polish cochain complex
![]() $C^{\bullet }(\boldsymbol {\mathcal {U}};G)$
, viewed as the group with a Polish cover
$C^{\bullet }(\boldsymbol {\mathcal {U}};G)$
, viewed as the group with a Polish cover
where
![]() $\mathrm {Z}^{n}(\boldsymbol {\mathcal {U}};G)= \mathrm {ker}(\delta ^{n})$
is the Polish group of n-dimensional G-valued cocycles of
$\mathrm {Z}^{n}(\boldsymbol {\mathcal {U}};G)= \mathrm {ker}(\delta ^{n})$
is the Polish group of n-dimensional G-valued cocycles of
![]() $\boldsymbol {\mathcal {U}}$
and
$\boldsymbol {\mathcal {U}}$
and
![]() $\mathrm {B}^{n}(\boldsymbol {\mathcal {U}};G)=\mathrm {im}(\delta ^{n-1})$
is the Polishable group of n-dimensional G-valued coboundaries of
$\mathrm {B}^{n}(\boldsymbol {\mathcal {U}};G)=\mathrm {im}(\delta ^{n-1})$
is the Polishable group of n-dimensional G-valued coboundaries of
![]() $\boldsymbol {\mathcal {U}}$
.
$\boldsymbol {\mathcal {U}}$
.
Notice that while the definition of
![]() $\mathrm {H}^{n}(X;G)$
involves a choice of covering system
$\mathrm {H}^{n}(X;G)$
involves a choice of covering system
![]() $\boldsymbol {\mathcal {U}}$
for X, the latter is not explicit in the notation
$\boldsymbol {\mathcal {U}}$
for X, the latter is not explicit in the notation ![]() . This is because, as we will show in Corollary 5.8, a different choice of
. This is because, as we will show in Corollary 5.8, a different choice of
![]() $\boldsymbol {\mathcal {U}}$
will induce the exact same definable cohomology groups up to definable isomorphism.
$\boldsymbol {\mathcal {U}}$
will induce the exact same definable cohomology groups up to definable isomorphism.
Since the Polish groups in
![]() $C^{\bullet }(\boldsymbol {\mathcal {U}};G)$
are non-archimedean, the rigidity results of [Reference Bergfalk and Lupini9] provide a powerful resource for analyzing the definable cohomology groups of any locally compact Polish space. Note that as a sequence of abstract groups,
$C^{\bullet }(\boldsymbol {\mathcal {U}};G)$
are non-archimedean, the rigidity results of [Reference Bergfalk and Lupini9] provide a powerful resource for analyzing the definable cohomology groups of any locally compact Polish space. Note that as a sequence of abstract groups,
![]() $\mathrm {H}^{\bullet }(X;G)$
coincides with the classical Čech cohomology groups of X with coefficients in G.
$\mathrm {H}^{\bullet }(X;G)$
coincides with the classical Čech cohomology groups of X with coefficients in G.
Theorem 2.12. As an abstract group, ![]() is isomorphic to the n-dimensional Čech cohomology group
is isomorphic to the n-dimensional Čech cohomology group ![]() of X with coefficients in G.
of X with coefficients in G.
Proof. Throughout this proof, every group is viewed as an abstract group. The proof of Theorem 2.12 follows by combining the two usual arguments which show (1) without loss of generality, the colimit in the definition of ![]() can be taken over any
can be taken over any
![]() $\preceq $
–cofinal collection of open covers and (2) the group
$\preceq $
–cofinal collection of open covers and (2) the group ![]() is isomorphic to the sheaf of germs of constant G-valued functions. We sketch the argument here, as the explicit abstract group isomorphism
is isomorphic to the sheaf of germs of constant G-valued functions. We sketch the argument here, as the explicit abstract group isomorphism ![]() generated by this argument will be needed in the proof of Theorem 5.7.
generated by this argument will be needed in the proof of Theorem 5.7.
Recall that in order to define the n-dimensional Čech cohomology group ![]() of X, one first considers the poset
of X, one first considers the poset
![]() $\mathrm {Cov}(X)$
of all open covers
$\mathrm {Cov}(X)$
of all open covers
![]() $\mathcal {U}$
of X ordered by the relation of refinement
$\mathcal {U}$
of X ordered by the relation of refinement
![]() $\mathcal {U}\preceq \mathcal {V}$
and observes that any two refinement maps
$\mathcal {U}\preceq \mathcal {V}$
and observes that any two refinement maps
![]() $r^{\mathcal {V}}_{\mathcal {U}},s^{\mathcal {V}}_{\mathcal {U}}\colon \mathcal {V}\to \mathcal {U}$
induce contiguous (see Section 4.2) simplicial maps
$r^{\mathcal {V}}_{\mathcal {U}},s^{\mathcal {V}}_{\mathcal {U}}\colon \mathcal {V}\to \mathcal {U}$
induce contiguous (see Section 4.2) simplicial maps
![]() $r^{\mathcal {V}}_{\mathcal {U}},s^{\mathcal {V}}_{\mathcal {U}}\colon \mathrm {Nv}(\mathcal {V})\to \mathrm {Nv}(\mathcal {U})$
. Hence, while the associated chain maps
$r^{\mathcal {V}}_{\mathcal {U}},s^{\mathcal {V}}_{\mathcal {U}}\colon \mathrm {Nv}(\mathcal {V})\to \mathrm {Nv}(\mathcal {U})$
. Hence, while the associated chain maps
![]() $(r^{\mathcal {V}}_{\mathcal {U}})^{\bullet },(s^{\mathcal {V}}_{\mathcal {U}})^{\bullet }\colon C^{\bullet }(\mathrm {Nv}(\mathcal {U}),G)\to C^{\bullet }(\mathrm {Nv}(\mathcal {V}),G)$
with
$(r^{\mathcal {V}}_{\mathcal {U}})^{\bullet },(s^{\mathcal {V}}_{\mathcal {U}})^{\bullet }\colon C^{\bullet }(\mathrm {Nv}(\mathcal {U}),G)\to C^{\bullet }(\mathrm {Nv}(\mathcal {V}),G)$
with
![]() $(r^{\mathcal {V}}_{\mathcal {U}})^{\bullet }(\zeta ):=\zeta \circ r^{\mathcal {V}}_{\mathcal {U}}$
and
$(r^{\mathcal {V}}_{\mathcal {U}})^{\bullet }(\zeta ):=\zeta \circ r^{\mathcal {V}}_{\mathcal {U}}$
and
![]() $(s^{\mathcal {V}}_{\mathcal {U}})^{\bullet }(\zeta ):=\zeta \circ s^{\mathcal {V}}_{\mathcal {U}}$
may differ, they induce the same homomorphism
$(s^{\mathcal {V}}_{\mathcal {U}})^{\bullet }(\zeta ):=\zeta \circ s^{\mathcal {V}}_{\mathcal {U}}$
may differ, they induce the same homomorphism
![]() $(r^{\mathcal {V}}_{\mathcal {U}})^{*}=(s^{\mathcal {V}}_{\mathcal {U}})^{*}$
on the level of simplicial cohomology
$(r^{\mathcal {V}}_{\mathcal {U}})^{*}=(s^{\mathcal {V}}_{\mathcal {U}})^{*}$
on the level of simplicial cohomology
![]() $\mathrm {H}^{n}(\mathrm {Nv}(\mathcal {U}),G)\to \mathrm {H}^{n}(\mathrm {Nv}(\mathcal {V}),G)$
for every
$\mathrm {H}^{n}(\mathrm {Nv}(\mathcal {U}),G)\to \mathrm {H}^{n}(\mathrm {Nv}(\mathcal {V}),G)$
for every
![]() $n\in \mathbb {N}$
; see [Reference Eilenberg and Steenrod29, Corollary IX.2.14], for example.
$n\in \mathbb {N}$
; see [Reference Eilenberg and Steenrod29, Corollary IX.2.14], for example.
As a consequence, we have a well-defined direct system of group homomorphisms
![]() $\mathrm {H}^{n}(\mathrm {Nv}(\mathcal {U}),G)\to \mathrm {H}^{n}(\mathrm {Nv}(\mathcal {V}),G)$
indexed by the poset
$\mathrm {H}^{n}(\mathrm {Nv}(\mathcal {U}),G)\to \mathrm {H}^{n}(\mathrm {Nv}(\mathcal {V}),G)$
indexed by the poset
![]() $(\mathrm {Cov}(X),\preceq )$
. By definition, see [Reference Eilenberg and Steenrod29, Definition IX.3.1], we have that
$(\mathrm {Cov}(X),\preceq )$
. By definition, see [Reference Eilenberg and Steenrod29, Definition IX.3.1], we have that
where
![]() $(r^{\mathcal {V}}_{\mathcal {U}}\colon \mathcal {V}\to \mathcal {U})_{\mathcal {U}\preceq \mathcal {V}}$
is any fixed pre-chosen collection of refinement maps.
$(r^{\mathcal {V}}_{\mathcal {U}}\colon \mathcal {V}\to \mathcal {U})_{\mathcal {U}\preceq \mathcal {V}}$
is any fixed pre-chosen collection of refinement maps.
Let now
![]() $(U_{\alpha }\colon \alpha \in \mathcal {N}^{*})$
and
$(U_{\alpha }\colon \alpha \in \mathcal {N}^{*})$
and
![]() $(r^{\beta }_{\alpha }\colon \alpha \leq \beta )$
be the open covers and refinement maps appearing in the covering system
$(r^{\beta }_{\alpha }\colon \alpha \leq \beta )$
be the open covers and refinement maps appearing in the covering system
![]() $\boldsymbol {\mathcal {U}}$
used in the definition of
$\boldsymbol {\mathcal {U}}$
used in the definition of ![]() , and set
, and set
![]() $N_{\alpha }:=\mathrm {Nv}(\mathcal {U}_{\alpha })$
. Since the colimit in (9) is isomorphic to the colimit taken over any cofinal collection of
$N_{\alpha }:=\mathrm {Nv}(\mathcal {U}_{\alpha })$
. Since the colimit in (9) is isomorphic to the colimit taken over any cofinal collection of
![]() $\mathcal {U}\in \mathrm {Cov}(X)$
, by Lemma 2.6(3), we have that
$\mathcal {U}\in \mathrm {Cov}(X)$
, by Lemma 2.6(3), we have that
However, the system
![]() $(r^{\beta }_{\alpha }\colon \alpha \leq \beta )$
coheres (i.e., for all
$(r^{\beta }_{\alpha }\colon \alpha \leq \beta )$
coheres (i.e., for all
![]() $\alpha \leq \beta \leq \gamma $
, we have
$\alpha \leq \beta \leq \gamma $
, we have
![]() $r^{\gamma }_{\alpha }=r^{\beta }_{\alpha }\circ r^{\gamma }_{\beta }$
); see Definition 2.3. Moreover, if
$r^{\gamma }_{\alpha }=r^{\beta }_{\alpha }\circ r^{\gamma }_{\beta }$
); see Definition 2.3. Moreover, if
![]() $\delta ^{\bullet }_{\alpha }$
and
$\delta ^{\bullet }_{\alpha }$
and
![]() $\delta ^{\bullet }_{\beta }$
are the coboundary maps of the cochain complexes
$\delta ^{\bullet }_{\beta }$
are the coboundary maps of the cochain complexes
![]() $\mathrm {C}^{\bullet }(N_{\alpha };G)$
and
$\mathrm {C}^{\bullet }(N_{\alpha };G)$
and
![]() $\mathrm {C}^{\bullet }(N_{\beta };G)$
with
$\mathrm {C}^{\bullet }(N_{\beta };G)$
with
![]() $\alpha \leq \beta $
, then for all
$\alpha \leq \beta $
, then for all
![]() $n\in \mathbb {N}$
, we have that
$n\in \mathbb {N}$
, we have that
![]() $(r^{\beta }_{\alpha })^{n+1}\circ \delta ^{n}_{\alpha }=\delta ^{n}_{\beta }\circ (r^{\beta }_{\alpha })^{n}$
. As a consequence, we have a direct system of chain complexes
$(r^{\beta }_{\alpha })^{n+1}\circ \delta ^{n}_{\alpha }=\delta ^{n}_{\beta }\circ (r^{\beta }_{\alpha })^{n}$
. As a consequence, we have a direct system of chain complexes
![]() $\big (\mathrm {C}^{\bullet }(N_{\alpha };G) ,(r^{\beta }_{\alpha })^{\bullet }\big )_{\alpha \in \mathcal {N}^{*}}$
. But then, by the definition of a colimit of a directed system of abelian groups (see, for example, [Reference Eilenberg and Steenrod29, Definition IX.4.1]), for every
$\big (\mathrm {C}^{\bullet }(N_{\alpha };G) ,(r^{\beta }_{\alpha })^{\bullet }\big )_{\alpha \in \mathcal {N}^{*}}$
. But then, by the definition of a colimit of a directed system of abelian groups (see, for example, [Reference Eilenberg and Steenrod29, Definition IX.4.1]), for every
![]() $n\in \mathbb {N}$
, we have that
$n\in \mathbb {N}$
, we have that
 $$ \begin{align} \mathrm{colim}_{\;\alpha \in\mathcal{N}^{*}} \;\big( \mathrm{C}^{n}(N_{\alpha};G) ,(r^{\beta}_{\alpha})^{n} \big)\quad :=\quad \bigg(\bigsqcup_{\alpha \in\mathcal{N}^{*}} C^{n}(N_{\alpha};G) \; \bigg)\bigg/\sim \quad = \quad C^n_{\mathrm{sem}}(\boldsymbol{\mathcal{U}};G)/\sim \quad = \quad C^{n}(\boldsymbol{\mathcal{U}};G), \end{align} $$
$$ \begin{align} \mathrm{colim}_{\;\alpha \in\mathcal{N}^{*}} \;\big( \mathrm{C}^{n}(N_{\alpha};G) ,(r^{\beta}_{\alpha})^{n} \big)\quad :=\quad \bigg(\bigsqcup_{\alpha \in\mathcal{N}^{*}} C^{n}(N_{\alpha};G) \; \bigg)\bigg/\sim \quad = \quad C^n_{\mathrm{sem}}(\boldsymbol{\mathcal{U}};G)/\sim \quad = \quad C^{n}(\boldsymbol{\mathcal{U}};G), \end{align} $$
where
![]() $\sim $
is the congruence we defined earlier in this section, and similarly have that
$\sim $
is the congruence we defined earlier in this section, and similarly have that
![]() $\delta ^n= \mathrm {colim}_{\alpha }\delta ^n_{\alpha }$
. Consequently,
$\delta ^n= \mathrm {colim}_{\alpha }\delta ^n_{\alpha }$
. Consequently,
But for every direct system of pairs of abelian groups
![]() $(H_i\leq G_{i},i\in I)$
, colimits commute with quotients (i.e.,
$(H_i\leq G_{i},i\in I)$
, colimits commute with quotients (i.e.,
![]() $\mathrm {colim}_i(G_i)/\mathrm {colim}_i( H_i) \cong \mathrm {colim}_i(G_i/H_i)$
); see [Reference Eilenberg and Steenrod29, Theorem IX.6.3]. Hence, by combining (10) and (12), we have
$\mathrm {colim}_i(G_i)/\mathrm {colim}_i( H_i) \cong \mathrm {colim}_i(G_i/H_i)$
); see [Reference Eilenberg and Steenrod29, Theorem IX.6.3]. Hence, by combining (10) and (12), we have
An explicit formula for the composition of these isomorphisms, ![]() , can be given as follows. First, let
, can be given as follows. First, let ![]() be any element of
be any element of ![]() , where
, where
![]() $\zeta \in \mathrm {Z}^{n}(\mathrm {Nv}(\mathcal {U});G)$
for some
$\zeta \in \mathrm {Z}^{n}(\mathrm {Nv}(\mathcal {U});G)$
for some
![]() $\mathcal {U}\in \mathrm {Cov}(X)$
, and
$\mathcal {U}\in \mathrm {Cov}(X)$
, and ![]() is the image of
is the image of
![]() $a\in \mathrm {H}^{n}(\mathrm {Nv}(\mathcal {U});G)$
under the inclusion
$a\in \mathrm {H}^{n}(\mathrm {Nv}(\mathcal {U});G)$
under the inclusion ![]() . Then,
. Then,
where
![]() $\alpha $
can be taken to be any element of
$\alpha $
can be taken to be any element of
![]() $\mathcal {N}^{*}$
with
$\mathcal {N}^{*}$
with
![]() $\mathcal {U}\preceq \mathcal {U}_{\alpha }.$
Such
$\mathcal {U}\preceq \mathcal {U}_{\alpha }.$
Such
![]() $\alpha $
exists by Lemma 2.6(3).
$\alpha $
exists by Lemma 2.6(3).
Remark 2.13. In this section, we developed definable cohomology groups with coefficients in a countable discrete abelian group G. Implicit in our definitions was the passage from classical definition of Čech cohomology to the sheaf-theoretic one. As outlined in the proof of Theorem 2.12, this passage was effected essentially by alternating the order between two processes – namely, taking the colimit of abelian groups and computing the cohomology groups of a cochain complex. One can more generally develop definable cohomology groups
![]() $\mathrm {H}_{\mathrm {def}}^{n}(X;G')$
for X with coefficients in an arbitrary Polish abelian group
$\mathrm {H}_{\mathrm {def}}^{n}(X;G')$
for X with coefficients in an arbitrary Polish abelian group
![]() $G'$
by endowing the sheaf of germs of all continuous
$G'$
by endowing the sheaf of germs of all continuous
![]() $G'$
-valued functions with an appropriate Polish structure. However, this would require significant amounts of bookkeeping. Perhaps one way of simplifying the process of endowing the aforementioned sheaf with a Polish structure would be to first pass to a ‘completion’ of the inverse system
$G'$
-valued functions with an appropriate Polish structure. However, this would require significant amounts of bookkeeping. Perhaps one way of simplifying the process of endowing the aforementioned sheaf with a Polish structure would be to first pass to a ‘completion’ of the inverse system
![]() $((\mathcal {U}_{\alpha }),(r^{\beta }_{\alpha }))$
by considering locally profinite topological simplicial complexes similar to the profinite topological simplicial complexes used in projective Fraïssé theory; see [Reference Panagiotopoulos and Solecki70]. This, however, is beyond the scope of the present paper.
$((\mathcal {U}_{\alpha }),(r^{\beta }_{\alpha }))$
by considering locally profinite topological simplicial complexes similar to the profinite topological simplicial complexes used in projective Fraïssé theory; see [Reference Panagiotopoulos and Solecki70]. This, however, is beyond the scope of the present paper.
2.5. Definable cohomology of pairs of spaces
The process of enriching the Čech cohomology groups of locally compact spaces with definable content readily extends to the Čech cohomology groups of locally compact pairs (i.e, pairs
![]() $(X,A)$
in which X is a locally compact Polish space and A is closed in X); see Section 4.1. In this section, we sketch the details. We begin by generalizing the theory from Section 2.1 to pairs
$(X,A)$
in which X is a locally compact Polish space and A is closed in X); see Section 4.1. In this section, we sketch the details. We begin by generalizing the theory from Section 2.1 to pairs
![]() $(K,L)$
of simplicial complexes.
$(K,L)$
of simplicial complexes.
Let K be a simplicial complex. A subcomplex L of K is any simplicial complex with
![]() $\mathrm {dom}(L)\subseteq \mathrm {dom}(K)$
for which
$\mathrm {dom}(L)\subseteq \mathrm {dom}(K)$
for which
![]() $\sigma \in L$
implies
$\sigma \in L$
implies
![]() $\sigma \in K$
. By a simplicial pair we mean a pair
$\sigma \in K$
. By a simplicial pair we mean a pair
![]() $(K,L)$
of simplicial complexes in which L is a subcomplex of K. A simplicial map (of pairs)
$(K,L)$
of simplicial complexes in which L is a subcomplex of K. A simplicial map (of pairs)
![]() $f\colon (K,L)\to (K',L')$
is any simplicial map
$f\colon (K,L)\to (K',L')$
is any simplicial map
![]() $f\colon K\to K'$
such that
$f\colon K\to K'$
such that
![]() $\{f(v)\colon v\in \sigma \}\in L'$
for all
$\{f(v)\colon v\in \sigma \}\in L'$
for all
![]() $\sigma \in L$
. For any abelian Polish group G and
$\sigma \in L$
. For any abelian Polish group G and
![]() $n\in \mathbb {N}$
, let
$n\in \mathbb {N}$
, let
![]() $C^{n}(K,L;G)$
is a closed subgroup of
$C^{n}(K,L;G)$
is a closed subgroup of
![]() $C^{n}(K;G)$
with respect to the product topology of the
$C^{n}(K;G)$
with respect to the product topology of the
![]() $K^{(n)}$
-fold product of copies of G; hence, it is a Polish group. The coboundary map
$K^{(n)}$
-fold product of copies of G; hence, it is a Polish group. The coboundary map
![]() $ \delta ^{n}:C^{n}(K;G) \rightarrow C^{n+1}(K;G)$
clearly restricts to a map
$ \delta ^{n}:C^{n}(K;G) \rightarrow C^{n+1}(K;G)$
clearly restricts to a map
![]() $C^{n}(K,L;G) \rightarrow C^{n+1}(K,L;G)$
which we will also denote by
$C^{n}(K,L;G) \rightarrow C^{n+1}(K,L;G)$
which we will also denote by
![]() $\delta ^{n}$
. This induces a Polish cochain complex
$\delta ^{n}$
. This induces a Polish cochain complex
The definable cohomology groups of
![]() $(K,L)$
with coefficients in G are the groups with a Polish cover
$(K,L)$
with coefficients in G are the groups with a Polish cover
Note that the natural homomorphisms determining the short exact sequences
are continuous and aggregate into a short exact sequence of Polish cochain complexes
For the rest of this section, let G be a countable abelian group and
![]() $(X,A)$
be a locally compact pair. Fix any covering system
$(X,A)$
be a locally compact pair. Fix any covering system
![]() $\boldsymbol {\mathcal {U}}=\big {(}(X_n),(\mathcal {U}_{\alpha }),(r^{\beta }_{\alpha })\big {)}$
for X, and notice that the triple
$\boldsymbol {\mathcal {U}}=\big {(}(X_n),(\mathcal {U}_{\alpha }),(r^{\beta }_{\alpha })\big {)}$
for X, and notice that the triple
![]() $\boldsymbol {\mathcal {V}}=\big {(}(A_n),(\mathcal {V}_{\alpha }),(s^{\beta }_{\alpha })\big {)}$
, where
$\boldsymbol {\mathcal {V}}=\big {(}(A_n),(\mathcal {V}_{\alpha }),(s^{\beta }_{\alpha })\big {)}$
, where
![]() $A_n:=A\cap X_n$
,
$A_n:=A\cap X_n$
,
![]() $\mathcal {V}_{\alpha }:=\mathcal {U}_{\alpha }\upharpoonright A\subseteq \mathcal {U}_{\alpha }$
and
$\mathcal {V}_{\alpha }:=\mathcal {U}_{\alpha }\upharpoonright A\subseteq \mathcal {U}_{\alpha }$
and
![]() $s^{\beta }_{\alpha }$
denotes the restriction of
$s^{\beta }_{\alpha }$
denotes the restriction of
![]() $r^{\beta }_{\alpha }$
to
$r^{\beta }_{\alpha }$
to
![]() $\mathcal {V}_{\beta }$
, is a covering system for A. Moreover, the inclusion
$\mathcal {V}_{\beta }$
, is a covering system for A. Moreover, the inclusion
![]() $\mathcal {V}_{\alpha }\subseteq \mathcal {U}_{\alpha }$
induces a simplicial pair
$\mathcal {V}_{\alpha }\subseteq \mathcal {U}_{\alpha }$
induces a simplicial pair
![]() $(N_{\alpha },M_{\alpha }):=\big {(}\mathrm {Nv}(\mathcal {U}_{\alpha }),\mathrm {Nv}(\mathcal {V}_{\alpha })\big {)}$
. For every
$(N_{\alpha },M_{\alpha }):=\big {(}\mathrm {Nv}(\mathcal {U}_{\alpha }),\mathrm {Nv}(\mathcal {V}_{\alpha })\big {)}$
. For every
![]() $n\in \mathbb {N}$
, we set
$n\in \mathbb {N}$
, we set
Then
![]() $C^{n}( \boldsymbol {\mathcal {U}}, \boldsymbol {\mathcal {V}};G)$
is a Polish group, as it is a closed subgroup of
$C^{n}( \boldsymbol {\mathcal {U}}, \boldsymbol {\mathcal {V}};G)$
is a Polish group, as it is a closed subgroup of
![]() $C^{n}( \boldsymbol {\mathcal {U}};G)$
. Moreover, the coboundary map
$C^{n}( \boldsymbol {\mathcal {U}};G)$
. Moreover, the coboundary map
![]() $ \delta ^{n}:C^{n}( \boldsymbol {\mathcal {U}};G) \rightarrow C^{n+1}( \boldsymbol {\mathcal {U}};G)$
restricts to
$ \delta ^{n}:C^{n}( \boldsymbol {\mathcal {U}};G) \rightarrow C^{n+1}( \boldsymbol {\mathcal {U}};G)$
restricts to
![]() $ \delta ^{n}:C^{n}( \boldsymbol {\mathcal {U}},\boldsymbol {\mathcal {V}};G) \rightarrow C^{n+1}( \boldsymbol {\mathcal {U}},\boldsymbol {\mathcal {V}};G)$
, inducing a Polish cochain complex
$ \delta ^{n}:C^{n}( \boldsymbol {\mathcal {U}},\boldsymbol {\mathcal {V}};G) \rightarrow C^{n+1}( \boldsymbol {\mathcal {U}},\boldsymbol {\mathcal {V}};G)$
, inducing a Polish cochain complex
The definable cohomology groups of
![]() $(X,A)$
with coefficients in G are the groups with a Polish cover
$(X,A)$
with coefficients in G are the groups with a Polish cover
Arguing exactly as for Theorem 2.12 shows that, as abstract groups, these are precisely the Čech cohomology groups ![]() of the pair
of the pair
![]() $(X,A)$
; see [Reference Eilenberg and Steenrod29, Chapter IX] for a definition of the latter. Moreover, these
$(X,A)$
; see [Reference Eilenberg and Steenrod29, Chapter IX] for a definition of the latter. Moreover, these ![]() groups array into a definable long exact sequence of the usual form; put differently, by the following theorem, they satisfy the Exactness Axiom as maps to the category of groups with a Polish cover.
groups array into a definable long exact sequence of the usual form; put differently, by the following theorem, they satisfy the Exactness Axiom as maps to the category of groups with a Polish cover.
Theorem 2.14. For any countable discrete group G and locally compact pair
![]() $(X,A)$
, there exists a long exact sequence of groups with a Polish cover and definable group homomorphisms
$(X,A)$
, there exists a long exact sequence of groups with a Polish cover and definable group homomorphisms
Theorem 2.14 is an instance of Theorem 2.16 below which, in turn, is a direct consequence of the following definable version of the Snake Lemma:
Lemma 2.15. Consider the following diagram of continuous homomorphisms of abelian Polish groups:

If the rows are exact, then there exists a Borel function
![]() $\varepsilon \colon \mathrm {ker}(c)\rightarrow A^{\prime }$
so that the map
$\varepsilon \colon \mathrm {ker}(c)\rightarrow A^{\prime }$
so that the map
![]() $x\mapsto \big (\varepsilon (x)+\mathrm {im}(A)\big )$
links the middle terms in the following exact sequence of groups with a Polish cover and definable group homomorphisms:
$x\mapsto \big (\varepsilon (x)+\mathrm {im}(A)\big )$
links the middle terms in the following exact sequence of groups with a Polish cover and definable group homomorphisms:
Observe that we have notationally conflated all other maps with those which they induce on subgroups and quotients.
Proof. By [Reference Kechris44, Theorem 12.15], there exists a Borel selector
![]() $\gamma $
for the
$\gamma $
for the
![]() $\mathrm {ker}(f)$
-coset relation on B; put differently, there exists a Borel function
$\mathrm {ker}(f)$
-coset relation on B; put differently, there exists a Borel function
![]() $\gamma \colon C\rightarrow B$
so that
$\gamma \colon C\rightarrow B$
so that
![]() $f\circ \gamma =\mathrm {id} _{C}.$
Being a continuous injection, g is a Borel isomorphism between
$f\circ \gamma =\mathrm {id} _{C}.$
Being a continuous injection, g is a Borel isomorphism between
![]() $A^{\prime }$
and
$A^{\prime }$
and
![]() $\mathrm {im}(g)$
and hence possesses a Borel inverse
$\mathrm {im}(g)$
and hence possesses a Borel inverse
![]() $\varphi \colon \mathrm {im}(g)\rightarrow A^{\prime }$
. Set
$\varphi \colon \mathrm {im}(g)\rightarrow A^{\prime }$
. Set
![]() $\varepsilon =\varphi \circ b\circ (\gamma \upharpoonright \mathrm {ker}(c))$
. Since the rightmost square commutes, for every
$\varepsilon =\varphi \circ b\circ (\gamma \upharpoonright \mathrm {ker}(c))$
. Since the rightmost square commutes, for every
![]() $x\in \mathrm {ker}(c)$
, we have that
$x\in \mathrm {ker}(c)$
, we have that
![]() $b\circ \gamma (x)\in \mathrm {ker}(h)=\mathrm {im}(g)$
so
$b\circ \gamma (x)\in \mathrm {ker}(h)=\mathrm {im}(g)$
so
![]() $\varepsilon $
is well defined and Borel. The rest of the argument is essentially algebraic and standard; see [Reference Lang48, Lemma 9.1].
$\varepsilon $
is well defined and Borel. The rest of the argument is essentially algebraic and standard; see [Reference Lang48, Lemma 9.1].
Theorem 2.16. Let
![]() $0\longrightarrow A^{\bullet } \overset {i^{\bullet }}{\longrightarrow } B^{\bullet } \overset {r^{\bullet }}{\longrightarrow } C^{\bullet } \longrightarrow 0$
be a short exact sequence of Polish cochain complexes where the group homomorphisms
$0\longrightarrow A^{\bullet } \overset {i^{\bullet }}{\longrightarrow } B^{\bullet } \overset {r^{\bullet }}{\longrightarrow } C^{\bullet } \longrightarrow 0$
be a short exact sequence of Polish cochain complexes where the group homomorphisms
![]() $i^n,r^n$
are continuous for all
$i^n,r^n$
are continuous for all
![]() $n\in \mathbb {Z}$
. Then there is a long exact sequence of definable homomorphisms between the associated groups with a Polish cover
$n\in \mathbb {Z}$
. Then there is a long exact sequence of definable homomorphisms between the associated groups with a Polish cover
Proof. On the level of abstract cochain complexes and abstract abelian groups, the long exact sequence (17) can be formed by taking
![]() $\widehat {\iota }^{n}$
and
$\widehat {\iota }^{n}$
and
![]() $\widehat {\rho }^{n}$
to be the maps induced by the homomorphisms
$\widehat {\rho }^{n}$
to be the maps induced by the homomorphisms
![]() $\iota _n\upharpoonright \mathrm {Z}^{n}(A^{\bullet })$
and
$\iota _n\upharpoonright \mathrm {Z}^{n}(A^{\bullet })$
and
![]() $\rho _n\upharpoonright \mathrm {Z}^{n}(B^{\bullet })$
, and setting
$\rho _n\upharpoonright \mathrm {Z}^{n}(B^{\bullet })$
, and setting
![]() $\partial ^{n}$
to be the map induced by an application of the classical Snake Lemma on the diagram
$\partial ^{n}$
to be the map induced by an application of the classical Snake Lemma on the diagram

But then,
![]() $\widehat {\iota }^{n}$
and
$\widehat {\iota }^{n}$
and
![]() $\widehat {\rho }^{n}$
are both definable since they admit
$\widehat {\rho }^{n}$
are both definable since they admit
![]() $\iota _n\upharpoonright \mathrm {Z}^{n}(A^{\bullet })$
and
$\iota _n\upharpoonright \mathrm {Z}^{n}(A^{\bullet })$
and
![]() $\rho _n\upharpoonright \mathrm {Z}^{n}(B^{\bullet })$
as continuous lifts. The homomorphism
$\rho _n\upharpoonright \mathrm {Z}^{n}(B^{\bullet })$
as continuous lifts. The homomorphism
![]() $\partial ^n$
is also definable as a consequence of Lemma 2.15.
$\partial ^n$
is also definable as a consequence of Lemma 2.15.
Theorem 2.14 now follows by an application of Theorem 2.16 to the short exact sequence (16).
3. Definable sets and groups
At work in the main results of [Reference Bergfalk and Lupini9] is the fact that the category
![]() $\mathsf {GPC}$
of groups with a Polish cover is well behaved in a number of ways. For example, if a group isomorphism
$\mathsf {GPC}$
of groups with a Polish cover is well behaved in a number of ways. For example, if a group isomorphism
![]() $G/H\to G'/H'$
lifts to a Borel function, then so too does its inverse; see [Reference Bergfalk and Lupini9, Remark 3.3]. Put differently, in
$G/H\to G'/H'$
lifts to a Borel function, then so too does its inverse; see [Reference Bergfalk and Lupini9, Remark 3.3]. Put differently, in
![]() $\mathsf {GPC}$
, every bijective morphism is an isomorphism; this is just as we would hope, of course, and sharply contrasts with with the behavior of categories of topological groups, for example. Deeper regularities of this construction manifest as the second author’s more recent result that the category of groups with an abelian Polish cover
$\mathsf {GPC}$
, every bijective morphism is an isomorphism; this is just as we would hope, of course, and sharply contrasts with with the behavior of categories of topological groups, for example. Deeper regularities of this construction manifest as the second author’s more recent result that the category of groups with an abelian Polish cover
![]() $\mathsf {APC}$
forms an abelian category [Reference Lupini52].
$\mathsf {APC}$
forms an abelian category [Reference Lupini52].
Algebraic topology, however, abounds in spaces possessing a group structure only modulo a homotopy relation; such H-groups, moreover, are fundamental to the homotopical representation of cohomology theories, and of Čech cohomology, in particular. We were led in this way to consideration of a more general category of what we term definable groups, one which contains
![]() $\mathsf {GPC}$
as a full subcategory, as well as the homotopical examples we have in mind, and we were gratified to discover how many of
$\mathsf {GPC}$
as a full subcategory, as well as the homotopical examples we have in mind, and we were gratified to discover how many of
![]() $\mathsf {GPC}$
’s regularity properties persist in this wider setting. In a nutshell, a definable group
$\mathsf {GPC}$
’s regularity properties persist in this wider setting. In a nutshell, a definable group
![]() $(X/E,*,\mu )$
is the quotient
$(X/E,*,\mu )$
is the quotient
![]() $X/E$
of a Polish space by an idealistic Borel equivalence relation E, together with a group structure given by a multiplication
$X/E$
of a Polish space by an idealistic Borel equivalence relation E, together with a group structure given by a multiplication
![]() $\mu \colon X/E \times X/E \to X/E$
so that both
$\mu \colon X/E \times X/E \to X/E$
so that both
![]() $\mu $
and the group-inverse map
$\mu $
and the group-inverse map
![]() $X/E\to X/E$
lift to Borel maps at the level of X. Just as in the category of groups with a Polish cover, maps in the category of definable groups are definable homomorphisms (i.e., group homomorphisms
$X/E\to X/E$
lift to Borel maps at the level of X. Just as in the category of groups with a Polish cover, maps in the category of definable groups are definable homomorphisms (i.e., group homomorphisms
![]() $X/E\to Y/F$
which lift to a Borel map
$X/E\to Y/F$
which lift to a Borel map
![]() $X\to Y$
).
$X\to Y$
).
We will be working with a slightly more general notion of an idealistic equivalence relation than is standard. This is introduced in Section 3.1, where we also record some technical preliminaries for our later work. Definable groups are then introduced as group objects in the category
![]() $\mathsf {DSet}$
of definable sets; see Sections 3.2 and 3.4. The prototypical example of a definable group is the group
$\mathsf {DSet}$
of definable sets; see Sections 3.2 and 3.4. The prototypical example of a definable group is the group
![]() $[X, K(G,n)]$
of homotopy classes of maps from a locally compact Polish space X to an Eilenberg–MacLane space
$[X, K(G,n)]$
of homotopy classes of maps from a locally compact Polish space X to an Eilenberg–MacLane space
![]() $K(G,n)$
; see Section 4. In Section 5, we will establish that
$K(G,n)$
; see Section 4. In Section 5, we will establish that
![]() $[X, K(G,n)]$
is essentially a group with a Polish cover (i.e., is definably isomorphic to a group with a Polish cover). It remains an open question whether every definable group is essentially a group with a Polish cover, as we note in our conclusion.
$[X, K(G,n)]$
is essentially a group with a Polish cover (i.e., is definably isomorphic to a group with a Polish cover). It remains an open question whether every definable group is essentially a group with a Polish cover, as we note in our conclusion.
3.1. Idealistic equivalence relations
We say that an equivalence relation E on a Polish space X is open, closed or Borel, respectively, if it is an open, closed or Borel subset of
![]() $X\times X$
endowed with the product topology. We will denote by
$X\times X$
endowed with the product topology. We will denote by
![]() $[x]_E$
, or simply by
$[x]_E$
, or simply by
![]() $[x]$
if E is understood, the E-equivalence class of x in X.
$[x]$
if E is understood, the E-equivalence class of x in X.
The following is a slight generalization of the classical notion of an idealistic equivalence relation; it coincides with [Reference Gao31, Definition 5.4.9] if we require that the map
![]() $\zeta :X\rightarrow X$
in Definition 3.1 is the identity map. And while our definition’s allowance for a potentially wider range of functions
$\zeta :X\rightarrow X$
in Definition 3.1 is the identity map. And while our definition’s allowance for a potentially wider range of functions
![]() $\zeta $
appears indispensible to the proof of Lemma 3.6 below, for example, it remains unclear whether [Reference Gao31, Definition 5.4.9] is, in fact, equivalent to Definition 3.1. Recall that a
$\zeta $
appears indispensible to the proof of Lemma 3.6 below, for example, it remains unclear whether [Reference Gao31, Definition 5.4.9] is, in fact, equivalent to Definition 3.1. Recall that a
![]() $\sigma $
-filter of subsets of a set C is a nonempty collection
$\sigma $
-filter of subsets of a set C is a nonempty collection
![]() $\mathcal {F} $
of nonempty subsets of C which is closed under supersets and countable intersections.
$\mathcal {F} $
of nonempty subsets of C which is closed under supersets and countable intersections.
Definition 3.1. An equivalence relation E on a Polish space X is idealistic if there exist an assignment
![]() $[x]\mapsto \mathcal {F}_{[x]}$
mapping each E-class
$[x]\mapsto \mathcal {F}_{[x]}$
mapping each E-class
![]() $[x]$
to a
$[x]$
to a
![]() $\sigma $
-filter
$\sigma $
-filter
![]() $\mathcal {F}_{[x]}$
of subsets of
$\mathcal {F}_{[x]}$
of subsets of
![]() $[x]$
and a Borel function
$[x]$
and a Borel function
![]() $\zeta :X\rightarrow X$
satisfying
$\zeta :X\rightarrow X$
satisfying
-
•
 $x\,E\, \zeta ( x) $
for every
$x\,E\, \zeta ( x) $
for every
 $x\in X$
, and
$x\in X$
, and -
• for each Borel subset A of
 $X\times X$
, the set
$X\times X$
, the set
 $A_{\mathcal {F}}\subseteq X$
defined by is Borel.
$A_{\mathcal {F}}\subseteq X$
defined by is Borel. $$ \begin{align*} x\in A_{\mathcal{F}}\Leftrightarrow \left\{ x^{\prime }\in \left[ x\right] :( \zeta( x) ,x^{\prime }) \in A\right\} \in \mathcal{F}_{\left[ x\right]} \end{align*} $$
$$ \begin{align*} x\in A_{\mathcal{F}}\Leftrightarrow \left\{ x^{\prime }\in \left[ x\right] :( \zeta( x) ,x^{\prime }) \in A\right\} \in \mathcal{F}_{\left[ x\right]} \end{align*} $$
A common convention facilitates statements like the second bulleted point above: if
![]() $ \mathcal {F}$
is a filter of subsets of C and
$ \mathcal {F}$
is a filter of subsets of C and
![]() $P(x) $
is a property which elements of C may or may not have, write ‘
$P(x) $
is a property which elements of C may or may not have, write ‘
![]() $\mathcal {F}x\:\:P( x) $
’ for the assertion ‘
$\mathcal {F}x\:\:P( x) $
’ for the assertion ‘
![]() $\{x\in C:P( x) $
holds
$\{x\in C:P( x) $
holds
![]() $\}\in \mathcal {F}$
’. We may then rephrase the second item of Definition 3.1 as the requirement that for every Borel
$\}\in \mathcal {F}$
’. We may then rephrase the second item of Definition 3.1 as the requirement that for every Borel
![]() $A\subseteq X\times X$
, the set
$A\subseteq X\times X$
, the set
![]() $\{x\in X:\mathcal {F}_{\left [ x\right ] }x^{\prime }\:\:( \zeta ( x) ,x^{\prime }) \in A\}$
is Borel.
$\{x\in X:\mathcal {F}_{\left [ x\right ] }x^{\prime }\:\:( \zeta ( x) ,x^{\prime }) \in A\}$
is Borel.
Example 3.2. Let
![]() $G/N$
be a group with a Polish cover, and let
$G/N$
be a group with a Polish cover, and let
![]() $\mathcal {R}(G/N)$
be the coset equivalence relation on G, so that
$\mathcal {R}(G/N)$
be the coset equivalence relation on G, so that
![]() $x \, \mathcal {R}(G/N) \, x' \iff xN= x'N$
. Then
$x \, \mathcal {R}(G/N) \, x' \iff xN= x'N$
. Then
![]() $\mathcal {R}(G/N)$
is idealistic, as witnessed by
$\mathcal {R}(G/N)$
is idealistic, as witnessed by
![]() $\zeta :=\mathrm {id}_{G}$
, and the assignment
$\zeta :=\mathrm {id}_{G}$
, and the assignment
![]() $[x]\mapsto \mathcal {F}_{[x]}$
, with
$[x]\mapsto \mathcal {F}_{[x]}$
, with
![]() $D\in \mathcal {F}_{[x]}\iff $
“
$D\in \mathcal {F}_{[x]}\iff $
“
![]() $x^{-1}D$
is a comeager subset of the Polish group N”; see [Reference Gao31, Proposition 5.4.10].
$x^{-1}D$
is a comeager subset of the Polish group N”; see [Reference Gao31, Proposition 5.4.10].
The collection of idealistic equivalence relations enjoys several desirable closure properties. It is clear, for example, that if E is an idealistic equivalence relation on X and
![]() $ X_{0}\subseteq X$
is an E-invariant Borel subset, then
$ X_{0}\subseteq X$
is an E-invariant Borel subset, then
![]() $E|_{X_0}$
is idealistic.
$E|_{X_0}$
is idealistic.
Lemma 3.3. Suppose that
![]() $E,F$
are idealistic equivalence relations on Polish spaces
$E,F$
are idealistic equivalence relations on Polish spaces
![]() $X,Y$
, respectively. Define
$X,Y$
, respectively. Define
![]() $E\times F$
to be the equivalence relation on
$E\times F$
to be the equivalence relation on
![]() $X\times Y$
defined by
$X\times Y$
defined by
![]() $( x,y) (E\times F) ( x^{\prime },y^{\prime }) $
if and only if
$( x,y) (E\times F) ( x^{\prime },y^{\prime }) $
if and only if
![]() $x\,E\,x^{\prime }$
and
$x\,E\,x^{\prime }$
and
![]() $y\,F\,y^{\prime }$
. Then
$y\,F\,y^{\prime }$
. Then
![]() $E\times F$
is idealistic.
$E\times F$
is idealistic.
Proof. Let the assignments
![]() $[x]\mapsto \mathcal {F}_{[x]}^{X}$
and
$[x]\mapsto \mathcal {F}_{[x]}^{X}$
and
![]() $\zeta ^{X}:X\rightarrow X$
witness that E is idealistic, and let
$\zeta ^{X}:X\rightarrow X$
witness that E is idealistic, and let
![]() $[y]\mapsto \mathcal {F }_{[y]}^{Y}$
and
$[y]\mapsto \mathcal {F }_{[y]}^{Y}$
and
![]() $\zeta ^{Y}:Y\rightarrow Y$
witness that F is idealistic. Observe that an
$\zeta ^{Y}:Y\rightarrow Y$
witness that F is idealistic. Observe that an
![]() $( E\times F) $
-class
$( E\times F) $
-class
![]() $[(x,y)]$
is of the form
$[(x,y)]$
is of the form
![]() $[x]\times [y]$
where
$[x]\times [y]$
where
![]() $[x]$
is an E-class and
$[x]$
is an E-class and
![]() $[y]$
is an F-class. Define
$[y]$
is an F-class. Define
![]() $\mathcal {F}_{[(x,y)]}$
by setting
$\mathcal {F}_{[(x,y)]}$
by setting
![]() $S\in \mathcal {F}_{[(x,y)]}$
if and only if
$S\in \mathcal {F}_{[(x,y)]}$
if and only if
![]() $[\mathcal {F}_{[x]}^{X}x'\:\:\mathcal {F}_{[y]}^{Y}y'\:\:( x',y') \in S]$
, and observe that
$[\mathcal {F}_{[x]}^{X}x'\:\:\mathcal {F}_{[y]}^{Y}y'\:\:( x',y') \in S]$
, and observe that
![]() $\mathcal {F}_{[(x,y)]}$
is indeed a
$\mathcal {F}_{[(x,y)]}$
is indeed a
![]() $\sigma $
-filter. Define also the function
$\sigma $
-filter. Define also the function
![]() $\zeta :X\times Y\rightarrow X\times Y$
,
$\zeta :X\times Y\rightarrow X\times Y$
,
![]() $( x,y) \mapsto ( \zeta ^{X}( x) ,\zeta ^{Y}( y) ) $
.
$( x,y) \mapsto ( \zeta ^{X}( x) ,\zeta ^{Y}( y) ) $
.
For any
![]() $( x,y) \in X\times Y$
and Borel
$( x,y) \in X\times Y$
and Borel
![]() $A\subseteq ( X\times Y) \times ( X\times Y) $
, we have that
$A\subseteq ( X\times Y) \times ( X\times Y) $
, we have that
![]() $[\mathcal {F}_{ \left [ ( x,y) \right ] }( x^{\prime },y^{\prime }) \:\: ( \zeta ( x,y) ,( x^{\prime },y^{\prime }) ) \in A]$
if and only if
$[\mathcal {F}_{ \left [ ( x,y) \right ] }( x^{\prime },y^{\prime }) \:\: ( \zeta ( x,y) ,( x^{\prime },y^{\prime }) ) \in A]$
if and only if
![]() $[\mathcal {F}_{\left [ x\right ] }^{X}x^{\prime }\:\:\mathcal {F}_{\left [ y\right ] }^{Y}y^{\prime }\:\:( ( \zeta ^{X}( x^{\prime }) ,\zeta ^{Y}( y^{\prime }) ) ,( x^{\prime },y^{\prime }) ) \in A]$
. The set
$[\mathcal {F}_{\left [ x\right ] }^{X}x^{\prime }\:\:\mathcal {F}_{\left [ y\right ] }^{Y}y^{\prime }\:\:( ( \zeta ^{X}( x^{\prime }) ,\zeta ^{Y}( y^{\prime }) ) ,( x^{\prime },y^{\prime }) ) \in A]$
. The set
is Borel by the assumption that the assignments
![]() $[x]\mapsto \mathcal {F}_{[x]}^{X}$
and
$[x]\mapsto \mathcal {F}_{[x]}^{X}$
and
![]() $\zeta ^{X}$
and
$\zeta ^{X}$
and
![]() $ [y]\mapsto \mathcal {F}_{[y]}^{Y}$
and
$ [y]\mapsto \mathcal {F}_{[y]}^{Y}$
and
![]() $\zeta ^{Y}$
, respectively, witness that E and
$\zeta ^{Y}$
, respectively, witness that E and
![]() $ F$
are idealistic. Hence,
$ F$
are idealistic. Hence,
![]() $[(x,y)]\mapsto \mathcal {F}_{[(x,y)]}$
and
$[(x,y)]\mapsto \mathcal {F}_{[(x,y)]}$
and
![]() $ \zeta :X\times Y\rightarrow X\times Y$
witness that
$ \zeta :X\times Y\rightarrow X\times Y$
witness that
![]() $E\times F$
is idealistic.
$E\times F$
is idealistic.
Lemma 3.4. Suppose that F is an idealistic equivalence relation on a Polish space Y and Z is an F-invariant Borel subset of Y. Define
![]() $F_Z$
to be the equivalence relation on Y given by
$F_Z$
to be the equivalence relation on Y given by
![]() $ x\,F_Z\,x^{\prime }$
if and only if
$ x\,F_Z\,x^{\prime }$
if and only if
![]() $x\,F\,x^{\prime }$
or
$x\,F\,x^{\prime }$
or
![]() $x,x^{\prime }\in Z$
. Then
$x,x^{\prime }\in Z$
. Then
![]() $F_Z$
is idealistic.
$F_Z$
is idealistic.
Proof. Suppose that the assignments
![]() $[x]\mapsto \mathcal {F}_{[x]}$
and
$[x]\mapsto \mathcal {F}_{[x]}$
and
![]() $\zeta :Y\rightarrow Y$
witness that F is idealistic. Fix a Polish topology
$\zeta :Y\rightarrow Y$
witness that F is idealistic. Fix a Polish topology
![]() $\tau _Z$
on Z that is compatible with the Borel structure inherited from Y. Let C be an
$\tau _Z$
on Z that is compatible with the Borel structure inherited from Y. Let C be an
![]() $F_Z$
-equivalence class. Set
$F_Z$
-equivalence class. Set
![]() $\mathcal {F}_{C}^{\prime }:= \mathcal {F}_{C}$
if
$\mathcal {F}_{C}^{\prime }:= \mathcal {F}_{C}$
if
![]() $C=[x]$
with
$C=[x]$
with
![]() $x\not \in Z$
, and let
$x\not \in Z$
, and let
![]() $\mathcal {F}_Z^{\prime }=\{S\subseteq Z:S$
contains a
$\mathcal {F}_Z^{\prime }=\{S\subseteq Z:S$
contains a
![]() $\tau _Z$
-comeager Borel subset of
$\tau _Z$
-comeager Borel subset of
![]() $Z\}$
. Notice that for a Borel subset A of
$Z\}$
. Notice that for a Borel subset A of
![]() $Y\times Y$
and
$Y\times Y$
and
![]() $x\in Y$
, we have
$x\in Y$
, we have
![]() $[\mathcal {F}_{\left [ x\right ] }^{\prime }x^{\prime }\:\:( \zeta ( x) ,x^{\prime }) \in A]$
if and only if either
$[\mathcal {F}_{\left [ x\right ] }^{\prime }x^{\prime }\:\:( \zeta ( x) ,x^{\prime }) \in A]$
if and only if either
![]() $x\in Z$
and
$x\in Z$
and
![]() $A_{\zeta (x)}=\left \{ x^{\prime }\in Y:( \zeta ( x) ,x^{\prime }) \in A\right \} $
is comeager in Z or
$A_{\zeta (x)}=\left \{ x^{\prime }\in Y:( \zeta ( x) ,x^{\prime }) \in A\right \} $
is comeager in Z or
![]() $x\notin Z$
and
$x\notin Z$
and
![]() $[\mathcal {F}_{\left [ x\right ] }x^{\prime }\:\:( \zeta ( x) ,x^{\prime }) \in A]$
. It then follows from the reasoning, for example, of [Reference Kechris44, Theorem 16.1] that
$[\mathcal {F}_{\left [ x\right ] }x^{\prime }\:\:( \zeta ( x) ,x^{\prime }) \in A]$
. It then follows from the reasoning, for example, of [Reference Kechris44, Theorem 16.1] that
is Borel. Thus, the assignments
![]() $C\mapsto \mathcal {F}_{C}^{\prime }$
and
$C\mapsto \mathcal {F}_{C}^{\prime }$
and
![]() $ \zeta $
witness that
$ \zeta $
witness that
![]() $F_Z$
is idealistic.
$F_Z$
is idealistic.
We now recall several notions of reduction between equivalence relations; see [Reference Gao31, Definition 5.1.1] and [Reference Ros66, Definitions 2.1 and 2.2]. Suppose that E and F are equivalence relations on Polish spaces X and Y, respectively, and let
![]() $ X/ E$
and
$ X/ E$
and
![]() $Y/ F$
be the set of E and F-equivalence classes on X and Y, respectively. If
$Y/ F$
be the set of E and F-equivalence classes on X and Y, respectively. If
![]() $f:X/ E \rightarrow Y/ F$
is a function, then a lift of f is a function
$f:X/ E \rightarrow Y/ F$
is a function, then a lift of f is a function
![]() $\hat {f}:X\rightarrow Y$
such that
$\hat {f}:X\rightarrow Y$
such that
![]() $f( [x]_{E}) =[\hat {f} ( x) ]_{F}$
for every
$f( [x]_{E}) =[\hat {f} ( x) ]_{F}$
for every
![]() $x\in X$
; if some such
$x\in X$
; if some such
![]() $\hat {f}$
is, furthermore, Borel, then we say that f lifts to a Borel function
$\hat {f}$
is, furthermore, Borel, then we say that f lifts to a Borel function
![]() $ X\rightarrow Y$
.
$ X\rightarrow Y$
.
Definition 3.5. Suppose that E and F are equivalence relations on Polish spaces X and Y.
A Borel homomorphism from E to F is a function
![]() $X/E\rightarrow Y/ F$
which lifts to a Borel function
$X/E\rightarrow Y/ F$
which lifts to a Borel function
![]() $X\rightarrow Y$
.
$X\rightarrow Y$
.
A Borel reduction from E to F is an injective function
![]() $X/ E\rightarrow Y/ F$
which lifts to a Borel function
$X/ E\rightarrow Y/ F$
which lifts to a Borel function
![]() $X\rightarrow Y$
.
$X\rightarrow Y$
.
A classwise Borel isomorphism from E to F is a bijective function
![]() $X/ E\rightarrow Y/ F$
which lifts to a Borel function
$X/ E\rightarrow Y/ F$
which lifts to a Borel function
![]() $X\rightarrow Y$
and whose inverse also lifts to a Borel function
$X\rightarrow Y$
and whose inverse also lifts to a Borel function
![]() $Y\rightarrow X$
;
$Y\rightarrow X$
;
A classwise Borel embedding from E to F is a classwise Borel isomorphism from E to
![]() $F|_{Z}$
for some F-invariant Borel subset Z of Y.
$F|_{Z}$
for some F-invariant Borel subset Z of Y.
By the following lemma, Borel and idealistic equivalence relations are downwards closed with respect to Borel reducibility and classwise Borel embedding relations, respectively.
Lemma 3.6. Suppose that E and F are equivalence relations on Polish spaces X and Y. If E classwise Borel embeds into F and F is idealistic, then E is idealistic.
Proof. Suppose that F is idealistic and E classwise Borel embeds into F. Without loss of generality, we may assume E and F to be classwise Borel isomorphic. Thus, there exists a bijection
![]() $f:X/ E \rightarrow Y/ F$
such that f lifts to a Borel function
$f:X/ E \rightarrow Y/ F$
such that f lifts to a Borel function
![]() $\hat {f}:X\rightarrow Y$
and
$\hat {f}:X\rightarrow Y$
and
![]() $f^{-1}$
lifts to a Borel function
$f^{-1}$
lifts to a Borel function
![]() $\hat {f}^{\ast }:X\rightarrow Y$
.
$\hat {f}^{\ast }:X\rightarrow Y$
.
Suppose that the assignment
![]() $[y]\mapsto \mathcal {F}_{[y]}$
and the map
$[y]\mapsto \mathcal {F}_{[y]}$
and the map
![]() $\tau :Y\rightarrow Y$
witness that F is idealistic. We define an assignment
$\tau :Y\rightarrow Y$
witness that F is idealistic. We define an assignment
![]() $[x]\mapsto \mathcal {E}_{[x]}$
from E-classes to
$[x]\mapsto \mathcal {E}_{[x]}$
from E-classes to
![]() $\sigma $
-filters as follows: for each E-class
$\sigma $
-filters as follows: for each E-class
![]() $[x]$
and subset S of
$[x]$
and subset S of
![]() $[x]$
, let S be in
$[x]$
, let S be in
![]() $\mathcal {E}_{[x]}$
if and only if
$\mathcal {E}_{[x]}$
if and only if
![]() $\hat {f}^{\ast -1}( S) \in \mathcal {F}_{f([x])}$
(i.e.,
$\hat {f}^{\ast -1}( S) \in \mathcal {F}_{f([x])}$
(i.e.,
![]() $ \mathcal {F}_{[f(x)]}\:\:\hat {f}^{\ast }( y) \in S$
). Notice that for a Borel subset A of
$ \mathcal {F}_{[f(x)]}\:\:\hat {f}^{\ast }( y) \in S$
). Notice that for a Borel subset A of
![]() $X\times X$
and
$X\times X$
and
![]() $x\in X$
, we have that
$x\in X$
, we have that
![]() $[\mathcal {E} _{\left [ x\right ] }x^{\prime }\:\:( x,x^{\prime }) \in X]$
if and only if
$[\mathcal {E} _{\left [ x\right ] }x^{\prime }\:\:( x,x^{\prime }) \in X]$
if and only if
![]() $[\mathcal {F}_{f( \left [ x\right ] ) }y^{\prime }\:\:(x, \hat {f}^{\ast }( y^{\prime }) )\in A]$
. We also define the Borel map
$[\mathcal {F}_{f( \left [ x\right ] ) }y^{\prime }\:\:(x, \hat {f}^{\ast }( y^{\prime }) )\in A]$
. We also define the Borel map
![]() $\zeta =\hat {f}^{\ast }\circ \tau \circ \hat {f}:X\rightarrow X$
. Notice that
$\zeta =\hat {f}^{\ast }\circ \tau \circ \hat {f}:X\rightarrow X$
. Notice that
![]() $\zeta (x)\,E\,x$
for every
$\zeta (x)\,E\,x$
for every
![]() $x\in X$
.
$x\in X$
.
Let A be a Borel subset of
![]() $X\times X$
. Consider the Borel subset B of
$X\times X$
. Consider the Borel subset B of
![]() $Y\times Y$
defined by
$Y\times Y$
defined by
![]() $( y,y^{\prime }) \in B$
if and only if
$( y,y^{\prime }) \in B$
if and only if
![]() $(\hat {f}^{\ast }( y) ,\hat {f}^{\ast }( y^{\prime }) )\in A$
. Then, by assumption, we have that
$(\hat {f}^{\ast }( y) ,\hat {f}^{\ast }( y^{\prime }) )\in A$
. Then, by assumption, we have that
![]() $\{y\in Y: \mathcal {F}_{\left [ y\right ] }y^{\prime }\:\:( \tau ( y) ,y^{\prime }) \in B\}$
is Borel. Hence,
$\{y\in Y: \mathcal {F}_{\left [ y\right ] }y^{\prime }\:\:( \tau ( y) ,y^{\prime }) \in B\}$
is Borel. Hence,
![]() $\hat {f}^{-1}( \{y\in Y:\mathcal {F}_{\left [ y\right ] }y^{\prime }\:\:( \tau ( y) ,y^{\prime }) \in B\}) \subseteq X$
is Borel. We then have
$\hat {f}^{-1}( \{y\in Y:\mathcal {F}_{\left [ y\right ] }y^{\prime }\:\:( \tau ( y) ,y^{\prime }) \in B\}) \subseteq X$
is Borel. We then have
if and only if
if and only if
if and only if
Hence,
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
![]() $\zeta $
witness that E is idealistic.
$\zeta $
witness that E is idealistic.
We now recall some results from [Reference Gao31] and [Reference Kechris and Macdonald45]. We will always assume E and F to be analytic equivalence relations on Polish spaces
![]() $X,Y$
, respectively. The following result is essentially [Reference Kechris and Macdonald45, Lemmas 3.7, 3.8], although a slightly more restrictive notion of idealistic equivalence relation is considered there; its proof readily adapts to our more generous notion.
$X,Y$
, respectively. The following result is essentially [Reference Kechris and Macdonald45, Lemmas 3.7, 3.8], although a slightly more restrictive notion of idealistic equivalence relation is considered there; its proof readily adapts to our more generous notion.
Proposition 3.7 (Kechris–Macdonald).
Suppose that E is idealistic and F is Borel. Then a Borel reduction from E to F is a classwise Borel embedding.
Proof. Suppose that
![]() $[x]\mapsto \mathcal {F}_{[x]}$
and
$[x]\mapsto \mathcal {F}_{[x]}$
and
![]() $\zeta :X\rightarrow X$
witness that E is idealistic. Suppose that
$\zeta :X\rightarrow X$
witness that E is idealistic. Suppose that
![]() $f:X/E \rightarrow Y/F $
is a Borel reduction from E to F, and let
$f:X/E \rightarrow Y/F $
is a Borel reduction from E to F, and let
![]() $\hat {f} :X\rightarrow Y$
be a Borel lift of f. We will show that the F-saturation
$\hat {f} :X\rightarrow Y$
be a Borel lift of f. We will show that the F-saturation
 $$ \begin{align*} \lbrack \hat{f}( X) ]_{F} &=\{y\in Y:\exists x\in X\:\,y\,F\hat{f} ( x) \} \\ &=\{y\in Y:\exists x\in X\:\,y\,F\,(\hat{f}\circ \zeta )( x) \} \end{align*} $$
$$ \begin{align*} \lbrack \hat{f}( X) ]_{F} &=\{y\in Y:\exists x\in X\:\,y\,F\hat{f} ( x) \} \\ &=\{y\in Y:\exists x\in X\:\,y\,F\,(\hat{f}\circ \zeta )( x) \} \end{align*} $$
of
![]() $\hat {f}( X) $
is a Borel subset Z of Y and that there exists a Borel lift
$\hat {f}( X) $
is a Borel subset Z of Y and that there exists a Borel lift
![]() $\hat {f}^{*}$
of
$\hat {f}^{*}$
of
![]() $f^{-1}:Z/F\to X/E$
.
$f^{-1}:Z/F\to X/E$
.
Define the subset P of
![]() $Y\times X$
by setting
$Y\times X$
by setting
![]() $( y,x) \in P$
if and only if
$( y,x) \in P$
if and only if
![]() $y\,F\,(\hat {f}\circ \zeta )( x) $
. Then
$y\,F\,(\hat {f}\circ \zeta )( x) $
. Then
![]() $[\hat {f}( X) ]_{F}$
is the projection of P onto the first coordinate. By the ‘large sections’ uniformization theorem figuring in the proof of [Reference Kechris and Macdonald45, Lemma 3.7], it will suffice to show that there is a map
$[\hat {f}( X) ]_{F}$
is the projection of P onto the first coordinate. By the ‘large sections’ uniformization theorem figuring in the proof of [Reference Kechris and Macdonald45, Lemma 3.7], it will suffice to show that there is a map
![]() $y\mapsto \mathcal {G}_{y}$
that assigns to each
$y\mapsto \mathcal {G}_{y}$
that assigns to each
![]() $y\in \lbrack \hat {f}( X) ]_{F}$
a
$y\in \lbrack \hat {f}( X) ]_{F}$
a
![]() $\sigma $
-filter
$\sigma $
-filter
![]() $\mathcal {G} _{y}$
of subsets of
$\mathcal {G} _{y}$
of subsets of
![]() $f^{-1}( [ y]) $
such that for each Borel subset R of
$f^{-1}( [ y]) $
such that for each Borel subset R of
![]() $Y\times X$
, there exist a
$Y\times X$
, there exist a
![]() $\boldsymbol {\Sigma } _{1}^{1}$
set
$\boldsymbol {\Sigma } _{1}^{1}$
set
![]() $S\subseteq Y$
and a
$S\subseteq Y$
and a
![]() $\boldsymbol {\Pi }_{1}^{1}$
set
$\boldsymbol {\Pi }_{1}^{1}$
set
![]() $ T\subseteq Y$
such that, setting
$ T\subseteq Y$
such that, setting
one has
for every
![]() $y\in \lbrack \hat {f}( X) ]_{F}$
. The uniformization given by the aforementioned theorem will then be such an
$y\in \lbrack \hat {f}( X) ]_{F}$
. The uniformization given by the aforementioned theorem will then be such an
![]() $\hat {f}^{*}$
as we had desired.
$\hat {f}^{*}$
as we had desired.
To this end, define
![]() $\mathcal {G}_{y}=\mathcal {F}_{f^{-1}([y])}$
for
$\mathcal {G}_{y}=\mathcal {F}_{f^{-1}([y])}$
for
![]() $y\in \lbrack \hat {f}( X) ]_{F}$
. To see that the assignment
$y\in \lbrack \hat {f}( X) ]_{F}$
. To see that the assignment
![]() $y\mapsto \mathcal {F}_{f^{-1}([y])}$
satisfies the above requirement, suppose
$y\mapsto \mathcal {F}_{f^{-1}([y])}$
satisfies the above requirement, suppose
![]() $R\subseteq Y\times X$
is Borel. Then for
$R\subseteq Y\times X$
is Borel. Then for
![]() $y\in \lbrack \hat {f}( X) ]_{F}$
, we have that
$y\in \lbrack \hat {f}( X) ]_{F}$
, we have that
![]() $R_{y}\in \mathcal {F} _{f^{-1}([y])}$
if and only if
$R_{y}\in \mathcal {F} _{f^{-1}([y])}$
if and only if
![]() $[\mathcal {F}_{f^{-1}([y])}x^{\prime }\:\:( y,x^{\prime }) \in R]$
, if and only if
$[\mathcal {F}_{f^{-1}([y])}x^{\prime }\:\:( y,x^{\prime }) \in R]$
, if and only if
if and only if
This concludes the proof.
Corollary 3.8. Suppose that E is idealistic and F is Borel. Then a surjective Borel reduction from E to F is a classwise Borel isomorphism.
The following related result is [Reference Ros66, Proposition 2.3].
Proposition 3.9 (Motto Ros).
If there is a classwise Borel embedding from E to F and there is a classwise Borel embedding from F to E, then there is a classwise Borel isomorphism from E to F.
Recall that a Borel selector for a Borel equivalence relation E on a Polish space X is a function
![]() $s:X\rightarrow X$
such that
$s:X\rightarrow X$
such that
![]() $s(x)\,E\,x$
and
$s(x)\,E\,x$
and
![]() $ x\,E\,y\Leftrightarrow s( x) =s( y) $
for every
$ x\,E\,y\Leftrightarrow s( x) =s( y) $
for every
![]() $x,y\in X$
. The principal filters that selectors determine on the classes of E witness that E is idealistic.
$x,y\in X$
. The principal filters that selectors determine on the classes of E witness that E is idealistic.
Lemma 3.10. Let E be a Borel equivalence relation on a Polish space X. If E admits a Borel selector, then E is idealistic.
Proof. Let s be a Borel selector for E. Then s determines a function
![]() $f:X/ E \rightarrow X$
,
$f:X/ E \rightarrow X$
,
![]() $\left [ x\right ] \mapsto s( x) $
. For each E-class
$\left [ x\right ] \mapsto s( x) $
. For each E-class
![]() $[x]$
, let
$[x]$
, let
![]() $ \mathcal {F}_{[x]}=\{S\subseteq [x]\mid f([x])\in S\}$
. For every Borel subset A of
$ \mathcal {F}_{[x]}=\{S\subseteq [x]\mid f([x])\in S\}$
. For every Borel subset A of
![]() $ X\times X$
and
$ X\times X$
and
![]() $x\in X$
, then, [
$x\in X$
, then, [
![]() $\mathcal {F}_{\left [ x\right ] }x^{\prime }\:\: (x,x^{\prime }) \in A]$
if and only if
$\mathcal {F}_{\left [ x\right ] }x^{\prime }\:\: (x,x^{\prime }) \in A]$
if and only if
![]() $(x,s(x)) \in A$
. Hence,
$(x,s(x)) \in A$
. Hence,
![]() $A_{\mathcal {F}}=\left \{ x\in X: \mathcal {F}_{\left [ x\right ] }x^{\prime }\:\:(x,x^{\prime }) \in A\right \}$
is a Borel subset of X, as desired.
$A_{\mathcal {F}}=\left \{ x\in X: \mathcal {F}_{\left [ x\right ] }x^{\prime }\:\:(x,x^{\prime }) \in A\right \}$
is a Borel subset of X, as desired.
3.2. Definable sets
A definable set is a pair
![]() $\left ( X,E\right ) $
such that X is a Polish space and E is a Borel and idealistic equivalence relation on X. We will indulge below in the common abuse whereby the notation
$\left ( X,E\right ) $
such that X is a Polish space and E is a Borel and idealistic equivalence relation on X. We will indulge below in the common abuse whereby the notation
![]() $X/E$
may stand either for this pair or for its associated quotient set, as context will indicate. A definable subset of a definable set
$X/E$
may stand either for this pair or for its associated quotient set, as context will indicate. A definable subset of a definable set
![]() $X/E$
is a definable set of the form
$X/E$
is a definable set of the form
![]() $Y/E \subseteq X/E$
where Y is an E-invariant Borel subset of
$Y/E \subseteq X/E$
where Y is an E-invariant Borel subset of
![]() $ X $
. We regard a Polish space X, in particular, as a definable set
$ X $
. We regard a Polish space X, in particular, as a definable set
![]() $ X/E$
, where E is the relation of equality.
$ X/E$
, where E is the relation of equality.
If
![]() $X/E$
and
$X/E$
and
![]() $Y/F$
are definable sets, then a definable function
$Y/F$
are definable sets, then a definable function
![]() $X/E \rightarrow Y/F$
is a Borel homomorphism from E to F (i.e., a function
$X/E \rightarrow Y/F$
is a Borel homomorphism from E to F (i.e., a function
![]() $X/E \rightarrow Y/F$
that lifts to a Borel function
$X/E \rightarrow Y/F$
that lifts to a Borel function
![]() $ X\rightarrow Y$
). We let
$ X\rightarrow Y$
). We let
![]() $\mathsf {DSet}$
be the category that has definable sets as objects and definable functions as morphisms. The identity morphism on
$\mathsf {DSet}$
be the category that has definable sets as objects and definable functions as morphisms. The identity morphism on
![]() $X/E$
is the identity function, and composition of morphisms is given by composition of functions. We now observe that this category has similar properties to the paradigmatic category
$X/E$
is the identity function, and composition of morphisms is given by composition of functions. We now observe that this category has similar properties to the paradigmatic category
![]() $\mathsf {Set}$
of sets.
$\mathsf {Set}$
of sets.
In the framework of
![]() $\mathsf {DSet}$
, for example, Corollary 3.8 takes the following form:
$\mathsf {DSet}$
, for example, Corollary 3.8 takes the following form:
Proposition 3.11 (Kechris–Macdonald).
Suppose that
![]() $X/E$
and
$X/E$
and
![]() $Y/F$
are definable sets, and
$Y/F$
are definable sets, and
![]() $f:X/E \rightarrow Y/F$
is a definable function. The following assertions are equivalent:
$f:X/E \rightarrow Y/F$
is a definable function. The following assertions are equivalent:
-
(1) f is a bijection;
-
(2) f is an isomorphism in
 $\mathsf {DSet}$
.
$\mathsf {DSet}$
.
The following also is a consequence of Proposition 3.7.
Proposition 3.12 (Kechris–Macdonald).
Suppose that
![]() $X/E$
and
$X/E$
and
![]() $ Y/F$
are definable sets, and
$ Y/F$
are definable sets, and
![]() $f:X/E\rightarrow Y/F$
is an injective definable function. Then there is a definable subset
$f:X/E\rightarrow Y/F$
is an injective definable function. Then there is a definable subset
![]() $Z/F$
of
$Z/F$
of
![]() $Y/F$
such that
$Y/F$
such that
![]() $f:X/E \rightarrow Z/F $
is a definable bijection.
$f:X/E \rightarrow Z/F $
is a definable bijection.
Proposition 3.9 above, similarly, may be rephrased as a Cantor–Bernstein theorem for definable sets.
Proposition 3.13 (Motto Ros).
Suppose that
![]() $X/E$
and
$X/E$
and
![]() $ Y/F$
are definable sets. If there exist an injective definable function
$ Y/F$
are definable sets. If there exist an injective definable function
![]() $X/E \rightarrow Y/F $
and an injective definable function
$X/E \rightarrow Y/F $
and an injective definable function
![]() $Y/F \rightarrow X/E$
, then there exists a bijective definable function
$Y/F \rightarrow X/E$
, then there exists a bijective definable function
![]() $X/E \rightarrow Y/F $
.
$X/E \rightarrow Y/F $
.
The category
![]() $\mathsf {DSet}$
has a number of further pleasant and
$\mathsf {DSet}$
has a number of further pleasant and
![]() $\mathsf {Set}$
-like properties. Observe, for example, that if the definable sets
$\mathsf {Set}$
-like properties. Observe, for example, that if the definable sets
![]() $X/E$
and
$X/E$
and
![]() $Y/F$
are countable sets, then there is a definable bijection from
$Y/F$
are countable sets, then there is a definable bijection from
![]() $ X/E$
to
$ X/E$
to
![]() $Y/F$
if and only if there is a bijection from
$Y/F$
if and only if there is a bijection from
![]() $X/E$
to
$X/E$
to
![]() $Y/F$
.
$Y/F$
.
Recall that a morphism
![]() $f:x\rightarrow y$
in a category
$f:x\rightarrow y$
in a category
![]() $\mathcal {C}$
is
$\mathcal {C}$
is
-
• monic if for any two morphisms
 $g_{0},g_{1}:z\rightarrow x$
, if
$g_{0},g_{1}:z\rightarrow x$
, if
 $fg_{0}=fg_{1}$
, then
$fg_{0}=fg_{1}$
, then
 $g_{0}=g_{1}$
, and
$g_{0}=g_{1}$
, and -
• epic if for any two morphisms
 $g_{0},g_{1}:y\rightarrow z$
, if
$g_{0},g_{1}:y\rightarrow z$
, if
 $g_{0}f=g_{1}f$
, then
$g_{0}f=g_{1}f$
, then
 $g_{0}=g_{1}$
.
$g_{0}=g_{1}$
.
It is easy to see that a definable function is monic in
![]() $\mathsf {DSet}$
if and only if it is injective, and epic in
$\mathsf {DSet}$
if and only if it is injective, and epic in
![]() $\mathsf {DSet}$
if and only if it is surjective. The initial object is
$\mathsf {DSet}$
if and only if it is surjective. The initial object is
![]() $\mathsf {DSet}$
is the empty definable set, and a final object in
$\mathsf {DSet}$
is the empty definable set, and a final object in
![]() $\mathsf {DSet}$
is a definable set with only one element.
$\mathsf {DSet}$
is a definable set with only one element.
If
![]() $X/E$
and
$X/E$
and
![]() $Y/F $
are definable sets, then the coproduct
$Y/F $
are definable sets, then the coproduct
![]() $X/E\amalg Y/F $
is the definable set obtained as the quotient of the disjoint union
$X/E\amalg Y/F $
is the definable set obtained as the quotient of the disjoint union
![]() $X\amalg Y$
of
$X\amalg Y$
of
![]() $ X$
and Y by the equivalence relation on
$ X$
and Y by the equivalence relation on
![]() $X\amalg Y$
that restricts to E on X and to F on Y. Coproducts of sequences
$X\amalg Y$
that restricts to E on X and to F on Y. Coproducts of sequences
![]() $\left ( X_{n}/ E_{n}\right ) _{n\in \omega }$
of definable sets are defined similarly.
$\left ( X_{n}/ E_{n}\right ) _{n\in \omega }$
of definable sets are defined similarly.
The product of
![]() $X/E$
and
$X/E$
and
![]() $Y/F$
is the definable set obtained as the quotient of the product
$Y/F$
is the definable set obtained as the quotient of the product
![]() $X\times Y$
by the equivalence relation
$X\times Y$
by the equivalence relation
![]() $E\times F$
defined as in Lemma 3.3. In our conclusion, we record the question of whether the category
$E\times F$
defined as in Lemma 3.3. In our conclusion, we record the question of whether the category
![]() $\mathsf {DSet}$
possesses arbitrary countable products. Given two definable functions
$\mathsf {DSet}$
possesses arbitrary countable products. Given two definable functions
![]() $f,g:X/ E \rightarrow Y/ F$
, the equalizer of f and g is the definable subset of
$f,g:X/ E \rightarrow Y/ F$
, the equalizer of f and g is the definable subset of
![]() $X/E$
given by
$X/E$
given by
The existence of products and equalizers ensures the existence of pullbacks of definable functions
![]() $f:X/E\to Y/F$
and
$f:X/E\to Y/F$
and
![]() $f^{\prime }:X^{\prime }/E^{\prime } \rightarrow Y/F$
. These are the definable subsets of
$f^{\prime }:X^{\prime }/E^{\prime } \rightarrow Y/F$
. These are the definable subsets of
![]() $X/E \times X^{\prime }/E^{\prime }$
consisting of pairs
$X/E \times X^{\prime }/E^{\prime }$
consisting of pairs
![]() $(x,y) $
such that
$(x,y) $
such that
![]() $f( x) =f^{\prime }( x^{\prime })$
.
$f( x) =f^{\prime }( x^{\prime })$
.
3.3. Pointed definable sets
We will also consider pointed definable sets, which are just definable sets
![]() $X/E$
with a distinguished point (the basepoint). A basepoint-preserving definable function between pointed definable sets is simply a function that maps the basepoint to the basepoint. This defines a category
$X/E$
with a distinguished point (the basepoint). A basepoint-preserving definable function between pointed definable sets is simply a function that maps the basepoint to the basepoint. This defines a category
![]() $\mathsf {DSet}_{\ast }$
, which may be seen as the under category
$\mathsf {DSet}_{\ast }$
, which may be seen as the under category
![]() $\left \{ \ast \right \} \downarrow \mathsf {DSet}$
of
$\left \{ \ast \right \} \downarrow \mathsf {DSet}$
of
![]() $\mathsf {DSet}$
-morphisms from
$\mathsf {DSet}$
-morphisms from
![]() $\left \{ \ast \right \} $
, where
$\left \{ \ast \right \} $
, where
![]() $\left \{ \ast \right \} $
is a definable set with just one point. In
$\left \{ \ast \right \} $
is a definable set with just one point. In
![]() $\mathsf {DSet}_{\ast }$
, the set
$\mathsf {DSet}_{\ast }$
, the set
![]() $\left \{ \ast \right \} $
is a null object (i.e., it is both initial and terminal). For any two pointed definable sets, there exists a unique basepoint-preserving constant function or zero arrow. Thus, we may define the cokernel of a basepoint-preserving injective definable function
$\left \{ \ast \right \} $
is a null object (i.e., it is both initial and terminal). For any two pointed definable sets, there exists a unique basepoint-preserving constant function or zero arrow. Thus, we may define the cokernel of a basepoint-preserving injective definable function
![]() $f:X/E \rightarrow Y/F$
. This is the definable set obtained as follows. We have that
$f:X/E \rightarrow Y/F$
. This is the definable set obtained as follows. We have that
![]() $f(X/E) =Z/F$
for some definable subset
$f(X/E) =Z/F$
for some definable subset
![]() $Z/F$
of
$Z/F$
of
![]() $Y/F$
. Define the equivalence relation
$Y/F$
. Define the equivalence relation
![]() $F_{Z}$
on Y in terms of Z as in Lemma 3.4. The cokernel of f is then
$F_{Z}$
on Y in terms of Z as in Lemma 3.4. The cokernel of f is then
![]() $Y/F_{Z}$
. Intuitively,
$Y/F_{Z}$
. Intuitively,
![]() $ Y/F_{Z}$
is the definable set obtained from
$ Y/F_{Z}$
is the definable set obtained from
![]() $Y/F$
by identifying the definable subset
$Y/F$
by identifying the definable subset
![]() $Z/F$
to a single basepoint.
$Z/F$
to a single basepoint.
3.4. Definable monoids and definable groups
One may interpret definable monoids and definable groups as monoids and groups in
![]() $\mathsf {DSet}$
, as a particular instance of monoids and groups in a category in the sense of [Reference MacLane53, Section III.6]. Explicitly, a definable monoid is a pointed definable set
$\mathsf {DSet}$
, as a particular instance of monoids and groups in a category in the sense of [Reference MacLane53, Section III.6]. Explicitly, a definable monoid is a pointed definable set
![]() $X/E$
together with a definable function
$X/E$
together with a definable function
![]() $\mu :X/E\times X/E \rightarrow X/E$
that is an associative binary operation with the basepoint as identity element. A definable group is a definable monoid
$\mu :X/E\times X/E \rightarrow X/E$
that is an associative binary operation with the basepoint as identity element. A definable group is a definable monoid
![]() $ \left ( X/E,\mu \right ) $
that is a also a group, and such that the function
$ \left ( X/E,\mu \right ) $
that is a also a group, and such that the function
![]() $X/E \rightarrow X/E$
mapping each element to its inverse is a definable function. Evidently, definable monoids and groups form subcategories of the category of pointed definable sets. A definable group homomorphism between definable groups is a definable function that is also a group homomorphism. A definable subgroup of
$X/E \rightarrow X/E$
mapping each element to its inverse is a definable function. Evidently, definable monoids and groups form subcategories of the category of pointed definable sets. A definable group homomorphism between definable groups is a definable function that is also a group homomorphism. A definable subgroup of
![]() $ X/E$
is a simply a definable subset
$ X/E$
is a simply a definable subset
![]() $Y/E$
that is also a subgroup. Notice that the kernel of a definable group homomorphism is a definable subgroup. A definable exact sequence of definable groups is a sequence
$Y/E$
that is also a subgroup. Notice that the kernel of a definable group homomorphism is a definable subgroup. A definable exact sequence of definable groups is a sequence
of definable groups and definable group homomorphisms such that f is injective, g is surjective, and the kernel of g is the image of f. Notice that the category of groups with a Polish cover
![]() $G/N$
is a full subcategory of the category of definable groups. We say that a definable group
$G/N$
is a full subcategory of the category of definable groups. We say that a definable group
![]() $X/E$
is essentially a group with a Polish cover if it definably isomorphic to a group with a Polish cover.
$X/E$
is essentially a group with a Polish cover if it definably isomorphic to a group with a Polish cover.
3.5. Semidefinable sets
In the following, we will also consider analytic equivalence relations on Polish spaces that we do not know or have not yet shown to be Borel or idealistic. We will call a quotient
![]() $X/E$
of a Polish space by an analytic equivalence relation a semidefinable set. Such pairs form the objects of a category
$X/E$
of a Polish space by an analytic equivalence relation a semidefinable set. Such pairs form the objects of a category
![]() $\mathsf {SemiDSet}$
of semidefinable sets in which morphisms are, as above, definable functions
$\mathsf {SemiDSet}$
of semidefinable sets in which morphisms are, as above, definable functions
![]() $f:X/E\to Y/F$
(i.e., functions f which lift to Borel functions
$f:X/E\to Y/F$
(i.e., functions f which lift to Borel functions
![]() $X\to Y$
). Notice that an isomorphism in this category is a definable bijection whose inverse is also definable. By definition, the category of definable sets is a full subcategory of the category of semidefinable sets. The notions of semidefinable subset, semidefinable group and semidefinable subgroup may be defined just as in the definable case. The following is immediate from Lemma 3.6.
$X\to Y$
). Notice that an isomorphism in this category is a definable bijection whose inverse is also definable. By definition, the category of definable sets is a full subcategory of the category of semidefinable sets. The notions of semidefinable subset, semidefinable group and semidefinable subgroup may be defined just as in the definable case. The following is immediate from Lemma 3.6.
Lemma 3.14. If a semidefinable set
![]() $X/E$
is isomorphic in
$X/E$
is isomorphic in
![]() $\mathsf {SemiDSet}$
to a definable set
$\mathsf {SemiDSet}$
to a definable set
![]() $Y/F$
, then
$Y/F$
, then
![]() $X/E$
is a definable set.
$X/E$
is a definable set.
As in Section 3.1, the existence of a Borel selector may entail that a semidefinable object is, in fact, in
![]() $\mathsf {DSet}$
.
$\mathsf {DSet}$
.
Lemma 3.15. Suppose that
![]() $X/E$
is a semidefinable group and
$X/E$
is a semidefinable group and
![]() $Y/E$
is a semidefinable subgroup. Define the equivalence relation F on X by setting
$Y/E$
is a semidefinable subgroup. Define the equivalence relation F on X by setting
![]() $x\,F\,x^{\prime }$
if and only if
$x\,F\,x^{\prime }$
if and only if
![]() $ \left [ x\right ] _{E}\cdot \left [ x^{\prime }\right ] _{E}^{-1}\in Y/E$
. Suppose that F admits a Borel selector. Then
$ \left [ x\right ] _{E}\cdot \left [ x^{\prime }\right ] _{E}^{-1}\in Y/E$
. Suppose that F admits a Borel selector. Then
-
(1) if
 $E|_{Y}$
is Borel, then E is Borel.
$E|_{Y}$
is Borel, then E is Borel. -
(2) if
 $E|_{Y}$
is idealistic, then E is idealistic.
$E|_{Y}$
is idealistic, then E is idealistic.
Proof. We let
![]() $X\times X\rightarrow X$
,
$X\times X\rightarrow X$
,
![]() $\left ( x,y\right ) \mapsto x\cdot y$
be a Borel lift of the group operation on
$\left ( x,y\right ) \mapsto x\cdot y$
be a Borel lift of the group operation on
![]() $X/E$
. Let s be a Borel selector for F. Notice that the relation E is finer than F; hence, the Borel selector s for F induces a definable function
$X/E$
. Let s be a Borel selector for F. Notice that the relation E is finer than F; hence, the Borel selector s for F induces a definable function
![]() $ \hat {s}:X/E\rightarrow X$
,
$ \hat {s}:X/E\rightarrow X$
,
![]() $\left [ x\right ] \mapsto s( x) $
. Observe that if
$\left [ x\right ] \mapsto s( x) $
. Observe that if
![]() $T=\left \{ s( x) :x\in X\right \} $
, then
$T=\left \{ s( x) :x\in X\right \} $
, then
![]() $T\subseteq X$
is a Borel transversal for F (i.e., T meets each F-equivalence class in exactly one point). Notice that the map
$T\subseteq X$
is a Borel transversal for F (i.e., T meets each F-equivalence class in exactly one point). Notice that the map
 $$ \begin{align*} Y/ E\times T &\rightarrow X/ E\\ \left( \left[ y\right] _{E},t\right) &\mapsto [y\cdot t]_{E} \end{align*} $$
$$ \begin{align*} Y/ E\times T &\rightarrow X/ E\\ \left( \left[ y\right] _{E},t\right) &\mapsto [y\cdot t]_{E} \end{align*} $$
is a definable bijection with definable inverse
 $$ \begin{align*} X/E &\rightarrow Y/E \times T \\ \left[ x\right] _{E} &\mapsto (\left[ x\right] _{E}\cdot \left[ s( x) \right] _{E}^{-1},s(x) )\text{.} \end{align*} $$
$$ \begin{align*} X/E &\rightarrow Y/E \times T \\ \left[ x\right] _{E} &\mapsto (\left[ x\right] _{E}\cdot \left[ s( x) \right] _{E}^{-1},s(x) )\text{.} \end{align*} $$
This shows that the semidefinable set
![]() $X/ E$
is isomorphic in
$X/ E$
is isomorphic in
![]() $ \mathsf {SemiDSet}$
to
$ \mathsf {SemiDSet}$
to
![]() $Y/E \times T$
. If
$Y/E \times T$
. If
![]() $Y/E$
is Borel or idealistic, respectively, then
$Y/E$
is Borel or idealistic, respectively, then
![]() $Y/E\times T$
is Borel or idealistic, respectively; see Lemma 3.3. The conclusion thus follows from Lemma 3.6.
$Y/E\times T$
is Borel or idealistic, respectively; see Lemma 3.3. The conclusion thus follows from Lemma 3.6.
4. Homotopy is idealistic
Let X and Y be locally compact metrizable spaces, and let
![]() $[X,Y]$
be the set of all homotopy classes of maps from X to Y. Since the space
$[X,Y]$
be the set of all homotopy classes of maps from X to Y. Since the space
![]() $\mathrm {Map}(X,Y)$
of all maps from X to Y is Polish when endowed with the compact-open topology and the homotopy relation between elements of
$\mathrm {Map}(X,Y)$
of all maps from X to Y is Polish when endowed with the compact-open topology and the homotopy relation between elements of
![]() $\mathrm {Map}(X,Y)$
is clearly analytic,
$\mathrm {Map}(X,Y)$
is clearly analytic,
![]() $[X,Y]$
is naturally viewed as an object in the category
$[X,Y]$
is naturally viewed as an object in the category
![]() $\mathsf {SemiDSet}$
of semidefinable sets. By a theorem of Becker’s, any analytic equivalence relation on the Cantor space may be realized as
$\mathsf {SemiDSet}$
of semidefinable sets. By a theorem of Becker’s, any analytic equivalence relation on the Cantor space may be realized as
![]() $[*,Y]$
for some compact
$[*,Y]$
for some compact
![]() $Y\subseteq \mathbb {R}^3$
(see [Reference Becker5, Theorem 4.1]); hence,
$Y\subseteq \mathbb {R}^3$
(see [Reference Becker5, Theorem 4.1]); hence,
![]() $[X,Y]$
is not in general a definable set. In contrast, for any locally compact Polish space X, if
$[X,Y]$
is not in general a definable set. In contrast, for any locally compact Polish space X, if
![]() $Y=P$
is a polyhedral H-group, then
$Y=P$
is a polyhedral H-group, then
![]() $[X,Y]$
is a definable set; this is the result appearing as Theorem 1.2 in our introduction. A main ingredient in this theorem is the more general fact that for any locally compact Polish space X and countable polyhedron Y, the homotopy relation on
$[X,Y]$
is a definable set; this is the result appearing as Theorem 1.2 in our introduction. A main ingredient in this theorem is the more general fact that for any locally compact Polish space X and countable polyhedron Y, the homotopy relation on
![]() $\mathrm {Map}(X,Y)$
is idealistic. This we show in Section 4.4 below. This and several subsequent arguments make use of Borsuk’s Homotopy Extension Theorem; we record the classical version in the present section, proving and applying its definable version in Section 6 below.
$\mathrm {Map}(X,Y)$
is idealistic. This we show in Section 4.4 below. This and several subsequent arguments make use of Borsuk’s Homotopy Extension Theorem; we record the classical version in the present section, proving and applying its definable version in Section 6 below.
4.1. Homotopy
Let
![]() $\mathsf {LC}$
denote the category of locally compact Polish spaces and continuous functions; we will often term the latter maps, simply. For any two locally compact spaces X and Y, we endow the hom-set
$\mathsf {LC}$
denote the category of locally compact Polish spaces and continuous functions; we will often term the latter maps, simply. For any two locally compact spaces X and Y, we endow the hom-set
![]() $\mathsf {LC}( X,Y)$
with the compact-open topology. This is the topology with subbasis the collection of all sets of the form
$\mathsf {LC}( X,Y)$
with the compact-open topology. This is the topology with subbasis the collection of all sets of the form
![]() $\{f\in \mathsf {LC}(X,Y):f(K) \subseteq U\} $
for some compact subset
$\{f\in \mathsf {LC}(X,Y):f(K) \subseteq U\} $
for some compact subset
![]() $K\subseteq X$
and open subset
$K\subseteq X$
and open subset
![]() $U\subseteq Y$
. With this topology, each such
$U\subseteq Y$
. With this topology, each such
![]() $\mathsf {LC}( X,Y) $
is a Polish space, and what is more, the composition functions
$\mathsf {LC}( X,Y) $
is a Polish space, and what is more, the composition functions
![]() $\mathsf {LC}( Y,Z) \times \mathsf {LC}( X,Y) \rightarrow \mathsf {LC}(X,Z)$
are all continuous. In this way, we regard
$\mathsf {LC}( Y,Z) \times \mathsf {LC}( X,Y) \rightarrow \mathsf {LC}(X,Z)$
are all continuous. In this way, we regard
![]() $\mathsf {LC}$
as a Polish category, by which we mean a category enriched over the category of Polish spaces [Reference Kelly46]. We denote by
$\mathsf {LC}$
as a Polish category, by which we mean a category enriched over the category of Polish spaces [Reference Kelly46]. We denote by
![]() $\mathsf {C}$
the full subcategory of
$\mathsf {C}$
the full subcategory of
![]() $\mathsf {LC}$
consisting of compact spaces.
$\mathsf {LC}$
consisting of compact spaces.
Let
![]() $\mathcal {C}$
be a category with small (i.e., set-sized) hom-sets. A congruence
$\mathcal {C}$
be a category with small (i.e., set-sized) hom-sets. A congruence
![]() $\equiv $
on
$\equiv $
on
![]() $\mathcal {C}$
[Reference MacLane53, Section I.8] is given by an assignment to each pair of objects
$\mathcal {C}$
[Reference MacLane53, Section I.8] is given by an assignment to each pair of objects
![]() $x,y$
of
$x,y$
of
![]() $\mathcal {C}$
of an equivalence relation
$\mathcal {C}$
of an equivalence relation
![]() $\equiv _{x,y}$
on
$\equiv _{x,y}$
on
![]() $\mathcal {C}( x,y) $
such that for objects
$\mathcal {C}( x,y) $
such that for objects
![]() $x,y,z$
and morphisms
$x,y,z$
and morphisms
![]() $f_{1},f_{2}:x\rightarrow y$
and
$f_{1},f_{2}:x\rightarrow y$
and
![]() $ g_{1},g_{2}:y\rightarrow z$
in
$ g_{1},g_{2}:y\rightarrow z$
in
![]() $\mathcal {C}$
, if
$\mathcal {C}$
, if
![]() $f_{1}\equiv _{x,y}f_{2}$
and
$f_{1}\equiv _{x,y}f_{2}$
and
![]() $g_{1}\equiv _{y,z}g_{2}$
, then
$g_{1}\equiv _{y,z}g_{2}$
, then
![]() $g_{1}f_{1} \equiv _{x,z} g_{2}f_{2} $
. One may regard the pair
$g_{1}f_{1} \equiv _{x,z} g_{2}f_{2} $
. One may regard the pair
![]() $\left ( \mathcal {C},\equiv \right ) $
as a (strict)
$\left ( \mathcal {C},\equiv \right ) $
as a (strict)
![]() $2$
-category by declaring that for objects
$2$
-category by declaring that for objects
![]() $ x,y$
and morphisms
$ x,y$
and morphisms
![]() $f,g:x\rightarrow y$
in
$f,g:x\rightarrow y$
in
![]() $\mathcal {C}$
, there exists a unique
$\mathcal {C}$
, there exists a unique
![]() $2$
-cell
$2$
-cell
![]() $f\Rightarrow g$
if and only if
$f\Rightarrow g$
if and only if
![]() $f\equiv _{x,y}g$
. The corresponding quotient category
$f\equiv _{x,y}g$
. The corresponding quotient category
![]() $\mathcal {C}/\!\equiv $
is the category whose objects are those of
$\mathcal {C}/\!\equiv $
is the category whose objects are those of
![]() $\mathcal {C} $
and whose morphisms from x to y are the quotient set
$\mathcal {C} $
and whose morphisms from x to y are the quotient set
![]() $\mathcal {C}(x,y)/\!\equiv _{x,y}$
.
$\mathcal {C}(x,y)/\!\equiv _{x,y}$
.
Let X and Y be topological spaces; henceforth, we will let I denote the closed unit interval
![]() $[0,1]$
. A homotopy
$[0,1]$
. A homotopy
![]() $h:f\Rightarrow g:X\rightarrow Y$
from the map
$h:f\Rightarrow g:X\rightarrow Y$
from the map
![]() $f:X\to Y$
to the map
$f:X\to Y$
to the map
![]() $g:X\to Y$
is a function
$g:X\to Y$
is a function
![]() $h:X\times I\rightarrow Y$
such that
$h:X\times I\rightarrow Y$
such that
![]() $h\left ( -,0\right ) =f$
and
$h\left ( -,0\right ) =f$
and
![]() $ h\left ( -,1\right ) =g$
. The homotopy relation
$ h\left ( -,1\right ) =g$
. The homotopy relation
![]() $\simeq _{\mathsf {LC}}$
on
$\simeq _{\mathsf {LC}}$
on
![]() $\mathsf {LC}(X,Y)$
is defined by setting
$\mathsf {LC}(X,Y)$
is defined by setting
![]() $ f\simeq _{\mathsf {LC}}g$
if and only if there exists a homotopy
$ f\simeq _{\mathsf {LC}}g$
if and only if there exists a homotopy
![]() $ h:f\Rightarrow g:X\rightarrow Y$
; evidently,
$ h:f\Rightarrow g:X\rightarrow Y$
; evidently,
![]() $\simeq _{\mathsf {LC}}$
defines a congruence on
$\simeq _{\mathsf {LC}}$
defines a congruence on
![]() $\mathsf {LC}$
. We let
$\mathsf {LC}$
. We let
![]() $\mathsf {Ho}( \mathsf {LC}) $
denote the corresponding quotient category, which may be regarded as a category enriched over the category
$\mathsf {Ho}( \mathsf {LC}) $
denote the corresponding quotient category, which may be regarded as a category enriched over the category
![]() $\mathsf {SemiDSet}$
;
$\mathsf {SemiDSet}$
;
![]() $[X,Y] $
will denote the semidefinable set of homotopy classes of maps
$[X,Y] $
will denote the semidefinable set of homotopy classes of maps
![]() $X\rightarrow Y$
or, equivalently, of the path-components of
$X\rightarrow Y$
or, equivalently, of the path-components of
![]() $\mathsf {LC}(X,Y)$
. A homotopy equivalence
$\mathsf {LC}(X,Y)$
. A homotopy equivalence
![]() $f\in \mathsf {LC}(X,Y)$
is a map whose image in the quotient category
$f\in \mathsf {LC}(X,Y)$
is a map whose image in the quotient category
![]() $\mathsf {Ho}(\mathsf {LC})$
is an isomorphism.
$\mathsf {Ho}(\mathsf {LC})$
is an isomorphism.
More generally, we consider locally compact pairs; these are pairs of topological spaces
![]() $(X,A)$
in which X is locally compact and Polish and A is a closed subspace of X. These form the objects of the Polish category
$(X,A)$
in which X is locally compact and Polish and A is a closed subspace of X. These form the objects of the Polish category
![]() $\mathsf {LCP}$
of locally compact pairs. Its morphisms
$\mathsf {LCP}$
of locally compact pairs. Its morphisms
![]() $(X,A)\to (Y,B)$
are those maps
$(X,A)\to (Y,B)$
are those maps
![]() $f:X\rightarrow Y$
such that
$f:X\rightarrow Y$
such that
![]() $f(A) \subseteq B$
. The hom-sets
$f(A) \subseteq B$
. The hom-sets
![]() $\mathsf {LCP}((X,A),(Y,B)) $
then form
$\mathsf {LCP}((X,A),(Y,B)) $
then form
![]() $G_{\delta }$
subsets of
$G_{\delta }$
subsets of
![]() $\mathsf {LC}(X,Y) $
, and their subspace topologies are consequently Polish. Note also that the identification
$\mathsf {LC}(X,Y) $
, and their subspace topologies are consequently Polish. Note also that the identification
![]() $X\mapsto (X,\varnothing )$
embeds
$X\mapsto (X,\varnothing )$
embeds
![]() $\mathsf {LC}$
as a full subcategory of
$\mathsf {LC}$
as a full subcategory of
![]() $\mathsf {LCP}$
. We write
$\mathsf {LCP}$
. We write
![]() $f:(X,A) \rightarrow (Y,B) $
to indicate that
$f:(X,A) \rightarrow (Y,B) $
to indicate that
![]() $f\in \mathsf {LCP}(( X,A),(Y,B))$
. We let
$f\in \mathsf {LCP}(( X,A),(Y,B))$
. We let
![]() $\mathsf {CP}$
denote the full subcategory of
$\mathsf {CP}$
denote the full subcategory of
![]() $\mathsf {LCP}$
consisting of compact pairs (i.e., of locally compact pairs
$\mathsf {LCP}$
consisting of compact pairs (i.e., of locally compact pairs
![]() $(X,A)$
in which X is compact). Given maps
$(X,A)$
in which X is compact). Given maps
![]() $f,g:( X,A) \rightarrow (Y,B) $
a homotopy – sometimes termed pair homotopy –
$f,g:( X,A) \rightarrow (Y,B) $
a homotopy – sometimes termed pair homotopy –
![]() $h:f\Rightarrow g:( X,A) \rightarrow (Y,B)$
from f to g is a homotopy
$h:f\Rightarrow g:( X,A) \rightarrow (Y,B)$
from f to g is a homotopy
![]() $h:f\Rightarrow g:X\rightarrow Y$
such that
$h:f\Rightarrow g:X\rightarrow Y$
such that
![]() $h( -,t) :( X,A) \rightarrow (Y,B) $
for every
$h( -,t) :( X,A) \rightarrow (Y,B) $
for every
![]() $t\in I$
. This defines a congruence relation
$t\in I$
. This defines a congruence relation
![]() $\simeq _{\mathsf {LCP}}$
on
$\simeq _{\mathsf {LCP}}$
on
![]() $\mathsf {LCP}$
. We let Ho
$\mathsf {LCP}$
. We let Ho
![]() $(\mathsf {LCP}) $
denote the corresponding quotient category; note that Ho
$(\mathsf {LCP}) $
denote the corresponding quotient category; note that Ho
![]() $(\mathsf {LC})$
and Ho
$(\mathsf {LC})$
and Ho
![]() $(\mathsf {LCP})$
are the homotopy categories associated to the Hurewicz model category structures on
$(\mathsf {LCP})$
are the homotopy categories associated to the Hurewicz model category structures on
![]() $\mathsf {LC}$
and
$\mathsf {LC}$
and
![]() $\mathsf {LCP}$
, respectively (see [Reference Dwyer and Spaliński24]). We let
$\mathsf {LCP}$
, respectively (see [Reference Dwyer and Spaliński24]). We let
![]() $\left [(X,A),(Y,B) \right ] $
be the semidefinable set of homotopy classes of maps
$\left [(X,A),(Y,B) \right ] $
be the semidefinable set of homotopy classes of maps
![]() $(X,A) \rightarrow (Y,B) $
. Just as above, a homotopy equivalence
$(X,A) \rightarrow (Y,B) $
. Just as above, a homotopy equivalence
![]() $f\in \mathsf {LCP}((X,A),(Y,B))$
is a map whose image in the quotient category
$f\in \mathsf {LCP}((X,A),(Y,B))$
is a map whose image in the quotient category
![]() $\mathsf {Ho}(\mathsf {LCP})$
is an isomorphism.
$\mathsf {Ho}(\mathsf {LCP})$
is an isomorphism.
A pointed locally compact Polish space is a locally compact pair
![]() $(X,A) $
in which A is a singleton
$(X,A) $
in which A is a singleton
![]() $\{*\}$
; we call
$\{*\}$
; we call
![]() $*$
the basepoint of this space. Such spaces comprise a full subcategory
$*$
the basepoint of this space. Such spaces comprise a full subcategory
![]() $\mathsf {LC}_{\ast }$
of the category
$\mathsf {LC}_{\ast }$
of the category
![]() $\mathsf {LCP}$
of locally compact pairs. The morphisms in
$\mathsf {LCP}$
of locally compact pairs. The morphisms in
![]() $\mathsf {LC}_{\ast }$
are maps which are basepoint-preserving (i.e., they are exactly those maps which send basepoints to basepoints). Similarly, one defines the notion of basepoint-preserving homotopy, and the corresponding congruence relation
$\mathsf {LC}_{\ast }$
are maps which are basepoint-preserving (i.e., they are exactly those maps which send basepoints to basepoints). Similarly, one defines the notion of basepoint-preserving homotopy, and the corresponding congruence relation
![]() $\simeq _{\mathsf {LC}_{\ast }}$
on
$\simeq _{\mathsf {LC}_{\ast }}$
on
![]() $\mathsf {LC}_{\ast }$
(which is simply the restriction of
$\mathsf {LC}_{\ast }$
(which is simply the restriction of
![]() $\simeq _{\mathsf {LCP}}$
to the full subcategory
$\simeq _{\mathsf {LCP}}$
to the full subcategory
![]() $\mathsf {LC}_{\ast }$
).
$\mathsf {LC}_{\ast }$
).
A central concern in homotopy theory is the existence (or nonexistence) of extensions of maps or homotopies from a topological space A to some larger space
![]() $X\supseteq A$
. In the locally compact setting, a main theorem describing conditions of their existence is Borsuk’s Homotopy Extension Theorem (see [Reference Mardešić and Segal56, Chapter I.3, Theorem 9]):
$X\supseteq A$
. In the locally compact setting, a main theorem describing conditions of their existence is Borsuk’s Homotopy Extension Theorem (see [Reference Mardešić and Segal56, Chapter I.3, Theorem 9]):
Theorem 4.1. Suppose that A is a closed subspace of a locally compact Polish space X and that P is a polyhedron. Then for every map
![]() $f:A\times I\rightarrow P$
and
$f:A\times I\rightarrow P$
and
![]() $h:X\times \left \{ 0\right \} \rightarrow P$
such that
$h:X\times \left \{ 0\right \} \rightarrow P$
such that
![]() $h|_{A\times \left \{ 0\right \} }=f|_{A\times \left \{ 0\right \} }$
, there exists a map
$h|_{A\times \left \{ 0\right \} }=f|_{A\times \left \{ 0\right \} }$
, there exists a map
![]() $\tilde {h}:X\times I\rightarrow P$
which simultaneously extends both h and f.
$\tilde {h}:X\times I\rightarrow P$
which simultaneously extends both h and f.
Beginning in Section 4.4, we will make repeated use of this theorem; as noted, we will also prove its definable version in Section 6.2 below.
4.2. Polyhedra
Henceforth, all simplicial complexes will be tacitly understood to be countable and locally finite; let K be such a complex. We may assume without loss of generality that
![]() $\mathrm {dom}(K) \subseteq \mathbb {N}$
and then associate with K a locally compact Polish space
$\mathrm {dom}(K) \subseteq \mathbb {N}$
and then associate with K a locally compact Polish space
![]() $\left \vert K\right \vert \subseteq \mathbb {R}^{\mathbb {N}}$
, called its topological realization, as follows. Let
$\left \vert K\right \vert \subseteq \mathbb {R}^{\mathbb {N}}$
, called its topological realization, as follows. Let
![]() $( e_{v})_{v\in \mathbb {N}}$
denote the canonical basis of the
$( e_{v})_{v\in \mathbb {N}}$
denote the canonical basis of the
![]() $\mathbb {R}$
-vector space
$\mathbb {R}$
-vector space
![]() $\mathbb {R}^{\mathbb {N}}$
. For each simplex
$\mathbb {R}^{\mathbb {N}}$
. For each simplex
![]() $\sigma =\{ i_{0},\ldots ,i_{n}\} $
of K, define
$\sigma =\{ i_{0},\ldots ,i_{n}\} $
of K, define
The topological boundary
![]() $\left \vert \dot {\sigma } \right \vert $
of
$\left \vert \dot {\sigma } \right \vert $
of
![]() $\sigma $
is the set of points
$\sigma $
is the set of points
![]() $t_{0}e_{i_{0}}+\cdots +t_{n}e_{i_{n}}$
of
$t_{0}e_{i_{0}}+\cdots +t_{n}e_{i_{n}}$
of
![]() $\left \vert \sigma \right \vert $
for which at least one of the coordinates
$\left \vert \sigma \right \vert $
for which at least one of the coordinates
![]() $t_{0},\ldots ,t_{n}$
is zero. The topological interior of
$t_{0},\ldots ,t_{n}$
is zero. The topological interior of
![]() $ \left \vert \sigma \right \vert $
is
$ \left \vert \sigma \right \vert $
is
![]() $\left \langle \sigma \right \rangle :=\left \vert \sigma \right \vert \setminus \left \vert \dot {\sigma }\right \vert $
. We then define
$\left \langle \sigma \right \rangle :=\left \vert \sigma \right \vert \setminus \left \vert \dot {\sigma }\right \vert $
. We then define
![]() $\left \vert K\right \vert $
to be the union of
$\left \vert K\right \vert $
to be the union of
![]() $\left \vert \sigma \right \vert $
where
$\left \vert \sigma \right \vert $
where
![]() $\sigma $
ranges among the simplices of K. Hence, every
$\sigma $
ranges among the simplices of K. Hence, every
![]() $x\in |K|$
can be uniquely identified with some sum
$x\in |K|$
can be uniquely identified with some sum
where the coefficients
![]() $(x_v)_{v\in \mathrm {dom}(K)}$
satisfy
$(x_v)_{v\in \mathrm {dom}(K)}$
satisfy
![]() $\sum _{v\in \mathrm {dom}(K)}x_v=1$
. We call
$\sum _{v\in \mathrm {dom}(K)}x_v=1$
. We call
![]() $(x_v)$
the barycentric coordinates of x.
$(x_v)$
the barycentric coordinates of x.
Observe that if
![]() $ L $
is a subcomplex of K, then
$ L $
is a subcomplex of K, then
![]() $\left \vert L\right \vert $
forms a closed subspace of
$\left \vert L\right \vert $
forms a closed subspace of
![]() $\left \vert K\right \vert $
. A topological space is called a polyhedron if it is homeomorphic to the topological realization of a simplicial complex. We let
$\left \vert K\right \vert $
. A topological space is called a polyhedron if it is homeomorphic to the topological realization of a simplicial complex. We let
![]() $\mathsf {P}$
be the full subcategory of the category
$\mathsf {P}$
be the full subcategory of the category
![]() $\mathsf {LC}$
of locally compact Polish spaces consisting of polyhedra and let
$\mathsf {LC}$
of locally compact Polish spaces consisting of polyhedra and let
![]() $\mathsf {Ho}(\mathsf {P})$
be its quotient by
$\mathsf {Ho}(\mathsf {P})$
be its quotient by
![]() $\simeq _{\mathsf {LC}}$
. Note that a polyhedron is compact if and only if it is homeomorphic to the realization of a finite simplicial complex.
$\simeq _{\mathsf {LC}}$
. Note that a polyhedron is compact if and only if it is homeomorphic to the realization of a finite simplicial complex.
Call two simplicial maps
![]() $f,g:K\rightarrow L$
contiguous if for every
$f,g:K\rightarrow L$
contiguous if for every
![]() $\sigma \in K$
,
$\sigma \in K$
,
![]() $f(\sigma )$
and
$f(\sigma )$
and
![]() $g(\sigma )$
are faces of a single simplex in L, and let the relation of contiguous equivalence be the transitive closure of the contiguity relation (see [Reference Eilenberg and Steenrod29, Section VI.3] or [Reference Spanier80, Section 3.5]). This defines a congruence relation
$g(\sigma )$
are faces of a single simplex in L, and let the relation of contiguous equivalence be the transitive closure of the contiguity relation (see [Reference Eilenberg and Steenrod29, Section VI.3] or [Reference Spanier80, Section 3.5]). This defines a congruence relation
![]() $\simeq _{\mathsf {S}}$
on
$\simeq _{\mathsf {S}}$
on
![]() $\mathsf {S}$
, and an associated quotient category Ho
$\mathsf {S}$
, and an associated quotient category Ho
![]() $(\mathsf {S}):=\mathsf {S}/\!\simeq _{\mathsf {S}}$
. A simplicial map
$(\mathsf {S}):=\mathsf {S}/\!\simeq _{\mathsf {S}}$
. A simplicial map
![]() $f:K\rightarrow L$
between simplicial complexes induces a continuous function
$f:K\rightarrow L$
between simplicial complexes induces a continuous function
![]() $\left \vert f\right \vert :\left \vert K\right \vert \rightarrow \left \vert L\right \vert $
defined by setting
$\left \vert f\right \vert :\left \vert K\right \vert \rightarrow \left \vert L\right \vert $
defined by setting
for all
![]() $\{ i_{0},\ldots ,i_{n}\} \in K$
and
$\{ i_{0},\ldots ,i_{n}\} \in K$
and
![]() $t_{0},\ldots ,t_{n}\in \left [ 0,1\right ] $
such that
$t_{0},\ldots ,t_{n}\in \left [ 0,1\right ] $
such that
![]() $t_{0}+\cdots +t_{n}=1$
. Moreover, if
$t_{0}+\cdots +t_{n}=1$
. Moreover, if
![]() $f,g:K\rightarrow L$
are contiguously equivalent, then the corresponding maps
$f,g:K\rightarrow L$
are contiguously equivalent, then the corresponding maps
![]() $\left \vert f\right \vert ,\left \vert g\right \vert :\left \vert K\right \vert \rightarrow \left \vert L\right \vert $
are homotopic (a fact invoked in the proof of Theorem 2.12); put differently, the functor
$\left \vert f\right \vert ,\left \vert g\right \vert :\left \vert K\right \vert \rightarrow \left \vert L\right \vert $
are homotopic (a fact invoked in the proof of Theorem 2.12); put differently, the functor
![]() $K\mapsto \left \vert K\right \vert $
from
$K\mapsto \left \vert K\right \vert $
from
![]() $\mathsf {S}$
to
$\mathsf {S}$
to
![]() $\mathsf {P}$
induces a functor from Ho
$\mathsf {P}$
induces a functor from Ho
![]() $(\mathsf {S})$
to Ho
$(\mathsf {S})$
to Ho
![]() $(\mathsf {P})$
.
$(\mathsf {P})$
.
The barycentric subdivision
![]() $\beta K$
of a simplicial complex K is the simplicial complex with
$\beta K$
of a simplicial complex K is the simplicial complex with
![]() $\mathrm {dom}(\beta K) $
equal to the set of nonempty simplices of K. A simplex of
$\mathrm {dom}(\beta K) $
equal to the set of nonempty simplices of K. A simplex of
![]() $\beta K$
is a set
$\beta K$
is a set
![]() $\{ \sigma _{0},\ldots ,\sigma _{n}\} $
of simplices of K which is linearly ordered by inclusion. A selection map for K is a function
$\{ \sigma _{0},\ldots ,\sigma _{n}\} $
of simplices of K which is linearly ordered by inclusion. A selection map for K is a function
![]() $s:K\setminus \{ \varnothing \} \rightarrow \mathrm {dom}(K) $
such that
$s:K\setminus \{ \varnothing \} \rightarrow \mathrm {dom}(K) $
such that
![]() $s(\sigma ) \in \sigma $
for every
$s(\sigma ) \in \sigma $
for every
![]() $\sigma \in K\setminus \{ \varnothing \}$
; equivalently, s is a simplicial map
$\sigma \in K\setminus \{ \varnothing \}$
; equivalently, s is a simplicial map
![]() $\beta K\rightarrow K$
. Notice that any two selection maps are contiguous and therefore represent the same morphism in
$\beta K\rightarrow K$
. Notice that any two selection maps are contiguous and therefore represent the same morphism in
![]() $\mathsf {Ho}(\mathsf {S})$
.
$\mathsf {Ho}(\mathsf {S})$
.
Precomposing the realization construction (18) above with a bijection
![]() $b:\mathbb {N}^{<\mathbb {N}}\to \mathbb {N}$
determines a topological realization of a subdivided complex
$b:\mathbb {N}^{<\mathbb {N}}\to \mathbb {N}$
determines a topological realization of a subdivided complex
![]() $\beta K$
, and if
$\beta K$
, and if
![]() $s:\beta K\rightarrow K$
is a selection map, then the corresponding map
$s:\beta K\rightarrow K$
is a selection map, then the corresponding map
![]() $\left \vert s\right \vert :\left \vert \beta K\right \vert \rightarrow \left \vert K\right \vert $
is homotopic to the homeomorphism
$\left \vert s\right \vert :\left \vert \beta K\right \vert \rightarrow \left \vert K\right \vert $
is homotopic to the homeomorphism
![]() $ \left \vert \beta K\right \vert \rightarrow \left \vert K\right \vert $
defined by the maps
$ \left \vert \beta K\right \vert \rightarrow \left \vert K\right \vert $
defined by the maps
for each nonempty simplex
![]() $\left \{ v_{0},\ldots ,v_{n}\right \} $
of K, together with their linear extension.
$\left \{ v_{0},\ldots ,v_{n}\right \} $
of K, together with their linear extension.
For a vertex v of K, we let the open star St
![]() $_{K}(v) \subseteq \left \vert K\right \vert $
of v be the union of the interiors of
$_{K}(v) \subseteq \left \vert K\right \vert $
of v be the union of the interiors of
![]() $\left \vert \sigma \right \vert $
where
$\left \vert \sigma \right \vert $
where
![]() $\sigma $
ranges among the simplices that contain v as a vertex. Equivalently,
$\sigma $
ranges among the simplices that contain v as a vertex. Equivalently,
 $$ \begin{align*} \mathrm{St}_K( v) =\left\{ \sum_{w\in \mathrm{\mathrm{dom}}\left( K\right) }a_{w}e_{w}\;:\;a_{v}>0\right\}\cap\left\vert K\right\vert \text{.} \end{align*} $$
$$ \begin{align*} \mathrm{St}_K( v) =\left\{ \sum_{w\in \mathrm{\mathrm{dom}}\left( K\right) }a_{w}e_{w}\;:\;a_{v}>0\right\}\cap\left\vert K\right\vert \text{.} \end{align*} $$
We will sometimes omit the subscript K when it is contextually clear. In what follows, we will often make use of the following important well-known property of the open cover
![]() $\{\mathrm {St}_K(v)\colon v\in \mathrm {dom}(K)\}$
of
$\{\mathrm {St}_K(v)\colon v\in \mathrm {dom}(K)\}$
of
![]() $|K|$
.
$|K|$
.
Lemma 4.2. Let K be a simplicial complex, and let
![]() $D\subseteq |K|\times |K|$
be the union of all sets of the form
$D\subseteq |K|\times |K|$
be the union of all sets of the form
![]() $\mathrm {St}_K( v)\times \mathrm {St}_K( v)$
where v ranges over
$\mathrm {St}_K( v)\times \mathrm {St}_K( v)$
where v ranges over
![]() $\mathrm {dom}(K)$
. Then there exists a continuous map
$\mathrm {dom}(K)$
. Then there exists a continuous map
![]() $\lambda \colon D\times [0,1]\to P$
so that
$\lambda \colon D\times [0,1]\to P$
so that
-
(1) for all
 $(x,y)\in D$
, we have that
$(x,y)\in D$
, we have that
 $\lambda (x,y,0)=x, \quad \lambda (x,y,1)=y$
;
$\lambda (x,y,0)=x, \quad \lambda (x,y,1)=y$
; -
(2) if
 $x\in |\sigma |$
and
$x\in |\sigma |$
and
 $y\in |\tau |$
with
$y\in |\tau |$
with
 $\sigma ,\tau \in K$
, then for all
$\sigma ,\tau \in K$
, then for all
 $t\in [0,1]$
, we have that
$t\in [0,1]$
, we have that
 $\lambda (x,y,t)\in |\sigma |\cup |\tau |$
.
$\lambda (x,y,t)\in |\sigma |\cup |\tau |$
.
Proof. Following the proof of Theorem 2 from [Reference Milnor64], we first consider the map
![]() $\mu \colon D\to |K|$
which is defined as follows: if
$\mu \colon D\to |K|$
which is defined as follows: if
![]() $(x_v)$
and
$(x_v)$
and
![]() $(y_v)$
are the barycentric coordinates of
$(y_v)$
are the barycentric coordinates of
![]() $x,y$
where
$x,y$
where
![]() $(x,y)\in D$
, then
$(x,y)\in D$
, then
![]() $\mu (x,y):=(z_v\colon v\in \mathrm {dom}(K))$
, where
$\mu (x,y):=(z_v\colon v\in \mathrm {dom}(K))$
, where
 $$\begin{align*}z_w:= \min(x_w,y_w) \; \; \bigg/\sum_{v\in\mathrm{dom}(K)} \min(x_v,y_v). \end{align*}$$
$$\begin{align*}z_w:= \min(x_w,y_w) \; \; \bigg/\sum_{v\in\mathrm{dom}(K)} \min(x_v,y_v). \end{align*}$$
Notice that if
![]() $x\in |\sigma |$
and
$x\in |\sigma |$
and
![]() $y\in |\tau |$
with
$y\in |\tau |$
with
![]() $\sigma ,\tau \in K$
, then
$\sigma ,\tau \in K$
, then
![]() $\mu (x,y)\in |\sigma |\cap |\tau |$
. Then the map
$\mu (x,y)\in |\sigma |\cap |\tau |$
. Then the map
![]() $\lambda $
is defined by setting
$\lambda $
is defined by setting
The generalization to topological realizations
![]() $(|K|,|L|) $
of simplicial pairs
$(|K|,|L|) $
of simplicial pairs
![]() $(K,L) $
is straightforward. A polyhedral pair is a locally compact pair that arises in this fashion from a simplicial pair
$(K,L) $
is straightforward. A polyhedral pair is a locally compact pair that arises in this fashion from a simplicial pair
![]() $(K,L)$
. The category of polyhedral pairs is a full subcategory of
$(K,L)$
. The category of polyhedral pairs is a full subcategory of
![]() $\mathsf {LCP}$
; we denote it
$\mathsf {LCP}$
; we denote it
![]() $\mathsf {PP}$
, writing
$\mathsf {PP}$
, writing
![]() $\mathsf {P}_*$
for the full subcategory of pointed polyhedra.
$\mathsf {P}_*$
for the full subcategory of pointed polyhedra.
4.3. Maps from compact pairs to polyhedral pairs
It will be useful to henceforth adopt slightly strengthened notions of cover and refinement; portions of the next few paragraphs therefore amount to an updating of definitions first appearing in Section 2.
Let X be a locally compact Polish space. An (open) cover of X is a countable family
![]() $\mathcal {U}=\left ( U_{j}\right ) _{j\in J}$
of open subsets of X with compact closure such that X is the union of
$\mathcal {U}=\left ( U_{j}\right ) _{j\in J}$
of open subsets of X with compact closure such that X is the union of
![]() $\left \{ U_{j}:j\in J\right \} $
. The cover
$\left \{ U_{j}:j\in J\right \} $
. The cover
![]() $\mathcal {U}$
is star-finite if, for every
$\mathcal {U}$
is star-finite if, for every
![]() $j\in J$
, the set
$j\in J$
, the set
![]() $\left \{ i\in J:U_{i}\cap U_{j}\neq \varnothing \right \} $
is finite. The nerve of a star-finite cover
$\left \{ i\in J:U_{i}\cap U_{j}\neq \varnothing \right \} $
is finite. The nerve of a star-finite cover
![]() $\mathcal {U} =\left ( U_{j}\right ) _{j\in J}$
of X is the (countable, locally finite) simplicial complex with
$\mathcal {U} =\left ( U_{j}\right ) _{j\in J}$
of X is the (countable, locally finite) simplicial complex with
![]() $\mathrm {dom}(N_{\mathcal {U}})=\left \{ j\in J:U_{j}\neq \varnothing \right \} $
and
$\mathrm {dom}(N_{\mathcal {U}})=\left \{ j\in J:U_{j}\neq \varnothing \right \} $
and
![]() $\left \{ j_{0},\ldots ,j_{n}\right \} $
a simplex of
$\left \{ j_{0},\ldots ,j_{n}\right \} $
a simplex of
![]() $N_{\mathcal {U}}$
if and only if
$N_{\mathcal {U}}$
if and only if
![]() $U_{j_{0}}\cap \cdots \cap U_{j_{n}}\neq \varnothing $
. A canonical map for
$U_{j_{0}}\cap \cdots \cap U_{j_{n}}\neq \varnothing $
. A canonical map for
![]() $\mathcal {U}$
is a function
$\mathcal {U}$
is a function
![]() $f:X\rightarrow \left \vert N_{\mathcal {U}}\right \vert $
such that
$f:X\rightarrow \left \vert N_{\mathcal {U}}\right \vert $
such that
![]() $ f^{-1}\left ( \mathrm {St}_{N_{\mathcal {U}}}( j) \right ) \subseteq U_{j}$
, where
$ f^{-1}\left ( \mathrm {St}_{N_{\mathcal {U}}}( j) \right ) \subseteq U_{j}$
, where
![]() $\mathrm {St}_{N_{\mathcal {U}}}(j) $
is the open star of the vertex j of
$\mathrm {St}_{N_{\mathcal {U}}}(j) $
is the open star of the vertex j of
![]() $N_{\mathcal {U}}$
.
$N_{\mathcal {U}}$
.
A partition of unity subordinate to a star-finite cover
![]() $\mathcal {U}=\left ( U_{j}\right ) _{j\in J}$
is a family
$\mathcal {U}=\left ( U_{j}\right ) _{j\in J}$
is a family
![]() $\left ( f_{j}\right ) _{j\in J}$
of continuous functions
$\left ( f_{j}\right ) _{j\in J}$
of continuous functions
![]() $f_{j}:X\rightarrow I$
such that the closure of
$f_{j}:X\rightarrow I$
such that the closure of
![]() $\mathrm {supp}( f_{j}) $
is contained in
$\mathrm {supp}( f_{j}) $
is contained in
![]() $U_{j}$
for every
$U_{j}$
for every
![]() $j\in J$
, and
$j\in J$
, and
![]() $\sum _{j\in J}f_{j}( x) =1$
for every
$\sum _{j\in J}f_{j}( x) =1$
for every
![]() $x\in X$
. A partition of unity
$x\in X$
. A partition of unity
![]() $( f_{j}) _{j\in J}$
of
$( f_{j}) _{j\in J}$
of
![]() $\mathcal {U}$
gives rise to a canonical map
$\mathcal {U}$
gives rise to a canonical map
![]() $f:X\rightarrow \left \vert N_{\mathcal {U}}\right \vert $
for
$f:X\rightarrow \left \vert N_{\mathcal {U}}\right \vert $
for
![]() $\mathcal {U}$
defined by
$\mathcal {U}$
defined by
![]() $x\mapsto \sum _{j\in J}f_{j}( x) e_{j}$
.
$x\mapsto \sum _{j\in J}f_{j}( x) e_{j}$
.
A cover
![]() $\mathcal {V}$
of X refines a cover
$\mathcal {V}$
of X refines a cover
![]() $\mathcal {U}$
of X if for every
$\mathcal {U}$
of X if for every
![]() $V\in \mathcal {V}$
, there exists
$V\in \mathcal {V}$
, there exists
![]() $U\in \mathcal {U}$
such that
$U\in \mathcal {U}$
such that
![]() $\overline {V}\subseteq U$
. A refinement map from
$\overline {V}\subseteq U$
. A refinement map from
![]() $\mathcal {V}$
to
$\mathcal {V}$
to
![]() $ \mathcal {U}$
is a simplicial map
$ \mathcal {U}$
is a simplicial map
![]() $p:N_{\mathcal {V}}\rightarrow N_{\mathcal {U} }$
such that
$p:N_{\mathcal {V}}\rightarrow N_{\mathcal {U} }$
such that
![]() $\overline {V}_{j}\subseteq U_{p(j) }$
for every
$\overline {V}_{j}\subseteq U_{p(j) }$
for every
![]() $ j\in \mathrm {dom}( N_{\mathcal {U}}) $
. Note that any two refinement maps from
$ j\in \mathrm {dom}( N_{\mathcal {U}}) $
. Note that any two refinement maps from
![]() $\mathcal {V}$
to
$\mathcal {V}$
to
![]() $\mathcal {U}$
are contiguous.
$\mathcal {U}$
are contiguous.
Every cover of a locally compact Polish space admits a star-finite refinement [Reference Kaplan42], and every star-finite cover of such a space admits a subordinate partition of unity. If
![]() $( X,A) $
is a locally compact pair, then a cover of
$( X,A) $
is a locally compact pair, then a cover of
![]() $ ( X,A) $
is a cover
$ ( X,A) $
is a cover
![]() $\mathcal {U}=( U_{j}) _{j\in J}$
of X such that if
$\mathcal {U}=( U_{j}) _{j\in J}$
of X such that if
![]() $U_{j_{\ell }}\cap A\neq \varnothing $
for
$U_{j_{\ell }}\cap A\neq \varnothing $
for
![]() $\ell \in \left \{ 0,1,\ldots ,n\right \} $
and
$\ell \in \left \{ 0,1,\ldots ,n\right \} $
and
![]() $U_{j_{0}}\cap \cdots \cap U_{j_{n}}\neq \varnothing $
, then
$U_{j_{0}}\cap \cdots \cap U_{j_{n}}\neq \varnothing $
, then
![]() $U_{j_{0}}\cap \cdots \cap U_{j_{n}}\cap A\neq \varnothing $
. This condition ensures that
$U_{j_{0}}\cap \cdots \cap U_{j_{n}}\cap A\neq \varnothing $
. This condition ensures that
![]() $\mathcal {U}^{\prime }=( U_{j}\cap A) _{j\in J}$
is a cover of A such that the identity map
$\mathcal {U}^{\prime }=( U_{j}\cap A) _{j\in J}$
is a cover of A such that the identity map
![]() $J\rightarrow J$
induces an inclusion
$J\rightarrow J$
induces an inclusion
![]() $N_{\mathcal {U}^{\prime }}\rightarrow N_{\mathcal {U}}$
as a full subcomplex.
$N_{\mathcal {U}^{\prime }}\rightarrow N_{\mathcal {U}}$
as a full subcomplex.
If
![]() $( P,Q) $
is a polyhedral pair and
$( P,Q) $
is a polyhedral pair and
![]() $( K,L) $
is a simplicial pair and
$( K,L) $
is a simplicial pair and
![]() $(P,Q) =(|K|,|L|)$
, then there exists a canonical star-finite cover of
$(P,Q) =(|K|,|L|)$
, then there exists a canonical star-finite cover of
![]() $(P,Q)$
– namely,
$(P,Q)$
– namely,
![]() $\mathcal {U} _{K}^{P}:=\{\mathrm {St}_{K}(v)\mid v\in \mathrm {dom}(K)\}$
, where as above,
$\mathcal {U} _{K}^{P}:=\{\mathrm {St}_{K}(v)\mid v\in \mathrm {dom}(K)\}$
, where as above,
![]() $\mathrm {St}_{K}(v)$
is the open star of v in K. Notice that
$\mathrm {St}_{K}(v)$
is the open star of v in K. Notice that
![]() $\mathrm {St}_{K}(v)\cap |L| \neq \varnothing $
if and only if
$\mathrm {St}_{K}(v)\cap |L| \neq \varnothing $
if and only if
![]() $v\in L$
.
$v\in L$
.
Recall that an equivalence relation E on a Polish space Y is open (or closed) if it is an open (or closed) subset of
![]() $Y\times Y$
endowed with the product topology. Recall also that by a homotopy of maps in
$Y\times Y$
endowed with the product topology. Recall also that by a homotopy of maps in
![]() $\mathsf {LCP}$
, we mean a pair homotopy.
$\mathsf {LCP}$
, we mean a pair homotopy.
Lemma 4.3. For any
![]() $(Z,C)$
and homotopy equivalence
$(Z,C)$
and homotopy equivalence
![]() $f:(X,A)\to (Y,B)$
in
$f:(X,A)\to (Y,B)$
in
![]() $\mathsf {LCP}$
,
$\mathsf {LCP}$
,
-
(1) the map
 $f^{*}:\mathsf {LCP}((Y,B),(Z,C))\to \mathsf {LCP}((X,A),(Z,C))$
given by
$f^{*}:\mathsf {LCP}((Y,B),(Z,C))\to \mathsf {LCP}((X,A),(Z,C))$
given by
 $s\mapsto s\circ f$
is a homotopy equivalence, and
$s\mapsto s\circ f$
is a homotopy equivalence, and -
(2) the homotopy relation on
 $\mathsf {LCP}((Y,B),(Z,C))$
is open if and only if it is open on
$\mathsf {LCP}((Y,B),(Z,C))$
is open if and only if it is open on
 $\mathsf {LCP}((X,A),(Z,C))$
.
$\mathsf {LCP}((X,A),(Z,C))$
.
Proof. Item (1) is not particularly difficult to see, and appears as Corollary 2.4.14 of [Reference Dieck87]. Note, in particular, that the map
![]() $f^{*}$
is continuous and that
$f^{*}$
is continuous and that
![]() $s\simeq t$
if and only if
$s\simeq t$
if and only if
![]() $f^{*}(s)\simeq f^{*}(t)$
. Hence, if the homotopy relation on
$f^{*}(s)\simeq f^{*}(t)$
. Hence, if the homotopy relation on
![]() $\mathsf {LCP}((X,A),(Z,C))$
is open, then so too is its continuous preimage under the map
$\mathsf {LCP}((X,A),(Z,C))$
is open, then so too is its continuous preimage under the map
![]() $f^{*}$
, which is exactly the homotopy relation on
$f^{*}$
, which is exactly the homotopy relation on
![]() $\mathsf {LCP}((Y,B),(Z,C))$
. Repeating this argument for a homotopy equivalence
$\mathsf {LCP}((Y,B),(Z,C))$
. Repeating this argument for a homotopy equivalence
![]() $g:(Y,B)\to (X,A)$
in
$g:(Y,B)\to (X,A)$
in
![]() $\mathsf {LCP}$
completes the proof of item (2).
$\mathsf {LCP}$
completes the proof of item (2).
Lemma 4.4. Suppose that a locally compact pair
![]() $(X,A)$
is homotopy equivalent to a compact pair and that
$(X,A)$
is homotopy equivalent to a compact pair and that
![]() $(P,Q)$
is a polyhedral pair. Then the relation of homotopy among maps
$(P,Q)$
is a polyhedral pair. Then the relation of homotopy among maps
![]() $(X,A) \rightarrow (P,Q)$
is open (and, in consequence, closed as well).
$(X,A) \rightarrow (P,Q)$
is open (and, in consequence, closed as well).
Proof. By Lemma 4.3, we may without loss of generality assume that
![]() $(X,A)$
is a compact pair. Let
$(X,A)$
is a compact pair. Let
![]() $(K,L)$
be a locally finite simplicial pair such that
$(K,L)$
be a locally finite simplicial pair such that
![]() $(P,Q)=(|K|,|L|)$
, and let
$(P,Q)=(|K|,|L|)$
, and let
![]() $\mathcal {U}=\{\mathrm {St}_K(v)\colon v\in \mathrm {dom}(K)\}$
denote the canonical star-finite cover of
$\mathcal {U}=\{\mathrm {St}_K(v)\colon v\in \mathrm {dom}(K)\}$
denote the canonical star-finite cover of
![]() $(P,Q)$
. Let
$(P,Q)$
. Let
![]() $\mathcal {V}$
be any finite cover of
$\mathcal {V}$
be any finite cover of
![]() $(X,A)$
which refines
$(X,A)$
which refines
![]() $\{f^{-1}(U)\colon U\in \mathcal {U}\}$
; there must then exist a function
$\{f^{-1}(U)\colon U\in \mathcal {U}\}$
; there must then exist a function
![]() $p:\mathcal {V} \rightarrow \mathrm {dom}(K) $
such that
$p:\mathcal {V} \rightarrow \mathrm {dom}(K) $
such that
![]() $f(\overline {V}) \subseteq \mathrm {St}_K(p(V))$
for every
$f(\overline {V}) \subseteq \mathrm {St}_K(p(V))$
for every
![]() $V\in \mathcal {V}$
. Consider the open neighborhood
$V\in \mathcal {V}$
. Consider the open neighborhood
of f in
![]() $\mathsf {LC}((X,A),(P,Q))$
. We claim that every element g of
$\mathsf {LC}((X,A),(P,Q))$
. We claim that every element g of
![]() $N(f) $
is homotopic to f via a homotopy of pairs.
$N(f) $
is homotopic to f via a homotopy of pairs.
Indeed, consider the open neighborhood
![]() $D:=\bigcup _{U\in \mathcal {U}} U\times U$
of the diagonal of
$D:=\bigcup _{U\in \mathcal {U}} U\times U$
of the diagonal of
![]() $P\times P$
, and let
$P\times P$
, and let
![]() $\lambda \colon D\times [0,1]\to P$
be the map given by Lemma 4.2. Define
$\lambda \colon D\times [0,1]\to P$
be the map given by Lemma 4.2. Define
![]() $F\colon f \implies g$
by setting
$F\colon f \implies g$
by setting
![]() $F(x,t):=\lambda (f(x),g(x),t)$
. By Lemma 4.2(1), F is indeed a homotopy from f to g. Since
$F(x,t):=\lambda (f(x),g(x),t)$
. By Lemma 4.2(1), F is indeed a homotopy from f to g. Since
![]() $f(A)\subseteq Q$
, this implies that
$f(A)\subseteq Q$
, this implies that
![]() $p(V)\in \mathrm {dom}(L)$
for all
$p(V)\in \mathrm {dom}(L)$
for all
![]() $V\in \mathcal {V}$
with
$V\in \mathcal {V}$
with
![]() $V\cap A\neq \emptyset $
. From this observation and Lemma 4.2(2), we have that F is a homotopy of pairs.
$V\cap A\neq \emptyset $
. From this observation and Lemma 4.2(2), we have that F is a homotopy of pairs.
Corollary 4.5. Suppose that
![]() $(X,A)$
is a compact pair and
$(X,A)$
is a compact pair and
![]() $(P,Q)$
is a polyhedral pair. Then
$(P,Q)$
is a polyhedral pair. Then
![]() $[(X,A),(P,Q)]$
is countable.
$[(X,A),(P,Q)]$
is countable.
Letting A and Q denote basepoints of
![]() $X=S^n$
and an arbitrary polyhedron P, respectively, we recover the following well-known fact:
$X=S^n$
and an arbitrary polyhedron P, respectively, we recover the following well-known fact:
Corollary 4.6. For any
![]() $n\geq 0$
and countable, locally finite polyhedron P, the set
$n\geq 0$
and countable, locally finite polyhedron P, the set
![]() $\pi _n(P)$
is countable.
$\pi _n(P)$
is countable.
Remark 4.7. As indicated, the homotopy bracket
![]() $[-,-]$
will play an increasingly prominent role in the remainder of our paper, which might even be primarily regarded as a laying of foundations for its descriptive theoretic study. In part, for reasons noted in this section’s introduction, within such a program of study, some care is in order concerning the range of spaces permitted to appear in the target position. Allowing, accordingly, spaces to vary most freely in the source position meshes well with our present focus on cohomology, as will grow clearer below. That said, the reverse setup, the descriptive set theoretic study of the homotopy classes of maps from a fixed polyhedron P to a suitable range of spaces X, remains of considerable interest and would include the development of the definable homotopy groups as a special case. Such groups do, of course, tacitly figure in the present work, and it is only considerations of space and focus which have prevented us from saying more about them.
$[-,-]$
will play an increasingly prominent role in the remainder of our paper, which might even be primarily regarded as a laying of foundations for its descriptive theoretic study. In part, for reasons noted in this section’s introduction, within such a program of study, some care is in order concerning the range of spaces permitted to appear in the target position. Allowing, accordingly, spaces to vary most freely in the source position meshes well with our present focus on cohomology, as will grow clearer below. That said, the reverse setup, the descriptive set theoretic study of the homotopy classes of maps from a fixed polyhedron P to a suitable range of spaces X, remains of considerable interest and would include the development of the definable homotopy groups as a special case. Such groups do, of course, tacitly figure in the present work, and it is only considerations of space and focus which have prevented us from saying more about them.
4.4. Homotopy is idealistic
In this section, we show that the relation of homotopy for maps from a locally compact pair
![]() $(X,A) $
to a pointed polyhedron P is idealistic in the sense of Definition 3.1. We precede this result (Theorem 4.15) with a selection principle of general utility (Proposition 4.9); we then follow it with a more particular, and closely related, selection principle (Corollary 4.19) which we will apply to argue Theorem 7.10.
$(X,A) $
to a pointed polyhedron P is idealistic in the sense of Definition 3.1. We precede this result (Theorem 4.15) with a selection principle of general utility (Proposition 4.9); we then follow it with a more particular, and closely related, selection principle (Corollary 4.19) which we will apply to argue Theorem 7.10.
Suppose that
![]() $X,Y$
are Polish spaces and
$X,Y$
are Polish spaces and
![]() $R\subseteq X\times Y$
is a closed relation such that for every
$R\subseteq X\times Y$
is a closed relation such that for every
![]() $x\in X$
, the section
$x\in X$
, the section
![]() $R_{x}=\{ y\in Y:( x,y) \in R\} $
is nonempty. Let
$R_{x}=\{ y\in Y:( x,y) \in R\} $
is nonempty. Let
![]() $\mathcal {V}$
be a countable basis for the topology of Y. For any Borel set
$\mathcal {V}$
be a countable basis for the topology of Y. For any Borel set
![]() $B\subseteq R$
, let
$B\subseteq R$
, let
and
Notice that
Hence,
![]() $( R\setminus B) _{\Delta }=X\setminus B_{\ast }$
. In particular,
$( R\setminus B) _{\Delta }=X\setminus B_{\ast }$
. In particular,
![]() $B_{\ast }$
is Borel if and only if
$B_{\ast }$
is Borel if and only if
![]() $(R\setminus B)_{\Delta }$
is Borel, and
$(R\setminus B)_{\Delta }$
is Borel, and
![]() $B_{\Delta }$
is Borel if and only if
$B_{\Delta }$
is Borel if and only if
![]() $(R\setminus B)_{\ast }$
is Borel. If
$(R\setminus B)_{\ast }$
is Borel. If
![]() $\{B_{n}:n\in \mathbb {N}\}$
is a sequence of Borel subsets of R and
$\{B_{n}:n\in \mathbb {N}\}$
is a sequence of Borel subsets of R and
![]() $B=\bigcap _{n\in \mathbb {N}}B_{n}$
, then
$B=\bigcap _{n\in \mathbb {N}}B_{n}$
, then
Hence,
![]() $B_{\ast }$
is Borel if
$B_{\ast }$
is Borel if
![]() $(B_{n})_{\ast }$
is Borel for every
$(B_{n})_{\ast }$
is Borel for every
![]() $n\in \mathbb {N}$
. Similarly, if
$n\in \mathbb {N}$
. Similarly, if
![]() $C=\bigcup _{n\in \mathbb {N}}B_{n}$
, then
$C=\bigcup _{n\in \mathbb {N}}B_{n}$
, then
Hence,
![]() $C_{\Delta }$
is Borel if
$C_{\Delta }$
is Borel if
![]() $(B_{n})_{\Delta }$
is Borel for every
$(B_{n})_{\Delta }$
is Borel for every
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Lemma 4.8. Adopt the notations above. Suppose that for every
![]() $ V\in \mathcal {V}$
,
$ V\in \mathcal {V}$
,
is Borel. Then
![]() $B_{\ast }$
and
$B_{\ast }$
and
![]() $ B_{\Delta }$
are Borel subsets of X for each Borel set
$ B_{\Delta }$
are Borel subsets of X for each Borel set
![]() $B\subseteq R$
.
$B\subseteq R$
.
Proof. Notice that if
![]() $B\subseteq R$
is Borel and
$B\subseteq R$
is Borel and
![]() $x\in X$
, then
$x\in X$
, then
 $$ \begin{align} x \in B_{\ast }& \Leftrightarrow \forall\, V\in \mathcal{V}\,(V\cap R_{x}\neq \varnothing \Rightarrow B_{x}\cap V=(B\cap (X\times V))_{x}\text{ is nonmeager in }R_{x}) \notag \\ &\Leftrightarrow \forall\, V\in \mathcal{V}\,\left( x\in R^{V}\Rightarrow x\in \left( B\cap (X\times V)\right) _{\Delta }\right) \text{.} \end{align} $$
$$ \begin{align} x \in B_{\ast }& \Leftrightarrow \forall\, V\in \mathcal{V}\,(V\cap R_{x}\neq \varnothing \Rightarrow B_{x}\cap V=(B\cap (X\times V))_{x}\text{ is nonmeager in }R_{x}) \notag \\ &\Leftrightarrow \forall\, V\in \mathcal{V}\,\left( x\in R^{V}\Rightarrow x\in \left( B\cap (X\times V)\right) _{\Delta }\right) \text{.} \end{align} $$
Since
![]() $R^{V}$
is Borel for all
$R^{V}$
is Borel for all
![]() $V\in \mathcal {V}$
, it follows that
$V\in \mathcal {V}$
, it follows that
![]() $B_{\ast }$
is Borel whenever
$B_{\ast }$
is Borel whenever
![]() $( B\cap (X\times V)) _{\Delta }$
is Borel for every
$( B\cap (X\times V)) _{\Delta }$
is Borel for every
![]() $V\in \mathcal {V}$
. Since
$V\in \mathcal {V}$
. Since
![]() $\left ( R\setminus B\right ) _{\Delta }=X\setminus B_{\ast }$
, this implies that
$\left ( R\setminus B\right ) _{\Delta }=X\setminus B_{\ast }$
, this implies that
![]() $(R\setminus B)_{\Delta }$
is Borel whenever
$(R\setminus B)_{\Delta }$
is Borel whenever
![]() $( B\cap (X\times V)) _{\Delta }$
is Borel for every
$( B\cap (X\times V)) _{\Delta }$
is Borel for every
![]() $V\in \mathcal {V}$
. By these observations, the lemma will follow if we prove by induction on
$V\in \mathcal {V}$
. By these observations, the lemma will follow if we prove by induction on
![]() $\alpha <\omega _{1}$
that if
$\alpha <\omega _{1}$
that if
![]() $B\in \boldsymbol { \Sigma }_{\alpha }^{0}$
, then
$B\in \boldsymbol { \Sigma }_{\alpha }^{0}$
, then
![]() $B_{\Delta }$
is a Borel subset of X.
$B_{\Delta }$
is a Borel subset of X.
For the base case, suppose that
![]() $B=U\times V$
for some open set
$B=U\times V$
for some open set
![]() $U\subseteq X$
and
$U\subseteq X$
and
![]() $V\subseteq Y$
such that
$V\subseteq Y$
such that
![]() $V\in \mathcal {V}$
. Then
$V\in \mathcal {V}$
. Then
is Borel by hypothesis. It follows that
![]() $B_{\Delta }$
is Borel for every open
$B_{\Delta }$
is Borel for every open
![]() $B\subseteq R$
.
$B\subseteq R$
.
For successor steps, suppose that our induction hypothesis holds for some
![]() $\alpha <\omega _1$
. Then
$\alpha <\omega _1$
. Then
![]() $( B\cap (X\times V))_{\Delta }$
is Borel for every
$( B\cap (X\times V))_{\Delta }$
is Borel for every
![]() $V\in \mathcal {V}$
and
$V\in \mathcal {V}$
and
![]() $B\in \boldsymbol {\Sigma }_{\alpha }^{0}$
. Hence,
$B\in \boldsymbol {\Sigma }_{\alpha }^{0}$
. Hence,
![]() $B_{\Delta }$
is Borel for every
$B_{\Delta }$
is Borel for every
![]() $B\in \boldsymbol {\Pi }_{\alpha }^{0}$
. If
$B\in \boldsymbol {\Pi }_{\alpha }^{0}$
. If
![]() $C\in \boldsymbol { \Sigma }_{\alpha +1}^{0}$
, then
$C\in \boldsymbol { \Sigma }_{\alpha +1}^{0}$
, then
![]() $C=\bigcup _{n}B_{n}$
for
$C=\bigcup _{n}B_{n}$
for
![]() $B_{n}\in \boldsymbol {\Sigma }_{\alpha }^{0}$
. Hence,
$B_{n}\in \boldsymbol {\Sigma }_{\alpha }^{0}$
. Hence,
![]() $C_{\Delta }$
is Borel.
$C_{\Delta }$
is Borel.
Lastly, if
![]() $C\in \boldsymbol {\Sigma }_{\beta }^{0}$
for some limit ordinal
$C\in \boldsymbol {\Sigma }_{\beta }^{0}$
for some limit ordinal
![]() $\beta $
below which our inductive hypothesis holds, then since
$\beta $
below which our inductive hypothesis holds, then since
![]() $C=\bigcup _{n}B_{n}$
for some
$C=\bigcup _{n}B_{n}$
for some
![]() $B_{n}\in \boldsymbol {\Sigma }_{\alpha _{n}}^{0}$
with
$B_{n}\in \boldsymbol {\Sigma }_{\alpha _{n}}^{0}$
with
![]() $\alpha _{n}<\beta $
for all
$\alpha _{n}<\beta $
for all
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $C_{\Delta }$
is Borel. This concludes the limit case of our argument, and with it the proof.
$C_{\Delta }$
is Borel. This concludes the limit case of our argument, and with it the proof.
Proposition 4.9. There exists a Borel uniformization of any R as in Lemma 4.8; more precisely, there exists a Borel function
![]() $f:X\rightarrow Y$
such that
$f:X\rightarrow Y$
such that
![]() $f(x) \in R_{x}$
for every
$f(x) \in R_{x}$
for every
![]() $x\in X$
.
$x\in X$
.
Proof. Consider the map
![]() $x\mapsto I_{x}$
assigning to
$x\mapsto I_{x}$
assigning to
![]() $x\in X$
the
$x\in X$
the
![]() $\sigma $
-ideal of meager subsets of X. By Lemma 4.8, if
$\sigma $
-ideal of meager subsets of X. By Lemma 4.8, if
![]() $B\subseteq R$
is Borel, then
$B\subseteq R$
is Borel, then
![]() $\{ x\in X:B\cap R_{x}\in I_{x}\} $
is Borel. Therefore, the conclusion follows from the large section uniformization theorem [Reference Kechris44, Theorem 18.6], in the form appearing as Theorem 18.6
$\{ x\in X:B\cap R_{x}\in I_{x}\} $
is Borel. Therefore, the conclusion follows from the large section uniformization theorem [Reference Kechris44, Theorem 18.6], in the form appearing as Theorem 18.6
![]() $^{*}$
in [Reference Kechris43, p. 2] and featuring in [Reference Kechris and Macdonald45, p. 8] as well.
$^{*}$
in [Reference Kechris43, p. 2] and featuring in [Reference Kechris and Macdonald45, p. 8] as well.
We turn now more directly to the argument that the homotopy relation on
![]() $\mathsf {LC}((X,A),(P,*))$
is idealistic. We will argue this from a series of lemmas in which the closed relation R figuring in the definitions above will be the following set:
$\mathsf {LC}((X,A),(P,*))$
is idealistic. We will argue this from a series of lemmas in which the closed relation R figuring in the definitions above will be the following set:
In particular, for the remainder of this subsection, for any Borel
![]() $B\subseteq \mathsf {LCP}((X,A),( P,\ast ))\times \mathsf {LCP}((X\times I,A\times I),( P,\ast ))$
, it will be in reference to this R that the sets
$B\subseteq \mathsf {LCP}((X,A),( P,\ast ))\times \mathsf {LCP}((X\times I,A\times I),( P,\ast ))$
, it will be in reference to this R that the sets
![]() $B_{\ast }$
and
$B_{\ast }$
and
![]() $B_{\Delta }$
are defined. We begin by proving two lemmas concerning compact pairs
$B_{\Delta }$
are defined. We begin by proving two lemmas concerning compact pairs
![]() $(X,A)$
.
$(X,A)$
.
Lemma 4.10. Suppose that
![]() $(X,A) $
is a compact pair and
$(X,A) $
is a compact pair and
![]() $(P,\ast )$
is a pointed polyhedron. Fix a countable open basis
$(P,\ast )$
is a pointed polyhedron. Fix a countable open basis
![]() $\mathcal {V}$
for X, and let
$\mathcal {V}$
for X, and let
![]() $(K,\ast )$
be a pointed simplicial complex such that
$(K,\ast )$
be a pointed simplicial complex such that
![]() $(P,\ast ) =(|K|,\ast )$
. Then
$(P,\ast ) =(|K|,\ast )$
. Then
![]() $\mathsf {LCP}((X\times I,A\times I),(P,\ast ))$
has a countable basis consisting of open sets of the form
$\mathsf {LCP}((X\times I,A\times I),(P,\ast ))$
has a countable basis consisting of open sets of the form
where
-
•
 $s,\ell \in \mathbb {N}$
,
$s,\ell \in \mathbb {N}$
, -
•
 $\beta ^{s}K$
is the
$\beta ^{s}K$
is the
 $s^{\mathrm {th}}$
barycentric subdivision of K,
$s^{\mathrm {th}}$
barycentric subdivision of K, -
•
 $\mathcal {U}=(U_{i})_{i<\ell }$
is a finite open cover of X consisting of open sets from
$\mathcal {U}=(U_{i})_{i<\ell }$
is a finite open cover of X consisting of open sets from
 $\mathcal {V}$
,
$\mathcal {V}$
, -
•
 $\mathcal {L} =(L_{i}) _{i<\ell }$
is a finite cover of
$\mathcal {L} =(L_{i}) _{i<\ell }$
is a finite cover of
 $\left [ 0,1\right ] $
consisting of closed intervals
$\left [ 0,1\right ] $
consisting of closed intervals
 $L_{j}=[a_{j},a_{j+1}]$
with rational endpoints such that
$L_{j}=[a_{j},a_{j+1}]$
with rational endpoints such that
 $0=a_{0}<a_{1}<\cdots <a_{\ell }=1$
, and
$0=a_{0}<a_{1}<\cdots <a_{\ell }=1$
, and -
• p is a function
 $\ell \times \ell \rightarrow \mathrm {\mathrm {dom}}\left ( \beta ^{s}K\right ) $
.
$\ell \times \ell \rightarrow \mathrm {\mathrm {dom}}\left ( \beta ^{s}K\right ) $
.
Proof. Fix a nonempty open subset V of
![]() $\mathsf {LCP}((X\times I,A\times I),(P,\ast ))$
and
$\mathsf {LCP}((X\times I,A\times I),(P,\ast ))$
and
![]() $\alpha _{0}\in V$
. We prove that there exists an open set W as above such that
$\alpha _{0}\in V$
. We prove that there exists an open set W as above such that
![]() $\alpha _{0}\in W\subseteq V$
. Fix compatible metrics
$\alpha _{0}\in W\subseteq V$
. Fix compatible metrics
![]() $d_{X}$
on X and
$d_{X}$
on X and
![]() $d_{P}$
on P and endow
$d_{P}$
on P and endow
![]() $X\times I$
with the metric
$X\times I$
with the metric
Since
![]() $(X,A)$
is a compact pair, there exists a
$(X,A)$
is a compact pair, there exists a
![]() $\delta>0$
such that V contains
$\delta>0$
such that V contains
and there exists a finite subcomplex
![]() $L\subseteq K$
such that
$L\subseteq K$
such that
![]() $\alpha _{0}(X\times I) \subseteq |L|$
. And since L is a finite simplicial complex, there exists an
$\alpha _{0}(X\times I) \subseteq |L|$
. And since L is a finite simplicial complex, there exists an
![]() $s\in \omega $
such that every
$s\in \omega $
such that every
![]() $\mathrm {St}_{\beta ^{s}L}(v)$
has diameter less than
$\mathrm {St}_{\beta ^{s}L}(v)$
has diameter less than
![]() $\delta $
.
$\delta $
.
For every
![]() $z\in X\times I$
, there exists an open set
$z\in X\times I$
, there exists an open set
![]() $E_{z}\subseteq X\times I$
such that
$E_{z}\subseteq X\times I$
such that
![]() $z\in E_{z}$
and
$z\in E_{z}$
and
![]() $\alpha _{0}(\overline {E}_z)\subseteq \mathrm {St}_{\beta ^{s}L}(v_{z}) $
for some
$\alpha _{0}(\overline {E}_z)\subseteq \mathrm {St}_{\beta ^{s}L}(v_{z}) $
for some
![]() $v_{z}\in \beta ^s(L)$
. By compactness, there exists an
$v_{z}\in \beta ^s(L)$
. By compactness, there exists an
![]() $\ell \geq 1$
such that every subset of
$\ell \geq 1$
such that every subset of
![]() $X\times I$
of diameter at most
$X\times I$
of diameter at most
![]() $1/\ell $
is contained in
$1/\ell $
is contained in
![]() $E_z$
for some
$E_z$
for some
![]() $z\in X\times I$
. Therefore, let
$z\in X\times I$
. Therefore, let
![]() $\mathcal {U}=(U_i)_{i<\ell }$
be a finite open cover of X consisting of open sets from
$\mathcal {U}=(U_i)_{i<\ell }$
be a finite open cover of X consisting of open sets from
![]() $\mathcal {V}$
of diameter less than
$\mathcal {V}$
of diameter less than
![]() $1/\ell $
, and set
$1/\ell $
, and set
![]() $a_{i}=i/\ell $
for
$a_{i}=i/\ell $
for
![]() $0\leq i\leq \ell $
. For each
$0\leq i\leq \ell $
. For each
![]() $i,j<\ell $
, the set
$i,j<\ell $
, the set
![]() $\overline {U}_{i}\times [a_{j},a_{j+1}] $
has diameter at most
$\overline {U}_{i}\times [a_{j},a_{j+1}] $
has diameter at most
![]() $1/\ell $
and is contained in
$1/\ell $
and is contained in
![]() $E_{z(i,j)}$
for some
$E_{z(i,j)}$
for some
![]() $z(i,j) \in X\times I$
. Hence, if we let
$z(i,j) \in X\times I$
. Hence, if we let
![]() $p(i,j)=v_{z(i,j)}$
, then
$p(i,j)=v_{z(i,j)}$
, then
These parameters define a W as in equation 20 with
![]() $\alpha _{0}\in W\subseteq W'\subseteq V$
.
$\alpha _{0}\in W\subseteq W'\subseteq V$
.
Lemma 4.11. Suppose that
![]() $(X,A)$
is a compact pair and
$(X,A)$
is a compact pair and
![]() $(P,\ast )$
is a pointed polyhedron and that W is an open subset of
$(P,\ast )$
is a pointed polyhedron and that W is an open subset of
![]() $\mathsf {LCP}((X\times I,A\times I),(P,\ast ))$
. Then the set
$\mathsf {LCP}((X\times I,A\times I),(P,\ast ))$
. Then the set
is Borel.
Proof. We retain the notation of Lemma 4.10. It will suffice to argue the lemma when W is as in equation 20. In this case, we claim that
![]() $R^W$
equals the open set
$R^W$
equals the open set
where, of course, the sets
![]() $U_i$
and function p are those determining W. The relation
$U_i$
and function p are those determining W. The relation
![]() $R^W\subseteq S$
is clear, since
$R^W\subseteq S$
is clear, since
![]() $g(\overline {U}_i) \subseteq \mathrm {St}_{\beta ^{s}K}(p(i,0))$
for every
$g(\overline {U}_i) \subseteq \mathrm {St}_{\beta ^{s}K}(p(i,0))$
for every
![]() $g\in R_W$
and
$g\in R_W$
and
![]() $i<\ell $
, simply by the definition of W. For the reverse containment, suppose that
$i<\ell $
, simply by the definition of W. For the reverse containment, suppose that
![]() $ g_{0}\in \mathsf {LCP}((X,A),(P,\ast ))$
satisfies
$ g_{0}\in \mathsf {LCP}((X,A),(P,\ast ))$
satisfies
![]() $g_{0}(\overline {U}_i) \subseteq \mathrm {St}_{\beta ^{s}K}( p( i,0))$
for every
$g_{0}(\overline {U}_i) \subseteq \mathrm {St}_{\beta ^{s}K}( p( i,0))$
for every
![]() $i<\ell $
. Fix a partition of unity
$i<\ell $
. Fix a partition of unity
![]() $\left ( \rho _{i}\right )_{i\in \omega }$
subordinate to
$\left ( \rho _{i}\right )_{i\in \omega }$
subordinate to
![]() $\mathcal {U}$
, and consider the function
$\mathcal {U}$
, and consider the function
![]() $g_{1/2}:(X,A) \rightarrow (P,\ast )$
defined by
$g_{1/2}:(X,A) \rightarrow (P,\ast )$
defined by
Notice that
![]() $g_{1/2}^{-1}\left ( \mathrm {St}_{\beta ^{s}K}(p(i,0)) \right ) \subseteq U_{i}$
for every
$g_{1/2}^{-1}\left ( \mathrm {St}_{\beta ^{s}K}(p(i,0)) \right ) \subseteq U_{i}$
for every
![]() $i< \ell $
; hence,
$i< \ell $
; hence,
for every
![]() $i<\ell $
, and we may define a homotopy
$i<\ell $
, and we may define a homotopy
![]() $h_0:g_{0}\Rightarrow g_{1/2}:(X,A) \rightarrow (P,\ast )$
by letting
$h_0:g_{0}\Rightarrow g_{1/2}:(X,A) \rightarrow (P,\ast )$
by letting
![]() $\lambda $
and D be as in Lemma 4.2 and letting
$\lambda $
and D be as in Lemma 4.2 and letting
We now claim that if
![]() $\{ i_{0},\ldots ,i_{m}\} $
is a simplex in the nerve
$\{ i_{0},\ldots ,i_{m}\} $
is a simplex in the nerve
![]() $N_{\mathcal {U}}$
of the cover
$N_{\mathcal {U}}$
of the cover
![]() $\mathcal {U}$
of X, then
$\mathcal {U}$
of X, then
is a simplex in
![]() $\beta ^s K$
. To see this, fix an
$\beta ^s K$
. To see this, fix an
![]() $\alpha _0\in W$
and let
$\alpha _0\in W$
and let
![]() $g_1=\alpha _0\vert _{X\times \{a_1\}}$
, suppose that
$g_1=\alpha _0\vert _{X\times \{a_1\}}$
, suppose that
![]() $\{ i_{0},\ldots ,i_{m}\} \in N_{\mathcal {U}}$
, and hence that there exists an
$\{ i_{0},\ldots ,i_{m}\} \in N_{\mathcal {U}}$
, and hence that there exists an
![]() $x\in U_{i_{0}}\cap \cdots \cap U_{i_{m}}$
. We then have
$x\in U_{i_{0}}\cap \cdots \cap U_{i_{m}}$
. We then have
for
![]() $0\leq k\leq m$
; our claim follows immediately. In consequence, we may define a homotopy
$0\leq k\leq m$
; our claim follows immediately. In consequence, we may define a homotopy
![]() $ h_{1}:g_{1/2}\Rightarrow g_{1}:( X,A) \rightarrow (P,\ast ) $
by letting
$ h_{1}:g_{1/2}\Rightarrow g_{1}:( X,A) \rightarrow (P,\ast ) $
by letting
![]() $\lambda $
and D be as in Lemma 4.2 and letting
$\lambda $
and D be as in Lemma 4.2 and letting
To see that
![]() $h_{1}$
is well defined, observe as before that if
$h_{1}$
is well defined, observe as before that if
![]() $x\in X$
and
$x\in X$
and
![]() $\{ i_{0},\ldots ,i_{m}\} =\{i<\ell :\rho _{i}(x)>0\} $
, then
$\{ i_{0},\ldots ,i_{m}\} =\{i<\ell :\rho _{i}(x)>0\} $
, then
![]() $x\in U_{i_{0}}\cap \cdots \cap U_{i_{m}}$
, and hence, the set described by expression 21 above is again a simplex in
$x\in U_{i_{0}}\cap \cdots \cap U_{i_{m}}$
, and hence, the set described by expression 21 above is again a simplex in
![]() $\beta ^s K$
.
$\beta ^s K$
.
We now define an
![]() $\alpha \in W$
such that
$\alpha \in W$
such that
![]() $\alpha |_{X\times \left \{ 0\right \} }=g_{0}$
by setting
$\alpha |_{X\times \left \{ 0\right \} }=g_{0}$
by setting
 $$ \begin{align*} \alpha \left( x,t\right) =\left\{ \begin{array}{ll} h_{0}(x,\frac{2t}{a_{1}}) & 0\leq t\leq \frac{a_{1}}{2}\text{;} \\ h_{1}(x,\frac{2t}{a_{1}}-1)) & \frac{a_{1}}{2}\leq t\leq a_{1}\text{;} \\ \alpha _{0}\left( x,t\right) & a_{1}\leq t\leq 1\text{.} \end{array} \right. \end{align*} $$
$$ \begin{align*} \alpha \left( x,t\right) =\left\{ \begin{array}{ll} h_{0}(x,\frac{2t}{a_{1}}) & 0\leq t\leq \frac{a_{1}}{2}\text{;} \\ h_{1}(x,\frac{2t}{a_{1}}-1)) & \frac{a_{1}}{2}\leq t\leq a_{1}\text{;} \\ \alpha _{0}\left( x,t\right) & a_{1}\leq t\leq 1\text{.} \end{array} \right. \end{align*} $$
This concludes the proof.
We now extend this analysis to the locally compact setting.
Lemma 4.12. If
![]() $(X,A)$
is a locally compact pair and
$(X,A)$
is a locally compact pair and
![]() $(P,\ast )$
is a pointed polyhedron and W is an open subset of
$(P,\ast )$
is a pointed polyhedron and W is an open subset of
![]() $\mathsf {LCP}((X\times I,A\times I),(P,\ast ))$
, then the set
$\mathsf {LCP}((X\times I,A\times I),(P,\ast ))$
, then the set
is Borel.
Proof. Note first that by replacing X with
![]() $X/A$
(if A is nonempty) or with the space
$X/A$
(if A is nonempty) or with the space
![]() $X_{+}$
obtained by adding to X an additional basepoint (if A is empty), we may assume that A is a singleton
$X_{+}$
obtained by adding to X an additional basepoint (if A is empty), we may assume that A is a singleton
![]() $\{\star \}$
.
$\{\star \}$
.
As above, it will suffice to prove the statement for basic open subsets W subset
![]() $\mathsf {LCP}((X,A),(P,\ast ))$
. Therefore, we may assume that there exist compact subsets
$\mathsf {LCP}((X,A),(P,\ast ))$
. Therefore, we may assume that there exist compact subsets
![]() $K_{1},\ldots ,K_{n}\subseteq X\times I$
and open subsets
$K_{1},\ldots ,K_{n}\subseteq X\times I$
and open subsets
![]() $U_{1},\ldots ,U_{n}\subseteq P$
such that
$U_{1},\ldots ,U_{n}\subseteq P$
such that
Let
and let
By Lemma 4.11, the set
is Borel. By the Homotopy Extension Theorem applied to
![]() $K\subseteq X$
and P,
$K\subseteq X$
and P,
is a Borel subset of
![]() $\mathsf {LCP}((X,\star ),(P,\ast ))$
. This concludes the proof.
$\mathsf {LCP}((X,\star ),(P,\ast ))$
. This concludes the proof.
Lemma 4.13. If
![]() $(X,A)$
is a locally compact pair and
$(X,A)$
is a locally compact pair and
![]() $(P,\ast )$
is a pointed polyhedron and B is a Borel subset of
$(P,\ast )$
is a pointed polyhedron and B is a Borel subset of
![]() $\mathsf {LCP}((X\times I,A\times I),(P,\ast ))$
, then the subsets
$\mathsf {LCP}((X\times I,A\times I),(P,\ast ))$
, then the subsets
![]() $B_{\ast }$
and
$B_{\ast }$
and
![]() $B_{\Delta }$
of
$B_{\Delta }$
of
![]() $\mathsf {LCP}((X,A),(P,\ast ))$
are Borel as well.
$\mathsf {LCP}((X,A),(P,\ast ))$
are Borel as well.
Lemma 4.14. Suppose that
![]() $(X,A) $
is a locally compact pair and P is a pointed polyhedron. If
$(X,A) $
is a locally compact pair and P is a pointed polyhedron. If
![]() $S\subseteq X$
and
$S\subseteq X$
and
then the set
![]() $T_{\ast }\subseteq \mathsf {LCP}((X,A),(P,\ast ))$
is homotopy-invariant.
$T_{\ast }\subseteq \mathsf {LCP}((X,A),(P,\ast ))$
is homotopy-invariant.
Proof. Suppose that
![]() $f\in T_*$
and f is homotopic to g. Let
$f\in T_*$
and f is homotopic to g. Let
Notice that
![]() $\left \{ \alpha \in H_{f}:\alpha \left ( -,1\right ) \in S\right \} $
is comeager in
$\left \{ \alpha \in H_{f}:\alpha \left ( -,1\right ) \in S\right \} $
is comeager in
![]() $H_{f}$
, since
$H_{f}$
, since
![]() $f\in T_*$
.
$f\in T_*$
.
For
![]() $\left ( \alpha ,\beta \right ) \in L\times H_{g}$
, define
$\left ( \alpha ,\beta \right ) \in L\times H_{g}$
, define
![]() $\alpha \ast \beta \in H_{f}$
by setting
$\alpha \ast \beta \in H_{f}$
by setting
 $$ \begin{align*} \left( \alpha \ast \beta \right) \left( t\right) =\left\{ \begin{array}{ll} \alpha \left( 2t\right) & 0\leq t\leq 1/2\text{,} \\ \beta \left( 2t-1\right) & 1/2\leq t\leq 1\text{.} \end{array} \right. \end{align*} $$
$$ \begin{align*} \left( \alpha \ast \beta \right) \left( t\right) =\left\{ \begin{array}{ll} \alpha \left( 2t\right) & 0\leq t\leq 1/2\text{,} \\ \beta \left( 2t-1\right) & 1/2\leq t\leq 1\text{.} \end{array} \right. \end{align*} $$
This defines a continuous and open function
![]() $L\times H_{g}\rightarrow H_{f}$
. Therefore,
$L\times H_{g}\rightarrow H_{f}$
. Therefore,
is comeager in
![]() $L\times H_{g}$
. By the Kuratowski–Ulam theorem [Reference Kechris44, Theorem 8.41], this implies that
$L\times H_{g}$
. By the Kuratowski–Ulam theorem [Reference Kechris44, Theorem 8.41], this implies that
is comeager in
![]() $H_{g}$
, and hence that
$H_{g}$
, and hence that
![]() $g\in T_*$
.
$g\in T_*$
.
We turn now to this section’s main result.
Theorem 4.15. If
![]() $(X,A)$
is a locally compact pair and
$(X,A)$
is a locally compact pair and
![]() $(P,\ast )$
is a pointed polyhedron, then the relation of homotopy for maps
$(P,\ast )$
is a pointed polyhedron, then the relation of homotopy for maps
![]() $(X,A)\to (P,\ast )$
is idealistic.
$(X,A)\to (P,\ast )$
is idealistic.
Proof. For any map
![]() $f:(X,A)\to (P,\ast )$
, let
$f:(X,A)\to (P,\ast )$
, let
![]() $[f] \in [(X,A),(P,\ast )]$
denote its homotopy class. We define a
$[f] \in [(X,A),(P,\ast )]$
denote its homotopy class. We define a
![]() $\sigma $
-filter
$\sigma $
-filter
![]() $\mathcal {F}_{[f]}$
of subsets of
$\mathcal {F}_{[f]}$
of subsets of
![]() $[f]$
by letting
$[f]$
by letting
![]() $S\in \mathcal {F}_{[f]}$
if and only if
$S\in \mathcal {F}_{[f]}$
if and only if
is comeager in
By Lemma 4.14, the definition of
![]() $\mathcal {F}_{[f]}$
does not depend on the choice of representative f of the homotopy class
$\mathcal {F}_{[f]}$
does not depend on the choice of representative f of the homotopy class
![]() $[f]$
.
$[f]$
.
Suppose now that
![]() $E\subseteq \mathsf {LC}((X,A),P,\ast )) \times \mathsf {LC}((X,A),(P,\ast ))$
is Borel. In the notation of Definition 3.1, our task is to show that, for
$E\subseteq \mathsf {LC}((X,A),P,\ast )) \times \mathsf {LC}((X,A),(P,\ast ))$
is Borel. In the notation of Definition 3.1, our task is to show that, for
![]() $\zeta =\mathrm {id}$
and the filters
$\zeta =\mathrm {id}$
and the filters
![]() $\mathcal {F}_{[f]}$
described above, the set
$\mathcal {F}_{[f]}$
described above, the set
![]() $E_{\mathcal {F}}$
is Borel. This set unpacks as follows:
$E_{\mathcal {F}}$
is Borel. This set unpacks as follows:
 $$ \begin{align*} E_{\mathcal{F}} &=\{ f\in \mathsf{LC}(X,A),(P,\ast)):\mathcal{F}_{[f] }g,(f,g) \in E\} \\ &=\{ f\in \mathsf{LC}(X,A),(P,\ast)):\{ \alpha \in R_{f}:(f,\alpha |_{X\times\{1\}})\in E\} \text{ is comeager in } R_{f}\} \\ &=B_{\ast } \end{align*} $$
$$ \begin{align*} E_{\mathcal{F}} &=\{ f\in \mathsf{LC}(X,A),(P,\ast)):\mathcal{F}_{[f] }g,(f,g) \in E\} \\ &=\{ f\in \mathsf{LC}(X,A),(P,\ast)):\{ \alpha \in R_{f}:(f,\alpha |_{X\times\{1\}})\in E\} \text{ is comeager in } R_{f}\} \\ &=B_{\ast } \end{align*} $$
where
![]() $B\subseteq R$
is the Borel set
$B\subseteq R$
is the Borel set
By Lemma 4.13,
![]() $E_{\mathcal {F}}$
is Borel, as desired, showing that the assignment
$E_{\mathcal {F}}$
is Borel, as desired, showing that the assignment
![]() $[f]\mapsto \mathcal {F}_{[f]}$
indeed witnesses that the relation of homotopy for maps
$[f]\mapsto \mathcal {F}_{[f]}$
indeed witnesses that the relation of homotopy for maps
![]() $(X,A)\to (P,\ast )$
is idealistic.
$(X,A)\to (P,\ast )$
is idealistic.
We now deduce, from a sequence of minor variations on the lemmas just recorded, a selection principle which we will want in Section 7.
For any compact pair
![]() $(X,A)$
and pointed polyhedron and
$(X,A)$
and pointed polyhedron and
![]() $(P,*)$
, let
$(P,*)$
, let
![]() $\mathsf {LCP}_{0}((X,A),(P,*))$
denote the subspace of
$\mathsf {LCP}_{0}((X,A),(P,*))$
denote the subspace of
![]() $\mathsf {LCP}((X,A),(P,*))$
consisting of maps which are homotopic to the constant map
$\mathsf {LCP}((X,A),(P,*))$
consisting of maps which are homotopic to the constant map
![]() $\ast :(X,A)\to (P,*)$
. By Lemma 4.4,
$\ast :(X,A)\to (P,*)$
. By Lemma 4.4,
![]() $\mathsf {LCP}_{0}((X,A),(P,*))$
is open in
$\mathsf {LCP}_{0}((X,A),(P,*))$
is open in
![]() $\mathsf {LCP}((X,A),(P,*))$
. Let
$\mathsf {LCP}((X,A),(P,*))$
. Let
![]() $\mathcal {Z}((X,A),(P,*))$
denote the space of nullhomotopies; more precisely, let
$\mathcal {Z}((X,A),(P,*))$
denote the space of nullhomotopies; more precisely, let
![]() $\mathcal {Z}((X,A),(P,*))$
be the closed subset of
$\mathcal {Z}((X,A),(P,*))$
be the closed subset of
![]() $\mathsf {LCP}((X\times I,A\times I),(P,\ast ))$
consisting of those
$\mathsf {LCP}((X\times I,A\times I),(P,\ast ))$
consisting of those
![]() $\alpha $
for which
$\alpha $
for which
![]() $\alpha |_{X\times \{1\}}=\ast $
. As the proof of the following lemma is essentially identical to that of Lemma 4.10, we omit it.
$\alpha |_{X\times \{1\}}=\ast $
. As the proof of the following lemma is essentially identical to that of Lemma 4.10, we omit it.
Lemma 4.16. Suppose that
![]() $(X,A) $
is a compact pair and
$(X,A) $
is a compact pair and
![]() $(P,\ast )$
is a pointed polyhedron. Fix a countable open basis
$(P,\ast )$
is a pointed polyhedron. Fix a countable open basis
![]() $\mathcal {V}$
for X, and let
$\mathcal {V}$
for X, and let
![]() $(K,\ast )$
be a pointed simplicial complex such that
$(K,\ast )$
be a pointed simplicial complex such that
![]() $(P,\ast ) =(|K|,\ast )$
. Then
$(P,\ast ) =(|K|,\ast )$
. Then
![]() $\mathcal {Z}((X,A),(P,*))$
has a countable basis consisting of open sets of the form
$\mathcal {Z}((X,A),(P,*))$
has a countable basis consisting of open sets of the form
where
-
•
 $s,\ell \in \mathbb {N}$
,
$s,\ell \in \mathbb {N}$
, -
•
 $\beta ^{s}K$
is the
$\beta ^{s}K$
is the
 $s^{\mathrm {th}}$
barycentric subdivision of K,
$s^{\mathrm {th}}$
barycentric subdivision of K, -
•
 $\mathcal {U}=(U_{i})_{i<\ell }$
is a finite open cover of X consisting of open sets from
$\mathcal {U}=(U_{i})_{i<\ell }$
is a finite open cover of X consisting of open sets from
 $\mathcal {V}$
,
$\mathcal {V}$
, -
•
 $\mathcal {L} =(L_{i}) _{i<\ell }$
is a finite cover of
$\mathcal {L} =(L_{i}) _{i<\ell }$
is a finite cover of
 $\left [ 0,1\right ] $
consisting of closed intervals
$\left [ 0,1\right ] $
consisting of closed intervals
 $L_{j}=[a_{j},a_{j+1}]$
with rational endpoints such that
$L_{j}=[a_{j},a_{j+1}]$
with rational endpoints such that
 $0=a_{0}<a_{1}<\cdots <a_{\ell }=1$
, and
$0=a_{0}<a_{1}<\cdots <a_{\ell }=1$
, and -
• p is a function
 $\ell \times \ell \rightarrow \mathrm {\mathrm {dom}}\left ( \beta ^{s}K\right ) $
.
$\ell \times \ell \rightarrow \mathrm {\mathrm {dom}}\left ( \beta ^{s}K\right ) $
.
We also have the analogue of Lemma 4.11 (and its proof).
Lemma 4.17. Suppose that
![]() $(X,A)$
is a compact pair and
$(X,A)$
is a compact pair and
![]() $(P,\ast )$
is a pointed polyhedron and that W is an open subset of
$(P,\ast )$
is a pointed polyhedron and that W is an open subset of
![]() $\mathcal {Z}((X,A),(P,*))$
. Then the set
$\mathcal {Z}((X,A),(P,*))$
. Then the set
is Borel.
Proposition 4.18. If
![]() $(X,A)$
is a compact pair and
$(X,A)$
is a compact pair and
![]() $(P,*)$
is a pointed polyhedron, then there exists a Borel function
$(P,*)$
is a pointed polyhedron, then there exists a Borel function
![]() $\Phi :\mathsf {LCP}_{0}((X,A),(P,*))\to \mathcal {Z}((X,A),(P,*))$
,
$\Phi :\mathsf {LCP}_{0}((X,A),(P,*))\to \mathcal {Z}((X,A),(P,*))$
,
![]() $g\mapsto \Phi (g)$
such that
$g\mapsto \Phi (g)$
such that
![]() $\Phi (g)$
is a homotopy
$\Phi (g)$
is a homotopy
![]() $g\Rightarrow \ast :(X,A)\to (P,\ast )$
.
$g\Rightarrow \ast :(X,A)\to (P,\ast )$
.
We apply the following corollary in the proof of Theorem 7.10.
Corollary 4.19. Let
![]() $(Y,B)$
be a locally compact pair homotopy equivalent to the compact pair
$(Y,B)$
be a locally compact pair homotopy equivalent to the compact pair
![]() $(X,A)$
, and let
$(X,A)$
, and let
![]() $(P,\ast )$
be a pointed polyhedron. Then there exists a Borel function
$(P,\ast )$
be a pointed polyhedron. Then there exists a Borel function
![]() $\Phi _{Y}:\mathsf {LCP}_{0}((Y,B),(P,*))\to \mathcal {Z}((Y,B),(P,*))$
,
$\Phi _{Y}:\mathsf {LCP}_{0}((Y,B),(P,*))\to \mathcal {Z}((Y,B),(P,*))$
,
![]() $g\mapsto \Phi _Y(g)$
such that
$g\mapsto \Phi _Y(g)$
such that
![]() $\Phi _Y(g)$
is a homotopy
$\Phi _Y(g)$
is a homotopy
![]() $g\Rightarrow \ast :(Y,B)\to (P,\ast )$
.
$g\Rightarrow \ast :(Y,B)\to (P,\ast )$
.
Proof. By Proposition 4.18, there exists a Borel function
![]() $\Phi _X:\mathsf {LCP}_{0}((X,A),(P,*))\to \mathcal {Z}((X,A),(P,*))$
,
$\Phi _X:\mathsf {LCP}_{0}((X,A),(P,*))\to \mathcal {Z}((X,A),(P,*))$
,
![]() $g\mapsto \Phi _X(g)$
such that
$g\mapsto \Phi _X(g)$
such that
![]() $\Phi _X(g)$
is a homotopy
$\Phi _X(g)$
is a homotopy
![]() $g\Rightarrow \ast :(X,A)\to (P,\ast )$
. Fix a homotopy equivalence
$g\Rightarrow \ast :(X,A)\to (P,\ast )$
. Fix a homotopy equivalence
![]() $h:(X,A) \rightarrow (Y,B)$
, with homotopy inverse
$h:(X,A) \rightarrow (Y,B)$
, with homotopy inverse
![]() $k:(Y,B)\to (X,A)$
. Let also
$k:(Y,B)\to (X,A)$
. Let also
![]() $\alpha :\mathrm {id}_{(Y,B)}\Rightarrow h\circ k:(Y,B) \rightarrow (Y,B)$
be a homotopy.
$\alpha :\mathrm {id}_{(Y,B)}\Rightarrow h\circ k:(Y,B) \rightarrow (Y,B)$
be a homotopy.
For any
![]() $g\in \mathsf {LCP}_{0}((Y,B),(P,*))$
,
$g\in \mathsf {LCP}_{0}((Y,B),(P,*))$
,
![]() $\Phi _{X}( g\circ h)$
is a homotopy
$\Phi _{X}( g\circ h)$
is a homotopy
![]() $g\circ h\Rightarrow \ast :(X,A) \rightarrow (P,\ast )$
; hence,
$g\circ h\Rightarrow \ast :(X,A) \rightarrow (P,\ast )$
; hence,
![]() $\Phi _{X}(g\circ h) \circ (k\times \mathrm {id}_{I}) $
is a homotopy
$\Phi _{X}(g\circ h) \circ (k\times \mathrm {id}_{I}) $
is a homotopy
![]() $g\circ h\circ k\Rightarrow \ast :(Y,B) \rightarrow (P,\ast )$
. Define then
$g\circ h\circ k\Rightarrow \ast :(Y,B) \rightarrow (P,\ast )$
. Define then
![]() $\Phi _{Y}(g)$
to be the composition of the homotopy
$\Phi _{Y}(g)$
to be the composition of the homotopy
![]() $g\circ \alpha :g\Rightarrow g\circ h\circ k$
and the homotopy
$g\circ \alpha :g\Rightarrow g\circ h\circ k$
and the homotopy
![]() $\Phi _{X}( g\circ h) \circ ( k\times \mathrm {id}_{I}) : g\circ h\circ k\Rightarrow \ast $
.
$\Phi _{X}( g\circ h) \circ ( k\times \mathrm {id}_{I}) : g\circ h\circ k\Rightarrow \ast $
.
5. Definable cohomology: the homotopical approach
We showed in the previous section that
![]() $[X,P]$
is idealistic whenever P is a polyhedron. If P carries, in addition, an H-group structure, then
$[X,P]$
is idealistic whenever P is a polyhedron. If P carries, in addition, an H-group structure, then
![]() $[X,P]$
is naturally regarded as a semidefinable group; if the homotopy relation on
$[X,P]$
is naturally regarded as a semidefinable group; if the homotopy relation on
![]() $\mathsf {LC}(X,P)$
is, moreover, Borel, then by our previous results, we will have succeeded in showing that
$\mathsf {LC}(X,P)$
is, moreover, Borel, then by our previous results, we will have succeeded in showing that
![]() $[X,P]$
is a definable group. We show exactly this in Theorem 7.13 below.
$[X,P]$
is a definable group. We show exactly this in Theorem 7.13 below.
We show in the present section that when P is an Eilenberg-MacLane space of type
![]() $(G,n)$
, we can do even better. We adopt the standard abuse of denoting such a P (which is only well defined up to homotopy equivalence) by
$(G,n)$
, we can do even better. We adopt the standard abuse of denoting such a P (which is only well defined up to homotopy equivalence) by
![]() $K(G,n)$
. By a classical theorem of Huber’s,
$K(G,n)$
. By a classical theorem of Huber’s,
![]() $[X,K(G,n)]$
is naturally isomorphic to the Čech cohomology group
$[X,K(G,n)]$
is naturally isomorphic to the Čech cohomology group ![]() , and in this section, we show that this isomorphism is, in fact, definable. This carries several immediate and pleasant consequences – namely, (1)
, and in this section, we show that this isomorphism is, in fact, definable. This carries several immediate and pleasant consequences – namely, (1)
![]() $[X,K(G,n)]$
is essentially (i.e., is definably isomorphic to) a group with a Polish cover; (2) up to definable isomorphism,
$[X,K(G,n)]$
is essentially (i.e., is definably isomorphic to) a group with a Polish cover; (2) up to definable isomorphism, ![]() is homotopy invariant and does not depend on the choice of covering system
is homotopy invariant and does not depend on the choice of covering system
![]() $\boldsymbol {\mathcal {U}}$
; (3)
$\boldsymbol {\mathcal {U}}$
; (3) ![]() is a contravariant functor from
is a contravariant functor from
![]() $\mathsf {LC}$
(or more generally
$\mathsf {LC}$
(or more generally
![]() $\mathsf {LCP}$
) to
$\mathsf {LCP}$
) to
![]() $\mathsf {GPC}$
. The main ingredient of the proof of the definable version of Huber’s theorem is a definable version of the simplicial approximation theorem; see Lemma 5.5.
$\mathsf {GPC}$
. The main ingredient of the proof of the definable version of Huber’s theorem is a definable version of the simplicial approximation theorem; see Lemma 5.5.
In the remainder of the paper, we will argue our results in whichever of the settings
![]() $\mathsf {LC}$
,
$\mathsf {LC}$
,
![]() $\mathsf {LC}_{*}$
or
$\mathsf {LC}_{*}$
or
![]() $\mathsf {LCP}$
seems most representative or most encompassing, depending on the context, often only sketching their extension to any of the others. We note, looking ahead, that the hazards of such an approach are largely allayed by our results in Section 6.3, which help to definably mediate between these settings.
$\mathsf {LCP}$
seems most representative or most encompassing, depending on the context, often only sketching their extension to any of the others. We note, looking ahead, that the hazards of such an approach are largely allayed by our results in Section 6.3, which help to definably mediate between these settings.
5.1. Preliminaries: H-groups, H-cogroups and
 $K(G,n)$
spaces
$K(G,n)$
spaces
Before proceeding, we recall some of the basic materials and operations of homotopy theory – in particular, those which bear on the group and degree structures of
![]() $[-,-]$
and cohomology functors, respectively. The natural and standard context for these operations is the pointed setting (as in [Reference Arkowitz2, Reference May58, Reference Spanier80, Reference Switzer86]), any of which may be taken as a reference for this subsection); our initial framework, accordingly, will be
$[-,-]$
and cohomology functors, respectively. The natural and standard context for these operations is the pointed setting (as in [Reference Arkowitz2, Reference May58, Reference Spanier80, Reference Switzer86]), any of which may be taken as a reference for this subsection); our initial framework, accordingly, will be
![]() $\mathsf {LC}_{*}$
, although mild generalizations of these structures and operations will arise as we proceed.
$\mathsf {LC}_{*}$
, although mild generalizations of these structures and operations will arise as we proceed.
The
![]() $\mathsf {LC}_*$
-analogue of the well-known suspension operation
$\mathsf {LC}_*$
-analogue of the well-known suspension operation
![]() $SX$
on unbased spaces is the reduced suspension operation
$SX$
on unbased spaces is the reduced suspension operation
with the
![]() $\Sigma $
-image of the basepoint as the basepoint of
$\Sigma $
-image of the basepoint as the basepoint of
![]() $\Sigma (X,\ast )$
. The sum or wedge
$\Sigma (X,\ast )$
. The sum or wedge
![]() $(X\vee Y,\ast )$
of
$(X\vee Y,\ast )$
of
![]() $(X,\star )$
and
$(X,\star )$
and ![]() in
in
![]() $\mathsf {LC}_*$
simply identifies the basepoints in the spaces’ disjoint union. We will occasionally elide notation of basepoints in
$\mathsf {LC}_*$
simply identifies the basepoints in the spaces’ disjoint union. We will occasionally elide notation of basepoints in
![]() $\mathsf {LC}_*$
; the smash product
$\mathsf {LC}_*$
; the smash product
![]() $X\wedge Y$
of two pointed spaces, for example, is the quotient of
$X\wedge Y$
of two pointed spaces, for example, is the quotient of
![]() $X\times Y$
by the canonical copy of
$X\times Y$
by the canonical copy of
![]() $X\vee Y$
therein. Note that
$X\vee Y$
therein. Note that
![]() $\Sigma X\cong X\wedge S^1$
, where
$\Sigma X\cong X\wedge S^1$
, where
![]() $S^1$
is the basepointed sphere of dimension one.
$S^1$
is the basepointed sphere of dimension one.
An H-group (also called a grouplike space) is a group object in the category
![]() $\mathsf {Ho}(\mathsf {LC}_{\ast })$
(although it will occasionally be convenient to make this definition in
$\mathsf {Ho}(\mathsf {LC}_{\ast })$
(although it will occasionally be convenient to make this definition in
![]() $\mathsf {Ho}(\mathsf {Top}_{*})$
). Thus, an H-group is a pointed locally compact Polish space X endowed with a map
$\mathsf {Ho}(\mathsf {Top}_{*})$
). Thus, an H-group is a pointed locally compact Polish space X endowed with a map
![]() $\mu :( X\wedge X,\ast ) \rightarrow ( X,\ast ) $
(multiplication) such that
$\mu :( X\wedge X,\ast ) \rightarrow ( X,\ast ) $
(multiplication) such that
-
(1) the maps
 $\left ( X,\ast \right ) \rightarrow \left ( X,\ast \right ) $
,
$\left ( X,\ast \right ) \rightarrow \left ( X,\ast \right ) $
,
 $ x\mapsto \mu ( x,\ast ) $
and
$ x\mapsto \mu ( x,\ast ) $
and
 $x\mapsto ( \ast ,x) $
are homotopic to the identity map
$x\mapsto ( \ast ,x) $
are homotopic to the identity map
 $1_{X}$
of X (a homotopy identity);
$1_{X}$
of X (a homotopy identity); -
(2) the maps
 $\mu \circ \left ( \mu \wedge 1_{X}\right ) $
and
$\mu \circ \left ( \mu \wedge 1_{X}\right ) $
and
 $\mu \circ \left ( 1_{X}\wedge \mu \right ) $
, each taking
$\mu \circ \left ( 1_{X}\wedge \mu \right ) $
, each taking
 $\left ( X\wedge X\wedge X,\ast \right ) $
to
$\left ( X\wedge X\wedge X,\ast \right ) $
to
 $(X,*)$
, are homotopic (homotopy associativity);
$(X,*)$
, are homotopic (homotopy associativity); -
(3) there exists a map
 $z:\left ( X,\ast \right ) \rightarrow \left ( X,\ast \right ) $
such that the maps
$z:\left ( X,\ast \right ) \rightarrow \left ( X,\ast \right ) $
such that the maps
 $( X,\ast ) \rightarrow ( X,\ast ) $
,
$( X,\ast ) \rightarrow ( X,\ast ) $
,
 $x\mapsto \mu ( x,z( x)) $
and
$x\mapsto \mu ( x,z( x)) $
and
 $ x\mapsto \mu ( z( x) ,x) $
are nullhomotopic (a homotopy inverse).
$ x\mapsto \mu ( z( x) ,x) $
are nullhomotopic (a homotopy inverse).
Example 5.1. Any locally compact Polish group is an H-group, with its neutral element as basepoint. Less trivial examples of H-group structures are given by the spaces
![]() $\Omega X:=\mathsf {LC}_{*}((S^1,\ast ),(X,\star ))$
for X in
$\Omega X:=\mathsf {LC}_{*}((S^1,\ast ),(X,\star ))$
for X in
![]() $\mathsf {LC}_{*}$
(note, however, that
$\mathsf {LC}_{*}$
(note, however, that
![]() $\Omega X$
may itself fail to be locally compact); the multiplication operation is given by concatenation of maps in a manner subsumed (since
$\Omega X$
may itself fail to be locally compact); the multiplication operation is given by concatenation of maps in a manner subsumed (since
![]() $S^1=\Sigma S^0$
) by Example 5.2 below.
$S^1=\Sigma S^0$
) by Example 5.2 below.
The H-group X is abelian (or homotopy commutative) if the maps
![]() $\mu $
and
$\mu $
and
![]() $\mu\ \circ\ \sigma $
, where
$\mu\ \circ\ \sigma $
, where
![]() $ \sigma :\left ( X\wedge X,\ast \right ) \rightarrow \left ( X,\ast \right ) $
,
$ \sigma :\left ( X\wedge X,\ast \right ) \rightarrow \left ( X,\ast \right ) $
,
![]() $ \left ( x,y\right ) \mapsto \left ( y,x\right ) $
is the ‘flip’, are homotopic. If
$ \left ( x,y\right ) \mapsto \left ( y,x\right ) $
is the ‘flip’, are homotopic. If
![]() $(X,\ast ,\mu )$
is an H-group and
$(X,\ast ,\mu )$
is an H-group and
![]() $(Y,B)$
is locally compact pair, then
$(Y,B)$
is locally compact pair, then
![]() $[(Y,B),(X,\ast )]$
is a semidefinable group with respect to the operation defined by setting
$[(Y,B),(X,\ast )]$
is a semidefinable group with respect to the operation defined by setting
![]() $[f]\cdot [g] =[\mu \circ ( f\wedge g)]$
; here, the identity element of
$[f]\cdot [g] =[\mu \circ ( f\wedge g)]$
; here, the identity element of
![]() $[(Y,B),(X,\ast )]$
is represented by the constant map, which we also denote by
$[(Y,B),(X,\ast )]$
is represented by the constant map, which we also denote by
![]() $*$
.
$*$
.
Dually, an H-cogroup is a cogroup in the category
![]() $\mathsf {Ho}(\mathsf {LC}_{\ast })$
[Reference MacLane53, Section III.6]. Explicitly, an H-cogroup is a pointed locally compact Polish space X endowed with a continuous map
$\mathsf {Ho}(\mathsf {LC}_{\ast })$
[Reference MacLane53, Section III.6]. Explicitly, an H-cogroup is a pointed locally compact Polish space X endowed with a continuous map
![]() $\nu :X\rightarrow X\vee X$
(comultiplication) such that
$\nu :X\rightarrow X\vee X$
(comultiplication) such that
-
(1) the maps
 $\left ( X,\ast \right ) \rightarrow \left ( X,\ast \right ) $
given by
$\left ( X,\ast \right ) \rightarrow \left ( X,\ast \right ) $
given by
 $\left ( \ast \vee 1_{X}\right ) \circ \nu $
and
$\left ( \ast \vee 1_{X}\right ) \circ \nu $
and
 $\left ( 1_{X}\vee \ast \right ) \circ \nu $
are homotopic to
$\left ( 1_{X}\vee \ast \right ) \circ \nu $
are homotopic to
 $1_{X}$
;
$1_{X}$
; -
(2) the maps
 $\left ( X,\ast \right ) \rightarrow \left ( X\vee X\vee X,\ast \right ) $
defined by
$\left ( X,\ast \right ) \rightarrow \left ( X\vee X\vee X,\ast \right ) $
defined by
 $\left ( 1_{X}\vee \nu \right ) \circ \nu $
and
$\left ( 1_{X}\vee \nu \right ) \circ \nu $
and
 $\left ( \nu \vee 1_{X}\right ) \circ \nu $
are homotopic,
$\left ( \nu \vee 1_{X}\right ) \circ \nu $
are homotopic, -
(3) there exists a map
 $\zeta :\left ( X,\ast \right ) \rightarrow \left ( X,\ast \right ) $
such that the maps
$\zeta :\left ( X,\ast \right ) \rightarrow \left ( X,\ast \right ) $
such that the maps
 $\left ( X,\ast \right ) \rightarrow \left ( X,\ast \right ) $
defined by
$\left ( X,\ast \right ) \rightarrow \left ( X,\ast \right ) $
defined by
 $\left ( 1_{X}\vee \zeta \right ) \circ \nu $
and
$\left ( 1_{X}\vee \zeta \right ) \circ \nu $
and
 $\left ( \zeta \vee 1_{X}\right ) \circ \nu $
are homotopic to
$\left ( \zeta \vee 1_{X}\right ) \circ \nu $
are homotopic to
 $\ast $
.
$\ast $
.
Example 5.2. Main examples of H-cogroups are given by suspensions of spaces. Writing
![]() $\langle x,t\rangle $
for the image of
$\langle x,t\rangle $
for the image of
![]() $(x,t)\in X\times I$
in
$(x,t)\in X\times I$
in
![]() $\Sigma X$
, we have a comultiplication operation
$\Sigma X$
, we have a comultiplication operation
 $$ \begin{align*} \nu (\langle x,t\rangle) =\left\{ \begin{array}{ll} ( \langle x,2t\rangle ,\ast) & 0\leq t\leq 1/2 \\ ( \ast ,\langle x,2t-1\rangle) & 1/2\leq t\leq 1 \end{array} \right. \end{align*} $$
$$ \begin{align*} \nu (\langle x,t\rangle) =\left\{ \begin{array}{ll} ( \langle x,2t\rangle ,\ast) & 0\leq t\leq 1/2 \\ ( \ast ,\langle x,2t-1\rangle) & 1/2\leq t\leq 1 \end{array} \right. \end{align*} $$
(for ease of notation, we identify
![]() $X\vee X$
with its canonical copy in
$X\vee X$
with its canonical copy in
![]() $X\times X$
). The homotopy inverse
$X\times X$
). The homotopy inverse
![]() $\zeta :\Sigma X\rightarrow \Sigma X$
is defined by
$\zeta :\Sigma X\rightarrow \Sigma X$
is defined by
![]() $\langle x,t\rangle \mapsto \langle x,1-t\rangle $
.
$\langle x,t\rangle \mapsto \langle x,1-t\rangle $
.
The cogroup
![]() $\left ( X,\ast ,\nu \right ) $
is homotopy commutative if the maps
$\left ( X,\ast ,\nu \right ) $
is homotopy commutative if the maps
![]() $ X\rightarrow X\vee X$
defined by
$ X\rightarrow X\vee X$
defined by
![]() $\nu $
and
$\nu $
and
![]() $\sigma \circ \nu $
are homotopic. As above, for an H-cogroup
$\sigma \circ \nu $
are homotopic. As above, for an H-cogroup
![]() $\left ( X,\nu \right )$
and a pointed space Y, the operation
$\left ( X,\nu \right )$
and a pointed space Y, the operation
![]() $[f]\cdot [g] =[(f\vee g)\circ \nu ] $
defines a semidefinable group structure on
$[f]\cdot [g] =[(f\vee g)\circ \nu ] $
defines a semidefinable group structure on
![]() $[(X,\ast ),(Y,\star )]$
; again, the identity element is represented by the constant map.
$[(X,\ast ),(Y,\star )]$
; again, the identity element is represented by the constant map.
A natural question when the first and second arguments of
![]() $[(X,\ast ),(Y,\star )]$
carry H-cogroup and H-group structures, respectively, is how the induced group structures on
$[(X,\ast ),(Y,\star )]$
carry H-cogroup and H-group structures, respectively, is how the induced group structures on
![]() $[(X,\ast ),(Y,\star )]$
relate. This question has a pleasant answer even when
$[(X,\ast ),(Y,\star )]$
relate. This question has a pleasant answer even when
![]() $(Y,\star )$
is merely an H-space. Briefly put, an H -space is a unital magma in the homotopy category of pointed spaces [Reference Arkowitz2, Definition 2.2.1]. More explicitly, an H-space is a pointed locally compact Polish space X endowed with a map
$(Y,\star )$
is merely an H-space. Briefly put, an H -space is a unital magma in the homotopy category of pointed spaces [Reference Arkowitz2, Definition 2.2.1]. More explicitly, an H-space is a pointed locally compact Polish space X endowed with a map
![]() $\mu :X\wedge X\rightarrow X$
such that the maps
$\mu :X\wedge X\rightarrow X$
such that the maps
![]() $\left ( X,\ast \right ) \rightarrow \left ( X,\ast \right ) $
,
$\left ( X,\ast \right ) \rightarrow \left ( X,\ast \right ) $
,
![]() $x\mapsto \mu ( x,\ast ) $
and
$x\mapsto \mu ( x,\ast ) $
and
![]() $ x\mapsto \mu ( \ast ,x) $
are homotopic to
$ x\mapsto \mu ( \ast ,x) $
are homotopic to
![]() $1_{X}$
; its ‘group operation’
$1_{X}$
; its ‘group operation’
![]() $\mu $
, in other words, is free to violate items (2) and (3) of the definition of an H-group. The following lemma appears as [Reference Arkowitz2, Proposition 2.2.12].
$\mu $
, in other words, is free to violate items (2) and (3) of the definition of an H-group. The following lemma appears as [Reference Arkowitz2, Proposition 2.2.12].
Lemma 5.3. Let X be an H-cogroup, and let Y be an H-space. Then the group operation on
![]() $[(X,\ast ),(Y,\star )]$
induced by the H-cogroup structure on X coincides with the operation on
$[(X,\ast ),(Y,\star )]$
induced by the H-cogroup structure on X coincides with the operation on
![]() $[(X,\ast ),(Y,\star )]$
induced by the H-space structure on Y and is, moreover, commutative.
$[(X,\ast ),(Y,\star )]$
induced by the H-space structure on Y and is, moreover, commutative.
We turn now to a central focus of this section: the Eilenberg-MacLane spaces first introduced in [Reference Eilenberg and MacLane28]. These are specified up to homotopy equivalence by the following definition:
Definition 5.4. For any abelian group G and
![]() $n\geq 1$
, an Eilenberg-MacLane space of type
$n\geq 1$
, an Eilenberg-MacLane space of type
![]() $(G,n)$
is a pointed topological space Y satisfying the following condition:
$(G,n)$
is a pointed topological space Y satisfying the following condition:
 $$ \begin{align*} \pi_i(Y,*)= \begin{cases} \; G & \text{if } i=n \\ \{0\} & \text{if } i\neq n. \end{cases} \end{align*} $$
$$ \begin{align*} \pi_i(Y,*)= \begin{cases} \; G & \text{if } i=n \\ \{0\} & \text{if } i\neq n. \end{cases} \end{align*} $$
See this subsection’s initial references for multiple approaches to such spaces’ construction. More immediately relevant to our concerns are the following three main points:
-
• For any
 $n\geq 1$
and countable abelian group G, there exists a (countable, locally finite) polyhedral Eilenberg-MacLane space of type
$n\geq 1$
and countable abelian group G, there exists a (countable, locally finite) polyhedral Eilenberg-MacLane space of type
 $(G,n)$
, by any of the aforementioned constructions, together with [Reference Milnor64].
$(G,n)$
, by any of the aforementioned constructions, together with [Reference Milnor64]. -
• For any Eilenberg-MacLane spaces
 $Y,Z$
of type
$Y,Z$
of type
 $(G,n)$
and
$(G,n)$
and
 $(G,n+1)$
, respectively, we have
$(G,n+1)$
, respectively, we have
 $Y\simeq \Omega Z$
(this follows from the uniqueness of Eilenberg-MacLane spaces up to homotopy equivalence, together with the adjointness of the
$Y\simeq \Omega Z$
(this follows from the uniqueness of Eilenberg-MacLane spaces up to homotopy equivalence, together with the adjointness of the
 $\Sigma $
and
$\Sigma $
and
 $\Omega $
operations). It is easy to see that homotopy equivalences preserve H-group structures, and that the H-group operations on any
$\Omega $
operations). It is easy to see that homotopy equivalences preserve H-group structures, and that the H-group operations on any
 $\Omega Z$
referenced in Example 5.1 are continuous. Hence, any Eilenberg-MacLane space Y carries a natural H-group structure with continuous H-group operations.
$\Omega Z$
referenced in Example 5.1 are continuous. Hence, any Eilenberg-MacLane space Y carries a natural H-group structure with continuous H-group operations. -
• It will be convenient for our purposes to take any discrete group G itself to be an Eilenberg-MacLane space of type
 $(G,0)$
. Note that this extends the
$(G,0)$
. Note that this extends the
 $\Omega $
equation cited just above; moreover, as noted in [Reference Huber40], this convention extends the homotopical representation of the Čech cohomology groups to the degree zero.
$\Omega $
equation cited just above; moreover, as noted in [Reference Huber40], this convention extends the homotopical representation of the Čech cohomology groups to the degree zero.
5.2. A definable simplicial approximation theorem
For simplicity, we will conduct the discussion of the next two subsections in the category
![]() $\mathsf {LC}$
, touching on its generalization at their conclusion. Note that an H-group structure on P will continue in this context to translate to one on
$\mathsf {LC}$
, touching on its generalization at their conclusion. Note that an H-group structure on P will continue in this context to translate to one on
![]() $[X,P]$
, definably so, as is clear either from inspection or Corollary 6.6. Therefore, fix a locally compact Polish space X and a covering system
$[X,P]$
, definably so, as is clear either from inspection or Corollary 6.6. Therefore, fix a locally compact Polish space X and a covering system
![]() $\boldsymbol {\mathcal {U}}=\big {(}(X_n),(\mathcal {U}_{\alpha }),(r^{\beta }_{\alpha })\big {)}$
for X. Recall that by
$\boldsymbol {\mathcal {U}}=\big {(}(X_n),(\mathcal {U}_{\alpha }),(r^{\beta }_{\alpha })\big {)}$
for X. Recall that by
![]() $N_{\alpha }$
, we denote the simplicial complex
$N_{\alpha }$
, we denote the simplicial complex
![]() $\mathrm {Nv}(\mathcal {U}_{\alpha })$
. Fix also a countable locally finite simplicial complex K, and assume that
$\mathrm {Nv}(\mathcal {U}_{\alpha })$
. Fix also a countable locally finite simplicial complex K, and assume that
![]() $\mathrm {dom}(K)=\mathbb {N}$
.
$\mathrm {dom}(K)=\mathbb {N}$
.
We begin by defining the Polish space
![]() $\mathrm {SA}_{\boldsymbol {\mathcal {U}}}(X,K)$
of all simplicial approximations of functions from X to K. First, let
$\mathrm {SA}_{\boldsymbol {\mathcal {U}}}(X,K)$
of all simplicial approximations of functions from X to K. First, let
![]() $S:=\bigcup _{\alpha \in \mathcal {N}^{*}} \mathcal {U}_{\alpha }$
be the collection of all open sets contained in any open cover of our covering system. By Lemma 2.6, this set is countable, and without loss of generality, we may assume that
$S:=\bigcup _{\alpha \in \mathcal {N}^{*}} \mathcal {U}_{\alpha }$
be the collection of all open sets contained in any open cover of our covering system. By Lemma 2.6, this set is countable, and without loss of generality, we may assume that
![]() $\emptyset \not \in S$
. We endow the set
$\emptyset \not \in S$
. We endow the set
![]() $\mathrm {dom}(K)^S$
of all functions from S to
$\mathrm {dom}(K)^S$
of all functions from S to
![]() $\mathrm {dom}(K)$
with the product topology, rendering it a Polish space. For every
$\mathrm {dom}(K)$
with the product topology, rendering it a Polish space. For every
![]() $p\in \mathrm {dom}(K)^S$
and every
$p\in \mathrm {dom}(K)^S$
and every
![]() $\alpha \in \mathcal {N}^{*}$
, we denote by
$\alpha \in \mathcal {N}^{*}$
, we denote by
![]() $p|_{\alpha }$
the restriction of p to the set
$p|_{\alpha }$
the restriction of p to the set
![]() $\mathcal {U}_{\alpha }$
. We define the set
$\mathcal {U}_{\alpha }$
. We define the set
to consist of all pairs
![]() $(\alpha ,p)$
for which
$(\alpha ,p)$
for which
![]() $p|_{\alpha }$
is a simplicial map from
$p|_{\alpha }$
is a simplicial map from
![]() $N_{\alpha }$
to K and
$N_{\alpha }$
to K and
![]() $p(U)=0$
if
$p(U)=0$
if
![]() $U\not \in \mathcal {U}_{\alpha }$
. As a closed subset of the Polish space
$U\not \in \mathcal {U}_{\alpha }$
. As a closed subset of the Polish space
![]() $\mathcal {N}^{*}\times \mathrm {dom}(K)^S$
, the space
$\mathcal {N}^{*}\times \mathrm {dom}(K)^S$
, the space
![]() $\mathrm {SA}_{\boldsymbol {\mathcal {U}}}(X,K)$
is Polish. It is also clearly in bijective correspondence with the set all simplicial maps of the form
$\mathrm {SA}_{\boldsymbol {\mathcal {U}}}(X,K)$
is Polish. It is also clearly in bijective correspondence with the set all simplicial maps of the form
![]() $N_{\alpha }\to K$
from some complex of the form
$N_{\alpha }\to K$
from some complex of the form
![]() $N_{\alpha }$
. With reference to the canonical open cover
$N_{\alpha }$
. With reference to the canonical open cover
![]() $\{\mathrm {St}_K(k)\colon k\in \mathrm {dom}(K)\}$
of K, we now have the following definable version of the simplicial approximation theorem.
$\{\mathrm {St}_K(k)\colon k\in \mathrm {dom}(K)\}$
of K, we now have the following definable version of the simplicial approximation theorem.
Lemma 5.5. There is a Borel map
![]() $f\mapsto (\alpha _f,p_f)$
from
$f\mapsto (\alpha _f,p_f)$
from
![]() $\mathsf {LC}(X,|K|)$
to
$\mathsf {LC}(X,|K|)$
to
![]() $\mathrm {SA}_{\boldsymbol {\mathcal {U}}}(X,K)$
so that
$\mathrm {SA}_{\boldsymbol {\mathcal {U}}}(X,K)$
so that
Proof. For every
![]() $\alpha \in \mathcal {N}^{*}$
, set
$\alpha \in \mathcal {N}^{*}$
, set
![]() $\mathcal {U}^{\mathrm {cl}}_{\alpha }:=\{\mathrm {cl}(U)\colon U\in \mathcal {U}_{\alpha }\}$
. By Lemma 2.6(4), we may assume without loss of generality that for all
$\mathcal {U}^{\mathrm {cl}}_{\alpha }:=\{\mathrm {cl}(U)\colon U\in \mathcal {U}_{\alpha }\}$
. By Lemma 2.6(4), we may assume without loss of generality that for all
![]() $\alpha \in \mathcal {N}^{*}$
, every element of
$\alpha \in \mathcal {N}^{*}$
, every element of
![]() $\mathcal {U}^{\mathrm {cl}}_{\alpha }$
is compact.
$\mathcal {U}^{\mathrm {cl}}_{\alpha }$
is compact.
As before, for readability, we will omit the subscript of
![]() $\mathrm {St}_K(k)$
. For every
$\mathrm {St}_K(k)$
. For every
![]() $f\in \mathsf {LC}(X,|K|)$
and
$f\in \mathsf {LC}(X,|K|)$
and
![]() $k\in \mathrm {dom}(K)$
, set
$k\in \mathrm {dom}(K)$
, set
![]() $U_{f,k}:= f^{-1}(\mathrm {St}(k))$
; for each such f, collect these sets into an open cover
$U_{f,k}:= f^{-1}(\mathrm {St}(k))$
; for each such f, collect these sets into an open cover
![]() $\mathcal {U}_f:=(U_{f,k}\colon k\in \mathrm {dom}(K))$
of X. By Lemma 2.6(3), for each f, there exists some
$\mathcal {U}_f:=(U_{f,k}\colon k\in \mathrm {dom}(K))$
of X. By Lemma 2.6(3), for each f, there exists some
![]() $\alpha \in \mathcal {N}^{*}$
so that
$\alpha \in \mathcal {N}^{*}$
so that
![]() $\mathcal {U}_f\preceq \mathcal {U}^{\mathrm {cl}}_{\alpha }$
. Let
$\mathcal {U}_f\preceq \mathcal {U}^{\mathrm {cl}}_{\alpha }$
. Let
![]() $\alpha _f$
be the
$\alpha _f$
be the
![]() $\leq _{\mathrm {lex}}$
-least such; this specification is well defined by the fact that any
$\leq _{\mathrm {lex}}$
-least such; this specification is well defined by the fact that any
![]() $\leq _{\mathrm {lex}}$
-decreasing sequence in
$\leq _{\mathrm {lex}}$
-decreasing sequence in
![]() $\mathcal {N}^{*}$
has a limit, together with condition (L1) of Definition 2.3.
$\mathcal {N}^{*}$
has a limit, together with condition (L1) of Definition 2.3.
Claim 5.6. The assignment
![]() $f\mapsto \alpha _{f}$
is Borel.
$f\mapsto \alpha _{f}$
is Borel.
Proof of Claim.
Fix
![]() $t\in (\mathbb {N}^{<\mathbb {N}})^{*}$
with
$t\in (\mathbb {N}^{<\mathbb {N}})^{*}$
with
![]() $t= \alpha _{f}|n$
for some
$t= \alpha _{f}|n$
for some
![]() $n\in \mathbb {N}$
. We will show that the set of all
$n\in \mathbb {N}$
. We will show that the set of all
![]() $g\in \mathsf {LC}(X,|K|)$
with
$g\in \mathsf {LC}(X,|K|)$
with
![]() $\alpha _g \in \mathcal {N}^{*}_t$
is Borel.
$\alpha _g \in \mathcal {N}^{*}_t$
is Borel.
To that end, take g with
![]() $\alpha _g \in \mathcal {N}^{*}_t$
, and observe that there are only finitely many
$\alpha _g \in \mathcal {N}^{*}_t$
, and observe that there are only finitely many
![]() $s\in (\mathbb {N}^{n})^{*}$
with
$s\in (\mathbb {N}^{n})^{*}$
with
![]() $s<_{\mathrm {lex}} t$
. If for some
$s<_{\mathrm {lex}} t$
. If for some
![]() $s<_{\mathrm {lex}} t$
we had
$s<_{\mathrm {lex}} t$
we had
![]() $\mathcal {U}_g\preceq \mathcal {U}^{\mathrm {cl}}_{s}$
, then by Definition 2.3 (E1), there would exist some
$\mathcal {U}_g\preceq \mathcal {U}^{\mathrm {cl}}_{s}$
, then by Definition 2.3 (E1), there would exist some
![]() $\beta \in \mathcal {N}^{*}_s$
with
$\beta \in \mathcal {N}^{*}_s$
with
![]() $\mathcal {U}_g\preceq \mathcal {U}^{\mathrm {cl}}_{\beta }$
. As
$\mathcal {U}_g\preceq \mathcal {U}^{\mathrm {cl}}_{\beta }$
. As
![]() $\beta <_{\mathrm {lex}} \alpha _g$
, this is a contradiction. Hence, the condition
$\beta <_{\mathrm {lex}} \alpha _g$
, this is a contradiction. Hence, the condition
![]() $\alpha _g \in \mathcal {N}^{*}_t$
is equivalent to
$\alpha _g \in \mathcal {N}^{*}_t$
is equivalent to
-
(1) for every
 $U\in \mathcal {U}_t$
, there is some
$U\in \mathcal {U}_t$
, there is some
 $k\in \mathrm {dom}(K)$
with
$k\in \mathrm {dom}(K)$
with
 $g(\mathrm {cl}(U))\subseteq \mathrm {St}(k)$
; and
$g(\mathrm {cl}(U))\subseteq \mathrm {St}(k)$
; and -
(2) for every
 $s<_{\mathrm {lex}} t$
in
$s<_{\mathrm {lex}} t$
in
 $(\mathbb {N}^{n})^{*}$
, there is a
$(\mathbb {N}^{n})^{*}$
, there is a
 $U\in \mathcal {U}_s$
such that
$U\in \mathcal {U}_s$
such that
 $g(\mathrm {cl}(U))\not \subseteq \mathrm {St}(k)$
for all
$g(\mathrm {cl}(U))\not \subseteq \mathrm {St}(k)$
for all
 $k\in \mathrm {dom}(K)$
.
$k\in \mathrm {dom}(K)$
.
Condition (1) is open and condition (2) is closed.
Similarly, for every
![]() $f\in \mathsf {LC}(X,|K|)$
, let
$f\in \mathsf {LC}(X,|K|)$
, let
![]() $p_f\colon S\to \mathrm {dom}(K)$
be the map which sends every
$p_f\colon S\to \mathrm {dom}(K)$
be the map which sends every
![]() $U\in \mathcal {U}_{\alpha _f}$
to the least
$U\in \mathcal {U}_{\alpha _f}$
to the least
![]() $k\in \mathrm {dom}(K)=\mathbb {N}$
with
$k\in \mathrm {dom}(K)=\mathbb {N}$
with
![]() $f(\mathrm {cl}(U))\subseteq \mathrm {St}(k)$
and with
$f(\mathrm {cl}(U))\subseteq \mathrm {St}(k)$
and with
![]() $p_f(U)=0$
for
$p_f(U)=0$
for
![]() $U\not \in \mathcal {U}_{\alpha _f}$
.
$U\not \in \mathcal {U}_{\alpha _f}$
.
5.3. The definable version of Huber’s theorem
Let G be a countable abelian group. As noted above,
![]() $K(G,n)$
will denote for us a polyhedral Eilenberg-MacLane space of type
$K(G,n)$
will denote for us a polyhedral Eilenberg-MacLane space of type
![]() $(G,n)$
, despite the fact that such a space is only well defined up to homotopy equivalence. It will also be notationally simplifying to conflate
$(G,n)$
, despite the fact that such a space is only well defined up to homotopy equivalence. It will also be notationally simplifying to conflate
![]() $K(G,n)$
with its underlying simplicial complex in a few places below. The following is the definable version of Huber’s theorem [Reference Huber40] (that
$K(G,n)$
with its underlying simplicial complex in a few places below. The following is the definable version of Huber’s theorem [Reference Huber40] (that
![]() $[X,K(G,n)]_{\mathrm {def}}$
is a definable group follows from Theorem 4.15 and Theorem 7.13 below).
$[X,K(G,n)]_{\mathrm {def}}$
is a definable group follows from Theorem 4.15 and Theorem 7.13 below).
Theorem 5.7. Let X be a locally compact Polish space. For every
![]() $n\geq 0$
, the definable group
$n\geq 0$
, the definable group
![]() $[X,K(G,n)]_{\mathrm {def}}$
is naturally definably isomorphic to the group with a Polish cover
$[X,K(G,n)]_{\mathrm {def}}$
is naturally definably isomorphic to the group with a Polish cover ![]() .
.
Proof. Let ![]() be the classical Čech cohomology group as defined in the proof of Theorem 2.12. We start by recalling the definition of the Huber’s isomorphism
be the classical Čech cohomology group as defined in the proof of Theorem 2.12. We start by recalling the definition of the Huber’s isomorphism ![]() between abstract groups. For this, we follow the exposition from [Reference Bartik3], which explicitly takes (9) as its working definition for Čech cohomology.
between abstract groups. For this, we follow the exposition from [Reference Bartik3], which explicitly takes (9) as its working definition for Čech cohomology.
To define J, one begins with a fundamental cohomology class ![]() . While the explicit description of u will have no bearing on our definability considerations below, such a u is essentially provided by the Yoneda’s lemma. More concretely, note that, since G is abelian and
. While the explicit description of u will have no bearing on our definability considerations below, such a u is essentially provided by the Yoneda’s lemma. More concretely, note that, since G is abelian and
![]() $\pi _k(K(G,n))=0$
for
$\pi _k(K(G,n))=0$
for
![]() $k<n$
, by Hurewicz’s Theorem (when
$k<n$
, by Hurewicz’s Theorem (when
![]() $n=0$
, one may more directly argue the point), we have that
$n=0$
, one may more directly argue the point), we have that
By the Universal Coefficient Theorem, we then have the following natural isomorphisms:
The element ![]() is simply the pullback of the identity map
is simply the pullback of the identity map
![]() $G\to G$
under these isomorphisms.
$G\to G$
under these isomorphisms.
Notice now that by the functoriality of Čech cohomology, every continuous map
![]() $f\colon X\to K(G,n)$
induces an abstract group homomorphism
$f\colon X\to K(G,n)$
induces an abstract group homomorphism
Huber’s isomorphism is defined by simply setting
![]() $J([f]_{\simeq }):= f^{*}(u)$
, for every
$J([f]_{\simeq }):= f^{*}(u)$
, for every
![]() $[f]_{\simeq }\in [X,K(G,n)]$
; see [Reference Bartik3]. Our goal is to show that the abstract group isomorphism
$[f]_{\simeq }\in [X,K(G,n)]$
; see [Reference Bartik3]. Our goal is to show that the abstract group isomorphism ![]() , where
, where
![]() $\psi $
is defined by (14) in the proof of the Theorem 2.12, admits a Borel lift
$\psi $
is defined by (14) in the proof of the Theorem 2.12, admits a Borel lift
![]() $\mathsf {LC}(X,K(G,n))\to \mathrm {Z}^n(X;G)$
.
$\mathsf {LC}(X,K(G,n))\to \mathrm {Z}^n(X;G)$
.
Let
![]() $\mathcal {V}$
be the ‘canonical’ open cover
$\mathcal {V}$
be the ‘canonical’ open cover
![]() $\{\mathrm {St}_{K(G,n)}(v)\colon v\in \mathrm {dom}(K(G,n))\}$
of
$\{\mathrm {St}_{K(G,n)}(v)\colon v\in \mathrm {dom}(K(G,n))\}$
of
![]() $K(G,n)$
, consisting of all open stars. We have a simplicial complex isomorphism
$K(G,n)$
, consisting of all open stars. We have a simplicial complex isomorphism
![]() $\eta \colon K(G,n)\to \mathrm {Nv}(\mathcal {V})$
induced by the assignment
$\eta \colon K(G,n)\to \mathrm {Nv}(\mathcal {V})$
induced by the assignment
![]() $v\mapsto \mathrm {St}_{K(G,n)}(v)$
. Since
$v\mapsto \mathrm {St}_{K(G,n)}(v)$
. Since
![]() $\mathcal {V}$
is a good cover (i.e.,
$\mathcal {V}$
is a good cover (i.e.,
![]() $V_0\cap \cdots \cap V_k$
is either contractible or empty for all choices of
$V_0\cap \cdots \cap V_k$
is either contractible or empty for all choices of
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
![]() $V_i\in \mathcal {V}$
), there exists
$V_i\in \mathcal {V}$
), there exists
![]() $\hat {u}\in \mathrm {Z}^n(\mathrm {Nv}(\mathcal {V}),G)$
so that
$\hat {u}\in \mathrm {Z}^n(\mathrm {Nv}(\mathcal {V}),G)$
so that ![]() where, as in the proof of Theorem 2.12,
where, as in the proof of Theorem 2.12, ![]() is the image of
is the image of
![]() $a\in \mathrm {H}^{n}(\mathrm {Nv}(\mathcal {V});G)$
under the inclusion
$a\in \mathrm {H}^{n}(\mathrm {Nv}(\mathcal {V});G)$
under the inclusion ![]() ; see, for example, [Reference Eilenberg and Steenrod29, Section IX.9].
; see, for example, [Reference Eilenberg and Steenrod29, Section IX.9].
By the definition of the assignment
![]() $f\mapsto f^{*}$
(see, for example, [Reference Eilenberg and Steenrod29, Section IX.4]), for every
$f\mapsto f^{*}$
(see, for example, [Reference Eilenberg and Steenrod29, Section IX.4]), for every
![]() $f\in \mathsf {LC}(X,K(G,n))$
, the associated element
$f\in \mathsf {LC}(X,K(G,n))$
, the associated element ![]() is given by
is given by ![]() , where
, where
![]() $\mathcal {U}_f$
is any open cover of X which refines
$\mathcal {U}_f$
is any open cover of X which refines
![]() $\{f^{-1}(\mathrm {St}_{K(G,n)}(v))\colon v\in \mathrm {dom}(K(G,n))\}$
and
$\{f^{-1}(\mathrm {St}_{K(G,n)}(v))\colon v\in \mathrm {dom}(K(G,n))\}$
and
![]() $s_f\colon \mathrm {Nv}(\mathcal {U}_f)\to K(G,n)$
is any ‘canonical’ map (i.e., any (necessarily simplicial) map with
$s_f\colon \mathrm {Nv}(\mathcal {U}_f)\to K(G,n)$
is any ‘canonical’ map (i.e., any (necessarily simplicial) map with
![]() $s_f(U)= v \implies U\subseteq f^{-1}(\mathrm {St}_{K(G,n)}(v))$
). In particular, if
$s_f(U)= v \implies U\subseteq f^{-1}(\mathrm {St}_{K(G,n)}(v))$
). In particular, if
![]() $(\alpha _f,p_f)\in \mathrm {SA}_{\boldsymbol {\mathcal {U}}}(X,K(G,n))$
is the pair that is associated to
$(\alpha _f,p_f)\in \mathrm {SA}_{\boldsymbol {\mathcal {U}}}(X,K(G,n))$
is the pair that is associated to
![]() $f\in \mathsf {LC}(X,K(G,n))$
by Lemma 5.5, then we have
$f\in \mathsf {LC}(X,K(G,n))$
by Lemma 5.5, then we have
But then, by the definition of
![]() $\psi $
in the proof of the Theorem 2.12, and since
$\psi $
in the proof of the Theorem 2.12, and since
![]() $\alpha _f$
trivially satisfies
$\alpha _f$
trivially satisfies
![]() $\mathcal {U}_{\alpha _f}\preceq \mathcal {U}_{\alpha _f}$
and
$\mathcal {U}_{\alpha _f}\preceq \mathcal {U}_{\alpha _f}$
and
![]() $r^{\alpha _f}_{\alpha _f}:=\mathrm {id}$
, we have that
$r^{\alpha _f}_{\alpha _f}:=\mathrm {id}$
, we have that
But then the map
![]() $\mathsf {LC}(X,K(G,n))\to \mathrm {Z}^{n}(X;G)$
, given by
$\mathsf {LC}(X,K(G,n))\to \mathrm {Z}^{n}(X;G)$
, given by
![]() $f\mapsto [\hat {u}\circ \eta \circ p_f]$
, is a lift of
$f\mapsto [\hat {u}\circ \eta \circ p_f]$
, is a lift of
![]() $\psi \circ J$
. It is also Borel by Lemma 5.5, since both
$\psi \circ J$
. It is also Borel by Lemma 5.5, since both
![]() $\hat {u}$
and
$\hat {u}$
and
![]() $\eta $
are fixed and independent of f. By Proposition 3.11, it follows that
$\eta $
are fixed and independent of f. By Proposition 3.11, it follows that
![]() $\psi \circ J$
is a definable isomorphism.
$\psi \circ J$
is a definable isomorphism.
The following corollaries are all immediate.
Corollary 5.8. Up to definable isomorphism, the group with a Polish cover ![]() does not depend on the choice of covering system
does not depend on the choice of covering system
![]() $\boldsymbol {\mathcal {U}}$
for X.
$\boldsymbol {\mathcal {U}}$
for X.
Corollary 5.9. The definable group
![]() $[X,K(G,n)]$
is essentially – that is, is definably isomorphic to – a group with a Polish cover.
$[X,K(G,n)]$
is essentially – that is, is definably isomorphic to – a group with a Polish cover.
Altogether, we have the following; homotopy invariance follows, for example, from Lemma 4.3.
Corollary 5.10. For any morphism
![]() $g:X\to Y$
in
$g:X\to Y$
in
![]() $\mathsf {LC}$
, write
$\mathsf {LC}$
, write
![]() $g^{*}$
for the function
$g^{*}$
for the function
The assignments ![]() and
and
![]() $g\mapsto g^{*}$
determine a contravariant functor
$g\mapsto g^{*}$
determine a contravariant functor
![]() $\mathsf {LC}\to \mathsf {GPC}$
which factors through
$\mathsf {LC}\to \mathsf {GPC}$
which factors through
![]() $\mathsf {Ho}(\mathsf {LC})$
; in particular, they determine a functor which maps homotopy equivalent spaces to definably isomorphic groups with Polish cover.
$\mathsf {Ho}(\mathsf {LC})$
; in particular, they determine a functor which maps homotopy equivalent spaces to definably isomorphic groups with Polish cover.
Turning now to the category
![]() $\mathsf {LCP}$
of locally compact pairs, observe that the same map witnessing the isomorphism between
$\mathsf {LCP}$
of locally compact pairs, observe that the same map witnessing the isomorphism between
![]() $[X,K(G,n)]$
and
$[X,K(G,n)]$
and ![]() – namely,
– namely,
![]() $([f]\mapsto f^{*}(u))$
– will witness that
$([f]\mapsto f^{*}(u))$
– will witness that
![]() $[(X,A),(K(G,n),*)]$
and
$[(X,A),(K(G,n),*)]$
and ![]() are isomorphic as well. Hence the essential content of Theorem 5.7, which is that this map admits a Borel lift, holds in
are isomorphic as well. Hence the essential content of Theorem 5.7, which is that this map admits a Borel lift, holds in
![]() $\mathsf {LCP}$
by a verbatim argument.
$\mathsf {LCP}$
by a verbatim argument.
5.4. Remarks on axioms and notation
We have arrived by two distinct means to definably isomorphic cohomology groups; this is the sort of circumstance in which mathematicians begin to regard an object as canonical. One way to make this impulse precise is via axioms, and these are, indeed, a third main way of characterizing the classical Čech cohomology groups of locally compact Polish spaces. In [Reference Petkova71, Theorem 8], for example, Petkova showed that any cohomology theory coinciding with Čech cohomology on compact metric spaces and satisfying a natural additivity axiom coincides with Čech cohomology on locally compact metric spaces as well. We note that definable versions of the main ingredients of this argument – the Five Lemma and Urysohn’s Lemma, for example – already appear in either the present work or (in nuce) in its predecessor [Reference Bergfalk and Lupini9], so that the work of axiomatizing definable cohomology on locally compact Polish spaces reduces essentially to verifications, over the category of metric compacta, of the more classical Eilenberg-Steenrod and cluster axioms in the definable setting, or more precisely, that these axioms determine a cohomology theory up to definable isomorphism. Such verifications (along the lines of Theorem 2.14) do not appear to us to be either difficult or particularly illuminating and would detain us too long from the more interesting decompositions and applications of Sections 7 and 8, respectively; for these reasons, we leave their proper treatment for another occasion.
One might along different but related lines axiomatize the reduced definable Čech cohomology groups (see [Reference May58, Chapter 19]); this brings us to a more mundane consideration, which is the following. Though it has so far seemed valuable to notationally distinguish between classical and definable Čech cohomology, it will be convenient in what follows to reserve the subscript position for other purposes. And since we will be so primarily concerned with definable Čech cohomology in what follows, there is little danger of confusion in denoting its (definable) groups by
![]() $\mathrm {H}^n$
, simply – and similarly for the brackets
$\mathrm {H}^n$
, simply – and similarly for the brackets
![]() $[-,-]$
– and this henceforth will be our practice.
$[-,-]$
– and this henceforth will be our practice.
6. A definable homotopy extension theorem
In this section, we formulate and prove definable versions of three fundamental topological results – namely, Urysohn’s Lemma, Borsuk’s Homotopy Extension Theorem, and the presentation of the unbased homotopy classes of maps from
![]() $(X,\star )$
to
$(X,\star )$
to
![]() $(P,*)$
in terms of the action of
$(P,*)$
in terms of the action of
![]() $\pi _1(P,*)$
on the set of based homotopy classes of maps between them. Each of these definable results is applied in the proof of the one which follows it, and by facilitating the passage between pointed and unpointed settings, the last of them both simplifies the argument of some of our results and extends their scope, as we have noted already. That said, these definable results play a sufficiently minor role in later sections that readers may skip over this one without much loss of continuity; put differently, we have recorded them as much for their general interest and place in the development of the field as for any particular application herein.
$\pi _1(P,*)$
on the set of based homotopy classes of maps between them. Each of these definable results is applied in the proof of the one which follows it, and by facilitating the passage between pointed and unpointed settings, the last of them both simplifies the argument of some of our results and extends their scope, as we have noted already. That said, these definable results play a sufficiently minor role in later sections that readers may skip over this one without much loss of continuity; put differently, we have recorded them as much for their general interest and place in the development of the field as for any particular application herein.
6.1. The definable version of Urysohn’s Lemma
Let X be a locally compact Polish space. Fix a countable basis
![]() $ \mathcal {B}$
of open sets of X. Let
$ \mathcal {B}$
of open sets of X. Let
![]() $F( X) $
be the collection of closed subsets of X. We regard
$F( X) $
be the collection of closed subsets of X. We regard
![]() $F( X) $
as a topological space with respect to the Fell topology. This has a basis of sets of the form
$F( X) $
as a topological space with respect to the Fell topology. This has a basis of sets of the form
where
![]() $K\subseteq X$
is compact and
$K\subseteq X$
is compact and
![]() $U_{1},\ldots ,U_{n}$
are open subsets of X. This topology renders
$U_{1},\ldots ,U_{n}$
are open subsets of X. This topology renders
![]() $F(X) $
a Polish space [Reference Fell30].
$F(X) $
a Polish space [Reference Fell30].
We let
![]() $O(X) $
be the collection of open subsets of X. We regard
$O(X) $
be the collection of open subsets of X. We regard
![]() $O(X) $
as a topological space by declaring the bijection
$O(X) $
as a topological space by declaring the bijection
![]() $F( X) \rightarrow O( X) $
,
$F( X) \rightarrow O( X) $
,
![]() $F\mapsto X\backslash F$
to be a homeomorphism. Observe that the function
$F\mapsto X\backslash F$
to be a homeomorphism. Observe that the function
![]() $\mathcal {B} ^{\omega }\rightarrow O( X) $
which maps a sequence to its union is Borel, as is the function
$\mathcal {B} ^{\omega }\rightarrow O( X) $
which maps a sequence to its union is Borel, as is the function
![]() $O( X) \rightarrow F( X):\,U\mapsto \overline {U}$
.
$O( X) \rightarrow F( X):\,U\mapsto \overline {U}$
.
Lemma 6.1. The set
![]() $S=\{(F,O): F\subseteq O\}$
is a Borel subset of
$S=\{(F,O): F\subseteq O\}$
is a Borel subset of
![]() $F(X)\times O(X)$
, and there exists a Borel function
$F(X)\times O(X)$
, and there exists a Borel function
![]() $f:S\to O(X) $
such that
$f:S\to O(X) $
such that
![]() $F\subseteq f(F,O)\subseteq \overline {f(F,O)}\subseteq O$
for all
$F\subseteq f(F,O)\subseteq \overline {f(F,O)}\subseteq O$
for all
![]() $(F,O)\subseteq S$
.
$(F,O)\subseteq S$
.
Proof. First, fix a cofiltration of
![]() $X=\bigcup _{n\in \mathbb {N}} X_n$
of X by compact subsets
$X=\bigcup _{n\in \mathbb {N}} X_n$
of X by compact subsets
![]() $X_n$
(see Definition 7.1); note then that the collection
$X_n$
(see Definition 7.1); note then that the collection
![]() $K(X)$
of compact subsets of X is a Borel subset of
$K(X)$
of compact subsets of X is a Borel subset of
![]() $F(X)$
since
$F(X)$
since
![]() $F\in F(X)$
is in
$F\in F(X)$
is in
![]() $K(X)$
if and only if there exists an
$K(X)$
if and only if there exists an
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $F\subseteq X_n$
. Observe also that for any compact
$F\subseteq X_n$
. Observe also that for any compact
![]() $K\subseteq X$
, the function
$K\subseteq X$
, the function
![]() $f_K:F(X)\to K(X):F\mapsto F\cap K$
is Borel. To see this, fix a compatible metric d on X, and for all
$f_K:F(X)\to K(X):F\mapsto F\cap K$
is Borel. To see this, fix a compatible metric d on X, and for all
![]() $r>0$
, let
$r>0$
, let
![]() $B(K,r)=\{x\in X:\mathrm {inf}\{d(x,y):y\in K\}<r\}$
and observe that
$B(K,r)=\{x\in X:\mathrm {inf}\{d(x,y):y\in K\}<r\}$
and observe that
![]() $\{F: F\cap K\cap U\neq \varnothing \}=\bigcap _{n\in \mathbb {N}}\{F:F\cap B(K,\frac {1}{n+1})\neq \varnothing \}$
.
$\{F: F\cap K\cap U\neq \varnothing \}=\bigcap _{n\in \mathbb {N}}\{F:F\cap B(K,\frac {1}{n+1})\neq \varnothing \}$
.
Claim 6.2. The set
![]() $S_{c}=\{(K,O): K\subseteq O\}$
is a Borel subset of
$S_{c}=\{(K,O): K\subseteq O\}$
is a Borel subset of
![]() $K(X)\times O(X)$
.
$K(X)\times O(X)$
.
Proof of Claim.
Fix a dense
![]() $\{x_n:n\in \mathbb {N}\}\subseteq X$
and, as above, for any
$\{x_n:n\in \mathbb {N}\}\subseteq X$
and, as above, for any
![]() $x\in X$
and
$x\in X$
and
![]() $r>0$
, write
$r>0$
, write
![]() $B(x,r)$
for the open ball about x of d-radius r. Observe that
$B(x,r)$
for the open ball about x of d-radius r. Observe that
![]() $K\subseteq O$
if and only if there exist an N and
$K\subseteq O$
if and only if there exist an N and
![]() $i_0,\dots ,i_N$
in
$i_0,\dots ,i_N$
in
![]() $\mathbb {N}$
and positive rational
$\mathbb {N}$
and positive rational
![]() $q_0,\dots ,q_N$
such that
$q_0,\dots ,q_N$
such that
![]() $K\subseteq \overline {B(x_{i_0},q_0)\cup \dots \cup B(x_{i_N},q_N)}$
and
$K\subseteq \overline {B(x_{i_0},q_0)\cup \dots \cup B(x_{i_N},q_N)}$
and
![]() $B(x_{i_0},2q_0)\cup \dots \cup B(x_{i_N},2q_N)\subseteq O$
.
$B(x_{i_0},2q_0)\cup \dots \cup B(x_{i_N},2q_N)\subseteq O$
.
To establish our first assertion, it now suffices to observe that
![]() $F\subseteq O$
for
$F\subseteq O$
for
![]() $(F,O)\in F(X)\times O(X)$
if and only if
$(F,O)\in F(X)\times O(X)$
if and only if
![]() $f_{X_n}(F)\subseteq O$
for all
$f_{X_n}(F)\subseteq O$
for all
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
For the second assertion, let
![]() $\triangleleft $
well-order
$\triangleleft $
well-order
![]() $\mathcal {B}^2$
in order-type
$\mathcal {B}^2$
in order-type
![]() $\omega $
and recursively define
$\omega $
and recursively define
![]() $(U_k,V_k)$
to be the
$(U_k,V_k)$
to be the
![]() $\triangleleft $
-least
$\triangleleft $
-least
![]() $(U,V)$
such that
$(U,V)$
such that
-
•
 $U_k\cap V_k=\varnothing $
,
$U_k\cap V_k=\varnothing $
, -
•
 $U_k\subseteq O$
and
$U_k\subseteq O$
and
 $V_k\cap F =\varnothing $
,
$V_k\cap F =\varnothing $
, -
• either
 $F\subseteq \bigcup _{i<k} U_i$
or
$F\subseteq \bigcup _{i<k} U_i$
or
 $U_k\cap (F\backslash \bigcup _{i<k}U_i)\neq \varnothing $
, and
$U_k\cap (F\backslash \bigcup _{i<k}U_i)\neq \varnothing $
, and -
• letting
 $P=X\backslash O$
, either
$P=X\backslash O$
, either
 $P\subseteq \bigcup _{i<k} V_i$
or
$P\subseteq \bigcup _{i<k} V_i$
or
 $V_k\cap (P\backslash \bigcup _{i<k}V_i)\neq \varnothing $
.
$V_k\cap (P\backslash \bigcup _{i<k}V_i)\neq \varnothing $
.
This defines for each
![]() $k\in \mathbb {N}$
a Borel function
$k\in \mathbb {N}$
a Borel function
![]() $S\to \mathcal {B}^2$
given by
$S\to \mathcal {B}^2$
given by
![]() $(F,O)\mapsto (U_k,V_k)$
. The map
$(F,O)\mapsto (U_k,V_k)$
. The map
![]() $(F,O)\mapsto \bigcup _{k\in \mathbb {N}}U_k$
is then a Borel function
$(F,O)\mapsto \bigcup _{k\in \mathbb {N}}U_k$
is then a Borel function
![]() $f:S\to O(X)$
, as desired.
$f:S\to O(X)$
, as desired.
In the setting of
![]() $\mathsf {LC}$
, Urysohn’s Lemma takes the following form: if X is a locally compact Polish space and
$\mathsf {LC}$
, Urysohn’s Lemma takes the following form: if X is a locally compact Polish space and
![]() $A,B$
are disjoint closed subsets of X, then there exists a continuous function
$A,B$
are disjoint closed subsets of X, then there exists a continuous function
![]() $f:X\rightarrow [ 0,1] $
such that
$f:X\rightarrow [ 0,1] $
such that
![]() $f[A]=0$
and
$f[A]=0$
and
![]() $f[B]=1$
. The following should be regarded as the definable version of this statement.
$f[B]=1$
. The following should be regarded as the definable version of this statement.
Lemma 6.3. Let X be a locally compact Polish space, and let
![]() $\mathcal {P}$
denote the Borel set of pairs
$\mathcal {P}$
denote the Borel set of pairs
![]() $(A,B) \in F( X) \times F(X) $
such that
$(A,B) \in F( X) \times F(X) $
such that
![]() $A\cap B=\varnothing $
. For each such pair
$A\cap B=\varnothing $
. For each such pair
![]() $(A,B) $
, there exists a map
$(A,B) $
, there exists a map
![]() $f:X\rightarrow \left [ 0,1\right ] $
such that
$f:X\rightarrow \left [ 0,1\right ] $
such that
![]() $f[A]=0$
and
$f[A]=0$
and
![]() $f[B]=1$
; this map f may, moreover, be taken to depend in a Borel way on the pairs
$f[B]=1$
; this map f may, moreover, be taken to depend in a Borel way on the pairs
![]() $(A,B)$
, in the sense that there exists a choice function
$(A,B)$
, in the sense that there exists a choice function
witnessing this assertion which is Borel.
Proof. We adopt the notation of the proof of Urysohn’s Lemma in [Reference Munkres67, Theorem 33.1]. Endow
![]() $O( X)^{\mathbb {Q}}$
with the product topology. Let
$O( X)^{\mathbb {Q}}$
with the product topology. Let
![]() $\mathcal {Z}$
be the Borel subset of
$\mathcal {Z}$
be the Borel subset of
![]() $O( X)^{\mathbb {Q}}$
consisting of families
$O( X)^{\mathbb {Q}}$
consisting of families
![]() $\left ( U_{p}\right ) _{p\in \mathbb {Q}}\in O( X) ^{\mathbb {Q}}$
such that
$\left ( U_{p}\right ) _{p\in \mathbb {Q}}\in O( X) ^{\mathbb {Q}}$
such that
![]() $\overline {U}_{p}\subseteq U_{q}$
whenever
$\overline {U}_{p}\subseteq U_{q}$
whenever
![]() $p<q$
,
$p<q$
,
![]() $U_{p}=\varnothing $
for
$U_{p}=\varnothing $
for
![]() $ p<0$
, and
$ p<0$
, and
![]() $U_{q}=X$
for
$U_{q}=X$
for
![]() $q>1$
.
$q>1$
.
As in the proof of [Reference Munkres67, Theorem 33.1], for any disjoint A and B in
![]() $F( X) $
, there exists a
$F( X) $
, there exists a
![]() $\left ( U_{p}\right ) _{p\in \mathbb {Q}}\in \mathcal {Z}$
such that
$\left ( U_{p}\right ) _{p\in \mathbb {Q}}\in \mathcal {Z}$
such that
![]() $A\subseteq U_{0}$
and
$A\subseteq U_{0}$
and
![]() $U_{1}=X\backslash B$
; letting
$U_{1}=X\backslash B$
; letting
![]() $f( x) :=\mathrm {\inf }\{p\in \mathbb {Q}:x\in U_{p}\}$
then determines a function
$f( x) :=\mathrm {\inf }\{p\in \mathbb {Q}:x\in U_{p}\}$
then determines a function
![]() $f:X\rightarrow \left [ 0,1\right ] $
, as desired. The sequence
$f:X\rightarrow \left [ 0,1\right ] $
, as desired. The sequence
![]() $\left ( U_{p}\right ) _{p\in \mathbb {Q}}$
is defined by recursion, with respect to an enumeration
$\left ( U_{p}\right ) _{p\in \mathbb {Q}}$
is defined by recursion, with respect to an enumeration
![]() $\left ( p_{n}\right ) _{n\in \omega }$
of
$\left ( p_{n}\right ) _{n\in \omega }$
of
![]() $\mathbb {Q}$
, as follows. One lets
$\mathbb {Q}$
, as follows. One lets
![]() $U_{1}=X\backslash B$
and then chooses
$U_{1}=X\backslash B$
and then chooses
![]() $U_{0}$
so that
$U_{0}$
so that
By Lemma 6.1,
![]() $U_{0}$
can be chosen in a Borel fashion. Suppose that
$U_{0}$
can be chosen in a Borel fashion. Suppose that
![]() $U_{p_m}$
has been defined for
$U_{p_m}$
has been defined for
![]() $m<n$
(as is vacuously the case if
$m<n$
(as is vacuously the case if
![]() $n=0$
) and that
$n=0$
) and that
![]() $p_n\notin \{0,1\}$
. If
$p_n\notin \{0,1\}$
. If
![]() $p_n<0$
, then let
$p_n<0$
, then let
![]() $U_{p_n}=\varnothing $
, and if
$U_{p_n}=\varnothing $
, and if
![]() $p_n>1$
, then let
$p_n>1$
, then let
![]() $U_{p_n}=X$
. If
$U_{p_n}=X$
. If
![]() $p_n\in (0,1)$
, then let p and q be the immediate predecessor and immediate successor, respectively, of
$p_n\in (0,1)$
, then let p and q be the immediate predecessor and immediate successor, respectively, of
![]() $p_n$
in
$p_n$
in
![]() $\{p_m:m<n\} $
with respect to the standard ordering of
$\{p_m:m<n\} $
with respect to the standard ordering of
![]() $\mathbb {Q}$
, and let
$\mathbb {Q}$
, and let
![]() $U_{p_n}$
be such that
$U_{p_n}$
be such that
Again, by Lemma 6.1,
![]() $U_{p_n}$
may be chosen in a Borel fashion.
$U_{p_n}$
may be chosen in a Borel fashion.
It remains only to show that the function
![]() $\mathcal {Z}\rightarrow \mathsf {LC}( X,[0,1]) $
,
$\mathcal {Z}\rightarrow \mathsf {LC}( X,[0,1]) $
,
![]() $(U_{p}) _{p\in \mathbb {Q}}\mapsto f$
given by
$(U_{p}) _{p\in \mathbb {Q}}\mapsto f$
given by
is Borel. This, though, is immediate: for any
![]() $b\in [0,1] $
and compact
$b\in [0,1] $
and compact
![]() $ K\subseteq X$
, we have that
$ K\subseteq X$
, we have that
![]() $f(K) \subseteq ( -\infty ,b) $
if and only if there exist
$f(K) \subseteq ( -\infty ,b) $
if and only if there exist
![]() $\ell \in \omega $
and
$\ell \in \omega $
and
![]() $p_{0},\ldots ,p_{\ell }\in \mathbb {Q}\cap ( -\infty ,b) $
such that
$p_{0},\ldots ,p_{\ell }\in \mathbb {Q}\cap ( -\infty ,b) $
such that
![]() $K\subseteq U_{p_{0}}\cup \cdots \cup U_{p_{\ell }}$
. Similarly,
$K\subseteq U_{p_{0}}\cup \cdots \cup U_{p_{\ell }}$
. Similarly,
![]() $f(K) \subseteq ( b,+\infty )$
if and only if there exists a
$f(K) \subseteq ( b,+\infty )$
if and only if there exists a
![]() $q\in \mathbb {Q}$
such that
$q\in \mathbb {Q}$
such that
![]() $q>b$
and
$q>b$
and
![]() $[U_{p}\cap K\neq \varnothing \,\Rightarrow p>q]$
for every
$[U_{p}\cap K\neq \varnothing \,\Rightarrow p>q]$
for every
![]() $p\in \mathbb {Q}$
. This concludes the proof.
$p\in \mathbb {Q}$
. This concludes the proof.
6.2. The definable version of the Homotopy Extension Theorem
We recorded the classical framing of Borsuk’s Homotopy Extension Theorem for locally compact Polish spaces as Theorem 4.1 above. Implicit in its proof is its definable version:
Theorem 6.4. Suppose that A is a closed subspace of a locally compact Polish space X and that P is a polyhedron. Then for every map
![]() $g:\left ( A\times I\right ) \cup \left ( X\times \left \{ 0\right \} \right ) \rightarrow P$
, there exists a map
$g:\left ( A\times I\right ) \cup \left ( X\times \left \{ 0\right \} \right ) \rightarrow P$
, there exists a map
![]() $\tilde { g}:X\times I\rightarrow P$
which extends g. Furthermore,
$\tilde { g}:X\times I\rightarrow P$
which extends g. Furthermore,
![]() $\tilde {g}$
can be chosen in a Borel fashion from g, in the sense that there exists a choice function
$\tilde {g}$
can be chosen in a Borel fashion from g, in the sense that there exists a choice function
witnessing this assertion which is Borel.
Proof. By [Reference Mardešić and Segal56, Chapter I.3, Theorem 2], we may assume that P is a closed subspace of a convex subset D of a Banach space L. Since P is an absolute neighborhood retract [Reference Mardešić and Segal56, Tppendix 1, Theorem 1.11], there exists a neighborhood N of P in D and a retraction
![]() $s:N\rightarrow P$
.
$s:N\rightarrow P$
.
Consider now a map
![]() $g:( A\times I) \cup ( X\times \left \{ 0\right \} ) \rightarrow P$
. By [Reference Mardešić and Segal56, Chapter I.3, Theorem 2], there exists a map
$g:( A\times I) \cup ( X\times \left \{ 0\right \} ) \rightarrow P$
. By [Reference Mardešić and Segal56, Chapter I.3, Theorem 2], there exists a map
![]() $G:X\times I\rightarrow D$
that extends g. It is plain from the proof of this theorem that G depends in a Borel fashion on g, and that one may in a Borel manner choose along with G an open subset
$G:X\times I\rightarrow D$
that extends g. It is plain from the proof of this theorem that G depends in a Borel fashion on g, and that one may in a Borel manner choose along with G an open subset
![]() $V\supseteq A$
of X such that
$V\supseteq A$
of X such that
![]() $G( V\times I) \subseteq N$
. By the definable version of Urysohn’s Lemma, one may, in a Borel fashion, then choose for each V a continuous map
$G( V\times I) \subseteq N$
. By the definable version of Urysohn’s Lemma, one may, in a Borel fashion, then choose for each V a continuous map
![]() $\phi :X\rightarrow I$
such that
$\phi :X\rightarrow I$
such that
![]() $ \phi |_{A}=1$
and
$ \phi |_{A}=1$
and
![]() $\phi |_{X\setminus V}=0$
. As in the proof of [Reference Mardešić and Segal56, Chapter I.3, Lemma 2],
$\phi |_{X\setminus V}=0$
. As in the proof of [Reference Mardešić and Segal56, Chapter I.3, Lemma 2],
![]() $\phi $
determines an extension of the inclusion map
$\phi $
determines an extension of the inclusion map
to the continuous map
To conclude the construction, let
![]() $ \tilde {g}=s\circ G\circ r:X\times I\rightarrow P$
.
$ \tilde {g}=s\circ G\circ r:X\times I\rightarrow P$
.
6.3. The definable relation of based and unbased homotopy classes of maps
The following theorem, which relies on both our definable homotopy extension and homotopy selection theorems, is the definable version of the well-known isomorphism
![]() $[(X,\star ),(P,\ast )]/\pi _1(P,\ast )\cong [X,P]$
[Reference Spanier80, §7.3].
$[(X,\star ),(P,\ast )]/\pi _1(P,\ast )\cong [X,P]$
[Reference Spanier80, §7.3].
Theorem 6.5. Let P be a path-connected polyhedron with basepoint
![]() $\ast $
, and let X be an object of
$\ast $
, and let X be an object of
![]() $\mathsf {LC}_*$
. There exists a definable right action of the definable group
$\mathsf {LC}_*$
. There exists a definable right action of the definable group ![]() on the semidefinable set
on the semidefinable set
![]() $[(X,\star ),(P,\ast )]$
whose semidefinable set of orbits
$[(X,\star ),(P,\ast )]$
whose semidefinable set of orbits ![]() is definably isomorphic to the semidefinable set
is definably isomorphic to the semidefinable set
![]() $[X,P]$
.
$[X,P]$
.
Proof. We describe a Borel function
which induces the action in question. F is defined as follows. Any ![]() naturally identifies with a map
naturally identifies with a map
![]() $f\vee \gamma :X\vee I\to P$
. By the Homotopy Extension Theorem, this map extends to a homotopy
$f\vee \gamma :X\vee I\to P$
. By the Homotopy Extension Theorem, this map extends to a homotopy
![]() $h^{(f,\gamma )}:X\times I\to P$
for which
$h^{(f,\gamma )}:X\times I\to P$
for which
![]() $h^{(f,\gamma )}(-,0)=f$
and
$h^{(f,\gamma )}(-,0)=f$
and
![]() $h^{(f,\gamma )}(\ast ,-)=\gamma $
and
$h^{(f,\gamma )}(\ast ,-)=\gamma $
and
![]() $h^{(f,\gamma )}(-,1)\in \mathsf {LC}_*((X,\star ),(P,\ast ))$
; moreover, by Theorem 6.4, these extensions may be chosen in a Borel fashion. Assume that they have been, and let
$h^{(f,\gamma )}(-,1)\in \mathsf {LC}_*((X,\star ),(P,\ast ))$
; moreover, by Theorem 6.4, these extensions may be chosen in a Borel fashion. Assume that they have been, and let
![]() $F(f,g)=h^{(f,\gamma )}(-,1)$
for each
$F(f,g)=h^{(f,\gamma )}(-,1)$
for each ![]() .
.
Clearly, F is Borel. To see that F induces an action as claimed, suppose the pairs
![]() $f,g:(X,\star )\to (P,\ast )$
and
$f,g:(X,\star )\to (P,\ast )$
and ![]() are each homotopic; together with
are each homotopic; together with
![]() $h^{(f,\gamma )}$
and
$h^{(f,\gamma )}$
and
![]() $h^{(g,\delta )}$
, these homotopies determine a map r from
$h^{(g,\delta )}$
, these homotopies determine a map r from
to P. More precisely, r is defined by identifying
![]() $r\restriction X\times I\times \{0\}$
with
$r\restriction X\times I\times \{0\}$
with
![]() $f\Rightarrow g$
,
$f\Rightarrow g$
,
![]() $r\restriction \{\star \}\times I\times I$
with
$r\restriction \{\star \}\times I\times I$
with
![]() $\gamma \Rightarrow \delta $
, and
$\gamma \Rightarrow \delta $
, and
![]() $r\restriction X\times \{0\}\times I$
and
$r\restriction X\times \{0\}\times I$
and
![]() $r\restriction X\times \{1\}\times I$
with
$r\restriction X\times \{1\}\times I$
with
![]() $h^{(f,\gamma )}$
and
$h^{(f,\gamma )}$
and
![]() $h^{(g,\delta )}$
, respectively. By the Homotopy Extension Theorem, this map extends to an
$h^{(g,\delta )}$
, respectively. By the Homotopy Extension Theorem, this map extends to an
![]() $H:X\times I\times I\to P$
, and
$H:X\times I\times I\to P$
, and
![]() $H(-,-,1)$
is then the desired basepoint-preserving homotopy from
$H(-,-,1)$
is then the desired basepoint-preserving homotopy from
![]() $F(f,\gamma )$
to
$F(f,\gamma )$
to
![]() $F(g,\delta )$
. This shows that F induces a well-defined operation at the level of the quotients; that this operation is a right action is then immediate.
$F(g,\delta )$
. This shows that F induces a well-defined operation at the level of the quotients; that this operation is a right action is then immediate.
To see the isomorphism in question, regard ![]() as the semidefinable set
as the semidefinable set
![]() $(Y,E)$
wherein
$(Y,E)$
wherein
![]() $Y=\mathsf {LC}_*((X,\star ),(P,\ast ))$
and E is the equivalence relation defined by
$Y=\mathsf {LC}_*((X,\star ),(P,\ast ))$
and E is the equivalence relation defined by
![]() $f\,E\,g$
if and only if there exists an
$f\,E\,g$
if and only if there exists an
![]() $\alpha :(X,\star )\to (P,\ast )$
such that
$\alpha :(X,\star )\to (P,\ast )$
such that
![]() $[f]\cdot [\alpha ]=[g]$
. Observe then that the map
$[f]\cdot [\alpha ]=[g]$
. Observe then that the map
![]() $\mathsf {LC}_*((X,\star ),(P,\ast ))\to \mathsf {LC}(X,P):f\mapsto f$
induces a definable function
$\mathsf {LC}_*((X,\star ),(P,\ast ))\to \mathsf {LC}(X,P):f\mapsto f$
induces a definable function
We describe a definable inverse
![]() $\psi $
to
$\psi $
to
![]() $\phi $
. By Proposition 4.18, we may, in a Borel fashion, choose for each
$\phi $
. By Proposition 4.18, we may, in a Borel fashion, choose for each
![]() $f\in \mathsf {LC}(X,P)$
a homotopy
$f\in \mathsf {LC}(X,P)$
a homotopy
![]() $\gamma [f]:\{\star \}\times I\to P$
with
$\gamma [f]:\{\star \}\times I\to P$
with
![]() $\gamma [f](\star ,0)=f(\star )$
. As above, we may then apply the definable Homotopy Extension Theorem to, in a Borel fashion, extend each
$\gamma [f](\star ,0)=f(\star )$
. As above, we may then apply the definable Homotopy Extension Theorem to, in a Borel fashion, extend each
![]() $f\vee \gamma [f]$
to an
$f\vee \gamma [f]$
to an
![]() $h^{(f,\gamma [f])}:X\times I\to P$
. The definable function
$h^{(f,\gamma [f])}:X\times I\to P$
. The definable function
![]() $\psi $
is then that induced by the assignments
$\psi $
is then that induced by the assignments
![]() $f\mapsto h^{(f,\gamma [f])}(-,1)$
. The verification that
$f\mapsto h^{(f,\gamma [f])}(-,1)$
. The verification that
![]() $\psi $
is well defined is almost exactly as before: within the framework of this construction, any
$\psi $
is well defined is almost exactly as before: within the framework of this construction, any
![]() $f\Rightarrow g:X\to P$
induces maps from ‘walls’ of
$f\Rightarrow g:X\to P$
induces maps from ‘walls’ of
![]() $X\times I\times I$
which, by the Homotopy Extension Theorem, extend to a map
$X\times I\times I$
which, by the Homotopy Extension Theorem, extend to a map
![]() $X\times I\times I\to P$
whose restriction to
$X\times I\times I\to P$
whose restriction to
![]() $X\times I\times \{1\}$
defines a homotopy from
$X\times I\times \{1\}$
defines a homotopy from
![]() $h^{(f,\gamma [f])}(-,1)$
to
$h^{(f,\gamma [f])}(-,1)$
to
![]() $h^{(g,\gamma [g])}(-,1)$
. Unlike before, this homotopy need not be basepoint-preserving. Its restriction to
$h^{(g,\gamma [g])}(-,1)$
. Unlike before, this homotopy need not be basepoint-preserving. Its restriction to
![]() $\{\star \}\times I$
, however, determines an
$\{\star \}\times I$
, however, determines an ![]() , from which it follows that
, from which it follows that
![]() $[h^{(f,\gamma [f])}(-,1)]\cdot [\alpha ]=[h^{(g,\gamma [g])}(-,1)]$
, as desired. That
$[h^{(f,\gamma [f])}(-,1)]\cdot [\alpha ]=[h^{(g,\gamma [g])}(-,1)]$
, as desired. That
![]() $\psi $
is both a right and left inverse of
$\psi $
is both a right and left inverse of
![]() $\phi $
is now immediate from their definitions.
$\phi $
is now immediate from their definitions.
By an easy corollary, the semidefinable sets
![]() $[(X,\star ),(P,\ast )]$
and
$[(X,\star ),(P,\ast )]$
and
![]() $[X,P]$
may often be definably identified.
$[X,P]$
may often be definably identified.
Corollary 6.6. Let X and P be as above. If either (i) P is simply connected, or (ii) P is an H-space with identity element
![]() $\ast $
, then
$\ast $
, then
![]() $[(X,\star ),(P,\ast )]$
is definably isomorphic to
$[(X,\star ),(P,\ast )]$
is definably isomorphic to
![]() $[X,P]$
.
$[X,P]$
.
Proof. In both cases, the action of ![]() on
on
![]() $[(X,\star ),(P,\ast )]$
is trivial. In case (i), this is because the group is trivial. In case (ii), note first that without loss of generality, in the H-space structure on P, the homotopies of
$[(X,\star ),(P,\ast )]$
is trivial. In case (i), this is because the group is trivial. In case (ii), note first that without loss of generality, in the H-space structure on P, the homotopies of
![]() $\mu (-,\ast )$
and
$\mu (-,\ast )$
and
![]() $\mu (\ast ,-)$
with the identity may each be taken to be basepoint-preserving (see [Reference Hatcher33]). Note next that for any
$\mu (\ast ,-)$
with the identity may each be taken to be basepoint-preserving (see [Reference Hatcher33]). Note next that for any ![]() , the operation
, the operation
![]() $\mu $
on P determines a homotopy
$\mu $
on P determines a homotopy
where
![]() $\gamma $
is viewed as a map
$\gamma $
is viewed as a map
![]() $(I,\{0,1\})\to (P,\ast )$
. Since both
$(I,\{0,1\})\to (P,\ast )$
. Since both
![]() $h(-,0)$
and
$h(-,0)$
and
![]() $h(-,1)$
are (basepoint-preserving) homotopic to f and
$h(-,1)$
are (basepoint-preserving) homotopic to f and
![]() $h(\star ,-)$
is (basepoint-preserving) homotopic to
$h(\star ,-)$
is (basepoint-preserving) homotopic to
![]() $\gamma $
, we conclude that
$\gamma $
, we conclude that
![]() $[f]\cdot [\gamma ]=[f]$
.
$[f]\cdot [\gamma ]=[f]$
.
Remark 6.7. An upshot of our definable version of Huber’s Theorem is that the assignments of definable cohomology groups to spaces may be developed into definable cohomology functors from either a combinatorial or homotopical perspective. In this direction, we note in passing that a generalization of the preceding arguments constructs the definable connecting homomorphisms
![]() $\partial ^n:\mathrm {H}^n(A;G)\to \mathrm {H}^{n+1}(X,A;G)$
in the long exact cohomology sequence associated to a locally compact pair
$\partial ^n:\mathrm {H}^n(A;G)\to \mathrm {H}^{n+1}(X,A;G)$
in the long exact cohomology sequence associated to a locally compact pair
![]() $(X,A)$
from the homotopical perspective, in counterpoint to Section 2.5. The basic ingredients are application of the generalized reduced suspension operation
$(X,A)$
from the homotopical perspective, in counterpoint to Section 2.5. The basic ingredients are application of the generalized reduced suspension operation
![]() $\bar {\Sigma }$
, introduced in Section 7.3 below, to the subspace A (the key
$\bar {\Sigma }$
, introduced in Section 7.3 below, to the subspace A (the key
![]() $S^1$
term above may be regarded as
$S^1$
term above may be regarded as
![]() $\bar {\Sigma }(A)$
for
$\bar {\Sigma }(A)$
for
![]() $A=\star $
), together with the operation of its adjoint
$A=\star $
), together with the operation of its adjoint
![]() $\Omega $
on
$\Omega $
on
![]() $K(G,n)$
.
$K(G,n)$
.
7. The homotopy classification of maps and phantom maps
In this section, we study the homotopy relation on maps
![]() $(X,A) \rightarrow (P,\ast )$
where
$(X,A) \rightarrow (P,\ast )$
where
![]() $(X,A)$
is a locally compact pair and P is a path-connected pointed polyhedron with distinguished point
$(X,A)$
is a locally compact pair and P is a path-connected pointed polyhedron with distinguished point
![]() $\ast $
; notice that this includes the case when
$\ast $
; notice that this includes the case when
![]() $A=\varnothing $
, whereupon the problem reduces to the classification of maps
$A=\varnothing $
, whereupon the problem reduces to the classification of maps
![]() $X\rightarrow P$
. Working, in other words, in the setting of
$X\rightarrow P$
. Working, in other words, in the setting of
![]() $\mathsf {LCP}$
from a perspective essentially subsuming the cases of
$\mathsf {LCP}$
from a perspective essentially subsuming the cases of
![]() $\mathsf {LC}_*$
and
$\mathsf {LC}_*$
and
![]() $\mathsf {LC}$
affords a certain streamlining of arguments, requiring only some extra care around the operation of suspension; see the remarks early in Section 7.3. Below, we will let
$\mathsf {LC}$
affords a certain streamlining of arguments, requiring only some extra care around the operation of suspension; see the remarks early in Section 7.3. Below, we will let
![]() $\ast $
denote the map
$\ast $
denote the map
![]() $(X,A) \rightarrow (P,\ast )$
which is constantly equal to
$(X,A) \rightarrow (P,\ast )$
which is constantly equal to
![]() $\ast $
and say that a map
$\ast $
and say that a map
![]() $f:( X,A) \rightarrow (P,\ast )$
is nullhomotopic if there is a homotopy
$f:( X,A) \rightarrow (P,\ast )$
is nullhomotopic if there is a homotopy
![]() $h:f\Rightarrow \ast :(X,A) \rightarrow (P,\ast )$
. In this way, we regard
$h:f\Rightarrow \ast :(X,A) \rightarrow (P,\ast )$
. In this way, we regard
![]() $[(X,A),(P,\ast )]$
as a pointed semidefinable set with distinguished element equal to the homotopy class of
$[(X,A),(P,\ast )]$
as a pointed semidefinable set with distinguished element equal to the homotopy class of
![]() $\ast $
. For any cofiltration
$\ast $
. For any cofiltration
![]() $(X_n, A_n)_{n\in \mathbb {N}}$
of
$(X_n, A_n)_{n\in \mathbb {N}}$
of
![]() $(X,A)$
by compact pairs, we may consider also those maps f for which each
$(X,A)$
by compact pairs, we may consider also those maps f for which each
![]() $f\restriction X_n$
is nullhomotopic; these are the phantom maps from
$f\restriction X_n$
is nullhomotopic; these are the phantom maps from
![]() $(X,A)$
to
$(X,A)$
to
![]() $(P,*)$
, and they form this section’s main focus. Our primary results herein are the following:
$(P,*)$
, and they form this section’s main focus. Our primary results herein are the following:
-
• A series of decompositions of
 $[(X,A),(P,\ast )]$
in terms of its class of phantom maps (Theorems 7.10 and 7.11), culminating in the case when P is an H-group (Theorem 7.13), whereupon this decomposition takes the form of a short exact sequence specializing in Proposition 7.14 to a Milnor-type exact sequence of definable cohomology groups.
$[(X,A),(P,\ast )]$
in terms of its class of phantom maps (Theorems 7.10 and 7.11), culminating in the case when P is an H-group (Theorem 7.13), whereupon this decomposition takes the form of a short exact sequence specializing in Proposition 7.14 to a Milnor-type exact sequence of definable cohomology groups. -
• Using this decomposition, we show that
 $[(X,A),(P,\ast )]$
is a definable group whenever P is an H-group, thereby generalizing the results of Section 5.
$[(X,A),(P,\ast )]$
is a definable group whenever P is an H-group, thereby generalizing the results of Section 5. -
• Along the way, we prove a topological characterization of the class of phantom maps: they are the closure in
 $[(X,A),(P,\ast )]$
of
$[(X,A),(P,\ast )]$
of
 $[\{*\}]$
; see Proposition 7.9.
$[\{*\}]$
; see Proposition 7.9.
7.1. Cofiltrations and
 $\mathsf{Ind}_\omega (\mathcal {C})$
, and
$\mathsf{Ind}_\omega (\mathcal {C})$
, and
 $\mathsf{Pro}_\omega (\mathcal {C})$
and
$\mathsf{Pro}_\omega (\mathcal {C})$
and
 $\mathrm {lim}$
and
$\mathrm {lim}$
and
 $\mathrm {lim}^1$
$\mathrm {lim}^1$
Instrumental in the arguments of Section 2 was the existence, for any locally compact Polish space X, of a sequence of compact subspaces approximating to X; we now fix a slight refinement of this notion.
Definition 7.1. A cofiltration of a locally compact pair
![]() $(X,A)$
is an increasing sequence
$(X,A)$
is an increasing sequence
![]() $(X_i,A_i) _{i\in \mathbb {N}}$
of pairs of compact subspaces of X such that
$(X_i,A_i) _{i\in \mathbb {N}}$
of pairs of compact subspaces of X such that
![]() $X_{i}\subseteq \mathrm {int}(X_{i+1})$
and
$X_{i}\subseteq \mathrm {int}(X_{i+1})$
and
![]() $A_i=X_i\cap A$
for each
$A_i=X_i\cap A$
for each
![]() $i\in \mathbb {N}$
, and
$i\in \mathbb {N}$
, and
![]() $X=\bigcup _{i\in \mathbb {N}}X_i$
.
$X=\bigcup _{i\in \mathbb {N}}X_i$
.
Such a sequence is naturally viewed as a direct or inductive system
![]() $\mathbf {X}=((X_i,A_i),\eta _i)_{i\in \mathbb {N}}$
with each
$\mathbf {X}=((X_i,A_i),\eta _i)_{i\in \mathbb {N}}$
with each
![]() $\eta _i:(X_i,A_i)\to (X_{i+1},A_{i+1})$
an inclusion map. Such a system, of course, also contains the morphisms
$\eta _i:(X_i,A_i)\to (X_{i+1},A_{i+1})$
an inclusion map. Such a system, of course, also contains the morphisms
![]() $\eta _{i,j}:(X_i,A_i)\to (X_j,A_j)$
for any
$\eta _{i,j}:(X_i,A_i)\to (X_j,A_j)$
for any
![]() $i\leq j$
but is fully determined by those of the form
$i\leq j$
but is fully determined by those of the form
![]() $\eta _{i,i+1}$
, which we will continue to abbreviate as
$\eta _{i,i+1}$
, which we will continue to abbreviate as
![]() $\eta _i$
. It will be convenient below to view these and other inductive sequences in any given category
$\eta _i$
. It will be convenient below to view these and other inductive sequences in any given category
![]() $\mathcal {C}$
themselves as objects of a category
$\mathcal {C}$
themselves as objects of a category
![]() $\mathsf {Ind}_\omega (\mathcal {C})$
. To do so, we need only to describe the morphisms of the latter; to better motivate this description, let us first observe the following.
$\mathsf {Ind}_\omega (\mathcal {C})$
. To do so, we need only to describe the morphisms of the latter; to better motivate this description, let us first observe the following.
-
(i) Given cofiltrations
 $\mathbf {X}=((X_i,A_i),\eta ^X_i)_{i\in \mathbb {N}}$
and
$\mathbf {X}=((X_i,A_i),\eta ^X_i)_{i\in \mathbb {N}}$
and
 $\mathbf {Y}=((Y_i,B_i),\eta ^Y_i)_{i\in \mathbb {N}}$
of locally compact pairs
$\mathbf {Y}=((Y_i,B_i),\eta ^Y_i)_{i\in \mathbb {N}}$
of locally compact pairs
 $(X,A)$
and
$(X,A)$
and
 $(Y,B)$
, respectively, and a continuous function
$(Y,B)$
, respectively, and a continuous function
 $f:X\to Y$
, there exists for each
$f:X\to Y$
, there exists for each
 $i\in \mathbb {N}$
a least
$i\in \mathbb {N}$
a least
 $g(i)$
with
$g(i)$
with
 $f[X_i]\subseteq Y_{g(i)}$
. In other words, letting
$f[X_i]\subseteq Y_{g(i)}$
. In other words, letting
 $f_i=f\restriction X_i:X_i\to Y_{g(i)}$
for each i, any such f induces a family of morphisms
$f_i=f\restriction X_i:X_i\to Y_{g(i)}$
for each i, any such f induces a family of morphisms
 $(f_i,g)_{i\in \mathbb {N}}$
satisfying the following property: (23)
$(f_i,g)_{i\in \mathbb {N}}$
satisfying the following property: (23) $$ \begin{align} g(i)\leq g(j)\text{ and }f_j\,\eta^X_{i,j}=\eta^Y_{g(i),g(j)}\,f_i\text{ for all }i\leq j\text{ in }\mathbb{N}. \end{align} $$
$$ \begin{align} g(i)\leq g(j)\text{ and }f_j\,\eta^X_{i,j}=\eta^Y_{g(i),g(j)}\,f_i\text{ for all }i\leq j\text{ in }\mathbb{N}. \end{align} $$
-
(ii) Higher choices for each
 $g(i)$
above would not, for our purposes, make any essential difference; more broadly, we are much more interested in ‘cofinal’ relations among cofiltrations or functions between them than in strict ones. More formally, we would prefer not to distinguish between families
$g(i)$
above would not, for our purposes, make any essential difference; more broadly, we are much more interested in ‘cofinal’ relations among cofiltrations or functions between them than in strict ones. More formally, we would prefer not to distinguish between families
 $(f_i,g)_{i\in \mathbb {N}}$
as above which exhibit the following relation: (24)
$(f_i,g)_{i\in \mathbb {N}}$
as above which exhibit the following relation: (24) $$ \begin{align} (f_i,g)_{i\in\mathbb{N}}\thicksim (e_i,h)_{i\in\mathbb{N}}\hspace{.3 cm}\text{if}\hspace{.3 cm}g(i)\leq h(i)\text{ and }e_i=\eta^Y_{g(i),h(i)}\,f_i\text{ for all }i\in\mathbb{N}. \end{align} $$
$$ \begin{align} (f_i,g)_{i\in\mathbb{N}}\thicksim (e_i,h)_{i\in\mathbb{N}}\hspace{.3 cm}\text{if}\hspace{.3 cm}g(i)\leq h(i)\text{ and }e_i=\eta^Y_{g(i),h(i)}\,f_i\text{ for all }i\in\mathbb{N}. \end{align} $$
These considerations lead to the following definition.
Definition 7.2. Fix any category
![]() $\mathcal {C}$
. The category
$\mathcal {C}$
. The category
![]() $\mathsf {Ind}_\omega (\mathcal {C})$
has as objects the inductive sequences
$\mathsf {Ind}_\omega (\mathcal {C})$
has as objects the inductive sequences
![]() $\mathbf {X}=(X_i,\eta _i)_{i\in \mathbb {N}}$
in
$\mathbf {X}=(X_i,\eta _i)_{i\in \mathbb {N}}$
in
![]() $\mathcal {C}$
, or, in other words, the functors from the partial order category
$\mathcal {C}$
, or, in other words, the functors from the partial order category
![]() $\mathbb {N}$
to
$\mathbb {N}$
to
![]() $\mathcal {C}$
. Its morphisms are the
$\mathcal {C}$
. Its morphisms are the
![]() $\thicksim $
-equivalence classes of families
$\thicksim $
-equivalence classes of families
![]() $(f_i,g)_{i\in \mathbb {N}}$
of functions
$(f_i,g)_{i\in \mathbb {N}}$
of functions
![]() $f_i:X_i\to Y_{g(i)}$
coupled with a
$f_i:X_i\to Y_{g(i)}$
coupled with a
![]() $g:\mathbb {N}\to \mathbb {N}$
which together satisfy equation 23, where
$g:\mathbb {N}\to \mathbb {N}$
which together satisfy equation 23, where
![]() $\thicksim $
is the equivalence relation generated by line 24 above.
$\thicksim $
is the equivalence relation generated by line 24 above.
We may then define
![]() $\mathsf {Pro}_\omega (\mathcal {C})$
as
$\mathsf {Pro}_\omega (\mathcal {C})$
as
![]() $\mathsf {Ind}_\omega (\mathcal {C}^{\mathrm {op}})^{\mathrm {op}}$
. In particular, any contravariant functor
$\mathsf {Ind}_\omega (\mathcal {C}^{\mathrm {op}})^{\mathrm {op}}$
. In particular, any contravariant functor
![]() $\mathcal {C}\to \mathcal {D}$
induces a functor
$\mathcal {C}\to \mathcal {D}$
induces a functor
![]() $\mathsf {Ind}_\omega (\mathcal {C})^{\mathrm {op}}\to \mathsf {Pro}_\omega (\mathcal {D})$
; the composition of such a functor with the
$\mathsf {Ind}_\omega (\mathcal {C})^{\mathrm {op}}\to \mathsf {Pro}_\omega (\mathcal {D})$
; the composition of such a functor with the
![]() $\mathrm {lim}$
and
$\mathrm {lim}$
and
![]() $\mathrm {lim}^1$
functors is a basic motif in what follows. The latter functors were reviewed in abelian settings in some detail in [Reference Bergfalk and Lupini9, §5]; here, we will require and review their extension in [Reference Bousfield and Kan13, Section IX.2] to inverse sequences
$\mathrm {lim}^1$
functors is a basic motif in what follows. The latter functors were reviewed in abelian settings in some detail in [Reference Bergfalk and Lupini9, §5]; here, we will require and review their extension in [Reference Bousfield and Kan13, Section IX.2] to inverse sequences
![]() $(G^n,\eta ^n)_{n\in \mathbb {N}}$
of possibly nonabelian groups. Much as above,
$(G^n,\eta ^n)_{n\in \mathbb {N}}$
of possibly nonabelian groups. Much as above,
![]() $\eta ^n$
abbreviates
$\eta ^n$
abbreviates
![]() $\eta ^{n,n+1}:G^{n+1}\to G^n$
; for brevity, we will also sometimes term such inverse sequences towers. To simplify notation, we adopt the sometimes tacit convention that towers and the arguments of
$\eta ^{n,n+1}:G^{n+1}\to G^n$
; for brevity, we will also sometimes term such inverse sequences towers. To simplify notation, we adopt the sometimes tacit convention that towers and the arguments of
![]() $\mathrm {lim}$
and
$\mathrm {lim}$
and
![]() $\mathrm {lim}^1$
are always indexed by
$\mathrm {lim}^1$
are always indexed by
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Writing
![]() $\mathsf {CGrp}$
for the category of countable groups, it is straightforward first of all to see that the inverse limit defines a functor from
$\mathsf {CGrp}$
for the category of countable groups, it is straightforward first of all to see that the inverse limit defines a functor from
![]() $\mathsf {Pro}_\omega (\mathsf {CGrp})$
to the category of non-archimedean Polish groups and continuous homomorphisms. Suppose next that
$\mathsf {Pro}_\omega (\mathsf {CGrp})$
to the category of non-archimedean Polish groups and continuous homomorphisms. Suppose next that
![]() $\mathbf {G}=(G^n,\eta ^n)$
is a tower in
$\mathbf {G}=(G^n,\eta ^n)$
is a tower in
![]() $\mathsf {CGrp}$
, and consider the Polish group
$\mathsf {CGrp}$
, and consider the Polish group
![]() $C^0(\mathbf {G}):=\prod _{n\in \mathbb {N}}G^n$
. We then have a continuous action of the Polish group
$C^0(\mathbf {G}):=\prod _{n\in \mathbb {N}}G^n$
. We then have a continuous action of the Polish group
![]() $C^0(\mathbf {G})$
on the Polish space
$C^0(\mathbf {G})$
on the Polish space
![]() $\mathrm {Z}^{1}(\mathbf {G}) =\prod _{n\in \mathbb {N}}G^n$
defined by
$\mathrm {Z}^{1}(\mathbf {G}) =\prod _{n\in \mathbb {N}}G^n$
defined by
![]() $(g \cdot h) _{n}=g_n\cdot h_n\cdot (\eta ^n(g_{n+1}))^{-1}$
for each
$(g \cdot h) _{n}=g_n\cdot h_n\cdot (\eta ^n(g_{n+1}))^{-1}$
for each
![]() $n\in \mathbb {N}$
, which we call the
$n\in \mathbb {N}$
, which we call the
![]() $\mathrm {lim}^{1}$
-action of
$\mathrm {lim}^{1}$
-action of
![]() $\mathbf {G}$
. If
$\mathbf {G}$
. If
![]() $\mathrm {B}^{1}(\mathbf {G})$
is the corresponding orbit equivalence relation on
$\mathrm {B}^{1}(\mathbf {G})$
is the corresponding orbit equivalence relation on
![]() $\mathrm {Z}^{1}(\mathbf {G})$
, defined by setting
$\mathrm {Z}^{1}(\mathbf {G})$
, defined by setting
![]() $h\,\mathrm {B}^{1}(\mathbf {G})\,h^{\prime }$
if and only if there exists a
$h\,\mathrm {B}^{1}(\mathbf {G})\,h^{\prime }$
if and only if there exists a
![]() $g\in C^{0}(\mathbf {G})$
such that
$g\in C^{0}(\mathbf {G})$
such that
![]() $g\cdot h=h'$
, then
$g\cdot h=h'$
, then
![]() $\mathrm {lim}^{1}\,\mathbf {G}$
is the pointed semidefinable set
$\mathrm {lim}^{1}\,\mathbf {G}$
is the pointed semidefinable set
![]() $\mathrm {Z}^{1}(\mathbf {G})/\mathrm { B}^{1}(\mathbf {G})$
, with distinguished point corresponding to the identity element of
$\mathrm {Z}^{1}(\mathbf {G})/\mathrm { B}^{1}(\mathbf {G})$
, with distinguished point corresponding to the identity element of
![]() $\mathrm {Z}^{1}(\mathbf {G})$
(regarded as a group).
$\mathrm {Z}^{1}(\mathbf {G})$
(regarded as a group).
The construction clearly specializes to the more familiar
![]() $\mathrm {lim}^1$
of a tower
$\mathrm {lim}^1$
of a tower
![]() $\mathbf {G}$
of countable abelian groups: in this case,
$\mathbf {G}$
of countable abelian groups: in this case,
![]() $\mathrm {Z}^{1}(\mathbf {G})$
is also an abelian group, and
$\mathrm {Z}^{1}(\mathbf {G})$
is also an abelian group, and
![]() $\mathrm {B}^{1}(\mathbf {G})$
is the coset equivalence relation with respect to a Borel Polishable subgroup of
$\mathrm {B}^{1}(\mathbf {G})$
is the coset equivalence relation with respect to a Borel Polishable subgroup of
![]() $\mathrm {Z}^{1}(\mathbf {G})$
; hence,
$\mathrm {Z}^{1}(\mathbf {G})$
; hence,
![]() $\mathrm { lim}^{1}\,\mathbf {G}$
is a group with a Polish cover when endowed with the group operation inherited from
$\mathrm { lim}^{1}\,\mathbf {G}$
is a group with a Polish cover when endowed with the group operation inherited from
![]() $\mathrm {Z}^{1}(\mathbf {G})$
– a fact explored at length in [Reference Bergfalk and Lupini9].
$\mathrm {Z}^{1}(\mathbf {G})$
– a fact explored at length in [Reference Bergfalk and Lupini9].
7.2. Weak homotopy
As indicated, the broad focus of the remainder of this section is the sets or groups of homotopy classes of maps from a locally compact pair
![]() $(X,A)$
to a pointed polyhedron
$(X,A)$
to a pointed polyhedron
![]() $(P,*)$
; based maps
$(P,*)$
; based maps
![]() $(X,x)\to (P,*)$
or unbased maps
$(X,x)\to (P,*)$
or unbased maps
![]() $X\to P$
appear as special cases, by letting
$X\to P$
appear as special cases, by letting
![]() $A=\{x\}$
or
$A=\{x\}$
or
![]() $\varnothing $
, respectively.
$\varnothing $
, respectively.
Definition 7.3. Let f and g be maps from a locally compact pair
![]() $(X,A)$
to a pointed polyhedron
$(X,A)$
to a pointed polyhedron
![]() $(P,*)$
. We say that f and g are weakly homotopic, writing
$(P,*)$
. We say that f and g are weakly homotopic, writing
![]() $f\simeq _{\mathrm {w}} g$
, if for every compact subspace K of X, the maps
$f\simeq _{\mathrm {w}} g$
, if for every compact subspace K of X, the maps
![]() $f|_{K},g|_{K}:(K,K\cap A) \rightarrow ( P,*) $
are homotopic.
$f|_{K},g|_{K}:(K,K\cap A) \rightarrow ( P,*) $
are homotopic.
Lemma 7.4. Let f and g be as in Definition 7.3. The following are equivalent:
-
(1) f and g are weakly homotopic,
-
(2) for every subspace
 $(Y,B)$
of
$(Y,B)$
of
 $( X,A)$
that is homotopy equivalent to a compact pair,
$( X,A)$
that is homotopy equivalent to a compact pair,
 $f|_Y,g|_Y:( Y,B) \to (P,*)$
are homotopic.
$f|_Y,g|_Y:( Y,B) \to (P,*)$
are homotopic.
Proof. That (2) implies (1) is obvious; we will show that (1) implies (2). To that end, let
![]() $\alpha :(K,L) \rightarrow (Y,B) $
witness the homotopy equivalence of a compact pair
$\alpha :(K,L) \rightarrow (Y,B) $
witness the homotopy equivalence of a compact pair
![]() $(K,L)$
with
$(K,L)$
with
![]() $(Y,B)\subseteq (X,A)$
. By assumption, there exists a homotopy
$(Y,B)\subseteq (X,A)$
. By assumption, there exists a homotopy
![]() $h:f|_{\alpha (K)}\Rightarrow g|_{\alpha (K) }:( \alpha (K) ,\alpha (K) \cap A) \to ( P,*)$
. Thus,
$h:f|_{\alpha (K)}\Rightarrow g|_{\alpha (K) }:( \alpha (K) ,\alpha (K) \cap A) \to ( P,*)$
. Thus,
![]() $\tilde {h}:=h\circ ( \alpha \times \mathrm {id}_{I}) :(K\times I,L\times I) \to ( P,*) $
witnesses that
$\tilde {h}:=h\circ ( \alpha \times \mathrm {id}_{I}) :(K\times I,L\times I) \to ( P,*) $
witnesses that
![]() $\tilde {h}( -,0) =f\circ \alpha $
and
$\tilde {h}( -,0) =f\circ \alpha $
and
![]() $\tilde {h}( -,1) =g\circ \alpha $
are homotopic. Since
$\tilde {h}( -,1) =g\circ \alpha $
are homotopic. Since
![]() $\alpha :( K,L) \to (Y,B) $
is a homotopy equivalence, this implies that
$\alpha :( K,L) \to (Y,B) $
is a homotopy equivalence, this implies that
![]() $f|_Y,g|_Y:(Y,B) \to (P,*) $
are homotopic; this concludes the proof.
$f|_Y,g|_Y:(Y,B) \to (P,*) $
are homotopic; this concludes the proof.
Let
![]() $[(X,A),(P,*)]_{\mathrm {w}}$
denote the pointed semidefinable set of weak homotopy classes of maps
$[(X,A),(P,*)]_{\mathrm {w}}$
denote the pointed semidefinable set of weak homotopy classes of maps
![]() $(X,A) \to (P,*)$
.
$(X,A) \to (P,*)$
.
Lemma 7.5. Let
![]() $(X,A)$
be a locally compact pair, and let
$(X,A)$
be a locally compact pair, and let
![]() $(P,*)$
be a pointed polyhedron. The relation
$(P,*)$
be a pointed polyhedron. The relation
![]() $\simeq _{\mathrm {w}}$
of weak homotopy on maps
$\simeq _{\mathrm {w}}$
of weak homotopy on maps
![]() $(X,A)\to (P,*)$
is a closed equivalence relation with the property that the saturation
$(X,A)\to (P,*)$
is a closed equivalence relation with the property that the saturation
![]() $[ U] _{\simeq _{\mathrm {w}}}$
of any open subset U of
$[ U] _{\simeq _{\mathrm {w}}}$
of any open subset U of
![]() $\mathsf {LCP}((X,A),(P,*))$
is open.
$\mathsf {LCP}((X,A),(P,*))$
is open.
Furthermore,
![]() $\simeq _{\mathrm {w}}$
is the closure inside
$\simeq _{\mathrm {w}}$
is the closure inside
![]() $\mathsf {LCP}((X,A),(P,*))^2$
of the relation
$\mathsf {LCP}((X,A),(P,*))^2$
of the relation
![]() $\simeq $
of homotopy of maps
$\simeq $
of homotopy of maps
![]() $(X,A)\to (P,*)$
.
$(X,A)\to (P,*)$
.
Proof. Associated to any cofiltration
![]() $(X_n,A_n)_{n\in \mathbb {N}}$
of
$(X_n,A_n)_{n\in \mathbb {N}}$
of
![]() $(X,A)$
are restriction maps
$(X,A)$
are restriction maps
These, clearly, are continuous. The relation of weak homotopy for continuous maps
![]() $(X,A)\to (P,*)$
is the intersection of the
$(X,A)\to (P,*)$
is the intersection of the
![]() $(f_n\times f_n)$
-inverse images of the homotopy relation on
$(f_n\times f_n)$
-inverse images of the homotopy relation on
![]() $\mathsf {LCP}(( X_n,A_n) ,( P,*))$
. It then follows from Lemma 4.4 that
$\mathsf {LCP}(( X_n,A_n) ,( P,*))$
. It then follows from Lemma 4.4 that
![]() $ \simeq _{\mathrm {w}}$
is closed. It is also clear from this characterization (together with the Homotopy Extension Theorem 4.1 above) that
$ \simeq _{\mathrm {w}}$
is closed. It is also clear from this characterization (together with the Homotopy Extension Theorem 4.1 above) that
![]() $\simeq _{\mathrm {w}}$
is the closure of the homotopy relation
$\simeq _{\mathrm {w}}$
is the closure of the homotopy relation
![]() $\simeq $
.
$\simeq $
.
Suppose now that
![]() $U\subseteq \mathsf {LCP}((X,A) ,( P,*)) $
is open. We will show that
$U\subseteq \mathsf {LCP}((X,A) ,( P,*)) $
is open. We will show that
![]() $[U] _{\simeq _{\mathrm {w}}}$
is open. Since saturation commutes with unions, it will suffice to show this for
$[U] _{\simeq _{\mathrm {w}}}$
is open. Since saturation commutes with unions, it will suffice to show this for
![]() $U=\{ f\in \mathsf {LCP}(( X,A) ,( P,*)) :f( K) \subseteq W\} $
, where K and W are an arbitrary compact subset of X and an open subset of P, respectively. Fix an
$U=\{ f\in \mathsf {LCP}(( X,A) ,( P,*)) :f( K) \subseteq W\} $
, where K and W are an arbitrary compact subset of X and an open subset of P, respectively. Fix an
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
![]() $K\subseteq X_n$
.
$K\subseteq X_n$
.
Claim. A map
![]() $g\in \mathsf {LCP}((X,A) ,( P,* )) $
belongs to
$g\in \mathsf {LCP}((X,A) ,( P,* )) $
belongs to
![]() $[U] _{\simeq _{\mathrm {w}}}$
if and only if there exists an
$[U] _{\simeq _{\mathrm {w}}}$
if and only if there exists an
![]() $f \in \mathsf {LCP}(( X_n,A_n),( P,*)) $
such that
$f \in \mathsf {LCP}(( X_n,A_n),( P,*)) $
such that
![]() $f(K)\subseteq W$
and
$f(K)\subseteq W$
and
![]() $g|_{X_n}$
and f are homotopic.
$g|_{X_n}$
and f are homotopic.
Proof. By the Homotopy Extension Theorem, any f as in the statement of the claim extends to a map
![]() $f':(X,A) \rightarrow (P,*) $
which is homotopic to g. Since
$f':(X,A) \rightarrow (P,*) $
which is homotopic to g. Since
![]() $f'\in U$
, then,
$f'\in U$
, then,
![]() $g\in [U]_{\simeq _{\mathrm {w}}}$
. The converse implication is obvious.
$g\in [U]_{\simeq _{\mathrm {w}}}$
. The converse implication is obvious.
It is immediate from the claim and Lemma 4.4 that
![]() $[U] _{\simeq _{\mathrm {w}}}$
is indeed open.
$[U] _{\simeq _{\mathrm {w}}}$
is indeed open.
By Lemma 7.5, Lemma 3.10 and [Reference Kechris44, Theorem 12.16], we now have the following.
Corollary 7.6. Suppose that
![]() $(X,A)$
is a locally compact pair and P is a pointed polyhedron. Then the relation
$(X,A)$
is a locally compact pair and P is a pointed polyhedron. Then the relation
![]() $\simeq _{\mathrm {w}}$
on
$\simeq _{\mathrm {w}}$
on
![]() $\mathsf {LCP}((X,A),( P,*))$
has a Borel selector; there is, in other words, a Borel map
$\mathsf {LCP}((X,A),( P,*))$
has a Borel selector; there is, in other words, a Borel map
![]() $\mathsf {LCP}((X,A) ,( P,*))\to \mathsf {LCP}((X,A),( P,*)) :f\mapsto s(f)$
such that
$\mathsf {LCP}((X,A) ,( P,*))\to \mathsf {LCP}((X,A),( P,*)) :f\mapsto s(f)$
such that
![]() $f\simeq _{\mathrm {w}}s(f)$
for all
$f\simeq _{\mathrm {w}}s(f)$
for all
![]() $f,g\in \mathsf {LCP}((X,A) ,( P,*))$
, and
$f,g\in \mathsf {LCP}((X,A) ,( P,*))$
, and
![]() $f\simeq _{\mathrm {w}}g$
if and only if
$f\simeq _{\mathrm {w}}g$
if and only if
![]() $s(f)=s(g)$
. In particular,
$s(f)=s(g)$
. In particular,
![]() $[(X,A),(P,*)] _{\mathrm {w}}$
is a definable set.
$[(X,A),(P,*)] _{\mathrm {w}}$
is a definable set.
Let P be a polyhedron, and let
![]() $(X_n,A_n) _{n\in \mathbb {N}}$
be a cofiltration for the locally compact pair
$(X_n,A_n) _{n\in \mathbb {N}}$
be a cofiltration for the locally compact pair
![]() $(X,A)$
. Together with the natural restriction maps, the countable sets
$(X,A)$
. Together with the natural restriction maps, the countable sets
![]() $[(X_n,A_n),(P,*)] $
then assemble into an inverse sequence. Endow these sets with the discrete topology, and let
$[(X_n,A_n),(P,*)] $
then assemble into an inverse sequence. Endow these sets with the discrete topology, and let
denote the Polish space obtained as their limit. Having chosen a cofiltration for each locally compact pair
![]() $(X,A)$
, we may regard both
$(X,A)$
, we may regard both
![]() $[(X,A),(P,*)] _{\mathrm {w}}$
and
$[(X,A),(P,*)] _{\mathrm {w}}$
and
![]() $\mathrm {lim}\,[(X_n,A_n),(P,*)]$
as functors to the category of pointed definable sets, contravariant in the first coordinate (i.e., from
$\mathrm {lim}\,[(X_n,A_n),(P,*)]$
as functors to the category of pointed definable sets, contravariant in the first coordinate (i.e., from
![]() $\mathsf {LCP}$
) and covariant in the second (i.e., from
$\mathsf {LCP}$
) and covariant in the second (i.e., from
![]() $\mathsf {P}_*$
).
$\mathsf {P}_*$
).
Proposition 7.7. There is a definable bijection between the pointed definable sets
which is natural in each coordinate of the two bifunctors.
Proof. Consider for each n the definable function
![]() $[(X,A),(P,*)]_{\mathrm {w}}\to [(X_n,A_n),(P,*)]$
given by restriction; these functions together induce a definable function
$[(X,A),(P,*)]_{\mathrm {w}}\to [(X_n,A_n),(P,*)]$
given by restriction; these functions together induce a definable function
![]() $\Phi _{(X,A),(P,*)}:[(X,A),(P,*)]_{\mathrm {w}}\to \mathrm {lim}\,[(X_n,A_n),(P,*)]$
.
$\Phi _{(X,A),(P,*)}:[(X,A),(P,*)]_{\mathrm {w}}\to \mathrm {lim}\,[(X_n,A_n),(P,*)]$
.
We noted above that two maps
![]() $f,f':(X,A) \rightarrow (P,*)$
are weakly homotopic if and only if
$f,f':(X,A) \rightarrow (P,*)$
are weakly homotopic if and only if
![]() $f\restriction X_n$
and
$f\restriction X_n$
and
![]() $f' \restriction X_n$
are homotopic for every
$f' \restriction X_n$
are homotopic for every
![]() $n\in \mathbb {N}$
; it follows immediately that
$n\in \mathbb {N}$
; it follows immediately that
![]() $\Phi _{(X,A),(P,*)}$
is injective. To see that
$\Phi _{(X,A),(P,*)}$
is injective. To see that
![]() $\Phi _{(X,A),(P,*)}$
is surjective, let
$\Phi _{(X,A),(P,*)}$
is surjective, let
![]() $([f_n])_{n\in \mathbb {N}}$
be an element of
$([f_n])_{n\in \mathbb {N}}$
be an element of
![]() $\mathrm {lim}\,[(X_n,A_n),(P,*)]$
. In particular,
$\mathrm {lim}\,[(X_n,A_n),(P,*)]$
. In particular,
![]() $f_n:(X_n,A_n) \rightarrow (P,*) $
and
$f_n:(X_n,A_n) \rightarrow (P,*) $
and
![]() $f_{n+1}\restriction X_n$
are homotopic for each
$f_{n+1}\restriction X_n$
are homotopic for each
![]() $n\in \mathbb {N}$
. By the Homotopy Extension Theorem, we may, without leaving their homotopy classes, recursively modify each of the functions
$n\in \mathbb {N}$
. By the Homotopy Extension Theorem, we may, without leaving their homotopy classes, recursively modify each of the functions
![]() $f_{n}$
so that
$f_{n}$
so that
![]() $f_{n+1}\restriction X_n =f_n$
for each
$f_{n+1}\restriction X_n =f_n$
for each
![]() $n\in \mathbb {N}$
. If we then define
$n\in \mathbb {N}$
. If we then define
![]() $f:(X,A) \to (P,*)$
by letting
$f:(X,A) \to (P,*)$
by letting
![]() $f(x)=f_{n}(x)$
for
$f(x)=f_{n}(x)$
for
![]() $x\in X_{n}$
, then
$x\in X_{n}$
, then
![]() $\Phi _{(X,A),(P,\ast )}([f]) =([f_{n}])_{n\in \mathbb {N}}$
, as desired.
$\Phi _{(X,A),(P,\ast )}([f]) =([f_{n}])_{n\in \mathbb {N}}$
, as desired.
Naturality with respect to maps
![]() $g:(P,*)\to (Q,\star )$
in the second coordinate follows from the observation that
$g:(P,*)\to (Q,\star )$
in the second coordinate follows from the observation that
![]() $g\circ (f\restriction X_n)=(g\circ f)\restriction X_n$
for every
$g\circ (f\restriction X_n)=(g\circ f)\restriction X_n$
for every
![]() $f:(X,A)\to (P,*)$
and
$f:(X,A)\to (P,*)$
and
![]() $n\in \mathbb {N}$
, and naturality with respect to maps
$n\in \mathbb {N}$
, and naturality with respect to maps
![]() $(X,A)\to (Y,B)$
in the first coordinate follows from the same principle.
$(X,A)\to (Y,B)$
in the first coordinate follows from the same principle.
7.3. The classification of phantom maps
We turn now to the classification of phantom maps [Reference Gray and McGibbon32, Reference Mardešić55, Reference McGibbon60, Reference McGibbon and Roitberg61, Reference McGibbon and Steiner62]. Here we simply call phantom maps what in [Reference McGibbon60] are called phantom maps of the second kind.
Definition 7.8. Let
![]() $(X,A)$
be a locally compact pair, and let P be a pointed polyhedron. A phantom map from
$(X,A)$
be a locally compact pair, and let P be a pointed polyhedron. A phantom map from
![]() $(X,A)$
to
$(X,A)$
to
![]() $(P,*)$
is a map which is weakly homotopic to the constant map. We let
$(P,*)$
is a map which is weakly homotopic to the constant map. We let
![]() $\mathrm {Ph} ((X,A),(P,*)) $
denote the collection of phantom maps from
$\mathrm {Ph} ((X,A),(P,*)) $
denote the collection of phantom maps from
![]() $(X,A)$
to
$(X,A)$
to
![]() $(P,*)$
.
$(P,*)$
.
By Lemmas 7.4 and 7.5,
![]() $\mathrm {Ph}((X,A),(P,*))$
is a homotopy-invariant closed subspace of the space
$\mathrm {Ph}((X,A),(P,*))$
is a homotopy-invariant closed subspace of the space
![]() $\mathsf {LCP}((X,A),(P,*))$
. More precisely,
$\mathsf {LCP}((X,A),(P,*))$
. More precisely,
Proposition 7.9.
![]() $\mathrm {Ph}((X,A),(P,*))$
is the closure in
$\mathrm {Ph}((X,A),(P,*))$
is the closure in
![]() $\mathsf {LCP}((X,A),(P,*))$
of
$\mathsf {LCP}((X,A),(P,*))$
of
![]() $[\ast ]$
, the class of maps homotopic to the constant map.
$[\ast ]$
, the class of maps homotopic to the constant map.
Proof. As noted, by Lemma 7.5,
![]() $\mathrm {Ph}((X,A),(P,*))$
is closed in
$\mathrm {Ph}((X,A),(P,*))$
is closed in
![]() $\mathsf {LCP}((X,A),(P,*))$
and therefore contains the closure of
$\mathsf {LCP}((X,A),(P,*))$
and therefore contains the closure of
![]() $[\ast ]$
. For the reverse inclusion, fix
$[\ast ]$
. For the reverse inclusion, fix
![]() $f\in \mathrm {Ph}((X,A),(P,*))$
; applying Lemma 7.4 with
$f\in \mathrm {Ph}((X,A),(P,*))$
; applying Lemma 7.4 with
![]() $g=\ast $
then implies, together with the Homotopy Extension Theorem, that any basic open neighborhood of f in
$g=\ast $
then implies, together with the Homotopy Extension Theorem, that any basic open neighborhood of f in
![]() $\mathsf {LCP}((X,A),(P,*))$
contains some
$\mathsf {LCP}((X,A),(P,*))$
contains some
![]() $g'$
homotopic to g.
$g'$
homotopic to g.
Thus, we may consider the pointed semidefinable set
![]() $[(X,A),(P,*)]_{\infty }$
of homotopy classes of phantom maps
$[(X,A),(P,*)]_{\infty }$
of homotopy classes of phantom maps
![]() $(X,A)\rightarrow (P,*)$
. Just as for
$(X,A)\rightarrow (P,*)$
. Just as for
![]() $[-,-]_{\mathrm {w}}$
, this defines a functor to the category of pointed semidefinable sets which is contravariant in the first coordinate and covariant in the second.
$[-,-]_{\mathrm {w}}$
, this defines a functor to the category of pointed semidefinable sets which is contravariant in the first coordinate and covariant in the second.
Observe now that when
![]() $A=\{x\}$
for some single element x of X, then we may regard
$A=\{x\}$
for some single element x of X, then we may regard
![]() $(X,A)$
as a pointed space, and, in particular, may apply to it the reduced suspension operation
$(X,A)$
as a pointed space, and, in particular, may apply to it the reduced suspension operation
![]() $\Sigma :\mathsf {LC}_{*}\to \mathsf {LC}_{*}$
described in Section 5.1. In fact, in the present context of maps
$\Sigma :\mathsf {LC}_{*}\to \mathsf {LC}_{*}$
described in Section 5.1. In fact, in the present context of maps
![]() $(X,A)\to (P,*)$
, in which A functions as little more than a basepoint, it is reasonable to regard
$(X,A)\to (P,*)$
, in which A functions as little more than a basepoint, it is reasonable to regard
![]() $\Sigma $
as an instance of a generalized reduced suspension operation
$\Sigma $
as an instance of a generalized reduced suspension operation
![]() $\bar {\Sigma }:\mathsf {LCP}\to \mathsf {LC}_*$
defined for nonempty A as
$\bar {\Sigma }:\mathsf {LCP}\to \mathsf {LC}_*$
defined for nonempty A as
or, more concisely,
where
![]() $\star $
is the quotient-image of A. Doing so will allow us a more general unified statement and argument of this section’s main result. Note, however, that the second of the above formulations raises questions of interpretation when
$\star $
is the quotient-image of A. Doing so will allow us a more general unified statement and argument of this section’s main result. Note, however, that the second of the above formulations raises questions of interpretation when
![]() $A=\varnothing $
. We take the standard homotopy theoretic approach of defining
$A=\varnothing $
. We take the standard homotopy theoretic approach of defining
![]() $X/\varnothing $
to equal what is sometimes (as in [Reference May and Ponto59]) denoted
$X/\varnothing $
to equal what is sometimes (as in [Reference May and Ponto59]) denoted
![]() $X_{+}$
– namely, the union of X with a discrete basepoint
$X_{+}$
– namely, the union of X with a discrete basepoint
![]() $\{\star \}$
.Footnote
2
These conventions have the virtue of ensuring that any
$\{\star \}$
.Footnote
2
These conventions have the virtue of ensuring that any
![]() $\bar {\Sigma }(X,A)$
is an H-cogroup (
$\bar {\Sigma }(X,A)$
is an H-cogroup (
![]() $X\mapsto X_{+}$
is left adjoint to the forgetful functor from pointed to unpointed spaces and extends to a left adjoint to the inclusion
$X\mapsto X_{+}$
is left adjoint to the forgetful functor from pointed to unpointed spaces and extends to a left adjoint to the inclusion
![]() $\iota $
of pointed spaces in pairs of spaces;
$\iota $
of pointed spaces in pairs of spaces;
![]() $\bar {\Sigma }$
is simply
$\bar {\Sigma }$
is simply
![]() $\Sigma \circ \iota $
, and is consequently left adjoint to the standard loop-space functor
$\Sigma \circ \iota $
, and is consequently left adjoint to the standard loop-space functor
![]() $\Omega $
on
$\Omega $
on
![]() $\mathsf {LC}_{*}$
).
$\mathsf {LC}_{*}$
).
Now assume, as before, that we have assigned a cofiltration
![]() $(X_n,A_n)_{n\in \mathbb {N}}$
to each locally compact pair
$(X_n,A_n)_{n\in \mathbb {N}}$
to each locally compact pair
![]() $(X,A)$
. These assignments determine an inductive sequence of compact H-cogroups
$(X,A)$
. These assignments determine an inductive sequence of compact H-cogroups
![]() $(\bar {\Sigma }(X_n,A_n))_{n\in \mathbb {N}}$
and thereby, in turn, a tower
$(\bar {\Sigma }(X_n,A_n))_{n\in \mathbb {N}}$
and thereby, in turn, a tower
of countable groups. Taking
then determines a functor to the category of pointed semidefinable sets, which again is contravariant in the first coordinate and covariant in the second. Note that any other family of choices of cofiltrations for locally compact pairs
![]() $(X,A)$
would yield a definably isomorphic functor.
$(X,A)$
would yield a definably isomorphic functor.
We now present a definable version of a description of the set of phantom maps which has appeared in several contexts – all of them pointed. It may be found in [Reference Bousfield and Kan13, Section IX.3, Corollary 3.3] in the context of pointed simplicial sets, and in [Reference May and Ponto59, Section 2.1, Proposition 2.1.9 and Corollary 2.1.11] in the context of inductive sequences of pointed spaces and cofibrations, for example; see also [Reference McGibbon60, Section 5], where the fundamental insight is attributed to [Reference Steenrod81]. Readers may also find the heuristic discussion at [Reference McGibbon60, p. 1229] valuable.
Theorem 7.10. For each locally compact pair
![]() $(X,A)$
, let
$(X,A)$
, let
![]() $(X_n,A_n)_{n\in \mathbb {N}}$
denote the associated cofiltration described above. There exists a definable isomorphism of the bifunctors
$(X_n,A_n)_{n\in \mathbb {N}}$
denote the associated cofiltration described above. There exists a definable isomorphism of the bifunctors
![]() $\mathsf {LCP}^{\mathrm {op}}\times \mathsf {P}_*\to \mathsf {SemiDef}_*$
given by
$\mathsf {LCP}^{\mathrm {op}}\times \mathsf {P}_*\to \mathsf {SemiDef}_*$
given by
![]() $((X,A),(P,*))\mapsto [(X,A),(P,*)]_\infty $
and
$((X,A),(P,*))\mapsto [(X,A),(P,*)]_\infty $
and
![]() $((X,A),(P,*))\mapsto \mathrm {lim}^1\,[\bar {\Sigma }(X_n,A_n) ,(P,*)]$
which is natural in each coordinate.
$((X,A),(P,*))\mapsto \mathrm {lim}^1\,[\bar {\Sigma }(X_n,A_n) ,(P,*)]$
which is natural in each coordinate.
The following notation will render portions of our proof simpler and more intuitive. For any
![]() $0\leq a,b$
in
$0\leq a,b$
in
![]() $\mathbb {R}$
and
$\mathbb {R}$
and
![]() $f:X\times [0,a]\to Y$
and
$f:X\times [0,a]\to Y$
and
![]() $g:X\times [0,b]\to Y$
with
$g:X\times [0,b]\to Y$
with
![]() $f\restriction X\times \{a\}=g\restriction X\times \{0\}$
, define
$f\restriction X\times \{a\}=g\restriction X\times \{0\}$
, define
![]() $f\cdot g:X\times [0,a+b]\to Y$
by
$f\cdot g:X\times [0,a+b]\to Y$
by
 $$ \begin{align*} f\cdot g (x,t) = \left\{ \begin{array}{ll} f(x,t) & t\in [0,a]\text{,} \\ g(x,t-a) & t\in [a,b]\text{.} \end{array} \right. \end{align*} $$
$$ \begin{align*} f\cdot g (x,t) = \left\{ \begin{array}{ll} f(x,t) & t\in [0,a]\text{,} \\ g(x,t-a) & t\in [a,b]\text{.} \end{array} \right. \end{align*} $$
Define also
![]() $-f:X\times [0,a]\to Y$
by
$-f:X\times [0,a]\to Y$
by
![]() $-f(x,t)=f(x,a-t)$
and observe that
$-f(x,t)=f(x,a-t)$
and observe that
![]() $f\cdot -f$
is homotopic to the map
$f\cdot -f$
is homotopic to the map
![]() $X\times [0,2a]\to Y$
given by
$X\times [0,2a]\to Y$
given by
![]() $(x,t)\mapsto f(x,0)$
. Lastly, for any real
$(x,t)\mapsto f(x,0)$
. Lastly, for any real
![]() $k\geq 0$
, define
$k\geq 0$
, define
![]() $kf:X\times [0,ka]\to Y$
by
$kf:X\times [0,ka]\to Y$
by
![]() $kf(x,t)=f(x,kt)$
.
$kf(x,t)=f(x,kt)$
.
Proof. As indicated, we begin by describing a definable function
![]() $\varphi :[(X,A),(P,*)]_{\infty }\to \mathrm {lim}^1\,[\bar {\Sigma }(X_n,A_n) ,(P,*)]$
. We will then verify that
$\varphi :[(X,A),(P,*)]_{\infty }\to \mathrm {lim}^1\,[\bar {\Sigma }(X_n,A_n) ,(P,*)]$
. We will then verify that
![]() $\varphi $
is indeed an isomorphism in the category of pointed semidefinable sets. For ease of reading, let
$\varphi $
is indeed an isomorphism in the category of pointed semidefinable sets. For ease of reading, let
![]() $\mathbf {G}$
denote the tower of groups
$\mathbf {G}$
denote the tower of groups
![]() $([\bar {\Sigma }(X_n,A_n) ,(P,*)])_{n\in \mathbb {N}}$
for the duration of the proof.
$([\bar {\Sigma }(X_n,A_n) ,(P,*)])_{n\in \mathbb {N}}$
for the duration of the proof.
By Corollary 4.19, one may in a Borel fashion choose for each phantom map
![]() $f:(X,A)\to (P,*)$
and
$f:(X,A)\to (P,*)$
and
![]() $n\in \mathbb {N}$
a homotopy
$n\in \mathbb {N}$
a homotopy
![]() $h_{n}:\ast \Rightarrow f\restriction X_n:(X_n,A_n)\to (P,*)$
. Hence,
$h_{n}:\ast \Rightarrow f\restriction X_n:(X_n,A_n)\to (P,*)$
. Hence,
![]() $h_{n}:(X_{n}\times I,A_{n}\times I) \rightarrow (P,*)$
is a map such that
$h_{n}:(X_{n}\times I,A_{n}\times I) \rightarrow (P,*)$
is a map such that
![]() $h_{n}(\,\cdot \,,0) =\ast $
,
$h_{n}(\,\cdot \,,0) =\ast $
,
![]() $h_{n}(\,\cdot \,,1) =f\restriction X_n$
, and
$h_{n}(\,\cdot \,,1) =f\restriction X_n$
, and
![]() $h_{n}(x,\,\cdot \,) =\ast $
for each
$h_{n}(x,\,\cdot \,) =\ast $
for each
![]() $x\in A_n$
. As above, we let
$x\in A_n$
. As above, we let
![]() $ (x,t) \mapsto \langle x,t\rangle $
be the quotient map
$ (x,t) \mapsto \langle x,t\rangle $
be the quotient map
![]() $X_n\times I\to \bar {\Sigma }(X_n,A_n)$
.Footnote
3
Define then
$X_n\times I\to \bar {\Sigma }(X_n,A_n)$
.Footnote
3
Define then
![]() $D_n:\bar {\Sigma }(X_n,A_n)\rightarrow (P,*)$
by
$D_n:\bar {\Sigma }(X_n,A_n)\rightarrow (P,*)$
by
 $$ \begin{align} \langle x,t\rangle \mapsto \left\{ \begin{array}{ll} h_{n}( x,2t) & 0\leq t\leq 1/2\text{,} \\ h_{n+1}( x,2-2t) & 1/2\leq t\leq 1\text{.} \end{array} \right. \end{align} $$
$$ \begin{align} \langle x,t\rangle \mapsto \left\{ \begin{array}{ll} h_{n}( x,2t) & 0\leq t\leq 1/2\text{,} \\ h_{n+1}( x,2-2t) & 1/2\leq t\leq 1\text{.} \end{array} \right. \end{align} $$
In the notation introduced just above,
![]() $D_n$
is the map induced on
$D_n$
is the map induced on
![]() $\bar {\Sigma }(X_n,A_n)$
by
$\bar {\Sigma }(X_n,A_n)$
by
![]() $1/2(h_n\cdot -(h_{n+1}\restriction X_n\times I)):X_n\times I\to P$
. Writing
$1/2(h_n\cdot -(h_{n+1}\restriction X_n\times I)):X_n\times I\to P$
. Writing
![]() $[D_n] \in [\bar {\Sigma }(X_n,A_n) ,(P,*)]$
for the homotopy class of
$[D_n] \in [\bar {\Sigma }(X_n,A_n) ,(P,*)]$
for the homotopy class of
![]() $D_n$
, we then let
$D_n$
, we then let
![]() $\varphi ([f])$
be the element of
$\varphi ([f])$
be the element of
![]() $\mathrm {lim}^1\,\mathbf {G}$
represented by the sequence
$\mathrm {lim}^1\,\mathbf {G}$
represented by the sequence
![]() $([D_n])_{n\in \mathbb {N}}\in \prod _{n\in \mathbb {N}}G^n=\mathrm {Z}^1(\mathbf {G})$
.
$([D_n])_{n\in \mathbb {N}}\in \prod _{n\in \mathbb {N}}G^n=\mathrm {Z}^1(\mathbf {G})$
.
In the following three claims, we verify that
![]() $\varphi $
does not depend on our choices of homotopies
$\varphi $
does not depend on our choices of homotopies
![]() $h_n$
, or of representative of
$h_n$
, or of representative of
![]() $[f]$
, and hence that
$[f]$
, and hence that
![]() $\varphi : [(X,A),(P,*)]_{\infty }\to \mathrm {lim}^1\,\mathbf {G}$
is a well-defined basepoint-preserving definable function, as desired.
$\varphi : [(X,A),(P,*)]_{\infty }\to \mathrm {lim}^1\,\mathbf {G}$
is a well-defined basepoint-preserving definable function, as desired.
Claim. The element
![]() $\varphi ([f]) $
of
$\varphi ([f]) $
of
![]() $\mathrm {lim}^1\,\mathbf {G}$
does not depend on the choice of homotopies
$\mathrm {lim}^1\,\mathbf {G}$
does not depend on the choice of homotopies
![]() $h_{n}:\ast \Rightarrow f\restriction X_n:(X,A) \to (P,*)$
.
$h_{n}:\ast \Rightarrow f\restriction X_n:(X,A) \to (P,*)$
.
Proof. Let
![]() $f:(X,A) \to (P,*)$
be a phantom map, and let
$f:(X,A) \to (P,*)$
be a phantom map, and let
![]() $g_n,h_n:\ast \Rightarrow f\restriction X_n:(X_n,A_n)\to (P,*)$
be homotopies for each
$g_n,h_n:\ast \Rightarrow f\restriction X_n:(X_n,A_n)\to (P,*)$
be homotopies for each
![]() $n\in \mathbb {N}$
. Suppose that
$n\in \mathbb {N}$
. Suppose that
![]() $C_n,D_n:\bar {\Sigma }(X_n,A_n)\rightarrow (P,*)$
are defined as in equation (25) from
$C_n,D_n:\bar {\Sigma }(X_n,A_n)\rightarrow (P,*)$
are defined as in equation (25) from
![]() $g_n,g_{n+1}$
and
$g_n,g_{n+1}$
and
![]() $h_n,h_{n+1}$
, respectively. We will show that the corresponding sequences
$h_n,h_{n+1}$
, respectively. We will show that the corresponding sequences
![]() $([C_n])_{n\in \mathbb {N}},([D_n])_{n\in \mathbb {N}}\in Z^1(\mathbf {G}) $
define the same element of
$([C_n])_{n\in \mathbb {N}},([D_n])_{n\in \mathbb {N}}\in Z^1(\mathbf {G}) $
define the same element of
![]() $\mathrm {lim}^1\,\mathbf {G}$
. To this end, we define maps
$\mathrm {lim}^1\,\mathbf {G}$
. To this end, we define maps
![]() $E_n: \bar {\Sigma }(X_n,A_n)\rightarrow (P,*)$
for
$E_n: \bar {\Sigma }(X_n,A_n)\rightarrow (P,*)$
for
![]() $n\in \mathbb {N}$
such that
$n\in \mathbb {N}$
such that
for every
![]() $n\in \mathbb {N}$
; these maps
$n\in \mathbb {N}$
; these maps
![]() $E_n$
are defined by
$E_n$
are defined by
 $$ \begin{align*} \langle x,t\rangle \mapsto \left\{ \begin{array}{ll} g_n(x,2t) & 0\leq t\leq 1/2\text{,} \\ h_n(x,2-2t) & 1/2\leq t\leq 1\text{.} \end{array} \right. \text{.} \end{align*} $$
$$ \begin{align*} \langle x,t\rangle \mapsto \left\{ \begin{array}{ll} g_n(x,2t) & 0\leq t\leq 1/2\text{,} \\ h_n(x,2-2t) & 1/2\leq t\leq 1\text{.} \end{array} \right. \text{.} \end{align*} $$
Observe that
![]() $E_{n}$
is well defined for essentially the same reason that
$E_{n}$
is well defined for essentially the same reason that
![]() $D_n$
is, and that in our alternative notation,
$D_n$
is, and that in our alternative notation,
![]() $E_n$
is the map induced on
$E_n$
is the map induced on
![]() $\bar {\Sigma }(X_n,A_n)$
by
$\bar {\Sigma }(X_n,A_n)$
by
![]() $1/2(g_n\cdot -h_n):X_n\times I\to P$
. In this notation,
$1/2(g_n\cdot -h_n):X_n\times I\to P$
. In this notation,
![]() $[E_n]\cdot [D_n]\cdot [E_{n+1}\restriction \bar {\Sigma }(X_n,A_n)]^{-1}$
is the homotopy class of the map induced on
$[E_n]\cdot [D_n]\cdot [E_{n+1}\restriction \bar {\Sigma }(X_n,A_n)]^{-1}$
is the homotopy class of the map induced on
![]() $\bar {\Sigma }(X_n,A_n)$
by
$\bar {\Sigma }(X_n,A_n)$
by
![]() $1/6(g_n\cdot -h_n\cdot h_n\cdot -h_{n+1}\cdot h_{n+1}\cdot -g_{n+1})$
, where the last three functions are understood to be restricted to
$1/6(g_n\cdot -h_n\cdot h_n\cdot -h_{n+1}\cdot h_{n+1}\cdot -g_{n+1})$
, where the last three functions are understood to be restricted to
![]() $X_n\times I$
; it should be at least intuitively clear that this map is homotopic to the function induced on
$X_n\times I$
; it should be at least intuitively clear that this map is homotopic to the function induced on
![]() $\bar {\Sigma }(X_n,A_n)$
by
$\bar {\Sigma }(X_n,A_n)$
by
![]() $1/2(g_n\cdot -(g_{n+1}\restriction X_n\times I))$
or, in other words, to
$1/2(g_n\cdot -(g_{n+1}\restriction X_n\times I))$
or, in other words, to
![]() $C_n$
, as claimed. For the sake of thoroughness, we record explicit homotopies below.
$C_n$
, as claimed. For the sake of thoroughness, we record explicit homotopies below.
By definition,
![]() $[E_n]\cdot [D_n]\cdot [E_{n+1}\restriction \bar {\Sigma }(X_n,A_n)]^{-1}=[\tilde {D}_n]$
, where
$[E_n]\cdot [D_n]\cdot [E_{n+1}\restriction \bar {\Sigma }(X_n,A_n)]^{-1}=[\tilde {D}_n]$
, where
![]() $\tilde {D}_n:\bar {\Sigma }(X_n,A_n) \rightarrow (P,*)$
is defined by
$\tilde {D}_n:\bar {\Sigma }(X_n,A_n) \rightarrow (P,*)$
is defined by
 $$ \begin{align*} \langle x,t\rangle \mapsto \left\{ \begin{array}{ll} g_n( x,6t) & 0\leq t\leq 1/6\text{,} \\ h_n( x,1-6(t-1/6)) & 1/6\leq t\leq 2/6\text{,} \\ h_n(x,6(t-2/6)) & 2/6\leq t\leq 3/6\text{,} \\ h_{n+1}(x,1-6(t-3/6)) & 3/6\leq t\leq 4/6 \text{,} \\ h_{n+1}(x,6(t-4/6)) & 4/6\leq t\leq 5/6 \text{,} \\ g_{n+1}(x,1-6(t-5/6)) & 5/6\leq t\leq 1\text{.} \end{array} \right. \end{align*} $$
$$ \begin{align*} \langle x,t\rangle \mapsto \left\{ \begin{array}{ll} g_n( x,6t) & 0\leq t\leq 1/6\text{,} \\ h_n( x,1-6(t-1/6)) & 1/6\leq t\leq 2/6\text{,} \\ h_n(x,6(t-2/6)) & 2/6\leq t\leq 3/6\text{,} \\ h_{n+1}(x,1-6(t-3/6)) & 3/6\leq t\leq 4/6 \text{,} \\ h_{n+1}(x,6(t-4/6)) & 4/6\leq t\leq 5/6 \text{,} \\ g_{n+1}(x,1-6(t-5/6)) & 5/6\leq t\leq 1\text{.} \end{array} \right. \end{align*} $$
Define
![]() $\tilde {h}_{n}:\bar {\Sigma }(X_n,A_n)\times I \rightarrow (P,*)$
, a homotopy beginning at
$\tilde {h}_{n}:\bar {\Sigma }(X_n,A_n)\times I \rightarrow (P,*)$
, a homotopy beginning at
![]() $\tilde {h}_n(\,\cdot \,,0)=\tilde {D}_n$
, by setting
$\tilde {h}_n(\,\cdot \,,0)=\tilde {D}_n$
, by setting
 $$ \begin{align*} \tilde{h}_n(\langle x,t\rangle,s) =\left\{ \begin{array}{ll} \tilde{D}_{n}(\langle x,t\rangle) & t\in [0,1/6]\cup [5/6,1]\text{,} \\ h_n(x,1-6(t-1/6)) & 1/6\leq t\leq (2-s)/6\text{,} \\ h_n(x,1-6((2-s)/6-1/6)) & (2-s)/6\leq t\leq (2+s)/6\text{,} \\ h_n(x,6(t-2/6)) & (2+s)/6\leq t\leq 3/6\text{,} \\ h_{n+1}(x,1-6( t-3/6)) & 3/6\leq t\leq (4-s)/6\text{,} \\ h_{n+1}(x,1-6((4-s)/6-3/6)) & (4-s)/6\leq t\leq (4+s)/6\text{,} \\ h_{n+1}(x,6(t-4/6)) & (4+s)/6\leq t\leq 5/6 \end{array} \right. \end{align*} $$
$$ \begin{align*} \tilde{h}_n(\langle x,t\rangle,s) =\left\{ \begin{array}{ll} \tilde{D}_{n}(\langle x,t\rangle) & t\in [0,1/6]\cup [5/6,1]\text{,} \\ h_n(x,1-6(t-1/6)) & 1/6\leq t\leq (2-s)/6\text{,} \\ h_n(x,1-6((2-s)/6-1/6)) & (2-s)/6\leq t\leq (2+s)/6\text{,} \\ h_n(x,6(t-2/6)) & (2+s)/6\leq t\leq 3/6\text{,} \\ h_{n+1}(x,1-6( t-3/6)) & 3/6\leq t\leq (4-s)/6\text{,} \\ h_{n+1}(x,1-6((4-s)/6-3/6)) & (4-s)/6\leq t\leq (4+s)/6\text{,} \\ h_{n+1}(x,6(t-4/6)) & (4+s)/6\leq t\leq 5/6 \end{array} \right. \end{align*} $$
for all
![]() $\langle x,t\rangle \in \bar {\Sigma }(X_n,A_n)$
and
$\langle x,t\rangle \in \bar {\Sigma }(X_n,A_n)$
and
![]() $s\in I$
. Observe that
$s\in I$
. Observe that
![]() $\tilde {h}_n$
is a homotopy from
$\tilde {h}_n$
is a homotopy from
![]() $\tilde {D}_{n}$
to the function
$\tilde {D}_{n}$
to the function
![]() $\bar {\Sigma }(X_n,A_n) \rightarrow (P,*)$
given by
$\bar {\Sigma }(X_n,A_n) \rightarrow (P,*)$
given by
 $$ \begin{align*} \tilde{h}_n(\langle x,t\rangle,1) =\left\{ \begin{array}{ll} g_n(x,6t) & 0\leq t\leq 1/6\text{,} \\ f( x) & 1/6\leq t\leq 5/6\text{,} \\ g_{n+1}(x,1-6( t-5/6)) & 5/6\leq t\leq 1\text{.} \end{array} \right. \end{align*} $$
$$ \begin{align*} \tilde{h}_n(\langle x,t\rangle,1) =\left\{ \begin{array}{ll} g_n(x,6t) & 0\leq t\leq 1/6\text{,} \\ f( x) & 1/6\leq t\leq 5/6\text{,} \\ g_{n+1}(x,1-6( t-5/6)) & 5/6\leq t\leq 1\text{.} \end{array} \right. \end{align*} $$
![]() $\tilde {h}(\,\cdot \,,1) $
is clearly homotopic to
$\tilde {h}(\,\cdot \,,1) $
is clearly homotopic to
![]() $C_n:\bar {\Sigma }(X_n,A_n) \rightarrow (P,*)$
in turn. Since we have argued
$C_n:\bar {\Sigma }(X_n,A_n) \rightarrow (P,*)$
in turn. Since we have argued
![]() $[E_n]\cdot [D_n]\cdot [E_{n+1}\restriction \bar {\Sigma }(X_n,A_n)]^{-1}=[C_n]$
for arbitrary
$[E_n]\cdot [D_n]\cdot [E_{n+1}\restriction \bar {\Sigma }(X_n,A_n)]^{-1}=[C_n]$
for arbitrary
![]() $n\in \mathbb {N}$
, we conclude that the sequences
$n\in \mathbb {N}$
, we conclude that the sequences
![]() $([D_{n}]) _{n\in \mathbb {N}}$
and
$([D_{n}]) _{n\in \mathbb {N}}$
and
![]() $([C_{n}]) _{n\in \mathbb {N}}$
represent the same element of
$([C_{n}]) _{n\in \mathbb {N}}$
represent the same element of
![]() $\mathrm {lim}^1\,\mathbf {G}$
, as desired.
$\mathrm {lim}^1\,\mathbf {G}$
, as desired.
Claim. The element
![]() $\varphi ([f]) $
of
$\varphi ([f]) $
of
![]() $\mathrm {lim}^1\,\mathbf {G}$
does not depend on the choice of representative f of the homotopy class
$\mathrm {lim}^1\,\mathbf {G}$
does not depend on the choice of representative f of the homotopy class
![]() $[f]$
.
$[f]$
.
Proof. Fix a homotopy
![]() $\rho :f\Rightarrow f'$
between phantom maps
$\rho :f\Rightarrow f'$
between phantom maps
![]() $f,f':(X,A) \rightarrow (P,*) $
. We will show that
$f,f':(X,A) \rightarrow (P,*) $
. We will show that
![]() $\varphi ([f])=\varphi ([f'])$
. Fix homotopies
$\varphi ([f])=\varphi ([f'])$
. Fix homotopies
![]() $g_n:* \Rightarrow f\restriction X_n:(X_n,A_n) \rightarrow ( P,*)$
for each
$g_n:* \Rightarrow f\restriction X_n:(X_n,A_n) \rightarrow ( P,*)$
for each
![]() $n\in \mathbb {N}$
. Observe that these induce homotopies
$n\in \mathbb {N}$
. Observe that these induce homotopies
![]() $h_n:\ast \Rightarrow f'\restriction X_n:(X_n,A_n)\rightarrow ( P,*)$
defined by
$h_n:\ast \Rightarrow f'\restriction X_n:(X_n,A_n)\rightarrow ( P,*)$
defined by
 $$ \begin{align*} h_n(x,t) =\left\{ \begin{array}{ll} g_{n}(x,2t) & 0\leq t\leq 1/2,\\ \rho( x,2(t-1/2)) & 1/2\leq t\leq 1\text{.} \end{array} \right. \end{align*} $$
$$ \begin{align*} h_n(x,t) =\left\{ \begin{array}{ll} g_{n}(x,2t) & 0\leq t\leq 1/2,\\ \rho( x,2(t-1/2)) & 1/2\leq t\leq 1\text{.} \end{array} \right. \end{align*} $$
For
![]() $n\in \mathbb {N}$
, let
$n\in \mathbb {N}$
, let
![]() $D_n$
denote the map
$D_n$
denote the map
![]() $\bar {\Sigma }(X_n,A_n) \rightarrow (P,*)$
defined as above from
$\bar {\Sigma }(X_n,A_n) \rightarrow (P,*)$
defined as above from
![]() $g_n,g_{n+1}$
, and let
$g_n,g_{n+1}$
, and let
![]() $\tilde {D}_n$
denote the map
$\tilde {D}_n$
denote the map
![]() $\bar {\Sigma }(X_n,A_n) \rightarrow (P,*)$
defined as above from
$\bar {\Sigma }(X_n,A_n) \rightarrow (P,*)$
defined as above from
![]() $h_n,h_{n+1}$
. In our alternative notation,
$h_n,h_{n+1}$
. In our alternative notation,
![]() $D_n$
and
$D_n$
and
![]() $\tilde {D}_n$
are the functions induced on
$\tilde {D}_n$
are the functions induced on
![]() $\bar {\Sigma }(X_n,A_n)$
by
$\bar {\Sigma }(X_n,A_n)$
by
![]() $1/4(g_n\cdot \rho \cdot -\rho \cdot -g_{n+1})$
and
$1/4(g_n\cdot \rho \cdot -\rho \cdot -g_{n+1})$
and
![]() $1/2(g_n\cdot -g_{n+1})$
, respectively, where the constituent functions are all restricted to
$1/2(g_n\cdot -g_{n+1})$
, respectively, where the constituent functions are all restricted to
![]() $X_n\times I$
. It should now be clear that by arguments just as above,
$X_n\times I$
. It should now be clear that by arguments just as above,
![]() $D_n$
is homotopic to
$D_n$
is homotopic to
![]() $\tilde {D}_n$
for each
$\tilde {D}_n$
for each
![]() $n\in \mathbb {N}$
; the provision of explicit homotopies is left to the interested reader.
$n\in \mathbb {N}$
; the provision of explicit homotopies is left to the interested reader.
Claim. The
![]() $\varphi $
-image of the class
$\varphi $
-image of the class
![]() $[*]$
of nullhomotopic functions is the basepoint of
$[*]$
of nullhomotopic functions is the basepoint of
![]() $\mathrm {lim}^1\,\mathbf {G}$
.
$\mathrm {lim}^1\,\mathbf {G}$
.
Proof. When
![]() $f=\ast $
, we may choose
$f=\ast $
, we may choose
![]() $h_{n}:\ast \Rightarrow f\restriction X_n:(X_n,A_n) \rightarrow (P,*)$
to be the trivial homotopy. In this case,
$h_{n}:\ast \Rightarrow f\restriction X_n:(X_n,A_n) \rightarrow (P,*)$
to be the trivial homotopy. In this case,
![]() $D_n:\bar {\Sigma }(X_n,A_n) \rightarrow (P,*)$
is the constant map
$D_n:\bar {\Sigma }(X_n,A_n) \rightarrow (P,*)$
is the constant map
![]() $*$
. Clearly,
$*$
. Clearly,
![]() $(D_n)_{n\in \mathbb {N}}$
is the neutral element of
$(D_n)_{n\in \mathbb {N}}$
is the neutral element of
![]() $\mathrm {Z}^1(\mathbf {G}) $
, and hence,
$\mathrm {Z}^1(\mathbf {G}) $
, and hence,
![]() $\varphi ([f]) $
is the basepoint of
$\varphi ([f]) $
is the basepoint of
![]() $\mathrm {lim}^1\,\mathbf {G}$
.
$\mathrm {lim}^1\,\mathbf {G}$
.
By the foregoing claims,
![]() $\varphi :[(X,A),(P,*)]_\infty \to \mathrm {lim}^1\,\mathbf {G}$
is a well-defined basepoint-preserving definable function.
$\varphi :[(X,A),(P,*)]_\infty \to \mathrm {lim}^1\,\mathbf {G}$
is a well-defined basepoint-preserving definable function.
Claim. The function
![]() $\varphi :[(X,A),(P,*)] _{\infty }\rightarrow \mathrm {lim}^1\,\mathbf {G}$
is injective.
$\varphi :[(X,A),(P,*)] _{\infty }\rightarrow \mathrm {lim}^1\,\mathbf {G}$
is injective.
Proof. We will assume that
![]() $\varphi ([f]) =\varphi ([f'])$
for two phantom maps
$\varphi ([f]) =\varphi ([f'])$
for two phantom maps
![]() $f,f':(X,A) \rightarrow (P,*) $
and deduce that f and
$f,f':(X,A) \rightarrow (P,*) $
and deduce that f and
![]() $f'$
are homotopic.
$f'$
are homotopic.
Let
![]() $Y\subseteq X$
be the union of the boundaries
$Y\subseteq X$
be the union of the boundaries
![]() $\partial X_{n}$
for
$\partial X_{n}$
for
![]() $n\in \mathbb {N}$
. Note that Y is a closed subset of X, being the union of a locally finite family of closed subsets of X. Furthermore, as f is a phantom map, each
$n\in \mathbb {N}$
. Note that Y is a closed subset of X, being the union of a locally finite family of closed subsets of X. Furthermore, as f is a phantom map, each
![]() $f\restriction \partial X_{n}$
is nullhomotopic; hence,
$f\restriction \partial X_{n}$
is nullhomotopic; hence,
![]() $f\restriction Y$
is nullhomotopic as well. Thus, by the Homotopy Extension Theorem, after replacing f with a phantom map homotopic to f, we may assume that
$f\restriction Y$
is nullhomotopic as well. Thus, by the Homotopy Extension Theorem, after replacing f with a phantom map homotopic to f, we may assume that
![]() $f\restriction Y=\ast $
. By the same reasoning, we may assume that
$f\restriction Y=\ast $
. By the same reasoning, we may assume that
![]() $f'\restriction Y=\ast $
as well.
$f'\restriction Y=\ast $
as well.
Fix homotopies
![]() $h_n:* \Rightarrow f\restriction X_n:(X_n,A_n) \rightarrow (P,*)$
and
$h_n:* \Rightarrow f\restriction X_n:(X_n,A_n) \rightarrow (P,*)$
and
![]() $h^{\prime }_n:* \Rightarrow f'\restriction X_n:(X_n,A_n) \rightarrow (P,*)$
for each
$h^{\prime }_n:* \Rightarrow f'\restriction X_n:(X_n,A_n) \rightarrow (P,*)$
for each
![]() $n\in \mathbb {N}$
. These determine functions
$n\in \mathbb {N}$
. These determine functions
![]() $ D_{n}:\bar {\Sigma }\to (P,*)$
and
$ D_{n}:\bar {\Sigma }\to (P,*)$
and
![]() $ D^{\prime }_{n}:\bar {\Sigma }\to (P,*)$
in the manner described above, defining in turn the values
$ D^{\prime }_{n}:\bar {\Sigma }\to (P,*)$
in the manner described above, defining in turn the values
![]() $\varphi ([f])$
and
$\varphi ([f])$
and
![]() $\varphi ([f'])$
, respectively. Since
$\varphi ([f'])$
, respectively. Since
![]() $\varphi ([f])=\varphi ([f'])$
, there exist maps
$\varphi ([f])=\varphi ([f'])$
, there exist maps
![]() $E_{n}: \bar {\Sigma }(X_n,A_n)\rightarrow (P,*)$
such that
$E_{n}: \bar {\Sigma }(X_n,A_n)\rightarrow (P,*)$
such that
![]() $[E_n]\cdot [D_n]\cdot [E_{n+1}\restriction \bar {\Sigma }(X_n,A_n)]^{-1}=[D^{\prime }_n]$
for every
$[E_n]\cdot [D_n]\cdot [E_{n+1}\restriction \bar {\Sigma }(X_n,A_n)]^{-1}=[D^{\prime }_n]$
for every
![]() $n\in \mathbb {N}$
. Therefore, by replacing each
$n\in \mathbb {N}$
. Therefore, by replacing each
![]() $h_{n}:\ast \Rightarrow f\restriction X_n:(X_n,A_n) \rightarrow (P,*)$
with the homotopy defined by
$h_{n}:\ast \Rightarrow f\restriction X_n:(X_n,A_n) \rightarrow (P,*)$
with the homotopy defined by
 $$ \begin{align*} \left( x,t\right) \mapsto \left\{ \begin{array}{ll} E_{n}(\langle x,2t\rangle) & 0\leq t\leq 1/2 \\ h_{n}( 2t-1) & 1/2\leq t\leq 1 \end{array} \right. \end{align*} $$
$$ \begin{align*} \left( x,t\right) \mapsto \left\{ \begin{array}{ll} E_{n}(\langle x,2t\rangle) & 0\leq t\leq 1/2 \\ h_{n}( 2t-1) & 1/2\leq t\leq 1 \end{array} \right. \end{align*} $$
we may assume without loss of generality that
![]() $[D_n]=[D^{\prime }_n]$
for every
$[D_n]=[D^{\prime }_n]$
for every
![]() $n\in \mathbb {N}$
. Assume in other words that for each
$n\in \mathbb {N}$
. Assume in other words that for each
![]() $n\in \mathbb {N}$
, there exists a homotopy
$n\in \mathbb {N}$
, there exists a homotopy
![]() $ \tilde {h}_{n}:D_{n}\Rightarrow D_{n}^{\prime }:\bar {\Sigma }(X_n,A_n) \rightarrow (P,*)$
.
$ \tilde {h}_{n}:D_{n}\Rightarrow D_{n}^{\prime }:\bar {\Sigma }(X_n,A_n) \rightarrow (P,*)$
.
Fix for each
![]() $n\in \mathbb {N}$
a continuous function
$n\in \mathbb {N}$
a continuous function
![]() $\lambda _{n}:X\rightarrow \left [ 0,1 \right ] $
such that
$\lambda _{n}:X\rightarrow \left [ 0,1 \right ] $
such that
![]() $\lambda _n\restriction X_{n-1}=0$
and
$\lambda _n\restriction X_{n-1}=0$
and
![]() $\lambda _{n}\restriction X\backslash \mathrm {int}(X_n)=1$
, letting
$\lambda _{n}\restriction X\backslash \mathrm {int}(X_n)=1$
, letting
![]() $X_{-1}=\varnothing $
. Define the phantom map
$X_{-1}=\varnothing $
. Define the phantom map
![]() $g:(X,A)\to (P,*)$
by
$g:(X,A)\to (P,*)$
by
![]() $x\mapsto D_{n}(\langle x,\lambda _{n}(x)\rangle ) $
for
$x\mapsto D_{n}(\langle x,\lambda _{n}(x)\rangle ) $
for
![]() $x\in X_n\setminus X_{n-1}$
. To see that g is continuous, observe that for
$x\in X_n\setminus X_{n-1}$
. To see that g is continuous, observe that for
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $x\in \partial X_{n-1}$
,
$x\in \partial X_{n-1}$
,
We then have a homotopy
![]() $f\Rightarrow g:(X,A)\to (P,*)$
, defined by setting
$f\Rightarrow g:(X,A)\to (P,*)$
, defined by setting
![]() $(x,t) \mapsto D_{n}(\langle x,(1-t)/2+t\lambda _{n}(x)\rangle )$
for all
$(x,t) \mapsto D_{n}(\langle x,(1-t)/2+t\lambda _{n}(x)\rangle )$
for all
![]() $t\in [0,1] $
,
$t\in [0,1] $
,
![]() $x\in X_n\setminus X_{n-1}$
, and
$x\in X_n\setminus X_{n-1}$
, and
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Similarly,
![]() $f^{\prime }$
is homotopic to the map
$f^{\prime }$
is homotopic to the map
![]() $g^{\prime }:(X,A)\rightarrow (P,*)$
defined by
$g^{\prime }:(X,A)\rightarrow (P,*)$
defined by
![]() $g^{\prime }( x) =D_{n}^{\prime }(\langle x,\lambda _{n}(x)\rangle )$
for all
$g^{\prime }( x) =D_{n}^{\prime }(\langle x,\lambda _{n}(x)\rangle )$
for all
![]() $x\in X_{n}\setminus X_{n-1}$
and
$x\in X_{n}\setminus X_{n-1}$
and
![]() $n\in \mathbb {N}$
. Hence, our task reduces to showing that g and
$n\in \mathbb {N}$
. Hence, our task reduces to showing that g and
![]() $g^{\prime }$
are homotopic. One may define a homotopy
$g^{\prime }$
are homotopic. One may define a homotopy
![]() $g\Rightarrow g^{\prime }:(X,A)\to (P,*)$
by
$g\Rightarrow g^{\prime }:(X,A)\to (P,*)$
by
for
![]() $x\in X_{n}\setminus X_{n-1}$
and
$x\in X_{n}\setminus X_{n-1}$
and
![]() $t\in I$
, where
$t\in I$
, where
![]() $\tilde {h}_{n}$
is the homotopy
$\tilde {h}_{n}$
is the homotopy
![]() $D_{n}\Rightarrow D_{n}^{\prime }:\bar {\Sigma }( X_n,A_n) \rightarrow (P,*) $
described above. This concludes the proof.
$D_{n}\Rightarrow D_{n}^{\prime }:\bar {\Sigma }( X_n,A_n) \rightarrow (P,*) $
described above. This concludes the proof.
We have established that
![]() $\varphi :[(X,A),(P,*)]_\infty \to \mathrm {lim}^1\,\mathbf {G}$
is an injective basepoint-preserving definable function. In order to conclude the proof that
$\varphi :[(X,A),(P,*)]_\infty \to \mathrm {lim}^1\,\mathbf {G}$
is an injective basepoint-preserving definable function. In order to conclude the proof that
![]() $\varphi $
is an isomorphism in the category of pointed semidefinable sets, it will suffice to describe a definable function
$\varphi $
is an isomorphism in the category of pointed semidefinable sets, it will suffice to describe a definable function
![]() $\psi :\mathrm {lim}^1\,\mathbf {G}\to [(X,A),(P,*)]_\infty $
which is a right inverse of
$\psi :\mathrm {lim}^1\,\mathbf {G}\to [(X,A),(P,*)]_\infty $
which is a right inverse of
![]() $\varphi $
.
$\varphi $
.
Begin by fixing a continuous function
![]() $\lambda _{n}:X\rightarrow I$
as above for each
$\lambda _{n}:X\rightarrow I$
as above for each
![]() $n\in \mathbb {N}$
. We define
$n\in \mathbb {N}$
. We define
![]() $\psi $
via representatives
$\psi $
via representatives
![]() $([\tilde {D}_n])_{n\in \mathbb {N}}\in \mathrm {Z}^{1}( \mathbf {G}) $
of elements of
$([\tilde {D}_n])_{n\in \mathbb {N}}\in \mathrm {Z}^{1}( \mathbf {G}) $
of elements of
![]() $\mathrm {lim}^1\,\mathbf {G}$
. Let
$\mathrm {lim}^1\,\mathbf {G}$
. Let
![]() $\psi ([([ \tilde {D}_{n}])_{n\in \mathbb {N}}])=[f]$
, where
$\psi ([([ \tilde {D}_{n}])_{n\in \mathbb {N}}])=[f]$
, where
![]() $f:(X,A)\to (P,*)$
is the phantom map defined by setting
$f:(X,A)\to (P,*)$
is the phantom map defined by setting
for all
![]() $x\in X_{n}\backslash X_{n-1}$
.
$x\in X_{n}\backslash X_{n-1}$
.
Claim. The map
![]() $f:(X,A) \rightarrow \left ( P,\ast \right ) $
is a well-defined phantom map.
$f:(X,A) \rightarrow \left ( P,\ast \right ) $
is a well-defined phantom map.
Proof. Just as above, for all
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $x\in \partial X_{n}$
, we have
$x\in \partial X_{n}$
, we have
This shows that f is well defined and continuous. Define for each
![]() $n\in \mathbb {N}$
a homotopy
$n\in \mathbb {N}$
a homotopy
![]() $h_{n}:\ast \Rightarrow f\restriction X_n:(X_n,A_n) \rightarrow (P,*)$
by setting
$h_{n}:\ast \Rightarrow f\restriction X_n:(X_n,A_n) \rightarrow (P,*)$
by setting
This shows that f is a phantom map.
Claim. Adopt the notation above, and suppose that
![]() $[f]=\psi ([([\tilde {D}_{n}])_{n\in \mathbb {N}}])$
. Then
$[f]=\psi ([([\tilde {D}_{n}])_{n\in \mathbb {N}}])$
. Then
![]() $\phi ( \lbrack f]) =[([\tilde {D}_{n}])_{n\in \mathbb {N}}]$
.
$\phi ( \lbrack f]) =[([\tilde {D}_{n}])_{n\in \mathbb {N}}]$
.
Proof. The argument amounts to computing
![]() $\varphi ([f]) \in \mathrm {lim}^1\,\mathbf {G}$
. Let
$\varphi ([f]) \in \mathrm {lim}^1\,\mathbf {G}$
. Let
![]() $h_{n}:\ast \Rightarrow f\restriction X_n:(X_n,A_n) \rightarrow ( P,\ast ) $
be the homotopy recorded in the proof of the previous claim, and consider the map
$h_{n}:\ast \Rightarrow f\restriction X_n:(X_n,A_n) \rightarrow ( P,\ast ) $
be the homotopy recorded in the proof of the previous claim, and consider the map
![]() $D_{n}:\bar {\Sigma }(X_n,A_n) \rightarrow (P,*)$
defined from
$D_{n}:\bar {\Sigma }(X_n,A_n) \rightarrow (P,*)$
defined from
![]() $h_{n},h_{n+1}$
as in the definition of
$h_{n},h_{n+1}$
as in the definition of
![]() $\varphi ([f])$
. Thus,
$\varphi ([f])$
. Thus,
 $$ \begin{align*} D_{n}(\langle x,t\rangle) =\left\{ \begin{array}{ll} h_{n}( x,2t) =\tilde{D}_{n}(\langle x,2t\lambda _{n}( x)\rangle) & 0\leq t\leq 1/2\text{,} \\ h_{n+1}( x,2t-1) =\tilde{D}_{n+1}(\langle x,( 2t-1) \lambda _{n+1}( x)\rangle)=\ast & 1/2\leq t\leq 1\text{.} \end{array} \right. \end{align*} $$
$$ \begin{align*} D_{n}(\langle x,t\rangle) =\left\{ \begin{array}{ll} h_{n}( x,2t) =\tilde{D}_{n}(\langle x,2t\lambda _{n}( x)\rangle) & 0\leq t\leq 1/2\text{,} \\ h_{n+1}( x,2t-1) =\tilde{D}_{n+1}(\langle x,( 2t-1) \lambda _{n+1}( x)\rangle)=\ast & 1/2\leq t\leq 1\text{.} \end{array} \right. \end{align*} $$
Observe that
![]() $D_{n},\tilde {D}_{n}:\bar {\Sigma }(X_n,A_n) \rightarrow (P,\ast )$
are homotopic, as witnessed by the homotopy
$D_{n},\tilde {D}_{n}:\bar {\Sigma }(X_n,A_n) \rightarrow (P,\ast )$
are homotopic, as witnessed by the homotopy
 $$ \begin{align*} ([x,t],s) \mapsto \left\{ \begin{array}{cc} D_{n}(\langle x,2t(1-s)\lambda_{n}(x)+st\rangle) & 0\leq t\leq 1/2+s/2\text{,} \\ \ast & 1/2+s/2\leq t\leq 1\text{.} \end{array} \right. \end{align*} $$
$$ \begin{align*} ([x,t],s) \mapsto \left\{ \begin{array}{cc} D_{n}(\langle x,2t(1-s)\lambda_{n}(x)+st\rangle) & 0\leq t\leq 1/2+s/2\text{,} \\ \ast & 1/2+s/2\leq t\leq 1\text{.} \end{array} \right. \end{align*} $$
Therefore,
![]() $[ D_{n}] =[\tilde {D}_{n}]$
for every
$[ D_{n}] =[\tilde {D}_{n}]$
for every
![]() $n\in \mathbb {N}$
. This shows that
$n\in \mathbb {N}$
. This shows that
![]() $\varphi ([f]) =[([\tilde {D}_{n}])_{n\in \mathbb {N}}]$
, as desired.
$\varphi ([f]) =[([\tilde {D}_{n}])_{n\in \mathbb {N}}]$
, as desired.
By the previous claim, the function
![]() $\psi :\mathrm {lim}^1\,\mathbf {G}\rightarrow [(X,A),(P,*)]_{\infty }$
is well defined and basepoint-preserving and is a right inverse for
$\psi :\mathrm {lim}^1\,\mathbf {G}\rightarrow [(X,A),(P,*)]_{\infty }$
is well defined and basepoint-preserving and is a right inverse for
![]() $\varphi $
. Since
$\varphi $
. Since
![]() $\varphi $
is injective,
$\varphi $
is injective,
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are, in fact, mutually inverse functions. Since
$\psi $
are, in fact, mutually inverse functions. Since
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are definable functions, they are mutually inverse isomorphisms in the category of pointed semidefinable sets.
$\psi $
are definable functions, they are mutually inverse isomorphisms in the category of pointed semidefinable sets.
It is quite clear from our construction and claims above that
![]() $\varphi $
defines a transformation of functors which is natural in the polyhedral coordinate. Naturality in the first coordinate follows for the same reasons, coupled with the fact that maps
$\varphi $
defines a transformation of functors which is natural in the polyhedral coordinate. Naturality in the first coordinate follows for the same reasons, coupled with the fact that maps
![]() $(X,A)\to (Y,B)$
induce
$(X,A)\to (Y,B)$
induce
![]() $\mathsf {Ind}_\omega $
maps at the level of the cofiltrations in the manner described in Section 7.1.
$\mathsf {Ind}_\omega $
maps at the level of the cofiltrations in the manner described in Section 7.1.
7.4. Phantom maps to H-spaces
We now restrict our analysis to phantom maps from a locally compact pair
![]() $(X,A)$
to a polyhedral H -space
$(X,A)$
to a polyhedral H -space
![]() $(P,\ast ,m)$
. Recall that such a P is a pointed polyhedron endowed with a map
$(P,\ast ,m)$
. Recall that such a P is a pointed polyhedron endowed with a map
![]() $m:P\wedge P\rightarrow P$
such that the maps
$m:P\wedge P\rightarrow P$
such that the maps
![]() $m( \ast ,-)$
and
$m( \ast ,-)$
and
![]() $m( -,\ast ) :P\rightarrow P$
are each homotopic to the identity; m then induces a binary operation on
$m( -,\ast ) :P\rightarrow P$
are each homotopic to the identity; m then induces a binary operation on
![]() $[(X,A),(P,\ast )]$
with
$[(X,A),(P,\ast )]$
with
![]() $[\ast ]$
as identity element defined by
$[\ast ]$
as identity element defined by
for any maps
![]() $f,g:(X,A) \rightarrow (P,\ast )$
. This renders
$f,g:(X,A) \rightarrow (P,\ast )$
. This renders
![]() $[(X,A),(P,\ast )]$
a semidefinable unital magma (i.e., a pointed (semidefinable) set with a (definable) binary operation in which the basepoint serves as the neutral element).
$[(X,A),(P,\ast )]$
a semidefinable unital magma (i.e., a pointed (semidefinable) set with a (definable) binary operation in which the basepoint serves as the neutral element).
It is clear that
![]() $[(X,A),(P,\ast )]_{\infty }$
is a semidefinable unital submagma of
$[(X,A),(P,\ast )]_{\infty }$
is a semidefinable unital submagma of
![]() $[(X,A),(P,\ast )]$
. We now show that
$[(X,A),(P,\ast )]$
. We now show that
![]() $[(X,A),(P,\ast )]_{\infty }$
is, in fact, a definable abelian group, and even a group with a Polish cover.
$[(X,A),(P,\ast )]_{\infty }$
is, in fact, a definable abelian group, and even a group with a Polish cover.
Theorem 7.11. Suppose that
![]() $(X_n,A_n)_{n\in \mathbb {N}}$
is a cofiltration of a locally compact pair
$(X_n,A_n)_{n\in \mathbb {N}}$
is a cofiltration of a locally compact pair
![]() $(X,A)$
and
$(X,A)$
and
![]() $(P,\ast ,m)$
is a polyhedral H-space. Then
$(P,\ast ,m)$
is a polyhedral H-space. Then
![]() $[(X,A),(P,\ast )]_{\infty }$
is a definable abelian group naturally isomorphic to
$[(X,A),(P,\ast )]_{\infty }$
is a definable abelian group naturally isomorphic to
![]() $\mathrm {lim}^{1}\,[ \bar {\Sigma }(X_n,A_n),(P,*)]$
; in particular, it is naturally definably isomorphic to a group with a Polish cover.
$\mathrm {lim}^{1}\,[ \bar {\Sigma }(X_n,A_n),(P,*)]$
; in particular, it is naturally definably isomorphic to a group with a Polish cover.
The term natural here should be understood in the sense more precisely articulated in the statement of Theorem 7.10 and the conclusion of its proof; as is standard, for concision, we will omit those sorts of details from now on.
Proof. Since P is an H-space,
![]() $[\bar {\Sigma }(X_n,A_n),(P,\ast )]$
is a countable abelian group for every
$[\bar {\Sigma }(X_n,A_n),(P,\ast )]$
is a countable abelian group for every
![]() $n\in \mathbb {N}$
, by Lemmas 5.3 and 4.4. Therefore,
$n\in \mathbb {N}$
, by Lemmas 5.3 and 4.4. Therefore,
![]() $\mathrm {lim}^{1}\,[\bar {\Sigma }(X_n,A_n),(P,\ast )]$
is a group with a Polish cover and, hence, a definable abelian group.
$\mathrm {lim}^{1}\,[\bar {\Sigma }(X_n,A_n),(P,\ast )]$
is a group with a Polish cover and, hence, a definable abelian group.
Thus, it suffices to check that the definable basepoint-preserving map
defined in the proof of Theorem 7.10 is a magma homomorphism (i.e., that it satisfies
for
![]() $[f],[f^{\prime }]\in [(X,A),(P,\ast )]_{\infty }$
). To this end, suppose that
$[f],[f^{\prime }]\in [(X,A),(P,\ast )]_{\infty }$
). To this end, suppose that
![]() $f,f^{\prime }:X\rightarrow P$
are phantom maps, and choose for each
$f,f^{\prime }:X\rightarrow P$
are phantom maps, and choose for each
![]() $n\in \mathbb {N}$
homotopies
$n\in \mathbb {N}$
homotopies
![]() $h_{n}:\ast \Rightarrow f|_{X_{n}}$
and
$h_{n}:\ast \Rightarrow f|_{X_{n}}$
and
![]() $ h_{n}^{\prime }:\ast \Rightarrow f'|_{X_{n}}$
; we then have homotopies
$ h_{n}^{\prime }:\ast \Rightarrow f'|_{X_{n}}$
; we then have homotopies
![]() $m\circ \left ( h_{n}\wedge h_{n}^{\prime }\right ) :\ast \Rightarrow m\circ \left ( f\wedge f^{\prime }\right ) |_{X_{n}}$
for each
$m\circ \left ( h_{n}\wedge h_{n}^{\prime }\right ) :\ast \Rightarrow m\circ \left ( f\wedge f^{\prime }\right ) |_{X_{n}}$
for each
![]() $n\in \mathbb {N}$
as well.
$n\in \mathbb {N}$
as well.
By the definition of
![]() $\varphi $
,
$\varphi $
,
where
![]() $D_{n},D_{n}^{\prime },E_{n}:\bar {\Sigma }(X_{n},A_n)\rightarrow (P,\ast )$
are defined for each
$D_{n},D_{n}^{\prime },E_{n}:\bar {\Sigma }(X_{n},A_n)\rightarrow (P,\ast )$
are defined for each
![]() $n\in \mathbb {N}$
by
$n\in \mathbb {N}$
by
 $$ \begin{align*} D_{n}(\langle x,t\rangle) =\left\{ \begin{array}{ll} h_{n}( x,2t) & 0\leq t\leq 1/2 \\ h_{n+1}( x,2-2t) & 1/2\leq t\leq 1 \end{array} \right. \end{align*} $$
$$ \begin{align*} D_{n}(\langle x,t\rangle) =\left\{ \begin{array}{ll} h_{n}( x,2t) & 0\leq t\leq 1/2 \\ h_{n+1}( x,2-2t) & 1/2\leq t\leq 1 \end{array} \right. \end{align*} $$
 $$ \begin{align*} D_{n}^{\prime }( \langle x,t\rangle) =\left\{ \begin{array}{ll} h_{n}^{\prime }( x,2t) & 0\leq t\leq 1/2 \\ h_{n+1}^{\prime }\left( x,2-2t)\right) & 1/2\leq t\leq 1 \end{array} \right. \end{align*} $$
$$ \begin{align*} D_{n}^{\prime }( \langle x,t\rangle) =\left\{ \begin{array}{ll} h_{n}^{\prime }( x,2t) & 0\leq t\leq 1/2 \\ h_{n+1}^{\prime }\left( x,2-2t)\right) & 1/2\leq t\leq 1 \end{array} \right. \end{align*} $$
 $$ \begin{align*} E_{n}(\langle x,t\rangle) &=\left\{ \begin{array}{ll} \left( m\circ \left( h_{n}\wedge h_{n}^{\prime }\right) \right) ( x,2t) & 0\leq t\leq 1/2 \\ \left( m\circ \left( h_{n+1}\wedge h_{n+1}^{\prime }\right) \right) (x,2-2t)) & 1/2\leq t\leq 1 \end{array} \right. \\ &= \left( m\circ \left( D_{n}\wedge D_{n}^{\prime }\right) \right) ( \langle x,t\rangle) \text{.} \end{align*} $$
$$ \begin{align*} E_{n}(\langle x,t\rangle) &=\left\{ \begin{array}{ll} \left( m\circ \left( h_{n}\wedge h_{n}^{\prime }\right) \right) ( x,2t) & 0\leq t\leq 1/2 \\ \left( m\circ \left( h_{n+1}\wedge h_{n+1}^{\prime }\right) \right) (x,2-2t)) & 1/2\leq t\leq 1 \end{array} \right. \\ &= \left( m\circ \left( D_{n}\wedge D_{n}^{\prime }\right) \right) ( \langle x,t\rangle) \text{.} \end{align*} $$
In short,
![]() $E_{n}=m\circ \left ( D_{n}\wedge D_{n}^{\prime }\right )$
. And since, by Lemma 5.3, the operation on
$E_{n}=m\circ \left ( D_{n}\wedge D_{n}^{\prime }\right )$
. And since, by Lemma 5.3, the operation on
![]() $[\bar {\Sigma }(X_{n},A_n),(P,\ast )]$
defined in terms of the H-space structure on P coincides with the operation induced by the H-cogroup structure on
$[\bar {\Sigma }(X_{n},A_n),(P,\ast )]$
defined in terms of the H-space structure on P coincides with the operation induced by the H-cogroup structure on
![]() $\bar {\Sigma }(X_{n},A_n)$
,
$\bar {\Sigma }(X_{n},A_n)$
,
and hence,
![]() $\varphi ([f]\cdot [f']) =\varphi ([f]) +\varphi ([f'])$
. This concludes the proof that
$\varphi ([f]\cdot [f']) =\varphi ([f]) +\varphi ([f'])$
. This concludes the proof that
![]() $\varphi $
is a magma homomorphism.
$\varphi $
is a magma homomorphism.
7.5. The homotopy classification of maps to H-groups
We now consider the even more restrictive case in which
![]() $( P,\ast ,m)$
is a polyhedral H-group. To this end, let
$( P,\ast ,m)$
is a polyhedral H-group. To this end, let
![]() $(X,A)$
be a locally compact pair, and let
$(X,A)$
be a locally compact pair, and let
![]() $(P,\ast )$
be a pointed polyhedron with H-group operation
$(P,\ast )$
be a pointed polyhedron with H-group operation
![]() $m:P\wedge P\rightarrow P$
. In this case, the H-group structure on P renders
$m:P\wedge P\rightarrow P$
. In this case, the H-group structure on P renders
![]() $[(X,A),(P,\ast )]$
a (not necessarily abelian) semidefinable group. The group operation on
$[(X,A),(P,\ast )]$
a (not necessarily abelian) semidefinable group. The group operation on
![]() $[(X,A) ,(P,\ast )]$
is defined as before by setting
$[(X,A) ,(P,\ast )]$
is defined as before by setting
![]() $[f]\cdot [g]=[m\circ (f\wedge g)]$
. Similarly, if
$[f]\cdot [g]=[m\circ (f\wedge g)]$
. Similarly, if
![]() $\zeta :( P,\ast ) \rightarrow (P,\ast ) $
is a map such that the map
$\zeta :( P,\ast ) \rightarrow (P,\ast ) $
is a map such that the map
![]() $(P,\ast ) \rightarrow (P,\ast ):\, x\mapsto m(x,\zeta (x)) $
is homotopic to the constant map, then the inverse
$(P,\ast ) \rightarrow (P,\ast ):\, x\mapsto m(x,\zeta (x)) $
is homotopic to the constant map, then the inverse
![]() $[f]^{-1}$
of
$[f]^{-1}$
of
![]() $[f]\in [(X,A),(P,\ast )]$
is given by
$[f]\in [(X,A),(P,\ast )]$
is given by
![]() $[\zeta \circ f]$
.
$[\zeta \circ f]$
.
Lemma 7.12. Suppose that
![]() $(X,A)$
is a locally compact Polish space and
$(X,A)$
is a locally compact Polish space and
![]() $(P,\ast ,m)$
is a polyhedral H-group. Any two maps
$(P,\ast ,m)$
is a polyhedral H-group. Any two maps
![]() $f,g:(X,A) \rightarrow (P,\ast )$
are weakly homotopic if and only if
$f,g:(X,A) \rightarrow (P,\ast )$
are weakly homotopic if and only if
![]() $ [f]\cdot [g]^{-1}\in [(X,A),(P,\ast )]_{\infty }$
.
$ [f]\cdot [g]^{-1}\in [(X,A),(P,\ast )]_{\infty }$
.
Proof. Begin by observing that the map
![]() $p_{n}:[(X,A),(P,\ast )]\rightarrow [(X_n,A_n),(P,\ast )]$
given by function restriction is a group homomorphism. By definition,
$p_{n}:[(X,A),(P,\ast )]\rightarrow [(X_n,A_n),(P,\ast )]$
given by function restriction is a group homomorphism. By definition,
![]() $[(X,A),(P,\ast )]_{\infty }$
is the intersection of
$[(X,A),(P,\ast )]_{\infty }$
is the intersection of
![]() $\{\mathrm {ker}(p _n)\mid n\in \mathbb {N}\}$
. Thus,
$\{\mathrm {ker}(p _n)\mid n\in \mathbb {N}\}$
. Thus,
![]() $ f\simeq _w g$
if and only if
$ f\simeq _w g$
if and only if
![]() $p _{n}([f]) =p_{n}([g])$
for every
$p _{n}([f]) =p_{n}([g])$
for every
![]() $n\in \mathbb {N}$
, if and only if
$n\in \mathbb {N}$
, if and only if
![]() $p_{n}([f]\cdot [g]^{-1}) =0=[\ast ]$
for every
$p_{n}([f]\cdot [g]^{-1}) =0=[\ast ]$
for every
![]() $n\in \mathbb {N}$
, if and only if
$n\in \mathbb {N}$
, if and only if
![]() $[f]\cdot [g]^{-1}\in [(X,A),(P,\ast )]_{\infty }$
.
$[f]\cdot [g]^{-1}\in [(X,A),(P,\ast )]_{\infty }$
.
Under the present assumptions,
![]() $[(X,A),(P,\ast )]$
is, by the foregoing lemmas, a definable group.
$[(X,A),(P,\ast )]$
is, by the foregoing lemmas, a definable group.
Theorem 7.13. Suppose that
![]() $(X,A)$
is a locally compact Polish space with cofiltration
$(X,A)$
is a locally compact Polish space with cofiltration
![]() $(X_n,A_n)_{n\in \mathbb {N}}$
and
$(X_n,A_n)_{n\in \mathbb {N}}$
and
![]() $(P,\ast ,m)$
is a polyhedral H-group. Then,
$(P,\ast ,m)$
is a polyhedral H-group. Then,
-
(1)
 $[(X,A),(P,\ast )] _{\infty }$
is a definable abelian group, naturally definably isomorphic to the group with a Polish cover
$[(X,A),(P,\ast )] _{\infty }$
is a definable abelian group, naturally definably isomorphic to the group with a Polish cover
 $\mathrm {lim}^{1}\,[\bar {\Sigma }(X_n,A_n),(P,\ast )]$
;
$\mathrm {lim}^{1}\,[\bar {\Sigma }(X_n,A_n),(P,\ast )]$
; -
(2)
 $[(X,A),(P,\ast )]$
is a definable group;
$[(X,A),(P,\ast )]$
is a definable group; -
(3)
 $[(X,A),(P,\ast )]_{\mathrm {w}}$
is a definable group, naturally definably isomorphic to the pro-countable Polish group
$[(X,A),(P,\ast )]_{\mathrm {w}}$
is a definable group, naturally definably isomorphic to the pro-countable Polish group
 $\mathrm {lim}\,[(X_n,A_n),(P,\ast )]$
.
$\mathrm {lim}\,[(X_n,A_n),(P,\ast )]$
.
Furthermore, these groups naturally array in the definable exact sequence of definable groups
Proof. (1) This just a particular instance of Theorem 7.11.
(2) Since the group operations on
![]() $[(X,A),(P,\ast )]$
are definable,
$[(X,A),(P,\ast )]$
are definable,
![]() $[(X,A),(P,\ast )]$
is a semidefinable group. Furthermore,
$[(X,A),(P,\ast )]$
is a semidefinable group. Furthermore,
![]() $[(X,A),(P,\ast )]_{\infty }$
is a definable subgroup of
$[(X,A),(P,\ast )]_{\infty }$
is a definable subgroup of
![]() $[(X,A),(P,\ast )]$
by (1). The conclusion that
$[(X,A),(P,\ast )]$
by (1). The conclusion that
![]() $[(X,A),(P,\ast )]$
is a definable set now follows from Lemma 3.15 and Corollary 7.6.
$[(X,A),(P,\ast )]$
is a definable set now follows from Lemma 3.15 and Corollary 7.6.
(3) It suffices to notice that, under our assumptions, the natural definable bijection in Proposition 7.7 is a group homomorphism.
The last assertion now follows immediately from definitions.
7.6. A definable exact sequence decomposition of Čech cohomology
By Theorem 5.7 (or its version for
![]() $\mathsf {LCP}$
pairs), we may identify the Čech cohomology groups
$\mathsf {LCP}$
pairs), we may identify the Čech cohomology groups
![]() $\mathrm {H}^{q}(X,A;G)$
with the representable, or homotopical, cohomology groups
$\mathrm {H}^{q}(X,A;G)$
with the representable, or homotopical, cohomology groups
![]() $[(X,A),(K( G,q) ,\ast )]$
. We may then consider its definable subgroup
$[(X,A),(K( G,q) ,\ast )]$
. We may then consider its definable subgroup
which we term the asymptotic cohomology group. We may also consider the weak cohomology group
Also by Theorem 7.13, we have a natural definable exact sequence
More precisely, Theorem 7.13 gives us the following, which shows that this exact sequence is naturally isomorphic to the exact sequence (26) above.
Proposition 7.14. Suppose that q is a positive integer, G is a countable discrete abelian group, and
![]() $(X,A)$
is a locally compact pair with cofiltration
$(X,A)$
is a locally compact pair with cofiltration
![]() $(X_n,A_n)_{n\in \mathbb {N}}$
. Then,
$(X_n,A_n)_{n\in \mathbb {N}}$
. Then,
-
(1)
 $\mathrm {H}_{\infty }^{q}(X,A;G) $
is naturally definably isomorphic to
$\mathrm {H}_{\infty }^{q}(X,A;G) $
is naturally definably isomorphic to  $$ \begin{align*} \mathrm{lim}^1\,\mathrm{H}^q(\bar{\Sigma}(X_n,A_n),\ast;G) \cong \mathrm{lim}^1\,\mathrm{H}^{q-1}(X_n,A_n;G); \end{align*} $$
$$ \begin{align*} \mathrm{lim}^1\,\mathrm{H}^q(\bar{\Sigma}(X_n,A_n),\ast;G) \cong \mathrm{lim}^1\,\mathrm{H}^{q-1}(X_n,A_n;G); \end{align*} $$
-
(2)
 $\mathrm {H}_{\mathrm {w}}^{q}(X,A;G)$
is naturally definably isomorphic to the pro-countable abelian group
$\mathrm {H}_{\mathrm {w}}^{q}(X,A;G)$
is naturally definably isomorphic to the pro-countable abelian group  $$ \begin{align*} \mathrm{lim}\,\mathrm{H}^{q}(X_n,A_n;G). \end{align*} $$
$$ \begin{align*} \mathrm{lim}\,\mathrm{H}^{q}(X_n,A_n;G). \end{align*} $$
Proof. Only the isomorphism in item (1) requires comment; it follows from the sequence of definable isomorphisms
 $$ \begin{align*} \mathrm{H}^q(\bar{\Sigma}(X_n,A_n),\ast;G) & \cong [(\bar{\Sigma}(X_n,A_n),\ast),(K(G,q),\star)]\cong [(X_n,A_n),\Omega(K(G,q),\star)]\\ & \cong [(X_n,A_n),(K(G,q-1),\star)]\cong\mathrm{H}^{q-1}(X_n,A_n;G) \end{align*} $$
$$ \begin{align*} \mathrm{H}^q(\bar{\Sigma}(X_n,A_n),\ast;G) & \cong [(\bar{\Sigma}(X_n,A_n),\ast),(K(G,q),\star)]\cong [(X_n,A_n),\Omega(K(G,q),\star)]\\ & \cong [(X_n,A_n),(K(G,q-1),\star)]\cong\mathrm{H}^{q-1}(X_n,A_n;G) \end{align*} $$
of countable groups.
In [Reference Lupini52], this work’s second author showed that the map taking
![]() $(G,N)$
to the closure of
$(G,N)$
to the closure of
![]() $\{0\}$
in
$\{0\}$
in
![]() $G/N$
is functorial in the category
$G/N$
is functorial in the category
![]() $\mathsf {APC}$
of groups with an abelian Polish cover. More precisely, by the
$\mathsf {APC}$
of groups with an abelian Polish cover. More precisely, by the
![]() $\alpha =0$
case of [Reference Lupini52, Theorem 6.3], this is a subfunctor of the identity. Hence, by Proposition 7.9, the definable functor
$\alpha =0$
case of [Reference Lupini52, Theorem 6.3], this is a subfunctor of the identity. Hence, by Proposition 7.9, the definable functor
![]() $\mathrm {H}^q_{\infty }$
as well as its definable quotient
$\mathrm {H}^q_{\infty }$
as well as its definable quotient
![]() $\mathrm {H}^q/\mathrm {H}^q_{\infty }\cong \mathrm {H}^q_{\mathrm {w}}$
may each be definably recovered from the single definable functor
$\mathrm {H}^q/\mathrm {H}^q_{\infty }\cong \mathrm {H}^q_{\mathrm {w}}$
may each be definably recovered from the single definable functor
![]() $\mathrm {H}^q$
– facts we summarize in the following proposition.
$\mathrm {H}^q$
– facts we summarize in the following proposition.
Proposition 7.15. For any
![]() $q\geq 0$
and countable abelian group G, the definable functors
$q\geq 0$
and countable abelian group G, the definable functors
![]() $\mathrm {H}^q_\infty (-;G)$
and
$\mathrm {H}^q_\infty (-;G)$
and
![]() $\mathrm {H}^q_{\mathrm {w}}(-;G)$
each map
$\mathrm {H}^q_{\mathrm {w}}(-;G)$
each map
![]() $\mathsf {LCP}$
to
$\mathsf {LCP}$
to
![]() $\mathsf {APC}$
. Each of these, moreover, definably derives from the definable functor
$\mathsf {APC}$
. Each of these, moreover, definably derives from the definable functor
![]() $\mathrm {H}^q$
in the sense that the first is its postcomposition with a subfunctor of the identity, and the second is its postcomposition with that subfunctor’s cokernel.
$\mathrm {H}^q$
in the sense that the first is its postcomposition with a subfunctor of the identity, and the second is its postcomposition with that subfunctor’s cokernel.
7.7. Hopf’s Theorem
Čech cohomology is a main tool for the study and classification of maps up to homotopy. This is due to descriptions, like those above, of Čech cohomology groups as groups of homotopy classes of maps, whereby homotopy classification problems for maps between spaces may reduce to a corresponding problem for maps to Eilenberg–MacLane spaces.
One of the first such results was Hopf’s theorem for maps to spheres [Reference Hu37, Chapter VII, Theorem 11.5]. We cite it both for a quick application of our machinery and for use in the following section. Henceforth, we will omit notation of the cohomology coefficient group when
![]() $G=\mathbb {Z}$
. Viewing the n -dimensional sphere
$G=\mathbb {Z}$
. Viewing the n -dimensional sphere
![]() $S^{n}$
as a pointed space, we have that
$S^{n}$
as a pointed space, we have that
![]() $\mathrm {H}^{n}(S^{n},\star ) =\mathbb {Z}$
. One may choose, as generator of this group, an
$\mathrm {H}^{n}(S^{n},\star ) =\mathbb {Z}$
. One may choose, as generator of this group, an
![]() $[\iota ]\in [(S^{n},\star ),(K(\mathbb {Z},n),\ast )]$
such that
$[\iota ]\in [(S^{n},\star ),(K(\mathbb {Z},n),\ast )]$
such that
![]() $\iota $
is an inclusion of
$\iota $
is an inclusion of
![]() $(S^{n},\star )$
as a closed subspace of
$(S^{n},\star )$
as a closed subspace of
![]() $(K(\mathbb {Z},n),\ast )$
; see [Reference Arkowitz2, Theorem 2.5.14]. Any map f from a locally compact pair
$(K(\mathbb {Z},n),\ast )$
; see [Reference Arkowitz2, Theorem 2.5.14]. Any map f from a locally compact pair
![]() $(X,A)$
to
$(X,A)$
to
![]() $(S^n,\star )$
then determines a map
$(S^n,\star )$
then determines a map
![]() $\iota \circ f:(X,A) \rightarrow ( K(\mathbb {Z},n),\ast ) $
, a determination amounting to a definable function
$\iota \circ f:(X,A) \rightarrow ( K(\mathbb {Z},n),\ast ) $
, a determination amounting to a definable function
![]() $[(X,A),(S^n,\star )]\rightarrow \mathrm {H}^{n}(X,A)$
.
$[(X,A),(S^n,\star )]\rightarrow \mathrm {H}^{n}(X,A)$
.
Theorem 7.16 (Hopf).
Fix
![]() $n\geq 1$
. For every polyhedral pair
$n\geq 1$
. For every polyhedral pair
![]() $(P,Q)$
satisfying
$(P,Q)$
satisfying
![]() $\mathrm {H}^q(P,Q) =0$
for
$\mathrm {H}^q(P,Q) =0$
for
![]() $q>n$
, the definable function
$q>n$
, the definable function
![]() $[(P,Q),(S^{n},\star )]\rightarrow \mathrm {H}^n(P,Q) $
is a bijection.
$[(P,Q),(S^{n},\star )]\rightarrow \mathrm {H}^n(P,Q) $
is a bijection.
Corollary 7.17. Under the assumptions of Theorem 7.16,
![]() $[(P,Q),(S^{n},\star )]$
is a pointed definable set.
$[(P,Q),(S^{n},\star )]$
is a pointed definable set.
Proof. This amounts to saying that the relation of homotopy for maps
![]() $(P,Q) \rightarrow (S^n,\star )$
is Borel and idealistic. This relation is idealistic by Theorem 4.15. As the relation of homotopy for maps
$(P,Q) \rightarrow (S^n,\star )$
is Borel and idealistic. This relation is idealistic by Theorem 4.15. As the relation of homotopy for maps
![]() $(P,Q)\rightarrow (K( \mathbb {Z},n),\ast )$
is Borel by Theorem 7.13, it follows from Theorem 7.16 that the relation of homotopy for maps
$(P,Q)\rightarrow (K( \mathbb {Z},n),\ast )$
is Borel by Theorem 7.13, it follows from Theorem 7.16 that the relation of homotopy for maps
![]() $(P,Q)\rightarrow (S^n,\star )$
is Borel as well.
$(P,Q)\rightarrow (S^n,\star )$
is Borel as well.
8. The Borsuk-Eilenberg problem and the definable cohomology of mapping telescopes
This section records several sample applications of the definable cohomology functors and decomposition theorems of the preceding pages. We begin by reviewing the core construction in these applications – namely, the mapping telescope or homotopy colimit of a sequence of maps
![]() $\langle f_n:X_n\to X_{n+1}\mid n\in \mathbb {N}\rangle $
of topological spaces. The results of this section reconnect with those of [Reference Bergfalk and Lupini9], from which, together with Proposition 8.8, it will follow almost immediately that definable Čech cohomology is, in strong contrast to classical Čech cohomology, a complete homotopy invariant both of mapping telescopes of d-tori and of d-spheres. Equally immediate from the machinery we have developed are solutions to the natural generalizations of the Borsuk-Eilenberg problem of classifying the maps from the complement of a canonically embedded p-adic solenoid
$\langle f_n:X_n\to X_{n+1}\mid n\in \mathbb {N}\rangle $
of topological spaces. The results of this section reconnect with those of [Reference Bergfalk and Lupini9], from which, together with Proposition 8.8, it will follow almost immediately that definable Čech cohomology is, in strong contrast to classical Čech cohomology, a complete homotopy invariant both of mapping telescopes of d-tori and of d-spheres. Equally immediate from the machinery we have developed are solutions to the natural generalizations of the Borsuk-Eilenberg problem of classifying the maps from the complement of a canonically embedded p-adic solenoid
![]() $\Sigma _p\subset S^3$
to a
$\Sigma _p\subset S^3$
to a
![]() $2$
-sphere. This problem played a critical role in the development of multiple areas of mathematics, in historical senses that we briefly pause to review. We show that definable cohomology is a complete invariant of the homotopy classes of maps to
$2$
-sphere. This problem played a critical role in the development of multiple areas of mathematics, in historical senses that we briefly pause to review. We show that definable cohomology is a complete invariant of the homotopy classes of maps to
![]() $S^{d+1}$
from mapping telescopes of d-spheres. We conclude with an analysis of the problems of classifying those maps up to homotopy, as well as up to homotopy modulo a homotopy equivalence of their domain. Put differently, we study the problem of equivariant classification; the affinity of the associated quotients with the structure sets of manifold theory should be noted as well [Reference Ramesh73, Definition 2.1]. We describe lower bounds for the Borel complexity degrees of these problems and the existence of an infinite antichain of complexity degrees among them, and we show also that this complexity rises with dimension.
$S^{d+1}$
from mapping telescopes of d-spheres. We conclude with an analysis of the problems of classifying those maps up to homotopy, as well as up to homotopy modulo a homotopy equivalence of their domain. Put differently, we study the problem of equivariant classification; the affinity of the associated quotients with the structure sets of manifold theory should be noted as well [Reference Ramesh73, Definition 2.1]. We describe lower bounds for the Borel complexity degrees of these problems and the existence of an infinite antichain of complexity degrees among them, and we show also that this complexity rises with dimension.
In subsections 8.1 and 8.2, we conduct our review of homotopy colimits in the unbased category
![]() $\mathsf {LC}$
. This is solely for conceptual clarity; the discussion applies with only superficial modifications to the context of
$\mathsf {LC}$
. This is solely for conceptual clarity; the discussion applies with only superficial modifications to the context of
![]() $\mathsf {LC}_*$
, as readers may easily verify. Results in which the homotopy bracket figures thereafter will, by Corollary 6.6, admit interpretation in either category, as we will note below.
$\mathsf {LC}_*$
, as readers may easily verify. Results in which the homotopy bracket figures thereafter will, by Corollary 6.6, admit interpretation in either category, as we will note below.
8.1. Colimits and homotopy colimits
First, recall the notion of a colimit of a diagram in a category
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Definition 8.1 [Reference Margolis57].
Let
![]() $\mathcal {J}$
be a small category; as above, write
$\mathcal {J}$
be a small category; as above, write
![]() $\mathcal {J}(W,X)$
for the collection of morphisms in
$\mathcal {J}(W,X)$
for the collection of morphisms in
![]() $\mathcal {J}$
from W to X. By a diagram of shape
$\mathcal {J}$
from W to X. By a diagram of shape
![]() $\mathcal {J}$
in a category
$\mathcal {J}$
in a category
![]() $\mathcal {C}$
, we simply mean a functor
$\mathcal {C}$
, we simply mean a functor
![]() $F:\mathcal {J}\to \mathcal {C}$
. For any such diagram a collection of morphisms,
$F:\mathcal {J}\to \mathcal {C}$
. For any such diagram a collection of morphisms,
![]() $\{f_W:F(W)\to Y \mid W\in \mathrm {obj}(\mathcal {J})\}$
is coherent if
$\{f_W:F(W)\to Y \mid W\in \mathrm {obj}(\mathcal {J})\}$
is coherent if
![]() $f_W=f_X\circ F(g)$
for all
$f_W=f_X\circ F(g)$
for all
![]() $g\in \mathcal {J}(W,X)$
. An object Y of
$g\in \mathcal {J}(W,X)$
. An object Y of
![]() $\mathcal {C}$
is a colimit of a diagram F if it admits a coherent collection of morphisms
$\mathcal {C}$
is a colimit of a diagram F if it admits a coherent collection of morphisms
![]() $\{f_W:F(W)\to Y\mid W\in \mathrm {obj}(\mathcal {J})\}$
such that for any coherent collection
$\{f_W:F(W)\to Y\mid W\in \mathrm {obj}(\mathcal {J})\}$
such that for any coherent collection
![]() $\{g_W:F(W)\to Z\mid W\in \mathrm {obj}(\mathcal {J})\}$
of morphisms to any object Z of
$\{g_W:F(W)\to Z\mid W\in \mathrm {obj}(\mathcal {J})\}$
of morphisms to any object Z of
![]() $\mathcal {C}$
, there exists a unique
$\mathcal {C}$
, there exists a unique
![]() $h:Y\to Z$
such that
$h:Y\to Z$
such that
![]() $g_W=h\circ f_W$
for all
$g_W=h\circ f_W$
for all
![]() $W\in \mathrm {obj}(\mathcal {J})$
. A weak colimit of the diagram F is a Y satisfying these same conditions, but without the requirement that all such maps
$W\in \mathrm {obj}(\mathcal {J})$
. A weak colimit of the diagram F is a Y satisfying these same conditions, but without the requirement that all such maps
![]() $h:Y\to Z$
be unique.
$h:Y\to Z$
be unique.
In more concrete contexts, colimits admit more concrete descriptions; for example, the colimit of a pushout diagram of topological spaces (i.e., of a diagram of the form
is
where
![]() $\sim $
is the equivalence relation generated by
$\sim $
is the equivalence relation generated by
![]() $\{f(x)\sim g(x)\mid x\in X\}$
. This brings us to a standard motivating example (see [Reference Dugger23]): consider the diagrams
$\{f(x)\sim g(x)\mid x\in X\}$
. This brings us to a standard motivating example (see [Reference Dugger23]): consider the diagrams
and
in which, as usual,
![]() $*$
denotes the one-point space, and the only nontrivial map is the inclusion into
$*$
denotes the one-point space, and the only nontrivial map is the inclusion into
![]() $D^n$
of its boundary
$D^n$
of its boundary
![]() $\partial D^n\cong S^{n-1}$
. What interests us is the following: each of the corresponding terms of (29) and (30) are homotopy equivalent; the colimits of (29) and (30), however, are not (the latter are homeomorphic to
$\partial D^n\cong S^{n-1}$
. What interests us is the following: each of the corresponding terms of (29) and (30) are homotopy equivalent; the colimits of (29) and (30), however, are not (the latter are homeomorphic to
![]() $S^n$
and
$S^n$
and
![]() $*$
, respectively, as the reader may verify). More formally, what these diagrams together show is that colimits in the topological category are not, in general, homotopy invariant; indeed, as the example might suggest, colimits in the category
$*$
, respectively, as the reader may verify). More formally, what these diagrams together show is that colimits in the topological category are not, in general, homotopy invariant; indeed, as the example might suggest, colimits in the category
![]() $\mathsf {Ho}(\mathsf {LC})$
may even fail altogether to exist (see [Reference Strom84, pp. 245–246]).
$\mathsf {Ho}(\mathsf {LC})$
may even fail altogether to exist (see [Reference Strom84, pp. 245–246]).
What do more generally exist, however, are homotopy colimits; these are particular representatives of weak colimits in homotopy categories in the sense of Definition 8.1. We follow [Reference May and Ponto59, 2] in foregoing their rather abstract general definition, focusing instead on their construction in the contexts which are our immediate interest; their idea, in the process, will grow clear. The first of these is pushout diagrams of topological spaces, as in (27), (29) and (30) above. The homotopy colimit
![]() $\mathrm {hocolim}\, D$
of any diagram D of spaces of the form (27) is
$\mathrm {hocolim}\, D$
of any diagram D of spaces of the form (27) is
where the equivalence relation
![]() $\sim $
is that given by the identifications
$\sim $
is that given by the identifications
![]() $f(x)\sim (x,0)$
and
$f(x)\sim (x,0)$
and
![]() $(x,1)\sim g(x)$
for each
$(x,1)\sim g(x)$
for each
![]() $x\in X$
. Observe that this construction resolves the discord of (29) and (30) above, in the sense that the homotopy colimits of these two diagrams are, indeed, homotopy equivalent. Just as we would hope, this holds more generally for any two naturally homotopy equivalent pushout diagrams of polyhedra (and even for naturally weakly homotopy equivalent pushout diagrams of arbitrary topological spaces; see [Reference Dugger23, p. 5]). We record in the lemma below the special instance of this fact which we will need.
$x\in X$
. Observe that this construction resolves the discord of (29) and (30) above, in the sense that the homotopy colimits of these two diagrams are, indeed, homotopy equivalent. Just as we would hope, this holds more generally for any two naturally homotopy equivalent pushout diagrams of polyhedra (and even for naturally weakly homotopy equivalent pushout diagrams of arbitrary topological spaces; see [Reference Dugger23, p. 5]). We record in the lemma below the special instance of this fact which we will need.
Observe first, though, how many of homotopy theory’s most fundamental constructions arise in the above manner: the homotopy colimits of the diagrams
are the suspension
![]() $SX$
of X and the mapping cone
$SX$
of X and the mapping cone
![]() $C(g)$
and mapping cylinder
$C(g)$
and mapping cylinder
![]() $M_g$
of the map
$M_g$
of the map
![]() $g:X\to Y$
, respectively. The last of these is the basic building block of the homotopy colimits of towers of topological spaces, the so-called mapping telescopes at the center of our applications below. Note also the natural identification of the homotopy colimit of (27) with two mapping cylinders
$g:X\to Y$
, respectively. The last of these is the basic building block of the homotopy colimits of towers of topological spaces, the so-called mapping telescopes at the center of our applications below. Note also the natural identification of the homotopy colimit of (27) with two mapping cylinders
![]() $M_f$
and
$M_f$
and
![]() $M_g$
glued together along their respective copies of X. Hence, to show that the homotopy type of the homotopy colimit of (27) depends only upon the homotopy classes of the maps f and g, it suffices to observe the following.
$M_g$
glued together along their respective copies of X. Hence, to show that the homotopy type of the homotopy colimit of (27) depends only upon the homotopy classes of the maps f and g, it suffices to observe the following.
Lemma 8.2. For any two homotopic maps
![]() $g,h:X\to Y$
, the mapping cylinders
$g,h:X\to Y$
, the mapping cylinders
![]() $M_g$
and
$M_g$
and
![]() $M_h$
are homotopy equivalent.
$M_h$
are homotopy equivalent.
The proof is, at the referee’s suggestion, left to the reader, but it is worth lingering over its essential mechanism: in contrast with colimits, homotopy colimits like (31) identify spaces only ‘up to a homotopy factor’ of
![]() $\times I$
; put differently, the
$\times I$
; put differently, the
![]() $\times I$
component in homotopy colimits supplies a space ‘within which’ to realize homotopies between various connecting maps. Each of these components also readily collapses, furnishing a canonical map from the homotopy colimit of a diagram to its colimit, as is easily seen in the case of (31) and (28), for example. The deformation retract of
$\times I$
component in homotopy colimits supplies a space ‘within which’ to realize homotopies between various connecting maps. Each of these components also readily collapses, furnishing a canonical map from the homotopy colimit of a diagram to its colimit, as is easily seen in the case of (31) and (28), for example. The deformation retract of
![]() $M_g$
to its target space Y is a special case. With these recognitions in place, we turn our attention to mapping telescopes.
$M_g$
to its target space Y is a special case. With these recognitions in place, we turn our attention to mapping telescopes.
8.2. Mapping telescopes
The following construction may first have appeared in Milnor’s [Reference Milnor63] which, not coincidentally, was a seminal first appearance of the
![]() $\mathrm {lim}^1$
functor within algebraic topology as well. In general, though, this section’s results have the status of folklore.
$\mathrm {lim}^1$
functor within algebraic topology as well. In general, though, this section’s results have the status of folklore.
Definition 8.3. The mapping telescope associated to a diagram of the form
is the space
where
![]() $\sim $
is the equivalence relation generated by the identifications
$\sim $
is the equivalence relation generated by the identifications
![]() $(x,n+1) \sim ( \eta _n(x),n+1)$
for each
$(x,n+1) \sim ( \eta _n(x),n+1)$
for each
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $x\in X_n$
. This space is the homotopy colimit of the diagram
$x\in X_n$
. This space is the homotopy colimit of the diagram
![]() $\mathbf {X}$
and henceforth will accordingly be denoted
$\mathbf {X}$
and henceforth will accordingly be denoted
![]() $\mathrm {hocolim}\,\mathbf {X}$
[Reference May and Ponto59]. We will sometimes refer to diagrams of the form (32) as towers or inductive sequences below.
$\mathrm {hocolim}\,\mathbf {X}$
[Reference May and Ponto59]. We will sometimes refer to diagrams of the form (32) as towers or inductive sequences below.
Clearly, the space (33) may equivalently be viewed as an assemblage of mapping cylinders in the following way:
where
![]() $\sim $
identifies the copy of
$\sim $
identifies the copy of
![]() $X_n$
in
$X_n$
in
![]() $M_{\eta _{n-1}}$
with
$M_{\eta _{n-1}}$
with
![]() $X_n\times \{0\}$
in
$X_n\times \{0\}$
in
![]() $M_{\eta _n}$
, for each
$M_{\eta _n}$
, for each
![]() $n>0$
. From this observation, the following lemma is immediate (what we are proving is simply an aspect of the fact that mapping telescopes are homotopy colimits which we will later invoke).
$n>0$
. From this observation, the following lemma is immediate (what we are proving is simply an aspect of the fact that mapping telescopes are homotopy colimits which we will later invoke).
Lemma 8.4. If
![]() $\left ( X_{n}\right )_{n\in \mathbb {N}}$
is a sequence of topological spaces and
$\left ( X_{n}\right )_{n\in \mathbb {N}}$
is a sequence of topological spaces and
![]() $\eta _{n },\eta ^{\prime }_{n}:X_{n}\rightarrow X_{n+1}$
are homotopic for each
$\eta _{n },\eta ^{\prime }_{n}:X_{n}\rightarrow X_{n+1}$
are homotopic for each
![]() $n\in \mathbb {N}$
, then the corresponding mapping telescopes
$n\in \mathbb {N}$
, then the corresponding mapping telescopes
![]() $\mathrm {hocolim}\,( X_{n},\eta _n) $
and
$\mathrm {hocolim}\,( X_{n},\eta _n) $
and
![]() $\mathrm {hocolim}\,( X_{n},\eta ^{\prime }_n) $
are homotopy equivalent.
$\mathrm {hocolim}\,( X_{n},\eta ^{\prime }_n) $
are homotopy equivalent.
Proof. Observe simply that the homotopy equivalences (and the witnessing homotopies) between each
![]() $M_{\eta _n}$
and
$M_{\eta _n}$
and
![]() $M_{\eta ^{\prime }_n}$
are compatible with the identifications of (34), and consequently assemble to define homotopy equivalences of
$M_{\eta ^{\prime }_n}$
are compatible with the identifications of (34), and consequently assemble to define homotopy equivalences of
![]() $\mathrm {hocolim}\,( X_{n},\eta _n) $
and
$\mathrm {hocolim}\,( X_{n},\eta _n) $
and
![]() $\mathrm {hocolim}\,( X_{n},\eta ^{\prime }_n) $
, as desired.
$\mathrm {hocolim}\,( X_{n},\eta ^{\prime }_n) $
, as desired.
Corollary 8.5. If
![]() $\mathbf {X}$
is an inductive sequence of polyhedra, then
$\mathbf {X}$
is an inductive sequence of polyhedra, then
![]() $\mathrm {hocolim}\,\mathbf {X}$
is homotopy equivalent to a polyhedron.
$\mathrm {hocolim}\,\mathbf {X}$
is homotopy equivalent to a polyhedron.
Proof. This is immediate from Proposition 8.4, the Simplicial Approximation Theorem and the fact that mapping cylinders of simplicial maps are polyhedra.
We will require two more basic facts before proceeding. For the first, recall the previous section’s reference to a canonical map
![]() $\mathrm {hocolim}\,\mathbf {X}\to \mathrm {colim}\,\mathbf {X}$
. Under the conditions of the following lemma, this is a homotopy equivalence.
$\mathrm {hocolim}\,\mathbf {X}\to \mathrm {colim}\,\mathbf {X}$
. Under the conditions of the following lemma, this is a homotopy equivalence.
Lemma 8.6. The homotopy colimit of an inductive sequence
![]() $\mathbf {X}$
of embeddings of compact Polish spaces is homotopy equivalent to
$\mathbf {X}$
of embeddings of compact Polish spaces is homotopy equivalent to
![]() $\mathrm {colim}\,\mathbf {X}$
.
$\mathrm {colim}\,\mathbf {X}$
.
Proof. Let
![]() $Y=\mathrm {colim}\,\mathbf {X}$
. For each
$Y=\mathrm {colim}\,\mathbf {X}$
. For each
![]() $n\in \mathbb {N} $
, we have a canonical embedding
$n\in \mathbb {N} $
, we have a canonical embedding
![]() $\psi _n:X_{n}\rightarrow Y$
with range a compact
$\psi _n:X_{n}\rightarrow Y$
with range a compact
![]() $Y_{n}\subseteq Y$
. By passing to a subsequence, we may assume that
$Y_{n}\subseteq Y$
. By passing to a subsequence, we may assume that
![]() $ ( Y_{n}) _{n\in \mathbb {N}}$
is a sequence of compact subsets of Y such that
$ ( Y_{n}) _{n\in \mathbb {N}}$
is a sequence of compact subsets of Y such that
![]() $Y_{n}\subseteq \mathrm {int}( Y_{n+1}) $
for every
$Y_{n}\subseteq \mathrm {int}( Y_{n+1}) $
for every
![]() $ n\in \mathbb {N} $
, and Y is the union of
$ n\in \mathbb {N} $
, and Y is the union of
![]() $\{ Y_{n}\mid n\in \mathbb {N} \} $
(if we cannot, then
$\{ Y_{n}\mid n\in \mathbb {N} \} $
(if we cannot, then
![]() $(X_n)_{n\in \mathbb {N}}$
eventually stabilizes, in which case the conclusion of the lemma is clear). Let also
$(X_n)_{n\in \mathbb {N}}$
eventually stabilizes, in which case the conclusion of the lemma is clear). Let also
![]() $Y_{-1}=\varnothing $
. For each
$Y_{-1}=\varnothing $
. For each
![]() $n\in \mathbb {N}$
, fix a continuous function
$n\in \mathbb {N}$
, fix a continuous function
![]() $\lambda _{n}:Y_{n}\rightarrow [ n,n+1] $
such that
$\lambda _{n}:Y_{n}\rightarrow [ n,n+1] $
such that
![]() $\lambda _{n}[Y_{n-1}]\subseteq \{n\}$
and
$\lambda _{n}[Y_{n-1}]\subseteq \{n\}$
and
![]() $\lambda _{n}[\partial Y_{n}]=\{n+1\}$
. Define the function
$\lambda _{n}[\partial Y_{n}]=\{n+1\}$
. Define the function
![]() $\lambda :Y\rightarrow [ 0,\infty )$
by setting
$\lambda :Y\rightarrow [ 0,\infty )$
by setting
![]() $\lambda ( x) =\lambda _n( x) $
for all
$\lambda ( x) =\lambda _n( x) $
for all
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $x\in Y_{n}\setminus Y_{n-1}$
, and let
$x\in Y_{n}\setminus Y_{n-1}$
, and let
and
Notice that L is a subset of B and that
-
• L is a deformation retract of B, via the map
 $\left ( x,t\right ) \mapsto ( x,\lambda (x)) $
, and
$\left ( x,t\right ) \mapsto ( x,\lambda (x)) $
, and -
• Y is homeomorphic to L, via the map
 $Y\rightarrow L$
,
$Y\rightarrow L$
,
 $x\mapsto \left ( x,\lambda \left ( x\right ) \right ) $
, and
$x\mapsto \left ( x,\lambda \left ( x\right ) \right ) $
, and -
•
 $\mathrm {hocolim}\,\mathbf {X}$
is homeomorphic to B, via the map
$\mathrm {hocolim}\,\mathbf {X}$
is homeomorphic to B, via the map
 $\mathrm {hocolim}\,\mathbf {X}\rightarrow B$
,
$\mathrm {hocolim}\,\mathbf {X}\rightarrow B$
,
 $ \langle x,t\rangle \mapsto ( \psi _{n}( x) ,t) $
for all
$ \langle x,t\rangle \mapsto ( \psi _{n}( x) ,t) $
for all
 $n\in \mathbb {N} $
,
$n\in \mathbb {N} $
,
 $n\leq t\leq n+1$
and
$n\leq t\leq n+1$
and
 $x\in X_{n}$
.
$x\in X_{n}$
.
This concludes the proof.
The last of the mapping telescope facts we will collect was tacitly invoked in the ‘passage to a subsequence” step of the above argument; namely, it is the following:
Proposition 8.7. The mapping telescope construction determines a functor from the category
![]() $\mathsf {Ind}_{\omega }( \mathsf {C}) $
of inductive sequences of compact Polish spaces to the homotopy category
$\mathsf {Ind}_{\omega }( \mathsf {C}) $
of inductive sequences of compact Polish spaces to the homotopy category
![]() $\mathsf {Ho}(\mathsf {LC}) $
of locally compact Polish spaces.
$\mathsf {Ho}(\mathsf {LC}) $
of locally compact Polish spaces.
See again Section 7.1 for the definition of
![]() $\mathsf {Ind}_{\omega }( \mathsf {C}) $
.
$\mathsf {Ind}_{\omega }( \mathsf {C}) $
.
Proof. Suppose that
![]() $\mathbf {X}=\left ( X_{n }\right ) _{n\in \mathbb {N}}$
and
$\mathbf {X}=\left ( X_{n }\right ) _{n\in \mathbb {N}}$
and
![]() $\mathbf {Y}=\left ( Y_{n}\right ) _{n\in \mathbb {N}}$
are inductive sequences of compact spaces and
$\mathbf {Y}=\left ( Y_{n}\right ) _{n\in \mathbb {N}}$
are inductive sequences of compact spaces and
![]() $( \ell _{k},f_{k})_{k\in \mathbb {N}}$
represents a morphism from
$( \ell _{k},f_{k})_{k\in \mathbb {N}}$
represents a morphism from
![]() $ \mathbf {X}$
to
$ \mathbf {X}$
to
![]() $\mathbf {Y}$
. We define the corresponding map
$\mathbf {Y}$
. We define the corresponding map
![]() $f=\mathrm {hocolim}\left ( \ell _{k},f_{k}\right ) :\mathrm {hocolim}\,\mathbf {X}\rightarrow \mathrm {hocolim}\,\mathbf {Y}$
as follows. We denote the constituent maps
$f=\mathrm {hocolim}\left ( \ell _{k},f_{k}\right ) :\mathrm {hocolim}\,\mathbf {X}\rightarrow \mathrm {hocolim}\,\mathbf {Y}$
as follows. We denote the constituent maps
![]() $Y_k\to Y_\ell $
of
$Y_k\to Y_\ell $
of
![]() $\mathbf {Y}$
by
$\mathbf {Y}$
by
![]() $\eta _{(k,\ell )}$
and let
$\eta _{(k,\ell )}$
and let
![]() $d_{k}=\ell _{k+1}-\ell _{k}$
for
$d_{k}=\ell _{k+1}-\ell _{k}$
for
![]() $k\in \mathbb {N}$
. For
$k\in \mathbb {N}$
. For
![]() $k\in \mathbb {N}$
and
$k\in \mathbb {N}$
and
![]() $x\in X_{k}$
and
$x\in X_{k}$
and
![]() $s\in [ 0,1]$
, let
$s\in [ 0,1]$
, let
where we write
![]() $\langle \eta _{\left (\ell ,t \right ) }( y) ,t\rangle $
for
$\langle \eta _{\left (\ell ,t \right ) }( y) ,t\rangle $
for
![]() $\langle \eta _{\left (\ell ,n \right ) }( y) ,t\rangle $
when t is in
$\langle \eta _{\left (\ell ,n \right ) }( y) ,t\rangle $
when t is in
![]() $[n,n+1] $
and y is in
$[n,n+1] $
and y is in
![]() $Y_{n}$
. It is easy to see that this gives a well-defined continuous function
$Y_{n}$
. It is easy to see that this gives a well-defined continuous function
![]() $\mathrm {hocolim}\,\mathbf {X}\rightarrow \mathrm {hocolim}\,\mathbf {Y}$
.
$\mathrm {hocolim}\,\mathbf {X}\rightarrow \mathrm {hocolim}\,\mathbf {Y}$
.
We now show that if
![]() $\left ( \ell _{k},f_{ k}\right ) _{k\in \mathbb {N}}$
and
$\left ( \ell _{k},f_{ k}\right ) _{k\in \mathbb {N}}$
and
![]() $(\ell _{k}^{\prime },f_{k }^{\prime })_{k\in \mathbb {N}}$
represent the same morphism from
$(\ell _{k}^{\prime },f_{k }^{\prime })_{k\in \mathbb {N}}$
represent the same morphism from
![]() $\mathbf {X}$
to
$\mathbf {X}$
to
![]() $\mathbf {Y }$
, then
$\mathbf {Y }$
, then
![]() $f=\mathrm {hocolim}\,( \ell _{k},f_{k}) $
and
$f=\mathrm {hocolim}\,( \ell _{k},f_{k}) $
and
![]() $f'=\mathrm {hocolim}\,( \ell ^{\prime }_{k},f^{\prime }_{k}) $
are homotopic maps
$f'=\mathrm {hocolim}\,( \ell ^{\prime }_{k},f^{\prime }_{k}) $
are homotopic maps
![]() $\mathrm {hocolim}\,\mathbf {X}\rightarrow \mathrm {hocolim}\,\mathbf {Y}$
. By definition, under these assumptions, there exists an increasing sequence
$\mathrm {hocolim}\,\mathbf {X}\rightarrow \mathrm {hocolim}\,\mathbf {Y}$
. By definition, under these assumptions, there exists an increasing sequence
![]() $\left ( \ell _{k}^{\prime \prime }\right ) _{k\in \mathbb {N}}$
such that
$\left ( \ell _{k}^{\prime \prime }\right ) _{k\in \mathbb {N}}$
such that
![]() $\max \{\ell _{k},\ell _{k}^{\prime }\}\leq \ell _{k}^{\prime \prime }$
and
$\max \{\ell _{k},\ell _{k}^{\prime }\}\leq \ell _{k}^{\prime \prime }$
and
![]() $\eta _{(\ell _{k},\ell ^{\prime \prime }_{k})}f_{k}=\eta _{\left ( \ell _{k}^{\prime },\ell ^{\prime \prime }_{k}\right ) }f_{k}^{\prime }$
for every
$\eta _{(\ell _{k},\ell ^{\prime \prime }_{k})}f_{k}=\eta _{\left ( \ell _{k}^{\prime },\ell ^{\prime \prime }_{k}\right ) }f_{k}^{\prime }$
for every
![]() $k\in \mathbb {N}$
. Hence, by the transitivity of the homotopy relation, it suffices to consider the case when
$k\in \mathbb {N}$
. Hence, by the transitivity of the homotopy relation, it suffices to consider the case when
![]() $\ell _{k}\leq \ell _{k}^{\prime }$
and
$\ell _{k}\leq \ell _{k}^{\prime }$
and
![]() $f_{k}^{\prime }=\eta _{\left ( \ell _{k},\ell ' _{k}\right ) }f_{k}$
for every
$f_{k}^{\prime }=\eta _{\left ( \ell _{k},\ell ' _{k}\right ) }f_{k}$
for every
![]() $k\in \mathbb {N}$
. Again, let
$k\in \mathbb {N}$
. Again, let
![]() $d_{k}=\ell _{k+1}-\ell _{k}$
and
$d_{k}=\ell _{k+1}-\ell _{k}$
and
![]() $d_{k}^{\prime }=\ell _{k+1}^{\prime }-\ell _{k}^{\prime }$
for all
$d_{k}^{\prime }=\ell _{k+1}^{\prime }-\ell _{k}^{\prime }$
for all
![]() $k\in \mathbb {N}$
. For all such k and
$k\in \mathbb {N}$
. For all such k and
![]() $ x\in X_{k}$
and
$ x\in X_{k}$
and
![]() $s\in \left [ 0,1\right ] $
, we then have
$s\in \left [ 0,1\right ] $
, we then have
and
We may then define a homotopy
![]() $h:f\Rightarrow f^{\prime }$
by setting
$h:f\Rightarrow f^{\prime }$
by setting
This shows that the homotopy class of
![]() $\mathrm {hocolim}\,( \ell _{k},f_{k}) $
does not depend on the choice of representative
$\mathrm {hocolim}\,( \ell _{k},f_{k}) $
does not depend on the choice of representative
![]() $(\ell _k, f_f)$
of a morphism from
$(\ell _k, f_f)$
of a morphism from
![]() $\mathbf {X}$
to
$\mathbf {X}$
to
![]() $\mathbf {Y}$
. Thus, given an
$\mathbf {Y}$
. Thus, given an
![]() $\mathsf {Ind}_\omega $
-morphism
$\mathsf {Ind}_\omega $
-morphism
![]() $ [(\ell _k,f_k)]$
from
$ [(\ell _k,f_k)]$
from
![]() $\mathbf {X}$
to
$\mathbf {X}$
to
![]() $\mathbf {Y}$
, we may let
$\mathbf {Y}$
, we may let
![]() $\mathrm {hocolim}\,[( \ell _{k},f_{k})]$
be the homotopy class of
$\mathrm {hocolim}\,[( \ell _{k},f_{k})]$
be the homotopy class of
![]() $\mathrm {hocolim}\,( \ell _{k},f_{k})$
, thereby defining a functor from the category of inductive sequences of compact Polish spaces to the homotopy category of locally compact Polish spaces, as desired.
$\mathrm {hocolim}\,( \ell _{k},f_{k})$
, thereby defining a functor from the category of inductive sequences of compact Polish spaces to the homotopy category of locally compact Polish spaces, as desired.
8.3. The cohomology of mapping telescopes
Suppose now that
![]() $\mathbf {X}=( X_{n}) _{n\in \mathbb {N}}$
is an inductive sequence of compact spaces. Then
$\mathbf {X}=( X_{n}) _{n\in \mathbb {N}}$
is an inductive sequence of compact spaces. Then
![]() $\mathrm {hocolim}\,\mathbf {X}$
has a canonical cofiltration
$\mathrm {hocolim}\,\mathbf {X}$
has a canonical cofiltration
![]() $(\tilde {X}_{n})_{n\in \mathbb {N}}$
obtained by letting
$(\tilde {X}_{n})_{n\in \mathbb {N}}$
obtained by letting
![]() $\tilde {X}_{n}$
be the set
$\tilde {X}_{n}$
be the set
It is easy to see that
![]() $\tilde {X}_{n}$
is a compact subset of
$\tilde {X}_{n}$
is a compact subset of
![]() $\mathrm {hocolim}\,\mathbf {X}$
that is homotopy equivalent to
$\mathrm {hocolim}\,\mathbf {X}$
that is homotopy equivalent to
![]() $X_{n}$
(via a sequence of mapping cylinder deformation retractions of the sort alluded to at the end of Section 8.1). Furthermore, the inductive sequence
$X_{n}$
(via a sequence of mapping cylinder deformation retractions of the sort alluded to at the end of Section 8.1). Furthermore, the inductive sequence
![]() $(\tilde {X}_{n})_{n\in \mathbb {N}}$
, with inclusions as bonding maps, is naturally isomorphic in
$(\tilde {X}_{n})_{n\in \mathbb {N}}$
, with inclusions as bonding maps, is naturally isomorphic in
![]() $ \mathsf {Ind}_{\omega }( \mathsf {Ho}( \mathsf {C})) $
to
$ \mathsf {Ind}_{\omega }( \mathsf {Ho}( \mathsf {C})) $
to
![]() $\mathbf {X}$
. Thus, as a particular instance of Proposition 7.14, we have the following.
$\mathbf {X}$
. Thus, as a particular instance of Proposition 7.14, we have the following.
Proposition 8.8. Suppose that q is a positive integer and G is a countable discrete group and
![]() $\mathbf {X}=( X_{n},\eta _n)_{n\in \mathbb {N}}$
is an inductive sequence of compact spaces. Then,
$\mathbf {X}=( X_{n},\eta _n)_{n\in \mathbb {N}}$
is an inductive sequence of compact spaces. Then,
-
(1)
 $\mathrm {H}_{\infty }^{q}(\mathrm {hocolim}\,\mathbf {X} ;G)$
is naturally definably isomorphic to
$\mathrm {H}_{\infty }^{q}(\mathrm {hocolim}\,\mathbf {X} ;G)$
is naturally definably isomorphic to
 $ \mathrm {lim}^{1}\,\mathrm {H}^{q}( S( X_n) ,\,\ast \,;G) \cong \mathrm {lim}^{1}\,\mathrm {H}^{q-1}( X_n;G) $
;
$ \mathrm {lim}^{1}\,\mathrm {H}^{q}( S( X_n) ,\,\ast \,;G) \cong \mathrm {lim}^{1}\,\mathrm {H}^{q-1}( X_n;G) $
; -
(2)
 $\mathrm {H}_{\mathrm {w}}^q(\mathrm {hocolim}\,\mathbf {X} ;G)$
is naturally definably isomorphic to the pro-countable abelian group
$\mathrm {H}_{\mathrm {w}}^q(\mathrm {hocolim}\,\mathbf {X} ;G)$
is naturally definably isomorphic to the pro-countable abelian group
 $\mathrm {lim}\,\mathrm {H}^{q}(X_n;G) $
.
$\mathrm {lim}\,\mathrm {H}^{q}(X_n;G) $
.
8.4. Mapping telescopes of tori
Call an inductive sequence
![]() $\mathbf {X}=\left ( X_{n},\eta _n\right ) _{n\in \mathbb {N}}$
of d-dimensional tori
$\mathbf {X}=\left ( X_{n},\eta _n\right ) _{n\in \mathbb {N}}$
of d-dimensional tori
![]() $X_n=\mathbb {T}^{d}$
nontrivial if its bonding maps
$X_n=\mathbb {T}^{d}$
nontrivial if its bonding maps
![]() $\eta _n:X_{n}\rightarrow X_{n+1}$
are each of nonzero degree. In this section, we show that definable Čech cohomology is a complete invariant for homotopy colimits of such sequences.
$\eta _n:X_{n}\rightarrow X_{n+1}$
are each of nonzero degree. In this section, we show that definable Čech cohomology is a complete invariant for homotopy colimits of such sequences.
Theorem 8.9. The definable Čech cohomology groups completely classify homotopy colimits of nontrivial towers of d-tori up to homotopy equivalence, for all
![]() $d\geq 1$
. In fact, the mapping telescopes associated to any two such towers are homotopy equivalent if and only if they have definably isomorphic weak and asymptotic Čech cohomology groups.
$d\geq 1$
. In fact, the mapping telescopes associated to any two such towers are homotopy equivalent if and only if they have definably isomorphic weak and asymptotic Čech cohomology groups.
In contrast, there exist uncountable families of homotopy inequivalent mapping telescopes of d-tori whose weak and asymptotic Čech cohomology — and, moreover, classical Čech cohomology — groups are isomorphic, as we show in Theorem 8.15 below.
We will precede the proof of Theorem 8.9 with a few observations. Most immediately, observe that by Proposition 7.15, the first assertion of Theorem 8.9 follows from its second; it is the latter which we will prove below.
Next, recall the notion of mapping degree:
Definition 8.10. Fix closed, connected, oriented d-dimensional manifolds M and N; the degree
![]() $\mathrm {deg}(f)$
of a continuous function
$\mathrm {deg}(f)$
of a continuous function
![]() $f:M\to N$
is the integer k for which
$f:M\to N$
is the integer k for which
![]() $f^{*}:\mathrm {H}^d(N)\to \mathrm {H}^d(M)$
is multiplication by k.Footnote
4
$f^{*}:\mathrm {H}^d(N)\to \mathrm {H}^d(M)$
is multiplication by k.Footnote
4
The value of restricting our attention to telescopes of maps of nonzero degree will grow clearer momentarily; we return to the question of its necessity in a concluding remark. We may, in fact, without any loss of generality, restrict our attention yet further: by [Reference Scheffer76, Corollary 2], any map
![]() $\mathbb {T}^d\to \mathbb {T}^d$
is homotopic to a group homomorphism. Hence, by Lemma 8.4, it will suffice to argue Theorem 8.9 for nontrivial inductive sequences
$\mathbb {T}^d\to \mathbb {T}^d$
is homotopic to a group homomorphism. Hence, by Lemma 8.4, it will suffice to argue Theorem 8.9 for nontrivial inductive sequences
![]() $(X_n,\eta _n)$
in which all bonding maps are homomorphisms. For ease of reference, we term the full subcategory of
$(X_n,\eta _n)$
in which all bonding maps are homomorphisms. For ease of reference, we term the full subcategory of
![]() $\mathsf {Ind}_\omega (\mathsf {C})$
consisting of such sequences the category of monomorphic inductive sequences of d-tori. The prefix ‘mono’ references firstly the injectivity of the induced
$\mathsf {Ind}_\omega (\mathsf {C})$
consisting of such sequences the category of monomorphic inductive sequences of d-tori. The prefix ‘mono’ references firstly the injectivity of the induced
![]() $d^{\mathrm {th}}$
cohomology maps but will apply as well in the first and second of the related contexts which we now describe.
$d^{\mathrm {th}}$
cohomology maps but will apply as well in the first and second of the related contexts which we now describe.
Let
![]() $\Lambda $
be a torsion-free rank d abelian group. A cofiltration of
$\Lambda $
be a torsion-free rank d abelian group. A cofiltration of
![]() $\Lambda $
is an increasing sequence
$\Lambda $
is an increasing sequence
![]() $\left ( \Lambda _{n}\right ) _{n\in \mathbb {N} }$
of finitely generated rank d free abelian subgroups of
$\left ( \Lambda _{n}\right ) _{n\in \mathbb {N} }$
of finitely generated rank d free abelian subgroups of
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $\Lambda =\bigcup _{n\in \mathbb {N}} \Lambda _{n}$
. A cofiltration
$\Lambda =\bigcup _{n\in \mathbb {N}} \Lambda _{n}$
. A cofiltration
![]() $\left ( \Lambda _{n}\right ) _{n\in \mathbb {N}}$
gives rise to an inverse sequence
$\left ( \Lambda _{n}\right ) _{n\in \mathbb {N}}$
gives rise to an inverse sequence
![]() $ \left ( \mathrm {Hom}( \Lambda _{n},\mathbb {Z}) \right ) _{n\in \mathbb {N}}$
of finitely generated rank d free abelian groups. By Pontryagin duality, this tower, in turn, induces a monomorphic inductive sequence
$ \left ( \mathrm {Hom}( \Lambda _{n},\mathbb {Z}) \right ) _{n\in \mathbb {N}}$
of finitely generated rank d free abelian groups. By Pontryagin duality, this tower, in turn, induces a monomorphic inductive sequence
![]() $ \mathbf {X}_{\Lambda }:=\left ( \mathrm {Hom}( \Lambda _{n},\mathbb {Z}) ^{\ast }\right ) _{n\in \mathbb {N}}$
of d-tori. In this way, a choice of cofiltration for each torsion-free rank d abelian group determines a functor
$ \mathbf {X}_{\Lambda }:=\left ( \mathrm {Hom}( \Lambda _{n},\mathbb {Z}) ^{\ast }\right ) _{n\in \mathbb {N}}$
of d-tori. In this way, a choice of cofiltration for each torsion-free rank d abelian group determines a functor
![]() $\Lambda \mapsto \mathbf {X}_{\Lambda }$
from the category of rank d torsion-free abelian groups to the category of monomorphic inductive sequences of d-tori. As shown in [Reference Bergfalk and Lupini9], the group invariant
$\Lambda \mapsto \mathbf {X}_{\Lambda }$
from the category of rank d torsion-free abelian groups to the category of monomorphic inductive sequences of d-tori. As shown in [Reference Bergfalk and Lupini9], the group invariant
![]() $\mathrm {Ext}(C,A)$
for countable abelian groups A and C first defined in [Reference Eilenberg and MacLane26] admits a canonical definable abelian group structure. Using Proposition 8.8, we may formulate the definable cohomology of
$\mathrm {Ext}(C,A)$
for countable abelian groups A and C first defined in [Reference Eilenberg and MacLane26] admits a canonical definable abelian group structure. Using Proposition 8.8, we may formulate the definable cohomology of
![]() $ \mathbf {X}_{\Lambda }$
in terms of this definable
$ \mathbf {X}_{\Lambda }$
in terms of this definable
![]() $\textrm {Ext}$
.
$\textrm {Ext}$
.
We therefore pause to recall this functor’s essentials from [Reference Bergfalk and Lupini9, §7]. By an extension
![]() $\mathcal {E}$
of a countable abelian group C by a countable abelian group A, we mean any short exact sequence
$\mathcal {E}$
of a countable abelian group C by a countable abelian group A, we mean any short exact sequence
of abelian groups. The extensions
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
![]() $\mathcal {E}'$
are isomorphic if there is a group isomorphism
$\mathcal {E}'$
are isomorphic if there is a group isomorphism
![]() $E\to E'$
which makes the following diagram commute:
$E\to E'$
which makes the following diagram commute:

We denote by
![]() $\mathrm {Ext}(C,A)$
the collection of all isomorphism classes of extensions of C by A. As is well known, this collection admits a natural abelian group structure, and
$\mathrm {Ext}(C,A)$
the collection of all isomorphism classes of extensions of C by A. As is well known, this collection admits a natural abelian group structure, and
![]() $\mathrm {Ext}$
is more generally the first derived functor of the bifunctor
$\mathrm {Ext}$
is more generally the first derived functor of the bifunctor
![]() $\mathrm {Hom}:\mathsf {Ab}^{\mathrm {op}}\times \mathsf {Ab}\to \mathsf {Ab}$
. The definable versions of
$\mathrm {Hom}:\mathsf {Ab}^{\mathrm {op}}\times \mathsf {Ab}\to \mathsf {Ab}$
. The definable versions of
![]() $\mathrm {Hom}$
and
$\mathrm {Hom}$
and
![]() $\mathrm {Ext}$
are each bifunctors from the category of countable abelian groups to the category
$\mathrm {Ext}$
are each bifunctors from the category of countable abelian groups to the category
![]() $\mathsf {APC}$
of groups with an abelian Polish cover: A and C being discrete, the compact-open topology (or equivalently the product topology) renders
$\mathsf {APC}$
of groups with an abelian Polish cover: A and C being discrete, the compact-open topology (or equivalently the product topology) renders
![]() $\mathrm {Hom}(C,A)$
itself a Polish abelian group. And
$\mathrm {Hom}(C,A)$
itself a Polish abelian group. And
![]() $\mathrm {Ext}(C,A)$
, in a definition tracing to [Reference Eilenberg and MacLane26], is the group with a Polish cover
$\mathrm {Ext}(C,A)$
, in a definition tracing to [Reference Eilenberg and MacLane26], is the group with a Polish cover
![]() $\mathrm {Z}(C,A) /\mathrm {B}(C,A)$
, where
$\mathrm {Z}(C,A) /\mathrm {B}(C,A)$
, where
-
•
 $\mathrm {Z}(C,A)$
is the closed subgroup of the abelian Polish group
$\mathrm {Z}(C,A)$
is the closed subgroup of the abelian Polish group
 $A^{C\times C}$
, consisting of all cocycles on C with coefficients in A. Here,
$A^{C\times C}$
, consisting of all cocycles on C with coefficients in A. Here,
 $A^{C\times C}$
is, as above, endowed with the compact-open topology; by a cocycle on C with coefficients in A, we mean any function
$A^{C\times C}$
is, as above, endowed with the compact-open topology; by a cocycle on C with coefficients in A, we mean any function
 $g:C\times C\rightarrow A$
such that for all
$g:C\times C\rightarrow A$
such that for all
 $x,y,z \in C$
, we have
$x,y,z \in C$
, we have-
(1)
 $g( x,0) =g( 0,y) =0$
;
$g( x,0) =g( 0,y) =0$
; -
(2)
 $g( x,y) +g( x+y,z) =g( x,y+z)+g( y,z)$
;
$g( x,y) +g( x+y,z) =g( x,y+z)+g( y,z)$
; -
(3)
 $g( x,y) =g( y,x)$
, for all
$g( x,y) =g( y,x)$
, for all
 $x,y \in C$
.
$x,y \in C$
.
-
-
•
 $\delta $
is the continuous group homomorphism
$\delta $
is the continuous group homomorphism
 $\mathrm {Hom}(C,A)\to \mathrm {Z}(C,A)$
given by
$\mathrm {Hom}(C,A)\to \mathrm {Z}(C,A)$
given by  $$\begin{align*}\delta(g)(x,y):= g(x)+g(y)-g(x+y).\end{align*}$$
$$\begin{align*}\delta(g)(x,y):= g(x)+g(y)-g(x+y).\end{align*}$$
-
•
 $\mathrm {B}(C,A)$
is the Polishable Borel subgroup
$\mathrm {B}(C,A)$
is the Polishable Borel subgroup
 $\delta [\mathrm {Hom}(C,A)]$
of
$\delta [\mathrm {Hom}(C,A)]$
of
 $\mathrm {Z}(C,A)$
.
$\mathrm {Z}(C,A)$
.
Returning to our cohomology computations, we have the following.
Proposition 8.11. Let
![]() $\Lambda $
be a rank d torsion-free abelian group. Then
$\Lambda $
be a rank d torsion-free abelian group. Then
-
(1)
 $\mathrm {H}^{d+1}(\mathrm {hocolim}\, \mathbf {X}_{\Lambda }) =\mathrm {H}_{\infty }^{d+1}(\mathrm {hocolim}\, \mathbf {X}_{\Lambda }) $
is naturally definably isomorphic to
$\mathrm {H}^{d+1}(\mathrm {hocolim}\, \mathbf {X}_{\Lambda }) =\mathrm {H}_{\infty }^{d+1}(\mathrm {hocolim}\, \mathbf {X}_{\Lambda }) $
is naturally definably isomorphic to
 $\mathrm {Ext}( \Lambda ,\mathbb {Z}) $
;
$\mathrm {Ext}( \Lambda ,\mathbb {Z}) $
; -
(2)
 $\mathrm {H}_{\mathrm {w}}^{d}(\mathrm {hocolim}\, \mathbf {X}_{\Lambda }) $
is naturally definably isomorphic to
$\mathrm {H}_{\mathrm {w}}^{d}(\mathrm {hocolim}\, \mathbf {X}_{\Lambda }) $
is naturally definably isomorphic to
 $\mathrm {Hom}( \Lambda ,\mathbb {Z}) $
;
$\mathrm {Hom}( \Lambda ,\mathbb {Z}) $
; -
(3)
 $\mathrm {H}^{k}( \mathrm {hocolim}\, \mathbf {X}_{\Lambda }) =0$
for
$\mathrm {H}^{k}( \mathrm {hocolim}\, \mathbf {X}_{\Lambda }) =0$
for
 $k> d+1$
.
$k> d+1$
.
Proof. (1) By Proposition 8.8,
![]() $ \mathrm {H}_{\infty }^{d+1}(\mathrm {hocolim}\, \mathbf {X}_{\Lambda })$
is naturally definably isomorphic to
$ \mathrm {H}_{\infty }^{d+1}(\mathrm {hocolim}\, \mathbf {X}_{\Lambda })$
is naturally definably isomorphic to
![]() $\mathrm {lim}^{1}\,\mathrm {H}^{d}( \mathrm {Hom}( \Lambda _{n},\mathbb {Z}) ^{\ast }) $
. Furthermore,
$\mathrm {lim}^{1}\,\mathrm {H}^{d}( \mathrm {Hom}( \Lambda _{n},\mathbb {Z}) ^{\ast }) $
. Furthermore,
![]() $\mathrm {H}^{d}( \mathrm {Hom}( \Lambda _{n}, \mathbb {Z}) ^{\ast }) $
is naturally isomorphic to the countable group
$\mathrm {H}^{d}( \mathrm {Hom}( \Lambda _{n}, \mathbb {Z}) ^{\ast }) $
is naturally isomorphic to the countable group
![]() $\mathrm {Hom}( \Lambda _{n},\mathbb {Z}) $
[Reference Hofmann and Morris36, Theorem 8.83]. Hence, by the definable version of Jensen’s Theorem [Reference Bergfalk and Lupini9, Theorem 7.4], we have natural definable isomorphisms
$\mathrm {Hom}( \Lambda _{n},\mathbb {Z}) $
[Reference Hofmann and Morris36, Theorem 8.83]. Hence, by the definable version of Jensen’s Theorem [Reference Bergfalk and Lupini9, Theorem 7.4], we have natural definable isomorphisms
 $$ \begin{align*} \mathrm{lim}^{1}\,\mathrm{H}^{d}( \mathrm{Hom}(\Lambda _{n},\mathbb{Z}) ^{\ast }) &\cong \mathrm{lim}^{1}\,\mathrm{Hom}(\Lambda _{n},\mathbb{Z}) \\ &\cong \mathrm{Ext}(\mathrm{colim}\,\Lambda _{n},\mathbb{Z)} \\ &\cong \mathrm{Ext}(\Lambda,\mathbb{Z}) \text{.} \end{align*} $$
$$ \begin{align*} \mathrm{lim}^{1}\,\mathrm{H}^{d}( \mathrm{Hom}(\Lambda _{n},\mathbb{Z}) ^{\ast }) &\cong \mathrm{lim}^{1}\,\mathrm{Hom}(\Lambda _{n},\mathbb{Z}) \\ &\cong \mathrm{Ext}(\mathrm{colim}\,\Lambda _{n},\mathbb{Z)} \\ &\cong \mathrm{Ext}(\Lambda,\mathbb{Z}) \text{.} \end{align*} $$
This is definably isomorphic to the entirety of
![]() $\mathrm {H}^{d+1}(\mathrm {hocolim}\,\mathbf {X}_{\Lambda })$
by Proposition 7.14, together with the observation that
$\mathrm {H}^{d+1}(\mathrm {hocolim}\,\mathbf {X}_{\Lambda })$
by Proposition 7.14, together with the observation that
![]() $\mathrm {H}^{d+1}( \mathrm {Hom}(\Lambda _{n},\mathbb {Z}) ^{\ast })=0$
for every
$\mathrm {H}^{d+1}( \mathrm {Hom}(\Lambda _{n},\mathbb {Z}) ^{\ast })=0$
for every
![]() $n\in \mathbb {N}$
implies that
$n\in \mathbb {N}$
implies that
(2) By Proposition 8.8,
![]() $\mathrm {H}_{\mathrm {w}}^{d}(\mathrm {hocolim}\,\mathbf {X}_{\Lambda })$
is naturally definably isomorphic to
$\mathrm {H}_{\mathrm {w}}^{d}(\mathrm {hocolim}\,\mathbf {X}_{\Lambda })$
is naturally definably isomorphic to
(3) This is an immediate consequence of Proposition 8.8, upon observation that
![]() $\mathrm {H}^{k}( \mathrm {Hom}( \Lambda _{n},\mathbb {Z}) ^{\ast }) =0$
for
$\mathrm {H}^{k}( \mathrm {Hom}( \Lambda _{n},\mathbb {Z}) ^{\ast }) =0$
for
![]() $ k>d$
.
$ k>d$
.
Observe that the functor
![]() $\Lambda \mapsto \mathbf {X}_{\Lambda } $
described above, from the category of countable torsion-free rank d abelian groups to the category of monomorphic inductive sequences of d-tori, is fully faithful. To see this, observe that a choice of cofibrations
$\Lambda \mapsto \mathbf {X}_{\Lambda } $
described above, from the category of countable torsion-free rank d abelian groups to the category of monomorphic inductive sequences of d-tori, is fully faithful. To see this, observe that a choice of cofibrations
![]() $(\Lambda _n)$
and
$(\Lambda _n)$
and
![]() $(\Lambda ^{\prime }_n)$
of
$(\Lambda ^{\prime }_n)$
of
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Lambda '$
, respectively, induces a bijection
$\Lambda '$
, respectively, induces a bijection
and that the sequences of matrices
![]() $(M_n:\Lambda _n\to \Lambda ^{\prime }_n)$
representing maps in the latter correspond precisely to those representing maps in
$(M_n:\Lambda _n\to \Lambda ^{\prime }_n)$
representing maps in the latter correspond precisely to those representing maps in
![]() $\mathrm {Hom}_{\mathsf {Ind}_\omega (\mathsf {C})}((\mathbb {T}(\Lambda _n)),(\mathbb {T}(\Lambda ^{\prime }_n)))$
, where
$\mathrm {Hom}_{\mathsf {Ind}_\omega (\mathsf {C})}((\mathbb {T}(\Lambda _n)),(\mathbb {T}(\Lambda ^{\prime }_n)))$
, where
![]() $(\mathbb {T}(\Lambda _n))$
and
$(\mathbb {T}(\Lambda _n))$
and
![]() $(\mathbb {T}(\Lambda ^{\prime }_n))$
denote the sequences of tori comprising
$(\mathbb {T}(\Lambda ^{\prime }_n))$
denote the sequences of tori comprising
![]() $\mathbf {X}_\Lambda $
and
$\mathbf {X}_\Lambda $
and
![]() $\mathbf {X}_{\Lambda '}$
, respectively. It is also easy to see that each monomorphic inductive sequence of d-tori is isomorphic in Ind
$\mathbf {X}_{\Lambda '}$
, respectively. It is also easy to see that each monomorphic inductive sequence of d-tori is isomorphic in Ind
![]() $_{\omega }( \mathsf {C}) $
to
$_{\omega }( \mathsf {C}) $
to
![]() $\mathbf {X}_{\Lambda }$
for some torsion-free rank d abelian group
$\mathbf {X}_{\Lambda }$
for some torsion-free rank d abelian group
![]() $\Lambda $
. Hence, the functor
$\Lambda $
. Hence, the functor
![]() $ \Lambda \mapsto \mathbf {X}_{\Lambda }$
is an equivalence of categories from the category of countable torsion-free rank d abelian groups to the category of monomorphic inductive sequences of d-tori. Thus, in order to establish Theorem 8.9, it suffices to prove the following.
$ \Lambda \mapsto \mathbf {X}_{\Lambda }$
is an equivalence of categories from the category of countable torsion-free rank d abelian groups to the category of monomorphic inductive sequences of d-tori. Thus, in order to establish Theorem 8.9, it suffices to prove the following.
Theorem 8.12. The asymptotic and weak definable cohomology groups of
![]() $\mathrm {hocolim}\,\mathbf {X} _{\Lambda }$
together provide a complete invariant for a finite rank torsion-free abelian group
$\mathrm {hocolim}\,\mathbf {X} _{\Lambda }$
together provide a complete invariant for a finite rank torsion-free abelian group
![]() $\Lambda $
up to isomorphism.
$\Lambda $
up to isomorphism.
Proof. A finite rank torsion-free abelian group
![]() $\Lambda $
uniquely decomposes as
$\Lambda $
uniquely decomposes as
![]() $\Lambda _{\infty }\oplus \Lambda _{\mathrm {w}}$
where
$\Lambda _{\infty }\oplus \Lambda _{\mathrm {w}}$
where
![]() $\Lambda _{\mathrm { w}}$
is finitely generated and
$\Lambda _{\mathrm { w}}$
is finitely generated and
![]() $\Lambda _{\infty }$
has no finitely generated summand. Hence, it will suffice to show that the asymptotic and weak definable cohomology groups of
$\Lambda _{\infty }$
has no finitely generated summand. Hence, it will suffice to show that the asymptotic and weak definable cohomology groups of
![]() $\mathrm {hocolim}\,\mathbf {X} _{\Lambda }$
provide complete invariants for such groups
$\mathrm {hocolim}\,\mathbf {X} _{\Lambda }$
provide complete invariants for such groups
![]() $\Lambda _{\infty }$
and
$\Lambda _{\infty }$
and
![]() $\Lambda _{\mathrm {w}}$
, respectively.
$\Lambda _{\mathrm {w}}$
, respectively.
By Proposition 8.11, we have definable isomorphisms
and
By [Reference Bergfalk and Lupini9, Corollary 7.6], the definable group
![]() $\mathrm {Ext}\left ( -,\mathbb {Z}\right ) $
is a complete invariant for torsion-free finite rank groups with no finitely generated summands. The complementary fact, that
$\mathrm {Ext}\left ( -,\mathbb {Z}\right ) $
is a complete invariant for torsion-free finite rank groups with no finitely generated summands. The complementary fact, that
![]() $\mathrm {Hom}\left ( -,\mathbb {Z} \right ) $
is a complete invariant for finitely generated torsion-free abelian groups, is trivial.
$\mathrm {Hom}\left ( -,\mathbb {Z} \right ) $
is a complete invariant for finitely generated torsion-free abelian groups, is trivial.
In the setting of finite rank torsion-free abelian groups with no finitely generated direct summand, the proof of Theorem 8.12 allows for a strengthening of its conclusion as follows:
Theorem 8.13. The map
![]() $\Lambda \mapsto \mathrm {H}^{d+1}(\mathrm {hocolim}\,\mathbf {X}_{\Lambda })$
is a fully faithful functor from the category of rank d torsion-free abelian groups with no finitely generated direct summand to the category of groups with a Polish cover.
$\Lambda \mapsto \mathrm {H}^{d+1}(\mathrm {hocolim}\,\mathbf {X}_{\Lambda })$
is a fully faithful functor from the category of rank d torsion-free abelian groups with no finitely generated direct summand to the category of groups with a Polish cover.
Remark 8.14. To see that the assumption that bonding maps are of nonzero degree is needed for our arguments, let
![]() $X_n=Y_n=\mathbb {T}\times \mathbb {T}$
for all
$X_n=Y_n=\mathbb {T}\times \mathbb {T}$
for all
![]() $n\in \omega $
; let each
$n\in \omega $
; let each
![]() $\eta _n:X_n\to X_{n+1}$
be the projection to the first factor, and let each
$\eta _n:X_n\to X_{n+1}$
be the projection to the first factor, and let each
![]() $Y_n\to Y_{n+1}$
be constant. Letting X and Y denote
$Y_n\to Y_{n+1}$
be constant. Letting X and Y denote
![]() $\mathrm {hocolim}\,(X_n,\eta _n)$
and
$\mathrm {hocolim}\,(X_n,\eta _n)$
and
![]() $\mathrm {hocolim}\,(Y_n,\beta _n)$
, respectively, we then have that
$\mathrm {hocolim}\,(Y_n,\beta _n)$
, respectively, we then have that
![]() $X\not \simeq Y$
but
$X\not \simeq Y$
but
Here, then, the reasoning of Theorems 8.11 and 8.12 no longer applies. Note that it remains quite plausible that definable cohomology classifies mapping telescopes of tori even without assumptions on maps’ degrees; the example simply suggests that ascertaining this would require a deeper analysis of the cohomology groups than is in the spirit of the present work.
As indicated, the sensitivities of definable cohomology recorded above contrast strongly with those of classical cohomology.
Theorem 8.15. There exist size-continuum families of pairwise homotopy inequivalent mapping telescopes of monomorphic inductive sequences of tori whose classical Čech cohomology groups are, viewed as graded abelian groups, all isomorphic.
Proof. Recall the following notations from [Reference Bergfalk and Lupini9, p. Reference Eilenberg and MacLane28]: for every sequence
![]() $\boldsymbol {m}=\left ( m_{p}\right ) _{p\in \mathcal {P}}\in \mathbb {N }^{\mathcal {P}}$
, where
$\boldsymbol {m}=\left ( m_{p}\right ) _{p\in \mathcal {P}}\in \mathbb {N }^{\mathcal {P}}$
, where
![]() $\mathbb {N}$
is the set of strictly positive integers, define
$\mathbb {N}$
is the set of strictly positive integers, define
![]() $\mathbb {Z}[\frac {1}{\mathcal {P}^{\boldsymbol {m}}}]$
to be the set of rational numbers of the form
$\mathbb {Z}[\frac {1}{\mathcal {P}^{\boldsymbol {m}}}]$
to be the set of rational numbers of the form
![]() $a/b$
where
$a/b$
where
![]() $a\in \mathbb {Z}$
,
$a\in \mathbb {Z}$
,
![]() $b\in \mathbb {N}$
, and for every
$b\in \mathbb {N}$
, and for every
![]() $p\in \mathcal {P}$
and
$p\in \mathcal {P}$
and
![]() $k\in \mathbb {N}$
, if
$k\in \mathbb {N}$
, if
![]() $ p^{k}$
divides b, then
$ p^{k}$
divides b, then
![]() $k\leq m_{p}$
. Write
$k\leq m_{p}$
. Write
![]() $\boldsymbol {m}=^{\ast } \boldsymbol {n}$
if and only if
$\boldsymbol {m}=^{\ast } \boldsymbol {n}$
if and only if
![]() $\{ p\in \mathcal {P} :m_{p}\neq m_{p}^{\prime }\} $
is finite. The following appears as Corollary 7.9 in [Reference Bergfalk and Lupini9].
$\{ p\in \mathcal {P} :m_{p}\neq m_{p}^{\prime }\} $
is finite. The following appears as Corollary 7.9 in [Reference Bergfalk and Lupini9].
Proposition 8.16. Fix
![]() $d\geq 1$
. For every
$d\geq 1$
. For every
![]() $ \boldsymbol {m},\boldsymbol {n}\in \mathbb {N}^{\mathcal {P}}$
,
$ \boldsymbol {m},\boldsymbol {n}\in \mathbb {N}^{\mathcal {P}}$
,
![]() $ \mathrm {Ext}(\mathbb {Z}[\frac {1}{\mathcal {P}^{\boldsymbol {m}}}]^{d},\mathbb {Z })$
and
$ \mathrm {Ext}(\mathbb {Z}[\frac {1}{\mathcal {P}^{\boldsymbol {m}}}]^{d},\mathbb {Z })$
and
![]() $\mathrm {Ext}(\mathbb {Z}[\frac {1}{\mathcal {P}^{\boldsymbol {n}}}]^{d}, \mathbb {Z})$
are isomorphic as discrete groups, and are Borel isomorphic if and only if
$\mathrm {Ext}(\mathbb {Z}[\frac {1}{\mathcal {P}^{\boldsymbol {n}}}]^{d}, \mathbb {Z})$
are isomorphic as discrete groups, and are Borel isomorphic if and only if
![]() $\boldsymbol {m}=^{\ast }\boldsymbol {n}$
. In particular, the collection
$\boldsymbol {m}=^{\ast }\boldsymbol {n}$
. In particular, the collection
 $$ \begin{align*} \left\{ \mathrm{Ext}(\mathbb{Z}\Big[\frac{1}{\mathcal{P}^{\boldsymbol{m}}}\Big]^{d}, \mathbb{Z}):\boldsymbol{m}\in \mathbb{N}^{\mathcal{P}}\right\} \end{align*} $$
$$ \begin{align*} \left\{ \mathrm{Ext}(\mathbb{Z}\Big[\frac{1}{\mathcal{P}^{\boldsymbol{m}}}\Big]^{d}, \mathbb{Z}):\boldsymbol{m}\in \mathbb{N}^{\mathcal{P}}\right\} \end{align*} $$
contains a continuum of groups with a Polish cover that are pairwise isomorphic as discrete groups but not definably isomorphic.
Though this result carries implications contrasting with Proposition 8.11 and Theorem 8.12 for all
![]() $d\geq 1$
, for simplicity, we focus on the case of
$d\geq 1$
, for simplicity, we focus on the case of
![]() $d=1$
. Choosing
$d=1$
. Choosing
![]() $\boldsymbol {m}\in \mathbb {N}^{\mathcal {P}}$
and letting
$\boldsymbol {m}\in \mathbb {N}^{\mathcal {P}}$
and letting
![]() $\Lambda =\mathbb {Z}[\frac {1}{\mathcal {P}^{\boldsymbol {m}}}]$
, we may represent
$\Lambda =\mathbb {Z}[\frac {1}{\mathcal {P}^{\boldsymbol {m}}}]$
, we may represent
![]() $\mathrm {hocolim}\, \mathbf {X}_{\Lambda }$
as the mapping telescope
$\mathrm {hocolim}\, \mathbf {X}_{\Lambda }$
as the mapping telescope
![]() $\mathrm {tel}(\boldsymbol {m})$
of the sequence of maps
$\mathrm {tel}(\boldsymbol {m})$
of the sequence of maps
![]() $\eta _n:\mathbb {T}\to \mathbb {T}$
$\eta _n:\mathbb {T}\to \mathbb {T}$
![]() $(n\in \mathbb {N})$
defined by
$(n\in \mathbb {N})$
defined by
![]() $z\mapsto z^{p^{m_p}}$
, where p is the
$z\mapsto z^{p^{m_p}}$
, where p is the
![]() $n^{\mathrm {th}}$
prime number. It is straightforward to verify that
$n^{\mathrm {th}}$
prime number. It is straightforward to verify that
![]() $\mathrm {H}^0(\mathrm {tel}(\boldsymbol {m}))=\mathrm {H}^1(\mathrm {tel}(\boldsymbol {m}))=\mathbb {Z}$
; it then follows from Proposition 8.11 that for any family M of sequences
$\mathrm {H}^0(\mathrm {tel}(\boldsymbol {m}))=\mathrm {H}^1(\mathrm {tel}(\boldsymbol {m}))=\mathbb {Z}$
; it then follows from Proposition 8.11 that for any family M of sequences
![]() $\boldsymbol {m}$
witnessing Proposition 8.16, the family
$\boldsymbol {m}$
witnessing Proposition 8.16, the family
![]() $\{\mathrm {tel}(\boldsymbol {m})\mid \boldsymbol {m}\in M\}$
is a witness to Theorem 8.15.
$\{\mathrm {tel}(\boldsymbol {m})\mid \boldsymbol {m}\in M\}$
is a witness to Theorem 8.15.
8.5. Mapping telescopes of spheres
Similarly, definable cohomology classifies mapping telescopes of spheres up to homotopy equivalence.
Theorem 8.17. The definable Čech cohomology groups completely classify homotopy colimits of nontrivial inductive sequences of d-spheres up to homotopy equivalence, for all
![]() $d\geq 1$
. In fact, the mapping telescopes associated to any two such inductive sequences are homotopy equivalent if and only if they have definably isomorphic weak and asymptotic Čech cohomology groups.
$d\geq 1$
. In fact, the mapping telescopes associated to any two such inductive sequences are homotopy equivalent if and only if they have definably isomorphic weak and asymptotic Čech cohomology groups.
Just as for Theorem 8.9, Theorem 8.17 contrasts with the fact that there exist uncountable families of pairwise homotopy inequivalent mapping telescopes of sequences of spheres whose classical Čech cohomology groups, viewed as graded abelian groups, are all isomorphic; the handiest examples of such are the families
![]() $\{\mathrm {tel}(\boldsymbol {m})\mid \boldsymbol {m}\in M\}$
concluding the proof of Theorem 8.15 above.
$\{\mathrm {tel}(\boldsymbol {m})\mid \boldsymbol {m}\in M\}$
concluding the proof of Theorem 8.15 above.
As in that proof, for each (cofiltered) rank
![]() $1$
torsion-free abelian group
$1$
torsion-free abelian group
![]() $\Lambda $
, let
$\Lambda $
, let
![]() $\mathbf {X}_{\Lambda }$
denote the corresponding inductive sequence
$\mathbf {X}_{\Lambda }$
denote the corresponding inductive sequence
![]() $\left ( X_{n }\right ) _{n\in \mathbb {N}}$
of
$\left ( X_{n }\right ) _{n\in \mathbb {N}}$
of
![]() $1$
-dimensional tori, which we regard as pointed
$1$
-dimensional tori, which we regard as pointed
![]() $1$
-spheres. Let
$1$
-spheres. Let
![]() $S^{d-1}( \mathbf {X}_{\Lambda }) =\left ( S^{d-1}( X_{n}\right ) ) _{n\in \mathbb {N}}$
, where
$S^{d-1}( \mathbf {X}_{\Lambda }) =\left ( S^{d-1}( X_{n}\right ) ) _{n\in \mathbb {N}}$
, where
![]() $S^{k}$
for
$S^{k}$
for
![]() $k\geq 0$
denotes the k-fold iterated reduced suspension of a pointed space, defined by setting
$k\geq 0$
denotes the k-fold iterated reduced suspension of a pointed space, defined by setting
![]() $S^{k+1}( X)=S(S^{k}(X)) $
for every
$S^{k+1}( X)=S(S^{k}(X)) $
for every
![]() $k\in \mathbb {N}$
; evidently,
$k\in \mathbb {N}$
; evidently,
![]() $S^{d-1}( \mathbf {X}_{\Lambda }) $
is an inductive sequence of d-spheres. Conversely, by Hopf’s Theorem 7.16, since
$S^{d-1}( \mathbf {X}_{\Lambda }) $
is an inductive sequence of d-spheres. Conversely, by Hopf’s Theorem 7.16, since
![]() $\tilde {H}^{d}( S^{d}) $
is isomorphic to
$\tilde {H}^{d}( S^{d}) $
is isomorphic to
![]() $\mathbb {Z}$
, every inductive sequence of d-spheres and maps of nonzero degree is isomorphic in
$\mathbb {Z}$
, every inductive sequence of d-spheres and maps of nonzero degree is isomorphic in
![]() $\mathsf {Ind}_\omega ( \mathsf {Ho}( \mathsf {C})) $
to an inductive sequence of this form. Thus, by Proposition 8.4, it suffices to show that definable cohomology is a complete invariant for
$\mathsf {Ind}_\omega ( \mathsf {Ho}( \mathsf {C})) $
to an inductive sequence of this form. Thus, by Proposition 8.4, it suffices to show that definable cohomology is a complete invariant for
![]() $\mathrm {hocolim}\,S^{d-1}(\mathbf {X}_{\Lambda }) $
where
$\mathrm {hocolim}\,S^{d-1}(\mathbf {X}_{\Lambda }) $
where
![]() $\Lambda $
is a rank
$\Lambda $
is a rank
![]() $1$
torsion-free abelian group. This is immediate from the following proposition, whose proof is the same as the proof of Proposition 8.11.
$1$
torsion-free abelian group. This is immediate from the following proposition, whose proof is the same as the proof of Proposition 8.11.
Proposition 8.18. Let
![]() $\Lambda $
be a rank
$\Lambda $
be a rank
![]() $1$
torsion-free abelian group. Then,
$1$
torsion-free abelian group. Then,
-
(1)
 $\mathrm {H}_{\infty }^{d+1}(S^{d-1}(\mathbf {X}_{\Lambda }))$
is naturally definably isomorphic to
$\mathrm {H}_{\infty }^{d+1}(S^{d-1}(\mathbf {X}_{\Lambda }))$
is naturally definably isomorphic to
 $\mathrm {Ext}(\Lambda ,\mathbb {Z}) $
;
$\mathrm {Ext}(\Lambda ,\mathbb {Z}) $
; -
(2)
 $\mathrm {H}_{\mathrm {w}}^{d}(S^{d-1}(\mathbf {X}_{\Lambda }))$
is naturally definably isomorphic to
$\mathrm {H}_{\mathrm {w}}^{d}(S^{d-1}(\mathbf {X}_{\Lambda }))$
is naturally definably isomorphic to
 $\mathrm {Hom}(\Lambda ,\mathbb {Z})$
.
$\mathrm {Hom}(\Lambda ,\mathbb {Z})$
.
8.6. The Borsuk–Eilenberg classification problem
A d-dimensional solenoid is an indecomposable continuum and, in particular, a compact Polish space which is homeomorphic to the Pontryagin dual of an infinitely generated rank d torsion-free abelian group. One-dimensional solenoids played a prominent role in the work of Smale and Williams in the context of dynamical systems, as they provided the first examples of uniformly hyperbolic (or Axiom A) attractors that are strange; see [Reference Ruelle74, Reference Smale79, Reference Williams90]. In these contexts, a
![]() $1$
-dimensional solenoid arising as a uniformly hyperbolic attractor of a dynamical system is termed a Smale (solenoid) attractor or Smale–Williams (solenoid) attractor. For any
$1$
-dimensional solenoid arising as a uniformly hyperbolic attractor of a dynamical system is termed a Smale (solenoid) attractor or Smale–Williams (solenoid) attractor. For any
![]() $p\geq 2$
(not necessarily prime), let
$p\geq 2$
(not necessarily prime), let
![]() $\Sigma _{p}$
be the p-adic solenoid (i.e., the Pontryagin dual of
$\Sigma _{p}$
be the p-adic solenoid (i.e., the Pontryagin dual of
![]() $\mathbb {Z}[1/p]$
). An explicit construction of an orientation-preserving diffeomorphism
$\mathbb {Z}[1/p]$
). An explicit construction of an orientation-preserving diffeomorphism
![]() $h_{p}$
of
$h_{p}$
of
![]() $S^{3}$
with
$S^{3}$
with
![]() $\Sigma _{p}$
as attractor is also given in [Reference Hubbard and Oberste-Vorth38, Reference Hubbard and Oberste-Vorth39]; we now recall some definitions from that work.
$\Sigma _{p}$
as attractor is also given in [Reference Hubbard and Oberste-Vorth38, Reference Hubbard and Oberste-Vorth39]; we now recall some definitions from that work.
Let
![]() $\mathbb {T}\times D^{2}$
be the solid torus, viewing
$\mathbb {T}\times D^{2}$
be the solid torus, viewing
![]() $\mathbb {T}$
as the unit circle in the complex plane, and let
$\mathbb {T}$
as the unit circle in the complex plane, and let
![]() $\phi :\mathbb {T} \rightarrow \mathbb {T}$
be the map
$\phi :\mathbb {T} \rightarrow \mathbb {T}$
be the map
![]() $\zeta \mapsto \zeta ^{p}$
. The canonical unbraided solenoidal mapping
$\zeta \mapsto \zeta ^{p}$
. The canonical unbraided solenoidal mapping
![]() $\mathbb {T}\times D^{2}\rightarrow \mathbb {T}\times D^{2}$
of degree p is the mapping
$\mathbb {T}\times D^{2}\rightarrow \mathbb {T}\times D^{2}$
of degree p is the mapping
where
![]() $\varepsilon $
is a fixed positive real number chosen to be small enough that
$\varepsilon $
is a fixed positive real number chosen to be small enough that
![]() $e_{\phi }$
is injective. An intrinsic characterization of
$e_{\phi }$
is injective. An intrinsic characterization of
![]() $e_{\phi }$
up to conjugacy is given in [Reference Hubbard and Oberste-Vorth38, Theorem 3.11]. It is shown in [Reference Hubbard and Oberste-Vorth38, Section 4] that there exists an orientation-preserving diffeomorphism h of
$e_{\phi }$
up to conjugacy is given in [Reference Hubbard and Oberste-Vorth38, Theorem 3.11]. It is shown in [Reference Hubbard and Oberste-Vorth38, Section 4] that there exists an orientation-preserving diffeomorphism h of
![]() $S^{3}$
and a smooth embedding
$S^{3}$
and a smooth embedding
![]() $j^{+}:\mathbb {T}\times D^{2}\rightarrow S^{3}$
such that h lifts
$j^{+}:\mathbb {T}\times D^{2}\rightarrow S^{3}$
such that h lifts
![]() $e_{\phi }$
through
$e_{\phi }$
through
![]() $j^{+}$
, in the sense that
$j^{+}$
, in the sense that
![]() $h\circ j^{+}=j^{+}\circ e_{\phi }$
. Setting
$h\circ j^{+}=j^{+}\circ e_{\phi }$
. Setting
![]() $T^{+}:=j^{+}( \mathbb {T}\times D^{2}) $
and
$T^{+}:=j^{+}( \mathbb {T}\times D^{2}) $
and
one has that
is an attractor for h homeomorphic to
![]() $\Sigma _{p}$
. Furthermore, if one lets
$\Sigma _{p}$
. Furthermore, if one lets
![]() $T^{-}$
be the closure of the complement of
$T^{-}$
be the closure of the complement of
![]() $T^{+}$
, then one has that
$T^{+}$
, then one has that
![]() $ h^{-1}|_{T^{-}}$
is conjugate to
$ h^{-1}|_{T^{-}}$
is conjugate to
![]() $e_{\phi }$
, meaning that there exists a diffeomorphism
$e_{\phi }$
, meaning that there exists a diffeomorphism
![]() $j^{-}:\mathbb {T}\times D^{2}\rightarrow T^{-}$
such that
$j^{-}:\mathbb {T}\times D^{2}\rightarrow T^{-}$
such that
![]() $ h^{-1}\circ j^{-}=e_{\phi }$
. Hence,
$ h^{-1}\circ j^{-}=e_{\phi }$
. Hence,
is homeomorphic to
This colimit, in turn, is homotopy equivalent to the mapping telescope
![]() $\mathrm {hocolim}\left ( \mathbb {T},\phi \right ) $
, by Lemma 8.6.
$\mathrm {hocolim}\left ( \mathbb {T},\phi \right ) $
, by Lemma 8.6.
The complement
![]() $S^{3}\setminus \Sigma _{p}( h) $
of
$S^{3}\setminus \Sigma _{p}( h) $
of
![]() $\Sigma _{p}( h) $
is called a (one-dimensional) solenoid complement. The problem of classifying the maps
$\Sigma _{p}( h) $
is called a (one-dimensional) solenoid complement. The problem of classifying the maps
![]() $S^{3}\setminus \Sigma _{p}(h) \rightarrow S^{2}$
up to homotopy was posed by Borsuk and Eilenberg in [Reference Borsuk and Eilenberg11], and we conclude this subsection with a brief review of this question’s rather striking history. More immediately, though, we have the following.
$S^{3}\setminus \Sigma _{p}(h) \rightarrow S^{2}$
up to homotopy was posed by Borsuk and Eilenberg in [Reference Borsuk and Eilenberg11], and we conclude this subsection with a brief review of this question’s rather striking history. More immediately, though, we have the following.
Theorem 8.19. Fix
![]() $p\geq 2$
. Then
$p\geq 2$
. Then
![]() $[S^{3}\setminus \Sigma _{p}( h) ,S^{2}]=[ S^{3}\setminus \Sigma _{p}( h) ,S^{2}] _{\infty }$
is a definable set, and there is a basepoint-preserving definable bijection between
$[S^{3}\setminus \Sigma _{p}( h) ,S^{2}]=[ S^{3}\setminus \Sigma _{p}( h) ,S^{2}] _{\infty }$
is a definable set, and there is a basepoint-preserving definable bijection between
![]() $[S^{3}\setminus \Sigma _{p}(h) ,S^{2}]$
and
$[S^{3}\setminus \Sigma _{p}(h) ,S^{2}]$
and
![]() $\mathrm {Ext}( \mathbb {Z}[1/p],\mathbb {Z}) $
.
$\mathrm {Ext}( \mathbb {Z}[1/p],\mathbb {Z}) $
.
Proof. By the foregoing discussion,
![]() $S^{3}\setminus \Sigma _{p}(h)$
is homotopy equivalent to
$S^{3}\setminus \Sigma _{p}(h)$
is homotopy equivalent to
![]() $\mathbf {X}_\Lambda $
for
$\mathbf {X}_\Lambda $
for
![]() $\Lambda =\mathbb {Z}[1/p]$
. By the
$\Lambda =\mathbb {Z}[1/p]$
. By the
![]() $d=1$
instance of Proposition 8.11(3), Hopf’s Theorem 7.16 applies, giving a definable bijection of
$d=1$
instance of Proposition 8.11(3), Hopf’s Theorem 7.16 applies, giving a definable bijection of
![]() $[S^{3}\setminus \Sigma _{p}( h) ,S^{2}]$
and
$[S^{3}\setminus \Sigma _{p}( h) ,S^{2}]$
and
![]() $\mathrm {H}^2(S^{3}\setminus \Sigma _{p}(h))$
, and the latter, by Proposition 8.11(1), is definably isomorphic to
$\mathrm {H}^2(S^{3}\setminus \Sigma _{p}(h))$
, and the latter, by Proposition 8.11(1), is definably isomorphic to
![]() $\mathrm {Ext}( \mathbb {Z}[1/p],\mathbb {Z})$
. That the composite bijection is basepoint-preserving is clear, and just as in Corollary 7.17,
$\mathrm {Ext}( \mathbb {Z}[1/p],\mathbb {Z})$
. That the composite bijection is basepoint-preserving is clear, and just as in Corollary 7.17,
![]() $[S^{3}\setminus \Sigma _{p}( h) ,S^{2}]$
is then a definable set. Proposition 8.11(1) also gives the first definable bijection in the series
$[S^{3}\setminus \Sigma _{p}( h) ,S^{2}]$
is then a definable set. Proposition 8.11(1) also gives the first definable bijection in the series
Proposition 8.8 supplies the second, and the last follows again from Hopf’s Theorem 7.16, together with Theorem 7.10.
As
![]() $S^{3}\setminus \Sigma _{p}(h) $
is homotopy equivalent to the mapping telescope
$S^{3}\setminus \Sigma _{p}(h) $
is homotopy equivalent to the mapping telescope
![]() $\mathrm {hocolim}\,( \mathbb {T},\phi ) $
, one may consider the following generalization of Theorem 8.19 to arbitrary homotopy colimits of d-tori. This theorem follows just as above from Hopf’s Theorem 7.16 and Propositions 8.8 and 8.11.
$\mathrm {hocolim}\,( \mathbb {T},\phi ) $
, one may consider the following generalization of Theorem 8.19 to arbitrary homotopy colimits of d-tori. This theorem follows just as above from Hopf’s Theorem 7.16 and Propositions 8.8 and 8.11.
Theorem 8.20. Fix
![]() $d\geq 1$
, and let
$d\geq 1$
, and let
![]() $\Lambda $
be a torsion-free rank
$\Lambda $
be a torsion-free rank
![]() $ d$
abelian group. Then there are basepoint-preserving definable bijections between
$ d$
abelian group. Then there are basepoint-preserving definable bijections between
![]() $[\mathrm {hocolim}\,\mathbf {X}_{\Lambda },S^{d+1}]_{\infty }$
and
$[\mathrm {hocolim}\,\mathbf {X}_{\Lambda },S^{d+1}]_{\infty }$
and
![]() $\mathrm {Ext}( \Lambda ,\mathbb {Z}) $
, and between
$\mathrm {Ext}( \Lambda ,\mathbb {Z}) $
, and between
![]() $[\mathrm {hocolim}\,\mathbf {X}_{\Lambda },S^{d+1}]_{\mathrm {w }}$
and
$[\mathrm {hocolim}\,\mathbf {X}_{\Lambda },S^{d+1}]_{\mathrm {w }}$
and
![]() $\mathrm {Hom}( \Lambda ,\mathbb {Z}) $
.
$\mathrm {Hom}( \Lambda ,\mathbb {Z}) $
.
Turning now to the question’s history, we quote from Eilenberg’s memoirs of his work with Karol Borsuk:
The main problem concerning us was the following: given a solenoid
![]() $\Sigma $
in
$\Sigma $
in
![]() $S^3$
, how big is the set S of homotopy classes of maps
$S^3$
, how big is the set S of homotopy classes of maps
![]() $f: S^3\setminus \Sigma \rightarrow S^{2}$
? Our algebraic equipment was so poor that we could not tackle the problem in the whole generality even though all the tools needed were in our paper. In 1938, using the newly developed “obstruction theory,” I established that the set S in question is equipotent to [the second Čech cohomology group of
$f: S^3\setminus \Sigma \rightarrow S^{2}$
? Our algebraic equipment was so poor that we could not tackle the problem in the whole generality even though all the tools needed were in our paper. In 1938, using the newly developed “obstruction theory,” I established that the set S in question is equipotent to [the second Čech cohomology group of
![]() $S^3\setminus \Sigma $
]. [Reference Eilenberg25]
$S^3\setminus \Sigma $
]. [Reference Eilenberg25]
This motivated Steenrod [Reference Steenrod81] to introduce a homology theory dual to Čech cohomology; this theory is now known as Steenrod homology. Steenrod’s duality principle (a form of Alexander duality) entailed that
![]() $\tilde {\mathrm {H}}_{0}\left ( \Sigma \right ) \cong \mathrm {H}^{2}(S^{3}\setminus \Sigma )$
. Steenrod then computed the group
$\tilde {\mathrm {H}}_{0}\left ( \Sigma \right ) \cong \mathrm {H}^{2}(S^{3}\setminus \Sigma )$
. Steenrod then computed the group
![]() $\tilde {\mathrm {H}}_{0}(\Sigma )$
and showed that it – and hence the set of homotopy classes of maps
$\tilde {\mathrm {H}}_{0}(\Sigma )$
and showed that it – and hence the set of homotopy classes of maps
![]() $f: S^3\setminus \Sigma \rightarrow S^{2}$
– is uncountable. Eilenberg continues:
$f: S^3\setminus \Sigma \rightarrow S^{2}$
– is uncountable. Eilenberg continues:
When Saunders MacLane lectured in 1940 at the University of Michigan on group extensions one of the groups appearing on the blackboard was exactly the group calculated by Steenrod. I recognized it and spoke about it to MacLane. The result was the joint paper “Group extensions and homology,” Ann. of Math., 43, 1942. This was the birth of Homological Algebra.
This joint paper, which introduced the functors
![]() $\mathrm {Hom}$
and
$\mathrm {Hom}$
and
![]() $\mathrm {Ext}$
, is often cited as the beginning of category theory as well: a central concern of the work is canonical or so-called ‘natural homomorphisms’ between groups – a notion category theory was in part developed to make precise [Reference Eilenberg and MacLane27, Reference Weibel89].Footnote
5
$\mathrm {Ext}$
, is often cited as the beginning of category theory as well: a central concern of the work is canonical or so-called ‘natural homomorphisms’ between groups – a notion category theory was in part developed to make precise [Reference Eilenberg and MacLane27, Reference Weibel89].Footnote
5
The affinity of that concern with our own concern for definable homomorphisms should be clear. The novelty of this subsection’s theorems consists in both the generalization to higher dimensions (Theorem 8.20), and in their formulation within the category of DSet. This latter point allows both for finer characterizations (in the sense of Borel complexity) of the sets in question and an analysis of their orbits under automorphism actions, the subjects of the following subsection.
8.7. Actions and Borel complexity
Let us begin by recalling that a definable set
![]() $X/E$
is
$X/E$
is
-
• smooth if and only if and only if there is an injective definable function
 $X/E \rightarrow Y$
where Y is a Polish space;
$X/E \rightarrow Y$
where Y is a Polish space; -
• essentially hyperfinite if and only if there is an injective definable function
 $X/E \rightarrow Y/F$
where Y is a Polish space, and F is the orbit equivalence relation associated with a Borel action of
$X/E \rightarrow Y/F$
where Y is a Polish space, and F is the orbit equivalence relation associated with a Borel action of
 $\mathbb {Z}$
on Y;
$\mathbb {Z}$
on Y; -
• essentially treeable if and only if there exists an injective definable function
 $X/E \rightarrow Y/F$
where Y is a Polish space, and F is the orbit equivalence relation associated with a Borel action of a free group on Y.
$X/E \rightarrow Y/F$
where Y is a Polish space, and F is the orbit equivalence relation associated with a Borel action of a free group on Y.
Consider next the definable sets
![]() $\mathrm {Ext}(\Lambda ,\mathbb {Z})$
featuring in Theorem 8.20 above; more generally, consider
$\mathrm {Ext}(\Lambda ,\mathbb {Z})$
featuring in Theorem 8.20 above; more generally, consider
![]() $\mathrm {Ext}(\Lambda ,\mathbb {Z})$
for any countable torsion-free group
$\mathrm {Ext}(\Lambda ,\mathbb {Z})$
for any countable torsion-free group
![]() $\Lambda $
. Since
$\Lambda $
. Since
![]() $\Lambda $
has no finite subgroup,
$\Lambda $
has no finite subgroup,
![]() $\mathrm {Ext}(\Lambda ,\mathbb {Z})$
equals, in modern notation,
$\mathrm {Ext}(\Lambda ,\mathbb {Z})$
equals, in modern notation,
![]() $\mathrm {PExt}(\Lambda ,\mathbb {Z})$
, or in other words the group which Eilenberg and MacLane denote
$\mathrm {PExt}(\Lambda ,\mathbb {Z})$
, or in other words the group which Eilenberg and MacLane denote
![]() $\mathrm {Ext}_f( \Lambda ,\mathbb {Z})$
and identify as the closure of
$\mathrm {Ext}_f( \Lambda ,\mathbb {Z})$
and identify as the closure of
![]() $\{0\} $
in
$\{0\} $
in
![]() $\mathrm {Ext}(\Lambda ,\mathbb {Z})$
in [Reference Eilenberg and MacLane26]; more succinctly,
$\mathrm {Ext}(\Lambda ,\mathbb {Z})$
in [Reference Eilenberg and MacLane26]; more succinctly,
![]() $\{ 0\} $
is dense in
$\{ 0\} $
is dense in
![]() $\mathrm {Ext}( \Lambda ,\mathbb {Z})$
(here,
$\mathrm {Ext}( \Lambda ,\mathbb {Z})$
(here,
![]() $\{0\}$
is a convenient locution for N in the presentation
$\{0\}$
is a convenient locution for N in the presentation
![]() $G/N$
of
$G/N$
of
![]() $\mathrm {Ext}(\Lambda ,\mathbb {Z})$
as a group with a Polish cover). From this, the first item of the following theorem is almost immediate.
$\mathrm {Ext}(\Lambda ,\mathbb {Z})$
as a group with a Polish cover). From this, the first item of the following theorem is almost immediate.
Theorem 8.21. Let
![]() $\Lambda $
be a countable torsion-free abelian group.
$\Lambda $
be a countable torsion-free abelian group.
-
• The equivalence relation of isomorphism of extensions of
 $\Lambda $
by
$\Lambda $
by
 $\mathbb {Z}$
is smooth if and only if
$\mathbb {Z}$
is smooth if and only if
 $\{0\} $
is closed in
$\{0\} $
is closed in
 $ \mathrm {Ext}(\Lambda ,\mathbb {Z})$
if and only if
$ \mathrm {Ext}(\Lambda ,\mathbb {Z})$
if and only if
 $\mathrm {Ext}(\Lambda ,\mathbb {Z})=0$
if and only if
$\mathrm {Ext}(\Lambda ,\mathbb {Z})=0$
if and only if
 $\Lambda $
is free abelian.
$\Lambda $
is free abelian. -
• The equivalence relation of isomorphism of extensions of
 $ \Lambda $
by
$ \Lambda $
by
 $\mathbb {Z}$
is essentially hyperfinite if and only if
$\mathbb {Z}$
is essentially hyperfinite if and only if
 $\{0\} $
is
$\{0\} $
is
 $\boldsymbol {\Sigma }_{2}^{0}$
in
$\boldsymbol {\Sigma }_{2}^{0}$
in
 $\mathrm {Ext}( \Lambda ,\mathbb {Z})$
if and only if
$\mathrm {Ext}( \Lambda ,\mathbb {Z})$
if and only if
 $\Lambda =\Lambda _{\infty }\oplus \Lambda _{\mathrm {free}}$
where
$\Lambda =\Lambda _{\infty }\oplus \Lambda _{\mathrm {free}}$
where
 $\Lambda _{\mathrm {free}}$
is free and
$\Lambda _{\mathrm {free}}$
is free and
 $\Lambda _{\infty }$
is finite-rank.
$\Lambda _{\infty }$
is finite-rank.
In particular, for any prime
![]() $p\geq 2$
, the problem of classifying extensions of
$p\geq 2$
, the problem of classifying extensions of
![]() $\mathbb {Z}[1/p]$
by
$\mathbb {Z}[1/p]$
by
![]() $\mathbb {Z}$
is essentially hyperfinite and not smooth, and so, in consequence, is the problem of classifying maps
$\mathbb {Z}$
is essentially hyperfinite and not smooth, and so, in consequence, is the problem of classifying maps
![]() $S^{3}\setminus \Sigma _{p}( h) \rightarrow S^{2}$
up to homotopy.
$S^{3}\setminus \Sigma _{p}( h) \rightarrow S^{2}$
up to homotopy.
Proof. The third of the first item’s bi-implications is due to [Reference Stein83]; the second simply restates our above observation that
![]() $\{0\}$
is dense in
$\{0\}$
is dense in
![]() $\mathrm {Ext}(\Lambda ,\mathbb {Z})$
. For the left-to-right portion of its first bi-implication, again recast that observation as the orbit equivalence relation given by
$\mathrm {Ext}(\Lambda ,\mathbb {Z})$
. For the left-to-right portion of its first bi-implication, again recast that observation as the orbit equivalence relation given by
![]() $\{0\}$
is generically ergodic [Reference Gao31, Prop. 6.1.9] and apply the contrapositive of [Reference Gao31, Prop. 6.1.10] to conclude that
$\{0\}$
is generically ergodic [Reference Gao31, Prop. 6.1.9] and apply the contrapositive of [Reference Gao31, Prop. 6.1.10] to conclude that
![]() $\{0\}$
is comeager and, hence, by Pettis’s Lemma [Reference Gao31, Thm. 2.3.2], is closed, as claimed. The right-to-left portion of its first bi-implication is trivial.
$\{0\}$
is comeager and, hence, by Pettis’s Lemma [Reference Gao31, Thm. 2.3.2], is closed, as claimed. The right-to-left portion of its first bi-implication is trivial.
Let us turn now to the theorem’s second item, from which our last assertion directly follows by an application of Theorem 8.19. Note that since
![]() $\mathrm {Ext}(-,\mathbb {Z})$
commutes with sums, in arguing the second item’s right-to-left implications, we may suppose at the outset that
$\mathrm {Ext}(-,\mathbb {Z})$
commutes with sums, in arguing the second item’s right-to-left implications, we may suppose at the outset that
![]() $\Lambda $
is finite-rank. Next, let
$\Lambda $
is finite-rank. Next, let
![]() $E\subseteq \Lambda $
be a free abelian group such that
$E\subseteq \Lambda $
be a free abelian group such that
![]() $\Lambda /E$
is torsion. To see that
$\Lambda /E$
is torsion. To see that
![]() $\{ 0\} $
is
$\{ 0\} $
is
![]() $\boldsymbol {\Sigma }_{2}^{0}$
in
$\boldsymbol {\Sigma }_{2}^{0}$
in
![]() $\mathrm {Ext}(\Lambda ,\mathbb {Z})$
, consider the tail of the long definable exact sequence relating
$\mathrm {Ext}(\Lambda ,\mathbb {Z})$
, consider the tail of the long definable exact sequence relating
![]() $\mathrm {Hom}$
and
$\mathrm {Hom}$
and
![]() $\mathrm {Ext}$
:
$\mathrm {Ext}$
:
whereby
where
![]() $\mathrm {ran}(f)$
denotes the range, of course, of a function f. Considering next the fragment
$\mathrm {ran}(f)$
denotes the range, of course, of a function f. Considering next the fragment
of the long definable exact sequence associating to
![]() $\mathbb {Z}\to \mathbb {Q}\to \mathbb {Q}/\mathbb {Z}$
, we see that
$\mathbb {Z}\to \mathbb {Q}\to \mathbb {Q}/\mathbb {Z}$
, we see that
![]() $\mathrm {Ext}(\Lambda /E, \mathbb {Z})$
is definably isomorphic to the Polish group
$\mathrm {Ext}(\Lambda /E, \mathbb {Z})$
is definably isomorphic to the Polish group
![]() $\mathrm {Hom}(\Lambda /E, \mathbb {Q}/\mathbb {Z})$
. Hence, the complexity of
$\mathrm {Hom}(\Lambda /E, \mathbb {Q}/\mathbb {Z})$
. Hence, the complexity of
![]() $\{ 0\} $
in
$\{ 0\} $
in
![]() $\mathrm {Ext}(\Lambda , \mathbb {Z})$
equals the complexity of
$\mathrm {Ext}(\Lambda , \mathbb {Z})$
equals the complexity of
![]() $\mathrm {ran}( \mathrm {Hom}(E,\mathbb {Z}) \rightarrow \mathrm {Ext}(\Lambda /E,\mathbb {Z}))$
in
$\mathrm {ran}( \mathrm {Hom}(E,\mathbb {Z}) \rightarrow \mathrm {Ext}(\Lambda /E,\mathbb {Z}))$
in
![]() $\mathrm {Ext}(\Lambda /E,\mathbb {Z})$
(for the preservation of this complexity by definable isomorphisms, see [Reference Lupini52, Proposition 4.12]). Since E is finite-rank,
$\mathrm {Ext}(\Lambda /E,\mathbb {Z})$
(for the preservation of this complexity by definable isomorphisms, see [Reference Lupini52, Proposition 4.12]). Since E is finite-rank,
![]() $\mathrm {Hom}(E,\mathbb {Z})$
is countable; hence
$\mathrm {Hom}(E,\mathbb {Z})$
is countable; hence
![]() $\mathrm {ran}(\mathrm {Hom}( E,\mathbb {Z}) \rightarrow \mathrm {Ext}(\Lambda /E,\mathbb {Z}))$
is also countable, and consequently
$\mathrm {ran}(\mathrm {Hom}( E,\mathbb {Z}) \rightarrow \mathrm {Ext}(\Lambda /E,\mathbb {Z}))$
is also countable, and consequently
![]() $\boldsymbol {\Sigma }_{2}^{0}$
in
$\boldsymbol {\Sigma }_{2}^{0}$
in
![]() $\mathrm {Ext}(\Lambda /E,\mathbb {Z})$
. From this, we conclude that the equivalence relation of isomorphism of extensions of
$\mathrm {Ext}(\Lambda /E,\mathbb {Z})$
. From this, we conclude that the equivalence relation of isomorphism of extensions of
![]() $ \Lambda $
by
$ \Lambda $
by
![]() $\mathbb {Z}$
is essentially hyperfinite by [Reference Gao31, Theorem 12.5.7] and [Reference Ding and Gao22, Theorem 6.1].
$\mathbb {Z}$
is essentially hyperfinite by [Reference Gao31, Theorem 12.5.7] and [Reference Ding and Gao22, Theorem 6.1].
The second item’s left-to-right implications are as follows: the essential hyperfiniteness of the relation implies that
![]() $\{0\}$
is
$\{0\}$
is
![]() $\boldsymbol {\Sigma }_{2}^{0}$
in
$\boldsymbol {\Sigma }_{2}^{0}$
in
![]() $\mathrm {Ext}( \Lambda ,\mathbb {Z})$
by [Reference Lupini52, Proposition 4.14], and this, in turn, implies that
$\mathrm {Ext}( \Lambda ,\mathbb {Z})$
by [Reference Lupini52, Proposition 4.14], and this, in turn, implies that
![]() $\Lambda $
is a sum of a finite-rank abelian group and a free one by [Reference Lupini51, Proposition 6.4].
$\Lambda $
is a sum of a finite-rank abelian group and a free one by [Reference Lupini51, Proposition 6.4].
We turn now to an analysis of actions on definable sets. Suppose that
![]() $\Gamma $
is a group and
$\Gamma $
is a group and
![]() $X/E$
is a semidefinable set. A definable left action
$X/E$
is a semidefinable set. A definable left action
![]() $\Gamma \curvearrowright X/E$
of
$\Gamma \curvearrowright X/E$
of
![]() $\Gamma $
on
$\Gamma $
on
![]() $X\left / E \right. $
is a function
$X\left / E \right. $
is a function
![]() $\Gamma \times X\left / E \right. \rightarrow X/E$
,
$\Gamma \times X\left / E \right. \rightarrow X/E$
,
![]() $(\gamma ,x) \mapsto \gamma \cdot x$
such that
$(\gamma ,x) \mapsto \gamma \cdot x$
such that
-
• for every
 $\gamma \in \Gamma $
, the map
$\gamma \in \Gamma $
, the map
 $f_{\gamma }:X/E \rightarrow X/E$
,
$f_{\gamma }:X/E \rightarrow X/E$
,
 $x\mapsto \gamma \cdot x$
is definable, and
$x\mapsto \gamma \cdot x$
is definable, and -
• the assignment
 $ \gamma \mapsto f_{\gamma }$
is a group homomorphism from
$ \gamma \mapsto f_{\gamma }$
is a group homomorphism from
 $\Gamma $
to the group of definable bijections of X.
$\Gamma $
to the group of definable bijections of X.
The orbit space of the action is the semidefinable set
![]() $(X/E)/\Gamma =X/F$
where F is the equivalence relation on X defined by setting
$(X/E)/\Gamma =X/F$
where F is the equivalence relation on X defined by setting
![]() $ xFy$
if and only if there exists
$ xFy$
if and only if there exists
![]() $\gamma \in \Gamma $
such that
$\gamma \in \Gamma $
such that
![]() $\left ( \gamma \cdot x\right ) E\,y$
. A definable morphism of actions from
$\left ( \gamma \cdot x\right ) E\,y$
. A definable morphism of actions from
![]() $\Gamma \curvearrowright X/E$
to
$\Gamma \curvearrowright X/E$
to
![]() $\Gamma ^{\prime }\curvearrowright X^{\prime }/E^{\prime }$
is a pair
$\Gamma ^{\prime }\curvearrowright X^{\prime }/E^{\prime }$
is a pair
![]() $\left ( \varphi ,f\right ) $
such that
$\left ( \varphi ,f\right ) $
such that
![]() $\varphi :\Gamma \rightarrow \Gamma ^{\prime }$
is a group homomorphism and
$\varphi :\Gamma \rightarrow \Gamma ^{\prime }$
is a group homomorphism and
![]() $f:X/E\rightarrow X^{\prime }/ E^{\prime }$
is a definable function satisfying
$f:X/E\rightarrow X^{\prime }/ E^{\prime }$
is a definable function satisfying
![]() $\varphi ( \gamma ) \cdot f(x) =f( \gamma \cdot x) $
for all
$\varphi ( \gamma ) \cdot f(x) =f( \gamma \cdot x) $
for all
![]() $\gamma \in \Gamma $
and
$\gamma \in \Gamma $
and
![]() $x\in X/E$
. A definable right action is simply a definable left action of its opposite group.
$x\in X/E$
. A definable right action is simply a definable left action of its opposite group.
Consider the group
![]() $\mathcal {E}(X) $
of Ho
$\mathcal {E}(X) $
of Ho
![]() $( \mathsf {LC})$
-automorphisms of a locally compact Polish space X. If P is a polyhedron, then
$( \mathsf {LC})$
-automorphisms of a locally compact Polish space X. If P is a polyhedron, then
![]() $\mathcal {E}(X) $
possesses a canonical right action on the space
$\mathcal {E}(X) $
possesses a canonical right action on the space
![]() $[X,P] $
. If we let
$[X,P] $
. If we let
![]() $\mathcal {K}_{P}(X)$
be the kernel of this action, then we obtain a faithful right action
$\mathcal {K}_{P}(X)$
be the kernel of this action, then we obtain a faithful right action
![]() $[ X,P] \curvearrowleft \mathcal {E}(X) / \mathcal {K}_{P}(X)$
. Similarly, if
$[ X,P] \curvearrowleft \mathcal {E}(X) / \mathcal {K}_{P}(X)$
. Similarly, if
![]() $\mathcal {G}$
is a definable group, and
$\mathcal {G}$
is a definable group, and
![]() $\mathrm {Aut}( \mathcal {G}) $
is the group of definable group automorphisms of
$\mathrm {Aut}( \mathcal {G}) $
is the group of definable group automorphisms of
![]() $\mathcal {G}$
, then we have a faithful left action
$\mathcal {G}$
, then we have a faithful left action
![]() $\mathrm {Aut}( \mathcal {G}) \curvearrowright \mathcal {G}$
.
$\mathrm {Aut}( \mathcal {G}) \curvearrowright \mathcal {G}$
.
Consider now the case in which d is a positive integer, X is a polyhedron with
![]() $H^{q}(X) =0$
for
$H^{q}(X) =0$
for
![]() $q>d+1$
, and
$q>d+1$
, and
![]() $P=S^{d+1}$
. In this case, by Hopf’s theorem, we have a natural definable bijection
$P=S^{d+1}$
. In this case, by Hopf’s theorem, we have a natural definable bijection
![]() $f:[ X,S^{d+1}] \rightarrow \mathrm {H}^{d+1}(X) $
. By the functoriality of definable Čech cohomology, we have also a group anti-homomorphism
$f:[ X,S^{d+1}] \rightarrow \mathrm {H}^{d+1}(X) $
. By the functoriality of definable Čech cohomology, we have also a group anti-homomorphism
![]() $\varphi :\mathcal {E}(X)/ \mathcal {K}_{S^{d+1}}(X)\rightarrow \mathrm {Aut}(\mathrm {H}^{d+1}(X)) $
such that
$\varphi :\mathcal {E}(X)/ \mathcal {K}_{S^{d+1}}(X)\rightarrow \mathrm {Aut}(\mathrm {H}^{d+1}(X)) $
such that
![]() $(\varphi ,f)$
is a morphism of actions from
$(\varphi ,f)$
is a morphism of actions from
![]() $[ X,S^{d+1}] \curvearrowleft \mathcal {E}(X)/ \mathcal {K}_{S^{d+1}}(X)$
to
$[ X,S^{d+1}] \curvearrowleft \mathcal {E}(X)/ \mathcal {K}_{S^{d+1}}(X)$
to
![]() $\mathrm {Aut}(\mathrm {H}^{d+1}(X)) \curvearrowright \mathrm {H}^{d+1}(X)$
.
$\mathrm {Aut}(\mathrm {H}^{d+1}(X)) \curvearrowright \mathrm {H}^{d+1}(X)$
.
In particular, when
![]() $X=\mathrm {hocolim}\,\mathbf {X} _{\Lambda }$
for some a rank d torsion-free abelian group
$X=\mathrm {hocolim}\,\mathbf {X} _{\Lambda }$
for some a rank d torsion-free abelian group
![]() $\Lambda $
with no finitely generated summands, then by Theorem 7.16, Theorem 8.13 and Proposition 8.11 we have the following (see, for example, [Reference Kerr and Li47, p. 15] for the notion of a conjugacy of actions).
$\Lambda $
with no finitely generated summands, then by Theorem 7.16, Theorem 8.13 and Proposition 8.11 we have the following (see, for example, [Reference Kerr and Li47, p. 15] for the notion of a conjugacy of actions).
Theorem 8.22. Suppose that
![]() $\Lambda $
is a rank d torsion-free abelian group with no finitely generated direct summand. Let
$\Lambda $
is a rank d torsion-free abelian group with no finitely generated direct summand. Let
![]() $X_{\Lambda }:=\mathrm {hocolim}\,\mathbf {X} _{\Lambda }$
. Then the natural definable bijection
$X_{\Lambda }:=\mathrm {hocolim}\,\mathbf {X} _{\Lambda }$
. Then the natural definable bijection
and the group anti-homomorphism
establish a conjugacy between the actions
![]() $\mathcal {E}(X_{\Lambda }) \left / \mathcal {K}_{S^{d+1}}( X_{\Lambda }) \right. \curvearrowright [X_{\Lambda },S^{d+1}]$
and the action
$\mathcal {E}(X_{\Lambda }) \left / \mathcal {K}_{S^{d+1}}( X_{\Lambda }) \right. \curvearrowright [X_{\Lambda },S^{d+1}]$
and the action
![]() $\mathrm {Aut}( \Lambda ) \curvearrowright \mathrm {Ext}( \Lambda ,\mathbb {Z}) $
.
$\mathrm {Aut}( \Lambda ) \curvearrowright \mathrm {Ext}( \Lambda ,\mathbb {Z}) $
.
Corollary 8.23. Suppose that
![]() $\Lambda $
is a rank d torsion-free abelian group with no finitely generated direct summand. Set
$\Lambda $
is a rank d torsion-free abelian group with no finitely generated direct summand. Set
![]() $X_{\Lambda }:=\mathrm {hocolim}\,\mathbf {X} _{\Lambda }$
. Then the orbit space
$X_{\Lambda }:=\mathrm {hocolim}\,\mathbf {X} _{\Lambda }$
. Then the orbit space
![]() $[X_{\Lambda },S^{d+1}]/\mathcal {E}( X_{\Lambda })$
is a definable set, and there is a definable bijection between
$[X_{\Lambda },S^{d+1}]/\mathcal {E}( X_{\Lambda })$
is a definable set, and there is a definable bijection between
and
The next corollary follows immediately from Corollary 8.23 and [Reference Bergfalk and Lupini9, Theorem 1.3].
Corollary 8.24. Suppose that
![]() $n,m\geq 2$
, and
$n,m\geq 2$
, and
![]() $p,q$
are prime numbers. Consider the groups
$p,q$
are prime numbers. Consider the groups
![]() $\Lambda =\mathbb {Z}[1/p]^{n}$
and
$\Lambda =\mathbb {Z}[1/p]^{n}$
and
![]() $\Gamma = \mathbb {Z}[1/q]^{m}$
. Then,
$\Gamma = \mathbb {Z}[1/q]^{m}$
. Then,
-
(1)
 $[X_{\Lambda },S^{n+1}]/\mathcal {E}( X_{\Lambda })$
is not smooth;
$[X_{\Lambda },S^{n+1}]/\mathcal {E}( X_{\Lambda })$
is not smooth; -
(2)
 $[X_{\Lambda },S^{n+1}]/\mathcal {E}( X_{\Lambda })$
is essentially hyperfinite if and only if
$[X_{\Lambda },S^{n+1}]/\mathcal {E}( X_{\Lambda })$
is essentially hyperfinite if and only if
 $n=1$
;
$n=1$
; -
(3)
 $[X_{\Lambda },S^{n+1}]/\mathcal {E}( X_{\Lambda })$
is not essentially treeable if
$[X_{\Lambda },S^{n+1}]/\mathcal {E}( X_{\Lambda })$
is not essentially treeable if
 $n>1$
;
$n>1$
; -
(4) if
 $m>n$
, then there is no injective definable function from
$m>n$
, then there is no injective definable function from
 $[X_{\Gamma },S^{m+1}]/\mathcal {E}(X_{\Gamma })$
to
$[X_{\Gamma },S^{m+1}]/\mathcal {E}(X_{\Gamma })$
to
 $[X_{\Lambda },S^{n+1}]/\mathcal {E}( X_{\Lambda })$
;
$[X_{\Lambda },S^{n+1}]/\mathcal {E}( X_{\Lambda })$
; -
(5) if
 $m,n\geq 3$
and
$m,n\geq 3$
and
 $p,q$
are distinct, then there is no injective definable function from
$p,q$
are distinct, then there is no injective definable function from
 $[X_{\Gamma },S^{m+1}]/\mathcal {E}(X_{\Gamma })$
to
$[X_{\Gamma },S^{m+1}]/\mathcal {E}(X_{\Gamma })$
to
 $[X_{\Lambda },S^{n+1}]/\mathcal {E}( X_{\Lambda })$
.
$[X_{\Lambda },S^{n+1}]/\mathcal {E}( X_{\Lambda })$
.
9. Conclusion
This work opens onto further tasks and questions in a number of directions, and of various degrees of concreteness; we close with a few of the most conspicuous among them.
Question 9.1. Is our definition of an idealistic equivalence relation in Definition 3.1 equivalent to the classical one?
Question 9.2. Does the category
![]() $\mathsf {DSet}$
possess arbitrary countable products?
$\mathsf {DSet}$
possess arbitrary countable products?
Question 9.3. Is every abelian group with a Polish cover definably isomorphic to a group with an abelian Polish cover?
Question 9.4. Is every definable group essentially a group with a Polish cover?
Since an affirmative answer would imply one for Is the category of definable abelian groups an exact category?, one may regard the latter as a weaker version of Question 9.4 (note, though, that multiple notions of exact category circulate; those of Quillen and of [Reference Iversen41] both seem interesting here. See [Reference Bühler20]).
Question 9.5. Which of the major generalized homology and cohomology theories – for example, topological K-theory, cobordism, or stable homotopy [Reference Switzer86] – lift to functors to the category of definable groups?
This question condenses several. Its primary background, of course, is our work on the homotopical representation of Čech cohomology, and it, in part, asks how far in the Brown representability [Reference Brown15] direction this work may be extended; it is arguably also a question of extending our analysis to categories of spectra. We may take it more generally to stand for the further development, in the spirit of the present work, of any of contemporary algebraic topology’s extraordinary array of computational resources, including, perhaps most immediately, homotopy groups and the ring structure of cohomology theories, which we simply lacked the space to treat herein; we should further note in this connection the second author’s [Reference Lupini49, Reference Lupini50, Reference Lupini52].
Any such developments should tend, as in the present work, to shed light on the complexity of a number of classification problems, but we are at least as interested in the possibilities of their more direct application to the fields of algebraic or geometric topology. As this work’s authors have shown, for example, the existence of definable homology functors very readily implies the topological rigidity of solenoids, and although this fact may also be argued by classical means, it seems also to underscore the prospect of others which may not be.
Question 9.6. Do there exist classes of topological spaces for which the rigidities of definable (co)homological functors carry implications not accessible by classical means?
Not unrelated is the following line of inquiry, best phrased as a task:
Task 9.7. Characterize those locally compact Polish spaces whose definable cohomology groups are all of the form
![]() $(G,N)$
with N countable, or locally profinite, or procountable, respectively.
$(G,N)$
with N countable, or locally profinite, or procountable, respectively.
Returning to the Borel complexity framework, in recent joint work [Reference Allison and Panagiotopoulos1], this work’s third author exhibited a dynamical obstruction to classification by actions of TSI Polish groups, roughly paralleling Hjorth’s turbulence obstruction to classification by countable structures. Recall that a Polish group is TSI if it admits a two-sided invariant metric. As abelian groups are TSI, the dynamical condition from [Reference Allison and Panagiotopoulos1] can also serve as an obstruction to classification by cohomological invariants.
Question 9.8. Does there exist a dynamical obstruction to classification by cohomological invariants sharper than the obstruction by TSI-groups appearing in [Reference Allison and Panagiotopoulos1]?
Question 9.9. Can Corollary 8.24(5) be extended to the cases when one or both of the variables m and n are
![]() $2$
?
$2$
?
One last question has as partial background the first author’s independence results in homology and cohomology computations. As shown in the joint work [Reference Bergfalk and Lambie-Hanson6], for example, both the vanishing and the nonvanishing of the first Čech cohomology group of the locally compact Hausdorff space
![]() $\omega _2$
are consistent relative to large cardinals; similar independence phenomena arise for strong homology even within the category
$\omega _2$
are consistent relative to large cardinals; similar independence phenomena arise for strong homology even within the category
![]() $\mathsf {LC}$
, even in the absence of large cardinal hypotheses (see [Reference Bergfalk and Lambie-Hanson7, Reference Mardešić and Prasolov54]). On the other hand, the homotopy-bracket representation of Čech cohomology on the category
$\mathsf {LC}$
, even in the absence of large cardinal hypotheses (see [Reference Bergfalk and Lambie-Hanson7, Reference Mardešić and Prasolov54]). On the other hand, the homotopy-bracket representation of Čech cohomology on the category
![]() $\mathsf {LC}$
, as well as our analysis of its complexity, suggests that
$\mathsf {LC}$
, as well as our analysis of its complexity, suggests that ![]() may, on that category, be immune to independence phenomena of this sort, a possibility we evoke in the following question:
may, on that category, be immune to independence phenomena of this sort, a possibility we evoke in the following question:
Question 9.10. Are the values of the Čech cohomology groups of a locally compact Polish space X in some suitable sense forcing absolute?
A more precise framing of any such prospect should, of course, be taken to be part of the question.
Acknowledgements
We would like to thank Alexander Kechris for many valuable discussions, particularly of idealistic equivalence relations, in the course of this paper’s composition. We also thank the anonymous referee for an alert and valuable reading.
Competing interests
The authors have no competing interest to declare.

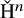 on the category of locally compact separable metric spaces each factor into (i) what we term their
on the category of locally compact separable metric spaces each factor into (i) what we term their 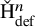 taking values in the category
taking values in the category 

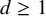
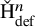 to show that a seminal problem in the development of algebraic topology – namely, Borsuk and Eilenberg’s 1936 problem of classifying, up to homotopy, the maps from a solenoid complement
to show that a seminal problem in the development of algebraic topology – namely, Borsuk and Eilenberg’s 1936 problem of classifying, up to homotopy, the maps from a solenoid complement 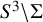
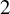
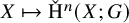 admit two main formulations: a more combinatorial one and a more homotopical formulation as the group
admit two main formulations: a more combinatorial one and a more homotopical formulation as the group 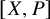
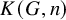
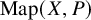
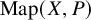
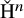 , embodies a substantial variety of classification problems arising throughout mathematics. We show, in particular, that if
, embodies a substantial variety of classification problems arising throughout mathematics. We show, in particular, that if