Hostname: page-component-7dd5485656-s6l46 Total loading time: 0 Render date: 2025-10-30T22:30:13.401Z Has data issue: false hasContentIssue false
  • English
  • Français

The monodromy of unit-root F-isocrystals with geometric origin

Part of: Arithmetic algebraic geometry (Co)homology theory

Published online by Cambridge University Press:  18 April 2022

Joe Kramer-Miller
Joe Kramer-Miller*
Affiliation:
Department of Mathematics, Lehigh University, Bethlehem, PA 18015, USA jjk221@lehigh.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 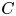$C$ be a smooth curve over a finite field of characteristic 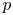$p$ and let 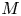$M$ be an overconvergent 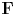$\mathbf {F}$-isocrystal over 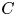$C$. After replacing 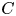$C$ with a dense open subset, 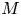$M$ obtains a slope filtration. This is a purely 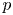$p$-adic phenomenon; there is no counterpart in the theory of lisse 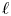$\ell$-adic sheaves. The graded pieces of this slope filtration correspond to lisse 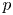$p$-adic sheaves, which we call geometric. Geometric lisse 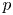$p$-adic sheaves are mysterious, as there is no 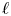$\ell$-adic analogue. In this article, we study the monodromy of geometric lisse 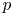$p$-adic sheaves with rank one. More precisely, we prove exponential bounds on their ramification breaks. When the generic slopes of 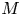$M$ are integers, we show that the local ramification breaks satisfy a certain type of periodicity. The crux of the proof is the theory of 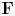$\mathbf {F}$-isocrystals with log-decay. We prove a monodromy theorem for these 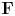$\mathbf {F}$-isocrystals, as well as a theorem relating the slopes of 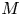$M$ to the rate of log-decay of the slope filtration. As a consequence of these methods, we provide a new proof of the Drinfeld–Kedlaya theorem for irreducible 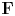$\mathbf {F}$-isocrystals on curves.

Keywords

unit-root F-isocrystalsp-adic cohomologyramification theory

MSC classification

Primary: 14F30: $p$-adic cohomology, crystalline cohomology
Secondary: 11G20: Curves over finite and local fields

Information

Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 2 , February 2022 , pp. 334 - 365
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abbes, A. and Saito, T., Ramification of local fields with imperfect residue fields, Amer. J. Math. 125 (2002), 879--920.Google Scholar
Berthelot, P., Cohomologie cristalline des schémas de caractéristique $p>0$, Lecture Notes in Mathematics, vol. 407 (Springer, Berlin, New York, 1974); MR 0384804.Google Scholar
Berthelot, P., Cohomologie rigide et cohomologie rigide à supports propres, Preprint (1996), https://perso.univ-rennes1.fr/pierre.berthelot/publis/Cohomologie_Rigide_I.pdf.Google Scholar
Berthelot, P. and Ogus, A., Notes on crystalline cohomology (Princeton University Press, Princeton, NJ, 1978); University of Tokyo Press, Tokyo; MR 0491705.Google Scholar
Chiarellotto, B. and Pulita, A., Arithmetic and differential swan conductors of rank one representations with finite local monodromy, Amer. J. Math. 131 (2009), 1743–1794.CrossRefGoogle Scholar
Crew, R., F-isocrystals and p-adic representations, in Algebraic geometry, Bowdoin, 1985, Proceedings of Symposia in Pure Mathematics, vol. 46 (American Mathematical Society, Providence, RI, 1987), 111–138.CrossRefGoogle Scholar
de Jong, A. J., Smoothness, semi-stability and alterations, Publ. Math. Inst. Hautes Études Sci. 83 (1996), 51–93; MR 1423020.CrossRefGoogle Scholar
Drinfeld, V. and Kedlaya, K. S., Slopes of indecomposable $F$-isocrystals, Pure Appl. Math. Q. 13 (2017), 131–192; MR 3858017.CrossRefGoogle Scholar
Dwork, B. and Sperber, S., Logarithmic decay and overconvergence of the unit root and associated zeta functions, Ann. Sci. Éc. Norm. Supér. (4) 24 (1991), 575–604; MR 1132758.CrossRefGoogle Scholar
Hyodo, O. and Kato, K., Semi-stable reduction and crystalline cohomology with logarithmic poles, in Périodes $p$-adiques (Bures-sur-Yvette, 1988), Astérisque, vol. 223 (Société Mathmatique de France, 1994), 221–268; MR 1293974.Google Scholar
Katz, N. and Mazur, B., Arithmetic moduli of elliptic curves, Annals of Mathematics Studies, vol. 108 (Princeton University Press, Princeton, NJ, 1985); MR 772569.CrossRefGoogle Scholar
Katz, N. M., p-adic properties of modular schemes and modular forms, in Modular functions of one variable, III (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972), Lecture Notes in Mathematics, vol. 350 (Springer, 1973), 69–190; MR 0447119.Google Scholar
Katz, N. M., Slope filtration of F-crystals, in Journées de Géométrie Algébrique de Rennes (Rennes, 1978), vol. I, Astérisque, vol. 63 (Société Mathématique de France, Paris, 1979), 113–163; MR 563463.Google Scholar
Kedlaya, K., Descent theorems for overconvergent f-crystals, PhD thesis, Massachusetts Institute of Technology (2000).Google Scholar
Kedlaya, K. S., Full faithfulness for overconvergent F-isocrystals, Geometric Aspects of Dwork Theory, vol. I, II (Walter de Gruyter, Berlin, 2004), 819–835; MR 2099088.Google Scholar
Kedlaya, K., Swan conductors for $p$-adic differential modules, I: A local construction, Algebra Number Theory 1 (2007), 269–300.CrossRefGoogle Scholar
Kedlaya, K., Notes on isocrystals, J. Number Theory (2022), doi:10.1016/j.jnt.2021.12.004.CrossRefGoogle Scholar
Kleiman, S. L., Algebraic cycles and the Weil conjectures, in Dix exposés sur la cohomologie des schémas, Advanced Studies in Pure Mathematics, vol. 3 (North-Holland, Amsterdam, 1968), 359–386; MR 292838.Google Scholar
Kosters, M. and Wan, D., Genus growth in $\Bbb {Z}_p$-towers of function fields, Proc. Amer. Math. Soc. 146 (2018), 1481–1494; MR 3754335.CrossRefGoogle Scholar
Kramer-Miller, J., Slope filtrations of F-isocrystals and logarithmic decay, Math. Res. Lett. 28 (2021), 107–125.CrossRefGoogle Scholar
Matsuda, S., Local indices of $p$-adic differential operators corresponding to Artin-Schreier-Witt coverings, Duke Math. J. 77 (1995), 607–625.CrossRefGoogle Scholar
Oort, F., The Riemann–Hurwitz formula, in The legacy of Bernhard Riemann after one hundred and fifty years, Vol. II, Advanced Lectures in Mathematics (ALM), vol. 35 (International Press, Somerville, MA, 2016), 567–594; MR 3525904.Google Scholar
Ribet, K. A., p-adic interpolation via Hilbert modular forms, in Algebraic geometry—Arcata 1974, Proceedings of Symposia in Pure Mathematics, vol. 29 (American Mathematical Society location Providence, RI, 1975), 581–592; MR 0419414.Google Scholar
Sen, S., Ramification in $p$-adic Lie extensions, Invent. Math. 17 (1972), 44–50; MR 0319949.CrossRefGoogle Scholar
Serre, J.-P., Local fields, Graduate Texts in Mathematics, vol. 67 (Springer, New York, Berlin, 1979), translated from the French by Marvin Jay Greenberg; MR 554237.CrossRefGoogle Scholar
Sperber, S., Congruence properties of the hyper-Kloosterman sum, Compos. Math. 40 (1980), 3–33; MR 558257.Google Scholar
Tsuzuki, N., Finite local monodromy of overconvergent unit-root $F$-isocrystals on a curve, Amer. J. Math. 120 (1998), 1165–1190; MR 1657158.CrossRefGoogle Scholar
Tsuzuki, N., Slope filtration of quasi-unipotent overconvergent $F$-isocrystals, Ann. Inst. Fourier (Grenoble) 48 (1998), 379–412; MR 1625537.CrossRefGoogle Scholar
Wan, D., Dwork's conjecture on unit root zeta functions, Ann. of Math. (2) 150 (1999), 867–927; MR 1740990.CrossRefGoogle Scholar
Wan, D., Class numbers and $p$-ranks in $\Bbb {Z}_p^d$-towers, J. Number Theory 203 (2019), 139–154; MR 3991398.CrossRefGoogle Scholar
Xiao, L., On ramification filtrations and $p$-adic differential modules, I: the equal characteristic case, Algebra Number Theory 4 (2011), 969–1027.CrossRefGoogle Scholar