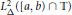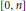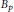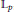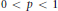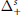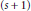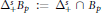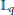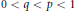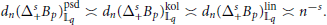Contents
Research Article
Wirtinger's Inequalities on Time Scales
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 161-171
-
- Article
-
- You have access
- Export citation
Consecutive Large Gaps in Sequences Defined by Multiplicative Constraints
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 172-181
-
- Article
-
- You have access
- Export citation
Group Gradings on Associative Algebras with Involution
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 182-194
-
- Article
-
- You have access
- Export citation
Boundedness from Below of Composition Operators on α-Bloch Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 195-204
-
- Article
-
- You have access
- Export citation
On Gâteaux Differentiability of Pointwise Lipschitz Mappings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 205-216
-
- Article
-
- You have access
- Export citation
A Multivalued Nonlinear System with the Vector p-Laplacian on the Semi-Infinity Interval
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 217-228
-
- Article
-
- You have access
- Export citation
Existence of Solutions to Poisson's Equation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 229-235
-
- Article
-
- You have access
- Export citation
Kolmogorov, Linear and Pseudo-Dimensional Widths of Classes of s-Monotone Functions in 𝕃p , 0 < p < 1
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 236-248
-
- Article
-
- You have access
- Export citation
On the Inner Radius of a Nodal Domain
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 249-260
-
- Article
-
- You have access
- Export citation
On the Classification of Rational Quantum Tori and the Structure of Their Automorphism Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 261-282
-
- Article
-
- You have access
- Export citation
The Noether–Lefschetz Theorem Via Vanishing of Coherent Cohomology
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 283-290
-
- Article
-
- You have access
- Export citation
Group Algebras with Minimal Strong Lie Derived Length
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 291-297
-
- Article
-
- You have access
- Export citation
The Kostrikin Radical and the Invariance of the Core of Reduced Extended Affine Lie Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 298-309
-
- Article
-
- You have access
- Export citation
Relative Homotopy in Relational Structures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 310-320
-
- Article
-
- You have access
- Export citation