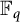1 Introduction
Let
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $d\geq 1$
, and let
$d\geq 1$
, and let
![]() ${\mathbb {F}}_q$
be a finite field. Let
${\mathbb {F}}_q$
be a finite field. Let
![]() $X\subset \mathbb {P}^n$
be a geometrically irreducible hypersurface of degree
$X\subset \mathbb {P}^n$
be a geometrically irreducible hypersurface of degree
![]() $d$
over
$d$
over
![]() ${\mathbb {F}}_q$
. Lang and Weil [Reference Lang and Weil4] have established the bound
${\mathbb {F}}_q$
. Lang and Weil [Reference Lang and Weil4] have established the bound
where the implicit constant can depend only on
![]() $d$
and
$d$
and
![]() $n$
(but not on
$n$
(but not on
![]() $q$
or
$q$
or
![]() $X$
). We prove that, in fact, the implicit constant can be taken to be an absolute constant—independent of
$X$
). We prove that, in fact, the implicit constant can be taken to be an absolute constant—independent of
![]() $n$
and
$n$
and
![]() $d$
altogether—in the regime of interest
$d$
altogether—in the regime of interest
![]() $q\gg _d 1$
.
$q\gg _d 1$
.
Theorem 1.1 Let
![]() $X\subset \mathbb {P}^n_{{\mathbb {F}}_q}$
be a geometrically irreducible hypersurface of degree
$X\subset \mathbb {P}^n_{{\mathbb {F}}_q}$
be a geometrically irreducible hypersurface of degree
![]() $d$
. Then
$d$
. Then
 $$ \begin{align*} |X({\mathbb{F}}_q)|&\geq q^{n-1}-(d-1)(d-2)q^{n-3/2}-O_d(q^{n-5/2}) \qquad\text{and}\\ |X({\mathbb{F}}_q)|&\leq q^{n-1}+(d-1)(d-2)q^{n-3/2} +(1+\pi^2/6)q^{n-2}+O_d(q^{n-5/2}). \end{align*} $$
$$ \begin{align*} |X({\mathbb{F}}_q)|&\geq q^{n-1}-(d-1)(d-2)q^{n-3/2}-O_d(q^{n-5/2}) \qquad\text{and}\\ |X({\mathbb{F}}_q)|&\leq q^{n-1}+(d-1)(d-2)q^{n-3/2} +(1+\pi^2/6)q^{n-2}+O_d(q^{n-5/2}). \end{align*} $$
Example 1.2 (Cone over a maximal curve)
Let
![]() $(d,q_0)$
be such that there exists a (nonsingular) maximal curve
$(d,q_0)$
be such that there exists a (nonsingular) maximal curve
![]() $C=\{f=0\}$
in
$C=\{f=0\}$
in
![]() $\mathbb {P}^2$
over
$\mathbb {P}^2$
over
![]() ${\mathbb {F}}_{q_0}$
of degree
${\mathbb {F}}_{q_0}$
of degree
![]() $d$
. Let
$d$
. Let
![]() $q$
be a power of
$q$
be a power of
![]() $q_0$
, and let
$q_0$
, and let
![]() $X=\{f=0\}\subset \mathbb {P}^n_{{\mathbb {F}}_q}$
be a projective cone over
$X=\{f=0\}\subset \mathbb {P}^n_{{\mathbb {F}}_q}$
be a projective cone over
![]() $C$
. Then
$C$
. Then
with
![]() $\pm $
depending on whether
$\pm $
depending on whether
![]() $q$
is an odd or an even power of
$q$
is an odd or an even power of
![]() $q_0$
. Thus, the constant
$q_0$
. Thus, the constant
![]() $1+\pi ^2/6$
in the upper bound exhibited in Theorem 1.1 cannot possibly be improved by more than
$1+\pi ^2/6$
in the upper bound exhibited in Theorem 1.1 cannot possibly be improved by more than
![]() $\pi ^2/6$
, and the constant
$\pi ^2/6$
, and the constant
![]() $0$
in the lower bound in Theorem 1.1 cannot be improved by more than
$0$
in the lower bound in Theorem 1.1 cannot be improved by more than
![]() $1$
.
$1$
.
In most of this article, we work in affine space. For a geometrically irreducible hypersurface
![]() $X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
of degree
$X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
of degree
![]() $d$
, [Reference Lang and Weil4] states that
$d$
, [Reference Lang and Weil4] states that
where
![]() $C_d$
can depend only on
$C_d$
can depend only on
![]() $d$
and
$d$
and
![]() $n$
. Our notation highlights the more important dependence of
$n$
. Our notation highlights the more important dependence of
![]() $C_d$
on
$C_d$
on
![]() $d$
and suppresses the dependence on
$d$
and suppresses the dependence on
![]() $n$
(usually one thinks of
$n$
(usually one thinks of
![]() $n$
as being fixed from the beginning).
$n$
as being fixed from the beginning).
The problem of giving explicit versions of (1.2) and of improving the dependence of
![]() $C_d$
on
$C_d$
on
![]() $d$
has a long history, which we now briefly summarize. See [Reference Cafure and Matera2] for a more detailed account.
$d$
has a long history, which we now briefly summarize. See [Reference Cafure and Matera2] for a more detailed account.
-
• Schmidt has shown that in the case of the lower bound, one can take
 $C_d=6d^2$
for
$C_d=6d^2$
for
 $q\gg _{n,d} 1$
(see [Reference Schmidt5]) and in the case of the upper bound, one can take
$q\gg _{n,d} 1$
(see [Reference Schmidt5]) and in the case of the upper bound, one can take
 $C_d=4d^2 k^{2^k}$
, where
$C_d=4d^2 k^{2^k}$
, where
 $k=\binom {d+1}{2}$
(see Theorem 4C on page 208 and Theorem 5A on page 210 in [Reference Schmidt6]).
$k=\binom {d+1}{2}$
(see Theorem 4C on page 208 and Theorem 5A on page 210 in [Reference Schmidt6]). -
• Ghorpade and Lachaud [Reference Ghorpade and Lachaud3] use
 $\ell $
-adic étale cohomology techniques to prove that one can take
$\ell $
-adic étale cohomology techniques to prove that one can take
 $C_d$
to be a polynomial in
$C_d$
to be a polynomial in
 $d$
(of degree that depends on
$d$
(of degree that depends on
 $n$
) in the case of the upper bound as well. Explicitly, one can take
$n$
) in the case of the upper bound as well. Explicitly, one can take
 $C_d=12(d+3)^{n+1}$
in (1.2).
$C_d=12(d+3)^{n+1}$
in (1.2). -
• Cafure and Matera [Reference Cafure and Matera2] prove that one can take
 $C_d=5d^{13/3}$
in (1.2); moreover, if
$C_d=5d^{13/3}$
in (1.2); moreover, if
 $q>15d^{13/3}$
, one can take
$q>15d^{13/3}$
, one can take
 $C_d=5d^2+d+1$
(this is a polynomial whose degree does not grow with
$C_d=5d^2+d+1$
(this is a polynomial whose degree does not grow with
 $n$
).
$n$
). -
• The author [Reference Slavov7] has established the lower bound (for any
 $\varepsilon>0$
) for
$\varepsilon>0$
) for $$\begin{align*}|X({\mathbb{F}}_q)|\geq q^{n-1}-(d-1)(d-2)q^{n-3/2}-(d+2+\varepsilon)q^{n-2}\end{align*}$$
$$\begin{align*}|X({\mathbb{F}}_q)|\geq q^{n-1}-(d-1)(d-2)q^{n-3/2}-(d+2+\varepsilon)q^{n-2}\end{align*}$$
 $q\gg _\varepsilon 1$
.
$q\gg _\varepsilon 1$
.
-
• The author’s Theorem 8 in the preprint [Reference Slavov8] implies that for every
 $\varepsilon>0$
and
$\varepsilon>0$
and
 $\varepsilon '>0$
, we have as long as
$\varepsilon '>0$
, we have as long as $$\begin{align*}|X({\mathbb{F}}_q)|\leq q^{n-1}+(d-1)(d-2)q^{n-3/2}+((2+\varepsilon)d+1+\varepsilon')q^{n-2}\end{align*}$$
$$\begin{align*}|X({\mathbb{F}}_q)|\leq q^{n-1}+(d-1)(d-2)q^{n-3/2}+((2+\varepsilon)d+1+\varepsilon')q^{n-2}\end{align*}$$
 $q\gg _{\varepsilon ,\varepsilon '} 1$
.
$q\gg _{\varepsilon ,\varepsilon '} 1$
.
-
• When
 $\dim X=1$
(equivalently,
$\dim X=1$
(equivalently,
 $n=2$
), Aubry and Perret have proved (apply Corollary 2.5 in [Reference Aubry, Perret, Pellikaan, Perret and Vlădu1] to the closure of
$n=2$
), Aubry and Perret have proved (apply Corollary 2.5 in [Reference Aubry, Perret, Pellikaan, Perret and Vlădu1] to the closure of
 $X$
in
$X$
in
 $\mathbb {P}^2$
) that one can take
$\mathbb {P}^2$
) that one can take
 $C_d=d-1$
in the case of the lower bound and
$C_d=d-1$
in the case of the lower bound and
 $C_d=1$
in the case of the upper bound: (1.3)
$C_d=1$
in the case of the upper bound: (1.3) $$ \begin{align} q-(d-1)(d-2)\sqrt{q}-d+1\leq |X({\mathbb{F}}_q)| \leq q+(d-1)(d-2)\sqrt{q}+1. \end{align} $$
$$ \begin{align} q-(d-1)(d-2)\sqrt{q}-d+1\leq |X({\mathbb{F}}_q)| \leq q+(d-1)(d-2)\sqrt{q}+1. \end{align} $$
1.1 Upper bounds
The affine version of the asymptotic upper bound in Theorem 1.1 reads as follows.
Theorem 1.3 Let
![]() $X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
be a geometrically irreducible hypersurface of degree
$X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
be a geometrically irreducible hypersurface of degree
![]() $d$
. Then
$d$
. Then
where the implied constant depends only on
![]() $d$
and can be computed effectively.
$d$
and can be computed effectively.
We can give an explicit bound, as in the following theorem.
Theorem 1.4 Let
![]() $X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
be a geometrically irreducible hypersurface of degree
$X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
be a geometrically irreducible hypersurface of degree
![]() $d$
. Suppose that
$d$
. Suppose that
![]() $q>15d^{13/3}$
. Then
$q>15d^{13/3}$
. Then
Example 1.5 (Cylinder over a maximal curve)
Let
![]() $d\geq 3$
be such that
$d\geq 3$
be such that
![]() $d-1$
is a prime power. Let
$d-1$
is a prime power. Let
![]() $q$
be an odd power of
$q$
be an odd power of
![]() $(d-1)^2$
. Consider the curve
$(d-1)^2$
. Consider the curve
![]() $C=\{y^{d-1}+y=x^d\}$
in
$C=\{y^{d-1}+y=x^d\}$
in
![]() $\mathbb {A}^2_{{\mathbb {F}}_q}$
. It is known (see, for example, [Reference Stichtenoth9]) that
$\mathbb {A}^2_{{\mathbb {F}}_q}$
. It is known (see, for example, [Reference Stichtenoth9]) that
![]() $\#C({\mathbb {F}}_q)=q+(d-1)(d-2)\sqrt {q}$
. Then the number of
$\#C({\mathbb {F}}_q)=q+(d-1)(d-2)\sqrt {q}$
. Then the number of
![]() ${\mathbb {F}}_q$
-points on
${\mathbb {F}}_q$
-points on
![]() $C\times \mathbb {A}^{n-2}$
is
$C\times \mathbb {A}^{n-2}$
is
![]() $q^{n-1}+(d-1)(d-2)q^{n-3/2}$
. Thus, the constant
$q^{n-1}+(d-1)(d-2)q^{n-3/2}$
. Thus, the constant
![]() $5$
in (1.4) cannot possibly be improved by more than
$5$
in (1.4) cannot possibly be improved by more than
![]() $5$
.
$5$
.
Remark 1.6 While the cylinder
![]() $C\times \mathbb {A}^{n-2}$
in Example 1.5 is nonsingular, its Zariski closure in
$C\times \mathbb {A}^{n-2}$
in Example 1.5 is nonsingular, its Zariski closure in
![]() $\mathbb {P}^n$
has a large (in fact,
$\mathbb {P}^n$
has a large (in fact,
![]() $(n-3)$
-dimensional) singular locus. In general, let
$(n-3)$
-dimensional) singular locus. In general, let
![]() $X\subset \mathbb {A}^n$
be a geometrically irreducible hypersurface such that
$X\subset \mathbb {A}^n$
be a geometrically irreducible hypersurface such that
![]() $\#X({\mathbb {F}}_q)\geq q^{n-1}+ (d-1)(d-2)q^{n-3/2}-O_d(q^{n-2})$
for large
$\#X({\mathbb {F}}_q)\geq q^{n-1}+ (d-1)(d-2)q^{n-3/2}-O_d(q^{n-2})$
for large
![]() $q$
. Theorem 6.1 in [Reference Ghorpade and Lachaud3] implies that the Zariski closure of
$q$
. Theorem 6.1 in [Reference Ghorpade and Lachaud3] implies that the Zariski closure of
![]() $X$
in
$X$
in
![]() $\mathbb {P}^n$
must have singular locus of dimension
$\mathbb {P}^n$
must have singular locus of dimension
![]() $n-3$
or
$n-3$
or
![]() $n-2$
.
$n-2$
.
We exhibit a forbidden interval for
![]() $|X({\mathbb {F}}_q)|$
that improves Theorem 4 in [Reference Slavov7]. The statement below does not require
$|X({\mathbb {F}}_q)|$
that improves Theorem 4 in [Reference Slavov7]. The statement below does not require
![]() $X$
to be geometrically irreducible.
$X$
to be geometrically irreducible.
Theorem 1.7 Let
![]() $X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
be a hypersurface of degree
$X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
be a hypersurface of degree
![]() $d$
. If
$d$
. If
then in fact
Remark 1.8 Let us write
![]() $g(d)+\cdots $
for an effectively computable
$g(d)+\cdots $
for an effectively computable
![]() $g(d)+g_1(d)$
, where
$g(d)+g_1(d)$
, where
![]() $g_1(d)=o(g(d))$
for
$g_1(d)=o(g(d))$
for
![]() $d\to \infty $
. Theorem 1.7 has content when the right-hand side of (1.6) exceeds the right-hand side of (1.7), which takes place for
$d\to \infty $
. Theorem 1.7 has content when the right-hand side of (1.6) exceeds the right-hand side of (1.7), which takes place for
![]() $q>16d^4+\cdots $
. Thus, in the presence of Theorem 1.4, Theorem 1.7 addresses the range
$q>16d^4+\cdots $
. Thus, in the presence of Theorem 1.4, Theorem 1.7 addresses the range
![]() $16d^4+\cdots <q<15d^{13/3}$
. Notice that in the Lang–Weil bound (1.2), the approximation term
$16d^4+\cdots <q<15d^{13/3}$
. Notice that in the Lang–Weil bound (1.2), the approximation term
![]() $q^{n-1}$
dominates the error precisely when
$q^{n-1}$
dominates the error precisely when
![]() $q>d^4+\cdots $
. This is why it is reasonable to frame the entire discussion of the Lang–Weil bound in the range
$q>d^4+\cdots $
. This is why it is reasonable to frame the entire discussion of the Lang–Weil bound in the range
![]() $q>d^4+\cdots $
. For example, any lower Lang–Weil bound is trivial for
$q>d^4+\cdots $
. For example, any lower Lang–Weil bound is trivial for
![]() $q$
below this threshold.
$q$
below this threshold.
1.2 Lower bounds
The proof of Theorem 4 in [Reference Slavov7] actually gives a lower bound which is tighter for
![]() $q\gg 1$
than the one stated in [Reference Slavov7].
$q\gg 1$
than the one stated in [Reference Slavov7].
Theorem 1.9 Let
![]() $X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
be a geometrically irreducible hypersurface of degree
$X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
be a geometrically irreducible hypersurface of degree
![]() $d$
. Then
$d$
. Then
where the implied constant depends only on
![]() $d$
and can be computed explicitly.
$d$
and can be computed explicitly.
We give a version with an explicit lower bound as well.
Theorem 1.10 Let
![]() $X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
be a geometrically irreducible hypersurface of degree
$X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
be a geometrically irreducible hypersurface of degree
![]() $d$
. Suppose that
$d$
. Suppose that
![]() $q>15d^{13/3}$
. Then
$q>15d^{13/3}$
. Then
Example 1.11 As in Example 1.5, let
![]() $d\geq 3$
be such that
$d\geq 3$
be such that
![]() is a prime power. The curve
is a prime power. The curve
![]() $\{y^{d-1}z+yz^{d-1}=x^d\}$
in
$\{y^{d-1}z+yz^{d-1}=x^d\}$
in
![]() $\mathbb {P}^2$
over
$\mathbb {P}^2$
over
![]() ${\mathbb {F}}_{q_0}$
intersects the line
${\mathbb {F}}_{q_0}$
intersects the line
![]() $x=0$
at
$x=0$
at
![]() $d$
distinct points defined over an extension
$d$
distinct points defined over an extension
![]() ${\mathbb {F}}_{q_1}$
of
${\mathbb {F}}_{q_1}$
of
![]() ${\mathbb {F}}_{q_0}$
. Let
${\mathbb {F}}_{q_0}$
. Let
![]() $q$
be an even power of
$q$
be an even power of
![]() $q_1$
. Then the affine curve
$q_1$
. Then the affine curve
![]() in
in
![]() $\mathbb {A}^2_{{\mathbb {F}}_q}$
satisfies
$\mathbb {A}^2_{{\mathbb {F}}_q}$
satisfies
![]() $\#C({\mathbb {F}}_q)= q-(d-1)(d-2)\sqrt {q}-d+1$
. Consequently, the number of
$\#C({\mathbb {F}}_q)= q-(d-1)(d-2)\sqrt {q}-d+1$
. Consequently, the number of
![]() ${\mathbb {F}}_q$
-points on the hypersurface
${\mathbb {F}}_q$
-points on the hypersurface
![]() $C\times \mathbb {A}^{n-2}$
in
$C\times \mathbb {A}^{n-2}$
in
![]() $\mathbb {A}^n$
is
$\mathbb {A}^n$
is
![]() $q^{n-1}-(d-1)(d-2)q^{n-3/2}-(d-1)q^{n-2}$
. Therefore, the constant
$q^{n-1}-(d-1)(d-2)q^{n-3/2}-(d-1)q^{n-2}$
. Therefore, the constant
![]() $d+0.6$
in (1.9) cannot possibly be improved by more than
$d+0.6$
in (1.9) cannot possibly be improved by more than
![]() $1.6$
.
$1.6$
.
We can elaborate on (1.8) by pushing the implied constant further down.
Corollary 1.12 Let
![]() $X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
be a geometrically irreducible hypersurface of degree
$X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
be a geometrically irreducible hypersurface of degree
![]() $d$
. Then
$d$
. Then
 $$ \begin{align} |X({\mathbb{F}}_q)|&\geq q^{n-1}-(d-1)(d-2)q^{n-3/2}-dq^{n-2} -2(d-1)(d-2)q^{n-5/2}\nonumber\\ &-(2(d-1)^2(d-2)^2+d^2/2+d+2+\pi^2/6)q^{n-3}-O_d(q^{n-7/2}). \end{align} $$
$$ \begin{align} |X({\mathbb{F}}_q)|&\geq q^{n-1}-(d-1)(d-2)q^{n-3/2}-dq^{n-2} -2(d-1)(d-2)q^{n-5/2}\nonumber\\ &-(2(d-1)^2(d-2)^2+d^2/2+d+2+\pi^2/6)q^{n-3}-O_d(q^{n-7/2}). \end{align} $$
A lower Lang–Weil bound can be useful in proving that a geometrically irreducible hypersurface
![]() $X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
has an
$X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
has an
![]() ${\mathbb {F}}_q$
-rational point. It is known (see Theorem 5.4 in [Reference Cafure and Matera2] and its proof) that if
${\mathbb {F}}_q$
-rational point. It is known (see Theorem 5.4 in [Reference Cafure and Matera2] and its proof) that if
![]() $q>1.5d^4+\cdots $
, then
$q>1.5d^4+\cdots $
, then
![]() $X({\mathbb {F}}_q)\neq \emptyset $
. Notice that the approximation term
$X({\mathbb {F}}_q)\neq \emptyset $
. Notice that the approximation term
![]() $q^{n-1}$
in (1.10) dominates the remaining explicit terms already for
$q^{n-1}$
in (1.10) dominates the remaining explicit terms already for
![]() $q>d^4+\cdots $
. Based on this heuristic, we state the following conjecture.
$q>d^4+\cdots $
. Based on this heuristic, we state the following conjecture.
Conjecture 1.13 There exists an effectively computable function
![]() $g_1(d)=O(d^{7/2})$
as
$g_1(d)=O(d^{7/2})$
as
![]() $d\to \infty $
with the following property. Let
$d\to \infty $
with the following property. Let
![]() $X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
be a geometrically irreducible hypersurface of degree
$X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
be a geometrically irreducible hypersurface of degree
![]() $d$
. Then
$d$
. Then
![]() $X({\mathbb {F}}_q)\neq \emptyset $
as long as
$X({\mathbb {F}}_q)\neq \emptyset $
as long as
![]() $q>d^4+g_1(d)$
.
$q>d^4+g_1(d)$
.
1.3 Outline
This paper builds upon the author’s earlier work [Reference Slavov7] and is inspired by Tao’s discussion [Reference Tao10] of the Lang–Weil bound through random sampling and the idea of Cafure–Matera [Reference Cafure and Matera2] to slice
![]() $X$
with planes (a plane is a two-dimensional affine linear subvariety of
$X$
with planes (a plane is a two-dimensional affine linear subvariety of
![]() $\mathbb {A}^n_{{\mathbb {F}}_q}$
). If
$\mathbb {A}^n_{{\mathbb {F}}_q}$
). If
![]() $H\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
is any plane, then
$H\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
is any plane, then
![]() $\#(X\cap H)({\mathbb {F}}_q)$
is either
$\#(X\cap H)({\mathbb {F}}_q)$
is either
![]() $q^2$
,
$q^2$
,
![]() $0$
, or
$0$
, or
![]() $\approx kq$
, where
$\approx kq$
, where
![]() $k$
is the number of geometrically irreducible
$k$
is the number of geometrically irreducible
![]() ${\mathbb {F}}_q$
-irreducible components of
${\mathbb {F}}_q$
-irreducible components of
![]() $X\cap H$
. For
$X\cap H$
. For
![]() $0\leq k\leq d$
, we exhibit a small interval
$0\leq k\leq d$
, we exhibit a small interval
![]() $I_k=[a_k,b_k]$
containing
$I_k=[a_k,b_k]$
containing
![]() $kq$
so that if we also define
$kq$
so that if we also define
![]() $I_\infty =\{q^2\}$
, then each
$I_\infty =\{q^2\}$
, then each
![]() $\#(X\cap H)({\mathbb {F}}_q)$
belongs to
$\#(X\cap H)({\mathbb {F}}_q)$
belongs to
![]() $\bigcup I_k$
.
$\bigcup I_k$
.

The problem when it comes to the upper bound is that when
![]() $k$
is large, planes
$k$
is large, planes
![]() $H$
with
$H$
with
![]() $\#(X\cap H)({\mathbb {F}}_q)\in I_k$
contribute significantly toward the count
$\#(X\cap H)({\mathbb {F}}_q)\in I_k$
contribute significantly toward the count
![]() $\#X({\mathbb {F}}_q)$
. However, it turns out that the number of such
$\#X({\mathbb {F}}_q)$
. However, it turns out that the number of such
![]() $H$
’s decreases quickly as
$H$
’s decreases quickly as
![]() $k$
grows.
$k$
grows.
2 A collection of small intervals
Lemma 2.1 [Reference Schmidt5, Lemma 5]
Let
![]() $C\subset \mathbb {A}^2_{{\mathbb {F}}_q}$
be a curve of degree
$C\subset \mathbb {A}^2_{{\mathbb {F}}_q}$
be a curve of degree
![]() $d$
. Let
$d$
. Let
![]() $k$
be the number of geometrically irreducible
$k$
be the number of geometrically irreducible
![]() ${\mathbb {F}}_q$
-irreducible components of
${\mathbb {F}}_q$
-irreducible components of
![]() $C$
. Then
$C$
. Then
It will be crucial to give a refined upper bound when
![]() $k=1$
.
$k=1$
.
Lemma 2.2 Let
![]() $C\subset \mathbb {A}^2_{{\mathbb {F}}_q}$
be a curve of degree
$C\subset \mathbb {A}^2_{{\mathbb {F}}_q}$
be a curve of degree
![]() $d$
. Suppose that
$d$
. Suppose that
![]() $C$
has exactly one geometrically irreducible
$C$
has exactly one geometrically irreducible
![]() ${\mathbb {F}}_q$
-irreducible component. Then
${\mathbb {F}}_q$
-irreducible component. Then
Proof Let
![]() $C_1,\dots ,C_s$
be the
$C_1,\dots ,C_s$
be the
![]() ${\mathbb {F}}_q$
-irreducible components of
${\mathbb {F}}_q$
-irreducible components of
![]() $C$
. Suppose that
$C$
. Suppose that
![]() $C_1$
is geometrically irreducible, but
$C_1$
is geometrically irreducible, but
![]() $C_i$
is not for
$C_i$
is not for
![]() $i\geq 2$
. Let
$i\geq 2$
. Let
![]() $e=\deg (C_1)$
. Note that
$e=\deg (C_1)$
. Note that
![]() $(d,e)\neq (2,1)$
.
$(d,e)\neq (2,1)$
.
Using the Aubry–Perret bound (1.3) for
![]() $C_1$
and Lemma 2.3 in [Reference Cafure and Matera2] for each
$C_1$
and Lemma 2.3 in [Reference Cafure and Matera2] for each
![]() $C_i$
with
$C_i$
with
![]() $i\geq 2$
, we estimate
$i\geq 2$
, we estimate
 $$ \begin{align*} |C({\mathbb{F}}_q)| &\leq |C_1({\mathbb{F}}_q)|+\sum_{i=2}^s |C_i({\mathbb{F}}_q)|\\&\leq q+(e-1)(e-2)\sqrt{q}+1+\sum_{i=2}^s (\deg C_i)^2/4\\&\leq q+(e-1)(e-2)\sqrt{q}+1+(d-e)^2/4\\[3pt]&\leq q+(d-1)(d-2)\sqrt{q}+1; \end{align*} $$
$$ \begin{align*} |C({\mathbb{F}}_q)| &\leq |C_1({\mathbb{F}}_q)|+\sum_{i=2}^s |C_i({\mathbb{F}}_q)|\\&\leq q+(e-1)(e-2)\sqrt{q}+1+\sum_{i=2}^s (\deg C_i)^2/4\\&\leq q+(e-1)(e-2)\sqrt{q}+1+(d-e)^2/4\\[3pt]&\leq q+(d-1)(d-2)\sqrt{q}+1; \end{align*} $$
to justify the last inequality in the chain, note that it is equivalent to
and holds true because either
![]() $e=d$
, or else
$e=d$
, or else
![]() $d-e>0$
, and we can write
$d-e>0$
, and we can write
(using that
![]() $e\geq 1$
and
$e\geq 1$
and
![]() $d\geq 3$
on the last step).
$d\geq 3$
on the last step).
Let
![]() $a_0=0$
,
$a_0=0$
,
![]() $b_0=d^2/4$
,
$b_0=d^2/4$
,
![]() $a_1=q-(d-1)(d-2)\sqrt {q}-d+1$
, and
$a_1=q-(d-1)(d-2)\sqrt {q}-d+1$
, and
![]() $b_1=q+(d-1) (d-2)\sqrt {q}+1$
. For
$b_1=q+(d-1) (d-2)\sqrt {q}+1$
. For
![]() $2\leq k\leq d$
, set
$2\leq k\leq d$
, set
![]() $a_k=kq-(d-1)(d-2)\sqrt {q}-d^2-d-1$
and
$a_k=kq-(d-1)(d-2)\sqrt {q}-d^2-d-1$
and
![]() $b_k=kq+(d-1)(d-2)\sqrt {q}+d^2+d+1$
. Finally, set
$b_k=kq+(d-1)(d-2)\sqrt {q}+d^2+d+1$
. Finally, set
![]() $a_\infty =b_\infty =q^2$
. Define
$a_\infty =b_\infty =q^2$
. Define
![]() for
for
![]() $k\in \{0,\dots ,d\}\cup \{\infty \}$
.
$k\in \{0,\dots ,d\}\cup \{\infty \}$
.
Lemma 2.3 Let
![]() $X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
be a hypersurface of degree
$X\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
be a hypersurface of degree
![]() $d$
. Let
$d$
. Let
![]() $H\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
be a plane. Then
$H\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
be a plane. Then
![]() $\#(X\cap H)({\mathbb {F}}_q)\in I_k$
for some
$\#(X\cap H)({\mathbb {F}}_q)\in I_k$
for some
![]() $k\in \{0,\dots ,d\}\cup \{\infty \}$
.
$k\in \{0,\dots ,d\}\cup \{\infty \}$
.
Proof If
![]() $X\cap H=\emptyset $
, then
$X\cap H=\emptyset $
, then
![]() $\#(X\cap H)({\mathbb {F}}_q)=0\in I_0$
. If
$\#(X\cap H)({\mathbb {F}}_q)=0\in I_0$
. If
![]() $H\subset X$
, then
$H\subset X$
, then
![]() $X\cap H=H$
and
$X\cap H=H$
and
![]() $\#(X\cap H)({\mathbb {F}}_q)=q^2\in I_\infty $
. Suppose that
$\#(X\cap H)({\mathbb {F}}_q)=q^2\in I_\infty $
. Suppose that
![]() $X\cap H\neq \emptyset $
and
$X\cap H\neq \emptyset $
and
![]() $H\not \subset X$
. Let
$H\not \subset X$
. Let
![]() $k$
be the number of geometrically irreducible
$k$
be the number of geometrically irreducible
![]() ${\mathbb {F}}_q$
-irreducible components of the degree
${\mathbb {F}}_q$
-irreducible components of the degree
![]() $d$
plane curve
$d$
plane curve
![]() $X\cap H\subset H\simeq \mathbb {A}^2_{{\mathbb {F}}_q}$
. Then
$X\cap H\subset H\simeq \mathbb {A}^2_{{\mathbb {F}}_q}$
. Then
![]() $0\leq k\leq d$
. If
$0\leq k\leq d$
. If
![]() $k=0$
, the proof of Lemma 11 in [Reference Slavov7] gives
$k=0$
, the proof of Lemma 11 in [Reference Slavov7] gives
![]() $\#(X\cap H)({\mathbb {F}}_q)\leq d^2/4$
. If
$\#(X\cap H)({\mathbb {F}}_q)\leq d^2/4$
. If
![]() $k=1$
, we use Lemma 2.2 and the lower bound from (1.3) applied to a geometrically irreducible
$k=1$
, we use Lemma 2.2 and the lower bound from (1.3) applied to a geometrically irreducible
![]() ${\mathbb {F}}_q$
-irreducible component (necessarily of degree
${\mathbb {F}}_q$
-irreducible component (necessarily of degree
![]() $\leq d$
) of
$\leq d$
) of
![]() $X$
. For
$X$
. For
![]() $2\leq k\leq d$
, use Lemma 2.1.
$2\leq k\leq d$
, use Lemma 2.1.
Alternatively, one could take
![]() $b_d=dq$
by the Schwartz–Zippel lemma.
$b_d=dq$
by the Schwartz–Zippel lemma.
When it comes to giving an upper bound for
![]() $|X({\mathbb {F}}_q)|$
, it will be more convenient to work with
$|X({\mathbb {F}}_q)|$
, it will be more convenient to work with
![]() and
and
![]() for
for
![]() $i\in \{2,\dots ,d\}\cup \{\infty \}$
.
$i\in \{2,\dots ,d\}\cup \{\infty \}$
.
3 Probability estimates
We spell out in detail the proof of Theorem 1.3; the proofs of the remaining results will then require only slight modifications. The implied constant in each
![]() $O$
-notation is allowed to depend only on
$O$
-notation is allowed to depend only on
![]() $d$
(a priori, possibly also on
$d$
(a priori, possibly also on
![]() $n$
), but not on
$n$
), but not on
![]() $q$
or
$q$
or
![]() $X$
.
$X$
.
Proof of Theorem 1.3
Set
![]() . For a plane
. For a plane
![]() $H\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
chosen uniformly at random, consider
$H\subset \mathbb {A}^n_{{\mathbb {F}}_q}$
chosen uniformly at random, consider
![]() $\#(X\cap H)({\mathbb {F}}_q)$
as a random variable. Let
$\#(X\cap H)({\mathbb {F}}_q)$
as a random variable. Let
![]() $\mu $
and
$\mu $
and
![]() $\sigma ^2$
denote its mean and variance. Lemma 10 in [Reference Slavov7] and (1.2) imply
$\sigma ^2$
denote its mean and variance. Lemma 10 in [Reference Slavov7] and (1.2) imply
Write
 $$ \begin{align} \frac{N}{q^{n-2}}=\mu\leq \sum_{k\in\{1,\dots,d\}\cup\{\infty\}}\operatorname{\mathrm{Prob}}\Big(\#(X\cap H)({\mathbb{F}}_q)\in J_k\Big)b_k. \end{align} $$
$$ \begin{align} \frac{N}{q^{n-2}}=\mu\leq \sum_{k\in\{1,\dots,d\}\cup\{\infty\}}\operatorname{\mathrm{Prob}}\Big(\#(X\cap H)({\mathbb{F}}_q)\in J_k\Big)b_k. \end{align} $$
For
![]() $k\in \{1,\dots ,d\}\cup \{\infty \}$
, denote
$k\in \{1,\dots ,d\}\cup \{\infty \}$
, denote
We can assume that
![]() $q$
is large enough so that the intervals
$q$
is large enough so that the intervals
![]() $J_1,\dots ,J_d$
are pairwise disjoint.
$J_1,\dots ,J_d$
are pairwise disjoint.
Let
![]() $k\in \{2,\dots ,d\}$
. If
$k\in \{2,\dots ,d\}$
. If
![]() $H$
is a plane such that
$H$
is a plane such that
![]() $\#(X\cap H)({\mathbb {F}}_q)\in J_k\cup \dots \cup J_d$
, then
$\#(X\cap H)({\mathbb {F}}_q)\in J_k\cup \dots \cup J_d$
, then
Define
![]() $t$
via
$t$
via
![]() $(k-1)q-O(\sqrt {q})=t\sigma $
; then Chebyshev’s inequality and the variance bound (3.1) imply
$(k-1)q-O(\sqrt {q})=t\sigma $
; then Chebyshev’s inequality and the variance bound (3.1) imply
 $$ \begin{align} p_k+\cdots+p_d =\operatorname{\mathrm{Prob}}\Big(\#(X\cap H)({\mathbb{F}}_q)\in J_k\cup\dots\cup J_d\Big) &\leq\frac{1}{t^2}\notag \\ &=\frac{\sigma^2}{((k-1)q-O(\sqrt{q}))^2}\notag \\ &\leq\frac{q+O(\sqrt{q})}{((k-1)q-O(\sqrt{q}))^2}\notag \\ &=\frac{1}{(k-1)^2 q}+O(q^{-3/2}). \end{align} $$
$$ \begin{align} p_k+\cdots+p_d =\operatorname{\mathrm{Prob}}\Big(\#(X\cap H)({\mathbb{F}}_q)\in J_k\cup\dots\cup J_d\Big) &\leq\frac{1}{t^2}\notag \\ &=\frac{\sigma^2}{((k-1)q-O(\sqrt{q}))^2}\notag \\ &\leq\frac{q+O(\sqrt{q})}{((k-1)q-O(\sqrt{q}))^2}\notag \\ &=\frac{1}{(k-1)^2 q}+O(q^{-3/2}). \end{align} $$
If
![]() $H$
is a plane such that
$H$
is a plane such that
![]() $\#(X\cap H)({\mathbb {F}}_q)=q^2$
, then
$\#(X\cap H)({\mathbb {F}}_q)=q^2$
, then
Define
![]() $t$
via
$t$
via
![]() $q^2-O(q)=t\sigma $
; then
$q^2-O(q)=t\sigma $
; then
 $$\begin{align*}p_\infty\leq \frac{1}{t^2}=\frac{\sigma^2}{(q^2-O(q))^2}\leq \frac{q+O(\sqrt{q})}{(q^2-O(q))^2}= q^{-3}+O(q^{-7/2}),\!\quad\text{and hence}\quad\! p_\infty b_\infty=O(q^{-1}). \end{align*}$$
$$\begin{align*}p_\infty\leq \frac{1}{t^2}=\frac{\sigma^2}{(q^2-O(q))^2}\leq \frac{q+O(\sqrt{q})}{(q^2-O(q))^2}= q^{-3}+O(q^{-7/2}),\!\quad\text{and hence}\quad\! p_\infty b_\infty=O(q^{-1}). \end{align*}$$
Note that
![]() $b_k-b_{k-1}=q+O(1)$
for
$b_k-b_{k-1}=q+O(1)$
for
![]() $2\leq k\leq d$
. We now go back to (3.2) and apply the Abel summation formula:
$2\leq k\leq d$
. We now go back to (3.2) and apply the Abel summation formula:
 $$ \begin{align*} \frac{N}{q^{n-2}}=\mu&\leq (p_1+\cdots+p_d)b_1+(p_2+\cdots+p_d)(b_2-b_1)+\cdots+p_d(b_d-b_{d-1})+p_\infty b_\infty\\ &\leq b_1+\frac{1}{1^2}+\cdots+\frac{1}{(d-1)^2}+O(q^{-1/2})\\ &\leq q+(d-1)(d-2)\sqrt{q}+1+\pi^2/6+O(q^{-1/2}). \end{align*} $$
$$ \begin{align*} \frac{N}{q^{n-2}}=\mu&\leq (p_1+\cdots+p_d)b_1+(p_2+\cdots+p_d)(b_2-b_1)+\cdots+p_d(b_d-b_{d-1})+p_\infty b_\infty\\ &\leq b_1+\frac{1}{1^2}+\cdots+\frac{1}{(d-1)^2}+O(q^{-1/2})\\ &\leq q+(d-1)(d-2)\sqrt{q}+1+\pi^2/6+O(q^{-1/2}). \end{align*} $$
Multiply both sides by
![]() $q^{n-2}$
to arrive at (1.4).
$q^{n-2}$
to arrive at (1.4).
Going through all the explicit inequalities with an
![]() $O$
-term, one can compute explicitly a possible value of the constant implicit in (1.4). In fact, since the Cafure–Matera bound gives a choice of
$O$
-term, one can compute explicitly a possible value of the constant implicit in (1.4). In fact, since the Cafure–Matera bound gives a choice of
![]() $C_d$
in the Lang–Weil bound that depends only on
$C_d$
in the Lang–Weil bound that depends only on
![]() $d$
and not on
$d$
and not on
![]() $n$
, a second look at all the inequalities written down in the proof above reveals that the implied constant in (1.4) can likewise be chosen not to depend on
$n$
, a second look at all the inequalities written down in the proof above reveals that the implied constant in (1.4) can likewise be chosen not to depend on
![]() $n$
.
$n$
.
For the rest of the paper, we follow the notation and proof of Theorem 1.3.
Proof of Theorem 1.9
Say that a plane
![]() $H$
is “bad” if
$H$
is “bad” if
![]() $\#(X\cap H)({\mathbb {F}}_q)\in I_0$
and “good” otherwise. If
$\#(X\cap H)({\mathbb {F}}_q)\in I_0$
and “good” otherwise. If
![]() $H\subset \mathbb {A}^2_{{\mathbb {F}}_q}$
is a bad plane, then
$H\subset \mathbb {A}^2_{{\mathbb {F}}_q}$
is a bad plane, then
 $$\begin{align*}|\#(X\cap H)({\mathbb{F}}_q)-\mu|\geq \frac{N}{q^{n-2}}-\frac{d^2}{4}\geq q-O(\sqrt{q}).\end{align*}$$
$$\begin{align*}|\#(X\cap H)({\mathbb{F}}_q)-\mu|\geq \frac{N}{q^{n-2}}-\frac{d^2}{4}\geq q-O(\sqrt{q}).\end{align*}$$
By computations similar to the ones in the proof of Theorem 1.3, the probability that a plane is bad is at most
![]() $q^{-1}+O(q^{-3/2})$
. Every good plane contributes at least
$q^{-1}+O(q^{-3/2})$
. Every good plane contributes at least
![]() $a_1$
to the mean. Therefore,
$a_1$
to the mean. Therefore,
giving (1.8).
Proof of Corollary 1.12
In fact, the proofs of Theorems 1.3 and 1.9 give an algorithm that takes as input a half-integer
![]() $r\geq 0$
and constantsFootnote
1
$r\geq 0$
and constantsFootnote
1
![]() $C_d^{(j)}$
and
$C_d^{(j)}$
and
![]() $D_d^{(j)}$
for each half-integer
$D_d^{(j)}$
for each half-integer
![]() $1/2\leq j\leq r$
such that
$1/2\leq j\leq r$
such that
 $$\begin{align*}|X({\mathbb{F}}_q)|\leq q^{n-1}+\sum_{j=1/2}^r C_d^{(j)} q^{n-1-j}+O_d(q^{n-r-3/2}) \!\!\qquad\text{(summation over half-integers)}\end{align*}$$
$$\begin{align*}|X({\mathbb{F}}_q)|\leq q^{n-1}+\sum_{j=1/2}^r C_d^{(j)} q^{n-1-j}+O_d(q^{n-r-3/2}) \!\!\qquad\text{(summation over half-integers)}\end{align*}$$
and
 $$\begin{align*}|X({\mathbb{F}}_q)|\geq q^{n-1}-\sum_{j=1/2}^r D_d^{(j)} q^{n-1-j}-O_d(q^{n-r-3/2}) \!\!\!\qquad\text{(summation over half-integers)},\end{align*}$$
$$\begin{align*}|X({\mathbb{F}}_q)|\geq q^{n-1}-\sum_{j=1/2}^r D_d^{(j)} q^{n-1-j}-O_d(q^{n-r-3/2}) \!\!\!\qquad\text{(summation over half-integers)},\end{align*}$$
and returns as output four additional
![]() $C_d^{(r+1/2)}$
,
$C_d^{(r+1/2)}$
,
![]() $C_d^{(r+1)}$
,
$C_d^{(r+1)}$
,
![]() $D_d^{(r+1/2)}$
, and
$D_d^{(r+1/2)}$
, and
![]() $D_d^{(r+1)}$
such that
$D_d^{(r+1)}$
such that
 $$\begin{align*}|X({\mathbb{F}}_q)|\leq q^{n-1}+\sum_{j=1/2}^{r+1} C_d^{(j)} q^{n-1-j}+O_d(q^{n-r-5/2}) \!\!\qquad\text{(summation over half-integers)}\end{align*}$$
$$\begin{align*}|X({\mathbb{F}}_q)|\leq q^{n-1}+\sum_{j=1/2}^{r+1} C_d^{(j)} q^{n-1-j}+O_d(q^{n-r-5/2}) \!\!\qquad\text{(summation over half-integers)}\end{align*}$$
and
 $$\begin{align*}|X({\mathbb{F}}_q)|\geq q^{n-1}-\sum_{j=1/2}^{r+1} D_d^{(j)} q^{n-1-j}-O_d(q^{n-r-5/2}) \!\!\!\qquad\text{(summation over half-integers)}.\end{align*}$$
$$\begin{align*}|X({\mathbb{F}}_q)|\geq q^{n-1}-\sum_{j=1/2}^{r+1} D_d^{(j)} q^{n-1-j}-O_d(q^{n-r-5/2}) \!\!\!\qquad\text{(summation over half-integers)}.\end{align*}$$
Initiating the algorithm with
![]() $r=0$
and the rather weak version
$r=0$
and the rather weak version
of (1.2), we obtained (1.4) and (1.8). In turn, taking the upper bound for
![]() $N$
from (1.4) and the lower bound for
$N$
from (1.4) and the lower bound for
![]() $N$
from (1.8) as input, we obtain (1.10).
$N$
from (1.8) as input, we obtain (1.10).
Proof of Theorem 1.1
We now slice with a random plane
![]() $H\subset \mathbb {P}^n_{{\mathbb {F}}_q}$
. The mean
$H\subset \mathbb {P}^n_{{\mathbb {F}}_q}$
. The mean
![]() $\mu $
of
$\mu $
of
![]() $\#(X\cap H)({\mathbb {F}}_q)$
is
$\#(X\cap H)({\mathbb {F}}_q)$
is
![]() $N\rho _1$
, where
$N\rho _1$
, where
![]() $N=|X({\mathbb {F}}_q)|$
and
$N=|X({\mathbb {F}}_q)|$
and
![]() $\rho _1=(q^3-1)/(q^{n+1}-1)$
is the probability that a plane passes through a given point. Let
$\rho _1=(q^3-1)/(q^{n+1}-1)$
is the probability that a plane passes through a given point. Let
![]() $\rho _2$
be the probability that a plane passes through two distinct given points. Explicitly (in terms of
$\rho _2$
be the probability that a plane passes through two distinct given points. Explicitly (in terms of
![]() $q$
-binomial coefficients),
$q$
-binomial coefficients),
![]() $\rho _2=\binom {n-1}{1}_q/\binom {n+1}{3}_q$
. One verifies directly that
$\rho _2=\binom {n-1}{1}_q/\binom {n+1}{3}_q$
. One verifies directly that
![]() $\rho _2\leq \rho _1^2$
and expresses
$\rho _2\leq \rho _1^2$
and expresses
![]() $\sigma ^2$
as in [Reference Tao10]:
$\sigma ^2$
as in [Reference Tao10]:
to deduce
![]() $\sigma ^2\leq \mu $
.
$\sigma ^2\leq \mu $
.
We can still take
![]() $I_0=[0,d^2/4]$
. Use the projective version of (1.3) (Corollary 2.5 in [Reference Aubry, Perret, Pellikaan, Perret and Vlădu1]). Adapt
$I_0=[0,d^2/4]$
. Use the projective version of (1.3) (Corollary 2.5 in [Reference Aubry, Perret, Pellikaan, Perret and Vlădu1]). Adapt
![]() $I_1$
with
$I_1$
with
![]() $a_1=q-(d-1)(d-2)\sqrt {q}+1$
. Use
$a_1=q-(d-1)(d-2)\sqrt {q}+1$
. Use
![]() $I_\infty =\{q^2+q+1\}$
. Up to a summand
$I_\infty =\{q^2+q+1\}$
. Up to a summand
![]() $d$
to account for points at infinity, the remaining
$d$
to account for points at infinity, the remaining
![]() $a_k$
and
$a_k$
and
![]() $b_k$
are unchanged.
$b_k$
are unchanged.
Proceed as in the proof of Theorems 1.3 and 1.9. On the very last step in proving either bound, multiply by
![]() $1/\rho _1$
rather than by
$1/\rho _1$
rather than by
![]() $q^{n-2}$
and use that
$q^{n-2}$
and use that
![]() $1/\rho _1=q^{n-2}+ O(q^{n-5})$
.
$1/\rho _1=q^{n-2}+ O(q^{n-5})$
.
4 Explicit versions
Proof of Theorem 1.4
The statement clearly holds for
![]() $d=1$
, so assume that
$d=1$
, so assume that
![]() $d\geq 2$
. We will use the explicit Cafure–Matera bound for
$d\geq 2$
. We will use the explicit Cafure–Matera bound for
![]() $N$
. Replace the variance bound (3.1) by
$N$
. Replace the variance bound (3.1) by
to verify the last inequality above, we argue as follows. For any
![]() $c_1>0$
and
$c_1>0$
and
![]() $c_2>0$
, the function
$c_2>0$
, the function
![]() $q\mapsto q/(c_1\sqrt {q}+c_2)$
is increasing. Therefore,
$q\mapsto q/(c_1\sqrt {q}+c_2)$
is increasing. Therefore,
 $$\begin{align*}\frac{q}{(d-1)(d-2)\sqrt{q}+5d^2+d+1}>\frac{15d^{13/3}}{(d-1)(d-2)\sqrt{15}d^{13/6}+5d^2+d+1}.\end{align*}$$
$$\begin{align*}\frac{q}{(d-1)(d-2)\sqrt{q}+5d^2+d+1}>\frac{15d^{13/3}}{(d-1)(d-2)\sqrt{15}d^{13/6}+5d^2+d+1}.\end{align*}$$
It remains to check that the function
![]() $g(d)$
on the right-hand side above satisfies
$g(d)$
on the right-hand side above satisfies
![]() $g(d)>7.44$
for any integer
$g(d)>7.44$
for any integer
![]() $d\geq 2$
. On the one hand,
$d\geq 2$
. On the one hand,
![]() $g$
grows like
$g$
grows like
![]() $d^{1/6}$
, so one easily exhibits a
$d^{1/6}$
, so one easily exhibits a
![]() $d_0$
such that
$d_0$
such that
![]() $g(d)>7.44$
for
$g(d)>7.44$
for
![]() $d>d_0$
. Then a simple computer calculation checks that
$d>d_0$
. Then a simple computer calculation checks that
![]() $g(d)>7.44$
for integers
$g(d)>7.44$
for integers
![]() $d\in \{2,\dots ,d_0\}$
as well.
$d\in \{2,\dots ,d_0\}$
as well.
In the same way, one readily checks that the intervals
![]() $J_1,\dots ,J_d$
are pairwise disjoint.
$J_1,\dots ,J_d$
are pairwise disjoint.
For
![]() $k\in \{2,\dots ,d\}$
, replace (3.3) by
$k\in \{2,\dots ,d\}$
, replace (3.3) by
to check the last inequality, one has to consider only
![]() $k=2$
and to argue as above.
$k=2$
and to argue as above.
For
![]() $k\in \{2,\dots ,d\}$
, (3.4) is now replaced by
$k\in \{2,\dots ,d\}$
, (3.4) is now replaced by
 $$\begin{align*}p_k+\cdots+p_d\leq \frac{(8.44/7.44)q}{\left((5.45/7.45)(k-1)q\right)^2}<\frac{2.12}{(k-1)^2q}.\end{align*}$$
$$\begin{align*}p_k+\cdots+p_d\leq \frac{(8.44/7.44)q}{\left((5.45/7.45)(k-1)q\right)^2}<\frac{2.12}{(k-1)^2q}.\end{align*}$$
To bound
![]() $p_\infty b_\infty $
, note that
$p_\infty b_\infty $
, note that
![]() $q>15d^{13/3}>15\times 2^{13/3}>302$
, so
$q>15d^{13/3}>15\times 2^{13/3}>302$
, so
 $$\begin{align*}p_\infty b_\infty\leq\frac{(8.44/7.44)q}{(q^2-(8.44/7.44)q)^2}q^2 =\frac{8.44\times 7.44q}{(7.44q-8.44)^2}<0.01.\end{align*}$$
$$\begin{align*}p_\infty b_\infty\leq\frac{(8.44/7.44)q}{(q^2-(8.44/7.44)q)^2}q^2 =\frac{8.44\times 7.44q}{(7.44q-8.44)^2}<0.01.\end{align*}$$
Since
![]() $b_k-b_{k-1}=q$
for
$b_k-b_{k-1}=q$
for
![]() $3\leq k\leq d$
, but
$3\leq k\leq d$
, but
![]() $b_2-b_1=q+d^2+d$
, we have to estimate
$b_2-b_1=q+d^2+d$
, we have to estimate
![]() $(d^2+d)/q<(d^2+d)/15d^{13/3}<0.02$
. The Abel summation argument now gives
$(d^2+d)/q<(d^2+d)/15d^{13/3}<0.02$
. The Abel summation argument now gives
Proof of Theorem 1.7
Again, assume
![]() $d\geq 2$
. We can assume that the right-hand side of (1.7) is less than the right-hand side of (1.6); i.e.,
$d\geq 2$
. We can assume that the right-hand side of (1.7) is less than the right-hand side of (1.6); i.e.,
This inequality implies in particular that the intervals
![]() $J_1,\dots ,J_d$
are pairwise disjoint. Note that it is equivalent to
$J_1,\dots ,J_d$
are pairwise disjoint. Note that it is equivalent to
![]() $q>r(d)^2$
, where
$q>r(d)^2$
, where
![]() $r(d)$
is the positive root of the quadratic equation
$r(d)$
is the positive root of the quadratic equation
![]() $x^2-4(d-1)(d-2)x-2(d^2+d+13)=0$
.
$x^2-4(d-1)(d-2)x-2(d^2+d+13)=0$
.
Due to (1.6), now we can use the variance bound
![]() $\sigma ^2\leq N/q^{n-2}\leq (3/2)q$
. Furthermore, (1.6) gives
$\sigma ^2\leq N/q^{n-2}\leq (3/2)q$
. Furthermore, (1.6) gives
 $$\begin{align*}a_k-\frac{N}{q^{n-2}}= kq-(d-1)(d-2)\sqrt{q}-(d^2+d+1)-\frac{N}{q^{n-2}}\geq \frac{k-1}{2}q\end{align*}$$
$$\begin{align*}a_k-\frac{N}{q^{n-2}}= kq-(d-1)(d-2)\sqrt{q}-(d^2+d+1)-\frac{N}{q^{n-2}}\geq \frac{k-1}{2}q\end{align*}$$
for
![]() $2\leq k\leq d$
. Therefore,
$2\leq k\leq d$
. Therefore,
![]() $p_k+\cdots +p_d$
is now bounded by
$p_k+\cdots +p_d$
is now bounded by
![]() $6/((k-1)^2q)$
.
$6/((k-1)^2q)$
.
We bound
![]() $(d^2+d)/q$
by
$(d^2+d)/q$
by
![]() $(d^2+d)/(r(d))^2<0.16$
for
$(d^2+d)/(r(d))^2<0.16$
for
![]() $d\geq 2$
. Finally, note that
$d\geq 2$
. Finally, note that
![]() $q>r(2)^2=38$
, so
$q>r(2)^2=38$
, so
![]() $q\geq 41$
, and we can bound
$q\geq 41$
, and we can bound
![]() $p_\infty b_\infty $
by
$p_\infty b_\infty $
by
![]() $6q/(2q-3)^2<0.04$
. Therefore,
$6q/(2q-3)^2<0.04$
. Therefore,
Proof of Theorem 1.10
As above, assume that
![]() $d\geq 2$
. We bound the variance as
$d\geq 2$
. We bound the variance as
Moreover,
 $$\begin{align*}\frac{N}{q^{n-2}}-\frac{d^2}{4}\geq q-(d-1)(d-2)\sqrt{q}-21d^2/4-d-1\geq (6.44/7.44)q.\end{align*}$$
$$\begin{align*}\frac{N}{q^{n-2}}-\frac{d^2}{4}\geq q-(d-1)(d-2)\sqrt{q}-21d^2/4-d-1\geq (6.44/7.44)q.\end{align*}$$
From here, we bound the probability that a plane is bad by
![]() $1.6/q$
. Thus,
$1.6/q$
. Thus,
 $$\begin{align*}\frac{N}{q^{n-2}}\geq \left(1-\frac{1.6}{q}\right)(q-(d-1)(d-2)\sqrt{q}-d+1)\geq q-(d-1)(d-2)\sqrt{q}-(d+0.6).\end{align*}$$
$$\begin{align*}\frac{N}{q^{n-2}}\geq \left(1-\frac{1.6}{q}\right)(q-(d-1)(d-2)\sqrt{q}-d+1)\geq q-(d-1)(d-2)\sqrt{q}-(d+0.6).\end{align*}$$