Hostname: page-component-7dd5485656-frp75 Total loading time: 0 Render date: 2025-10-31T08:29:53.065Z Has data issue: false hasContentIssue false
  • English
  • Français

Harmonic Polynomials Associated With Reflection Groups

Published online by Cambridge University Press:  20 November 2018

Yuan Xu
Yuan Xu*
Affiliation:
Department of Mathematics, University of Oregon, Eugene, Oregon 97403-1222, USA, e-mail: yuan@math.uoregon.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We extend Maxwell’s representation of harmonic polynomials to $h$ -harmonics associated to a reflection invariant weight function 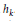${{h}_{k}}$ . Let 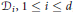${{\mathcal{D}}_{i}},\,1\,\le \,i\,\le \,d$ , be Dunkl’s operators associated with a reflection group. For any homogeneous polynomial 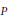$P$ of degree 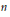$n$ ,we prove the polynomial 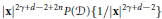${{\left| x \right|}^{2\gamma +d-2+2n}}P\left( \mathcal{D} \right)\left\{ 1/{{\left| x \right|}^{2\gamma +d-2}} \right\}$ is a $h$ -harmonic polynomial of degree 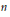$n$ , where 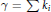$\gamma \,=\,\sum \,ki$ and 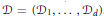$\mathcal{D}\,=\,\left( {{\mathcal{D}}_{1}},\ldots ,{{\mathcal{D}}_{d}} \right)$ . The construction yields a basis for $h$ -harmonics. We also discuss self-adjoint operators acting on the space of $h$ -harmonics.

Keywords

33C5033C45h-harmonicsreflection groupDunkl’s operators

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 4 , 01 December 2000 , pp. 496 - 507
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Baker, T. H. and Forrester, P. J., The Calogero-Sutherland model and generalized classical polynomials. Comm. Math. Phys. 188 (1997), 175–216.Google Scholar
[2] van Diejen, J. F., Confluent hypergeometric orthogonal polynomials related to the rational quantum Calogero system with harmonic confinement. Comm. Math. Phys. 188 (1997), 467–497.Google Scholar
[3] Dunkl, C., Reflection groups and orthogonal polynomials on the sphere. Math. Z. 197 (1988) 33–60.Google Scholar
[4] Dunkl, C., Differential-difference operators associated to reflection groups. Trans. Amer.Math. Soc. 311 (1989), 167–183.Google Scholar
[5] Dunkl, C., Integral kernels with reflection group invariance. Canad. J. Math. 43 (1991), 1213–1227.Google Scholar
[6] Dunkl, C., Intertwining operators associated to the group S3. Trans. Amer.Math. Soc. 347 (1995), 3347–3374.Google Scholar
[7] Dunkl, C., Computing with differential-difference operators. J. Symb. Comput. 28 (1999), 819–826.Google Scholar
[8] Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G., Higher transcendental functions. McGraw-Hill 2, New York, 1953.Google Scholar
[9] Hobson, E. W., The theory of spherical and ellipsoidal harmonics. Chelsea, New York, 1955.Google Scholar
[10] Müller, C., Analysis of spherical symmetries in Euclidean spaces. Springer, New York, 1997.Google Scholar
[11] Murphy, G. E., A new construction of Young's seminormal representation of the symmetric groups. J. Algebra 62 (1981), 287–297.Google Scholar
[12] Rösler, M., Positivity of Dunkl's intertwining operator, q-alg /9710029. DukeMath. J. 98 (1999), 445–463.Google Scholar
[13] Xu, Y., Orthogonal polynomials for a family of product weight functions on the spheres. Canad. J. Math. 49 (1997), 175–192.Google Scholar
[14] Xu, Y., Integration of the intertwining operator for h-harmonic polynomials associated to reflection groups. Proc. Amer.Math. Soc. 125 (1997), 2963–2973.Google Scholar