A set 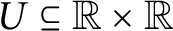$U \subseteq {\mathbb {R}} \times {\mathbb {R}}$ is universal for countable subsets of 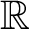${\mathbb {R}}$ if and only if for all 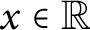$x \in {\mathbb {R}}$, the section 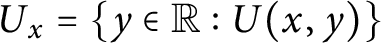$U_x = \{y \in {\mathbb {R}} : U(x,y)\}$ is countable and for all countable sets 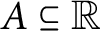$A \subseteq {\mathbb {R}}$, there is an 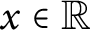$x \in {\mathbb {R}}$ so that 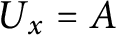$U_x = A$. Define the equivalence relation 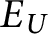$E_U$ on 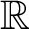${\mathbb {R}}$ by 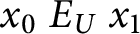$x_0 \ E_U \ x_1$ if and only if 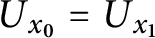$U_{x_0} = U_{x_1}$, which is the equivalence of codes for countable sets of reals according to U. The Friedman–Stanley jump, 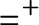$=^+$, of the equality relation takes the form 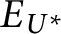$E_{U^*}$ where 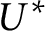$U^*$ is the most natural Borel set that is universal for countable sets. The main result is that 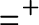$=^+$ and 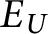$E_U$ for any U that is Borel and universal for countable sets are equivalent up to Borel bireducibility. For all U that are Borel and universal for countable sets, 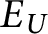$E_U$ is Borel bireducible to 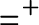$=^+$. If one assumes a particular instance of 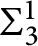$\mathbf {\Sigma }_3^1$-generic absoluteness, then for all 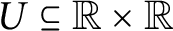$U \subseteq {\mathbb {R}} \times {\mathbb {R}}$ that are 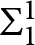$\mathbf {\Sigma }_1^1$ (continuous images of Borel sets) and universal for countable sets, there is a Borel reduction of 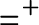$=^+$ into 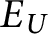$E_U$.