Hostname: page-component-7dd5485656-j7khd Total loading time: 0 Render date: 2025-10-31T01:41:15.039Z Has data issue: false hasContentIssue false
  • English
  • Français

Diagonal Plus Tridiagonal Representatives for Symplectic Congruence Classes of Symmetric Matrices

Published online by Cambridge University Press:  20 November 2018

D. Ž. Đoković ,
F. Szechtman  and
K. Zhao
D. Ž. Đoković
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, ON, N2L 3G1 e-mail: djokovic@uwaterloo.ca
F. Szechtman
Affiliation:
Department of Mathematics and Statistics, University of Regina, Regina, SK, S4S 0A2 e-mail: szechtf@math.uregina.ca
K. Zhao
Affiliation:
Department of Mathematics, Wilfrid Laurier University, Waterloo, ON, N2L 3C5 and Mathematics Department, Henan University, Henan, China e-mail: kzhao@wlu.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 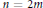$n=2m$ be even and denote by 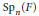$\text{S}{{\text{p}}_{n}}\left( F \right)$ the symplectic group of rank 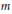$m$ over an infinite field 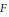$F$ of characteristic different from 2. We show that any 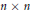$n\times n$ symmetric matrix 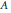$A$ is equivalent under symplectic congruence transformations to the direct sum of 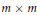$m\times m$ matrices 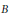$B$ and 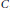$C$ , with 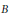$B$ diagonal and 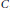$C$ tridiagonal. Since the 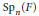$\text{S}{{\text{p}}_{n}}\left( F \right)$ -module of symmetric 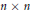$n\times n$ matrices over 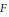$F$ is isomorphic to the adjoint module 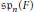$\mathfrak{s}{{\mathfrak{p}}_{n}}\left( F \right)$ , we infer that any adjoint orbit of 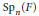$\text{S}{{\text{p}}_{n}}\left( F \right)$ in 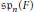$\mathfrak{s}{{\mathfrak{p}}_{n}}\left( F \right)$ has a representative in the sum of 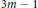$3m-1$ root spaces, which we explicitly determine.

Keywords

11E3915A6317B20

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 3 , 01 September 2005 , pp. 394 - 404
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Antonyan, L. V., On the classification of homogeneous elements of Z 2 -graded semisimple Lie algebras. (in Russian). Vestnik Moskov. Univ. Ser. I Mat. Mekh. (1982), 29–34.Google Scholar
[2] Arnold, V. I., Mathematical Methods of Classical Mechanics. Graduate Texts in Mathematics 60, Springer-Verlag, New York, 1978.Google Scholar
[3] Ballantine, C. S. and Yip, E. L., Congruence and conjunctivity of matrices. Linear Algebra Appl. 32(1980), 159–198.Google Scholar
[4] Bourgoyne, N. and Cushman, R., Conjugacy classes in linear groups. J. Algebra 44(1977), 339–362.Google Scholar
[5] Đoković, D.Ž., Patera, J., Winternitz, P., and Zassenhaus, H., Normal forms of elements of classical real and complex Lie and Jordan algebras. J. Math. Phys. 24(1983), 1363–1374.Google Scholar
[6] Đoković, D.Ž., Szechtman, F. and Zhao, K., An algorithm that carries a square matrix into its transpose by an involutory congruence transformation., Electron. J. Linear Algebra 10(2003), 320–340.Google Scholar
[7] Gabriel, P., Appendix: degenerate bilinear forms. J. Algebra, 31(1974), 67–72.Google Scholar
[8] Gow, R., The equivalence of an invertible matrix to its transpose. Linear and Multilinear Algebra, 8(1979/80), 329–336.Google Scholar
[9] Riehm, C., The equivalence of bilinear forms. J. Algebra 31(1974), 45–66.Google Scholar
[10] Springer, T. A. and Steinberg, R., Conjugacy classes. In: Seminar on Algebraic Groups and Related Finite Groups, Lecture Notes in Mathematics 131, Springer, Berlin, 1970, pp. 167–266.Google Scholar
[11] Wall, G. E., On the conjugacy classes in the unitary, symplectic and orthogonal groups. J. Austral. Math. Soc. 3(1963), 1–62.Google Scholar
[12] Williamson, J., On the algebraic problem concerning the normal forms of linear dynamical systems. Amer. J. Math. 58(1936), 141–163.Google Scholar