Hostname: page-component-7dd5485656-tbj44 Total loading time: 0 Render date: 2025-10-31T07:24:14.729Z Has data issue: false hasContentIssue false
  • English
  • Français

Compatibility of theta lifts and tempered condition

Part of: Lie groups

Published online by Cambridge University Press:  21 June 2023

Zhe Li  and
Shanwen Wang Open the ORCID record for Shanwen Wang [Opens in a new window]
Zhe Li
Affiliation:
School of Mathematical Sciences, Fudan University, 220 Handan Road, Shanghai, China e-mail: zli17@fudan.edu.cn
Shanwen Wang*
Affiliation:
School of Mathematics, Renmin University of China, No. 59, Zhongguancun Street, Haidian District, Beijing 100872, China
*
e-mail: s_wang@ruc.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this note, assuming the nonvanishing result of explicit theta correspondence for the symplectic–orthogonal dual pair over quaternion algebra $\mathbb {H}$, we show that, for metapletic–orthogonal dual pair over 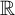$\mathbb {R}$ and the symplectic–orthogonal dual pair over quaternion algebra $\mathbb {H}$, the theta correspondence is compatible with tempered condition by directly estimating the matrix coefficients, without using the classification theorem.

Keywords

Tempered representationstheta correspondencemetaplectic groupsWeil representations

MSC classification

Primary: 22E45: Representations of Lie and linear algebraic groups over real fields

Information

Type
Article
Information
Canadian Mathematical Bulletin , Volume 67 , Issue 1 , March 2024 , pp. 60 - 73
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adams, J. and Barbasch, D., Genuine representation of the metaplectic group. Comp. Math. 113(1998), 23–66. https://doi.org/10.1023/A:1000450504919 CrossRefGoogle Scholar
Cowling, M., Haagerup, U., and Howe, R., Almost ${{L}}^2$ matrix coefficients . J. Reine Angew. Math. 387(1988), 97–110. https://doi.org/10.1515/crll.1988.387.97 Google Scholar
Gan, W. T. and Ichino, A., On endoscopy and the refined Gross–Prasad conjecture for $\left({{SO}}_5,{{SO}}_4\right)$ . J. Inst. Math. Jussieu 10(2011), 235–324. https://doi.org/10.1017/S1474748010000198 CrossRefGoogle Scholar
Gan, W. T. and Ichino, A., Formal degrees and local theta correspondence . Invent. Math. 195(2014), 509–672. https://doi.org/10.1007/s00222-013-0460-5 CrossRefGoogle Scholar
Gan, W. T., Qiu, Y. N., and Takeda, S., The regularized Siegel–Weil formula (the second term identity) and the Rallis inner product formula . Invent. Math. 198(2014), no. 3, 739–831. https://doi.org/10.1007/s00222-014-0509-0 CrossRefGoogle Scholar
He, H., Unitary representations and theta correspondence for type I classical groups . J. Funct. Anal. 199(2003), no. 1, 92–121. https://doi.org/10.1016/S0022-1236(02)00170-2 CrossRefGoogle Scholar
He, H., Composition of theta correspondences . Adv. Math. 190(2005), 225–263. https://doi.org/10.1016/j.aim.2004.01.001 CrossRefGoogle Scholar
Howe, R., Transcending invariant theory . J. Amer. Math. Soc. 2(1989), no. 3, 535–552. https://doi.org/10.1090/S0894-0347-1989-0985172-6 CrossRefGoogle Scholar
Ichino, A., Theta lifting for tempered representations of real unitary groups . Adv. Math. 398(2022), 108188.CrossRefGoogle Scholar
Ichino, A. and Ikeda, T., On the periods of automorphic forms on special orthogonal groups and the Gan–Gross–Prasad conjecture . Geom. Funct. Anal. 19(2010), 1378–1425. https://doi.org/10.1007/S00039-009-0040-4 CrossRefGoogle Scholar
Lee, S. T. and Zhu, C. B., Degenerate principal series and local theta correspondence . Trans. Amer. Math. Soc. 350(1998), no. 12, 5017–5046. https://doi.org/10.1090/S0002-9947-98-02036-4 CrossRefGoogle Scholar
Li, J., Paul, A., Tan, E., and Zhu, C., The explicit duality correspondence of $\left({Sp}\left({p},{q}\right),{{O}}^{\ast}\left(2{n}\right)\right)$ . J. Funct. Anal. 200(2003), 71–100.CrossRefGoogle Scholar
Li, J. S., Singular unitary representations of classical groups . Invent. Math. 97(1989), 237–255. https://doi.org/10.1007/BF01389041 CrossRefGoogle Scholar
Sun, B., Bounding matrix coefficients for smooth vectors of tempered representations . Proc. Amer. Math. Soc. 137(2009), no. 1, 353–357. https://doi.org/10.1090/S0002-9939-08-09598-1 CrossRefGoogle Scholar
Trèvres, F., Topological vector spaces, distributions and kernels. Academic Press, New York, 1967. https://doi.org/10.1112/BLMS/1.3.444 Google Scholar
Varadarajan, V. S., Harmonic analysis on real reductive groups. Lecture Notes in Mathematics, 576, Springer, Berlin–Heidelberg, 1977. https://doi.org/10.1007/BF01390004 CrossRefGoogle Scholar
Wallach, N. R., Real reductive groups I. Pure and Applied Mathematics, 132, Academic Press, Boston, MA, 1988.Google Scholar
Wallach, N. R., Real reductive groups II. Pure and Applied Mathematics, 132, Academic Press, Boston, MA, 1992. https://doi.org/10.1016/0378-4754(92)90088-x Google Scholar
Xue, H., Bessel model for real unitary groups: the tempered case. Duke Math. J. 172(2023), no. 5, 995–1031.Google Scholar