Hostname: page-component-7dd5485656-npwhs Total loading time: 0 Render date: 2025-10-30T12:04:15.854Z Has data issue: false hasContentIssue false
  • English
  • Français

The Cardinality of the Center of a PI Ring

Published online by Cambridge University Press:  20 November 2018

Charles Lanski
Charles Lanski*
Affiliation:
Department of Mathematics University of Southern California Los Angeles, CA 90089-1113 USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The main result shows that if 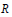$R$ is a semiprime ring satisfying a polynomial identity, and if 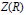$Z(R)$ is the center of 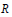$R$ , then card 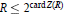$R\,\le \,{{2}^{\text{card}\,Z\text{(}R\text{)}}}$ . Examples show that this bound can be achieved, and that the inequality fails to hold for rings which are not semiprime.

Keywords

16R2016N6016R9916U50

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 41 , Issue 1 , 01 March 1998 , pp. 81 - 85
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Formanek, E., Central polynomials for matrix rings. J.Algebra 23 (1972), 129–132.Google Scholar
2. Formanek, E., Noetherian PI-rings. Comm. Algebra 1 (1974), 79–86.Google Scholar
3. Herstein, I. N., Rings with involution. Chicago Lectures in Mathematics, University of Chicago Press, Chicago, 1976.Google Scholar
4. Jacobson, N., Structure of rings. Amer. Math. Soc. Colloq. Publ. 37, Amer. Math. Soc., Providence, RI, 1964.Google Scholar
5. Jacobson, N., PI-algebras. Lecture Notes in Math. 441, Springer-Verlag, New York, 1975.Google Scholar
6. Rowen, L., Some results on the center of a ring with polynomial identity. Bull. Amer.Math. Soc. 79 (1973), 219–223.Google Scholar