Hostname: page-component-7f64f4797f-7vqc4 Total loading time: 0 Render date: 2025-11-04T13:35:51.693Z Has data issue: false hasContentIssue false
  • English
  • Français

Specht property for the algebra of upper triangular matrices of size two with a Taft’s algebra action

Part of: Hopf algebras, quantum groups and related topics Rings with polynomial identity

Published online by Cambridge University Press:  16 May 2022

Lucio Centrone Open the ORCID record for Lucio Centrone [Opens in a new window]  and
Alejandro Estrada
Lucio Centrone*
Affiliation:
Dipartimento di Matematica, Università degli Studi di Bari “Aldo Moro”, via E. Orabona 4, Bari, 70125, Italy
Alejandro Estrada
Affiliation:
IMECC, UNICAMP, Rua Sérgio Buarque de Holanda 651, 13083-859 Campinas, SP, Brazil e-mail: a227983@dac.unicamp.br
*
e-mail: lucio.centrone@uniba.it
Get access Rights & Permissions [Opens in a new window]

Abstract

Let F be a field of characteristic zero, and let 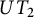$UT_2$ be the algebra of $2 \times 2$ upper triangular matrices over F. In a previous paper by Centrone and Yasumura, the authors give a description of the action of Taft’s algebras 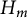$H_m$ on 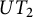$UT_2$ and its 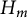$H_m$-identities. In this paper, we give a complete description of the space of multilinear 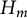$H_m$-identities in the language of Young diagrams through the representation theory of the hyperoctahedral group. We finally prove that the variety of 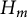$H_m$-module algebras generated by 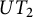$UT_2$ has the Specht property, i.e., every 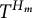$T^{H_m}$-ideal containing the 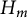$H_m$-identities of 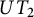$UT_2$ is finitely based.

Keywords

Specht propertyH-module algebrasTaft’s algebrasH-identitiescocharacter

MSC classification

Primary: 16R10: $T$-ideals, identities, varieties of rings and algebras
Secondary: 16R50: Other kinds of identities (generalized polynomial, rational, involution) 16T05: Hopf algebras and their applications

Information

Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 1 , March 2023 , pp. 303 - 323
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

A. Estrada was partially supported by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES)—Finance Code 001.

References

Aljadeff, E. and Kanel-Belov, A., Representability and Specht problem for  $G$ -graded algebras . Adv. Math. 225(2010), no. 5, 2391–2428.CrossRefGoogle Scholar
Aljadeff, E. and Kanel-Belov, A., Hilbert series of PI relatively free G-graded algebras are rational functions . Bull. Lond. Math. Soc. 44(2012), no. 3, 520–532.CrossRefGoogle Scholar
Bahturin, Y. and Yasumura, F., Distinguishing simple algebras by means of polynomial identities . São Paulo J. Math. Sci. 13(2019), no. 1, 39–72.CrossRefGoogle Scholar
Belov, A. Y., The Gel’fand–Kirillov dimension of relatively free associative algebras. Mat. Sb. 195(2004), no. 12, 3–26 (in Russian). Transl: Sb. Math. 195(2004), nos. 11–12, 1703–1726.Google Scholar
Belov, A. Y., Borisenko, V. V., and Latyshev, V. N., Monomial algebras . J. Math. Sci. 87(1997), 3463–3575.CrossRefGoogle Scholar
Berele, A., Homogeneous polynomial identities . Israel J. Math. 42(1982), no. 3, 258–272.CrossRefGoogle Scholar
Berele, A., Generic verbally prime PI-algebras and their GK-dimensions . Comm. Algebra 21(1993), 1487–1504.CrossRefGoogle Scholar
Centrone, L., A note on graded Gelfand–Kirillov dimension of graded algebras . J. Algebra Appl. 10(2011), no. 5, 865–889.CrossRefGoogle Scholar
Centrone, L., The graded Gelfand–Kirillov dimension of verbally prime algebras . Linear Multilinear Algebra 59(2011), no. 12, 1433–1450.CrossRefGoogle Scholar
Centrone, L., On some recent results about the graded Gelfand–Kirillov dimension of graded PI-algebras . Serdica Math. J. 38(2012), nos. 1–3, 43–68.Google Scholar
Centrone, L., The GK dimension of relatively free algebras of PI-algebras . J. Pure Appl. Algebra 223(2019), no. 7, 2977–2996.CrossRefGoogle Scholar
Centrone, L., Estrada, A., and Ioppolo, A., Algebras with superinvolution and H-module algebras: Specht problem and rationality of Hilbert series of relatively free algebras . J. Algebra 592(2022), 300–356.CrossRefGoogle Scholar
Centrone, L., Martino, F., and Souza, M. S., Specht property for some varieties of Jordan algebras of almost polynomial growth . J. Algebra 521(2019), 137–165.CrossRefGoogle Scholar
Centrone, L. and Yasumura, F., Actions of Taft’s algebras on finite dimensional algebras . J. Algebra 560(2020), 725–744.CrossRefGoogle Scholar
Curtis, C. W. and Reiner, I., Representation theory of finite groups and associative algebras, Wiley Classics Library, John Wiley & Sons, Inc., New York, 1988.Google Scholar
Dăscălescu, S., Năstăsescu, C., and Raianu, Ş., Hopf algebras. An introduction, Monographs and Textbooks in Pure and Applied Mathematics, 235, Marcel Dekker, Inc., New York, 2001.Google Scholar
Drensky, V., Gelfand–Kirillov dimension of PI-algebras . In: Methods in ring theory: Proceedings of the Trento Conference, Trento, Italy, Lecture Notes in Pure and Applied Mathematics, 198, Marcel Dekker, New York, 1998, pp. 97–113.Google Scholar
Drensky, V., Free algebras and PI-algebras. Graduate course in algebra, Springer-Verlag, Singapore, 2000.Google Scholar
Eilenberg, S., Automata, languages, and machines. Vol. A, Pure and Applied Mathematics, 58, Academic Press, New York, 1974.Google Scholar
Giambruno, A. and Rizzo, C., Differential identities, $2\times 2$ upper triangular matrices and varieties of almost polynomial growth. J. Pure Appl. Algebra 223(2019), no. 4, 1710–1727.Google Scholar
Giambruno, A. and Zaicev, M., On codimension growth of finitely generated associative algebras . Adv. Math. 140(1998), 145–155.CrossRefGoogle Scholar
Giambruno, A. and Zaicev, M., Exponential codimension growth of PI algebras: an exact estimate . Adv. Math. 142(1999), 221–243.CrossRefGoogle Scholar
Giambruno, A. and Zaicev, M., Polynomial identities and asymptotic methods, Mathematical Surveys and Monographs, 122, American Mathematical Society, Providence, RI, 2005.CrossRefGoogle Scholar
Gordienko, A., Lie algebras simple with respect to a Taft algebra action . J. Algebra 517(2019), 249–275.CrossRefGoogle Scholar
Gordienko, A. S., Algebras simple with respect to a Sweedler’s algebra action . J. Pure Appl. Algebra 219(2015), no. 8, 3279–3291.CrossRefGoogle Scholar
Higman, G., Ordering by divisibility in abstract algebras . Proc. Lond. Math. Soc. (3) 2(1952), 326–336.CrossRefGoogle Scholar
Karasik, Y., Kemer’s theory for H-module algebras with application to the PI exponent . J. Algebra 457(2016), 194–227.CrossRefGoogle Scholar
Kemer, A. R., Varieties of finite rank . In: Proc. 15-th All the Union Algebraic Conf., Krasnoyarsk. Vol. 2, 1979, p. 73 (in Russian).Google Scholar
Kemer, A. R., Varieties and $\ {\mathbb{Z}}_2$ -graded algebras . Izv. Akad. Nauk SSSR Ser. Mat. 48 (1984), no. 5, 1042–1059 (in Russian).Google Scholar
Kemer, A. R., Finite basability of identities of associative algebras . Algebra Logika 26(1987), no. 5, 597–641, 650.CrossRefGoogle Scholar
Kemer, A. R., Ideals of identities of associative algebras, AMS Translations of Mathematical Monograph, 87, American Mathematical Society, Providence, RI, 1988.Google Scholar
Kleene, S. C., On notation for ordinal numbers . J. Symb. Log. 3(1938), no. 4, 150–155.CrossRefGoogle Scholar
Krause, G. R. and Lenagan, T. H., Growth of algebras and Gelfand–Kirillov dimension. Revised edition, Graduate Studies in Mathematics, 22, American Mathematical Society, Providence, RI, 2000.Google Scholar
McConnell, J. C. and Robson, J. C., Noncommutative Noetherian rings. Revised edition, Graduate Studies in Mathematics, 30, American Mathematical Society, Providence, RI, 2001. With the cooperation of L. W. Small.CrossRefGoogle Scholar
Mishchenko, S. and Valenti, A., A star-variety with almost polynomial growth . J. Algebra 223(2000), no. 1, 66–84.CrossRefGoogle Scholar
Montgomery, S., Hopf algebras and their actions on rings, CBMS Regional Conference Series in Mathematics, 82, American Mathematical Society, Providence, RI, 1993. Published for the Conference Board of the Mathematical Sciences, Washington, DC.CrossRefGoogle Scholar
Radford, D. E., Hopf algebras, Series on Knots and Everything, 49, World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, 2012.Google Scholar
Regev, A., Existence of identities in $\ A\otimes B$ . Israel J. Math. 11(1972), 131–152.CrossRefGoogle Scholar
Sagan, B. E., The symmetric group. Representations, combinatorial algorithms, and symmetric functions. 2nd ed., Graduate Texts in Mathematics, 203, Springer-Verlag, New York, 2001.Google Scholar
Sviridova, I., Identities of PI-algebras graded by a finite abelian group . Comm. Algebra 39(2011), no. 9, 3462–3490.CrossRefGoogle Scholar
Sweedler, M. E., Hopf algebras, Mathematics Lecture Note Series, W. A. Benjamin, Inc., New York, 1969.Google Scholar
Valenti, A., The graded identities of upper triangular matrices of size two . J. Pure Appl. Algebra 172(2002), 325–335.CrossRefGoogle Scholar