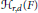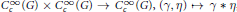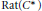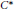Contents
Research Article
On Hilbert Covariants
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-30
-
- Article
-
- You have access
- Export citation
Symplectic Foliations and Generalized Complex Structures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 31-56
-
- Article
-
- You have access
- Export citation
Perfect Orderings on Finite Rank Bratteli Diagrams
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 57-101
-
- Article
-
- You have access
- Export citation
Continuity of Convolution of Test Functions on Lie Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 102-140
-
- Article
-
- You have access
- Export citation
Existence of Taut Foliations on Seifert Fibered Homology 3-spheres
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 141-169
-
- Article
-
- You have access
- Export citation
Modular Abelian Varieties Over Number Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 170-196
-
- Article
-
- You have access
- Export citation
On Hyperbolicity of Domains with StrictlyPseudoconvex Ends
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 197-204
-
- Article
-
- You have access
- Export citation
Generalized Frobenius Algebras and Hopf Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 205-240
-
- Article
-
- You have access
- Export citation