Hostname: page-component-cb9f654ff-nr592 Total loading time: 0 Render date: 2025-08-28T03:34:50.514Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniqueness of the von Neumann Continuous Factor

Published online by Cambridge University Press:  20 November 2018

Pere Ara  and
Joan Claramunt
Pere Ara
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, 08193 Bellaterra (Barcelona), Spain. e-mail: para@mat.uab.cat
Joan Claramunt
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, 08193 Bellaterra (Barcelona), Spain., e-mail: jclaramunt@mat.uab.cat
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a division ring 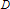$D$ , denote by 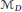${{\mathcal{M}}_{D}}$ the 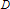$D$ -ring obtained as the completion of the direct limit 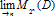$\underset{\to n}{\mathop \lim }\,{{M}_{{{2}^{n}}}}(D)$ with respect to themetric induced by its unique rank function. We prove that, for any ultramatricial 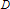$D$ -ring 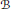$B$ and any non-discrete extremal pseudo-rank function 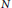$N$ on 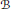$B$ , there is an isomorphism of 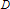$D$ -rings 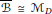$\overline{B}\,\cong \,{{\mathcal{M}}_{D}}$ , where 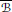$\overline{B}$ stands for the completion of 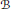$B$ with respect to the pseudo-metric induced by 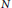$N$ . This generalizes a result of von Neumann. We also show a corresponding uniqueness result for $*$ -algebras over fields 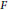$\text{F}$ with positive definite involution, where the algebra 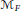${{\mathcal{M}}_{\text{F}}}$ is endowed with its natural involution coming from the $*$ -transpose involution on each of the factors 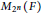${{M}_{{{2}^{n}}}}\,(F)$ .

Keywords

16E5016D70rank functionvon Neumann regular ringcompletionfactorultramatricial

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 5 , 01 October 2018 , pp. 961 - 982
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Ara, P., Matrix rings over *-regular rings and pseudo-rank functions. Pacific J. Math. 129 (1987), 209–241. http://dx.doi.org/10.2140/pjm.1987.129.209Google Scholar
[2] Ara, P. and Claramunt, J., Approximating the group algebra of the lamplighter by finite-dimensional algebras. In preparation.Google Scholar
[3] Berberian, S. K., Baer *-rings. Die Grundlehren der Mathematischen Wissenschaften, 195. Springer-Verlag, New York, 1972.Google Scholar
[4] Blackadar, B. and Handelman, D., Dimension functions and traces on C* -algebras. J. Funct. Anal. 45 (1982), 297–340. http://dx.doi.org/10.1016/0022-1236(82)90009-XGoogle Scholar
[5] Cohn, P. M., Algebra. Vol. 3, second edition. John Wiley, Chichester, 1991.Google Scholar
[6] Connes, A., Classification of injective factors. Cases II1 II∞, IIIλ, λ ≠ 1. Ann. of Math. (2) 104 (1976), 73–115. http://dx.doi.Org/10.2307/1 971057Google Scholar
[7] Elek, G., Connes embeddings and von Neumann regular closures of amenable group algebras. Trans. Amer. Math. Soc. 365 (2013), 3019–3039. http://dx.doi.org/10.1090/S0002-9947-2012-05687-XGoogle Scholar
[8] Elek, G., Lamplighter groups and von Neumann continuous regular rings. Proc. Amer. Math. Soc. 144 (2016), 2871–2883. http://dx.doi.Org/10.1090/proc/13066Google Scholar
[9] Elek, G., Infinite dimensional representations of finite dimensional algebras and amenability. Math. Ann. 369 (2017), 397–439. http://dx.doi.org/10.1007/s00208-017-1552-0Google Scholar
[10] Handelman, D., Completions of rank rings. Canad. Math. Bull. 20 (1977), 199–205. http://dx.doi.Org/10.41 53/CMB-1977-032-3Google Scholar
[11] Handelman, D., Coordinatization applied to finite Baer *-rings. Trans. Amer. Math. Soc. 235 (1978), 1–34.Google Scholar
[12] Handelman, D., Rings with involution as partially ordered abelian groups. Rocky Mountain J. Math. 11 (1981), 337–381. http://dx.doi.org/10.1216/RMJ-1981-11-3-337Google Scholar
[13] Murray, E. J. and von Neumann, J., On rings of operators. IV. Ann. of Math. (2) 44 (1943), 716–808. http://dx.doi.Org/10.2307/1969107Google Scholar
[14] Goodearl, K. R., Centers of regular self-injective rings. Pacific J. Math. 76 (1978), 381–395. http://dx.doi.org/10.2140/pjm.1978.76.381Google Scholar
[15] Goodearl, K. R., Von Neumann Regular Rings. Second edition. Krieger, Malabar, FL, 1991.Google Scholar
[16] Halperin, I., Von Neumann's manuscript on inductive limits of regular rings. Canad. J. Math. 20 (1968), 477–483. http://dx.doi.org/10.4153/CJM-1968-045-0Google Scholar
[17] Jaikin-Zapirain, A., L2-Betti numbers and their analogues in positive characteristic. To appear, Proceedings of Groups St. Andrews, 2017.Google Scholar
[18] Sinclair, A. M., and Smith, R. R., Finite von Neumann algebras and masas. London Mathematical Society Lecture Note Series, 351. Cambridge University Press, Cambridge, 2008.Google Scholar