Hostname: page-component-7dd5485656-wxk4p Total loading time: 0 Render date: 2025-10-30T08:37:58.021Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniquely D-colourable Digraphs with Large Girth

Published online by Cambridge University Press:  20 November 2018

Ararat Harutyunyan ,
P. Mark Kayll ,
Bojan Mohar  and
Liam Rafferty
Ararat Harutyunyan
Affiliation:
Department of Mathematics, Simon Fraser University, Burnaby, BC V5A 1S6 email: aha43@sfu.ca mohar@sfu.ca
P. Mark Kayll
Affiliation:
Department of Mathematical Sciences, University of Montana, Missoula MT 59812-0864, USA email: mark.kayll@umontana.edu rafferty@member.ams.org
Bojan Mohar
Affiliation:
Department of Mathematics, Simon Fraser University, Burnaby, BC V5A 1S6 email: aha43@sfu.ca mohar@sfu.ca
Liam Rafferty
Affiliation:
Department of Mathematical Sciences, University of Montana, Missoula MT 59812-0864, USA email: mark.kayll@umontana.edu rafferty@member.ams.org
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 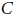$C$ and 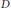$D$ be digraphs. A mapping 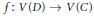$f:V\left( D \right)\to V\left( C \right)$ is a 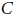$C$ -colouring if for every arc 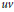$uv$ of 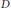$D$ , either 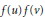$f\left( u \right)f\left( v \right)$ is an arc of 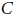$C$ or 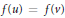$f\left( u \right)=f\left( v \right)$ , and the preimage of every vertex of 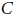$C$ induces an acyclic subdigraph in 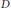$D$ . We say that 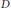$D$ is 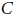$C$ -colourable if it admits a 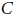$C$ -colouring and that 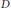$D$ is uniquely 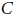$C$ -colourable if it is surjectively 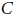$C$ -colourable and any two 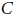$C$ -colourings of 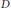$D$ differ by an automorphism of 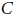$C$ . We prove that if a digraph 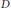$D$ is not 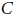$C$ -colourable, then there exist digraphs of arbitrarily large girth that are 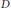$D$ -colourable but not 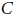$C$ -colourable. Moreover, for every digraph 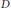$D$ that is uniquely 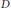$D$ -colourable, there exists a uniquely 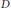$D$ -colourable digraph of arbitrarily large girth. In particular, this implies that for every rational number 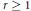$r\ge 1$ , there are uniquely circularly 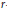$r$ -colourable digraphs with arbitrarily large girth.

Keywords

05C1505C2060C05digraph colouringacyclic homomorphismcircular chromatic numbergirth

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 6 , 01 December 2012 , pp. 1310 - 1328
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Aigner, M. and Ziegler, G. M., Proofs from The Book. Fourth ed. Springer-Verlag, Berlin, 2010. http://dx.doi.org/10.1007/978-3-642-00856-6 Google Scholar
[2] Alon, N. and Spencer, J. H., The probabilistic method. Second ed. Wiley-Interscience Series in Discrete Mathematics and Optimization, Wiley-Interscience, New York, 2000. http://dx.doi.org/10.1002/0471722154 Google Scholar
[3] Bang-Jensen, J. and Gutin, G., Digraphs. Theory, algorithms and applications. Second ed., Springer Monographs in Mathematics, Springer-Verlag, London, 2009. http://dx.doi.org/10.1007/978-1-84800-998-1 Google Scholar
[4] Bokal, D., G. Fijavž, Juvan, M., Kayll, P. M., and Mohar, B., The circular chromatic number of a digraph. J. Graph Theory 46(2004), no. 3, 227–240. http://dx.doi.org/10.1002/jgt.20003 Google Scholar
[5] Bollobás, B., Modern graph theory. Graduate Texts in Mathematics, 184, Springer-Verlag, New York, 1998.Google Scholar
[6] Bollobás, B. and Sauer, N., Uniquely colourable graphs with large girth. Canad. J. Math. 28(1976), no. 6, 1340–1344. http://dx.doi.org/10.4153/CJM-1976-133-5 Google Scholar
[7] Bondy, J. A. and Murty, U. S. R., Graph theory. Graduate Texts in Mathematics, 244, Springer, New York, 2008. http://dx.doi.org/10.1007/978-1-84628-970-5 Google Scholar
[8] Descartes, B., A three-colour problem. Eureka 9 (April 1947), 21; solution in Eureka 10 (March 1948), 24–25.Google Scholar
[9] Descartes, B., Solution to advanced problem no. 4526, proposed by P. Ungar. Amer. Math. Monthly 61(1954), no. 5, 352–353. http://dx.doi.org/10.2307/2307489 Google Scholar
[10] Diestel, R., Graph theory. Fourth ed., Graduate Texts in Mathematics, 173, Springer, Heidelberg, 2010.Google Scholar
[11] Emden-Weinert, T., Hougardy, S., and Kreuter, B., Uniquely colourable graphs and the hardness of colouring graphs of large girth. Combin. Probab. Comput. 7(1998), no. 4, 375–386. http://dx.doi.org/10.1017/S0963548398003678 Google Scholar
[12] Erdʺos, P., Graph theory and probability. Canad. J. Math. 11(1959), 34–38. http://dx.doi.org/10.4153/CJM-1959-003-9 Google Scholar
[13] Godsil, C. and Royle, G., Algebraic graph theory. Graduate Texts in Mathematics, 207, Springer-Verlag, New York, 2001.Google Scholar
[14] Harutyunyan, A., Brooks-type results for colouring of digraphs. Ph. D. dissertation, Simon Fraser University, 2011.Google Scholar
[15] Hell, P. and Něsetřil, J., Graphs and homomorphisms. Oxford Lecture Series in Mathematics and its Applications, 28, Oxford University Press, Oxford, 2004. http://dx.doi.org/10.1093/acprof:oso/9780198528173.001.0001 Google Scholar
[16] Kelly, J. B. and Kelly, L. M., Paths and circuits in critical graphs. Amer. J. Math. 76(1954), 786–792. http://dx.doi.org/10.2307/2372652 Google Scholar
[17] Kostochka, A. V. and Něsetřil, J., Properties of Descartes’ construction of triangle-free graphs with high chromatic number. Combin. Probab. Comput. 8(1999), no. 5, 467–472. http://dx.doi.org/10.1017/S0963548399004022 Google Scholar
[18] Křıž, I., A hypergraph-free construction of highly chromatic graphs without short cycles. Combinatorica 9(1989), no. 2, 227–229. http://dx.doi.org/10.1007/BF02124683 Google Scholar
[19] Lin, S. and Zhu, X., Uniquely circular colourable and uniquely fractional colourable graphs of large girth. Contrib. Discrete Math. 1(2006), no. 1, 57–67 (electronic).Google Scholar
[20] Lovász, L., On chromatic number of finite set-systems. Acta Math. Acad. Sci. Hungar. 19(1968), 59–67. http://dx.doi.org/10.1007/BF01894680 Google Scholar
[21] Mohar, B., Circular colorings of edge-weighted graphs. J. Graph Theory 43(2003), no. 2, 107–116. http://dx.doi.org/10.1002/jgt.10106 Google Scholar
[22] Molloy, M. and Reed, B., Graph colouring and the probabilistic method. Algorithms and Combinatorics, 23, Springer-Verlag, Berlin, 2002.Google Scholar
[23] Müller, V., On colorings of graphs without short cycles. Discrete Math. 26(1979), no. 2, 165–176. http://dx.doi.org/10.1016/0012-365X(79)90121-3 Google Scholar
[24] Mycielski, J., Sur le coloriage des graphs. Colloq. Math. 3(1955), 161–162.Google Scholar
[25] Něsetřil, J., On uniquely colorable graphs without short cycles. Časopis Pěst. Mat. 98(1973), 122–125, 212.Google Scholar
[26] Něsetřil, J. and V. Rödl, A short proof of the existence of highly chromatic hypergraphs without short cycles. J. Combin. Theory Ser. B 27(1979), no. 2, 225–227. http://dx.doi.org/10.1016/0095-8956(79)90084-4 Google Scholar
[27] Něsetřil, J. and Zhu, X., Construction of sparse graphs with prescribed circular colorings. Graph theory (Prague, 1998). Discrete Math. 233(2001), no. 1–3, 277–291. http://dx.doi.org/10.1016/S0012-365X(00)00246-6 Google Scholar
[28] Něsetřil, J. and Zhu, X., On sparse graphs with given colorings and homomorphisms. J. Combin. Theory Ser. B 90(2004), no. 1, 161–172. http://dx.doi.org/10.1016/j.jctb.2003.06.001 Google Scholar
[29] Pan, Z. and Zhu, X., Graphs of large girth with prescribed partial circular colourings. Graphs Combin. 21(2005), no. 1, 119–129. http://dx.doi.org/10.1007/s00373-004-0596-6 Google Scholar
[30] Rafferty, L., D-colorable digraphs with large girth. Ph. D. dissertation, University of Montana, 2011.Google Scholar
[31] Zhu, X., Uniquely H-colorable graphs with large girth. J. Graph Theory 23(1996), no. 1, 33–41. http://dx.doi.org/10.1002/(SICI)1097-0118(199609)23:1h33::AID-JGT3i3.0.CO;2-L Google Scholar
[32] Zhu, X., Construction of uniquely H-colorable graphs. J. Graph Theory 30(1999), no. 1, 1–6. http://dx.doi.org/10.1002/(SICI)1097-0118(199901)30:1h1::AID-JGT1i3.0.CO;2-P Google Scholar
[33] Zhu, X., Circular chromatic number: a survey. Combinatorics, graph theory, algorithms and applications. Discrete Math. 229(2001), no. 1–3, 371–410. http://dx.doi.org/10.1016/S0012-365X(00)00217-X Google Scholar
[34] Zykov, A. A., On some properties of linear complexes. (Russian) Mat. Sbornik N. S. 24(66)(1949), 163–188; English translation in Amer. Math. Soc. Translation 1952(1952), no. 79, 33pp.Google Scholar