Article contents
Stability of rotation relations in 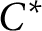 $C^*$-algebras
$C^*$-algebras
Published online by Cambridge University Press: 21 May 2020
Abstract
Let 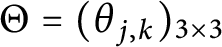 $\Theta =(\theta _{j,k})_{3\times 3}$ be a nondegenerate real skew-symmetric
$\Theta =(\theta _{j,k})_{3\times 3}$ be a nondegenerate real skew-symmetric  $3\times 3$ matrix, where
$3\times 3$ matrix, where 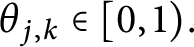 $\theta _{j,k}\in [0,1).$ For any
$\theta _{j,k}\in [0,1).$ For any 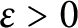 $\varepsilon>0$, we prove that there exists
$\varepsilon>0$, we prove that there exists 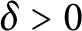 $\delta>0$ satisfying the following: if
$\delta>0$ satisfying the following: if 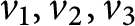 $v_1,v_2,v_3$ are three unitaries in any unital simple separable
$v_1,v_2,v_3$ are three unitaries in any unital simple separable 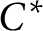 $C^*$-algebra A with tracial rank at most one, such that
$C^*$-algebra A with tracial rank at most one, such that 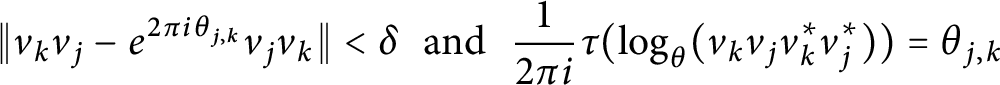
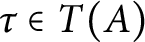 $\tau \in T(A)$ and
$\tau \in T(A)$ and 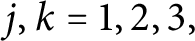 $j,k=1,2,3,$ where
$j,k=1,2,3,$ where 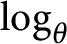 $\log _{\theta }$ is a continuous branch of logarithm (see Definition 4.13) for some real number
$\log _{\theta }$ is a continuous branch of logarithm (see Definition 4.13) for some real number 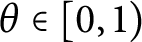 $\theta \in [0, 1)$, then there exists a triple of unitaries
$\theta \in [0, 1)$, then there exists a triple of unitaries 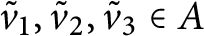 $\tilde {v}_1,\tilde {v}_2,\tilde {v}_3\in A$ such that
$\tilde {v}_1,\tilde {v}_2,\tilde {v}_3\in A$ such that 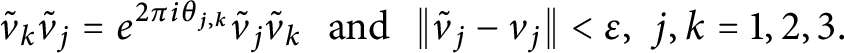
The same conclusion holds if  $\Theta $ is rational or nondegenerate and A is a nuclear purely infinite simple
$\Theta $ is rational or nondegenerate and A is a nuclear purely infinite simple  $C^*$-algebra (where the trace condition is vacuous).
$C^*$-algebra (where the trace condition is vacuous).
If  $\Theta $ is degenerate and A has tracial rank at most one or is nuclear purely infinite simple, we provide some additional injectivity conditions to get the above conclusion.
$\Theta $ is degenerate and A has tracial rank at most one or is nuclear purely infinite simple, we provide some additional injectivity conditions to get the above conclusion.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
References
- 4
- Cited by


