Hostname: page-component-54dcc4c588-gwv8j Total loading time: 0 Render date: 2025-09-29T03:40:20.776Z Has data issue: false hasContentIssue false
  • English
  • Français

Sigma-Prikry forcing I: The Axioms

Part of: Set theory

Published online by Cambridge University Press:  26 May 2020

Alejandro Poveda ,
Assaf Rinot  and
Dima Sinapova
Alejandro Poveda
Affiliation:
Departament de Matemàtiques i Informàtica, Universitat de Barcelona. Gran Via de les Corts Catalanes, Barcelona 585, 08007, Catalonia e-mail: alejandro.poveda@ub.edu
Assaf Rinot*
Affiliation:
Department of Mathematics, Bar-Ilan University, Ramat-Gan 5290002, Israel URL: http://www.assafrinot.com
Dima Sinapova
Affiliation:
Department of Mathematics, Statistics, and Computer Science University of Illinois at Chicago, Chicago, IL 60607-7045, USA e-mail: sinapova@uic.edu URL: https://homepages.math.uic.edu/~sinapova/
*
e-mail: rinotas@math.biu.ac.il
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We introduce a class of notions of forcing which we call 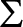$\Sigma $-Prikry, and show that many of the known Prikry-type notions of forcing that centers around singular cardinals of countable cofinality are 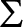$\Sigma $-Prikry. We show that given a 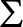$\Sigma $-Prikry poset 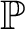$\mathbb P$ and a name for a non-reflecting stationary set T, there exists a corresponding 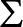$\Sigma $-Prikry poset that projects to 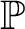$\mathbb P$ and kills the stationarity of T. Then, in a sequel to this paper, we develop an iteration scheme for 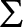$\Sigma $-Prikry posets. Putting the two works together, we obtain a proof of the following.

Theorem. If 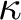$\kappa $ is the limit of a countable increasing sequence of supercompact cardinals, then there exists a forcing extension in which 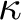$\kappa $ remains a strong limit cardinal, every finite collection of stationary subsets of 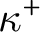$\kappa ^+$ reflects simultaneously, and 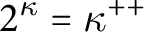$2^\kappa =\kappa ^{++}$.

Keywords

Sigma-Prikry forcingstationary reflectionsingular cardinals hypothesis

MSC classification

Primary: 03E35: Consistency and independence results
Secondary: 03E04: Ordered sets and their cofinalities; pcf theory

Information

Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 5 , October 2021 , pp. 1205 - 1238
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Canadian Mathematical Society 2020

Footnotes

Poveda was partially supported by the Spanish Government under grant MTM2017-86777-P, by Generalitat de Catalunya (Catalan Government) under grant SGR 270-2017 and by MECD Grant FPU15/00026. Rinot was partially supported by the European Research Council (grant agreement ERC-2018-StG 802756) and by the Israel Science Foundation (grant agreement 2066/18). Sinapova was partially supported by the National Science Foundation, Career-1454945.

References

Ben-Neria, O., Hayut, Y., and Unger, S., Statinoary reflection and the failure of SCH. Preprint, 2019. arXiv:1908.11145Google Scholar
Cohen, P. J., The independence of the continuum hypothesis . Proc. Natl. Acad. Sci. 50(1963), 1143–1148. https://doi.org/10.1073/pnas.50.6.1143 CrossRefGoogle ScholarPubMed
Cohen, P. J., The independence of the continuum hypothesis. II . Proc. Natl. Acad. Sci. 51(1964), 105–110. https://doi.org/10.1073/pnas.51.1.105 CrossRefGoogle ScholarPubMed
Cummings, J., Iterated forcing and elementary embeddings. In: Handbook of set theory, Vols. 1–3, Springer, Dordrecht, The Netherlands, 2010, pp. 775–883. http://dx.doi.org/10.1007/978-1-4020-5764-9_13 CrossRefGoogle Scholar
Cummings, J., Džamonja, M., Magidor, M., Morgan, C., and Shelah, S., A framework for forcing constructions at successors of singular cardinals . Trans. Am. Math. Soc. 369(2017), no. 10, 7405–7441. https://doi.org/10.1090/tran/6974 CrossRefGoogle Scholar
Cummings, J., Foreman, M., and Magidor, M., Squares, scales and stationary reflection . J. Math. Log. 1(2001), no. 1, 35–98. https://doi.org/10.1142/s021906130100003x CrossRefGoogle Scholar
Cummings, J., Friedman, S.-D., Magidor, M., Rinot, A., and Sinapova, D., Ordinal definable subsets of singular cardinals . Israel J. Math. 226(2018), no. 2, 781–804. https://doi.org/10.1007/s11856-018-1712-2 CrossRefGoogle Scholar
Dzamonja, M. and Shelah, S., Universal graphs at the successor of a singular cardinal . J. Symb. Log. 68(2003), 366–388. https://doi.org/10.2178/jsl/1052669056 CrossRefGoogle Scholar
Eisworth, T., On iterated forcing for successors of regular cardinals . Fundam. Math. 179(2003), no. 3, 249–266. https://doi.org/10.4064/fm179-3-4 CrossRefGoogle Scholar
Fremlin, D. H., Consequences of Martin’s axiom . Cambridge Tracts in Mathematics, 84, Cambridge University Press, Cambridge, MA, 1984. https://doi.org/10.1017/CBO9780511896972 CrossRefGoogle Scholar
Gitik, M., Prikry-type forcings . In: Handbook of set theory, Vols. 1–3, Springer, Dordrecht, The Netherlands, 2010, pp. 1351–1447. https://doi.org/10.1007/978-1-4020-5764-9_17 CrossRefGoogle Scholar
Gitik, M. and Magidor, M., Extender based forcings . J. Symb. Log. 59(1994), no. 2, 445–460. https://doi.org/10.2307/2275399 CrossRefGoogle Scholar
Gitik, M. and Rinot, A., The failure of diamond on a reflecting stationary set . Trans. Am. Math. Soc. 364(2012), no. 4, 1771–1795. https://doi.org/10.1090/s0002-9947-2011-05355-9 CrossRefGoogle Scholar
Gitik, M. and Sharon, A., On SCH and the approachability property . Proc. Am. Math. Soc. 136(2008), no. 1, 311–320. https://doi.org/10.1090/s0002-9939-07-08716-3 CrossRefGoogle Scholar
Gödel, K., The consistency of the continuum hypothesis . Annals of Mathematics Studies, 3, Princeton University Press, Princeton, NJ, 1940.Google Scholar
Kanamori, A., The higher infinite. Large cardinals in set theory from their beginnings . 2nd ed. Springer Monographs in Mathematics, Springer-Verlag, Berlin, Germany, 2009. Paperback reprint of the 2003 edition.Google Scholar
Lambie-Hanson, C. and Rinot, A., Knaster and friends I: Closed colorings and precalibers . Algebr. Univ. 79(2018), no. 4, 39, Art. 90. https://doi.org/10.1007/s00012-018-0565-1 CrossRefGoogle Scholar
Poveda, A., Rinot, A., and Sinapova, D., Sigma-Prikry forcing II: iteration scheme . J. Math. Log., to appear. http://assafrinot.com/paper/42 Google Scholar
Rinot, A., Chain conditions of products, and weakly compact cardinals . Bull. Symb. Log. 20(2014), no. 3, 293–314. https://doi.org/10.1017/bsl.2014.24 CrossRefGoogle Scholar
Rosłanowski, A., Explicit example of collapsing ${\kappa}^{+}$ in iteration of $\kappa$ -proper forcings. Preprint, 2018. arXiv:1808.01636Google Scholar
Rosłanowski, A. and Shelah, S., The last forcing standing with diamonds . Fundam. Math. 246(2019), no. 2, 109–159. https://doi.org/10.4064/fm898-9-2018 CrossRefGoogle Scholar
Rosłanowski, A. and Shelah, S., Iteration of $\lambda$ -complete forcing notions not collapsing $\lambda^+$ . Int. J. Math. Math. Sci. 28(2001), 63–82. https://doi.org/10.1155/s016117120102018x CrossRefGoogle Scholar
Rosłanowski, A. and Shelah, S., Lords of the iteration . In: Set theory and its applications, Contemporary Mathematics (CONM), 533, Amer. Math. Soc., Providence, RI, 2011, pp. 287–330. https://doi.org/10.1090/conm/533/10514 CrossRefGoogle Scholar
Rosłanowski, A. and Shelah, S., More about $\lambda$ -support iterations of $\left(<\lambda \right)$ -complete forcing notions . Arch. Math. Log. 52(2013), 603–629. https://doi.org/10.1007/s00153-013-0334-y CrossRefGoogle Scholar
Sharon, A., Weak squares, scales, stationary reflection and the failure of SCH. Ph.D. thesis, Tel Aviv University, Tel Aviv, 2005.Google Scholar
Shelah, S., A weak generalization of MA to higher cardinals . Israel J. Math. 30(1978), 297–306. https://doi.org/10.1007/bf02761994 CrossRefGoogle Scholar
Shelah, S., Diamonds, uniformization . J. Symb. Log. 49(1984), 1022–1033. https://doi.org/10.2307/2274258 CrossRefGoogle Scholar
Shelah, S., Cardinal arithmetic . Oxford Logic Guides, 29, The Clarendon Press Oxford University Press, Oxford Science Publications, New York, NY, 1994.Google Scholar
Shelah, S., Not collapsing cardinals $\le \kappa$ in $\left(<\kappa \right)$ -support iterations . Israel J Math. 136(2003), 29–115. https://doi.org/10.1007/bf02807192 CrossRefGoogle Scholar
Shelah, S., Successor of singulars: combinatorics and not collapsing cardinals $\le \kappa$ in $\left(<\kappa \right)$ -support iterations . Israel J. Math. 134(2003), 127–155. https://doi.org/10.1007/bf02787405 CrossRefGoogle Scholar
Solovay, R. M. and Tennenbaum, S., Iterated Cohen extensions and Souslin’s problem . Ann. Math. 94(1971), no. 2, 201–245. https://doi.org/10.2307/1970860 CrossRefGoogle Scholar