Hostname: page-component-7f64f4797f-pmsz9 Total loading time: 0 Render date: 2025-11-04T04:07:54.270Z Has data issue: false hasContentIssue false
  • English
  • Français

Global Units Modulo Circular Units: Descent Without Iwasawa’s Main Conjecture

Published online by Cambridge University Press:  20 November 2018

Jean-Robert Belliard
Jean-Robert Belliard*
Affiliation:
Université de Franche-Comté, Laboratoire de mathématiques UMR 6623, 16 route de Gray, 25030 Besanc¸on cedex, France, belliard@math.univ-fcomte.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Iwasawa's classical asymptotical formula relates the orders of the 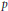$p$ -parts 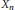${{X}_{n}}$ of the ideal class groups along a 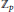${{\mathbb{Z}}_{p}}$ -extension 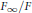${{F}_{\infty }}/F$ of a number field $F$ to Iwasawa structural invariants $\lambda $ and 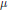$\mu $ attached to the inverse limit 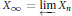${{X}_{\infty }}=\underleftarrow{\lim }\,{{X}_{n}}$ . It relies on “good” descent properties satisfied by 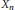${{X}_{n}}$ . 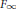If $F$ is abelian and ${{F}_{\infty }}$ is cyclotomic, it is known that the 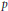$p$ -parts of the orders of the global units modulo circular units 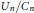${{U}_{n}}/{{C}_{n}}$ are asymptotically equivalent to the 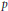$p$ -parts of the ideal class numbers. This suggests that these quotients 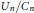${{U}_{n}}/{{C}_{n}}$ , so to speak unit class groups, also satisfy good descent properties. We show this directly, i.e., without using Iwasawa's Main Conjecture.

Keywords

11R23

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 3 , 01 June 2009 , pp. 518 - 533
Copyright
Copyright © Canadian Mathematical Society 2009

References

[Bt] Beliaeva, T., Unitès semi-locales modulo sommes de Gauß en thèorie d’Iwasawa, Thèse de l’universit è de Franche-Comtè Besancon (2004).Google Scholar
[Bjr] Belliard, J.-R., Sous-modules d’unitès en thèorie d’Iwasawa. Thèorie des nombres, Annèes 1998/2001, Publ. Math. UFR Sci. Tech. Besancon, 2002, 12 p.Google Scholar
[FG] Flach, M., The equivariant Tamagawa number conjecture: a survey. With an appendix by C. Greither. In: Stark's conjectures: recent work and new directions, Contemp. Math. 358, American Mathematical Society, Providence, RI, 2004, pp. 79–125.Google Scholar
[FW] Ferrero, B. and L.Washington, The Iwasawa invariant μp vanishes for abelian number fields. Ann. of Math. 109(1979), no. 2, 377–395.Google Scholar
[G] Greither, C., Class groups of abelian fields, and the main conjecture. Ann. Inst. Fourier (Grenoble)). 42(1992), no. 3, 449–499.Google Scholar
[I1] Iwasawa, K., On some modules in the theory of cyclotomic fields. J. Math. Soc. Japa. 16(1964), 42–82.Google Scholar
[I2] Iwasawa, K., On Zℓ-extensions of algebraic number fields. Ann. of Math. 98(1973), 246–326.Google Scholar
[KNF] Kolster, M., Nguy˜en Quang D˜o, T., and Fleckinger, V., Twisted S-units, p-adic class number formulas, and the Lichtenbaum conjectures. Duke Math. J. 84(1996), no. 3, 679–717.Google Scholar
[K] Kuz, L. V.′min, The Tate module of algebraic number fields. Izv. Akad. Nauk SSSR Ser. Mat. 36(1972), 267–327.Google Scholar
[N1] Nguy˜ên Quang D˜õ, T., Formations de classes et modules d’Iwasawa. In: Number theory, Noordwijkerhout 1983, Lecture Notes in Mathematics 1068, Springer, Berlin, 1984, pp. 167–185.Google Scholar
[N2] Nguy˜ên Quang D˜õ, T., Sur la conjecture faible de Greenberg dans le cas abèlien p-dècomposè. Int. J. Number Theor. 2(2006), no. 1, 49–64.Google Scholar
[NSW] Neukirch, J., Schmidt, A., and Wingberg, K., Cohomology of number fields. Grundlehren der MathematischenWissenschaften 323, Springer-Verlag, Berlin, 2000.Google Scholar
[Si] Sinnott, W., On the Stickelberger ideal and the circular units of an abelian field. Invent. Math. 62(1980/81), no. 2, 181–234.Google Scholar
[T] Tsuji, T., Semi-local units modulo cyclotomic units. J. Number Theor. 78(1999), no. 1, 1–26.Google Scholar
[W] Washington, L. C., Introduction to cyclotomic fields. Second ed., Graduate Texts in Mathematics 83, Springer-Verlag, New York, 1997.Google Scholar