Hostname: page-component-7f64f4797f-vhqbp Total loading time: 0 Render date: 2025-11-04T08:56:14.898Z Has data issue: false hasContentIssue false
  • English
  • Français

Equivariant Map Queer Lie Superalgebras

Published online by Cambridge University Press:  20 November 2018

Lucas Calixto ,
Adriano Moura  and
Alistair Savage
Lucas Calixto
Affiliation:
UNICAMP - IMECC, Campinas - SP - Brazil, 13083-859 e-mail: lhcalixto@ime.unicamp.br aamoura@ime.unicamp.br
Adriano Moura
Affiliation:
UNICAMP - IMECC, Campinas - SP - Brazil, 13083-859 e-mail: lhcalixto@ime.unicamp.br aamoura@ime.unicamp.br
Alistair Savage
Affiliation:
Department of Mathematics and Statistics, University of Ottawa, Ottawa, ON e-mail: alistair.savage@uottawa.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An equivariant map queer Lie superalgebra is the Lie superalgebra of regular maps from an algebraic variety (or scheme) 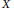$X$ to a queer Lie superalgebra 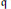$\mathfrak{q}$ that are equivariant with respect to the action of a finite group 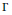$\Gamma $ acting on 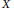$X$ and 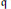$\mathfrak{q}$ . In this paper, we classify all irreducible finite-dimensional representations of the equivariant map queer Lie superalgebras under the assumption that 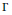$\Gamma $ is abelian and acts freely on 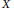$X$ . We show that such representations are parameterized by a certain set of 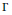$\Gamma $ -equivariant finitely supported maps from 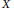$X$ to the set of isomorphism classes of irreducible finite-dimensional representations of 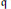$\mathfrak{q}$ . In the special case where 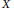$X$ is the torus, we obtain a classification of the irreducible finite-dimensional representations of the twisted loop queer superalgebra.

Keywords

17B6517B10Lie superalgebraqueer Lie superalgebraloop superalgebraequivariant map superalgebrafinite-dimensional representationfinite-dimensional module

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 2 , 01 April 2016 , pp. 258 - 279
Copyright
Copyright © Canadian Mathematical Society 2016

References

[Che95] Cheng, S.-J., Differentiably simple Lie superalgebras and representations of semisimple Lie superalgebras. J. Algebra 173(1995), no. 1,1–43.http://dx.doi.Org/10.1006/jabr.1995.1076 Google Scholar
[CW12] Cheng, S.-J. and Wang, W., Dualities and representations of Lie superalgebras. Graduate Studies in Mathematics, 144, American Mathematical Society, Providence, RI, 2012.Google Scholar
[Gor06] Gorelik, M., Shapovalov determinants of Q-type Lie superalgebras. IMRP Int. Math. Res. Pap. 2006, Art. ID 96895, 71.Google Scholar
[GP04] Grantcharov, D. and Pianzola, A., Automorphisms and twisted loop algebras of finite-dimensional simple Lie superalgebras. Int. Math. Res. Not. 73(2004), 3937–3962. http://dx.doi.Org/10.1155/S1073792804142141 Google Scholar
[GS08] Gorelik, M. and Serganova, V., On representations of the affine superalgebra q(n)(2). Mosc. Math. J. 8(2008), no. 1. 91-109, 184.Google Scholar
[Hus94] Husemoller, D., Vibre bundles. Third ed., Graduate Texts in Mathematics, 20, Springer-Verlag, New York, 1994.http://dx.doi.org/10.1007/978-1-4757-2261-1 Google Scholar
[Kac77] Kac, V. G., Lie superalgebras. Advances in Math. 26(1977), no. 1, 8–96.http://dx.doi.Org/10.1016/0001-8708(77)90017-2 Google Scholar
[Kac78] Kac, V. G., Representations of classical Lie superalgebras. In: Differential geometrical methods in mathematical physics, II (Proc. Conf., Univ. Bonn, Bonn, 1977), Lecture Notes in Math, 676, Springer, Berlin, 1978, pp. 597–626.Google Scholar
[Musl2] Musson, I. M., Lie superalgebras and enveloping algebras. Graduate Studies in Mathematics, 131, American Mathematical Society, Providence, RI, 2012.Google Scholar
[NS13] Neher, E. and Savage, A., A survey of equivariant map algebras with open problems. In: Recent developments in algebraic and combinatorial aspects of representation theory, Contemp. Math., 602, American Mathematical Society, Providence, RI, 2013, pp. 165–182.http://dx.doi.Org/10.1090/conm/602/12024 Google Scholar
[NSS12] Neher, E., Savage, A., and Senesi, P., Irreducible finite-dimensional representations of equivariant map algebras. Trans. Amer. Math. Soc. 364(2012), no. 5, 2619–2646.http://dx.doi.org/10.1090/S0002-9947-2011-05420-6 Google Scholar
[Pen86] Penkov, I. B., Characters of typical irreducible finite-dimensional q(n)-modules. Funktsional. Anal, i Prilozhen. 20(1986), no. 1, 37–45, 96.http://dx.doi.org/10.1007/BF01077312 Google Scholar
[PS97] Penkov, I. and Serganova, V., Characters of finite-dimensional irreducible q(n)-modules. Lett.Math. Phys. 40(1997), 147–158.http://dx.doi.Org/10.1023/A:1007367827082 Google Scholar
[Savl4] Savage, A., Equivariant map superalgebras. Math. Z. 277(2014), no. 1–2, 373–399.http://dx.doi.Org/10.1007/s00209-013-1261-7 Google Scholar
[Ser84] Serganova, V. V., Automorphisms of simple Lie superalgebras.(Russian) Izv. Akad. Nauk SSSR Ser. Mat. 48(1984), 585–598.Google Scholar