Hostname: page-component-cb9f654ff-5kfdg Total loading time: 0 Render date: 2025-08-30T11:12:55.723Z Has data issue: false hasContentIssue false
  • English
  • Français

A Counterexample in Lp Approximation by Harmonic Functions

Published online by Cambridge University Press:  20 November 2018

Joan Mateu
Joan Mateu*
Affiliation:
Departament de Matemàtiques, Universitat Autònoma de Barcelona, 08193 Bellaterra (Barcelona), Spain e-mail: mateu@manwe.mat.uab.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For 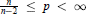we show that the conditions 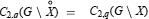for all open sets G, C 2,q denoting Bessel capacity, are not sufficient to characterize the compact sets X with the property that each function harmonic on 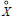and in Lp (X) is the limit in the Lp norm of a sequence of functions which are harmonic on neighbourhoods of X.

Keywords

41A3031C15

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 49 , Issue 3 , 01 June 1997 , pp. 568 - 582
Copyright
Copyright © Canadian Mathematical Society 1997

References

[AH] Adams, D.R., Hedberg, L.I., Function spaces and potential theory, Springer, Berlin and Heidelberg, 1996.Google Scholar
[Ba] Bagby, T., Approximation in the mean by solutions of elliptic equations, Trans. Amer. Math. Soc. 281(1984), 761–784.Google Scholar
[Br] Brelot, M., Sur les ensembles effilés, Bull. Sci. Math. 68(1944), 12–36.Google Scholar
[C] Carleson, L., Selected problems on exceptional sets, Van Nostrand, Princeton, New Jersey, 1967.Google Scholar
[G] Gamelin, T.W., Uniform Algebras, Prentice Hall, Englewood Cliff, New Jersey, 1969.Google Scholar
[H1] Hedberg, L.I., Non-linear potentials and approximation in the mean by analytic functions, Math. Z. 129(1972), 299–319.Google Scholar
[H2] Hedberg, L.I., Approximation in the mean by solutions of elliptic equations, Duke Math. J. 40(1973), 9–16.Google Scholar
[H3] Hedberg, L.I., Two approximation problems in function spaces, Ark.Mat. 16(1978), 51–81.Google Scholar
[H4] Hedberg, L.I., Spectral synthesis in Sobolev spaces, and uniqueness of solutions of the Dirichlet problem, Acta Math. 147(1981), 237–264.Google Scholar
[HW] Hedberg, L.I. and Wolff, T., Thin sets in nonlinear potential theory, Ann. Inst. Fourier (Grenoble) (4) 33(1983), 161–187.Google Scholar
[MNOV] Mateu, J., Netrusov, Y., Orobitg, J. and Verdera, J., BMO and Lipschitz approximation by solutions of elliptic equations, Ann. Inst. Fourier (Grenoble) (4) 46(1996), 1057–1081.Google Scholar
[Me] Meyers, N.G., A theory of capacities for potentials of functions in Lebesgue classes, Math. Scand. 26(1970), 225–292.Google Scholar
[O] O’Farrell, A.G., Hausdorff content and rational approximation in fractional Lipschitz norms, Trans.Amer. Math. Soc. 228(1977), 187–206.Google Scholar
[P] Polking, J.C., Approximation in Lp by solutions of elliptic partial differential equations, Amer. J. Math. 94(1972), 1231–1244.Google Scholar
[S] Stein, E.M., Singular integrals and differentiability properties of functions, Princeton University Press, Princeton, New Jersey, 1970.Google Scholar