Hostname: page-component-7dd5485656-g8tfn Total loading time: 0 Render date: 2025-10-29T22:04:00.886Z Has data issue: false hasContentIssue false
  • English
  • Français

A new way to tackle a conjecture of Rémond

Part of: Algebraic number theory: global fields Arithmetic algebraic geometry

Published online by Cambridge University Press:  31 October 2023

Arnaud Plessis
Arnaud Plessis*
Affiliation:
Morningside Center of Mathematics, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China
*
e-mail: plessis@amss.ac.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 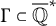$\Gamma \subset \overline {\mathbb {Q}}^*$ be a finitely generated subgroup. Denote by 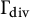$\Gamma _{\mathrm {div}}$ its division group. A recent conjecture due to Rémond, related to the Zilber–Pink conjecture, predicts that the absolute logarithmic Weil height of an element of 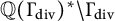$\mathbb {Q}(\Gamma _{\mathrm {div}})^*\backslash \Gamma _{\mathrm {div}}$ is bounded from below by a positive constant depending only on 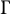$\Gamma $. In this paper, we propose a new way to tackle this problem.

Keywords

Weil heightRémond’s conjectureequidistribution

MSC classification

Primary: 11G50: Heights 11R04: Algebraic numbers; rings of algebraic integers

Information

Type
Article
Information
Canadian Journal of Mathematics , Volume 76 , Issue 6 , December 2024 , pp. 2049 - 2072
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work was funded by Morningside Center of Mathematics, CAS.

References

Amoroso, F., On a conjecture of G Rémond . Ann. Sc. Norm. Super. Pisa Cl. Sci. 15(2016), 599–608.Google Scholar
Amoroso, F., David, S., and Zannier, U., On fields with the property (B) . Proc. Amer. Math. Soc. 142(2014), no. 6, 1893–1910.CrossRefGoogle Scholar
Amoroso, F. and Dvornicich, R., A lower bound for the height in abelian extensions . J. Number Theory 595(2000), no. 2, 260–272.CrossRefGoogle Scholar
Amoroso, F. and Zannier, U., A relative Dobrowolski lower bound over abelian extensions . Ann. Sc. Norm. Super. Pisa Cl. Sci. (4) 29(2000), no. 3, 711–727.Google Scholar
Amoroso, F. and Zannier, U., A uniform relative Dobrowolski’s lower bound over abelian extensions . Bull. Lond. Math. Soc., 42(2010), no. 3, 489–498.CrossRefGoogle Scholar
Bilu, Y., Limit distribution of small points on algebraic tori . Duke Math. J. 89(1997), no. 3, 465–476.CrossRefGoogle Scholar
Blanksby, P. and Loxton, J., A note on the characterization of CM-fields . J. Aust. Math. Soc. Ser. A 26(1978), no. 1, 26–30.CrossRefGoogle Scholar
Bombieri, E. and Gubler, W., Heights in Diophantine geometry, Cambridge University Press, Cambridge, 2006.Google Scholar
Bombieri, E. and Zannier, U., A note on heights in certain infinite extensions of $\mathbb{Q}$ . Atti Accad. Naz. Lincei Cl. Sci. Fis. Mat. Natur. Rend. Lincei (9) Mat. Appl. 12(2001), 5–14.Google Scholar
Favre, C. and Rivera-Letelier, J., Équidistribution quantitative des points de petite hauteur sur la droite projective . Math. Ann. 335(2006), 311–361.CrossRefGoogle Scholar
Fili, P. and Milner, Z., Equidistribution and the heights of totally real and totally $p$ -adic numbers . Acta Arith. 170(2015), no. 1, 15–25.CrossRefGoogle Scholar
Frey, L., Height lower bounds in some non-abelian extensions . Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 23(2022), no. 3, 1357–1393.Google Scholar
Galateau, A., Small height in fields generated by singular moduli . Proc. Amer. Math. Soc. 144(2016), no. 7, 2771–2786.CrossRefGoogle Scholar
Grizzard, R., Relative Bogomolov extensions . Acta Arith. 170(2015), no. 1, 1–13.CrossRefGoogle Scholar
Grizzard, R., Remarks on Rémond’s generalized Lehmer problems. Preprint, 2017. arXiv:1710.11614v2 Google Scholar
Habegger, P., Small height and infinite nonabelian extensions . Duke Math. J. 162(2013), no. 11, 2027–2076.CrossRefGoogle Scholar
Onishchik, A. and Winberg, E. B., Lie groups and algebraic groups, Springer, Berlin, 1990.CrossRefGoogle Scholar
Pazuki, F. and Pengo, R., On the Northcott property for special values of L-functions. Preprint, 2020. arXiv:2012.00542 Google Scholar
Perucca, A. and Sgobba, P., Kummer theory for number fields and the reductions of algebraic numbers II . Unif. Distrib. Theory 15(2020), no. 1, 75–92.CrossRefGoogle Scholar
Petsche, C., The distribution of Galois orbits of low height. Ph.D. thesis, The University of Texas at Austin, Austin, 2003.Google Scholar
Plessis, A., Minoration de la hauteur de Weil dans un compositum de corps de rayon . J. Number Theory 205(2019), 246–276.CrossRefGoogle Scholar
Plessis, A., Bogomolov Property of some infinite nonabelian extensions of a totlly $v$ -adic field. Preprint, 2021. arXiv:2103.07270 Google Scholar
Plessis, A., Points de petite hauteur sur une variété semi-abélienne isotriviale de la forme ${G}_m^n\times A$ . Bull. Lond. Math. Soc. 54(2022), no. 6, 2278–2296.CrossRefGoogle Scholar
Plessis, A., Location of small points on an elliptic curve by an equidistribution argument . Int. Math. Res. Not. (2023), rnad051. https://doi.org/10.1093/imrn/rnad051 Google Scholar
Pottmeyer, L., A note on extensions of ${\mathbb{Q}}^{tr}$ . J. Théor. Nombres Bordeaux 28(2016), no. 3, 735–742.CrossRefGoogle Scholar
Pottmeyer, L., Fields generated by finite rank subsets of ${\overline{\mathbb{Q}}}^{\ast }$ . Int. J. Number Theory 17(2021), no. 5, 1079–1089.CrossRefGoogle Scholar
Rémond, G., Généralisations du problème de Lehmer et applications à la conjecture de Zilber-Pink . Panor. Synthèses 52(2017), 243–284.Google Scholar
Sahu, S., Points of small heights in certain nonabelian extensions. Ph.D. thesis, Chennai Mathematical Institute, Chennai, 2018.Google Scholar
Schinzel, A., On the product of the conjugates outside the unit circle of an algebraic number . Acta Arith. 24(1973), 385–399.CrossRefGoogle Scholar
Yuan, X., Big line bundles over arithmetic varieties . Invent. Math. 173(2008), 603–649.CrossRefGoogle Scholar