To every finite metric space X, including all connected unweighted graphs with the minimum edge-distance metric, we attach an invariant that we call its blowup-polynomial 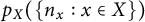$p_X(\{ n_x : x \in X \})$. This is obtained from the blowup 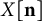$X[\mathbf {n}]$ – which contains 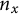$n_x$ copies of each point x – by computing the determinant of the distance matrix of 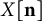$X[\mathbf {n}]$ and removing an exponential factor. We prove that as a function of the sizes 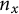$n_x$, 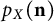$p_X(\mathbf {n})$ is a polynomial, is multi-affine, and is real-stable. This naturally associates a hitherto unstudied delta-matroid to each metric space X; we produce another novel delta-matroid for each tree, which interestingly does not generalize to all graphs. We next specialize to the case of 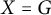$X = G$ a connected unweighted graph – so 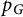$p_G$ is “partially symmetric” in 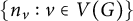$\{ n_v : v \in V(G) \}$ – and show three further results: (a) We show that the polynomial 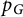$p_G$ is indeed a graph invariant, in that 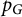$p_G$ and its symmetries recover the graph G and its isometries, respectively. (b) We show that the univariate specialization 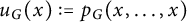$u_G(x) := p_G(x,\dots ,x)$ is a transform of the characteristic polynomial of the distance matrix 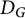$D_G$; this connects the blowup-polynomial of G to the well-studied “distance spectrum” of G. (c) We obtain a novel characterization of complete multipartite graphs, as precisely those for which the “homogenization at 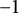$-1$” of 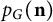$p_G(\mathbf { n})$ is real-stable (equivalently, Lorentzian, or strongly/completely log-concave), if and only if the normalization of 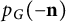$p_G(-\mathbf { n})$ is strongly Rayleigh.