Hostname: page-component-cb9f654ff-plnhv Total loading time: 0.001 Render date: 2025-09-07T08:14:58.806Z Has data issue: false hasContentIssue false
  • English
  • Français

THETA BLOCK FOURIER EXPANSIONS, BORCHERDS PRODUCTS AND A SEQUENCE OF NEWMAN AND SHANKS

Part of: Abelian varieties and schemes Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  14 June 2018

CRIS POOR Open the ORCID record for CRIS POOR [Opens in a new window] ,
JERRY SHURMAN Open the ORCID record for JERRY SHURMAN [Opens in a new window]  and
DAVID S. YUEN Open the ORCID record for DAVID S. YUEN [Opens in a new window]
CRIS POOR
Affiliation:
Department of Mathematics, Fordham University, Bronx, NY 10458, USA email poor@fordham.edu
JERRY SHURMAN*
Affiliation:
Department of Mathematics, Reed College, Portland, OR 97202, USA email jerry@reed.edu
DAVID S. YUEN
Affiliation:
Department of Mathematics, University of Hawaii, Honolulu, HI 96822, USA email yuen@math.hawaii.edu
*
✉ jerry@reed.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The ‘Borcherds products everywhere’ construction [Gritsenko et al., ‘Borcherds products everywhere’, J. Number Theory148 (2015), 164–195] creates paramodular Borcherds products from certain theta blocks. We prove that the 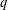$q$ -order of every such Borcherds product lies in a sequence 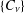$\{C_{\unicode[STIX]{x1D708}}\}$ , depending only on the 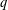$q$ -order $\unicode[STIX]{x1D708}$ of the theta block. Similarly, the 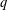$q$ -order of the leading Fourier–Jacobi coefficient of every such Borcherds product lies in a sequence 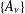$\{A_{\unicode[STIX]{x1D708}}\}$ , and this is the sequence 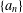$\{a_{n}\}$ from work of Newman and Shanks in connection with a family of series for $\unicode[STIX]{x1D70B}$ . Our proofs use a combinatorial formula giving the Fourier expansion of any theta block in terms of its germ.

Keywords

paramodular formBorcherds producttheta blockJacobi form

MSC classification

Primary: 11F46: Siegel modular groups; Siegel and Hilbert-Siegel modular and automorphic forms
Secondary: 11F55: Other groups and their modular and automorphic forms (several variables) 11F30: Fourier coefficients of automorphic forms 11F50: Jacobi forms 14K25: Theta functions

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 1 , August 2018 , pp. 48 - 59
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Bruinier, J. H., Borcherds Products on O (2, l) and Chern Classes of Heegner Divisors, Lecture Notes in Mathematics, 1780 (Springer, Berlin, 2002).CrossRefGoogle Scholar
Eichler, M. and Zagier, D., The Theory of Jacobi Forms, Progress in Mathematics, 55 (Birkhäuser Boston, Boston, MA, 1985).Google Scholar
Gritsenko, V. A. and Nikulin, V. V., ‘Automorphic forms and Lorentzian Kac–Moody algebras. II’, Internat. J. Math. 9(2) (1998), 201–275.Google Scholar
Gritsenko, V. A., Poor, C. and Yuen, D. S., ‘Borcherds products everywhere’, J. Number Theory 148 (2015), 164–195.Google Scholar
Gritsenko, V. A., Skoruppa, N.-P. and Zagier, D., ‘Theta blocks’, in preparation.Google Scholar
Newman, M. and Shanks, D., ‘On a sequence arising in series for 𝜋’, Math. Comp. 42(1655) (1984), 397–463.Google Scholar
Poor, C., Shurman, J. and Yuen, D. S., ‘Finding all Borcherds lift paramodular cusp forms of a given weight and level’, preprint, arXiv:1803.11092.Google Scholar
Shanks, D., ‘Dihedral quartic approximations and series for 𝜋’, J. Number Theory 14 (1982), 397–423.Google Scholar