Hostname: page-component-7dd5485656-zlgnt Total loading time: 0 Render date: 2025-10-31T16:35:30.942Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE 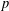$p$-LENGTH AND THE WIELANDT SERIES OF A FINITE 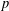$p$-SOLUBLE GROUP

Part of: Representation theory of groups

Published online by Cambridge University Press:  09 December 2014

NING SU  and
YANMING WANG
NING SU
Affiliation:
School of Mathematics, Sun Yat-sen University, Guangzhou 510275, PR China email suning3@mail.sysu.edu.cn
YANMING WANG*
Affiliation:
Lingnan College and Mathematics Department, Sun Yat-sen University, Guangzhou 510275, PR China email stswym@mail.sysu.edu.cn
*
✉stswym@mail.sysu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Wielandt subgroup of a group 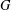$G$, denoted by 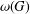${\it\omega}(G)$, is the intersection of the normalisers of all subnormal subgroups of 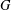$G$. The terms of the Wielandt series of 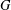$G$ are defined, inductively, by putting 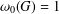${\it\omega}_{0}(G)=1$ and 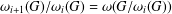${\it\omega}_{i+1}(G)/{\it\omega}_{i}(G)={\it\omega}(G/{\it\omega}_{i}(G))$. In this paper, we investigate the relations between the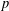$p$-length of a 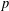$p$-soluble finite group and the Wielandt series of its Sylow 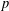$p$-subgroups. Some recent results are improved.

Keywords

p-lengthp-nilpotentWielandt seriesWielandt length

MSC classification

Primary: 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks
Secondary: 20D20: Sylow subgroups, Sylow properties, $pi$-groups, $pi$-structure

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 91 , Issue 2 , April 2015 , pp. 219 - 226
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Ballester-Bolinches, A. and Pedraza-Aguilera, M. C., ‘On minimal subgroups of finite groups’, Acta Math. Hungar. 73(4) (1996), 335–342.CrossRefGoogle Scholar
Doerk, K. and Hawkes, T. O., Finite Soluble Groups, Vol. 4 (Walter de Gruyter, Berlin–New York, 1992).Google Scholar
González-Sánchez, J. and Weigel, T. S., ‘Finite p-central groups of height k’, Israel J. Math. 181 (2011), 125–143.CrossRefGoogle Scholar
Gorenstein, D., Finite Groups (Chelsea, New York, 1980).Google Scholar
Hall, P. and Higman, G., ‘On the p-length of p-soluble groups and reduction theorems for Burnside’s problem’, Proc. Lond. Math. Soc. (3) 3(1) (1956), 1–42.CrossRefGoogle Scholar
Huppert, B., Endliche Gruppen. I, Die Grundlehren der Mathematischen Wissenschaften, 134 (Springer, Berlin, 1967).Google Scholar
Huppert, B. and Blackburn, N., Finite groups. II, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 242 (Springer, Berlin, 1982).Google Scholar
Su, N. and Wang, Y., ‘On the p-length and the Wielandt length of a finite p-soluble group’, Bull. Aust. Math. Soc. 88 (2013), 453–459.Google Scholar
Su, N. and Wang, Y., ‘On the intersection of the normalizers of the F-residuals of subgroups of a finite group’, Algebr. Represent. Theory 17(2) (2014), 507–518.CrossRefGoogle Scholar
Wielandt, H., ‘Über den normalisator der subnormalen untergruppen’, Math. Z. 69(1) (1958), 463–465.CrossRefGoogle Scholar