Article contents
A NOTE ON SPIRALLIKE FUNCTIONS
Published online by Cambridge University Press: 25 March 2021
Abstract
Let f be analytic in the unit disk  $\mathbb {D}=\{z\in \mathbb {C}:|z|<1 \}$ and let
$\mathbb {D}=\{z\in \mathbb {C}:|z|<1 \}$ and let 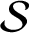 ${\mathcal S}$ be the subclass of normalised univalent functions with
${\mathcal S}$ be the subclass of normalised univalent functions with 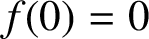 $f(0)=0$ and
$f(0)=0$ and 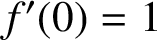 $f'(0)=1$, given by
$f'(0)=1$, given by 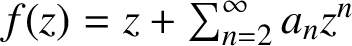 $f(z)=z+\sum _{n=2}^{\infty }a_n z^n$. Let F be the inverse function of f, given by
$f(z)=z+\sum _{n=2}^{\infty }a_n z^n$. Let F be the inverse function of f, given by 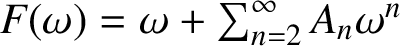 $F(\omega )=\omega +\sum _{n=2}^{\infty }A_n \omega ^n$ for
$F(\omega )=\omega +\sum _{n=2}^{\infty }A_n \omega ^n$ for 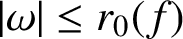 $|\omega |\le r_0(f)$. Denote by
$|\omega |\le r_0(f)$. Denote by 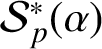 $ \mathcal {S}_p^{* }(\alpha )$ the subset of
$ \mathcal {S}_p^{* }(\alpha )$ the subset of 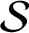 $ \mathcal {S}$ consisting of the spirallike functions of order
$ \mathcal {S}$ consisting of the spirallike functions of order 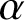 $\alpha $ in
$\alpha $ in 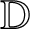 $\mathbb {D}$, that is, functions satisfying
$\mathbb {D}$, that is, functions satisfying 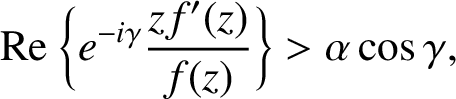
for 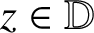 $z\in \mathbb {D}$,
$z\in \mathbb {D}$, 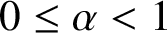 $0\le \alpha <1$ and
$0\le \alpha <1$ and 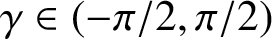 $\gamma \in (-\pi /2,\pi /2)$. We give sharp upper and lower bounds for both
$\gamma \in (-\pi /2,\pi /2)$. We give sharp upper and lower bounds for both 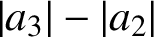 $ |a_3|-|a_2| $ and
$ |a_3|-|a_2| $ and 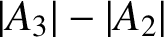 $ |A_3|-|A_2| $ when
$ |A_3|-|A_2| $ when 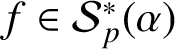 $f\in \mathcal {S}_p^{* }(\alpha )$, thus solving an open problem and presenting some new inequalities for coefficient differences.
$f\in \mathcal {S}_p^{* }(\alpha )$, thus solving an open problem and presenting some new inequalities for coefficient differences.
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 105 , Issue 1 , February 2022 , pp. 117 - 123
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
References
- 5
- Cited by


