Hostname: page-component-7dd5485656-bt4hw Total loading time: 0 Render date: 2025-10-31T21:29:32.237Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON 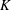$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}K$-SPACES

Part of: Fairly general properties Topological and differentiable algebraic systems

Published online by Cambridge University Press:  12 May 2014

HANFENG WANG  and
WEI HE
HANFENG WANG*
Affiliation:
Institute of Mathematics, Nanjing Normal University, Nanjing 210046, China Department of Mathematics, Shandong Agricultural University, Taian 271018, China email whfeng@sdau.edu.cn
WEI HE
Affiliation:
Institute of Mathematics, Nanjing Normal University, Nanjing 210046, China email weihe@njnu.edu.cn
*
✉whfeng@sdau.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, it is shown that every compact Hausdorff 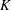$K$-space has countable tightness. This result gives a positive answer to a problem posed by Malykhin and Tironi [‘Weakly Fréchet–Urysohn and Pytkeev spaces’, Topology Appl.104 (2000), 181–190]. We show that a semitopological group 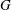$G$ that is a 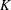$K$-space is first countable if and only if 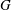$G$ is of point-countable type. It is proved that if a topological group 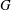$G$ is a 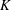$K$-space and has a locally paracompact remainder in some Hausdorff compactification, then 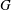$G$ is metrisable.

Keywords

K-spacetopological groupsemitopological groupmetrisablecountable tightness

MSC classification

Secondary: 54D40: Remainders 22A05: Structure of general topological groups

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 1 , August 2014 , pp. 144 - 148
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Arhangel’skii, A. V., ‘Quotients with respect to locally compact subgroups’, Houston J. Math. 31 (2005), 215–226.Google Scholar
Arhangel’skii, A. V., ‘Two types of remainders of topological groups’, Comment. Math. Univ. Carolin. 49 (2008), 119–126.Google Scholar
Arhangel’skii, A. V. and Tkachenko, M., Topological Groups and Related Structures (Atlantis Press, Amsterdam–Paris, 2008).Google Scholar
Engelking, R., General Topology, Revised and completed edition (Heldermann Verlag, Berlin, 1989).Google Scholar
Gruenhage, G., ‘Generalized metric spaces’, in: Handbook of Set-Theoretic Topology (eds. Kunen, K. and Vaughan, J. E.) (Elsevier, Amsterdam, 1984), 423–501.CrossRefGoogle Scholar
Henriksen, M. and Isbell, J. R., ‘Some properties of compactifications’, Duke Math. J. 25 (1958), 83–106.CrossRefGoogle Scholar
Hodel, R., ‘Cardinal functions I’, in: Handbook of Set-Theoretic Topology (eds. Kunen, K. and Vaughan, J. E.) (Elsevier, Amsterdam, 1984), 3–61.Google Scholar
Malykhin, V. I. and Tironi, G., ‘Weakly Fréchet–Urysohn and Pytkeev spaces’, Topology Appl. 104 (2000), 181–190.CrossRefGoogle Scholar
Pasynkov, B. A., ‘Almost-metrizable topological groups’, Dokl. Akad. Nauk SSSR 161 (1965), 281–284.Google Scholar
Shapirovskii, B., ‘On π-character and π-weight of compact Hausdorff spaces’, Soviet Math. Dokl. 16 (1975), 999–1003.Google Scholar
Wang, H. F. and He, W., ‘Notes on K-topological groups and homeomorphisms of topological groups’, Bull. Aust. Math. Soc. 87 (2013), 493–450.Google Scholar